三角形全等专题训练(一)
中考数学复习《全等三角形》专题(卷1)
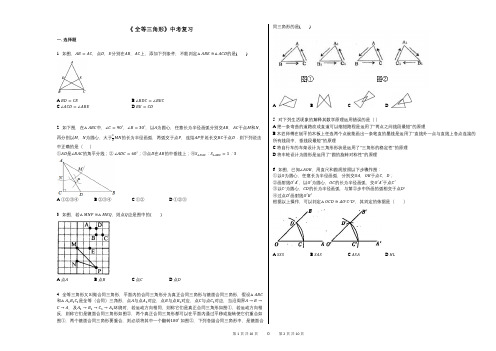
《全等三角形》中考复习一. 选择题1. 如图,AB=AC,点D,E分别在AB,AC上,添加下列条件,不能判定△ABE≅△ACD的是( )A.BD=CEB.∠BDC=∠BECC.∠ACD=∠ABED.BE=CD2. 如下图,在△ABC中,∠C=90∘,∠B=30∘,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N 为圆心,大于12MN的长为半径画弧,两弧交于点P ,连结AP 并延长交BC于点D.则下列说法中正确的是()①AD是∠BAC的角平分线;②∠ADC=60∘;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.A.①②③④B.②③④C.①②D.①②③3. 如图,若△MNP≅△MEQ,则点Q应是图中的()A.点AB.点BC.点CD.点D4. 全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC 和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形如图①,若运动方向相反,则称它们是镜面合同三角形如图②,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合如图①,两个镜面合同三角形要重合,则必须将其中一个翻转180∘如图②,下列各组合同三角形中,是镜面合同三角形的是( )A. B. C. D.5. 对下列生活现象的解释其数学原理运用错误的是()A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理6. 如图,已知∠AOB,用直尺和圆规按照以下步骤作图:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画射线O′A′,以O′为圆心,OC的长为半径画弧,交O′A′于点C′③以C′为圆心,CD的长为半径画弧,与第②步中所画的弧相交于点D′④过点D′画射线O′B′根据以上操作,可以判定△OCD≅ΔO′C′D′,其判定的依据是()A.SSSB.SASC.ASAD.HL7. 如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD//OA交OB于点D,点I是△OCD 的内心,连结OI,BI,∠AOB=β,则∠OIB等于()A.180∘−βB.180∘−12β C.90∘+12β D.90∘+β8. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )A.第1块B.第2块C.第3块D.第4块二. 填空题三角形具有稳定性,所以要使六边形木架不变形,至少要钉上________根木条.如图,在x、y轴上分别截取OA、OB,使OA=OB,再分别以点A、B 为圆心,以大于12AB的长度为半径画弧,两弧交于点C.若C的坐标为(3a,−a+8),则a=________.如图,在菱形ABCD中,已知AB=4,∠ABC=60∘,∠EAF=60∘,点E在CB的延长线上,点F在DC的延长线上,有下列结论:①BE=CF;②∠EAB=∠CEF;③△ABE∼△EFC;④若∠BAE=15∘,则点F到BC的距离为2√3−2.正确序号________.如图,△ABC中,点A的坐标为(0, 1),点C的坐标为(4, 3),如果要使△ABD与△ABC全等,那么点D的坐标是________.三. 解答题如图,小明用五根宽度相同的木条拼成了一个五边形,已知AE//CD,∠A=12∠C,∠B=120∘.(1)∠D+∠E=________度;(2)求∠A的度数;(3)要使这个五边形木架保持现在的稳定状态,小明至少还需钉上________根相同宽度的木条.根据要求完成下列各题.(1)如图1,在∠AOB的内部有一点P.①过点P画直线PC//OA交OB于点C;②过点P画直线PD⊥OA,垂足为D.(2)如图2,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E在下面解答中填空.解:∵AB⊥BF,CD⊥BF(已知),∴∠ABF=∠________=90∘(________),∴AB//CD(________)∵∠1=∠2(已知),∴AB//EF(________),∴CD//EF(平行于同一条直线的两条直线互相平行),∴∠3=∠E(________)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF= BD,连接BF.(1)线段BD与CD有何数量关系,为什么?(2)当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.(3)当△ABC满足________条件时,四边形AFBD是正方形?(直接写出结论,不用说明理由)一条大河两岸的A、B处分别立着高压线铁塔,如图所示.假设河的两岸平行,你在河的南岸,请利用现有的自然条件、皮尺和标杆,并结合你学过的全等三角形的知识,设计一个不过河便能测量河的宽度的好办法.(要求,画出示意图,并标出字母,结合图形简要叙述你的方案)参考答案与试题解析一. 选择题1.【答案】D【解析】欲使△ABE≅△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.2.【答案】A【解析】①连接NP,MP,根据SSS定理可得△ANP≅△AMP,故可得出结论;②先根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30∘,根据直角三角形的性质可知∠ADC=60∘;③根据∠1=∠B可知AD=BD,故可得出结论;④先根据直角三角形的性质得出∠2=30∘,CD=12AD,再由三角形的面积公式即可得出结论.3.【答案】D【解析】此题暂无解析4.【答案】B【解析】认真阅读题目,理解真正合同三角形和镜面合同三角形的定义,然后根据各自的定义或特点进行解答.5.【答案】B【解析】根据圆的有关定义、垂线段的性质、三角形的稳定性等知识结合生活中的实例确定正确的选项即可.6.【答案】A【解析】此题暂无解析7.【答案】B 【解析】此题暂无解析8.【答案】B【解析】本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.二. 填空题【答案】3【解析】三角形具有稳定性,所以要使六边形木架不变形需把它分成三角形,即过六边形的一个顶点作对角线,有几条对角线,就至少要钉上几根木条.【答案】2【解析】此题暂无解析【答案】①②【解析】①只要证明△BAE≅△CAF即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点F到BC的距离即可判断.【答案】(4, −1)或(−1, 3)或(−1, −1)【解析】因为△ABD与△ABC有一条公共边AB,故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论,计算即可得出答案.三. 解答题【答案】180(2)五边形的内角和为(5−2)×180∘=540∘,由(1)可知,∠D+∠E=180∘,又∠B=120∘,∠A=12∠C.设∠A=x,则∠C=2x,∴∠A+∠B+∠C+∠D+∠E=540∘,即x+120∘+2x+180∘=540∘,解得x=80∘,∴∠A=80∘.2【解析】(1)根据平行线性质,两直线平行同旁内角互补即可得到180∘.先由AE//CD,根据平行线的性质得出∠E+∠D=180∘.再根据∠B=120∘,∠A=12∠C,设∠A=x∘,则∠C=2x∘.利用五边形的内角和为540∘列出方程x+120+2x+180=540,求解即可.根据五边形不具有稳定性,而三角形具有稳定性即可求解.【答案】解:(1)①如图,直线PC即为所求;②如图,直线PD即为所求;(2)解:∵AB⊥BF,CD⊥BF(已知),∴∠ABF=∠CDF=90∘(垂直的定义),∴AB//CD(同位角相等,两直线平行)∵∠1=∠2(已知),∴AB//EF(内错角相等,两直线平行),∴CD//EF(平行于同一条直线的两条直线互相平行),∴∠3=∠E(两直线平行,同位角相等)【解析】此题暂无解析【答案】解:(1)BD=CD.理由如下:依题意得AF // BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,{∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,∴△AEF≅△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足AB=AC时,四边形AFBD是矩形.理由如下:∵AF // BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90∘,∴四边形AFBD是矩形.AB=AC,∠BAC=90∘【解析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90∘,由等腰三角形三线合一的性质可知必须是AB=AC.【答案】解:在河南岸AB的垂线BF上取两点C、E,使CE=BE,再定出BF的垂线CD,使A、E、D在同一条直线上,这时测得CD的长就是AB的长.如图所示:【解析】已知等边及垂直,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.。
八年级《全等三角形》专题训练

八年级上册《全等三角形》专题训练一.解答题(共14小题)1.如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.2.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.求证:(1)△ACD≌△BEC;(2)CF⊥DE.3.如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.(1)试猜想线段BG和AE的数量关系是;(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°),判断(1)中的结论是否仍然成立?请利用图2证明你的结论;4.如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB于N,PM⊥AC于点M,求证:BN=CM.5.已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.(1)求证:BF=AC;(2)求证:.6.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.7.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的数量关系,并说明理由.8.已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE的延长线上,CF=AB,求证:AF⊥AQ.9.问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;10.(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD 到点G,使DG=BE,连结EF,AG.求证:EF=FG.(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.11.如图在等边△ABC中,D、E分别是BC、AC上的点,且AE=CD,AD与BE相交于F,CF⊥BE.求证:(1)BE=AD;(2)BF=2AF.12.如图1,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图2,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.13.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC 于F,求证:AE=CF.14.△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.(1)如图1,若∠BAC=∠DAE=60°,判断△BEF的形状并说明理由.(2)若∠BAC=∠DAE≠60°如图2,当点D在线段BC上移动,判断△BEF的形状,不必说明理由。
全等三角形基本模型综合训练(一)(解析版)
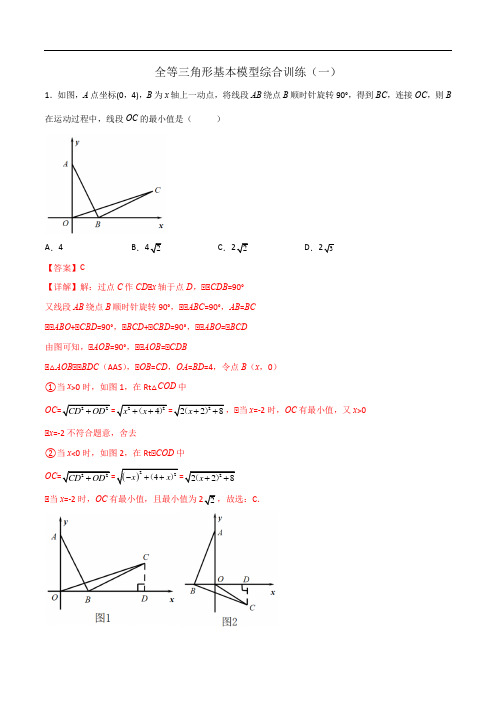
全等三角形基本模型综合训练(一)1.如图,A 点坐标(0,4),B 为x 轴上一动点,将线段AB 绕点B 顺时针旋转90°,得到BC ,连接OC ,则B 在运动过程中,线段OC 的最小值是( )A .4B .2C .2D .3【答案】C 【详解】解:过点C 作CD ⊥x 轴于点D ,⊥⊥CDB =90°又线段AB 绕点B 顺时针旋转90°,⊥⊥ABC =90°,AB =BC⊥⊥ABO +⊥CBD =90°,⊥BCD +⊥CBD =90°,⊥⊥ABO =⊥BCD由图可知,⊥AOB =90°,⊥⊥AOB =⊥CDB⊥△AOB ⊥⊥BDC (AAS ),⊥OB =CD ,OA =BD =4,令点B (x ,0)①当x >0时,如图1,在Rt △COD 中OC 22CD OD +224x x ++()2228x ++()⊥当x =-2时,OC 有最小值,又x >0⊥x =-2不符合题意,舍去②当x <0时,如图2,在Rt⊥COD 中OC 22CD OD +()224x x -++()2228x ++()⊥当x =-2时,OC 有最小值,且最小值为2,故选:C .2.如图,在ABC ∆中,40A ∠=︒,60C ∠=°,D 为AC 边上一点,DE BC ⊥于点E .若AD BD =,2BE =,则AB 的长为( )A 3B .2C .3D .4【答案】D【详解】解:如图,作DF ⊥AB 于点F ,⊥ AD =BD⊥△ADB 是等腰三角形,⊥ABD =⊥A =40°⊥AB =2AF =2BF⊥40A ∠=︒,60C ∠=°,⊥⊥ABC =180°-⊥A -⊥C =80°,⊥ ⊥DBE =⊥ABC -⊥ABD =40°⊥⊥DBE =⊥ABD⊥DE BC ⊥⊥ ⊥DE =DF⊥BD =BD⊥Rt △BDF ⊥Rt △BDE (HL )⊥BF =BE =2⊥AB =2BF =4,故选:D3.如图,Rt ABC ∆中,90C ∠=︒,AD 平分BAC ∠,交BC 于点D ,10AB =,15ABD S ∆=,则CD 的长为( )A .3B .4C .5D .6【答案】A 【详解】解:过点D 作DF ⊥AB 于点F ,⊥10AB =,15ABD S ∆=,⊥1152AB DF ⋅=,⊥110152DF ⨯=,得DF =3, ⊥90C ∠=︒,AD 平分BAC ∠,DF ⊥AB ,⊥CD =DF =3,故选:A .4.正方形ABCD 的边长为4,点E 是射线AD 上的一个动点,连结CE ,以CE 为边往右侧作正方形CEFG ,连结DF 、DG .(1)当点E在AD延长线上,且DE=AD时,DG=________.(2)当点E在线段AD上,且△DGF为等腰三角形时,DG=________.【答案】454或542【详解】解:(1)过点F作FH⊥AD交AD延长线于点H,⊥四边形ABCD是正方形,且DE=AD,⊥DE=AD=CD,⊥ADC=⊥CDE=90°,⊥△EDC是等腰直角三角形,⊥⊥DCE=⊥DEC=45°,⊥四边形CEFG是正方形,⊥CG=CE=EF,⊥GCE=⊥CEF=90°,⊥⊥DCG=⊥DEF=135°,⊥△DCG⊥△DEF,⊥DG=DF,⊥⊥DEC=45°,⊥CEF=90°,⊥⊥HEF=45°,⊥△EHF是等腰直角三角形,⊥CE=EF,⊥DE=CD=EH=FH=4,在Rt△DFH中,FH=4,DH=8,⊥DG=DF22+=4845(2)当点E与点A重合时,DG=DF,⊥DG=DE=DC=4;当DG=GF时,过点G作GI⊥CD于点I,⊥四边形CEFG是正方形,⊥CG=GF=CE,⊥GCE=90°,⊥DG=GC,CD=2,⊥CI=DI=12⊥DCE+⊥ICG=90°,⊥IGC+⊥ICG=90°,⊥⊥DCE=⊥IGC,⊥△DCE⊥△IGC,⊥IG=DC=4,⊥DG=GC22+=2425点E与点D重合时,DF=GF,此时,FG=FD=DC=4,⊥DG224442;综上,△DGF为等腰三角形时,DG=4或542故答案为:4或5425.如图,在边长为3的正方形ABCD中,点E是AB的中点,点F在BC上,且BF=2CF,DE,AF相交于点G,则DG的长为___________.958【详解】如图,延长DG、CB,二线交于点H,⊥四边形ABCD是正方形,E是AB的中点,⊥⊥DAE=⊥HBE=90°,AE=BE,⊥⊥AED =⊥BEH⊥△DAE ⊥△HBE ,⊥BH =AD =3,⊥BF =2CF ,BC =3,⊥BF =2,CF =1,⊥FH =FB +BH =3+2=5,CH =FH +CF =1+5=6,⊥四边形ABCD 是正方形,⊥⊥DCH =90°,AD ∥BC ,⊥△DAG ⊥△HFG ,DH 22223635CD CH ++=⊥35DG AD GH FH ==,⊥38DG DH =, ⊥333588DG DH ==⨯958958 6.如图,△ABC 中,AB =AC ,点 D 在 AC 上,连接 BD ,△ABD 的中线 AE 的延长线交 BC 于点 F ,⊥F AC =60°,若 AD =5,AB =7,则 EF 的长为__________.【答案】23【详解】解:延长AE 至点G ,使得AE =EG ,⊥E 是BD 的中点,⊥BE =DE ,在△ADE 和△GBE 中,DE BE AED GEB AE GE =⎧⎪∠=∠⎨⎪=⎩⊥⊥ADE ⊥⊥GBE (SAS ), ⊥AD =GB =5,⊥G=⊥F AC =60°,过点B 作BH ⊥GE 于点H ,在Rt ⊥BGH 中,⊥GBH =180°﹣90°﹣60°=30°,⊥GH =12BG =52,BH 22555()322-=, 在Rt ⊥ABH 中,AH 225117(3)22-,⊥AG =AH +GH =8,⊥AE =GE =4, 过点D 作DM AB 2AC =EF ,交BC 于点M .⊥12BE EF BD DM == , 设EF =x ,则DM =2x ,⊥DM AB 2AC =EF ,⊥225DM CD AF CA ==+,⊥AF =7x ,⊥AE =7x ﹣x =6x =4,⊥x =23,⊥EF =23, 故答案为:23. 7.如图,将矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,使点C 恰好落到线段AD 上的E 点处,连接CE ,连接CG 交BE 于点H .(1)求证:CE 平分⊥BED ;(2)取BC 的中点M ,连接MH ,求证:MH ∥BG ;(3)若BC =2AB =4,求CG 的长.【答案】(1)见解析;(2)见解析;(3)7【解析】(1)⊥四边形ABCD 是矩形,⊥BC =BE ,DE ∥BC ,⊥⊥BEC =⊥BCE ,⊥BCE =⊥DEC ,⊥⊥BEC =⊥DEC ,⊥CE 平分⊥BED .(2)过点C 作CN ⊥BE ,垂足为N ,⊥四边形ABCD 是矩形,⊥CD ⊥DE ,⊥CE 平分⊥BED ,⊥CD =CN ,⊥矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,⊥CD =BG ,⊥GBH =⊥CNH =90°,⊥CN =BG ,⊥BHG =⊥NHC ,⊥△BHG ⊥△CHN ,⊥HG =HC ,⊥H 是GC 的中点,⊥BC 的中点是M ,⊥MH 是△BGC 中位线,⊥MH ∥BG .(3)过点C 作CN ⊥BE ,垂足为N ,⊥四边形ABCD 是矩形,BC =2AB =4,矩形ABCD 绕着点B 逆时针旋转得到矩形GBEF ,⊥GB ⊥BH ,GB =BM =2,⊥MH 是△BGC 中位线,⊥MH =1,⊥⊥HBM =⊥QGB ,⊥GB =BM =2,⊥BHM =⊥GQB ,⊥△QBG ⊥△HMB ,⊥QB =MH =1,GQ =BH 3QC =5,⊥CG 22(3)52827+=.8.如图,在正方形ABCD 中,点E 是CD 中点,连接AE .过点C 作CF AE ⊥,交AE 的延长线于点F ,连接DF .过点D 作DG DF ⊥交AF 于点G .若2DF =,则正方形ABCD 的边长为________.10【详解】解:⊥四边形ABCD 是正方形,⊥AD =CD ,⊥ADC =90°,⊥⊥DAE +⊥AED =90°,⊥CF ⊥AE ,⊥⊥ECF +⊥CEF =90°,⊥⊥DAE =⊥ECF ,同理,⊥⊥ADG +⊥GDE =90°,⊥GDE +⊥CDF =90°,在⊥AGD 与⊥CFD 中,DAE ECF AD CD ADG CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥AGD ⊥⊥CFD (ASA ),⊥DG =DF ,AG =CF ,⊥DG ⊥DF ,⊥⊥DGF 是等腰直角三角形,⊥2222GF DG DF +=过点D 作DK ⊥AE 于点K ,则122DK GK GF === , 在⊥DKE 与⊥CFE 中,DEK CEF DKE CFE DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DKE ⊥⊥CFE (AAS ),⊥DK =CF ,⊥2AG CF DK GK ====⊥22AK =⊥2210AD AK DK +10.9.已知:如图,AC ⊥BD ,AE 、BE 分别平分⊥CAB 和⊥ABD ,点E 在CD上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.【答案】AC +BD =AB ,理由见见解析【详解】解:AC +BD =AB ,证明如下:在BA 上截取BF =BD ,连接EF ,如图所示:⊥AE 、BE 分别平分⊥CAB 和⊥ABD ,⊥⊥EAF =⊥EAC ,⊥EBF =⊥EBD ,在⊥BEF 和⊥BED 中,BF BD EBF EBD BE BE =⎧⎪∠=∠⎨⎪=⎩,⊥BEF BED ≌(SAS ),⊥⊥BFE =⊥D ,⊥AC ⊥BD ,⊥⊥C +⊥D =180°,⊥⊥AFE +⊥BFE =180°,⊥⊥AFE +⊥D =180°,⊥⊥AFE =⊥C ,在⊥AEF 和⊥AEC 中,EAF EAC AFE C AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥AEF AEC ≌(AAS ),⊥AF =AC ,⊥AF +BF =AB ,⊥AC +BD =AB .10.如图1,ΔΔRt ABF Rt CBE ≌,90ABC ∠=︒,点E ,F 分别在边AB,BC 上,点M 为AF 中点.(1)请直接写出线段CE 与BM 的关系;(2)连接EF ,将EBF ∆绕点B 逆时针旋转至如图2位置,请写出CE 与BM 的关系,并说明理由;(3)在EBF ∆绕点B 旋转的过程中,当B ,C ,E 三点共线时,若3BC =,2EF =CM 的长.【答案】(1)2CE BM = ,CE BM ⊥;(2)2CE BM = ,CE BM ⊥,理由见解析;(3)13CM =10【解析】(1)2CE BM =,CE BM ⊥,理由如下,设BM 与CE 相交于点N ,如图,⊥Rt ABF Rt CBE ≅△△,⊥ABC =90°,⊥AF =CE ,⊥A =⊥C ,⊥⊥A +⊥AFB =90°,⊥M 为AF 的中点,⊥BM =AM =FM =12AF ,⊥BM =12CE ,即2BM =CE ,⊥AFB =⊥CBM ,⊥⊥C +⊥CBM =90°,⊥⊥CNB =90°,⊥BM ⊥CE ,故BM 与CE 的关系为:2CE BM =,CE BM ⊥,(2)2CE BM =,CE BM ⊥,理由如下:证明:延长AB 至点N ,使NB AB =,连接NF⊥M 为AF 的中点,B 为AN 中点⊥BM 为ANF 的中位线⊥2NF BM =⊥90ABC ∠=︒,90EBF ∠=︒,⊥ABE ABF CBF ABF ∠+∠=∠+∠,⊥ABE CBF ∠=∠,⊥90ABC ∠=︒,AB BC BN ==,⊥CBA ABE CBN CBF ∠+∠=∠+∠,⊥CBE NBF ∠=∠,又⊥BE BF =,⊥()CBE NBF SAS ≅△△,⊥NF CE =,⊥2CE BM =,⊥BM 为ANF 的中位线,⊥BM FN ∥,⊥MBA N ∠=∠,⊥CBE NBF ≅△△,⊥ECB N ∠=∠,⊥MBA ECB ∠=∠,⊥90MBA CBM ∠+∠=︒,⊥90ECB CBM ∠+∠=︒,⊥CE BM ⊥,综上2CE BM =且CE BM ⊥;(3)当点E 在CB 的延长线上时,如图,⊥⊥ABC =⊥ABE =90°,AB =BC =3,BE =BF ,⊥在等腰Rt ⊥BEF 中,有EF 22,又⊥EF 2⊥BE =BF =1,⊥AF =AB -EF =3-1=2,⊥M 为AF 的中点,⊥FM =12AF =1,⊥22223213CM BC BM ++=当点E 在CB 上时,如图,同理可求得BF =BE =1,⊥AF =AB +BF =3+1=4,⊥M 为AF 的中点,⊥FM =12AF =2,⊥BM =FM -BF =2-1=1, ⊥22223110CM BC BM ++ 即CM 1310.11.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分⊥BAD .(1)推理证明:如图1,若120DAB ∠=︒,且90D ∠=︒,求证:AD AB AC +=;(2)问题探究:如图2,若120DAB ∠=︒,试探究AD 、AB 、AC 之间的数量关系;(3)迁移应用:如图3,若90DAB ∠=︒,AD =2,AB =4,求线段AC 的长度.【答案】(1)见解析;(2)AD AB AC +=;(3)32AC =【解析】(1)证明:⊥AC 平分BAD ∠,⊥12DAC BAC DAB ∠=∠=∠, 又⊥120DAB ∠=,⊥60DAC BAC ∠=∠=,又⊥180B D ∠+∠=,90D ∠=,⊥90B D ∠=∠=,⊥30ACD ACB ∠=∠=︒,⊥12AD AC =,12AB AC =, ⊥AD AB AC +=.(2)解:AD AB AC +=;过点C 作CE AD ⊥于点E ,过点C 作CF AE ⊥的延长线于点F ,⊥AC 平分BAD ∠,⊥CE CF =,90DEC CFB ∠=∠=,⊥180D ABC ∠+∠=,而180ABC FBC ∠+∠=,⊥D FBC ∠=∠,在BFC △与DEC 中D FBC DEC BFC CE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥()AAS BFC DEC ≌,⊥DF BF =,⊥AD AB AE DE AF BF AE AF +=++-=+,由(1)知AE AF AC +=,⊥AD AB AC +=.(3)过点C 作CM AB ⊥于点M ,过点C 作CN AD ⊥的延长线于点N ,由(2)知:CDN CBM ∆∆≌,⊥DN BM =,⊥AD AB AN DN AM BM AN AM +=-++=+,而90DAB ∠=︒,AC 平分BAD ∠,⊥45NAC MAC ACN ∠=∠=∠=︒,⊥2AN AM NC AC ===,⊥2AD AB AN AM +=+=, 又2AD =,4AB =,⊥32AC =12.如图,点F 在四边形ABCD 的边AB 上.(1)如图1,当四边形ABCD 是正方形时,过点B 作BE CF ⊥,垂足为O ,交AD 于点.E 求证:BE CF =;(2)当四边形ABCD 是矩形,6AD =,8AB =时,①如图2,点P 是BC 上的一点,过点P 作PE CF ⊥,垂足为O ,点O 恰好落在对角线BD 上,求OC OE 的值; ②如图3,点P 是BC 上的一点,过点P 作PE CF ⊥,垂足为O ,点O 恰好落在对角线BD 上,延长EP 、AB 交于点G,当2BG =时,请直接写出DE 的值.【答案】(1)证明见解析;(2)①34;②83. 【解析】(1)证明:四边形ABCD 是正方形,AB BC ∴=,90A FBC ∠=∠=︒,BE CF ⊥于点O ,90BOC ∴∠=︒,90ABE OBC BCF ∴∠=︒-∠=∠,ABE ∴⊥()BCF ASA , BE CF ∴=.(2)解:①如图2,过O 作OM AD ⊥于点M ,ON CD ⊥于点N ,则90OMD OND ∠=∠=︒,四边形ABCD 是矩形,6BC AD ∴==,8AB CD ==,90MDN A BCD ∠=∠=∠=︒,∴四边形OMDN 是矩形,90MON ∴∠=︒,PE CF ⊥于点O ,90COE ∴∠=︒,90CON EOM EON ∴∠=∠=︒-∠,90ONC OME ∠=∠=︒,ONC ∴⊥OME ,OC ON OE OM ∴=, OND BCD ∠=∠,//ON BC ∴, DON ∴⊥DBC △,ON OD BC BD ∴=,同理OM OD AB BD =, ON OM BC AB ∴=,ON BC OM AB ∴=,6384OC BC OE AB ∴===; ②如图3,连接CE 、CG ,90ABC ∠=︒,18090PBG ABC ∴∠=︒-∠=︒,90PBG POC ∴∠=∠=︒,BPG OPC ∠=∠,BPG ∴⊥OPC ,PB PG PO PC ∴=,PB PO PG PC ∴=,OPB CPG ∠=∠,OPB ∴⊥CPG △,CBD OGC ∴∠=∠, 34OC OE =,6384CB CD ==;OC CB OE CD ∴=, 90COE BOD ∠=∠=︒,COE ∴⊥BOD ,CDB OEC ∴∠=∠,90OGC OEC CBD CDB ∴∠+∠=∠+∠=︒,90ECG ∴∠=︒,90BCG DCE BCE ∴∠=∠=︒-∠,90CBG CDE ∠=∠=︒,CBG ∴△⊥CDE △,34BG CB DE CD ∴==,4482333DE BG ∴==⨯=. 13.将一块足够大的直角三角板的直角顶点P 放在边长为1的正方形ABCD 的对角线AC 上滑动,一条直角边始终经过点B ,另一条直角边与射线DC 交于点E .(1)当点E 在边DC 上时(如图1),求证:①⊥PBC ⊥⊥PDC ;②PB =PE .(2)当点E 在边DC 的延长线上时(如图2),(1)中的结论②还成立吗?如果不成立,请说明理由;如果成立,请给予证明.【答案】(1)①见解析;②见解析(2)(1)中的结论②仍然成立,证明见解析【解析】(1)①⊥四边形ABCD 是正方形,⊥BC =CD ,⊥BCP =⊥DCP=45°,又⊥CP =CP ,⊥⊥PBC ⊥⊥PDC ,②过点P 分别作PF ⊥BC 于点F ,PG ⊥CD 于点G ,易证四边形PFCG 为正方形,⊥⊥BFP =⊥EGP=90°,PF =PG ,⊥⊥EPG+⊥EPF=90°=⊥BPF+⊥EPF ,⊥⊥BFP =⊥EGP ⊥⊥PGE ⊥⊥PFB (ASA),⊥PB =PE .(2)PB =PE 成立,证明:设PE 交BC 于点O ,⊥⊥BPE =⊥BCE=90°,⊥BOP =⊥COE ,⊥⊥PBC =⊥PEC ,由(1)得:⊥PBC =⊥PDC ,⊥⊥PDC =⊥PEC ,PB =PD ,⊥PE =PD=PB ,故(1)中的结论②仍然成.14.在ABC 中,22BAC ABC ACB ∠=∠=∠,D 是BC 所在直线上的一个动点(点D 不与点B 、点C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF .(1)观察发现:如图1,当点D 在线段BC 上时,①BC 、CF 的位置关系为___________;②BC 、CD 、CF 之间的数量关系为___________.(2)探究证明:如图2,当点D 在线段CB 的延长线上时,(1)中的两个结论是否仍然成立?请说明理由.(3)问题解决:如图3,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE .若62AB =4BC CD =时,直接写出GE 的长.【答案】(1)①BC CF ⊥,②BC CF CD =+;(2)(1)中结论①成立,②不成立,理由见解析; (3)310【解析】(1)①在正方形ADEF 中,AD =AF ,⊥DAF =90°,⊥⊥BAC =90°,⊥⊥BAC =⊥DAF =90°⊥⊥BAD =⊥CAF ,在△DAB 与△F AC 中,AD AF BAD CAF AB AC =⎧⎪∠=∠⎨⎪=⎩,⊥⊥DAB ⊥⊥F AC (SAS ),⊥⊥ABD =⊥ACF ,⊥⊥ACB +⊥ACF =⊥ACB +⊥ABD =180°-⊥BAC =90°,⊥BC ⊥CF ;故答案为:BC ⊥CF ;②由①知,△DAB ⊥⊥F AC ,⊥BD =CF ,⊥BC =BD +CD ,⊥BC =CF +CD ;故答案为:BC =CF +CD ;(2)(1)中结论①成立.②不成立.理由如下:⊥四边形ADEF 是正方形:⊥AD AF =,90DAF ∠=︒.⊥22BAC ABC ACB ∠=∠=∠,180BAC ABC ACB ∠+∠+∠=︒,⊥90BAC ∠=︒,45ABC ACB ∠=∠=︒,⊥AB AC =,BAC DAF ∠=∠,⊥BAD CAF ∠=∠,⊥()SAS DAB FAC △△≌,⊥135ABD ACF ∠=∠=︒,=CF BD . ⊥45ACB ∠=︒,⊥1354590DCF ACF ACB ∠=∠-∠=︒-︒=︒,⊥CF BD ⊥. ⊥BC CD BD =-,⊥BC CD CF =-.⊥(1)中结论①成立.②不成立.(3)如图,作AH BC ⊥于点H ,EM BD ⊥于点M ,EN CF 于点N .易证90BAC ∠=︒,45ABC ACB ∠=∠=︒,⊥AB AC =,⊥BH CH =,⊥6212sin 452AB BC ==︒,⊥6AH BH CH ===. ⊥4BC CD =,3CD =,⊥9DH =.由(2)得BC CF ⊥,15CF BD ==.⊥BC CF ⊥,EM BD ⊥,EN CF ,⊥四边形CMEN 是矩形,⊥NE CM =,EM CN =. ⊥90AHD ADE EMD ∠=∠=∠=︒,⊥90ADH EDM ∠+∠=︒,90EDM DEM ∠+∠=︒,⊥ADH DEM =∠∠. ⊥AD DE =,⊥()ADH DEM AAS △△≌,⊥9EM DH ==,6DM AH ==, ⊥9CN EM ==,9669EN CM DH DM CH ==+-=+-=.⊥45ABC ∠=︒,⊥45BGC ∠=︒,⊥12CG BC ==,⊥1293GN CG CN =-=-=. ⊥2239310EG +=15.【探究建模】已知正方形ABCD ,E ,F 为平面内两点.(1)如图1,当点E 在边AB 上时,DE ⊥DF ,且B ,C ,F 三点共线.求证:AE =CF ;(2)【类比应用】如图2,当点E 在正方形ABCD 外部时,DE ⊥DF ,AE ⊥EF ,且E ,C ,F 三点共线.①(1)中的结论AE=CF还成立吗?请说明理由;②猜想并证明线段AE,CE,DE之间的数量关系.【答案】(1)见解析;(2)①成立,理由见解析;②EA+EC2,证明见解析【解析】(1)证明:⊥四边形ABCD是正方形,⊥DA=DC,⊥A=⊥ADC=⊥DCB=90°,⊥DE⊥DF,⊥⊥EDF=⊥ADC=90°,⊥⊥ADE=⊥CDF,在⊥DAE和⊥DCF中,ADE CDF AD CDA DCF∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥DAE⊥⊥DCF(ASA),⊥AE=CF.(2)解:①(1)中的结论AE=CF还成立.证明:⊥四边形ABCD是正方形,⊥DA=DC,⊥DAB=⊥ADC=⊥DCB=⊥DCF=90°,⊥DE⊥DF,⊥⊥EDF=⊥ADC=90°,⊥⊥ADE=⊥CDF,⊥AE⊥EF,⊥⊥AEF=90°,⊥⊥DAE+⊥DCE=180°,⊥⊥DCF+⊥DCE=180°,⊥⊥DAE=⊥DCF,在⊥DAE和⊥DCF中,ADE CDFAD CDDAE DCF∠=∠⎧⎪=⎨⎪∠=∠⎩,⊥⊥DAE⊥⊥DCF(ASA),⊥AE=CF.②解:结论:EA+EC2.理由:由①知,⊥DAE⊥⊥DCF(ASA),⊥AE=CF,DE=DF,∥ADE=∥CDF,⊥∥EDF=90°,⊥⊥DEF为等腰直角三角形,⊥EF2⊥FC+EC2.⊥AE+EC2.。
人教版数学八年级全等三角形证明题精选20题

三角形全等专题训练1已知:如图,四边形ABCD 中,AC 平分角BAD ,CE 垂直AB 于E ,且∠B+∠D=180度,求证:AE=AD+BE2,已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
3,如图,DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
① AB=AC ② BD=CD ③ BE=CFAEDCBDCABDCE 124,如图,在四边形ABCD 中,AB=BC ,BF 是∠ABC 的平分线,AF ∥DC ,连接AC 、CF ,求证:CA 是∠DCF 的平分线。
FDAC B5、如图,△ABC 中,AB=AC ,过A 作GE ∥BC ,角平分线BD 、CF 交于点H ,它们的延长线分别交GE 于E 、G ,试在图中找出三对全等三角形,并对其中一对给出证明。
6、已知:如图,AB 、CD 交于O 点,CE//DF ,CE=DF ,AE=BF 。
求证:∠ACE=∠BDF 。
EGABCDEFO7. 已知:如图,△ABC 中,AD ⊥BC 于D ,E 是AD 上一点,BE 的延长线交AC 于F ,若BD=AD ,DE=DC 。
求证:BF ⊥AC 。
8.已知:如图,AB=CD ,AD=BC ,O 是AC 中点,OE ⊥AB 于E ,OF ⊥D 于F 。
求证:OE=OF 。
9.已知:如图,AC ⊥OB ,BD ⊥OA ,AC 与BD 交于E 点,若OA=OB ,求证:AE=BE 。
AB CDEFA BCD E F OO B AC D E10.已知:如图,AB//DE ,AE//BD ,AF=DC ,EF=BC 。
求证:△AEF ≌△DBC 。
A BCDEF11.已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.12.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E . (1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.CBE D图1NMABC DEMN图2AC BEDN M 图313如图,已知AD 是△ABC 的中线, DE ⊥AB 于E , DF ⊥AC 于F , 且BE=CF , 求证:(1)AD 是∠BAC 的平分线;(2)AB=AC .14如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE⊥AD 交AB 于E .求证∠CDA =∠EDB .15在Rt △ABC 中,∠A =90°,CE 是角平分线,和高AD 相交于F ,作FG ∥BC 交AB 于G ,求证:AE =BG .F A 1 2 E CDBCD12ABCDE16.如图,已知△ABC是等边三角形,∠BDC=120º,说明AD=BD+CD的理由17如图,在△ABC中,AD是中线,BE交AD于F,且AE=EF,说明AC=BF的理由18如图,在△ABC中,∠ABC=100º,AM=AN,CN=CP,求∠MNP的度数19如图,已知∠BAC=90º,AD⊥BC, ∠1=∠2,EF⊥BC,FM⊥AC,说明FM=FD的理由20如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连结BD,AE,并延长AE交BD于F.求证:(1)△ACE≌△BCD(2)直线AE与BD互相垂直ABC D E F。
中考数学复习《全等三角形》专题训练-附带参考答案

中考数学复习《全等三角形》专题训练-附带参考答案一、选择题1.下列选项中表示两个全等的图形的是()A.形状相同的两个图形B.周长相等的两个图形C.面积相等的两个图形D.能够完全重合的两个图形2.如图,点D、E分别在线段AB、AC上,BE、CD相交于点O,AE=AD,则不一定能使△ABE≌△ACD的条件是()A.AB=AC B.∠B=∠CC.∠AEB=∠ADC D.CD=BE3.如图是用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是()A.SAS B.ASA C.AAS D.SSS4.如图△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为()A.25°B.30°C.35°D.65°5.如图EF=CF,BF=DF则下列结论不一定正确的是()A.△BEF≌△DCF B.△ABC≌△ADEC.DC=AC D.AB=AD6.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为()A.2 B.3 C.4 D.57.如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有()A.2对B.3对C.4对D.5对8.如图,AD 是△ABC中∠BAC的平分线,DE⊥AB于点E,△ABC的面积为12,DE =2,AB = 7,则 AC 的长是()A.3 B.4 C.5 D.6二、填空题9.如图,∠ACD=∠BCE,BC=EC,要使△ABC≌△DEC,则可以添加的一个条件是.10.如图所示,在△ABC中,∠C=90°,AB=8,AD是△ABC的一条角平分线.若CD=2,则△ABD的面积为.11.如图,在Rt△ABC中,∠BAC=90°,分别过点B,C作过点A的直线的垂线BD,若BD=4cm,CE=3cm则DE= cm.12.如图,把两根钢条AB,CD的中点连在一起做成卡钳,已知AC的长度是6cm,则工件内槽的宽BD是cm.13.如图,△ABC为等腰直角三角形AC=BC,若A(−3,0),C(0,2),则点B的坐标为.三、解答题14.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°(1)求证:△ADE≌△CDE.(2)求∠BDC度数.15.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.(1)求证:BC=DC;(2)若∠A =25°,∠D =15°,求∠ACB 的度数.16.如图,AB =AC ,AD =AE ,∠BAC =∠DAE.(1)求证:△ABD ≌△ACE ;(2)若∠1=25°,∠2=30°,求∠3的度数.17.如图,在ABC 中90C ∠=︒,BD 是ABC ∠的平分线,DE AB ⊥于点E ,点F 在BC 上,连接DF ,且AD DF =. (1)求证:CF AE =;(2)若3AE =,BF=4,求AB 的长.18.如图,∠BAD =∠CAE =90°,AB =AD ,AE =AC ,AF ⊥CB ,垂足为F .(1)求证:△ABC ≌△ADE ;(2)求∠FAE 的度数;(3)求证:CD =2BF+DE .1.D2.D3.D4.A5.C6.B7.C8.C9.AC =DC (答案不唯一)10.811.712.613.(2,-1)14.(1)证明:∵DE 是线段AC 的垂直平分线 ∴DA=DC ,AE=CE在△ADE 与△CDE 中:DA=DCAE=CEDE=DE∴△ADE ≌△CDE (SSS );(2)解:∵△ADE ≌△CDE .∴∠DCA=∠A=50°∴∠BDC=∠DCA+∠A=100°15.(1)证明:∵∠BCE =∠DCA∴∠BCE +∠ACE =∠DCA +∠ECA即∠BCA =∠DCE .在△BCA 和△DCE 中{∠BCA =∠DCE AC =EC ∠A =∠E∴△BCA ≌△DCE (ASA )(2)解:∵△BCA ≌△DCE∴∠B =∠D =15°.∵∠A =25°∴∠ACB =180°−∠A −∠B =140°.16.(1)证明:∵∠BAC =∠DAE∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC∴∠1=∠EAC在△ABD 和△ACE 中{AB =AC ∠1=∠EAC AD =AE∴△ABD ≌△ACE (SAS )(2)解:∵△ABD ≌△ACE∴∠ABD =∠2=30°∵∠1=25°∴∠3=∠1+∠ABD =25°+30°=55°.17.(1)证明:(1)∵90C ∠=︒∴DC BC ⊥又∵BD 是ABC ∠的平分线DE AB ⊥∴DE DC = 90AED ∠=︒在Rt AED △和Rt FCD △中∵AD DFDE DC =⎧⎨=⎩∴()Rt Rt AED FCD HL ≌△△∴CF AE =.(2)解:由(1)可得3CF AE ==∴437BC BF CF =+=+=∵DE AB ⊥∴90DEB ∠=︒∴DEB C ∠=∠∵BD 是ABC ∠的平分线∴ABD CBD ∠=∠在BED 和BCD △中∵DEB C EBD CBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BED BCD AAS ≌△△ ∴7BE BC ==∴7310AB BE AE =+=+=∴AB 的长为10.18.(1)证明:∵90BAD CAE ∠=∠=︒∴90BAC CAD ∠+∠=︒ 90CAD DAE ∠+∠=︒ ∴BAC DAE ∠=∠在△BAC 和△DAE 中∵AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴()BAC DAE SAS ≌△△;(2)解:∵90CAE ∠=︒,AC=AE∴45E ∠=︒由(1)知BAC DAE ≌△△∴45BCA E ∠=∠=︒∵AF BC ⊥∴90CFA ∠=︒∴45CAF ∠=︒∴4590135FAE FAC CAE ∠=∠+∠=︒+︒=︒;(3)证明:延长BF 到G ,使得FG FB = ∵AF BG ⊥∴90AFG AFB ∠=∠=︒在△AFB 和△AFG 中∴BF GF AFB AFG AF AF =⎧⎪∠=∠⎨⎪=⎩∴()AFB AFG SAS ≌△△∴AB AG = ABF G ∠=∠∵BAC DAE ≌△△∴AB AD = CBA EDA ∠=∠ CB=ED ∴AG AD = ABF CDA ∠=∠∴CGA CDA ∠=∠∵45GCA DCA ∠=∠=︒∴在△CGA 和△CDA 中GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CGA CDA AAS ≌△△∴CG CD =∵22CG CB BF FG CB BF DE BF =++=+=+ ∴2CD BF DE =+.。
八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,:在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为:在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用:如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解:(1)证实:BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下:: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下:由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实:PC=PE;〔2〕求N CPE的度数:〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论:⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案;(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE;⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>:⑶、AP = CE理由是:在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点:三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£>为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系:②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由;〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析:②成立,理由见解析:〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可:〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解:〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD:②成立,理由如下:如图2:VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD:(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证:△.所为等腰直角三角形:〔2〕假设△ABC的面积为7,求四边形AEDF•的面积:〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析;〔2〕 3.5:〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形;〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可;〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解:〔1〕证实:如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又;Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn;AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又;Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又:Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空:AABC的面积等于—;(2)连接CE,求证:CE是NAC3的平分线;(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—:〔2〕证实见解析:〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得:〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实:〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解:〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为:—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=;(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为:50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角 形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的 速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm :(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等?假设存在,请求出v的值:假设不存在,请说明理由.【答案】(1) (12-2/); (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长:(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得;(3)先分两种情况:当BP=CQ, AB=PC 时,△ABPgZ\PCQ:或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解:(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin:.PC = BC-BP = (n-2i)cm故答案为:(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下:①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item:.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.:在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证:MN = CN — BM ;(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析:(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM: (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实:・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由:•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA:.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现:如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证:△BADgZkCAE;(2)在(1)的条件下,求N8EC的度数:拓广探索:(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析:(2) 70°; (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实:如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,:.Z EAC=A DAB,AE=AD. AC=AB9:.△ BAD^ & CAE (SAS).(2)解:如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解:如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,:AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是;②设NBA尸=a,用.表示NBCF的大小;〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE;②NBCF=.:(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由釉对称性,得:AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解:(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,:.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下:作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证:CF = EG ;〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证:CD = CE+CF;〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解;〔2〕证实见详解:〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论:(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论;(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, :.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即:ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),:.CF = EG ;(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、:.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即:ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下:过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即:NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。
全等三角形的性质和判定专题训练
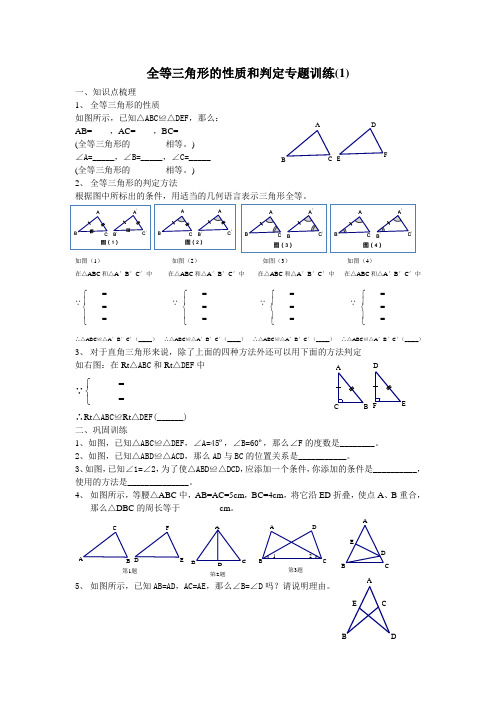
全等三角形的性质和判定专题训练(1)一、知识点梳理1、 全等三角形的性质如图所示,已知△ABC ≌△DEF ,那么:AB=____,AC=____,BC=______ (全等三角形的________相等。
)∠A=_____,∠B=_____,∠C=_____ (全等三角形的________相等。
) 2、 全等三角形的判定方法根据图中所标出的条件,用适当的几何语言表示三角形全等。
如图(1)如图(2) 如图(3)如图(4)在△ABC 和△A ′B ′C ′中在△ABC 和△A ′B ′C ′中 在△ABC 和△A ′B ′C ′中 在△ABC 和△A ′B ′C ′中∵⎪⎩⎪⎨⎧===_____________________ ∵ ⎪⎩⎪⎨⎧===_____________________ ∵ ⎪⎩⎪⎨⎧===_____________________ ∵ ⎪⎩⎪⎨⎧===_____________________ ∴△ABC ≌△A ′B ′C ′(_____) ∴△ABC ≌△A ′B ′C ′(_____) ∴△ABC ≌△A ′B ′C ′(_____) ∴△ABC ≌△A ′B ′C ′(_____)3、 对于直角三角形来说,除了上面的四种方法外还可以用下面的方法判定 如右图:在Rt △ABC 和Rt △DEF 中 ∵⎩⎨⎧==____________________∴Rt △ABC ≌Rt △DEF(______) 二、巩固训练1、如图,已知△ABC ≌△DEF ,∠A=45º,∠B=60º,那么∠F 的度数是________。
2、如图,已知△ABD ≌△ACD ,那么AD 与BC 的位置关系是___________。
3、如图,已知∠1=∠2,为了使△ABD ≌△DCD ,应添加一个条件,你添加的条件是__________,使用的方法是______________。
4、 如图所示,等腰△ABC 中,AB=AC=5cm ,BC=4cm ,将它沿ED 折叠,使点A 、B 重合,那么△DBC 的周长等于_________cm 。
2022年《直角三角形全等的判定》专题练习(附答案)

1.3 直角三角形全等的判定一、选择题(本大题共8小题)1. 在以下条件中,不能判定两个直角三角形全等的是( )2. 如下图,AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,那么图中全等的三角形有( )第2题图第5题图第6题图3.以下说法中正确的选项是〔〕A.a,b,c是三角形的三边长,那么a2+b2=c2B.在直角三角形中,两边长和的平方等于第三边长的平方C.在Rt△ABC中,假设∠C=90°,那么三角形对应的三边满足a2+b2=c2D.在Rt△ABC中,假设∠A=90°,那么三角形对应的三边满足a2+b2=c24. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=B′A,那么以下结论中正确的选项是〔〕A. AC=A′C′B.BC=B′C′C.AC=B′C′D.∠A=∠A′5. 如下图,△ABC中,AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点,那么图中全等三角形的对数是〔〕6. 如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,那么△BCE的面积等于〔〕A.10 B.7 C.5 D. 47. 在△ABC和△DEF中,∠A=∠D=90°,那么以下条件中不能判定△ABC和△DEF全等的是( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF8. 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,那么有( )A.DE=DBB.DE=AEC.AE=BED.AE=BD第8题图第9题图二、填空题(本大题共4小题)9. :如图,AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,AB=DC,那么△ABE≌△__________.10. 如图,BD⊥AE于点B,C是BD上一点,且BC=BE,要使Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D或__________或__________或__________.第10题图第11题图11. 如图,△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,假设根据“HL〞判定,还需要加一个条件__________.12. :如图,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,∠D=60°,那么∠A=__________.三、计算题(本大题共4小题)13. :如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE求证:OB=OC.14. :Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE15. 如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:〔1〕CF=EB.〔2〕AB=AF+2EB.16. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)假设CD=2,求AD的长.参考答案:一、选择题(本大题共8小题)1.A2. D3. C4. C5. D6. B7. B8. C二、填空题(本大题共6小题)9.分析:根据直角三角形全等的条件HL判定即可。
