魔术公式理论
魔术公式理论范文

魔术公式理论范文魔术公式理论是数学中的一个重要概念,旨在帮助解决各种数学问题。
它的核心思想是在一个特定的数学领域中,存在着一些固定的公式和规律,可以用来简化或解决复杂的问题。
本文将详细介绍魔术公式理论的定义、特点、应用以及相关的例子。
魔术公式理论最早由数学家斐波那契在13世纪提出,他发现了一些特殊的数列和公式,可以用来解决许多数学难题。
随后,这个概念在数学界得到了广泛认可,并逐渐发展成一种完整的理论体系。
魔术公式理论包括几何、代数、数论、微积分等各个数学领域,涉及面广泛,应用广泛。
魔术公式理论的主要特点是:简单易用、理论严谨、适用范围广。
这些特点使得魔术公式理论成为解决数学问题的重要工具。
魔术公式理论的应用范围非常广泛,从基础的加减乘除到高级的微分方程和线性代数等都可以使用魔术公式理论来解决。
同时,魔术公式理论也可以帮助学生更好地理解数学的本质和应用。
下面我们来看几个具体的例子来说明魔术公式理论的应用。
例一:求一个整数的平方。
根据魔术公式理论,整数的平方可以通过将该整数与自身相乘来得到。
例如,2的平方等于2乘2,即4;3的平方等于3乘3,即9、通过魔术公式理论,我们可以快速计算出任意整数的平方,从而解决这个问题。
例二:求一个数的对数。
根据魔术公式理论,数的对数可以通过对该数进行对数运算来得到。
例如,10的对数等于1,因为10的10次方等于10;100的对数等于2,因为100的2次方等于100;1000的对数等于3,因为1000的3次方等于1000。
通过魔术公式理论,我们可以简单地计算出任意数的对数,解决这个问题。
例三:求一个多项式的因式分解。
根据魔术公式理论,多项式的因式分解可以通过寻找该多项式的根来实现。
例如,对于多项式x^2-5x+6,我们可以通过找到满足(x-2)(x-3)的根来进行因式分解。
通过魔术公式理论,我们可以迅速找到多项式的因子,解决这个问题。
通过以上例子,我们可以看出魔术公式理论的应用非常广泛,并且在解决数学问题时起到了重要的作用。
即兴演讲 (3)

理查德“结构精选模式” 美国公共演讲专家理查德先生认为,即兴演讲应当记住四句话,这四句话是表述中四个步骤的提示信号。它们是: ——喂,请注意!(开头的悬念就激起听众的兴趣) ——为什么要费口舌?(进而强调指出听演讲的重要性) ——举例子。(么或怎么做) 理查德“结构精选模式”与常见模式之比较 美国一个高速公路边的小城镇经常出现交通事故,死伤情况日益严重。交通局长召集市民开会,他用“理查德模式”发表即兴讲话。下面的即兴讲话是理查德的“结构精选模式”与“常规模式”即兴成篇的比较。
魔术公式教学文案

魔术公式Pacejka的“魔术公式”是近期在汽车操纵动力学研究中比较流行的公式,它是用特殊正弦函数建立的轮胎的纵向力、横向力和自回正力矩模型。
因只用一套公式就完整地表达了纯工况下轮胎的力特性,故成为“魔术公式”。
“魔术公式”表达如下:sin(arctan((arctan())))vhY y Sy D C Bx E Bx Bxx X S=+=--=+其中,Y表示侧向力、纵向力或回正力矩,X表示侧偏角α或滑移率s。
现以侧向力为例说明公式中各系数的意义。
式中D--峰值因子,表示曲线的最大值B C D⋅⋅--侧偏角趋于零时轮胎的侧偏刚度,曲线中表示原点的斜率E--曲线形态因子,决定曲线最大值附近的形状C--决定曲线的形状,即曲线是像侧向力、纵向力还是回正力矩hS--水平方向漂移vS--垂直方向漂移除C外,“魔术公式”中的参数都是垂直载荷和侧倾角γ的函数。
以下为轮胎纵向动力学特性在MATLAB中的具体实现212x z zD a F a F=+1.65x C =2678x z z E a F a F a =++5234()///z a F x z z x x B a F a F e C D =+52342122678sin(arctan((arctan())))()///1.65zx x x x x x xa Fx z z x xxx z zx z zF D C B E B BB a F a F eC DCD a F a FE aF a F aκκκ=--=+==+=++sin(arctan((arctan())))(arctan((arctan()))) cos(arctan((arctan())))x xx x x x xz zx x x x x x x x x x xzdF dDC B E B BdF dFd B E B BD C BE B B CdFκκκκκκκκκ=--+----2(arctan((arctan())))(arctan()) 1((arctan())) 1((arctan()))x x x xzx x x xx x xx x x x z z zd B E B BdFdB dE d B BB B EB E B B dF dF dFκκκκκκκκκκκ--=----+--222(arctan())()11()1()x x x x x xz z x z x zd B B dB dB B dBdF dF B dF B dFκκκκκκκκ-=-=++555522343422234345(()///)()///(()///)(()///)zzz za Fa Fx z z x x z zx xz z za F a Fxz z x x z z x xzdB d a F a F e C D d a F a Fe C DdF dF dFdDa F a F e C D a F a F e C D adF++==-+-+sin(arctan((arctan())))x x x x x x xF D C B E B Bκκκ=--22cos(arctan((arctan())))(())1()1((arctan())xx x x x x x x x x xx xx x x xBD C BE B B C B E BdF Bd B E B Bκκκκκκκκ----+=+--车辆防抱死制动系统的控制技术研究东大,侯光钰,张为公 2.3.1 H.B.Pacejka 的魔术公式Pacejka 的“魔术公式”是汽车操纵动力学研究中应用比较广泛的轮胎力学模型,它用特殊的正弦函数建立轮胎的纵向力、横向力和回正力矩的函数表达式。
基于pac2002魔术公式的轮胎动力学特性分析

第34卷㊀第6期2019年12月北京信息科技大学学报JournalofBeijingInformationScience&TechnologyUniversityVol.34㊀No.6Dec.2019文章编号:1674-6864(2019)06-0076-06DOI:10 16508/j.cnki.11-5866/n.2019 06 014基于PAC2002魔术公式的轮胎动力学特性分析尚㊀强ꎬ王国权(北京信息科技大学机电工程学院ꎬ北京100192)摘㊀㊀㊀要:为了满足汽车动力学整车仿真的研究需要ꎬ基于Matlab/Simulinkꎬ用PAC2002魔术公式建立某轮胎动力学的仿真模型ꎬ对车辆稳态行驶时在轮胎纯驱动(制动)㊁纯转弯㊁驱动(制动)和转弯联合等工况下ꎬ分别进行纵向滑移率㊁侧偏角㊁垂直载荷等指标对纵向力㊁侧向力和回正力矩的仿真分析ꎮ仿真结果表明ꎬ基于PAC2002魔术公式的轮胎动力学模型能够比较准确地模拟出轮胎的动力学特性ꎮ关㊀键㊀词:PAC2002魔术公式ꎻ轮胎模型ꎻ纵向滑移率ꎻ侧偏角中图分类号:U461ꎻU463㊀㊀㊀文献标志码:ATiredynamicsanalysisbasedonPAC2002Magic ̄FormulaSHANGQiangꎬWANGGuoquan(MechanicalElectricalEnginneeringSchoolꎬBeijingInformationScience&TechnologyUniversityꎬBeijing100192ꎬChina)Abstract:InordertomeettheneedtoanalyzethevehicledynamicsꎬbasedontheMatlab/SimulinksoftwareꎬatiredynamicsmodelisestablishedaccordingtothePAC2002Magic ̄Formulatiremodel.Thenthemodelissolvedunderthesteady ̄stateconditionssuchasvehiclepurebrakingꎬdrivingꎬpurecorneringꎬbrakingꎬdrivingandcornering.Thetirelongitudinalforceꎬthelateralforceꎬandthealigningmomentarecaculatedindifferentslipratioꎬslipangleandtheverticalload.ItisshownthatthetiredynamicmodelbasedonPAC2002formulaeffectivelysimulatesitsdynamiccharacteristics.Keywords:PAC2002magic ̄formulaꎻtiremodelꎻlongitudinalslipratioꎻslipangle收稿日期:2018 ̄06 ̄16第一作者简介:尚㊀强ꎬ男ꎬ硕士研究生ꎻ通讯作者:王国权ꎬ男ꎬ博士ꎬ教授ꎮ0㊀引言轮胎动力学的研究先后经历了起始阶段㊁发展阶段和相对成熟阶段ꎮ汽车轮胎动力学的研究起源于对飞机轮胎的研究ꎮ20世纪20年代末至30年代初ꎬ美国空军建成了起落架系统卓越中心(LGSCE)ꎬ开发了航空轮胎六分力测试设备ꎮ此后ꎬ美国㊁德国㊁荷兰相继开发了Fiala㊁UA及MagicFormula(MF)等轮胎模型ꎬ在模型精度提高的同时ꎬ适用范围也从单一工况扩展至侧偏㊁纵滑等四维输入的复合工况[1]ꎮ轮胎模型从稳态到非稳态㊁从线性到非线性模型已经相当丰富ꎮ我国学者对轮胎动力学的研究始于20世纪60年代ꎬ起因是国产红旗轿车出现了高速稳定性的问题ꎮ1984年长春汽车研究所开发了QY7329轮胎试验台ꎬ改变了我国无法进行轮胎动力学测试的状况[2]ꎮ从此我国轮胎动力学的研究开始快速推进ꎮ郭孔辉院士在理论分析和试验研究基础上所提出的幂指数统一轮胎模型是代表性的成果ꎬ可用于轮胎的稳态侧偏㊁纵滑以及纵滑侧偏联合工况ꎬ并且可预测轮胎的稳定特性ꎮ该模型通过获得有效的滑移率ꎬ也可进行非稳态工况下的轮胎纵向力㊁侧偏力和回正力矩的计算[3]ꎮ国外ꎬ荷兰Delft工业大学提出了SWIFT轮胎模型ꎬ它由刚性圈理论和魔术公式[4]综合而成ꎬ在考虑侧向力和回正力矩时ꎬ采用魔术公式ꎻ在考虑纵向力和垂直力时ꎬ采用刚性圈理论ꎮSWIFT轮胎模型采用了胎体建模与接地区域分离的建模方法ꎬ可精确地描述小波长㊁大滑移时的轮胎特性ꎬ因而可计算从瞬态到稳态连续变化的轮胎动力学行为ꎮ此第6期尚㊀强等:基于PAC2002魔术公式的轮胎动力学特性分析㊀外ꎬ该模型也考虑到了在不同路面条件下行驶的情况ꎬ通过对模型的进一步细化ꎬ还可用来描述车轮外倾以及转弯纵滑联合工况下的轮胎特性[3]ꎮ目前ꎬ应用最广泛的是由H.BPacejka教授提出的轮胎经验模型 魔术公式 轮胎模型ꎬ它是通过对大量的轮胎动力特性的实验数据进行回归分析ꎬ以三角函数组合的形式来拟合实验数据ꎬ得出的一套形式相同但可同时表达纵向力㊁侧向力和回正力矩的轮胎模型[4]ꎮPacejka 89轮胎模型ꎬ由H.BPacejka㊁E.Bakker和L.Lidner教授在发表的论文中所提出[5]ꎻPacejka 94轮胎模型由H.BPacejka教授在1993年第一届国际车辆动力学分析轮胎模型座谈会上提出[6]ꎮ而PAC2002模型则由MSCSoftware公司根据Pacejka 89轮胎模型和Pacejka 94轮胎模型结合车辆动力学联合开发出来ꎬ该模型包含了已发布的Pacejka 89㊁Pacejka 94轮胎模型和车辆动力学的最新进展ꎮ相对于两个Pacejka轮胎模型ꎬPAC2002轮胎模型在参数表达式上有较大的变化ꎬ拟合精度有了更进一步的提高[7 ̄8]ꎮ本文以某品牌乘用车轮胎为研究对象ꎬ使用Matlab/Simulink软件建立了不同工况下轮胎的PAC2002轮胎模型ꎬ仿真绘制了轮胎的纵向滑移率㊁侧偏角㊁外倾角和垂直载荷对纵向力㊁侧向力以及回正力矩的关系曲线图ꎬ进而分析曲线的变化趋势ꎬ为汽车极限安全行驶性能评估提供了理论依据ꎮ1㊀轮胎模型的建立PAC2002轮胎模型是以 魔术公式 和车辆动力学为基础联合开发出来的ꎬ它用一套形式相同的数学公式描述稳态条件下轮胎与道路之间的相互作用力ꎮ无论对侧向力㊁纵向力和回正力矩ꎬ其拟合精度都相对比较高ꎬ公式统一性强ꎬ编程简单ꎬ需要拟合的参数较少ꎬ且各个参数都有明确的物理意义ꎮPAC2002轮胎模型采用SAE标准轮胎运动坐标系ꎬ轮胎力的计算输入和输出变量关系如图1所示ꎮ用魔术公式轮胎模型对轮胎建模时将轮胎的稳态工况分为以下3类ꎮ纯驱动(制动)工况:制动或驱动轮胎纵向滑动而不转弯ꎮ图1㊀魔术公式轮胎模型的输入和输出变量纯转弯工况:使用自由滚动轮胎半径转弯ꎮ㊀㊀纯驱动(制动)和纯转弯组合工况:同时转弯和纵向滑动ꎮ魔术公式如下:Yx()=DsinCtan-1Bx{[-EBx-(tan-1Bx())}](1)式中:Yx()为轮胎的侧向力㊁纵向力或者回正力矩ꎻx为轮胎的侧偏角或者纵向滑移率ꎻD为确定曲线特征的峰值ꎬ称为峰值因子ꎻC为决定正弦使用的部分ꎬ主要影响正弦的形状曲线ꎬ称为形状因子ꎻB为拉伸曲线因子ꎬ称为刚度系数ꎻE为修改曲线峰值周围的特征ꎬ称为曲率因子ꎮ在PAC2002轮胎模型中ꎬ滑移率的定义[7 ̄8]示意图如图2所示ꎮ图2㊀轮胎运动速度示意图横向滑移速度Vsy=Vyꎬ式中Vy为轮胎与地面接触点相对于路面的横向速度ꎮ滚动速度Vr=Ω Reꎬ式中Ω为车轮转速ꎻRe为有效滚动半径ꎮ接触点的纵向滑移速度Vsx=Vx-Vrꎬ式中Vx为接触点相对于路面的纵向速度ꎮ纵向滑移率κ=-VsxVxꎮ侧偏角α=tan-1VsyVxꎮ1 1㊀稳态纯驱动(制动)工况轮胎纯直线行驶的车轮运动ꎬ纵向力为Fx0=DxsinDxtan-1Bxκx{[-ExBxκx(-tan-1Bxκx())}]+Svx(2)κx=κ+SHxγx=γ λγx77㊀北京信息科技大学学报第34卷其中Cx=pCx1 λCxDx=μx Fz ζ1μx=pDx1+pDx2dfz() 1-pDx3γ2()λμxEx=pEx1+pEx2dfz+pEx3df2z()ˑ1-pEx4sgnκx(){}λEx㊀㊀纵向滑动刚度Kx=FzpKx1+pKx2dfz() exppKx3dfz()λKxKx=BxCxDx=∂Fx0∂κxtan-1κx()=0Bx=Kx/CxDx()SHx=pHx1+pHx2dfz()λHxSVx=FzpVx1+pVx2dfz()λVxλμxζ11 2㊀稳态纯转弯工况侧向力为Fy0=Fy0αꎬγꎬFZ()=DysinCy[tan-1Byαy{-EyByαy-tan-1Byαy()()}]+SVy(3)回正力矩为MZ0=MZ0αꎬγꎬFZ()= ̄t Fy0+Mzr气动路径为tαt()=DtcosCttan-1Btαt-Et{[Btαt-(tan-1Btαt())}]cosα残余力矩为Mαt()=DrcosCttan-1Brαr()[]cosα1 3㊀稳态驱动(制动)和转弯联合工况纵向力为FxαꎬγꎬκꎬFZ()=Fx0 GxααꎬκꎬFz()(4)加权函数为Gxα=cosCxα[tan-1Bxααs{-ExαBxααs(-tan-1Bxααs())}]/Gxα0Gxα0=cosCxα[tan-1BxαSHxα{-ExαˑBxαSHxα(-tan-1BxαSHxα())}]侧向力为㊀㊀Fy=FyαꎬγꎬκꎬFZ()=Fy0 GyκαꎬκꎬγꎬFz()+Svyk(5)加权函数为Gyκ=cosCyκtan-1Byκκs-Eyκ{[Byκκs(-tan-1Byκκs())}]/Gyκ0Gyκ0=cosCyκtan-1ByκSHyκ-Eyκ{[ˑByκSHyκ-tan-1ByκSHyκ())}](回正力矩为M=MαꎬγꎬκꎬFZ()= ̄t Fꎬy+Mzr+s Fx(6)Fꎬyꎬγ=0=Fy-SVykMzr=Mzrαγꎬeq()=Drcostan-1Brαrꎬeq()[]cosα2㊀仿真分析2 1㊀稳态纯驱动(制动)工况汽车在驱动(制动)直线行驶条件下ꎬ不可避免地会出现轮胎与地面的接触点相对于路面的纵向速度和接触点处的线速度不一致的情况ꎬ用车轮的滑动率(驱动工况时称为滑转率ꎬ被驱动或者制动时称为滑移率)表示车轮相对于纯滚动或者纯滑动状态的偏离程度[12]ꎮ滑动率是影响轮胎产生纵向力的一个重要因素ꎮ而在PAC2002轮胎模型中ꎬ统一用纵向滑移率来表示滑动率(匀速行驶时滑移率为0ꎬ加速行驶时滑移率为正值ꎬ减速行驶时滑移率为负值)ꎮ表1是纯驱动(制动)工况的测试条件ꎮ图3为在表1的测试条件下ꎬ轮胎纵向力和滑移率的关系曲线ꎮ表中FZ0为初载荷ꎬV为速度ꎬκ为滑移率ꎬγ为外倾角ꎬFZ为加载载荷ꎬP为胎压ꎬα为侧偏角ꎮ表1㊀纯驱动(制动)工况的测试条件编号Fz0/NV/(km h-1)κ/%γ/(ʎ)FN/NP/kPa1234400065-40~4001282320551287052220图3㊀轮胎纵向力和纵向滑移率的关系从图3可以看出ꎬ当驱动力矩传递到汽车轮胎时ꎬ在轮胎与路面的接触印迹处会产生切向力ꎬ即车轮驱动力ꎮ在地面切向力的作用下ꎬ轮胎胎面与地面接触处前端受到压缩ꎬ使轮胎后续有效滚动半径增加ꎬ此时轮胎接触点处的滚动速度大于纵向速度ꎬ滑移率为正ꎮ当滑移率在0~7%范围时ꎬ轮胎的滑移主要由胎面的弹性形变引起ꎬ这时车轮力矩与地面切向力随着滑移率近似呈线性关系增加ꎮ当驱动力矩和地面切向力进一步增加从而导致轮胎和地面接触处部分胎面在地面上滑移时ꎬ滑移率进入7%~87第6期尚㊀强等:基于PAC2002魔术公式的轮胎动力学特性分析㊀10%范围ꎮ地面切向力和滑移率呈非线性递增关系ꎬ当滑移率接近10%时地面切向力达到最大值ꎮ滑移率超过10%并且进一步增加时ꎬ轮胎与地面接触区域进入不稳定工况ꎬ地面切向力从峰值缓慢下降ꎬ直到进入纯滑移状态(即滑移率为100%)时的饱和地面切向力ꎮ当制动力作用于轮胎时ꎬ会出现类似的曲线变化关系ꎮ2 2㊀纯转弯工况汽车在行驶过程中ꎬ由于路面的侧向倾斜㊁侧向风或者转弯行驶时的离心力作用ꎬ在轮胎和地面的接触处会出现侧偏力ꎮ轮胎是具有弹性特性的结构部件ꎬ当车轮有侧向弹性时ꎬ车轮的行驶方向会偏离轮胎的车轮平面ꎮ侧偏角就是体现轮胎接触印迹中心线和车轮平面错开的程度ꎮ表2是纯转弯工况下的测试条件ꎮ表2㊀纯转弯工况下的测试条件编号Fz0/NV/(km h-1)α/(ʎ)γ/(ʎ)FN/NP/kPa1234400065-15~1551282320551287052220图4为在表2纯转弯工况的测试条件下仿真得到的轮胎侧向力和侧偏角的关系曲线ꎮ从图4可以看出ꎬ当侧偏角在0ʎ~4ʎ时ꎬ侧偏力随着侧偏角的增加而近似线性增加ꎮ这是由于轮胎是弹性部件ꎬ在弹性范围内ꎬ弹性变形与侧向力呈线性关系ꎮ当侧偏角在4ʎ~6ʎ时ꎬ侧偏力随着侧偏角的增加而缓慢呈非线性增加直到达到峰值侧偏力ꎬ即侧偏角以较大的速率增加时ꎬ侧偏力则以相对较小的速率增加ꎬ曲线的斜率逐渐减小ꎬ这时轮胎在接地面处已经发生部分侧滑ꎮ当侧偏角超过6ʎ以后ꎬ侧偏力逐渐减小ꎬ最终趋向定值ꎬ这时整个轮胎发生侧滑ꎮ另外ꎬ轮胎的侧偏力越大ꎬ轮胎能够产生的侧向加速度就越大ꎬ汽车的极限转弯性能就越好ꎮ汽车在路面上行驶时ꎬ轮胎上的垂直载荷常常会有所变化和转移ꎮ汽车在转弯时ꎬ外侧轮胎上的垂直载荷会增大ꎬ而内侧轮胎上的垂直载荷会有所减小ꎮ同理ꎬ在汽车直线加速或者减速时ꎬ前㊁后轮胎所负载的垂直载荷也会有所变化和转移ꎮ加速行驶时ꎬ前轴轮胎的垂直载荷减小ꎬ后轴轮胎的垂直载荷增大ꎬ减速行驶时ꎬ垂直载荷恰恰相反ꎮ图5为在表2纯转弯工况的测试条件下仿真得到的侧偏刚度与垂直载荷的关系曲线ꎮ图4㊀轮胎侧向力和侧偏角的关系图5㊀侧偏刚度和垂直载荷的关系从图5可以看出ꎬ侧偏刚度随着垂直载荷的增大而增大ꎮ当垂直载荷约为11kN时ꎬ侧偏刚度达到最大值ꎬ约为2100N/(ʎ)ꎬ但是ꎬ垂直载荷过大时ꎬ则会影响轮胎和地面的接触处的压力分布ꎬ并促使压力变得极其不均匀ꎬ从而使轮胎的侧偏刚度反而有所减小ꎮ然而ꎬ轮胎应该具有较高的侧偏刚度(指绝对值)ꎬ这样才能保证汽车具有良好的操作稳定性ꎮ在轮胎发生侧偏时ꎬ地面会产生作用于轮胎绕OZ轴的力矩ꎬ这个力矩称为回正力矩ꎬ大小为轮胎侧向力与轮胎气胎拖距的乘积ꎮ回正力矩是由接地面内分布的微元侧向反力产生的ꎬ圆周行驶时ꎬ回正力矩是使车轮恢复直线行驶位置的主要恢复力矩之一ꎬ它被用来描述实际轮胎侧向力相对于接地中心的非对称性ꎮ车轮滚动时ꎬ印迹长轴线不仅与车轮平面错开一定距离ꎬ而且还转动了一定的角度ꎬ因而印迹前端离车轮平面近ꎬ侧向变形小ꎻ印迹后端离车轮平面远ꎬ侧向变形大ꎮ图6为在表2纯转弯工况的测试条件下仿真得到的回正力矩和侧偏角的关系曲线ꎮ从图6可以看出ꎬ侧偏角在0~3ʎ时ꎬ回正力矩随侧偏角的增大而近似线性迅速增大ꎮ在侧偏角为3ʎ时ꎬ回正力矩达到最大值ꎮ侧偏角继续增大ꎬ回正97㊀北京信息科技大学学报第34卷图6㊀回正力矩和侧偏角的关系曲线力矩开始逐渐下降ꎮ当侧偏角为10ʎ时ꎬ回正力矩减小到零ꎮ侧偏角继续增大ꎬ回正力矩开始成为负值ꎮ这是因为接地面后部发生侧向滑动的速度过大ꎬ摩擦因数较小从而导致的ꎮ此外ꎬ回正力矩也随着垂直载荷的增加而增加ꎮ2 3㊀稳态驱动(制动)和转弯联合工况在驱动(制动)和转弯联合工况下ꎬ轮胎的纵向力㊁侧向力和垂向载荷三者之间是彼此相互影响的ꎮ汽车在路面上转弯驱动和转弯制动时ꎬ必须考虑上述纯转弯㊁纯驱动(制动)这两种轮胎特性的关联情况ꎮ在汽车转弯驱动或转弯制动两种联合工况下ꎬ轮胎会同时产生侧向力和纵向力ꎮ下面分析上述联合工况下ꎬ滑移率㊁侧偏角对侧偏力㊁纵向力㊁侧向力系数(轮胎侧向力与轮胎垂直力之比)以及制动力系数(地面制动力与垂直载荷之比)的影响ꎮ图7为在表3驱动(制动)和转弯联合工况测试条件下得到的制动力系数㊁侧向力系数与滑移率的关系曲线ꎮ表3㊀驱动(制动)和转弯联合工况下的测试条件编号Fz/NV/(km h-1)κ/%γ/(ʎ)α/(ʎ)P/kPa123457052650~100512468220从图7可以看出ꎬ同一侧偏角条件下ꎬ滑移率越低ꎬ侧向力系数越大ꎬ即轮胎保持转向㊁防止侧滑的能力越大ꎬ汽车的稳定性越好ꎮ同时ꎬ制动力系数随着滑动率的增加先近似线性增加ꎬ后缓慢增加ꎬ达到峰值后ꎬ又逐渐减小ꎮ所以ꎬ在汽车转弯制动时ꎬ若能保证滑移率在较低值(如图7中侧偏角为8ʎꎬ滑移率为13%时)ꎬ汽车的轮胎便能获得较大的制动力系数和侧向力系数ꎮ这样ꎬ车辆的制动性能最好ꎬ图7㊀制动力系数㊁侧向力系数与滑移率的关系曲线稳定性能也很好ꎬ两者相对比较均衡ꎮ具有一般制动系的汽车是无法同时满足这一点的ꎬ而制动防抱死系统却能比较完美地平衡制动力系数和侧向力系数ꎬ可以明显改善汽车在制动时的制动效能与方向稳定性ꎮ另外ꎬ应尽量避免制动时轮胎滑移率接近100%ꎬ或者加速时滑移率接近100%ꎬ此时ꎬ轮胎附着力几乎全部都分配给了轮胎制动力ꎬ轮胎侧向力近似为零ꎬ转弯失效ꎮ这就是制动防抱死系统和驱动力控制系统的重要理论依据之一[12]ꎮ图8是在表3驱动(制动)和转弯联合工况的图8㊀纵向力与侧向力之间的关系曲线测试条件下得到的纵向力与侧向力之间的关系曲线图ꎮ从图8可以看出ꎬ在侧偏角一定时ꎬ随着驱动力增加ꎬ侧偏力逐渐减小ꎬ这是由于轮胎侧向弹性有所改变造成的ꎮ当驱动力比较大且接近一定值(如图8中侧偏角为4ʎꎬ驱动力为6000N)时ꎬ侧偏力快速下降ꎬ这时轮胎与地面的摩擦接近附着极限ꎬ纵向驱动力已占用绝大部分的地面附着力ꎬ而侧向力所占附着力比例很小ꎮ当有制动力时ꎬ侧偏力也有相似的变化特征ꎮ另外ꎬ纵向力和侧向力关系的包络线近似为一椭圆ꎬ称为附着椭圆ꎬ它在一定程度上确定了在一定的轮胎附着条件下纵向力与侧偏力合力所08第6期尚㊀强等:基于PAC2002魔术公式的轮胎动力学特性分析㊀能达到的极限值ꎮ轮胎在接地印迹范围内所产生的纵向力和侧向力的合力是一定的ꎬ因此ꎬ汽车在转弯时ꎬ通过控制油门踏板和制动踏板合力分配侧向力和制动的比例关系ꎬ使汽车尽量快速通过弯道ꎮ3 结束语本文基于PAC2002魔术公式轮胎模型ꎬ利用Matalab/Simnlink仿真分析了在3种工况下ꎬ轮胎纵向力㊁侧向力㊁回正力矩与滑移率ꎬ侧偏角和垂直载荷的曲线关系ꎬ做出附着椭圆曲线ꎮ得到了以下结果:1)该型轮胎当侧偏角超过6ʎ以后ꎬ侧偏力逐渐减小ꎬ因此在转向系统设计和驾驶过程中应限制轮胎的侧偏角在6ʎ左右ꎮ2)轮胎垂直载荷达到11kN时ꎬ轮胎的侧偏刚度达到峰值2100N/(ʎ)ꎬ因此该轮胎应使用在总垂直载荷小于11kN的汽车上ꎮ3)汽车转弯制动(驱动)时ꎬ滑移率超过17%以后ꎬ侧向力系数快速减小ꎬ路面不能提供足够的侧向力ꎬ在确定防抱死制动系统参数时必须给予注意ꎮ进一步的工作将是建立整车多自由度仿真模型ꎬ在特定的速度范围内ꎬ着重分析汽车极限工况时的轮胎纵向力和侧向力ꎬ为汽车设计和性能评估提供理论基础ꎮ参考文献:[1]㊀PacejkaHBꎬBesselinkI.Tireandvehicledynamics(third ̄edition)[M].Netherlands:ElsevierLtdꎬ2012:5-12.[2]㊀郭孔辉ꎬ卢荡ꎬ吴海东.轮胎动力学协同发展策略研究[J].中国工程科学.2018(01):91-96.[3]㊀喻凡ꎬ林逸.汽车系统动力学[M].北京:机械工业出版社ꎬ2008:38-70.[4]㊀王和毅ꎬ谷正气.汽车轮胎模型研究现状及其发展分析[J].橡胶工业ꎬ2005ꎬ52(1):58-63.[5]㊀PacejkaHBꎬSharpRS.Shearforcedevelopmentbypneumatictyresinsteadystateconditions:areviewofmodellingaspects[J].VehicleSystemDynamicsꎬ1991ꎬ20(3/4):1212176.[6]㊀李军.ADAMS实用教程[M].北京:北京理工大学出版社ꎬ2002:128-142.[7]㊀任光胜.用MagicFormula对轮胎特性曲线的拟合与优化[J].重庆大学学报:自然科学版ꎬ2001(3):22-24.[8]㊀张剑威.汽车轮胎力学模型研究[D].武汉:武汉理工大学ꎬ2006.[9]㊀余志生.汽车理论[M].北京:机械工业出版社ꎬ2009:92-96.[10]㊀徐志新.车辆轮胎模型 MagicFormula 的模式作用探讨[J].上海汽车ꎬ1998(5):4-6. [11]㊀李松焱ꎬ闵永军ꎬ王良模ꎬ等.轮胎动力学模型的建立与仿真分析[J].南京工程学院学报:自然科学版ꎬ2009(3):34-38.[12]㊀郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社ꎬ2011:236-325.18。
葛底斯堡的演说

课前90秒
自主学习
合作探究
他山之玉
同时,这篇演讲词处处洋溢着炽烈而真挚的感情,极富 有鼓动性。“我们要从这些光荣的死者身上汲取更多的献身精 神,来完成他们已经完全彻底为之献身的事业”,这是对生者 的召唤与鼓励;“使国家在上帝福佑下得到自由的新生,要使 这个民有、民治、民享的政府永世长存”,这是对未来坚定的 信念。文章善于寓理于情,引起听众的强烈共鸣。
牲者的伟大奉献与活着的人的奋斗目标获得了统一。这个开场
白,也是林肯这次演说的理论基础与发展主线,贯穿全篇。
开头谈的是“一切人生来平等”的立国意
义,最后提出活着的人的奋斗目标,前后所体现出的精神实质是
统一的。
课前90秒
自主学习
合作探究
走近作者
亚 伯 拉 罕 · 林 肯 (1809—1865) , 美 国第十六任总统。他自修法律,以反对奴 隶制的纲领当选为总统,导致南方诸州脱 离联邦。在由此引起的南北战争中,他作 为总统,发挥了美国历史上最有效、最鼓 舞人心的领导作用,以其坚定的信念、深 远的眼光和完美无缺的政治手腕,成功地 引导一个处于分裂的国家度过了其历史上 流血最多的内战时期,从而挽救了联邦。
牺牲的烈士们,引导听众超越一场战役去思索其背后所蕴含的伟
大意义。战争是为了孕育于自由和奉行一切人生来平等原则的国
家“能够长久存在下去”,烈士们是“为使这个国家能够生存下
去而献出了自己的生命”,葛底斯堡则是这场战争中的一个伟大
的战场,并且因为勇士们的奉献而被神圣化了。这是“承”。
课前90秒
自主学习
合作探究
亚伯拉罕·林肯
课前90秒
自主学习
合作探究
他山之玉
要领点拨
1.演讲的结尾有哪些方式? 提示 演讲中结尾的方式有多种多样:用简洁的语句归纳
即席演讲

即席演讲目的:1、学习和掌握即兴演讲的知识和技能2、学会即兴演讲一生中,人们不可能每次讲话前都能深思熟虑,写成讲稿。
常常是站起来就讲话,或者演讲,这种讲话或演讲就是即席演讲。
即席演讲与命题演讲虽然没有本质的区别,没有优劣之分,但即席演讲使用的范围更广,频率更高,难度更大。
一、即席演讲的含义及特征即席演讲,是指事先没有准备,没有现成讲稿,因事而发,触景生情的演讲。
这类演讲,有的虽然没有讲稿,但是有所准备,有腹稿。
譬如出席某种会议,估计要讲话,或者因为某种话题某种情境,引发了说话的欲望,在讲话之前,已选定了话题,形成了思路,打好了腹稿。
还有的是毫无准备,压根就没有打算讲话也不想讲话,可迫于情势,不得不讲话。
这两种情势的讲话或演讲,虽然都可以视为即席演讲,但后者更是严格意义上的即席演讲。
即席演讲是即席成篇,出口成章,因而与其它类型的演讲比较,有其自身的特殊性:(一)时境的突发性也许正当你和别人窃窃私语,也许正当你在潜心思索别的什么,也许当你朝窗外张望的时候,被突然提名就某个问题发表看法;或者你参加校长主持的一次座谈会,或者被同学邀请参加茶话会,或者参加即席演讲比赛,你明明知道要讲话,也有了准备,可临近讲话时,话题被指定了,一切都发生的那么突然,不讲不行。
因而迅速成篇,这是即席演讲的一个内在特点。
(二)情境的复杂性因为突然发生,演讲者常常很少或根本没有留心当时当地的讲话情景以及听众的需求。
一下站起来讲话,茫然不知所措。
尤其是处在不同意见分歧的情势下,就更加左右为难了。
因此面对复杂的情景演讲只能就地取材,当场捕捉话机。
因此比起命题演讲来,即席演讲的现场感和针对性更鲜明。
(三)话境的多样性因为时境紧迫,情景复杂,由此而导致第三种情况的出现。
站起来以后,要么什么话也没有,呆若木鸡;要么什么都可以说上几句。
一般前者较少,后者居多。
演讲者虽然面临的是话题的多样选择,但有经验的演讲者往往是机敏地选准一点,迅速组合思维,把话讲少些,讲风趣些。
魔术公式——精选推荐
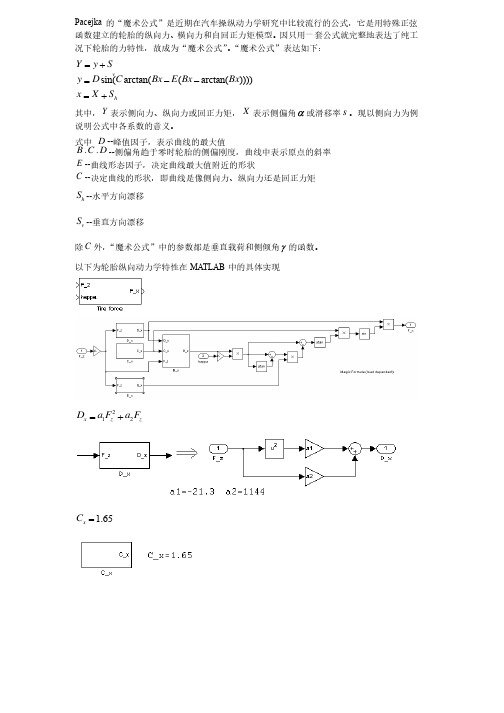
Pacejka 的“魔术公式”是近期在汽车操纵动力学研究中比较流行的公式,它是用特殊正弦函数建立的轮胎的纵向力、横向力和自回正力矩模型。
因只用一套公式就完整地表达了纯工况下轮胎的力特性,故成为“魔术公式”。
“魔术公式”表达如下:sin(arctan((arctan())))vhY y Sy D C Bx E Bx Bx x X S =+=--=+其中,Y 表示侧向力、纵向力或回正力矩,X 表示侧偏角a 或滑移率s 。
现以侧向力为例说明公式中各系数的意义。
式中D --峰值因子,表示曲线的最大值B C D ××--侧偏角趋于零时轮胎的侧偏刚度,曲线中表示原点的斜率E --曲线形态因子,决定曲线最大值附近的形状C --决定曲线的形状,即曲线是像侧向力、纵向力还是回正力矩h S --水平方向漂移v S --垂直方向漂移除C 外,“魔术公式”中的参数都是垂直载荷和侧倾角g 的函数。
以下为轮胎纵向动力学特性在MA TLAB中的具体实现212x z zD a F a F =+1.65x C=2678x zz E a F a F a =++5234()///za F x z z x x B a F a F e C D =+52342122678sin(arctan((arctan())))()///1.65zx x x x x x x a F x z z x xx xz zxzz F D C B E B B B a F a F e C D C D a F a F E a F a F a k k k =--=+==+=++sin(arctan((arctan())))(arctan((arctan())))cos(arctan((arctan())))x xx x x x x z zx x x x xxxxxxxzdF dD C B E B B dF dF d B E B B D C B E B B CdF k k k k k k k k k =--+----2(arctan((arctan())))(arctan())1((arctan()))1((arctan()))x x x x z x x x x x x xx x x x z z z d B E B B dF dB dE d B B B B E B E B B dFdF dF k k k k k k k k k k k --=----+--222(arctan())()11()1()xx xxxx zz x z x z d B B dB dB B dB dF dF B dF B dFk k k k k k k k -=-=++ 555522343422234345(()///)()///(()///)(()///)zzzza F a F xzzx x z z xxz zza F a F x z z x x z z x x zdBd a F a F eC D d a F a F eC D dF dF dF dD a F a F eC D a F a F eC D a dF ++==-+-+sin(arctan((arctan())))x x x x x x x F D C B E B B k k k =--22cos(arctan((arctan())))(())1()1((arctan())x xxxxxxxxxxxxx x x x B D C BE BB C B E B dF B d B E B B kkkk kk k k ----+=+--车辆防抱死制动系统的控制技术研究车辆防抱死制动系统的控制技术研究 东大,侯光钰,张为公东大,侯光钰,张为公2.3.1 H.B.Pacejka 的魔术公式的魔术公式Pacejka 的“魔术公式”是汽车操纵动力学研究中应用比较广泛的轮胎力学模型,它用特殊的正弦函数建立轮胎的纵向力、横向力和回正力矩的函数表达式。
车辆系统动力学-复习汇总

车轮滑动率 s 定义如下:
车轮的滑动率数值在0~1之间变化。当车轮作纯滚动时,即 uw=rd ω ,此时 s=0;当被 驱动轮处于纯滑动状态时,s=1。 8. 车轮滚动阻尼
9. 轮胎滚动阻力 当充气轮胎在理想路面(通常指平坦的干、硬路面)上直线滚动时,其外缘中心对 称面与车轮滚动方向一致,所受到的与滚动方向相反的阻力即为轮胎滚动阻力。轮胎滚 动阻力还可以进一步分解为弹性迟滞阻力、摩擦阻力和风扇效应力。 10. 轮胎侧偏角: (影响轮胎侧向力的一个重要因素)
车轮前束角 t 是车轮中心平面水平轴线与车轮行驶方向之间的夹角。 17. 车轮外倾角 车轮中心平面与路面垂线的夹角被称为车轮外倾角 。 18. 静刚度,动刚度 静载荷下抵抗变形的能力称为静刚度。动载荷下抵抗变形的能力称为动刚度。 19. 刷子模型 刷子模型是一个简化了的物理模型,它将轮胎看做是由连接在刚性基座(轮缘)上的一 系列可以伸缩变形的弹性刷毛所组成, 这些刷毛能起着承受垂向载荷以及产生轮胎纵向和侧 向力的作用。 20. 低选控制,高选控制 所谓低选控制就是对同一车轴两侧车轮同时施加制动压力控制, 大小由附着系数低的那 侧车轮来决定。 高选控制就是对同一车轴两侧车轮同时施加制动压力控制, 大小由附着系数 高的那侧车轮来决定。 21. 当量转动惯量 当量转动惯量 J 是指传动系统中与曲轴不同速旋转零部件的转动惯量换算成曲轴同速 旋转条件下的转动惯量。 22. 车辆平动质量 Mt 的当量转动惯量
dL0 M0 dt
3. 拉格朗日方程
d ET dt qi
ET FQi q i
i 1, 2, , n
式中, qi 为第 i 个质点的广义坐标; FQi 为对应于广义坐标 qi 的广义主动力; n 为系 统方程的阶数。 4. 轮胎的弹性迟滞阻力 充气轮胎在静态压缩作用下会产生变形并且回弹, 并由于其内部的摩擦作用而引起能量 损失。当车轮在力或力矩作用下滚动时,对轮胎胎面上的每一单元而言,其压缩与回弹的过 程将重复不断地进行。 当这些单元进入轮胎与路面的接触印迹时, 其弹簧和阻尼便能充分做 功,并生成附加的摩擦效应,称为弹性迟滞阻力。 5. 摩擦椭圆 “摩擦椭圆”表示了一系列给定滑移率或给定侧偏角情况下, (车辆转弯加速或转弯制 动联合工况)轮胎侧向力与纵向力的关系曲线。 6. 阿克曼转向理论 假定车辆转弯时,轮胎作无侧偏滚动,内外车轮转角必须不同。前轮转向的车辆在转向 时,其外侧车轮转向角 o 和内侧车轮转向角 i 应符合如下关系:
