新冠肺炎疫情相关的数学高考模拟题18
高三数学下学期防疫期间 停课不停学 网上考试试题三理 试题

HY 中学2021届高三数学下学期防疫期间“停课不停学〞网上考试试题〔三〕理创 作人:历恰面 日 期: 2020年1月1日第一卷〔选择题 一共60分〕一、选择题〔本大题一一共12小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.请把答案填涂在答题卡上.〕{}2|60,A x x x x Z =--<∈,{}1,1,2,3B =-,那么以下判断正确的选项是〔 〕A. 2A -∈B. A B ⊆C. {}1,1,2AB =- D.{}1,1,2A B ⋃=- 02θπ≤<,()21cos sin 2i i θθ+=+,那么θ的值是〔 〕A. 0B. 4πC.2π D. π3.如图,一个装饰物的正视图、侧视图都是边长为2,且有一个内角为60︒的菱形,俯视图是正方形,那么这个装饰物的体积为〔 〕A.833B.823C. 83D. 824.首项为1,公比为q 的等比数列{}n a 的前n 项和为n S , 那么“33S =〞是“2q =-〞的〔 〕 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件C 被两直线10x y --=,30x y +-=分成面积相等的四局部,且截x C 的方程是〔 〕 A. ()()222125x y -+-= B. ()()22215x y -+-= C. ()()222125x y +++=D. ()()22215x y +++=cos 1xy x x=++的局部图象大致为〔 〕 A. B. C. D.7.如下图,在ABC ∆中,23AE AC =,13BD BC =, BE 交AD 于点F ,假设AF AB AC λμ=+,那么2λμ+=〔 〕 A.67 B. 87C. 1621D. 2621()()3sin 3cos 0f x x x ωωω=+>,对任意的1x ,2x ,当()()1212f x f x =-时,12min2x x π-=,那么以下判断正确的选项是〔 〕 A. 16f π⎛⎫=⎪⎝⎭B. 函数()f x 在,62ππ⎛⎫⎪⎝⎭上递增 C. 函数()f x 的一条对称轴是76x π=D. 函数()f x 的一个对称中心是,03π⎛⎫ ⎪⎝⎭9.某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难一共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励假设干慧币〔一种网络虚拟币〕.该软件提供了三种奖励方案:第一种,每闯过一关奖励80慧币;第二种,闯过第一关奖励8慧币,以后每一关比前一关多奖励8慧币;第三种,闯过第一关奖励1慧币,以后每一关比前一关奖励翻一番〔即增加1倍〕.游戏规定:闯关者须于闯关前任选一种奖励方案.一名闯关者冲关数一定超过3关但不会超过9关,为了得到更多的慧币,他应如何选择奖励方案?答〔 〕 A 选择第一种奖励方案 B. 选择第二种奖励方案C. 选择第三种奖励方案D. 选择的奖励方案与其冲关数有关24y x =的焦点F 的直线交抛物线于()11,A x y ,()22,B x y 两点,那么4AF BF +的最小值为〔 〕 A. 4B. 8C. 9D. 12()()2224x x f x x x a e e --+=--+有唯一零点,那么a =〔 〕A. 12-B. -2C.12D. 2ABCD 的棱长为2,动点P 在以BC 为直径的球面上,那么AP AD ⋅的最大值为〔 〕A. 2B. C. 4D. 第二卷〔非选择题 一共90分〕二、填空题〔本大题一一共4小题,每一小题5分,一共20分.〕x ∈R ,向量()2,2a =-,()1,b x =,且a b ⊥,那么a b -=______ x ,y 满足约束条件204430x y y x x y -≥⎧⎪≥⎨⎪+-≥⎩,那么2z x y =+的最小值为______.C :()222210,0x y a b a b-=>>的左焦点为F ,过原点的直线与双曲线相交于A 、B 10AB,AF =cos ABF ∠=,那么双曲线C 的实轴长2a =______. {}n a 的通项公式为cos 2n n n a =,其前n 项和记为n S ,那么以下命题正确的选项是______.①数列{}n a 为递减数列; ②对任意正整数n ,1n S <都成立; ③对任意正整数(),m n m n >,12m n nS S ->都成立;④对任意正整数(),m n m n >,12m n nS S -<都成立. 三、解答题〔本大题一一共6小题,一共70分,解容许写出文字说明,证明过程或者演算步骤.〕〔一〕必考题:一共60分.()()23sin 22cos 1f x x x m x R =-++∈的最小值为-2.〔1〕务实数m 的值;〔2〕在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,假设()2f A =,5c =,1cos 7B =,求AC 的长.18.如图,正方体1111ABCD A B C D -,点E ,M ,N 分别是棱1CC ,11B C ,1BB 的中点,动点F 在线段MN 上运动. 〔1〕证明:1//A F 平面1D AE ;〔2〕求直线EF 与平面1D AE 所成角的正弦值的最大值.19.HY 的HY 报告明确指出要坚决打赢脱贫攻坚战,让贫困人口和贫困地区同全国一道进入全面小康社会,要发动全HY 全国全社会力量,坚持精准扶贫、精准脱贫,确保到2021年我国现行HY 下农村贫困人口实现脱贫.现有扶贫工作组到某山区贫困村施行脱贫工作.经摸底排查,该村现有贫困农户100户,他们均从事水果种植,2021年底该村平均每户年纯收入为1万元,扶贫工作组一方面请有关专家对水果进展品种改进,进步产量;另一方面,抽出局部农户从事水果包装、销售工作,其户数必须小于种植的户数.从2021年初开场,假设该村抽出4x 户〔x ∈Z ,112x ≤≤〕从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年进步20x,而从事包装销售农户的年纯收入每户平均为135x ⎛⎫-⎪⎝⎭万元.〔参考数据:31.12 1.404=,31.15 1.520=,31.18 1.643=,31.2 1.728=〕. 〔1〕至2021年底,该村每户年均纯收入能否到达1.32万元?假设能,恳求出从事包装、销售的户数;假设不能,请说明理由;〔2〕至2021年底,为使从事水果种植农户能实现脱贫〔即每户〔水果种植农户〕年均纯收入不低于1.6万元〕,至少要抽出多少户从事包装、销售工作?C :()22116x y ++=,过()1,0D 且与圆C 相切的动圆圆心为P .〔1〕求点P 的轨迹E 的方程;〔2〕过点C 的两直线1l 和2l 互相垂直,且直线1l 交曲线E 于Q ,S 两点,直线2l 交曲线E 于R ,T 两点〔Q ,R ,S ,T 为不同的四个点〕,求四边形QRST 的面积的最小值.()2ln f x ax ax x =--.〔1〕讨论()f x 的单调性;〔2〕假设()f x 有两个极值点1x ,2x ,求证:()()21123ln 24x f x x f x +>+.〔二〕选考题:一共10分.请考生在第22、23两题中任选一题答题.假如多做,那么按所做第一个题目计分.xOy 中,曲线C的参数方程为11212x t t y t t ⎧⎛⎫=+ ⎪⎪⎝⎭⎪⎨⎫⎪=-⎪⎪⎝⎭⎩〔t 为参数〕.以坐标原点O 为极点,x l 的极坐标方程为2cos sin 0m ρθρθ-+=.〔1〕求C 和l 的直角坐标方程; 〔2〕l 与C 相切,求m 的值.23.a ,b ,c 为正数,且满足1a b c ++=,证明: 〔1〕1119a b c++≥;〔2≤.一中高三年级防疫期间 “停课不停学〞网上考试〔三〕理科数学参考答案 第一卷〔选择题 一共60分〕一、选择题〔本大题一一共12小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的〕1. C 。
2024届甘肃省天水市甘谷一中高考模拟(二)数学试题

2024届甘肃省天水市甘谷一中高考模拟(二)数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.将函数sin 2y x =的图像向左平移(0)ϕϕ>个单位得到函数sin 26y x π⎛⎫=+ ⎪⎝⎭的图像,则ϕ的最小值为( ) A .6π B .12πC .1112πD .56π 2.执行如图所示的程序框图,则输出的S 的值是( )A .8B .32C .64D .1283.如图是函数sin()R,A 0,0,02y A x x πωφωφ⎛⎫=+∈>><< ⎪⎝⎭在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象,为了得到这个函数的图象,只需将sin (R)y x x =∈的图象上的所有的点( )A .向左平移3π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 B .向左平移3π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变C .向左平移6π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 D .向左平移6π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 4.已知等差数列{}n a 的公差为-2,前n 项和为n S ,若2a ,3a ,4a 为某三角形的三边长,且该三角形有一个内角为120︒,则n S 的最大值为( ) A .5B .11C .20D .255.自2019年12月以来,在湖北省武汉市发现多起病毒性肺炎病例,研究表明,该新型冠状病毒具有很强的传染性各级政府反应迅速,采取了有效的防控阻击措施,把疫情控制在最低范围之内.某社区按上级要求做好在鄂返乡人员体格检查登记,有3个不同的住户属在鄂返乡住户,负责该小区体格检查的社区诊所共有4名医生,现要求这4名医生都要分配出去,且每个住户家里都要有医生去检查登记,则不同的分配方案共有( ) A .12种B .24种C .36种D .72种6.已知平面ABCD ⊥平面,,ADEF AB AD CD AD ⊥⊥,且3,6,AB AD CD ADEF ===是正方形,在正方形ADEF 内部有一点M ,满足,MB MC 与平面ADEF 所成的角相等,则点M 的轨迹长度为( )A .43B .16C .43π D .8π7.若()f x 是定义域为R 的奇函数,且()()2f x f x +=-,则 A .()f x 的值域为RB .()f x 为周期函数,且6为其一个周期C .()f x 的图像关于2x =对称D .函数()f x 的零点有无穷多个8.若2m >2n >1,则( ) A .11m n> B .πm ﹣n >1 C .ln (m ﹣n )>0 D .1122log m log n >9.已知全集,,则( )A .B .C .D .10.定义在R 上的函数()f x 满足()()2log 10()50x x f x f x x ⎧-≤⎪=⎨->⎪⎩,则()2019f =() A .-1B .0C .1D .211.已知函数()22cos sin 4f x x x π⎛⎫=++⎪⎝⎭,则()f x 的最小值为( ) A .212+B .12C .212-D .214-12.已知集合M ={y |y =,x >0},N ={x |y =lg (2x -)},则M∩N 为( ) A .(1,+∞)B .(1,2)C .[2,+∞)D .[1,+∞)二、填空题:本题共4小题,每小题5分,共20分。
2024高中数学高考高频考点经典题型模拟卷 (323)

一、单选题1.已知函数的一个零点是,当时函数取最大值,则当取最小值时,函数在上的最大值为( )A.B.C.D .02. 豆腐发酵后表面长出一层白绒绒的长毛就成了毛豆腐,将三角形豆腐ABC 悬空挂在发酵空间内,记发酵后毛豆腐所构成的几何体为T .若忽略三角形豆腐的厚度,设,点在内部.假设对于任意点,满足的点都在内,且对于内任意一点,都存在点,满足,则的体积为( )A.B.C.D.3. 已知实数a ,b均为正数,且满足,那么的最小值为( )A .1B .e C.D.4. 已知函数的值域为,则实数的取值范围是( )A.B.C.D.5. 已知双曲线与椭圆.过椭圆上一点作椭圆的切线l ,l 与x 轴交于M 点,l 与双曲线C 的两条渐近线分别交于N 、Q ,且N 为MQ 的中点,则双曲线C 的离心率为( )A.B.C.D.6.猜灯谜是中国元宵节特色活动之一.已知甲、乙、丙三名同学同时猜一个灯谜,每人猜对的概率均为,并且每人是否猜对相互独立在三人中至少有两人猜对的条件下,甲猜对的概率为( )A.B.C.D.7. 函数的大致图象为( )A.B.C.D.8. 已知函数的部分图象如图所示,其中.在已知的条件下,则下列选项中可以确定其值的量为()2024高中数学高考高频考点经典题型模拟卷二、多选题A .B.C.D.9. 下列推断错误的个数是①命题“若,则”的逆否命题为“若则”②命题“若,则”的否命题为:若“,则”③“”是“”的充分不必要条件④命题“,使得”的否定是:“,均有”.A .1B .2C .3D .410. 命题p :“∀x ∈(-∞,0),3x ≥4x ”的否定¬p 为( )A .,B .,C.D.11.把函数的图象向左平移个单位,再向上平移2个单位,得到的函数是( )A.B.C.D.12.若,,,则是( )A.B.C.D.13.已知、分别是双曲线:(,)的左、右焦点,且,若是该双曲线右支上一点,且满足,则面积的最大值是( )A.B.C.D.14. 已知,,,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件15. 已知,,则的值为( )A.B.C.D.16. 甲、乙,丙、丁,戊5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,裁判说:“很遗憾,你俩都没有得到冠军.但都不是最差的.”从回答分析,5人的名次排列的不同情况可能有( )A .27种B .72种C .36种D .54种17. 已知双曲线的左、右焦点分别为,,O 为双曲线的中心,为双曲线的右顶点,P 是双曲线右支上的点,与的角平分线的交点为I ,过作直线的垂线,垂足为B ,设双曲线C 的离心率为e,若,,则( )A.B.C.D.18. 在三棱锥中,,,是棱的中点,是棱上一点,,平面,则( )A .平面B .平面平面C.点到底面的距离为2D .二面角的正弦值为2024高中数学高考高频考点经典题型模拟卷三、填空题19. 下列说法正确的是( )A .用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体m 被抽到的概率是0.1B .已知一组数据1,2,3,3,4,5的众数等于中位数C .数据27,12,14,30,15,17,19,23的第70百分位数是21D .若一个样本容量为8的样本的平均数为5,方差为2.现样本中又加入一个新数据5,此时样本容量为9,平均数不变,方差为变小20. 在正方体中,,点满足,.下列结论正确的有( )A .直线与一定为异面直线B.直线与平面所成角正弦值为C.四面体的体积恒定且为2D .当时,的最小值为21. 下列说法正确的是( )A.B.集合C.函数的值域为D.在定义域内单调递增22. 已知是函数图像的一个最高点,B ,C 是与P 相邻的两个最低点.若△PBC 为等边三角形,则下列说法正确的是( )A.B.的最小正周期为8C.D.将图像上所有的点向右平移1个单位长度后得到的图像,是图像的一个对称中心23. 已知Р是圆上的动点,直线与交于点Q ,则( )A.B .直线与圆O 相切C .直线与圆O截得弦长为D.长最大值为24. 已知函数相邻对称中心之间的距离为,则下列结论正确的是( )A.图象的对称轴方程为B .在上单调递减C.将的图象向右平移个单位得到的图象D .若在上的值域为,则25. 如图,在四面体中,,,两两垂直,,以为球心,为半径作球,则该球的球面与四面体各面交线的长度和为___.四、解答题五、解答题26.若直线与圆相交于两点,且,则实数的值为________.27. 已知向量,,若,则______.28.矩形满足,点分别在射线上运动,为直角,当到点的距离最大时,的大小为__________.29.函数的最大值为________.30. 设锐角三角形的内角,,所对的边分别为,,,且,则的取值范围是______.31.已知抛物线经过第二象限,且其焦点到准线的距离大于4,请写出一个满足条件的的标准方程__________.32.已知在三棱锥中,是面积为的正三角形,平面平面,若三棱锥的外接球的表面积为,则三棱锥体积的最大值为______.33. (1)已知角终边上一点,求的值;(2)化简求值:34. 已知向量,(,),令().(1)化简,并求当时方程的解集;(2)已知集合,是函数与定义域的交集且不是空集,判断元素与集合的关系,说明理由.35. 化简或求值:(1);(2).36.已知函数(Ⅰ)将函数化简成的形式,并指出的周期;(Ⅱ)求函数上的最大值和最小值37.设,化简:.38.已知数列的前顶和为.且.(1)求数列的通项公式;(2)在数列中,,求数列的前项和.39. 某数学小组从医院和气象局获得今年1月至6月份每月20日的昼夜温差和患感冒人数人的数据,画出折线图.由折线图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;建立y关于x的回归方程精确到,预测昼夜温差为时患感冒的人数精确到整数.参考数据:,,,.参考公式:相关系数:,回归直线方程是,,40. 画出函数的图象,并写出该函数的单调区间与值域41. 如图,是底部不可到达的一个塔型建筑物,为塔的最高点.现需在塔对岸测出塔高,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底在同一水平面内的一条基线,使不在同一条直线上,测出及的大小(分别用表示测得的数据)以及间的距离(用表示测得的数据),另外需在点测得塔顶的仰角(用表示测量的数据),就可以求得塔高.乙同学的方法是:选一条水平基线,使三点在同一条直线上.在处分别测得塔顶的仰角(分别用表示测得的数据)以及间的距离(用表示测得的数据),就可以求得塔高.请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时按顺时针方向标注,按从左到右的方向标注;③求塔高.42. 随着全球经济一体化进程的不断加快,机械零件的加工质量决定了制造工厂的生存,零件加工精度逐渐成为供应商判断制造公司产品的标准.已知某公司生产不同规格的一种产品,根据检测精度的标准,其合格产品的质量y()与尺寸x()之间近似满足关系式(b,c为大于0的常数).现随机从中抽取6件合格产品,测得数据如下:尺寸x(〕384858687888质量y(〕16.818.820.722.42425.5根据测得数据作出如下处理:令,得相关统计量的值如下表:75.324.618.3101.4(1)根据所给统计数据,求y关于x的回归方程;(2)若从一批该产品中抽取n件进行检测,已知检测结果的误差满足,求至少需要抽取多少件该产品,才能使误差在(-0.1,0.1)的概率不少于0.9545?附:①对于样本,i)(i=1,2,…,n),其回归直线的斜率和截距的最小二乘估计公式分别为:,,.②,则43. 为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取100名学生,将他们的竞赛成绩(满分为100分)分为6组:,,,,,,得到如图所示的频率分布直方图.(1)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表),并估计这100名学生成绩的中位数(精确到0.01);(2)在抽取的100名学生中,规定:竞赛成绩不低于80分为“优秀”,竞赛成绩低于80分为“非优秀”.①请将下面的列联表补充完整,并判断是否有99%的把握认为“竞赛成绩是否优秀与性别有关”?②求出等高条形图需要的数据,并画出等高条形图(按图中“优秀”和“非优秀”所对应阴影线画),利用条形图判断竞赛成绩优秀与性别是否有关系?列联表优秀非优秀合计男生10女生50合计100六、解答题参考公式及数据:,,0.100.050.0250.0100.0050.0012.7063.841 5.024 6.6357.87910.82844. 设某幼苗从观察之日起,第天的高度为,测得的一些数据如下表所示:第天高度作出这组数据的散点图发现:与(天)之间近似满足关系式,其中,均为大于0的常数.(1)试借助一元线性回归模型,根据所给数据,用最小二乘法对,作出估计,并求出关于的经验回归方程;(2)在作出的这组数据的散点图中,甲同学随机圈取了其中的3个点,记这3个点中幼苗的高度大于的点的个数为,其中为表格中所给的幼苗高度的平均数,试求随机变量的分布列和数学期望.附:对于一组数据,,…,,其回归直线方程的斜率和截距的最小二乘估计分别为,.45. 已知数列是等比数列,,且成等差数列.数列满足:.(1)求数列和的通项公式;(2)求证:.46. 已知函数.(1)讨论函数的单调性:(2)若,求证:.47.如图,在多面体中,四边形与均为直角梯形,平面平面,,,,..(1)已知点为的中点,求证:平面;(2)求多面体的体积.七、解答题48. 在四棱锥中,底面是正方形,若.(1)证明:平面平面;(2)求二面角的平面角的余弦值.49.设函数.(1)求函数的单调区间;(2)若函数有两个极值点且,求证.50. 已知椭圆经过两点.(1)求椭圆C 的方程和离心率;(2)设P ,Q 为椭圆C 上不同的两个点,直线AP 与y 轴交于点E ,直线AQ 与y 轴交于点F ,若点满足,求证:P ,O ,Q 三点共线.51. 某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y (元)与生产该产品的数量x (千件)有关,经统计得到如下数据:x 12345678y1126144.53530.5282524根据以上数据,绘制了散点图.观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合,(反比例函数模型可用转化为线性回归模型;指数函数模型可转化为和x 的线性回归模型)现已求得:用指数函数模型拟合的回归方程为,与x 的相关系数;(1)用反比例函数模型求y 关于x 的回归方程;(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本.参考数据:,,,,,,(其中,参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘法估计分别为:,相关系数52. “低碳经济”是促进社会可持续发展的推进器,某企业现有100万元资金可用于投资,如果投资“传统型”经济项目,一年后可能获利20%,可能损失10%,也可能不赔不赚,这三种情况发生的概率分别为,,;如果投资“低碳型”经济项目,一年后可能获利30%,也可能损失20%,这两种情况发生的概率分别为a和b(其中a+b=1).(1)如果把100万元投资“传统型”经济项目,用ξ表示投资收益(投资收益=回收资金投资资金),求ξ的概率分布及均值(数学期望);(2)如果把100万元投资“低碳型”经济项目,预测其投资收益均值会不低于投资“传统型”经济项目的投资收益均值,求a的取值范围.53. 某学校组织“消防”知识竞赛,有A,B两类题目.每位参加比赛的同学先在两类题目中选择一类并从中随机抽取一道题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得40分,否则得0分;B类问题中的每个问题回答正确得60分,否则得0分已知小明能正确回答A类问题的概率为0.7,能正确回答B类问题的概率为0.5,且能正确回答问题的概率与回答次序无关(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.54. 年初,新冠肺炎疫情暴发,全国中小学生响应教育部关于“停课不停学”居家学习的号召.因此,网上教学授课在全国范围内展开,为了解线上教学效果,根据学情要对线上教学方法进行调整,从而使大幅度地提高教学效率.近期某市组织高一年级全体学生参加了某项技能操作比赛,等级分为至分,随机调阅了、校名学生的成绩,得到样本数据如下:成绩(分)人数(个)校样本数据统计图(1)计算两校样本数据的均值和方差,并根据所得数据进行比较;(2)从校样本数据成绩分别为分、分和分的学生中按分层抽样的方法抽取人,从抽取的人中任选人参加更高一级的比赛,求这人成绩之和不小于的概率.55. 如图是游乐场中一款抽奖游戏机的示意图,玩家投入一枚游戏币后,机器从上方随机放下一颗半径适当的小球,小球沿着缝隙下落,最后落入这6个区域中.假设小球从最上层4个缝隙落下的概率都相同,且下落过程中遇到障碍物会等可能地从左边或右边继续下落.(1)分别求小球落入和的概率;(2)已知游戏币售价为2元/枚.若小球落入和,则本次游戏中三等奖,小球落入和,则本次游戏中二等奖,小球落入和,则本次游戏中一等奖.假设给玩家准备的一、二、三等奖奖品的成本价格之比为,若要使玩家平均每玩一次该游戏,商家至少获利0.7元,那么三等奖奖品的成本价格最多为多少元?八、解答题56. 2022年第22届世界杯足球赛在卡塔尔举行,这是继韩日世界杯之后时隔20年第二次在亚洲举行的世界杯足球赛,本届世界杯还是首次在北半球冬季举行的世界杯足球赛.每届世界杯共32支球队参加,进行64场比赛,其中小组赛阶段共分为8个小组,每个小组的4支队伍进行单循环比赛共计48场,以积分的方式产生16强,之后的比赛均为淘汰赛,1/8决赛8场产生8强,1/4决赛4场产生4强,半决赛两场产生2强,三四名决赛一场,冠亚军决赛一场.下表是某五届世界杯32进16的情况统计:欧洲球队美洲球队非洲球队亚洲球队32强16强32强16强32强16强32强16强1131094515121310105514031361085240414108550515138835263合计66444525256245(1)根据上述表格完成列联表:16强非16强合计欧洲地区其他地区合计并判断是否有95%的把握认为球队进入世界杯16强与来自欧洲地区有关?(2)淘汰赛阶段全场比赛90分钟内进球多的球队获胜,如果参赛双方在90分钟内无法决出胜负,将进行30分钟的加时赛.加时赛阶段,如果两队仍未分出胜负,则通过点球决出胜负.若每支球队90分钟比赛中胜,负,平的概率均为,加时赛阶段胜,负,平的概率也均为,并且各阶段比赛相互独立.设半决赛中进行点球比赛的场次为,求的分布列及期望.附:,0.0500.0100.0013.8416.63510.82857. 已知函数.(1)若在上为增函数,求实数的取值范围;(2)若在上最小值为,求实数的值;(3)若在上只有一个零点,求实数的取值范围.58. 学生总人数为3000的某中学组织阳光体育活动,提倡学生每天运动1小时,教育管理部门到该校抽查200名学生,统计一个星期的运动时间,得到下面的统计表格.一周运动时间/分钟频数10203050503010(1)如果某名学生一个星期的运动时间超过500分钟,则称该学生为“运动达人”,用样本估计总体,该校的“运动达人”有多少人?(2)依据上面的数据,完成下面的样本频率分布直方图.(3)依据频率分布直方图估计该校学生一个星期运动时间的中位数.59. 已知椭圆的两个焦点分别为,且经过点.(1)求椭圆的标准方程;(2)直线过点,且与相交于两点,线段的中点为(异于坐标原点),延长与交于点若四边形为平行四边形,求直线的方程.60. 已知数列其前项和,其中正数为一常数,且.(1)求;(2)求数列的前项和.61. 设函数.(1)若曲线在点处的切线与x 轴平行,求;(2)若在处取得极小值,求的取值范围;(3)若存在最小值,写出的取值范围(不要求说明理由).62.已知,求的最小值.甲、乙两位同学的解答过程分别如下:甲同学的解答:因为,所以.上式中等号成立当且仅当,即,解得(舍).当时,. 所以当时,的最小值为2.乙同学的解答:因为,所以.上式中等号成立当且仅当,即,解得(舍).所以当时,的最小值为.以上两位同学写出的结论一个正确,另一个错误.请先指出哪位同学的结论错误,然后再指出该同学解答过程中的错误之处,并说明错误的原因.2024高中数学高考高频考点经典题型模拟卷2024高中数学高考高频考点经典题型模拟卷。
新冠肺炎疫情相关的数学高考模拟题23

新冠肺炎疫情相关的数学高考模拟题231、解答:(1) 由题意可得,被传染的概率是2/5,不被传染的概率是3/5,X 的可能取值是0,1,2,3 则1252753)0(3=⎪⎭⎫ ⎝⎛==X P , 125545253C )1(1213=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==X P 125365253C )2(2123=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==X P , 125852C )3(333=⎪⎭⎫ ⎝⎛==X P X 01 2 3 P27/125 54/125 36/125 8/125 E (X )=5612583125362125541125270=⨯+⨯+⨯+⨯(1)由题意可得 E 1ζ=200,2ζ的可能取值为1,201()200299.01==ζP ,()200299.01120-==ζP所以()174.299.0200201)99.01(20199.012002002002≈⨯-=-⨯+⨯=ζE200174.2< 即()()12ζζE E <所以,应采用混合检测。
2、解:(1)3.17, 由于, 故没有的把握认为“长潜伏期”与年龄有关; (2) (i) 若潜伏期,由, 得知潜伏期超过天的概率很低, 因此隔离天是合理的. (ii) 由于个病例中有个属于长潜伏期,若以样本频率估计概率,一个患者属于“长潜伏期”的概率是,于是则当时,当时,;所以, .故当时,取得最大值.疫情,妈妈眼中儿子的改变近段时间学校让每人上交一篇关于疫情期间的所感所闻,以最能打动你内心为主题。
我犹豫了半天,我写什么呢?由于疫情期间,一直呆在家中,除了每天看新闻接触医护人员和红马甲的社区志愿者之外,身边接触最多的是家人。
疫情对人的影响是方方面面的,没有人可以置身事外。
我这几天在想,疫情给孩子带来什么?我就谈谈我最亲爱的儿子吧。
记得不能下楼的最初两三天,你很开心,因为不需要再按照统一的计划过假期了,再加上不能下楼,就觉得每天在家的时间远远超于24小时。
2022届高三数学新时代NT抗疫爱心卷 文(含解析)

【答案】A
【解析】
【分析】
根据题意得到 ,得到 ,得到离心率
【详解】椭圆 的半焦距 ,
双曲线 的半焦距 ,
由题意可得 ,即 ,
∴椭圆的离心率为 .
应选:A.
【点睛】此题考查了椭圆离心率,双曲线焦点,意在考查学生的计算能力和转化能力.
7.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,那么该几何体的体积为〔 〕
2021届高三数学新时代NT抗疫爱心卷 文〔含解析〕
考前须知:1.本试卷分第一卷〔选择题〕和第二卷〔非选择题〕两局部.
2.考试时间为120分钟,总分值150分.
3.答题前,考生务必将自己的姓名、准考证号填写在答题卡相应的位置.
4.全部答案在答题卡上完成,答在本试卷上无效.
第一卷〔选择题 共60分〕
一、选择题:此题共12小题,每题5分,共计60分.在每题给出的四个选项中,只有一个选项正确.
有 、 、 、 、 、 、 、 、 、 ,共10种情况,
其中至少有1人学习积极性不高的有 、 、 、 、 、 、 、 、 ,共9种情况,
至少有1人学习积极性不高的概率 .
【点睛】此题考查了列联表,独立性检验,概率的计算,意在考查学生的计算能力和应用能力.
20.椭圆 ,点 、 、 在椭圆上,直线 与直线 的斜率之积 .
代入验证知 错误.
应选:D.
【点睛】此题考查了正切函数的对称中心,意在考查学生的计算能力.
4.根据党中央关于“精准〞脱贫的要求,某市农业经济部门派三位专家对 、 、 三个县区进行调研,每个县区派一位专家,那么甲专家恰好派遣至 县区的概率为〔 〕
A. B. C. D.
【答案】B
天津市南开中学2023届高三高考模拟数学试题
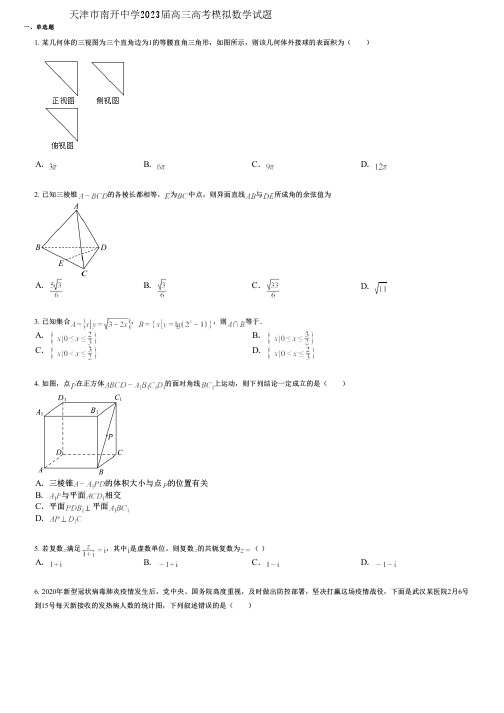
一、单选题1. 某几何体的三视图为三个直角边为1的等腰直角三角形,如图所示,则该几何体外接球的表面积为()A.B.C.D.2. 已知三棱锥的各棱长都相等,为中点,则异面直线与所成角的余弦值为A.B.C.D.3.已知集合,,则等于.A.B.C.D.4. 如图,点在正方体的面对角线上运动,则下列结论一定成立的是()A .三棱锥的体积大小与点的位置有关B.与平面相交C .平面平面D.5. 若复数满足,其中是虚数单位,则复数的共轭复数为( )A.B.C.D.6. 2020年新型冠状病毒肺炎疫情发生后,党中央、国务院高度重视,及时做出防控部署,坚决打赢这场疫情战役,下面是武汉某医院2月6号到15号每天新接收的发热病人数的统计图,下列叙述错误的是( )天津市南开中学2023届高三高考模拟数学试题A.从8号到10号,每天新接收的发热病人数逐渐增加B.这10天中每天新接收的发热病人数的平均数是49.3C.从这10天中随机选一天,这一天新接收的发热病人数小于35的概率是D.这10天中每天新接收的发热病人数的中位数是457. 若,且,则下列不等式成立的是( )A.B.C.D.8. 设,,则()A.B.C.D.9. 将函数的图象向右平移个单位长度得到函数的图象,下列结论正确的是()A.是最小正周期为的偶函数B.是最小正周期为的奇函数C .)在上单调递减D.在上的最大值为10. 已知正实数,,满足,,,则,,之间的大小关系为()A.B.C.D.11. 设函数的零点,函数的零点,其中,,若过点作圆的切线,则的方程为()A.B.C.D.,12. 图1中,正方体的每条棱与正八面体(八个面均为正三角形)的条棱垂直且互相平分.将该正方体的顶点与正八面体的顶点连结,得到图2的十二面体,该十二面体能独立密铺三维空间.若,则点M到直线的距离等于()A.B.C.D.13.设函数的最小正周期为.且过点.则下列说法正确的是()A.B .在上单调递增二、多选题C.的图象关于点对称D .把函数向右平移个单位得到的解析式是14.设复数,则( )A.B .4C.D .215.设函数,若在上有且仅有5个零点,则的取值范围为( )A.B.C.D.16.如图,在三棱柱中,底面ABC ,,点D是棱上的点,,若截面分这个棱柱为两部分,则这两部分的体积比为()A .1:2B .4:5C .4:9D .5:717. 已知向量,则( )A.B.C.D.18.如图,在正方体中,点是的中点,点是直线上的动点,则下列说法正确的是()A .是直角三角形B .异面直线与所成的角为C .当的长度为定值时,三棱锥的体积为定值D .平面平面19. 已知,,且,则下列判断正确的是( )A.的最小值为12B.的最小值为C .若不等式恒成立,则D.的最大值为820.设函数,则下列说法正确的是( )A.函数的图象可由的图象伸缩平移变换得到B .直线为函数的图象的对称轴C.函数的图象的对称中心是,三、填空题D.函数的单调递增区间是,21. 已知直线与曲线相切,则下列直线中可能与垂直的是( )A.B.C.D.22. 已知函数的定义域为R ,且为奇函数,为偶函数,且对任意的,且,都有,则下列结论正确的为( )A.是偶函数B.C.的图象关于对称D.23. 饮料瓶的主要成分是聚对苯二甲酸乙二醇酯,简称“PET ”.随着垃圾分类和可持续理念的普及,饮料瓶作为可回收材料的“主力军”之一,得以高效回收,获得循环再生,对于可持续发展具有重要意义.温州某高中随机调查了该校某两个班(A 班,B 班)4月份每天产生饮料瓶的数目(单位:个),并按,,,,,分组,分别得到频率分布直方图如下:下列说法正确的是()A.B .A 班该月平均每天产生的饮料瓶比B 班更多C .若A 班和B 班4月产生饮料瓶数的第75百分位数分别是和,则D .已知该校共有学生2000人,则约有400人4月份产生饮料瓶数在之间24.已知函数,则( )A.的图象关于直线轴对称B.的图象关于点中心对称C.的所有零点为D .是以为周期的函数25. 2021年9月17日,搭载着3名英航天员的神舟十二号载人飞船返回舱成功着陆于东风着陆场,标志着神舟十二号返回任务取得圆满成功.假设返回舱D 是垂直下落于点C,某时刻地面上点观测点观测到点D 的仰角分别为,若间距离为10千米(其中向量与同向),试估算该时刻返回舱距离地面的距离约为___________千米(结果保留整数,参考数据:).26. 若对任意正实数,不等式恒成立,则实数的最小值为________________.27. 把正整数按如下规律排列:1,2,2,3,3,3,4,4,4,4,5,……,构成数列,则__________.28.记函数的图象为,作关于直线的对称曲线得到,则曲线上任意一点与曲线上任意一点之间距离的最小值为__________.29. 已知,为单位向量,,且,则________.四、解答题五、解答题30. 直线与圆交,两点,若为等边三角形,则的值为______.31. 我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列就是二阶等差数列,数列的前3项和是________.32. 设表示不超过的最大整数,如,,则________.33.在数列中,,且.(1)求的通项公式;(2)若,数列的前项和为,求34. 如图,两射线、均与直线l 垂直,垂足分别为D 、E 且.点A 在直线l 上,点B 、C 在射线上.(1)若F 为线段BC 的中点(未画出),求的最小值;(2)若为等边三角形,求面积的范围.35.已知(1)求的值;(2)若是第三象限的角,化简三角式,并求值.36.已知数列满足.(1)求数列的通项公式;(2)求数列的前项和.37. (1)求值:;(2)已知,求的值.38. 我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.”事实上,很多代数问题可以转化为几何问题加以解决,已知曲线C上任意一点满足.(1)化简曲线的方程;(2)已知圆(为坐标原点),直线经过点且与圆相切,过点A 作直线的垂线,交于两点,求面积的最小值.39. 中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在内的频数为3.(1)求的值;(2)已知抽取的名参赛人员中,成绩在和女士人数都为2人,现从成绩在和的抽取的人员中各随机抽取2人,记这4人中女士的人数为,求的分布列与数学期望.40. 已知函数,其中[x]表示不超过的最大整数,例如(1)将的解析式写成分段函数的形式;(2)请在如图所示的平面直角坐标系中作出函数的图象;(3)根据图象写出函数的值域.41. 如图所示,在三棱锥A-BCD中,E,F分别是AD,BC的中点,且.(1)在∠BDC的角平分线上,是否存在一点O,使得AO∥平面EFC?若存在,请作出证明;若不存在,请说明理由;(2)若平面BCD⊥平面ADC,BD⊥DC,,求二面角F-EC-D的正切值.42. 如图,正方体的棱长为,为棱的中点.(1)画出过点且与直线垂直的平面,标出该平面与正方体各个面的交线(不必说明画法及理由);(2)求点到该平面的距离.43. 一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长与身高进行测量,得到数据(单位均为)作为样本如下表所示.20212223242526272829脚掌长(x)六、解答题身高(y )141146154160169176181188197203(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程;(2)若某人的脚掌长为,试估计此人的身高;(3)在样本中,从身高180cm 以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm 以上的概率.(参考数据:,,,)44. 某小型学院对所有入学新生进行了数学摸底考试,如果学生得分在35分以下,则不能进入正常数学班学习,必须进补习班补习,10名进入正常数学班的学生的摸底考试成绩和学期末考试成绩如下:摸底成绩50354055806065359050期末成绩53515668877146317968并计算得:(1)画出散点图;(2)建立一个回归方程,用摸底考试成绩来预测期末考试成绩(精确到0.1);(3)如果期末考试60分是某课程结业的最低标准,预测摸底考试成绩低于多少分学生将不能获得某课程结业.(附:)45. 如图,四棱柱中,平面平面,底面为菱形,与交于点O ,.(1)求证:平面;(2)线段上是否存在点F ,使得与平面所成角的正弦值是?若存在,求出;若不存在,说明理由.46. 如图,在四棱锥中,底面为直角梯形,,,平面底面,,,.(1)求证:;(2)求点到平面的距离.47. 如图,在五面体中,已知平面,,为正三角形,且.(1)求证:平面平面;(2)求二面角的余弦值.48. 如图,在多面体中,平面平面,平面,和均为正三角形,,,点为线段上一点.(1)求证:平面;(2)若与平面所成角为,求平面与平面所成角的余弦值.49. 如图,在长方体中,,,点是线段中点.(1)求证:;(2)求点到平面的距离.50. 如图,在四棱锥中,,平面平面,设平面与平面的交线为.七、解答题(1)证明:平面平面;(2)已知.若直线与直线所成的角为,求直线与平面所成角的正弦值.51. 某运动产品公司生产了一款足球,按行业标准这款足球产品可分为一级正品、二级正品、次品共三个等级.根据该公司测算:生产出一个一级正品可获利100元,一个二级正品可获利50元,一个次品亏损80元.该运动产品公司试生产这款足球产品2000个,并统计了这些产品的等级,如下表:等级一级正品二级正品次品频数1000800200(1)求这2000个产品的平均利润是多少;(2)该运动产品公司为了解人们对这款足球产品的满意度,随机调查了100名男性和100名女性,每位对这款足球产品给出满意或不满意的评价,得到下面的列联表:满意不满意总计男性3268100女性6139100总计93107200问:能否在犯错误的概率不超过0.001的前提下认为男性和女性对这款足球产品的评价有差异?附:,其中.0.100.050.0250.0100.0050.0012.7063.8415.0246.6357.87910.82852. 为了增强学生体质,茂名某中学的体育部计划开展乒乓球比赛,为了解学生对乒乓球运动的兴趣,从该校一年级学生中随机抽取了200人进行调查,男女人数相同,其中女生对乒乓球运动有兴趣的占80%,而男生有15人表示对乒乓球运动没有兴趣.(1)完成2×2列联表,并回答能否有90%的把握认为“对乒乓球运动是否有兴趣与性别有关”?有兴趣没兴趣合计男女合计(2)为了提高同学们对比赛的参与度,比赛分两个阶段进行.第一阶段的比赛赛制采取单循环方式,每场比赛采取三局二胜制,然后由积分的多少选出进入第二阶段比赛的同学,每场积分规则如下:比赛中以取胜的同学积3分,负的同学积0分;以取胜的同学积2分,负的同学积1分.其中,小强同学和小明同学的比赛倍受关注,设每局小强同学取胜的概率为,记小强同学所得积分为, 求的分布列和期望.附表:P (K 2≥k 0)0.500.400.250.1500.1000.050k 00.4550.7801.3232.0722.7063.84153. 根据中国造纸协会统计数据显示,2014年以来,我国纸及纸板生产量整体呈现震荡上行趋势,增速保持在低位运行.如图是2014~2020年八、解答题中国纸及纸板生产量统计图.(1)试计算2014~2020年中国纸及纸板生产量的平均值、中位数与极差(平均值结果保留两位小数);(2)2018年,行业景气度下滑,中国纸及纸板生产量小幅下滑,试计算2014~2017年、2018~2020年两个时间段中国纸及纸板生产量的平均值的大小,并比较这两个时间段中国纸及纸板生产量的方差的大小.54. 8年来,某地第年的第三产业生产总值(单位:百万元)统计图表如下图所示,根据该图提供的信息解决下列问题.(1)在所统计的8个生产总值中任取2个,记其中不低于平均值的个数为,求的分布列和数学期望;(2)由统计图表可看出,从第5年开始,该地第三产业生产总值呈直线上升趋势,试用线性回归模型预测该地第10年的第三产业生产总值.(参考公式:,)55. 某学校组织“一带一路”知识竞赛,有A ,B 两类问题,每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A 类问题中的每个问题回答正确得20分,否则得0分;B 类问题中的每个问题回答正确得80分,否则得0分,已知小明能正确回答A 类问题的概率为0.8,能正确回答B 类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.(1)若小明先回答A 类问题,记为小明的累计得分,求的分布列;(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.56. 在二十大报告中,体育、健康等关键词被多次提及,促进群众体育和竞技体育全面发展,加快建设体育强国是全面建设社会主义现代化国家的一个重要目标.某校为丰富学生的课外活动,加强学生体质健康,拟举行羽毛球团体赛,赛制采取局胜制,每局都是单打模式,每队有名队员,比赛中每个队员至多上场一次且是否上场是随机的,每局比赛结果互不影响.经过小组赛后,最终甲、乙两队进入最后的决赛,根据前期比赛的数据统计,甲队种子选手对乙队每名队员的胜率均为,甲队其余名队员对乙队每名队员的胜率均为.(注:比赛结果没有平局)(1)求甲队最终获胜且种子选手上场的概率;(2)已知甲队获得最终胜利,求种子选手上场的概率.57.设函数,.(1)若,,求函数的单调区间;(2)若曲线在点处的切线与直线平行.①求,的值;②求实数的取值范围,使得对恒成立.58. 已知函数(1)当时,①求曲线的单调区间和极值;②求曲线在点处的切线方程;(2)若函数有两个不同的零点,求实数的取值范围.59. 已知椭圆:上的点到左焦点的最大距离是,且点在椭圆上,其中为椭圆的离心率.(1)求椭圆的方程;(2)如图所示,是椭圆上的两点,且,求面积的取值范围.60. 如图,平面平面ABC,,,D分别为PA的中点,,.(1)设平面平面,若直线,证明:O为AC中点;(2)在(1)的条件下,求点P到平面BOD的距离.61. 一机械制造加工厂的某条生产线设备在正常运行的情况下,生产的零件尺寸z(单位:)服从正态分布,且.(1)求的概率;(2)若从该条生产线上随机选取2个零件,设X表示零件尺寸小于的零件个数,求X的分布列与数学期望.62. 如图,四棱锥P-ABCD的底面为梯形,底面ABCD,,,,E为PA的中点.(1)证明:平面平面BCE;(2)若二面角P-BC-E的余弦值为,求三棱锥P-BCE的体积.。
广东省珠海市2024高三冲刺(高考数学)部编版真题(预测卷)完整试卷

广东省珠海市2024高三冲刺(高考数学)部编版真题(预测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知,,,其中e为自然对数的底数,则()A.B.C.D.第(2)题在高三某次模拟考试中,甲、乙两个班级的数学成绩统计如下表:班级人数平均分数方差甲40705乙60808则两个班所有学生的数学成绩的方差为()A.B.13C.D.第(3)题复数的虚部是()A.1012B.1011C.D.第(4)题命题“”的否定是()A.B.C.D.第(5)题为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如图所示,根据该图可得这100名学生中体重在的学生人数是()A.20B.30C.40D.50第(6)题已知,则()A.B.C.D.第(7)题已知e是自然对数的底数,则下列不等关系中正确的是()A.B.C.D.第(8)题已知集合,,则等于()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题下列命题中是真命题的有()A.函数在其定义域上为减函数B.若随机变量服从正态分布,且,,则C.若,则D.若为等比数列,则,,,仍为等比数列第(2)题某市有A,B,C,D四个景点,一位游客来该市游览,已知该游客游览A的概率为,游览B,C,D的概率都是,且该游客是否游览这四个景点相互独立.用随机变量X表示该游客游览景点的个数,下列说法正确的是()A.该游客至多游览一个景点的概率为B.C.D.第(3)题已知球O的半径为4,球心O在大小为60°的二面角内,二面角的两个半平面所在的平面分别截球面得两个圆,,若两圆,的公共弦AB的长为4,E为AB的中点,四面体的体积为V,则正确的是()A.O,E,,四点共圆B.C.D.V的最大值为三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题甲、乙两位同学进行羽毛球比赛,约定赛制如下:累计赢2局者胜,分出胜负即停止比赛.已知甲每局赢的概率为,每局比赛的结果相互独立.本次比赛到第3局才分出胜负的概率为______,本次比赛甲获胜的概率为______.第(2)题设随机变量~,则 _____第(3)题已知抛物线的焦点在直线上,则______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题2020年新冠肺炎疫情肆虐全球,各个国家都翘首以盼疫苗上市.现在全球已经有多款疫苗上市,并且陆续在各个国家开始接种.如今我国有一款疫苗,经过三期临床试验以后,估计该款疫苗每次接种的有效率可达90%,并且已经陆续接到其他国家的订单.现已知该款疫苗需要接种两次,假设前后两次接种互不影响.(1)某人接种了我国的这款疫苗,则其可以接种成功的概率为多少?(2)已知某国家已经有意向与我国签订疫苗订单,买疫苗之后免费为本国首批10万人注射.但是由于部分人可能在两次注射疫苗之后未接种成功,所以该国决定购买一批预备疫苗为之后没有接种成功的人进行第二轮注射,第二轮注射仍为注射两次.根据以上信息,估计理想情况下该国需要从我国一共购买多少支疫苗?第(2)题甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表.机床品级合计一级品二级品甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)依据小概率值的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.附:χ2=.α0.0500.0100.001xα3.8416.63510.828第(3)题设函数.(1)若当时取得极值,求的值以及函数的单调区间;(2)若函数存在两个极值点,,证明:.第(4)题已知函数.(1)当时,求曲线在点处的切线方程;(2)设是函数的两个零点,求证:.第(5)题已知函数.(1)讨论的单调性;(2)若有3个不同的零点,求的取值范围.。
高考数学精选真题模拟测试卷含答案解析

精品基础教育教学资料,仅供参考,需要可下载使用!高考数学之精选真题+模拟重组卷(一)历年真题精选姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分150分,考试时间120分钟.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、单项选择题(本大题共8小题,每小题5分,共40分)1.(2020·全国高考真题(理))已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B 中元素的个数为( ) A .2 B .3C .4D .6【答案】C 【详解】由题意,A B 中的元素满足8y x x y ≥⎧⎨+=⎩,且*,x y N ∈,由82x y x +=≥,得4x ≤,所以满足8x y +=的有(1,7),(2,6),(3,5),(4,4), 故AB 中元素的个数为4.故选:C.2.(2020·北京高考真题)已知,R αβ∈,则“存在k Z ∈使得(1)kk απβ=+-”是“sin sin αβ=”的( ).A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C 【详解】(1)当存在k Z ∈使得(1)k k απβ=+-时,若k 为偶数,则()sin sin sin k απββ=+=;若k 为奇数,则()()()sin sin sin 1sin sin k k απβππβπββ=-=-+-=-=⎡⎤⎣⎦;(2)当sin sin αβ=时,2m αβπ=+或2m αβππ+=+,m Z ∈,即()()12kk k m απβ=+-=或()()121kk k m απβ=+-=+,亦即存在k Z ∈使得(1)kk απβ=+-.所以,“存在k Z ∈使得(1)kk απβ=+-”是“sin sin αβ=”的充要条件.故选:C.3.(2020·天津高考真题)函数241xy x =+的图象大致为( ) A . B .C .D .【答案】A 【详解】由函数的解析式可得:()()241xf x f x x --==-+,则函数()f x 为奇函数,其图象关于坐标原点对称,选项CD 错误; 当1x =时,42011y ==>+,选项B 错误. 故选:A.4.(2020·海南高考真题)已知函数2()lg(45)f x x x =--在(,)a +∞上单调递增,则a 的取值范围是( )A .(2,)+∞B .[2,)+∞C .(5,)+∞D .[5,)+∞【答案】D 【详解】由2450x x -->得5x >或1x <- 所以()f x 的定义域为(),1(5,)-∞-⋃+∞因为245y x x =--在(5,)+∞上单调递增所以2()lg(45)f x x x =--在(5,)+∞上单调递增 所以5a ≥ 故选:D5.(2015·北京高考真题(理))汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )A.消耗1升汽油,乙车最多可行驶5千米B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油【答案】D【详解】对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,故A错误;对于B,由图象可知当速度相同时,甲车的燃油效率最高,即当速度相同时,消耗1升汽油,甲车的行驶路程最远,∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B错误;对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,故C错误;对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,∴用丙车比用乙车更省油,故D正确故选D.6.(2016·全国高考真题(文))函数π()cos 26cos()2f x x x =+-的最大值为 A .4 B .5C .6D .7【答案】B 【解析】试题分析:因为22311()12sin 6sin 2(sin )22f x x x x =-+=--+,而sin [1,1]x ∈-,所以当sin 1x =时,()f x 取得最大值5,选B.7.(2017·全国高考真题(文))如图,在下列四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,则在这四个正方体中,直线AB 不平行与平面MNQ 的是( )A .B .C .D .【答案】D 【详解】对于A 选项,如下图所示,连接CD ,在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD ,N 、Q 分别为DE 、CE 的中点,则//NQ CD ,//AB NQ ∴, AB ⊄平面MNQ ,NQ ⊂平面MNQ ,//AB ∴平面MNQ ;对于B 选项,连接CD ,如下图所示:在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD ,M 、Q 分别为DE 、CE 的中点,则//MQ CD ,//AB MQ ∴,AB ⊄平面MNQ ,MQ 平面MNQ ,//AB ∴平面MNQ ;对于C 选项,连接CD ,如下图所示:在正方体中,//AD BC 且AD BC =,所以,四边形ABCD 为平行四边形,则//AB CD ,M 、Q 分别为DE 、CE 的中点,则//MQ CD ,//AB MQ ∴,AB ⊄平面MNQ ,MQ 平面MNQ ,//AB ∴平面MNQ ;对于D 选项,如下图所示,连接BE 交MN 于点F ,连接QF ,连接CD 交BE 于点O ,若//AB 平面MNQ ,AB 平面ABE ,平面ABE 平面MNQ FQ =,则//FQ AB ,则EF EQBE AE=, 由于四边形BCED 为正方形,对角线交于点O ,则O 为BE 的中点,M 、N 分别为DE 、CE 的中点,则//MN CD ,且MN BE F =,则12EF EN EO CE ==,1124EF OE BE ∴==, 则14EF BE =,又12EQ AE =,则EF EQBE AE≠,所以,AB 与平面MNQ 不平行;故选:D.8.(2014·浙江高考真题(文))如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小(仰角为直线与平面所成的角),若,,,则的最大值是()A.B.C.D.【答案】D【解析】试题分析:由勾股定理知,,过点作交于,连结,依题意,取最大值,点在点的左边,则,设,因为,则,在中,,在中由勾股定理得,整理得,令,当时,所以的最大值为,即的最大值是二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)9.(2020·海南高考真题)已知a >0,b >0,且a +b =1,则( )A .2212a b +≥B .122a b ->C .22log log 2a b +≥-D ≤【答案】ABD 【详解】对于A ,()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=,当且仅当12a b ==时,等号成立,故A 正确; 对于B ,211a b a -=->-,所以11222a b-->=,故B 正确;对于C ,2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭,当且仅当12a b==时,等号成立,故C不正确;对于D,因为2112a b=+≤++=,≤,当且仅当12a b==时,等号成立,故D正确;故选:ABD10.(2020·海南高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是()A.这11天复工指数和复产指数均逐日增加;B.这11天期间,复产指数增量大于复工指数的增量;C.第3天至第11天复工复产指数均超过80%;D.第9天至第11天复产指数增量大于复工指数的增量;【答案】CD【详解】由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11复工指数减少,第8天到第9天复产指数减少,故A错误;由图可知,第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;由图可知,第3天至第11天复工复产指数均超过80%,故C 正确; 由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D 正确;11.(2020·海南高考真题)下图是函数y = sin(ωx +φ)的部分图像,则sin(ωx +φ)= ( )A .πsin(3x +)B .πsin(2)3x - C .πcos(26x +)D .5πcos(2)6x - 【答案】BC 【详解】由函数图像可知:22362T πππ=-=,则222T ππωπ===,所以不选A, 当2536212x πππ+==时,1y =-∴()5322122k k Z ππϕπ⨯+=+∈, 解得:()223k k ϕππ=+∈Z , 即函数的解析式为:2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭故选:BC.12.(2020·海南高考真题)信息熵是信息论中的一个重要概念.设随机变量X 所有可能的取值为1,2,,n ,且1()0(1,2,,),1ni i i P X i p i n p ===>==∑,定义X 的信息熵21()log ni i i H X p p ==-∑.( )A .若n =1,则H (X )=0B .若n =2,则H (X )随着1p 的增大而增大C .若1(1,2,,)i p i n n==,则H (X )随着n 的增大而增大D .若n =2m ,随机变量Y 所有可能的取值为1,2,,m ,且21()(1,2,,)j m j P Y j p p j m +-==+=,则H (X )≤H (Y )【答案】AC 【详解】对于A 选项,若1n =,则11,1i p ==,所以()()21log 10H X =-⨯=,所以A 选项正确. 对于B 选项,若2n =,则1,2i =,211p p =-, 所以()()()121121X log 1log 1H p p p p =-⋅+-⋅-⎡⎤⎣⎦,当114p =时,()221133log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭, 当13p 4=时,()223311log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭,两者相等,所以B 选项错误. 对于C 选项,若()11,2,,i p i n n==,则()222111log log log H X n n nn n ⎛⎫=-⋅⨯=-= ⎪⎝⎭,则()H X 随着n 的增大而增大,所以C 选项正确.对于D 选项,若2n m =,随机变量Y 的所有可能的取值为1,2,,m ,且()21j m jP Y j p p +-==+(1,2,,j m =).()2222111log log mmi i i i i iH X p p p p ===-⋅=⋅∑∑ 122221222122121111log log log log m m m mp p p p p p p p --=⋅+⋅++⋅+⋅. ()H Y =()()()122221212122211111log log log m m m m m m m m p p p p p p p p p p p p -+-++⋅++⋅+++⋅+++12222122212221221121111log log log log m m m m m mp p p p p p p p p p p p ---=⋅+⋅++⋅+⋅++++由于()01,2,,2i p i m >=,所以2111i i m i p p p +->+,所以222111log log i i m ip p p +->+, 所以222111log log i i i i m ip p p p p +-⋅>⋅+, 所以()()H X H Y >,所以D 选项错误. 故选:AC三、填空题(本大题共4小题,每小题5分,共20分)13.(2020·江苏高考真题)已知y =f (x )是奇函数,当x ≥0时,()23f x x = ,则f (-8)的值是____. 【答案】4- 【详解】23(8)84f ==,因为()f x 为奇函数,所以(8)(8)4f f -=-=-故答案为:4-14.(2015·陕西高考真题(理))设曲线x y e =在点(0,1)处的切线与曲线1(0)y x x=>上点P 处的切线垂直,则P 的坐标为_____. 【答案】【详解】 设00(,)P x y .对y =e x 求导得y ′=e x ,令x =0,得曲线y =e x 在点(0,1)处的切线斜率为1,故曲线1(0)y x x=>上点P 处的切线斜率为-1,由02011x x y x ==-=-',得01x =,则01y =,所以P 的坐标为(1,1). 15.(2020·浙江高考真题)设52345123456(12)x a a x a x a x a x a x +=+++++,则5a =________;123a a a ++=________.【答案】80 51 【详解】5(12)x +的通项为155(2)2r r r r rr T C x C x +==,令4r =,则444455280T C x x ==,故580a =;11221235512251a a a C C ++=++=.故答案为:80;51.16.(2019·江苏高考真题)设(),()f x g x 是定义在R 上的两个周期函数,()f x 的周期为4,()g x 的周期为2,且()f x 是奇函数.当2(]0,x ∈时,()f x =,(2),01()1,122k x x g x x +<≤⎧⎪=⎨-<≤⎪⎩,其中0k >.若在区间(0]9,上,关于x 的方程()()f x g x =有8个不同的实数根,则k 的取值范围是_____.【答案】13⎡⎢⎣⎭. 【详解】当(]0,2x ∈时,()f x =即()2211,0.x y y -+=≥又()f x 为奇函数,其图象关于原点对称,其周期为4,如图,函数()f x 与()g x 的图象,要使()()f x g x =在(]0,9上有8个实根,只需二者图象有8个交点即可.当1g()2x =-时,函数()f x 与()g x 的图象有2个交点; 当g()(2)x k x =+时,()g x 的图象为恒过点()2,0-的直线,只需函数()f x 与()g x 的图象有6个交点.当()f x 与()g x 图象相切时,圆心()1,0到直线20kx y k -+=的距离为11=,得4k =,函数()f x 与()g x 的图象有3个交点;当g()(2)x k x =+过点1,1()时,函数()f x 与()g x 的图象有6个交点,此时13k =,得13k =. 综上可知,满足()()f x g x =在(]0,9上有8个实根的k 的取值范围为134⎡⎢⎣⎭,.四、解答题(本大题共6小题,共70分)17.(2019·天津高考真题(文)) 设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知113a b ==,23b a = ,3243b a =+.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅰ)设数列{}n c 满足21,,,n n n c bn ⎧⎪=⎨⎪⎩为奇数为偶数求()*112222n na c a c a c n N +++∈.【答案】(I )3n a n =,3nn b =;(II )22(21)369()2n n n n N +*-++∈【详解】(I )解:设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,依题意,得23323154q d q d =+⎧⎨=+⎩,解得33d q =⎧⎨=⎩, 故33(1)3n a n n =+-=,1333n nn b -=⨯=,所以,{}n a 的通项公式为3n a n =,{}n b 的通项公式为3nn b =;(II )112222n n a c a c a c +++135212142632()()n n n a a a a a b a b a b a b -=+++++++++123(1)[36](6312318363)2n n n n n -=⨯+⨯+⨯+⨯+⨯++⨯21236(13233)n n n =+⨯⨯+⨯++⨯,记 1213233n n T n =⨯+⨯++⨯ ∴ 则 231313233n n T n +=⨯+⨯++⨯ ∴∴-∴得,231233333n n n T n +=-----+⨯113(13)(21)333132n n n n n ++--+=-+⨯=-, 所以122112222(21)3336332n n n n n a c a c a c n T n +-++++=+=+⨯22(21)369()2n n n n N +*-++=∈.18.(2020·北京高考真题)在ABC 中,11a b +=,再从条件Ⅰ、条件Ⅰ这两个条件中选择一个作为已知,求:(Ⅰ)a 的值:(Ⅰ)sin C 和ABC 的面积. 条件Ⅰ:17,cos 7c A ==-; 条件Ⅰ:19cos ,cos 816A B ==. 注:如果选择条件Ⅰ和条件Ⅰ分别解答,按第一个解答计分.【答案】选择条件∴(∴)8(∴)sin C =, S =选择条件∴(∴)6(∴)sin C =, S =. 【详解】 选择条件∴(∴)17,cos 7c A ==-,11a b +=22222212cos (11)72(11)7()7a b c bc A a a a =+-∴=-+--⋅⋅-8a ∴=(∴)1cos (0,)sin 77A A A π=-∈∴==,由正弦定理得:7sin sin sin sin 2a c C A C C ==∴=11sin (118)822S ba C ==-⨯=选择条件∴(∴)19cos ,cos ,(0,)816A B A B π==∈,sin A B ∴====由正弦定理得:6sin sin a b a A B === (∴)91sin sin()sin cos sin cos 168C A B A B B A =+=+=+=11sin (116)622S ba C ==-⨯=19.(2020·海南高考真题)如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,QB PB 与平面QCD 所成角的正弦值.【答案】(1)证明见解析;(2. 【详解】 (1)证明:在正方形ABCD 中,//AD BC ,因为AD ⊄平面PBC ,BC ⊂平面PBC , 所以//AD 平面PBC ,又因为AD ⊂平面PAD ,平面PAD 平面PBC l =,所以//AD l ,因为在四棱锥P ABCD -中,底面ABCD 是正方形,所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ,所以,,AD PD l PD ⊥∴⊥ 因为CDPD D =所以l ⊥平面PDC ;(2)如图建立空间直角坐标系D xyz -,因为1PD AD ==,则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ,设(,0,1)Q m ,则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-,因为QB 1m =⇒=设平面QCD 的法向量为(,,)n x y z =,则00DC n DQ n ⎧⋅=⎨⋅=⎩,即00y x z =⎧⎨+=⎩,令1x =,则1z =-,所以平面QCD 的一个法向量为(1,0,1)n =-,则2cos ,1n PB n PB n PB⋅<>==== 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于6|cos ,|3n PB <>=所以直线PB 与平面QCD . 20.(2020·北京高考真题)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:假设所有学生对活动方案是否支持相互独立.(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;(Ⅰ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;(Ⅰ)将该校学生支持方案的概率估计值记为0p ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为1p ,试比较0p 与1p 的大小.(结论不要求证明)【答案】(∴)该校男生支持方案一的概率为13,该校女生支持方案一的概率为34; (∴)1336,(∴)01p p < 【详解】(∴)该校男生支持方案一的概率为2001200+4003=,该校女生支持方案一的概率为3003300+1004=;(∴)3人中恰有2人支持方案一分两种情况,(1)仅有两个男生支持方案一,(2)仅有一个男生支持方案一,一个女生支持方案一,所以3人中恰有2人支持方案一概率为:2121311313()(1)()(1)3433436C -+-=; (∴)01p p <21.(2020·浙江高考真题)如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(Ⅰ)若116=p ,求抛物线2C 的焦点坐标; (Ⅰ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.【答案】(∴)1(,0)32;(∴)40【详解】(∴)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(∴)设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+,由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩, 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++, 由M 在抛物线上,所以()222222244222m pm mp λλλλλ=⇒=+++,又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩, 012y y p λ∴+=,2101022x x y m y m p m λλλ∴+=+++=+,2122222mx p m λλ∴=+-+.由2222142,?22x y x px y px ⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-+222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+,18p ≥,21160p ≤,p ≤ 所以,p的最大值为40,此时(55A . 法2:设直线:(0,0)l x my t m t =+≠≠,()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得:()2222220m y mty t +++-=,所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得:2220y pmy pt --=,所以02M y y pt =-,解得()2022p m y m+=,因此()220222p m xm+=,由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,所以当m t ==时,p . 22.(2020·天津高考真题)已知函数3()ln ()f x x k x k R =+∈,()'f x 为()f x 的导函数.(Ⅰ)当6k =时,(i )求曲线()y f x =在点(1,(1))f 处的切线方程;(ii )求函数9()()()g x f x f x x'=-+的单调区间和极值; (Ⅰ)当3k -时,求证:对任意的12,[1,)x x ∈+∞,且12x x >,有()()()()1212122f x f x f x f x x x ''+->-.【答案】(∴)(i )98y x =-;(ii )()g x 的极小值为(1)1g =,无极大值;(∴)证明见解析.【详解】(∴) (i) 当k =6时,()36ln f x x x =+,()26'3f x x x=+.可得()11f =,()'19f =, 所以曲线()y f x =在点()()1,1f 处的切线方程为()191y x -=-,即98y x =-. (ii) 依题意,()()32336ln ,0,g x x x x x x=-++∈+∞. 从而可得()2263'36g x x x x x=-+-, 整理可得:323(1)(1)()x x g x x '-+=,令()'0g x =,解得1x =.当x 变化时,()()',g x g x 的变化情况如下表:所以,函数g (x )的单调递减区间为(0,1),单调递增区间为(1,+∞); g (x )的极小值为g (1)=1,无极大值.(∴)证明:由3()ln f x x k x =+,得2()3k f x x x'=+. 对任意的12,[1,)x x ∈+∞,且12x x >,令12(1)x t t x =>,则 ()()()()()()()1212122x x f x f x f x f x ''-+--()22331121212122332ln x k k x x x x x x k x x x ⎛⎫⎛⎫=-+++--+ ⎪ ⎪⎝⎭⎝⎭3322121121212212332ln x x x x x x x x x k k x x x ⎛⎫=--++-- ⎪⎝⎭()332213312ln x t t t k t t t ⎛⎫=-+-+-- ⎪⎝⎭. ∴令1()2ln ,[1,)h x x x x x=--∈+∞.当x >1时,22121()110h x x x x '⎛⎫=+-=-> ⎪⎝⎭,由此可得()h x 在[)1,+∞单调递增,所以当t >1时,()()1h t h >,即12ln 0t t t-->.因为21x ≥,323331(1)0t t t t -+-=->,3k ≥-,所以()()332322113312ln 33132ln x t t t k t t t t t t t t t ⎛⎫⎛⎫-+-+------- ⎪+ ⎪⎝⎭⎝⎭32336ln 1t t t t=-++-. ∴由(∴)(ii)可知,当1t >时,()()1g t g >,即32336ln 1t t t t-++>, 故32336ln 10t t t t-++-> ∴ 由∴∴∴可得()()()()()()()12121220x x fx f x f x f x ''-+-->.所以,当3k ≥-时,任意的[)12,1,x x ∈+∞,且12x x >,有()()()()1212122f x f x f x f x x x ''+->-.(二)2021新高考模拟卷姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分150分,考试时间120分钟.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、单项选择题(本大题共8小题,每小题5分,共40分)1.(2020·全国高三专题练习(文))已知复数5i5i 2iz =+-,则z =( )A B .C .D .【答案】B 【详解】由题,得()()()5i 2+i 5i5i 5i 1+7i 2i 2i 2+i z =+=+=---,所以z == 故选:B.2.(2020·阳江市第一中学高三其他模拟)已知全集为实数集R ,集合{}36A x x =-<<,{}29140B x x x =-+<,则()U A B ⋂=( )A .()2,6B .()2,7C .(]3,2-D .()3,2-【答案】C 【详解】{}{}2914027B x x x x x =-+<=<<, {2U B x x ∴=≤或}7x ≥,{}(]()323,2U A B x x ∴⋂=-<≤=-.故选:C.3.(2020·浙江杭州市·高一期末)已知集合(){}2ln 32,{}M xy x x N xx a ==+-=>∣∣,若M N ⊆,则实数a 的取值范围是( ) A .[3,)+∞B .(3,)+∞C .(,1]-∞-D .(,1)-∞-【答案】C 【详解】令2320x x +->,即()()310x x -+<,解得13x则(){}{}2ln 32|13M xy x x x x ==+-=-<<∣M N ⊆,1a ∴≤-故选:C4.(2020·霍邱县第二中学高二开学考试)若曲线()sin f x x x =在2x π=处的切线与直线210ax y ++=互相垂直,则实数a 等于( ) A .-2 B .-1C .1D .2【答案】D 【详解】由题可得:()sin cos f x x x x '=+,()12f π'=,∴曲线()sin f x x x =在2x π=处的切线的斜率为1,曲线()sin f x x x =在2x π=处的切线与直线210ax y ++=互相垂直,且直线210ax y ++=的斜率为2a -, ∴()1=12a -⨯-,解得:2a =;故答案选D.5.(2020·安徽金安区·六安一中高三月考(理))已知5log 2a =,7log 2b =,112c -⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系为( )A .b a c <<B .a b c <<C .c b a <<D .c a b <<【答案】A 【详解】5ln 2log 2ln 5a ==,7ln 2log 2ln 7b ==,0ln 2ln5ln7<<<,01b a ∴<<<, 11212c -⎛⎫==> ⎪⎝⎭,则b a c <<故选:A6.(2020·江苏高一课时练习)若方程2cos 2cos 10x x x m +--=在区间02π⎡⎤⎢⎥⎣⎦,上有实根,则实数m 的取值范围是( )A .[]02,B .[]12-, C .0⎡⎣ D .1⎡-⎣【答案】B 【详解】解:由题得2cos 2cos 10x x x m +--=,2cos 2x x m +=,则2sin 26x m π⎛⎫+= ⎪⎝⎭,由02x π⎡⎤∈⎢⎥⎣⎦,,得72666x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,,所以,1sin 2162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,, 得,[]2sin 2126x π⎛⎫+∈- ⎪⎝⎭,, 因为2sin 26x m π⎛⎫+= ⎪⎝⎭有实根, ∴[]12m ∈-,, 故选:B .7.(2020·全国高二课时练习)在数列{}n a 中,12a =-,111n na a +=-,则2019a 的值为( ) A .2- B .13C .5D .4【答案】B 【详解】解:由111n na a +=-,得2111111111n n n na a a a ++=-=-=--, 即32111111n nn na a a a ++=-=-=-, ∴数列{}n a 是以3为周期的周期数列,2019311113a a a ∴===-. 故选:B .8.(2020·广东广州市·高三月考)在长方体1111ABCD A B C D -中,1AB CC ==1BC =,点M 在正方形11CDD C 内,1C M ⊥平面1ACM ,则三棱锥11M ACC -的外接球表面积为( )A .11π2B .7πC .11πD .14π【答案】C 【详解】长方体1AC 中,11A D ⊥平面11CDD C ,1C M ⊂平面11CDD C ,∴111C M A D ⊥,又1C M ⊥平面1ACM ,1AC ⊂平面1ACM ,∴11C M AC ⊥, ∵1111AC A D A =,∴1C M ⊥平面11A CD ,而1CD ⊂平面11A CD ,∴11C M CD ⊥,11CDD C 是正方形,∴M 是1CD 与1C D 交点,即为1CD 的中点,也是1C D 的中点.1C MC △是直角三角形,设E 是1CC 中点,F 是1BB 中点,则由//EF BC 可得EF ⊥平面1MCC (长方体中棱与相交面垂直),E 是1C MC △的外心,三棱锥11A MCC -的外接球球心O 在直线EF 上(线段EF 或EF 的延长线上).设OE h =,则22222(1)22h h ⎛⎫⎛+=++- ⎪ ⎪ ⎝⎭⎝⎭,解得32h =,∴外接球半径为2r ==, 表面积为21144114S r πππ==⨯=. 故选:C .二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)9.(2020·福建福州市·高三期中)在ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若222sin a a b c ab C =+-=,cos sin a B b A c +=,则下列结论正确的是( )A .tan 2C =B .4A π=C .b =D .ABC 的面积为6【答案】ABD 【详解】因为222sin a b c ab C +-=,所以222sin sin cos 222a b c ab C C C ab ab +-===, 所以sin tan 2cos CC C==,故A 正确; 因为cos sin a B b A c +=,利用正弦定理可得sin cos sin sin sin A B B A C +=, 因为()C A B π=-+,所以sin sin[()]sin()C A B A B π=-+=+,所以sin cos sin si sin()sin cos cos sin n A A B B A B A B A B ++==+, 即sin sin cos sin B A A B =因为(0,)B π∈,所以sin 0B ≠,所以tan 1A =,又(0,)A π∈,所以4A π=,故B 正确;因为tan 2C =,(0,)C π∈所以sin C C ==所以sin sin()sin cos cos sin 22B A C A C A C =+=+=+=, 因为sin sin a bA B=,所以sin sin 2a Bb A===,故C 错误;11sin 622△===ABC S ab C ,故D 正确; 故选:ABD10.(2020·江苏连云港市·高三期中)已知ABC 是边长为2的等边三角形,D 是边AC 上的点,且2AD DC =,E 是AB 的中点,BD 与CE 交于点O ,那么( )A .0OE OC +=B .1AB CE ⋅=-C .32OA OB OC ++=D .132DE =【答案】AC【详解】建立平面直角坐标系如下图所示:取BD 中点M ,连接ME ,因为,M E 为,BD BA 中点,所以1//,2ME AD ME AD =,又因为12CD AD =, 所以//,ME CD ME CD =,所以易知EOM COD ≅,所以O 为CE 中点,A .因为O 为CE 中点,所以0OE OC +=成立,故正确;B .因为E 为AB 中点,所以AB CE ,所以0AB CE ⋅=,故错误;C .因为()()(0,,1,0,1,0,2O A B C ⎛- ⎝⎭,所以1,1,0,0,2222OA OB OC ⎛⎛⎫⎛⎫⎛++=-+--+=- ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭, 所以32OA OB OC ++=,故正确;D .因为()1,0,03DE ⎛ ⎝⎭,所以1,3DE ⎛=- ⎝⎭,所以133DE =,故错误, 故选:AC.11.(2020·深圳市高级中学高二期中)如图,在棱长为a 的正方体1111ABCD A B C D -中,P 为11A D 的中点,Q 为11A B 上任意一点,E 、F 为CD 上两点,且EF 的长为定值,则下面四个值中是定值的是( )A .点P 到平面QEF 的距离B .直线PQ 与平面PEF 所成的角C .三棱锥P QEF -的体积D .QEF △的面积【答案】ACD 【详解】平面QEF 就是平面11A B CD ,是确定的平面,因此点P 到平面QEF 的距离为定值,A 正确;平面PEF 即平面PCD ,而Q 在直线11A B 上,11//A B CD ,因此11A B 与平面PCD 平行,Q 到平面PEF 的距离为定值,但Q 运动时,PQ 的长度在变化,因此直线PQ 与平面PEF 所成的角也在变化,B 错误;P 点到直线CD 的距离是确定,而EF 的长度不变,因此PEF S △为定值,又Q 到平面PEF 的距离为定值,从而三棱锥P QEF -的体积为定值,C 正确;11//A B CD ,Q 到EF 的距离为定值,EF 的长度不变,∴QEF △的面积为定值,D 正确.故选:ACD .12.(2020·广东广州市·高三月考)已知直线2y x =-+分别与函数12xy e =和()ln 2y x =的图象交于点()11,A x y ,()22,B x y ,则( )A .122x x e e e +>B.124x x >C .1221ln ln 0x x x x +> D .()12ln 22xe x +>【答案】ABD 【详解】如图所示,由函数12xy e =和函数()ln 2y x =互为反函数, 所以函数12xy e =和()ln 2y x =的图象关于y x =对称, 从而直线2y x =-+与函数12xy e =和()ln 2y x =的图象的交点()11,A x y ,()22,B x y 也关于y x =对称,所以2112,x y x y ==,又由()11,A x y 在直线2y x =-+,可得112x y +=,所以122x x +=,则122x x e e e +≥=,又由12x x ≠,所以等号不成立, 所以122x x e e e +>,所以A 正确;记()2ln 2g x x x =--,则()1110,102g g =>=-<21x <<, 又121222(2)ln 2x x x x x x =-=,又由函数ln 2y x x =在单调递增,所以12x x >=B 正确; 由212120()12x x x x +<<=,则1201x x ,记()ln x f x x =,则()1ln x xf x x-'=, 当01x <<时,()0f x '>,则函数()f x 在(0,1)上单调递增,故121()()f x f x <,即1222121lnln ln 1x x x x x x <=-,所以1221ln ln 0x x x x +<,所以C 不正确; 由122x x +=,可得122y y +=,即()121ln 222x e x +=, 又由1112xx e e >,所以()121ln 222x e x +>,所以D 正确. 故选:ABD三、填空题(本大题共4小题,每小题5分,共20分)13.(2020·兴县友兰中学高一期中)“[]1,3x ∃∈-,220x x a -+<”为假命题,则实数a 的最小值为________. 【答案】1 【详解】[]“1,3x ∃∈-,220x x a -+<”为假命题,即在[-1,3]上,220x x a -+≥恒成立,分离参数得22a x x ≥-+,令()()22211f x x x x =-+=--+, 当1x =时()f x 取得最大值1,a∴的最小值为1,故答案为:1.14.(2020·上海闵行区·高三一模)新冠病毒爆发初期,全国支援武汉的活动中,需要从A医院某科室的6名男医生(含一名主任医师)、4名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有___________种.(用数字作答)【答案】90【详解】根据题意,从6名男医生(含一名主任医师)、4名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,共有3264206120C C⋅=⨯=种选派方案,如果所选的男女主任都没有参加,共有215330C C⨯=种选派方案,所以至少有一名主任医师参加有1203090-=种,故答案为:90.15.(2019·黄梅国际育才高级中学高二月考)下列说法:①线性回归方程y bx a=+必过(),x y;②命题“21,34x x∀≥+≥”的否定是“21,34x x∃<+<”③相关系数r越小,表明两个变量相关性越弱;④在一个22⨯列联表中,由计算得28.079K=,则有99%的把握认为这两个变量间有关系;其中正确..的说法是__________.(把你认为正确的结论都写在横线上)本题可参考独立性检验临界值表:【答案】①④【解析】线性回归方程ˆˆˆybx a =+必过样本中心点(),x y ,故①正确. 命题“21,34x x ∀≥+≥”的否定是“21,34x x ∃≥+<” 故②错误③相关系数r 绝对值越小,表明两个变量相关性越弱,故不正确;④在一个22⨯列联表中,由计算得28.079K =,则有99%的把握认为这两个变量间有关系,正确. 故答案为①④.16.(2020·浙江高三其他模拟)设椭圆22143x y +=的右焦点为F ,则F 的坐标是______;若A 为椭圆的右顶点,P 为椭圆上的动点.则当2PF PA -最小时,P 点的横坐标是______【答案】()1,0 8- 【详解】由椭圆方程22143x y +=知:右焦点F 的坐标为(1,0)由题意,知:(1,0)F ,(2,0)A ,令(,)P x y ,()22x -≤≤则2PF PA -=4x =--令()4g x x =-,则()1g x '=-当()0g x '<有28x -≤<-()g x 单调递减;当()0g x '>有82x -<≤,即()g x 单调递增,而()0g x '=有8x =-∴当8x =-()g x 有最小值,即2PF PA -最小 故答案为:()1,0;8-四、解答题(本大题共6小题,共70分)17.(2020·广东肇庆市·高三月考)已知数列{}n a 的前n 项和为n S ,()*112n n a S n =+∈N . (1)求n S ;(2)若21log 2n n n nb a a ⎛⎫=+⎪⎝⎭,求数列{}n b 的前n 项和n T . 【答案】(1)122n +-; (2)1(1)22n n n +-⋅++.【详解】(1)由题意,数列{}n a 满足()*112n n a S n =+∈N , 当2n ≥时,可得11112n n a S --=+, 两式相减,可得1111()22n n n n n a S S a a --==--,整理得12n n a a -=,即12n n a a -=, 当1n =时,可得111111122a S a =+=+,解得12a =, 所以数列{}n a 是首项为2,公比为2的等比数列,所以2nn a =,所以12(12)2212n n n S +-==--.(2)由(1)知2nn a =,则211log 2()212()2n n n n n n n b a a n n =+=+=⋅+设2,1nn n k n p =⋅=,数列{}{},n n k p 的前n 项和分别为,n n K P ,则1231122232(1)22n n n K n n -=⨯+⨯+⨯++-⨯+⨯ 23412122232(1)22n n n K n n +=⨯+⨯+⨯++-⨯+⨯,两式相减得23111223222222n n n n n K n n +++-=++⨯++-⨯=--⨯,所以1(1)22n n K n +=-⋅+,又由111n P n =+++=,所以数列{}n b 的前n 项和1(1)22n n n n T n n K P +-⋅=+++=.18.(2020·宁夏银川市·银川一中高三月考(理))如图,扇形ABC 是一块半径为2千米,圆心角为60的风景区,P 点在弧BC 上,现欲在风景区中规划三条商业街道,要求街道PQ 与AB 垂直,街道PR 与AC 垂直,线段RQ 表示第三条街道.(1)如果P 位于弧BC 的中点,求三条街道的总长度;(2)由于环境的原因,三条街道PQ 、PR 、RQ 每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?【答案】(1)2+;(2). 【详解】(1)由P 位于弧BC 的中点,在P 位于BAC ∠的角平分线上,则1||||||sin 2sin30212PQ PR PA PAB ==∠=⨯︒=⨯=,||cos 22AQ PA PAB =∠=⨯= 由60BAC ∠=︒,且AQ AR =,∴QAR 为等边三角形,则||RQ AQ ==三条街道的总长||||||112l PQ PR RQ =++=++ ; (2)设PAB θ∠=,060θ︒<<︒, 则sin 2sin PQ AP θθ==,PR AP =()()sin 602sin 603cos sin θθθθ-=-=-, cos 2cos AQ AP θθ==,||||cos(60)2cos(60)cos AR AP θθθθ=-=-=+,由余弦定理可知:2222cos60RQ AQ AR AQ AR =+-,22(2cos )(cos )22cos (cos )cos 603θθθθθθ=+-⨯+=,则|RQ =设三条街道每年能产生的经济总效益W ,300200400W PQ PR RQ =⨯+⨯+⨯,3002sin sin )200θθθ=⨯+-⨯+400sin θθ=++200(2sin )θθ=+)θϕ=++tan ϕ=当()sin 1θϕ+=时,W 取最大值,最大值为.19.(2020·全国高二专题练习)现有甲、乙两个规模一致的大型养猪场,均养有1万头猪.根据猪的体重,将其分为三个成长阶段,如下表:根据以往经验,两个养猪场内猪的体重X 均近似服从正态分布()250,16N .由于我国有关部门加强对大型养猪场即将投放市场的成年期的猪的监控力度,高度重视其质量保证,为了养出健康的成年期的猪,甲、乙两个养猪场引入两种不同的防控及养殖模式.已知甲,乙两个养猪场内一头成年期的猪能通过质检合格的概率分别为43,54. (1)试估算各养猪场三个阶段的猪的数量;(2)已知甲养猪场出售一头成年期的猪,若为健康合格的猪,则可盈利400元,若为不合格的猪,则亏损200元;乙养猪场出售--头成年期的猪,若为健康合格的猪,则可盈利500元,若为不合格的猪,则亏损100元记Y 为甲,乙养猪场各出售一头成年期的猪所得的总利润,求随机变量Y 的分布列,假设两个养猪场均能把成年期的猪售完,求两个养猪场的总利润的期望值. (参考数据:若()2~,Z Nμσ,则()0.683,(22)0.954,(33)0.997P Z P Z P Z μσμσμσμσμσμσ-+≈-+≈-+≈)【答案】(1)幼年期的猪215头,成长期的猪9540头,成年期的猪215头;(2)135450元.【详解】(1)设各阶段猪的数量分别为123,,n n n ,∵猪的体重X 近似服从正态分布2(50,16)N ,0.9970.954(218)(50316502 16) 0.02152P X P X -∴<=-⨯<-⨯≈=,1100000.0215215n ∴=⨯=(头);(1882)(5021650216)0.954P X P X <=-⨯<+⨯≈2100000.9549540n ∴=⨯=(头);0.9970.954(8298)(5021650316) 0.02152P X P X -=+⨯+⨯≈=,3100000.0215215n ∴=⨯=(头)∴甲、乙两个养猪场各有幼年期的猪215头,成长期的猪9540头,成年期的猪215头. (2)随机变量Y 的所有可能取值为900,300,300-.43341137111(900),(300),(300)5455454205420P Y P Y P Y ==⨯===⨯+⨯==-=⨯=,Y ∴的分布列为371()90030030063052020E Y ∴=⨯+⨯-⨯=(元),由于两个养猪场均有215头成年期的猪,且两个养猪场各出售一头成年期的猪所得的总利润的期望为630元,则总利润的期望为630215135450⨯=(元).20.(2020·全国高三其他模拟)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 为直角梯形,90CDA BAD ∠=∠=,1AD DC ==,2AB =, E 、F 分别为PD 、PB 的中点.(1)求证:平面PCB ⊥平面PAC ;(2)若平面CEF 与底面ABCD 所成的锐二面角为4π,求PA 的长.【答案】(1)证明见解析;(2)5. 【详解】(1)因为1AD DC ==,2AB =,90CDA BAD ∠=∠=,所以AC BC ==因为222AC BC AB +=,所以BC AC ⊥,因为PA ⊥底面ABCD ,BC ⊂平面ABCD ,所以PA BC ⊥, 因为AC PA A ⋂=,所以BC ⊥平面PAC , 因为BC ⊂平面PCB ,所以平面PCB ⊥平面PAC .(2)如图,以A 为坐标原点,分别以AD 、AB 、AP 所在直线为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,设(0)PA a a =>,则()0,2,0B =,()1,1,0C ,()1,0,0D ,()0,0,P a , 因为E 、F 分别为PD 、PB 的中点,所以1,0,22a E ⎛⎫⎪⎝⎭,0,1,2a F ⎛⎫ ⎪⎝⎭,1,1,22a CE ⎛⎫=-- ⎪⎝⎭,1,0,2a CF ⎛⎫=- ⎪⎝⎭, 易知平面ABCD 的一个法向量1(0,0,1)n =, 设平面CEF 的法向量为2(,,)n x y z =,则220,0,CE n CF n ⎧⋅=⎪⎨⋅=⎪⎩,即10,220,2az x y az x ⎧--+=⎪⎪⎨⎪-+=⎪⎩,不妨取4z =,则2x a =,y a =,即2(2,,4)a a n =,因为平面CEF 与底面ABCD 所成的锐二面角为4π,所以12122124cos ,5n n n n n n a ⋅===⋅,解得5a =,即PA 的长为5. 21.(2020·上海嘉定区·高三一模)在平面直角坐标系xOy 中,已知椭圆22221(0)x y a b a b+=>>的长轴长为6,且经过点3(2Q ,A 为左顶点,B 为下顶点,椭圆上的点P 在第一象限,PA 交y 轴于点C ,PB 交x 轴于点D .(1)求椭圆的标准方程(2)若20OB OC +=,求线段PA 的长(3)试问:四边形ABCD 的面积是否为定值?若是,求出该定值,若不是,请说明理由【答案】(1)22194x y +=;(2;(3)是定值,6. 【详解】(1)解:由题意得26a =,解得3a =.把点Q 的坐标代入椭圆C 的方程22221x y a b+=,得229314a b +=由于3a =,解得2b =所以所求的椭圆的标准方程为22194x y +=.(2)解:因为20OB OC +=,则得1(0,1)2OC OB =-=,即(0,1)C , 又因为(3,0)A -,所以直线AP 的方程为1(3)3y x =+.由221(3)3194y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩解得30x y =-⎧⎨=⎩(舍去)或27152415x y ⎧=⎪⎪⎨⎪=⎪⎩,即得2724,1515P ⎛⎫ ⎪⎝⎭所以||15AP ==即线段AP(3)由题意知,直线PB 的斜率存在,可设直线2:23PB y kx k ⎛⎫=->⎪⎝⎭. 令0y =,得2,0D k ⎛⎫⎪⎝⎭, 由222194y kx x y =-⎧⎪⎨+=⎪⎩得()2249360k x kx +-=,解得0x =(舍去)或23649k x k =+ 所以2218849k y k -=+,即22236188,4949k k P k k ⎛⎫- ⎪++⎝⎭于是直线AP 的方程为22218849(3)36314k k y x k k -+=⨯+++,即2(32)(3)3(32)k y x k -=++ 令0x =,得2(32)32k y k -=+,即2(32)0,32k C k -⎛⎫⎪+⎝⎭,所以四边形ABDC 的面积等于1||||2AD BC ⨯⨯ 122(32)13212326232232k k kk k k k -+⎛⎫⎛⎫=+⋅+=⋅⋅= ⎪ ⎪++⎝⎭⎝⎭ 即四边形ABDC 的面积为定值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新冠肺炎疫情相关的数学高考模拟题18
x
1 2 3 4 5 6
y (%) 1.08 0.76 0.53 0.72 0.95 1.09
x
7
8
9
10
11
12
y (%) 1.42 1.66 2.13 2.99 3.90 4.87
x
13
14
15
16
17
18
y (%) 6.23 7.72 9.75 11.98 14.10 15
根据此样本数据,试判断:y a bx =+与x
y c d =⋅哪一个更适合作为全国(除湖北)治愈率y 关于1月23日后天数x 的回归方程类型?请直接给出判断(不需说明理由),并求出该回归方程.
附:
y
v
18
2
1
i
i x
=∑
18
1
i
i
i x y
=∑ 18
1i i
i x v
=∑
0.186e 0.687e -
4.678 1.080 2109.000 1228.690 274.821 1.204 0.503
上述数据中,ln i i v y =,18
1
118i i v v ==∑
X (μm ) 0.054 0.057 0.060 0.063 0.066 0.069 0.072 0.075
件数
3
8
10
12
14
16
20
36
X(μm) 0.0780.0810.0840.0870.0900.0930.096合计
件数231014111094200
经计算,样本平均数为0.075,方差为0.0001.以此样本估计总体,回答以下问题:
【解答】(1)x
y c d
=⋅更适合作为全国(除湖北)治愈率y关于1月23日后天数x的回归方程类型.∵x
y c d
=⋅,两边同时取自然对数得ln ln ln
y c d x
=+⋅.
设ln
v y
=,ln c
α=,ln d
β=,则v x
αβ
=+.
由题意,()
1
1218
18
x=⨯+++
L
()
11818
1
9.5
182
+⨯
=⨯=,
代入相关数据,计算可得
µ1
2
2
1
n
i i
i
n
i
i
u v nuv
u nu
β=
=
-
=
-
∑
∑2
274.821189.51.080
2109.000189.5
-⨯⨯
=
-⨯
0.186
=.
将样本中心点()
9.5,1.080代入v x
αβ
=+得µµ
v u
αβ
=- 1.0800.1869.5
=-⨯0.687
=-,
∴0.6870.186
v x
=-+
$,即$
ln0.6870.186
y x
=-+,
从而
$0.6870.186
e x
y-+
=()
0.6870.186
e e x
-
=⋅0.503 1.204x
=⨯.
(2)(i )由样本数据可知过滤颗粒直径介于()2,2μσμσ-+的样本有193份,
故“从该口罩生产流水线上随意抽取1件口罩不符合N95标准”的概率为
3
200
, ∴35,
200Y B ⎛⎫ ⎪⎝⎭:,从而Y 的数学期望()33
=5==0.07520040
E Y ⨯. (ii )由题意,0.075μ=,20.0001σ=,0.01σ=, ∴()0.0750.0300.0750.0300.9974P X -<≤+=,
∴在10 000件口罩中符合标准的口罩有100000.99749974⨯=(件).。
