尺规绘图训练题
尺规作图(习题及答案)

尺规作图(习题)巩固练习1.下列作图语言描述正确的是()A.延长线段AB至点C,使AB=ACB.过∠AOB内部一点P,作∠AOB的平分线C.以点O为圆心,AC长为半径作弧D.在射线OA上截取OB=a,BC=b,则有OC=a+b2.已知边长作等边三角形.已知:线段a.求作:等边△ABC,使△ABC的三边长均为a.a作法:(1)作线段_____________;(2)分别以______,______为圆心,_______为半径作弧,两弧交于________;(3)连接________,_________.____________________.3.按下列要求作图,保留作图痕迹,不写作法.已知:如图,∠ABC.求作:∠DEF,使∠DEF=32∠ABC.A4.已知∠AOB=45°,点P在边OA上.请以点P为顶点,射线P A为一边作∠APC=∠O(作出所有可能的图形).5.如图,分别过A,B两个加油站的公路l1,l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足在两个加油站的连线上,且到两条公路l1,l2的距离相等.请用尺规作图作出点P(保留作图痕迹).6.请画出草图,并根据图形完成下列各题:(1)在△ABC中,AD平分∠BAC交BC于点D,过点B作BF∥AD交CA 的延长线于点F,则AF和AB的数量关系是_________________.(2)在△ABC中,点D是BC上的一点,过D作DE∥AC交AB于点E,DF∥AB交AC于点F,则∠EDF与∠A的数量关系是__________________.(3)已知,在锐角△ABC中,AD⊥BC于点D,CE⊥AB于点E,若AD与CE所夹的锐角是58°,则∠ABC=______.(4)已知,在锐角△ABC中,∠BAC=50°,AD平分∠BAC交BC于点D,BE⊥AC于点E,若∠EBC=20°,则∠ADC=_______.思考小结阅读材料:尺规作图是起源于古希腊的数学课题.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.古希腊的安那萨哥拉斯首先提出作图要有次数限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.尺规作图三大难题:①化圆为方问题求一个正方形的边长,使其面积与一已知圆的面积相等;②三等分角问题求一角,使其角度是一已知角度的三分之一;③倍立方问题求一立方体的棱长,使其体积是一已知立方体的二倍.【参考答案】1. C2.作法:(1)作线段AB使AB=a;(2)分别以点A,点B为圆心,a长为半径作弧,两弧交于点C;(3)连接AC,BC.△ABC即为所求.3.略4.略(有两种情况)5.略6.(1)AF=AB(2)∠EDF=∠A(3)58°(4)85°。
2023年九年级数学中考专题:尺规作图类训练题(含简单答案)

2023年九年级数学中考专题:尺规作图类训练题一、单选题1.如图,Rt ABC △中,由90ACB ∠=︒,30B ∠=︒,要求用圆规和直尺作图,分成两个三角形,其中至少有一个三角形是等腰三角形.其作法错误的是( )A .B .C .D .2.如图,在ABC 中,已知45B ∠=︒,30C ∠=︒,分别以点A 、C 为圆心,大于12AC长为半径画弧,两弧在AC 两侧分别交于P 、Q 两点,作直线PQ 交BC 于点D ,交AC 于点E .若3DE =,则AB 的长为( )A .B .5C .6D .3.如图,在ABC 中,分别以点B 和点C 为圆心,大于12BC 长为半径画弧,两弧相交于点M ,N ,作直线MN ,交AC 于点D ,交BC 于点E ,连接BD ,则ABD △的周长为( )A .AB BC + B .BC AC + C .+AB ACD .AB AC BC ++4.请仔细观察用直尺和圆规作一个角等于已知角的示意图如图所示,请你根据所学的三角形全等有关的知识,说明画出D O C DOC '''∠=∠的依据是( )A .SASB .AASC .SSSD .SSA5.如图,已知AOB ∠,以点O 为圆心,以任意长为半径画弧①,分别交OA ,OB 于点 E ,F , 再以点 E 为圆心,以EF 长为半径画弧,交弧①于点 D ,画射线OD .若28AOB ∠︒=,则BOD ∠的补角的度数为( )A .124︒B .39︒C .56︒D .144︒6.王师傅用角尺平分一个角,如图①,学生小顾用三角尺平分一个角,如图①,他们都在AOB ∠两边上分别取OM ON =,前者使角尺两边相同刻度分别与M ,N 重合,角尺顶点为P ;后者分别过M ,N 作OA ,OB 的垂线,交点为P ,则射线OP 平分AOB ∠,均可由OMP ONP ≌△△得知,其依据分别是( )A .SSS ;SASB .SAS ;SSSC .SSS ;HLD .SAS ;HL7.如图,在Rt ABC △中,90B ,分别以A 、C 为圆心,大于AC 长的一半为半径画弧,两弧相交于点M 、N ,连接MN ,与AC 、BC 分别相交于点D 、E ,连接AE ,当3AB =,5AC =时,ABE 周长为( )A .7B .8C .9D .108.如图,已知AOB ∠.按照以下步骤作图:①以点O 为圆心,以适当的长为半径作弧,分别交AOB ∠的两边于C ,D 两点,连接CD .①分别以点C ,D 为圆心,以大于线段OC 的长为半径作弧,两弧在AOB ∠内交于点E ,连接CE ,DE .①连接OE 交CD 于点M .下列结论中不正确的是( )A .CEO DEO ∠=∠B .CM MD =C .OCD ECD ∠=∠D .12OCED S CD OE =⋅四边形二、填空题9.如图,在ABC 中,AC BC =,以点A 为圆心,AB 长为半径作弧交BC 于点D ,交AC 于点E ,再分别以点C ,D 为圆心,大于CD 的长为半径作弧,两弧相交于F ,G两点,作直线FG .若直线FG 经过点E ,则C ∠的度数为______︒,AEG ∠的度数为______︒.10.如图,Rt ABC △中,90C ∠=︒,13AB =,5BC =,利用尺规在AC ,AB 上分别截取AD ,AE ,使AD AE =,分别以D ,E 为圆心,以大于12DE 为长的半径作弧,两弧在BAC ∠内交于点F ,作射线AF 交边BC 于点G ,点P 为边AB 上的一动点,则GP的最小值为______.11.如图,在ABC 中,90C ∠=︒.按以下步骤作图:①以点A 为圆心,适当长为半径作圆弧,分别交边AB 、AC 于点M 、N ;①分别以点M 和点N 为圆心、大于MN 一半的长为半径作圆弧,在BAC ∠内,两弧交于点P ;①作射线AP 交边BC 于点D .若DAC ABC ∽△△,则B ∠的大小为______度.12.如图,在Rt ABC △中,90C ∠=︒,以顶点B 为圆心,BC 长为半径画弧,交AB 于点D ,再分别以点C ,D 为圆心,大于12CD 长为半径画弧,两弧交于点E ,作射线BE交AC 于点F .若12BC =,15AB =,若BCF △的面积为24,则ABC 的面积为__________.13.如图,在四边形ABCD 中,30A ∠=︒,AB AD =,取大于12AB 的长为半径,分别以点A ,B 为圆心作弧相交于两点,过此两点的直线交AD 边于点E (作图痕迹如图所示),连接BE ,BD .则EBD ∠的度数为______.14.如图,在t R ABC 中,90C ∠=︒,以点B 为圆心,以任意长为半径作弧,分别交,AB BC于点M ,N ;①分别以M ,N 为圆心12MN 的长为半径作弧,两弧在ABC ∠内交于点P ,交AC 于点D .若16,8ABDSAB ==,则线段CD 的长为 ___________.15.如图,在ABCD 中,以A 为圆心,AB 长为半径画弧交AD 于F ,分别以F 、B 为圆心,大于12BF 长为半径画弧,两弧交于点G ,作射线AG 交BC 于点E ,6BF =,5AB =,则AE 的长为 ___________.16.如图,四边形ABCD 是平行四边形,以点B 为圆心,BC 的长为半径作弧交AD 于点E ,分别以点C ,E 为圆心、大于12CE 的长为半径作弧,两弧交于点P ,作射线BP交AD 的延长线于点F ,60CBE ∠=︒,6BC =,则BF =___________.三、解答题17.如图,在ABC 中,50A ∠=︒,30C ∠=,请用尺规作图法,在AC 上求作一点D ,使得BDC ABC ∽.(保留作图痕迹,不写作法)18.(1)操作实践:ABC 中,90A ∠=︒,22.5B ∠=︒,请画出一条直线把ABC 分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求画出一种分割方法即可)(2)分类探究:ABC 中,最小内角24B ∠=︒,若ABC 被一直线分割成两个等腰三角形,请画出相应示意图并写出ABC 最大内角的所有可能值;(3)猜想发现:若一个三角形能被一直线分割成两个等腰三角形,需满足什么条件?(请你至少写出两个条件,无需证明)19.如图,在ABC 中,点P ,Q 分别在边BC 及CB 的延长线上,且BQ CP =.(1)实践与探索:利用尺规按下列要求作图(不写作法,保留作图痕迹). ①作PQM CBA ∠=∠,且点M 在QC 的上方; ①在QM 上截取QR BA =; ①连接PR .(2)猜想与验证:试猜想线段AC 和RP 的数量关系,并证明你的猜想.20.如图,点D 是等边ABC 内部一点,且DB DC =,请仅用无刻度的直尺......,分别按下列要求画图.(1)在图①中BC 上找一点E ,使12BE BC =; (2)若2BDC A ∠=∠,在图①中AB AC 、边上分别找点M 、N ,使12MN BC =.参考答案:1.B2.A3.C4.C5.A6.C7.A8.C9.3612610.12 511.30 12.54 13.45︒14.4 15.816.18.(2)ABC的最大内角可能值是117︒或108︒或90︒或84︒;19.(2)RP AC=,答案第1页,共1页。
尺规作图习题

1画线段
一、用直尺能否作出下列图形
1、作直线( )
2、以O 为端点作过P 的射线( )
3、连结M 、N 并反向延长线段MN ( )
4、延长线段AB 到C ,使BC =AC ( )
二、已知线段AB ,求作一条线段,使它等于3AB
A B
三、已知线段a 、b (a<b ),求作一条线段使它等于b-a
a b
四、作等边三角形,使边长等于已知线段AB
A B
2画角
一、已知∠α、∠β,求作一个角使它等于∠α+∠β
二、巳知:线段a 、c ,∠α。
求作:△ABC ,使BC=a ,AB=c ,∠ABC=∠α a
c
α
3画垂线
一、画出⊿ABC 的外接圆
a b A B
C
二、已知⊿ABC画出BC边上的高
三、已知直角三角形斜边为a,直角边为b,求作直角三角形
a b
四、已知等腰三角形底边为a,底边上的高h,求作等腰三角形
a h
4画角平分线
一、补全“求作∠AOB的角平分线”的作法:
①在OA和OB上分别载取OD、OE,使OD=OE。
②分别以D、E为圆心,以()为半径画弧,两弧在∠AOB内交于点C。
③连OC即为∠AOB的平分线。
二、已知∠AOB,求作它的平分线
三、已知两角及其中一个角的对边,求作三角形
四、求作三角形ABC的内切圆
五、画一画
如图,在△ABC中:
(1)画出∠C的平分线CD
(2)画出BC边上的中线AM
(3)画出△ACM的边MC上的高
A A
B C
A
O B
a b
A
B C
B
C。
初二上册数学尺规作图练习题

初二上册数学尺规作图练习题1. 给定线段AB,利用尺规作图方法,构造平行于AB且离AB距离为3cm的直线段CD。
2. 给定线段EF和直线L,利用尺规作图方法,将直线L上的点P 与线段EF做垂线,垂足为点G。
3. 给定一个等边三角形ABC,利用尺规作图方法,找到三角形外部与三边等长的三点D、E、F,即DE=EF=FD。
4. 给定两个已知点A和B,利用尺规作图方法,找到与已知直线段AB等长的线段CD,使得CD垂直于已知直线段AB。
5. 给定两个已知点A和B,以及已知的一个直线段CD,利用尺规作图方法,找到一条经过点A且与线段CD垂直的直线L。
6. 给定一个已知角度,利用尺规作图方法,将已知角度的两边分别延长到任意长度,并找到它们的交点P。
7. 给定两个已知点A和B,以及已知的一个直线段CD,利用尺规作图方法,找到一条经过点A且与直线CD平行的直线L。
8. 给定两个已知点A和B,以及已知的一个直线段CD,利用尺规作图方法,找到一条经过点A且与直线CD相交于点E的直线L。
9. 给定一个已知角度,以及已知的一个直线段CD,利用尺规作图方法,找到一个与已知角度的一边重合且与线段CD相交于点F的直线L。
10. 给定一个已知角度,利用尺规作图方法,找到一个与已知角度的一边重合且经过点A的直线L。
以上是初二上册数学尺规作图的练习题。
通过这些练习题,可以帮助同学们熟悉数学尺规作图的基本方法和步骤,并提高他们的几何思维和空间想象能力。
尺规作图是一种重要的几何工具,对于解决几何问题和理解几何定理有着重要的作用。
通过反复练习和掌握尺规作图的技巧,同学们可以在几何学习中更加游刃有余,提高数学成绩。
在实际操作尺规作图时,同学们需要注意以下几点:1. 选取适当的比例尺:在作图中,要根据实际情况选择适当的比例尺,使得图形能够在纸上完整呈现,并且尽可能占用纸面的空间。
2. 使用准确的标志点:作图中需要准确的标记点、线段和角度大小。
尺规作图及真题训练

尺规作图及真题训练一.尺规作图的六大基本题型类型一作一条线段等于已知线段(已知线段a)1. 步骤①作射线OP;②以点O为圆心,线段a的长为半径作弧,交射线OP于A,OA即为所求线段2.图示3. 相关考点①已知三边作三角形;②作圆的六等分点类型二作一个角等于已知角(已知∠α)1. 步骤①在∠α上以点O为圆心,适当长为半径作弧,分别交∠α的两边于点P、Q;②作射线O′A;③以点O′为圆心,OP长为半径作弧,交O′A于点M;④以点M为圆心,PQ长为半径作弧,交步骤③中的弧于点N;⑤过点N作射线O′B,∠AO′B即为所求角2.图示3. 相关考点①作已知角一边的平行线(即作已知角的同位角或内错角);②过三角形边上一点,作一条直线使得其所分得三角形与原三角形相似类型三作已知角的平分线(已知∠AOB)1. 步骤①以点O为圆心,适当长为半径作弧,分别交OA、OB于点N、M;MN长为半径作弧,两弧在∠AOB的内部相交于②分别以点M、N为圆心,大于12点P;③作射线OP,OP即为所求角平分线2.图示3. 相关考点①在已知角的内部作到角两边距离相等的点;②作一个角的折痕,使得折叠后角两边可重叠;③作三角形内切圆圆心类型四作线段的垂直平分线(已知线段AB)1.步骤AB长为半径,在AB两侧作弧,分别交于点①分别以点A、B为圆心,大于12M、N;②过点M、N作直线交AB于点O,直线MN即为所求垂直平分线2.图示3.相关考点①过三角形顶点作一条直线平分三角形面积;②作到已知两点距离相等的点;③已知底边及腰长,作等腰三角形;④作三角形外接圆圆心类型五过一点作已知直线的垂线(已知点P和直线l)情形一:点P在直线l上1.步骤①以点P为圆心,适当长为半径向点P两侧的直线上作弧,分别交直线l于点A、B;AB长为半径向直线两侧作弧,两弧分别交于②分别以点A、B为圆心,大于12点M、N;③过点M、N作直线,直线MN即为所求垂线2.图示3. 相关考点①已知底边上的高线及腰长作等腰三角形;②已知半径长及直线上一点,作与直线相切的圆情形二:点P在直线l外1.步骤①任意取一点M ,使点M 和点P 在直线l 的两侧;③ 以点P 为圆心,PM 长为半径作弧,交直线l 于点A 、B ;④ 分别以点A 、B 为圆心,大于12AB 长为半径作弧,交于点M 同侧的点N ; ④过点P 、N 作直线,直线PN 即为所求垂线 2. 图示3. 相关考点①过直线外一点作与直线相切的圆;②过直角三角形顶点作垂线,使得到的两个三角形相似;③已知直线外同侧两点A 、B ,在直线上找一点P ,使得PA +PB 最小类型六 已知条件作三角形 情形一:已知三边作三角形。
初二数学尺规作图练习题

初二数学尺规作图练习题尺规作图是数学中的重要内容,通过使用尺规来解决几何问题。
在初二数学中,尺规作图是一项基础技能,帮助学生理解几何概念并锻炼解决问题的能力。
本文将介绍一些初二数学尺规作图的练习题,并提供相应的解答。
【练习题一】已知正方形ABCD的边长为2cm,E为边AB上的一点,连接DE并延长至与边BC相交于点F,请使用尺规作图的方法求出DF的长度。
解答:1. 作辅助线:过点D作DE的垂线,交边BC于点G。
2. 以尺规的一点放在点D上,另一点固定在边DE上,画弧与边BC相交于点G。
3. 以尺规的一点放在点G上,另一点放在点F上,画弧与边DC相交于点H。
4. 连接DH,DH即为所求的DF的长度。
【练习题二】已知直角三角形ABC,其中∠ABC=90°,AB=3cm,BC=4cm,请使用尺规作图的方法求出三角形ABC的内切圆的半径。
解答:1. 作辅助线:连接AB和AC,延长AC至点D。
2. 以尺规的一点放在点A上,另一点固定在边AC上,画弧与边AB相交于点E。
3. 以尺规的一点放在点E上,另一点放在点C上,画弧与边BC相交于点F。
4. 连接AF,AF即为三角形ABC的内切圆的半径。
【练习题三】已知正方形ABCD的边长为6cm,E为边AB上的一点,连接DE 并延长至与边BC相交于点F,连接CF,请使用尺规作图的方法求出三角形CEF的周长。
解答:1. 作辅助线:过点D作DE的垂线,交边BC于点G。
2. 以尺规的一点放在点D上,另一点固定在边DE上,画弧与边BC相交于点G。
3. 以尺规的一点放在点G上,另一点放在点F上,画弧与边FC相交于点H。
4. 连接CF和FH,CHFH即为三角形CEF。
5. 使用尺规测量边CH、HF和FC的长度,计算出三角形CEF的周长。
通过以上三个练习题,我们了解了尺规作图的基本方法和步骤。
在实际操作中,我们需要准确使用尺规,并且要仔细观察图形的性质和特点,以便选择合适的作图方法。
尺规作图练习
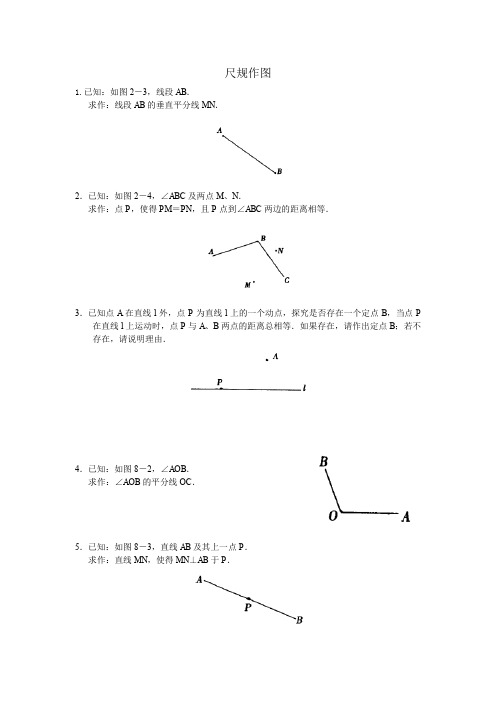
尺规作图1.已知:如图2-3,线段AB.求作:线段AB的垂直平分线MN.2.已知:如图2-4,∠ABC及两点M、N.求作:点P,使得PM=PN,且P点到∠ABC两边的距离相等.3.已知点A在直线l外,点P为直线l上的一个动点,探究是否存在一个定点B,当点P 在直线l上运动时,点P与A、B两点的距离总相等.如果存在,请作出定点B;若不存在,请说明理由.4.已知:如图8-2,∠AOB.求作:∠AOB的平分线OC.5.已知:如图8-3,直线AB及其上一点P.求作:直线MN,使得MN⊥AB于P.6.已知:如图8-4,△AB C.求作:点P,使得点P在△ABC内,且到三边AB、BC、CA的距离相等.7.已知:如图,△ABC中,∠C=90°,试在AC上找一点P,使P到斜边的距离等于PC.(画出图形,并写出画法)8.它到三条公路的距离都相等,试问:(1)可选择的地点有几处?(2)你能画出塔台的位置吗?9. 已知:如图,四条直线两两相交,相交部分的线段构成正方形ABCD.试问:是否存在到至少三边所在的直线的距离都相等的点?若存在,请找出此点,这样的点有几个?若不存在,请说明理由.8.已知:如图,A、B两点在直线l的同侧,点A'与A关于直线l对称,连接A'B交l于P 点,若A'B=a.(1)求AP+PB;(2)若点M是直线l上异于P点的任意一点,求证:AM+MB>AP+PB.9.已知:A、B两点在直线l的同侧,试分别画出符合条件的点M.(1)如图,在l上求作一点M,使得|AM-BM|最小;作法:(2)如图,在l上求作一点M,使得|AM-BM|最大;作法:(3)如图,在l上求作一点M,使得AM+BM最小.展、探究、思考10.(1)如图,点A、B、C在直线l的同侧,在直线l上,求作一点P,使得四边形APBC 的周长最小;(2)如图,已知线段a,点A、B在直线l的同侧,在直线l上,求作两点P、Q(点P 在点Q的左侧)且PQ=a,四边形APQB的周长最小.11.(1)已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得ΔPMQ的周长最小;(2)已知:如图,点M在锐角∠AOB的内部,在OB边上求作一点P,使得点P到点M的距离与点P到OA边的距离之和最小.12.若A、B是平面上的定点,在平面上找一点C,使ΔABC构成等腰直角三角形,问这样的C点有几个?并在图6-9中画出C点的位置.13.对于顶角∠A为36°的等腰ΔABC,请设计出三种不同的分法,将ΔABC分割为三个三角形,并且使每个三角形都是等腰三角形.。
尺规作图练习题

一 、基本作图:在几何里把限定用无刻度的直尺和无刻度的圆规来画图,称为尺规作图。
1.画一条线段等于已知线段 A B2.画一个角等于已知角3.画一个角的平分线4.画线段的垂直平分线 二、中考题展示1、如图点C 在∠AOB 的边OB 上,用尺规作出了CN ∥OA ,作图痕迹中,弧FG 是 ( ) A.以点C 为圆心,OD 为半径的弧 B.以点C 为圆心,DM 为半径的弧C.以点E 为圆心,OD 为半径的弧 D.以点E 为圆心,DM 为半径的弧《尺规作图》练习2、已知:线段a ,c ,∠α.求作:△ABC ,使BC=a,AB=c ,∠ABC=∠α.3、己知一个直角三角形的一条直角边为a ,斜边长为c ,求作这个三角形。
4、如图,画一个等腰△ABC ,使得底边BC=a ,它的高AD=h5、如下图,已知钝角△ABC ,∠B 是钝角.求作:(1)BC 边上的高;(2)BC 边上的中线6、已知:如图,在△ABC 中,∠A =30°,∠B =60°。
(1)作∠B 的平分线BD ,交AC 于点D ;作AB 的中点E (要求:尺规作图,保留作图痕迹) (2)连接DE ,求证:△ADE ≌△BDE 。
a cα《全等三角形》证明题1.已知:如图,E 、F 是平行四边行ABCD 的对角线AC 上的两点,AE =CF . 求证:(1)△ADF ≌△CBE ;(2)EB ∥DF .2.如图,在△ABC 中,AB =AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE .求证:△ABE ≌△ACE .3.把两个含有45°角的直角三角板如图放置,点D 在BC 上,连结BE ,AD ,AD 的延长线交BE 于点F .(1)求证:△BEC ≌△ADC ;(2)说明:AF ⊥BE .4、如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
