25.6三角形内切圆一
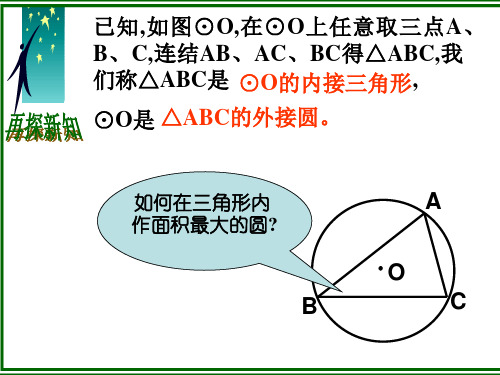
三角形的内切圆

三角形的内切圆三角形的内切圆是指一个能够完全嵌入于三角形内部、与三角形的三条边相切于一点的圆。
内切圆可以从许多不同角度来研究,它具有许多有趣的性质和应用。
本文将介绍三角形的内切圆的定义、性质和一些相关应用。
首先,让我们来定义三角形的内切圆。
给定一个三角形ABC,假设它的三条边分别为a、b和c。
现在我们想要找到一个圆,使得该圆内切于三角形ABC,并且与三角形的三边分别相切于点D、E和F。
圆心O位于三角形的内部,并且到三角形的三边的距离相等,我们将其距离记为r。
这个圆就是三角形ABC的内切圆。
三角形的内切圆具有许多有趣的性质。
首先,内切圆的圆心和三角形的每个顶点以及内切点D、E和F在一条直线上,这条直线叫做内切圆的欧拉线。
此外,内切圆的半径r等于三角形的面积S除以半周长s 的差值,即r = S/s,其中S = √[s(s-a)(s-b)(s-c)],s为半周长。
内切圆还有一些重要的性质。
首先,内切圆与三角形的每个外接圆相切于同一点D、E和F,并且它们的半径相等。
其次,内切圆的半径和三角形的面积成正比,当半径增加时,面积也增加,反之亦然。
此外,内切圆的面积等于三角形的面积,且内切圆的周长等于三角形的周长。
内切圆还有一些实际应用。
例如,在制作方程式赛车时,车轮的形状通常是一个内切圆,这样可以确保车轮与地面的接触面积最大,提供更好的牵引力和操控性能。
此外,在建筑和工程中,内切圆也被广泛应用,例如在圆形井盖、管道等设计中。
通过研究三角形的内切圆,我们可以更深入地了解几何学中的一些基本概念和性质。
同时,内切圆还有一些实际应用,使我们更好地理解它们在现实世界中的意义。
总结起来,三角形的内切圆是指一个能够完全嵌入于三角形内部、与三角形的三条边相切于一点的圆。
它具有许多有趣的性质,包括与三角形的每个外接圆相切、与三角形的三个顶点和内切点在一条直线上等。
它也有一些实际应用,如在方程式赛车和建筑工程中的应用。
通过研究三角形的内切圆,我们可以深入了解几何学中的一些基本概念和性质。
25.6三角形的内切圆

C
如图所示是一张三角形的铁皮,如何在它上 面剪下一块圆形的用料,并且使圆的面积尽 可能大呢?
A N A
·
B C B
·
D
I
M
C
与三角形各边都相切的圆叫做三角形的内 切圆;三角形内切圆的圆心是三角形三条 角平分线的交点,叫做三角形的内心;这个 三角形叫做圆的外切三角形。
G E
F H
1.学习了三角形内切圆、三角形的内心、圆的外切三 角形. 2.利用作三角形的内角平分线,任意两条角平分线的 交点就是内切圆的圆心,交点到任意一边的距离是圆 的半径. 3.在学习有关概念时,应注意区别“内”与“外”, “接”与“切”;还应注意“连结内心和三角形顶点” 这一辅助线的添加和应用.
1.什么是三角形的内切圆?
和三角形各边都相切的圆叫做三角形的内 切圆,内切圆的圆心叫做三角形的内心, 这个三角形叫做圆的外切三角形.
2、想一想,三角形内心和外心的区别?
名称 外 心 (三角 形外接 圆的圆 心)
确定方法
图形
A
性质
三角形三 边中垂线 的交点
B
O
(1)OA=OB=OC ; (2)外心不一 定在三角形的 内部.
基础题:
正方形 1.既有外接圆,又内切圆的平行四边形是______. 2.直角三角形的外接圆半径为5cm,内切圆半径为1cm, 22cm 则此三角形的周长是_______. 3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O 2cm 于P点,交AB、BC于E、F,则△BEF的周长是_____.形内切 条角平分 圆 的 圆 心 ) 线的交点
B
O C
(1)内心到三 边的距离相等 ; (2)OA、OB 、OC分别平分 ∠ BAC 、 ∠ ABC 、 ∠ACB; (3)内心在三 角形内部.
三角形的内切圆知识点总结

三角形的内切圆知识点总结三角形的内切圆是指能够与三角形的三条边都相切的圆。
它在三角形中起到了重要的几何作用,不仅在数学中有重要的应用,也在实际生活中有许多实际意义。
本文将从三角形的内切圆的定义、性质、构造方法、应用等方面进行探讨。
一、内切圆的定义三角形的内切圆是指能够与三角形的三条边都相切的圆。
换句话说,内切圆的圆心与三角形的三边的交点都在同一条直线上。
内切圆的半径被称为三角形的内切圆半径,通常用r表示。
二、内切圆的性质1. 内切圆的圆心与三角形的三边的交点都在同一条直线上,这条直线被称为内切圆的欧拉线。
2. 内切圆的半径与三角形的三边的长度有一定的关系。
根据欧拉定理,内切圆的半径r等于三角形的周长p与面积S的比值的一半,即r = S/p。
3. 内切圆的半径r与三角形的三个内角的正弦值的倒数之和有关,即1/r = (sinA + sinB + sinC)/p,其中A、B、C分别为三角形的三个内角。
4. 内切圆的圆心与三角形的三个内角的平分线相交。
三、内切圆的构造方法1. 根据内切圆的定义,可以通过直接计算三角形的内切圆半径和圆心的坐标来构造内切圆。
2. 另一种构造内切圆的方法是利用三角形的角平分线和垂直平分线的性质。
首先,通过角平分线找到三个内角的平分线交点,然后通过垂直平分线找到三个内边的中点,最后通过这些点来确定内切圆的圆心和半径。
四、内切圆的应用1. 在数学中,内切圆广泛应用于三角形的面积、周长、角度、长度等问题的计算中。
通过内切圆的性质,可以简化计算过程,提高计算的准确性。
2. 在几何建模中,内切圆可以用来确定三角形的外接圆和外接圆的圆心。
通过内切圆和外接圆的关系,可以更好地理解和描述三角形的形状和结构。
3. 在工程和建筑中,内切圆的应用十分广泛。
例如,在建筑物的设计和施工中,内切圆可以用来确定柱子和墙壁的形状和位置,从而提高建筑物的稳定性和美观性。
三角形的内切圆是与三角形的三条边都相切的圆,具有一系列重要的性质和应用。
《三角形的内切圆》 讲义

《三角形的内切圆》讲义一、引入同学们,在我们的数学世界中,三角形是一种非常基础且重要的图形。
而今天,我们要来一起探索三角形中的一个神秘而有趣的部分——三角形的内切圆。
想象一下,在一个三角形内部,有一个圆与三角形的三条边都相切,这个圆就像是被三角形紧紧地拥抱着,它有着独特的性质和规律等待我们去发现。
二、三角形内切圆的定义那什么是三角形的内切圆呢?简单来说,三角形的内切圆就是与三角形的三条边都相切的圆。
这个圆的圆心叫做三角形的内心,它是三角形三条角平分线的交点。
为了更直观地理解,我们可以画一个三角形 ABC,然后试着画出它的内切圆。
三、三角形内切圆的性质1、圆心到三角形三边的距离相等由于内切圆与三角形的三条边都相切,所以圆心到三条边的距离就是内切圆的半径,而且这个距离是相等的。
这是因为切线的性质决定了圆心到切线的距离等于圆的半径。
2、三角形的面积与内切圆半径之间的关系我们知道三角形的面积可以用底乘以高除以 2 来计算。
对于一个三角形 ABC,设其面积为 S,三边分别为 a、b、c,内切圆的半径为 r。
那么三角形的面积 S 还可以表示为:S = 1/2×(a + b + c)×r 。
这是一个非常有用的公式,通过它我们可以在已知三角形的边长和内切圆半径的情况下,轻松求出三角形的面积,或者在已知三角形的面积和边长的情况下,求出内切圆的半径。
3、内心的性质内心是三角形三条角平分线的交点,这意味着从内心到三角形三边的距离相等。
而且,内心是三角形内切圆的圆心,它决定了内切圆的位置。
四、三角形内切圆的画法那怎么画出一个三角形的内切圆呢?我们可以按照以下步骤进行:1、先作出三角形的两条角平分线,它们的交点就是内心。
2、以内心为圆心,从内心到三角形任意一边的距离为半径画圆,这个圆就是三角形的内切圆。
为了让大家更清楚,我们通过一个具体的例子来实际操作一下。
五、三角形内切圆的应用在实际生活中,三角形内切圆有很多应用。
三角形的内切圆

三角形的内切圆在几何学中,三角形是最基本的图形之一。
而内切圆是一种特殊的圆,它恰好与三角形的三条边相切于一点。
本文将探讨三角形的内切圆及其相关性质。
一. 内切圆的定义内切圆是指一个圆与一个三角形的三条边都相切于一点的情况。
这个相切点称为内切圆的切点。
二. 内切圆的特性1. 切点在三角形的角平分线上三角形的内切圆的切点在三角形的三个角的角平分线上。
这是因为切点到三角形的三条边的距离相等,而角平分线是与三角形的三条边相交且距离相等的直线。
2. 切点到三角形的三条边的距离相等内切圆的切点到三角形的三条边的距离都相等。
这是因为内切圆与三角形的边都相切于切点,根据切线与半径的性质,切点到切线的距离等于半径的长度。
3. 内切圆的半径与三角形的内角有关内切圆的半径与三角形的内角有一定的关系。
设三角形的内切圆的半径为r,三角形的三边长分别为a、b、c,那么有以下关系成立:r = √[(s-a)(s-b)(s-c)/s]其中,s为三角形的半周长,即s = (a+b+c)/2。
三. 内切圆与三角形的周长和面积的关系1. 内切圆与三角形的周长关系三角形的内切圆的半周长等于三角形的半周长,即2πr = a + b + c,其中r为内切圆的半径,a、b、c为三角形的三边长。
2. 内切圆与三角形的面积关系三角形的内切圆与三角形的面积有一定的关系。
设三角形的内切圆的半径为r,三角形的半周长为s,三角形的面积为A,则有以下关系成立:A = rs四. 内切圆的应用内切圆在几何学中有很多应用。
以下列举两个常见的应用:1. 利用内切圆求三角形的面积根据上述第三点的关系式A = rs,我们可以通过已知三角形的内切圆半径和半周长来求解三角形的面积。
2. 利用内切圆求三角形的周长根据上述第二点的关系式2πr = a + b + c,我们可以通过已知三角形的内切圆半径和三边长来求解三角形的周长。
总结:本文介绍了三角形的内切圆及其相关性质。
内切圆是指一个圆与一个三角形的三条边都相切于一点的情况。
《三角形的内切圆》 讲义

《三角形的内切圆》讲义一、三角形内切圆的定义在三角形中,如果一个圆与三角形的三边都相切,那么这个圆就叫做三角形的内切圆。
内切圆的圆心是三角形三条角平分线的交点,这个交点被称为三角形的内心。
想象一下,一个三角形就像是一块被包围的土地,而内切圆就是在这块土地中间挖的一个正好与三边都接触的圆形水池。
二、三角形内切圆的性质1、内心到三角形三边的距离相等因为角平分线的性质,内心到三角形三边的距离都等于内切圆的半径。
这就好比从圆心向三条边引垂线,这些垂线的长度都是一样的。
2、三角形的面积与内切圆半径的关系三角形的面积可以用“三角形的周长乘以内切圆半径的一半”来计算。
假设三角形的三条边分别为 a、b、c,周长为 L,内切圆半径为 r,那么三角形的面积 S = 1/2 × L × r 。
我们可以这样理解,把三角形分成三个小三角形,分别以三边为底,内切圆半径为高,那么三个小三角形的面积之和就是大三角形的面积。
3、内切圆半径的计算公式对于一个已知三边长度为 a、b、c 的三角形,其内切圆半径 r 可以通过公式 r =(a + b c) / 2 计算(前提是 c 为最长边)。
例如,一个三角形的三边分别为 6、8、10,因为 10 是最长边,所以内切圆半径 r =(6 + 8 10) / 2 = 2 。
三、三角形内切圆的作图方法1、角平分线法(1)首先作出三角形的两条角平分线,它们的交点就是内心。
(2)过内心向三角形的一边作垂线,这条垂线的长度就是内切圆的半径。
(3)以内心为圆心,以内切圆半径为半径作圆,这个圆就是三角形的内切圆。
2、切线长法(1)分别测量三角形的三边长度 a、b、c 。
(2)以三角形的顶点为圆心,分别以切线长(切线长可以通过公式:切线长=(a + b c) / 2 计算)为半径作弧,三条弧的交点就是内切圆的圆心。
(3)以内切圆的圆心为圆心,以切线长为半径作圆,即为三角形的内切圆。
四、三角形内切圆的应用1、求三角形的面积当知道三角形的三边长度时,可以先求出内切圆半径,然后利用面积公式计算三角形的面积。
三角形的内切圆定义

三角形的内切圆定义一、什么是三角形的内切圆内切圆是指与三角形的三条边都相切的圆,圆心位于三角形的内部。
三角形的内切圆是三角形内切圆心运动学的重要对象。
在三角形的内切圆中,圆心到三角形三边的距离是相等的,而且内切圆的半径等于三角形的面积除以半周长。
因此,研究三角形的内切圆不仅有助于理解三角形的性质,还有助于解决与三角形相关的问题。
二、三角形内切圆的性质1.圆心到三角形三边的距离相等:三角形的内切圆与三角形的三边都相切,因此圆心到三边的距离是相等的。
这个距离称为内切圆的半径。
2.内切圆的半径公式:内切圆的半径等于三角形的面积除以半周长,即r =A / s,其中r表示内切圆的半径,A表示三角形的面积,s表示半周长。
3.内切圆的圆心重心和内心重合:圆心、内心和重心在三角形的同一条高线上,且重心将内心和圆心一分为二。
4.内切圆的圆心和外心的连线垂直于三角形的内心和外心连线:内切圆的圆心和外心之间的连线与三角形的内心和外心之间的连线垂直。
5.内切圆的半径不超过外接圆的半径:对于任意三角形,内切圆的半径小于或等于外接圆的半径。
三、如何构造三角形的内切圆构造三角形的内切圆需要以下步骤:1.首先,画出给定的三角形ABC。
2.然后,分别作出三角形的三条角平分线,将角A、角B、角C分别平分为两部分。
这样可以得到三个交点,分别记为D、E、F,分别位于三角形的内部。
3.接下来,连接交点D、E、F和三角形的顶点A、B、C,得到三条边DA、EB和FC。
4.最后,以边DA、EB和FC为直径,画出三个圆。
这三个圆的交点即为三角形的内切圆的圆心O。
四、三角形内切圆的应用1.几何问题的解决:三角形的内切圆可以用来解决与三角形相关的几何问题,如计算三角形的面积、周长等。
通过内切圆的半径公式,可以简便地计算三角形的面积和半周长,进而得到三角形的各种性质。
2.工程测量:三角形的内切圆可以应用于工程测量中。
通过测量三角形的三个顶点和内切圆的圆心,可以确定三角形的形状和尺寸,为工程设计和施工提供参考。
三角形的内切圆(1)
巩固提高 2、判断。 (1)、三角形的外心到三角形各边的距离相等。 (2)、直角三角形的外心是斜边的中点。 3、填空: (1)、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆半径____,内切圆半径_____。 (2)、等边三角形外接圆半径与内切圆半径之比___。
A
B
C
D
E
F
2、如图,△ABC中,∠A=55度,其内切圆切△ABC 于D、E、F,则∠FDE=______度。
117.5
62.5
巩固提高 1. 下列命题正确的是( ) A、三角形外心到三边距离相等 B、三角形的内心不一定在三角形的内部 C、等边三角形的内心、外心重合 D、三角形一定有一个外切圆
C
A
F
E
D
O
已知等边三角形的边长,能求出三角形的内切圆的半径的吗?反之呢?
记忆:
例2.已知:△ABC的内切圆分别和BC、AC、AB相切于点D、E、F,∠DIE=120°,∠EIF=130°.求△ABC的三个内角的度数.
A
B
C
●
I
D
E
F
A
B
C
I
1、如图,△ABC中,∠A=55度,I是内心,则∠BIC=______度。
例1:已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
C
B
A
E
D
F
O
r
B
C
a
b
c
r
A
直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。
E
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
马鞍山中加双语学校九(上)数学清学稿 主备人:王军 2012年11月23日
25.6三角形的内切圆(一)(清学稿)
班级: 姓名: 日期: 节次: 知识梳理:
定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形。
性质:1.三角形的内心到三角形各边的距离相等;
2.三角形的内心在三角形的角平分线上;
当堂清学:
1、如图, △ABC 的顶点在⊙O 上, △ABC 的各边
与⊙I 都相切,则△ABC 是⊙I 的 三角形;
△ABC 是⊙O 的 三角形;
⊙I 叫△ABC 的 圆;
⊙O 叫△ABC 的 圆,点I 是△ABC 的 心,
点O 是△ABC 的 心
2、已知:在△ABC 中,BC=14,AC=9,AB=13,它的内切
圆分别和BC 、AC 、AB 切于点D 、E 、F ,求AF 、BD 和
CE 的长.
整洁(画√):A □B □C □D □ 得分: 批改日期:
A B C F D E。
