必修4 辅导:任意角的三角函数与诱导公式(教师)
人教A版数学必修四(六)任意角的三角函数、诱导公式、同角求值.docx

(六) 任意角的三角函数、诱导公式、同角求值一、知识整理:(一)角的概念的推广1.正角(逆时针旋转)、负角(顺时针旋转)、零角(不旋转)2.终边相同的角:设βα,是始边相同的角,则βα,的终边相同απβ+=⇔k 2,Z k ∈.3.坐标系中的角:(规定:角的顶点与原点重合,始边在x 轴的正半轴上)第一象限角 第二象限角第三象限角 第四象限角(二)角的度量换算关系10= 弧度;1弧度= 0 弧长l = = ;扇形面积S= =(三)角函数的概念:1.定义1:设α的终边与单位圆交于点),(y x P ,则sin α= ,cos α= ,tan α= .定义2:若α的终边上一点),(y x P 呢?2.象限角的三角函数值的符号表:(四)诱导公式:απ±k 2,π+α,π-α,-α:函数名不变,符号看象限;2π+α,2π-α简记: 函数名要变,符号看象限。
(五)同角三角函数的基本关系:二、典型例题例1.若角α=40°,若β终边在α的反向延长线上,则β= ;若β与α的终边关于x 轴对称,则β= 。
例2.已知角α为第二象限角,试确定-α、2α、2α终边所在象限。
例3.已知扇形AOB 圆心角为120°,半径为6,求这个扇形的弧长,周长,扇形面积和所含弓形的面积。
例4.求下列各角的三角函数值 例5.已知角α的终边过点P (3,4),求角α的各三角函数值。
已知角α的终边过点P (3r ,4r )(r ≠0),求角α的各三角函数值。
例6.已知4sin =5α ,求cos ,tan αα。
若cos130a =o ,则tan 50=o ___________.(用a 的代数式表示)例7.求值1.sin(1560)cos 210cos(300)sin(1410)______.-︒︒+-︒-︒=2.222sin 1sin 2sin 89_______.︒+︒++︒=L x 0 6π 4π 3π 2π 32π 43π 65πsin xcos x tan x3.已知1sin cos 2x x -=,且x 在第三象限,则sin cos _______,sin cos ________.x x x x =+=4.已知tan α=2,求:3cos sin (1),cos 2sin x x x x +- (2)x x x cos sin sin 12- 二、课后练习:一、选择题1.终边落在x 轴上的角的集合是 ( ) A. {|360,}a a k k Z =∈o gB. {|(21)180,}a a k k Z =+∈o gC. {|180,}a a k k Z =∈o gD. {|18090,}a a k k Z =+∈o o g 2.半径为π,中心角为120o 的弧长为 ( )A .cm 3πB .cm 32πC .cm 32π D .cm 322π 3.函数|tan |tan cos |cos ||sin |sin x x x x x x y ++=的值域是 ( ) A .{1} B .{1,3} C .{1}- D .{1,3}-4.若2cos sin 2cos sin =-+αααα,则=αtan ( ) A .1 B . 1- C .43 D .34- 5.若θ是第三象限角,且02cos <θ,则2θ是 ( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角6.若21cos sin =⋅θθ,则下列结论中一定成立的是 ( ) A .22sin =θ B .22sin -=θ C .1cos sin =+θθ D .0cos sin =-θθ 二、填空题7.已知α的终边经过点(39,2)a a -+,且sin 0,cos 0αα>≤ ,则a 的取值范围是_ ______.8.若求值sin12000= cos 647π= . 9.已知1sin cos (0)5αααπ+=-≤≤,则tan α=______ __.10.若21cos >α,则α的取值范围是 . 11.角α的终边上有一点P(m ,5),且)0(,13cos >=m m α,则sin α+cos α=________. 三、解答题12.若α在第四象限,化简:22sin (3)cos ()sin(5)cos(3)5312sin()cos()22παπαπαπαππαα+---++-++- 13.若关于x 的方程0sin )(cos 22=+-+a x x π有实数根,求实数a 的取值范围。
2020年高三总复习数学人教旧版-必修4[第1讲 三角函数的概念]讲义(教师版)
![2020年高三总复习数学人教旧版-必修4[第1讲 三角函数的概念]讲义(教师版)](https://img.taocdn.com/s3/m/7bb4ddacbe23482fb5da4c67.png)
第 4页
S扇
nr 2 360
。又因为扇形的弧长 l
nr 180
,扇形面积
nr 2 360
可以写成
1 . nr 2 180
.r
,所以又得
到扇形面积的另一个计算公式:
S扇
1 2
l
r
.
例 1. 给出下列说法:①锐角都是第一象限角;②第一象限角一定不是负角;③第
二象限角是钝角;④小于 180°的角是钝角、直角或锐角;⑤三角形的内角一定是第一、二
第 6页
令 720 k.360 1020 360 ,解得 5 k< 23 ,而 k Z ,∴ k 1、2 、3 .
6
6
当 k 1时, 660 ;
当 k 2 时, 300 ;
当 k 3 时, 60 .
故在 720 ~ 360 范围内与 1020 终边相同的角有三个,分别是 660 、 300 、60 .
原点)的坐标是 x, y,它与原点的距离为 r
2
x
y2
x2 y2 0 ,那么:
第 9页
(1)比值 y 叫做 的正弦,记做 sin ,即 sin y y ;
r
r
x2 y2
(2)比值 x 叫做 的余弦,记做 cos ,即 cos x x ;
r
r
x2 y2
(3)比值 y 叫做 的正切,记做 tan ,即 tan y ;
3、角度与弧度的互化
(1)将角度化为弧度:360 2 ;180 ;1 0.01745 rad ;n n rad .
180
180
(2)将弧度化为角度: 2 360 ; 180 ;1rad (180) ; n(rad ) (180n) .
高一数学必修4三角函数诱导公式

高一数学必修4三角函数诱导公式诱导公式是高一数学必修四三角函数知识点只必考的公式,我们在考前一定要掌握好这些公式的应用。
下面是店铺为大家整理的高一数学必修4三角函数诱导公式,希望对大家有所帮助!高一数学必修4三角函数诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα (k∈Z)cos(2kπ+α)=cosα (k∈Z)tan(2kπ+α)=tanα (k∈Z)cot(2kπ+α)=cotα (k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαco t(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)高一数学函数复习资料一、定义与定义式:自变量x和因变量y有如下关系:y=kx+b则此时称y是x的一次函数。
必修四任意角的三角函数、弧度制、诱导公式讲义

1.1——1.3 任意角的三角函数、弧度制、诱导公式一、任意角(一)、角的分类:(1)正角:按逆时针方向.....旋转形成的角叫做正角;(2)负角:按顺时针方向.....旋转形成的角叫做负角;(3)零角:如果一条射线没有做任何旋转.......,我们称它为零角; 说明:零角的始边和终边重合。
(二)、终边相同的角:所有与角α终边相同的角,和同角α的内,可构成一个集合S ={β|β=α+k ×3600,k ∈Z }。
注意:(1)对于集合S ={β|β=α+k ×3600,k ∈Z }的理解,注意集合中的角α是任意角;集合中的“k ∈Z ”是一个必不可少的条件;(2)当角的始边相同时,若角相等,则终边一定相同;始边相同,终边相同的角不一...................................定相等;终边相同的角有无数个,它................们相差...360...0.的整数倍。
.....(3)终边相同的角表示方式不唯一。
对于集合A ={β|β=300+k ×3600,k ∈Z }也可表示为A ={β|β=-3300+k ×3600,k ∈Z }(三)、象限角与轴线角1、象限角:若角的终边(端点除外)在第几象限,我们就说这个角是第几象限角。
2、轴线角:如角的终边在坐标轴上,就认为这个角不属于任何象限.......。
(四)、弧度制1、定义:长度等于半径长的弧所对的圆心角叫做.................1.弧度的角....;用弧度作为单位来度量角的单位制叫作弧度制;在弧度制下,1弧度记作1rad 。
2、度量:正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0。
如果半径为r 的圆心角所对的弧的长为l ,那么,角α的弧度数的绝对值是|α|=rl(其中l 是以角α为圆心角时所对的弧长,r 是圆的半径,角α的正负由角α终边的旋转方向决定)。
高中数学必修四 角度制 三角函数关系及诱导公式讲解
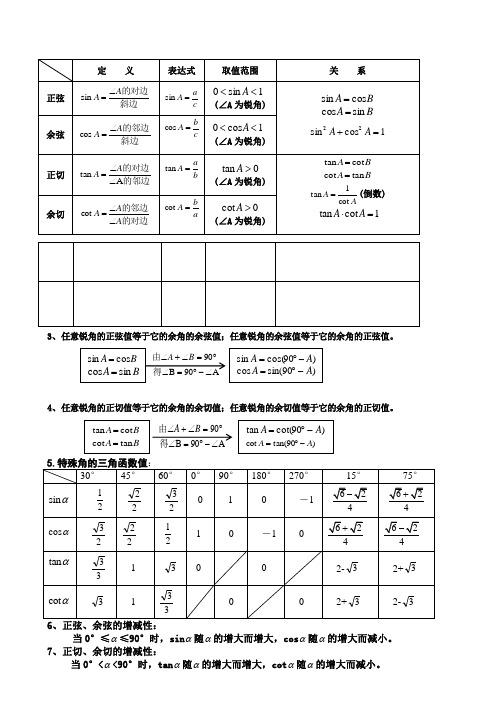
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
A90B 90∠-︒=∠︒=∠+∠得由B A一、任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =,那么sin ,cos y x r r αα==,()tan ,0y x x α=≠,cot xyα=(0)y ≠,sec r x α=()0x ≠,()csc 0ry yα=≠。
三角函数值只与角的大小有关,而与终边上点P 的位置无关。
设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为(cos_α,sin_α),即P (cos_α,sin_α),其中cos α=OM ,sin α=MP ,单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan α=AT .我们把有向线段OM 、MP 、AT 叫做α的余弦线、正弦线、正切线.三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.有向线段OM 为余弦线有向线段AT 为正切线比较)2,0(∈x ,x sin ,x tan ,x 的大小关系:三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
四、一条规律三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦.两个技巧(1)在利用三角函数定义时,点P 可取终边上任一点,如有可能则取终边与单位圆的交点,|OP |=r 一定是正值.(2)在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧.利用单位圆解三角不等式(组)的一般步骤是: (1)用边界值定出角的终边位置; (2)根据不等式(组)定出角的范围; (3)求交集,找单位圆中公共的部分; (4)写出角的表达式. (1)注意易混概念的区别:第一象限角、锐角、小于90°的角是概念不同的三类角,第一类是象限角,第二类、第三类是区间角.(2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.(3)α与2α的终边关系:由“两等分各象限、一二三四确定”.若α是第一象限,则2α是第一、三象限角;若α是第二象限,则2α是第一、三象限角;若α是第三象限角,则2α是第二、四象限;若α是第四象限角,则2α是第二、四象限。
高中数学必修4三角函数常考题型:三角函数的诱导公式

三角函数的引诱公式( 一 )【知识梳理】1.引诱公式二(1)角π+α 与角α 的终边对于原点对称.如下图.(2)公式: sin( π+α) =- sin_ α.cos( π+α) =- cos_ α .tan( π+α) = tan_ α.2.引诱公式三(1)角-α 与角α 的终边对于x轴对称.如下图.(2)公式: sin( -α) =- sin_ α .cos( -α) = cos_α.tan( -α) =- tan_ α.3.引诱公式四(1)角π-α 与角α 的终边对于y轴对称.如下图.(2)公式: sin( π-α) =sin_ α .cos( π-α) =- cos_ α .tan( π-α) =- tan_ α .【常考题型】题型一、给角求值问题【例 1】 求以下三角函数值:(1)sin( -1 200 °) ;(2)tan 945119π.°; (3)cos6[ 解 ] (1)sin( -1 200°) =- sin 1 200 °=- sin(3 ×360°+ 120°) =- sin 120 °=-sin(180 °- 60°) =- sin 60 °=-3 ;2(2)tan 945 °= tan(2 ×360°+ 225°) =tan 225 °= tan(180 °+ 45°) =tan 45 °=1;119ππ-π π 3(3)cos 6 = cos 20π-6 =cos 6 = 2 .6 = cos【类题通法】利用引诱公式解决给角求值问题的步骤【对点训练】求 sin 585°cos 1 290°+ cos( -30° )sin210°+ tan 135°的值.解: sin 585°cos 1 290°+ cos( -30° )sin210°+ tan 135°= sin( 360°+225° )cos( 3×360°+ 210) + cos 30°sin210°+ tan( 180°- 45° ) = sin 225°cos 210°+cos 30°sin 210°- tan 45°= sin( 180°+ 45° )cos( 180°+ 30° ) + cos 30°· sin ( 180°+30° ) - tan45°= sin45°cos30°- cos 30°sin30°- tan 45°=2×2 3 -23× 1-12 26- 3-4=.4题型二、化简求值问题【例 2】 (1)cos- α tan 7π+ α 化简: sinπ- α=________;(2) sin 1 440°+ α ·cos α-1 080°化简-180°- α.cos·sin - α-180°(1)[ 解 析 ]cos - α tan7π+ αcos αtan π+ αcos α·tan αsinπ-α =α==sin sin αsinαsinα= 1.[答案]1(2)[解 ]原式=sin4×360°+α·cos3×360°-α=sin α·cos -αcos180°+α·[ - sin180°+α ]- cos α·sin αcosα=- cos α=-1.【类题通法】利用引诱公式一~四化简应注意的问题(1)利用引诱公式主假如进行角的转变,进而达到一致角的目的;(2)化简时函数名没有改变,但必定要注意函数的符号有没有改变;(3)同时有切 ( 正切 ) 与弦 ( 正弦、余弦 ) 的式子化简,一般采纳切化弦,有时也将弦化切.【对点训练】化简:tan 2π-θsin2π-θ cos6π-θ.- cos θsin 5π+θ解:原式=tan-θsin-θ cos-θ=tanθsinθcosθ=tanθ.- cos θsin π+θcos θsin θ题型三、给角(或式)求值问题【例 3】 (1) 已知 sinβ =1,cos(α+β)=-1,则sin(α+2β )的值为() 3A. 1B.- 1D.-131(2)已知 cos( α-55° ) =-3,且α为第四象限角,求 sin(α+125°)的值.(1)[分析 ] ∵ cos( α+β ) =- 1,∴α+β=π+2kπ,k∈Z,1∴ sin(α+2β)=sin[(α +β)+β]=sin(π+β)=-sinβ =-3.[答案]D1(2)[解]∵ cos(α-55° )=-3<0,且α是第四象限角.∴α-55°是第三象限角.sin( α-55° ) =-1- cos 2α-55°=-22.3∵α+125°=180°+(α -55°),22∴sin( α+125° ) =sin[180 °+ ( α-55°)] =- sin( α-55° ) =3 .【类题通法】解决条件求值问题的策略(1)解决条件求值问题,第一要认真察看条件与所求式之间的角、函数名称及相关运算之间的差别及联系.(2)能够将已知式进行变形向所求式转变,或将所求式进行变形向已知式转变.【对点训练】1已知 sin( π+α) =-,求cos( 5π+α)的值.3解:由引诱公式得,sin( π+α ) =- sinα,1因此 sinα=3,因此α 是第一象限或第二象限角.当α 是第一象限角时,cos α=1- sin2α=232,此时, cos( 5π+α) = cos( π+α ) =- cos22α=-.3cos α=-1-sin 222当α 是第二象限角时,α=-3,此时, cos( 5π+α) = cos( π+α ) =- cos22α=.3【练习反应】1. 如下图,角θ的终边与单位圆交于点P -5,25,则 cos( π-55θ)的值为()255A.-5B.-55分析:选C∵r=1,∴ cosθ=-5,∴ cos( π-θ) =- cosθ =5. 52.已知sin(4π+α)=5,且α 是第四象限角,则cos(α-2π)的值是()A .-35 3C .± 5分析:选 B4sin α=- ,又 α 是第四象限角,523∴ cos( α-2π ) = cos α=1- sin α= 5.3.设 tan( 5π+ α) = m ,则sin α-3π+ cos π- α= ________.sin - α -cos π+ α分析:∵ tan( 5π+ α) =tanα= m ,- sin α - cos α - tan α- 1 - m - 1 m + 1∴原式= - sin α + cos α= - tan α+ 1= - m + 1= m - 1.m + 1答案: m - 1495°+ sin -570°) 的值是 ________.分析:原式= sincos 360°+ 225°360°+ 135° - sin 210°+ 360° =sin cos 225°210° = sincos 180°+ 45°135°- sin180°- 45° - sin 180°+ 30°2=- cos 45°- 2= 2-2.45°+ sin 30°=sin 2 1 2 + 2答案:2- 25.已知 cosπ3 ,求 cos α+ 5π6 - α =3 6 的值.解: cos π+ 5π=- cos 5π6 π- α+ 6 =π -3 - cos 6 α =- 3 .。
人教版必修四1.3三角函数的诱导公式课件

探究与归纳
角 与角的三角函数关系?
y
终边关系
关于原点对称
点的关系 P(x, y)
P(x, y)
O
P(x, y)
x
三角函数 定义
sin y
cos x
tan y
x
sin( ) y
cos( ) x
tan( ) y
x
P(x, y)
三角函数 关系
(公式二)
sin( ) sin
cos( ) cos
(3)化为锐角的三角函数。 概括为:“负化正,正化小,化到锐角就终了。”
用框图表示为:
用公式一
任意角的三角函数
任意正角的三角函数
或公式三
公式一
用公式二
锐角三角函数
0~2的角的三角函数
或公式四
当堂检测
1、计算
(1) tan120 0 3
3/2 (2)sin(240 0 )
2、化简
sin( ) cos(2 sin(3 ) cos(
,
cos(-α)= cosα
符
tan(-α)= -tanα
号
看
公式(四) sin(π-α)= sinα cos(π-α)= -cosα
象 限
tan(π-α)= -tanα
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”. 其含义是诱导公式两边的函数名称一致,符号则是将α看成锐 角时原角所在象限的三角函数值的符号.α看成锐角,只是公式 记忆的方便,实际上α可以是任意角.
cos( 2k ) cos
tan( 2k ) tan
(k Z)
终边相同角的同一三角函数的值相等
探要点·究所然
情境导学
高中必修4三角函数第二节任意角的三角函数_教师版

C.π4或54π
D.π4或74π
【答案】 C 作出角π4与54π的正弦线、余弦如图所示.
由图可知,角π4与54π的正弦线、余弦线长度相等,且符号相同.
5.下列不等式中,成立的是( ) A.sin1>sin2 C.tan1>tan2
B.cos1<cos2 D.cot1<cot2
【答案】 C 如图,由单位圆中的三角函数线可知,sin1<sin2,cos1>cos2,tan1>tan2,故选 C.
=3×222-2+4×12+1=1.
27.已知 tan(π+α)=-12,求下列各式的值.
(1)
-α - α- +
+α -α
;
(2)sin(α-7π)·cos(α+5π).
【答案】 tan(π+α)=-12⇒tanα=-12, (1)原式=-42ccoossαα-+s3insiαnα=-42-+t3antaαnα
一、以考查知识点为主试题
【容易题】
1.已知角 α 的终边经过点(-4,3),则 cosα=( )
A.45
B.35
C.-35
D.-45
【答案】 D 考查了三角函数的定义.
由条件知:x=-4,y=3,则 r=5,∴cosα=xr=-45.
2.如果角 α 的终边经过点(2sin30°,-2cos30°),则 sinα=( )
25.若 sinα=mm- +35,cosα=4m-+25m,π2<α<π,则 m=________.
【答案】 8
由题意,得
m-3 m+5>0 4-2m m+5 <0
,
m-3 m+5
2+
4-2m m+5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任意角的三角函数与诱导公式(教师)1.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P (x ,y ),它与原点的距离为(r r =,那么角α的正弦、余弦、正切分别是:sin α=y r ,cos α=x r ,tan α=yx.(三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦)3.特殊角的三角函数值1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1;(在利用同角三角函数的平方关系时,若开方,要特别注意判断符号) (2)商数关系:sin αcos α=tan α. (3)倒数关系:1cot tan =⋅αα 2.诱导公式公式一:sin(α+2k π)=sin α,cos(α+2k π)=cos_α,απαtan )2tan(=+k 其中k ∈Z . 公式二:sin(π+α)=-sin_α,cos(π+α)=-cos_α,tan(π+α)=tan α. 公式三:sin(π-α)=sin α,cos(π-α)=-cos_α,()tan tan παα-=-. 公式四:sin(-α)=-sin_α,cos(-α)=cos_α,()tan tan αα-=-. 公式五:sin ⎝⎛⎭⎫π2-α=cos_α,cos ⎝⎛⎭⎫π2-α=sin α. 公式六:sin ⎝⎛⎭⎫π2+α=cos_α,cos ⎝⎛⎭⎫π2+α=-sin_α. 口诀:奇变偶不变,符号看象限.口诀1、诱导公式的记忆口诀为:奇变偶不变,符号看象限.2、四种方法(1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (ααcos sin +、ααcos sin -、ααcos sin 三个式子知一可求二)(3)巧用“1”的变换:1=sin 2θ+cos 2θ= sin2π=tan π4 (4)齐次式化切法:已知k =αtan ,则n mk bak n m b a n m b a ++=++=++ααααααtan tan cos sin cos sin1.若sin cos 0αα⋅>,则角α的终边在( )A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限【详解】sin cos 0αα⋅>Q ,sin ,cos αα∴同号,所以角α的终边在第一、三象限 故选:B 2.若角θ满足sin 0θ<,tan 0θ<,则角θ是( )A .第三象限角B .第四象限角C .第三象限角或第四象限角D .第二象限角或第四象限角【详解】因为sin 0<θ时,角θ可以是第三、第四象限角,或终边在y 轴负半轴上; 又tan 0θ<时,角θ可以是第二、第四象限角;因此角θ是第四象限角.故选B 3.已知点(tan ,cos )P αα在第三象限,则角α的终边在( )A .第一象限B .第二象限C .第三象限D .第四象限【详解】因为点(tan ,cos )P αα在第三象限,则tan 0α<,cos 0α<, 所以sin tan cos 0ααα=>,则可知角α的终边在第二象限.故选:B. 4.已知角α的终边上有一点(7,24)P -,则sin α=()A .725B .725-C .2425D .2425-【详解】因为角α的终边上有一点(7,24)P -,所以24sin 25α==.故选:C. 5.已知tan 0,cos 0θθ<<,则θ的终边在( )象限A .第一B . 第二C . 第三D .第四【详解】由于tan 0θ<,故θ可能是第二或第四象限角;由于cos 0θ<,故θ可能是第二象限角,或第三象限角或终边落在x 轴的负半轴.由此判断出θ终边在第二象限.故选B. 6.已知角θ的终边过点(12,5)P -,则cos θ的值为A .513B .1213 C .513- D .1213-【详解】因为12cos 13x r θ===,故选B.7.若sin αtan α<0,且cos tan αα<0,则角α是( ) A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角【详解】由sin αtan α<0可知sin α,tan α异号,则α为第二象限角或第三象限角,由cos tan αα<0可知cos α,tan α异号,则α为第三象限角或第四象限角.综上可知,α为第三象限角.所以本题答案为C. 8.已知角θ的终边过点(3,4)-,则cos θ的值为( )A .23B .34C .35D .25【详解】∵角θ的终边过点(3,4)-,∴3x =,4y =-,=5r ,∴3cos 5x r θ==.故选C 9.角α的终边经过点(3,4),则sin cos sin cos αααα+=-A .35B .45 C .7D .17【详解】由角α的终边经过点(3,4),可得4sin 5α=,3cos 5α=,则43sin cos 55743sin cos 55αααα++==--.故选C . 10.已知角α的终边经过点()3,4P -,则cos α的值等于( )A .35-B .35C .45 D .45-【详解】由三角函数的定义可得3cos 5α==-,故选:A.11.0sin300=( )A .12B .12CD000036s 0))in300sin(300sin(60sin60-︒==-==- 12.如果点位于第三象限,那么角位于( )A .第一象限B .第二象限C .第三象限D .第四象限点位于第三象限,是第二象限角。
13.若α是第二象限角,则点()sin ,cos P αα在 ( )A .第一象限B .第二象限C .第三象限D .第四象限【详解】因为α是第二象限角,所以sin 0,cos 0αα><,所以点()sin ,cos P αα在第四象限,故选:D 14.已知(1,)P t -在角α终边上,若sin 5α=,则t =( ) A .12B .-2C .2D .2±【详解】sin α==0t >,∴2t =.故选C . 15.已知,,那么是( ) A .第一象限 B .第二象限C .第三象限D .第四象限详解】,在三四象限., 在一三象限,故在第三象限 答案为C16.若sin cos 4sin 5cos αααα+=-,则tan α等于( )A .17 B .13C .3D .7显然tan 0α≠,sin cos sin cos tan 1cos cos 444tan 7sin cos sin 5cos tan 55cos cos ααααααααααααααα+++=⇒=⇒=⇒=---,故本题选D. 17.已知3,2παπ⎛⎫∈ ⎪⎝⎭,tan 2α=,则cos α的值为( ).A.5-BC. D【详解】由3,2παπ⎛⎫∈ ⎪⎝⎭可知:sin 0α<,cos 0α<由22sin tan 2cos sin cos 1ααααα⎧==⎪⎨⎪+=⎩得:cos α=本题正确选项:A 18.若1cos ,,32πααπ⎛⎫=-∈⎪⎝⎭,则tan α等于( ) A.4-B.4C.-D.【详解】1cos ,,,sin 323πααπα⎛⎫=-∈∴== ⎪⎝⎭,sin tan cos ααα∴==-19.若,则 ( )A .1B .C .D .【详解】因为,所以,所以,故选A.20.若4sin 5α=,tan 0α<,则cos α=( ) A .35- B .35 C .45- D .45【详解】sin tan 0cos ααα=<且4sin 05α=> c o s 0α∴<3c o s 5α∴==-本题正确选项:A21.已知α是第二象限,5sin 13α=,则cos α=( )A .1213-B .513- C .513 D .1213【详解】α为第二象限角 cos 0α⇒<12cos 13α∴===- 22.若角α是第四象限角,满足1sin cos 5αα+=-,则sin 2α=( )A .2425B .2425-C .1225D .1225-【详解】解:∴角α满足1sin cos 5αα+=-,平方可得 1+sin2125α=,∴sin22425α=-,故选:B . 23.若α为锐角,4sin 5α=,则cos α= A .15- B .15 C .35- D .35【详解】4sin 5α=且α为锐角3cos 5α∴==本题正确选项:D24.若α∈(π2,π),tanα=( ) A.B.C.2-D【详解】∵α∈(2π,π),且sinα=3,∴cosα=tan α= .故选:C . 25.已知tan θ=2,θ为第三象项角,则sin θ=( )AB. CD .5-由于θ为第三象限角,故sin 0,cos 0θθ<<,依题意有22sin 2cos sin cos 1θθθθ⎧=⎪⎨⎪+=⎩,解得sin θ= B.26.若1tan 2θ=-,则sin cos θθ的值为( )A .15B .35C .45-D .25-【详解】因为222sin cos tan sin cos 1sin cos tan θθθθθθθθ==++,又1tan 2θ=-,所以122sin cos 1514θθ-==-+.故选D 27.已知(,)2παπ∈,tan 3α=-,则cos α=( )ABC. D. ,sin 3cos αα=-,且22sin cos 1αα+=,得21c o s 10α=,又因为,2παπ⎛⎫∈ ⎪⎝⎭,所以cos 0α<,cos α=,28.若sin =,0<<,则cos =( )A .B .C .D .【详解】解:∵sinα,0<α,∴cosα.故选:D .29.如果,,那么等于( )A .B .C .D .【详解】∵,可解得:.又,∴∴故选:A .30.已知,则值为( )A.B .C .D .【详解】解:由题意得:,=,==,==,故选D.31.已知,且为第二象限角,那么A .B .C .D .【详解】,且为第二象限角,,则,故选:D .32的结果为( )A .sin50cos50︒-︒B .cos50sin50︒-︒C .sin50cos50︒+︒D .sin50cos50-︒-︒5050?sin50cos50sin cos ︒-︒=︒-︒. 33.若1sin 3α=-,且α为第四象限角,则tan()πα-的值等于( )A.4B.-C.D.4-∵1sin 3α=-,且α为第四象限角,∴cosα3=,∴tan (π﹣α)=﹣tanα=﹣sin cos 4αα=. 34.已知sin 2cos 53sin 5cos αααα-=-+,那么tan α的值是( )A .-2B .2C .2316D .2316-【详解】由题意可知:cosα≠0,分子分母同除以cosα,得235tan tan αα-=-+5,∴tanα2316=-.故选:D .35.已知tan α=2παπ<<,则sinα的值为( ) A .12BC .12-D. 【详解】解:∵tan α=∴22sin cos sin cos 1αααα⎧=⎪⎨⎪+=⎩,解得12sin cos αα⎧=⎪⎪⎨⎪=-⎪⎩或12sin cos αα⎧=⎪⎪⎨⎪=⎪⎩.∵π2απ<<,∴sin α=.故选:B . 36.若3sin 5α=,且α为第二象限角,则tan α的值等于( ) A .45 B .45-C .34D .34-【详解】∵sinα35=,且α为第二象限角,∴cosα45==-,∴tanα34sin cos αα==-.故选:D . 37.已知3cos 5α=,α是第四象限角,则tan α的值是( ) A .34 B .34-C .43D .43-【详解】∵cosα35=,α为第四象限角,∴sinα45==-,则tanα43=-.故选:D .38.若sinα=-45,且α为第三象限的角,则cosα的值等于( ) A .35B .35-C .43D .43-【详解】解:由题意,αQ 为第三象限角cos 0α∴<4sin 5α=-,3cos 5α∴===-39.若1sin 3α=,且(0,)2πα∈,则tan α=( ) A.2 BCD.4【详解】∵1sin 3α=,且0,2πα⎛⎫∈ ⎪⎝⎭,∴cos 3α=,sin tan cos 4ααα==故选:D 40.若tan 3α4=,则222cos α4sin αcos αcos α4sin α++=( )A .6425 B .4825 C .1613D .413 【详解】∵tan 3α4=,∴2222314cos α4sin αcos α14tan α1649cos α4sin α14tan α131416+⨯++===+++⨯.故选:C . 41.若tan 2α=,则23sin cos sin cos αααα+-=( )A .5B .6C .7D .7±【详解】因为tan 2α=,所以2sin 3cos 2tan 32237sin cos tan 121αααααα++⨯+===---.42.已知tan α=3,则2212sin cos sin cos αααα+-的值是A .12B .2C .-12D .-2原式=()()222222sin cos ()tan?1312sin cos tan?131sin cos sin cos sin cos sin cos sin cos sin cos αααααααααααααααααα++++++=====-+----. 43.sin 240︒的值为( )A.2-B.2 C. D.2【详解】sin 240=sin(180+60)sin 602︒︒︒=-︒=-故选:C 44.1717cos tan 46ππ⎛⎫-⎪⎝⎭的值为( ) A. B.C. D【详解】因为1717cos cos cos 4cos 44442ππππ⎛⎫⎛⎫-==π+== ⎪ ⎪⎝⎭⎝⎭,17tantan 3tan 6663πππ⎛⎫=π-=-=- ⎪⎝⎭所以1717cos tan 466ππ⎛⎫-=- ⎪⎝⎭,故选:C . 45.23cos 3π⎛⎫- ⎪⎝⎭的值是( )A .12 B .12- CD. 【详解】231cos cos 8cos 3332ππππ⎛⎫⎛⎫-=-+== ⎪ ⎪⎝⎭⎝⎭故答案选A46.化简()()()()()23sin cos cos tan 2cos αππααπααπ--+-+--得到( )A .sin α-B .sin αC .cos α-D .cos α依题意,原式()()2sin cos cos tan cos ααααα⋅-⋅=⋅-22sin cos sin sin cos cos αααααα⋅==⋅.故选:B. 47.()cos 2040-= ( )A .12B.2C. D .12-()()1c o s 2040c o s 2040+3606=c o s (120)c o s (180120)c o s 602-=-⨯=--=-=-故选:D .48.sin80cos70sin1s n 00i 7+︒⋅︒︒︒=( )A. B .12-C .12D()1sin80cos70sin10sin70cos10cos70sin10sin70cos 7010cos602︒︒+︒︒=︒︒+︒︒=︒-︒=︒=,故选C.49.cos225︒=( )A .12B.2C.2-D. 【详解】由三角函数的诱导公式可知:2cos 225cos(18045)cos 452︒=+=-=-50.23πtan 6⎛⎫-⎪⎝⎭的值为A B.3C .2D .12【详解】23πππtan tan 4πtan 6663⎛⎫⎛⎫-=-+== ⎪ ⎪⎝⎭⎝⎭ B 51.已知1sin 5θ=,则()cos 450θ︒+的值是( )A .15 B .15-C .D .5【详解】()()()1cos 450cos 36090cos 90sin 5θθθθ︒+=︒+︒+=︒+=-=-,故选B.52.2017sin3π的值等于( )A .12B .12-C .2D .【详解】2017sinsin 672sin 333ππππ⎛⎫=+== ⎪⎝⎭。
