EBC初级讲义6
三角形优质讲义
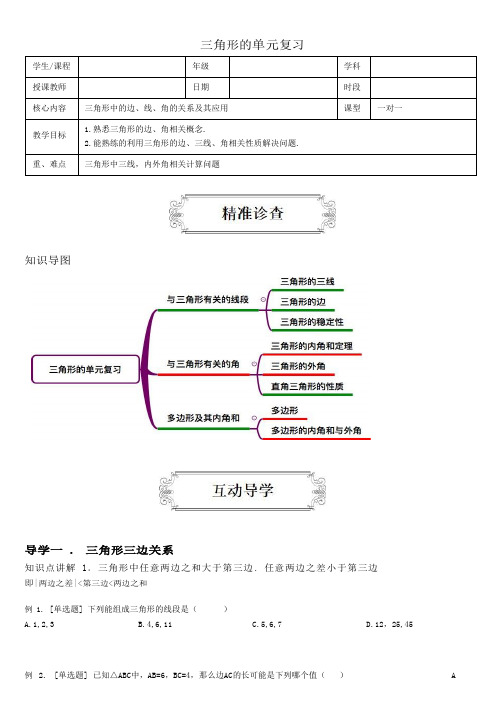
三角形的单元复习学生/课程年级学科授课教师日期时段核心内容三角形中的边、线、角的关系及其应用课型一对一教学目标1.熟悉三角形的边、角相关概念.2.能熟练的利用三角形的边、三线、角相关性质解决问题.重、难点三角形中三线,内外角相关计算问题知识导图导学一:三角形三边关系知识点讲解1:三角形中任意两边之和大于第三边,任意两边之差小于第三边即|两边之差|<第三边<两边之和例1. [单选题] 下列能组成三角形的线段是()A.1,2,3B.4,6,11C.5,6,7D.12,25,45例 2. [单选题] 已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值()A.1 B. 5 C.2 D. 1例3. [单选题] (2014广东)一个等腰三角形的两边长分别是3和7,则它的周长为()A. 17B. 15C. 13D. 13或17 【学有所获】判断给定线段能否围成三角形:只要最短的两边之和大于第三边即可组成三角形确定三角形第三边的取值范围:|两边之差|<第三边<两边之和等腰三角形问题:如果给出两边长,第三边边长分情况讨论,注意最后要建议这三边能为围成三角形。
我爱展示1.判别下列各组线段哪些能组成三角形,哪些不能组成三角形,并说明理由。
(1) 15cm、10cm、7cm (2) 4cm、5cm、10cm(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm2.[单选题] 在1,2,3,4,5这五个数中,任取三个组成三角形,方法有()种A.1B.2C.3D.43.三角形三边长分别为1,x,8,若x为正整数,则x的值为4.[单选题] 已知等腰三角形的两边长分别是5和6,则这个等腰三角形的周长为(). A.11 B.16 C.17 D.16或17导学二:三角形的高、中线与角平分线知识点讲解1例1. 如图,AD为三角形ABC的边BC上的中线,△ABC面积为20,则△ABD面积为多少?【学有所获】三角形中线把三角形分成等面积的两半例2. 在△ABC中,∠BAC为90度,AD为BC上的高,AB=4,BC=5,求AC与AD的比。
BEC初级讲义_第四章

Chapter Four Telephoning& Internal CommunicationI. Teaching ObjectivesOn completion of this Chapter, students should be able to:1. practice useful expression of telephoning (how to leave a message)2. practice listening comprehension from acquiring information of the content3. put functional sentences into practice4. write memo and E-mail5. expressing request and discuss responsibilityII. The Points to Be HighlightedStudents should know how to make effective communications by telephone.III. Teaching Approaches and FacilitiesApproaches: 1. Pair/Group work 2. Discussion 3 Task-based approach4. Communicative approach5. Questions and answers…… Facilities: blackboard, on-line research;IV. Background InformationGo over the basic telephone expressions.V. Teaching Procedures and Contents1. Leading-inGo over some telephone expressions learned before.2. Speacial ContentsLearning Difficulties1. easily answer and get through the phone2. understand the dialogue from the tape3. the process of leaving a message4. the process of leaving a memos, notes, and notice1. words and phrasesA: receptionist 接待员connect 连接,接通电话extension 电话分机put through(to) 为……接通电话cut off 中断。
培训教材(初级版)

黄石市科威自控有限公司——EC/EP系列嵌入式PLC培训教材(初级版)序言电控技术日异月新,市场需求日益苛刻。
作为一家“以复兴民族自动化工业为已任”的科技型公司,只是学习、消化、汲取、实践别人的产品和技术是远远不够的,一定有自己独创的产品,才能在没有硝烟的战场上取获成功。
在董事长龚云生同志的得力领导下,公司公司骨干一直朝着“创新是一个民族的灵魂,是国家兴盛发达的不停动力”的方向奋进。
十余年来,战胜了重重困难,坚韧不拔地走自己的路。
发场团队精神,仔细累积和总结经验;自主创新与借“脑袋”并举。
天道酬勤,科威公司的科技成就不停浮现,特别是2005年,EC/EP系列嵌入式PLC在黄石市科威自控有限公司研发成功了!为我国的自动化工业增加了光彩。
自嵌入式PLC的成就在网上公布后,感兴趣的同仁日新月异,渴求认识其技术性能。
正由于嵌入式PLC刚才问世,知者甚少,为此,科威公司决定创办嵌入式PLC培训班。
这是切合“科学发展观”的要求的。
培训班的教材内容,由表及里,由浅入深。
因受时间和要求所限,不系统,重视实践。
希望对初学者,有所补益。
卫工08 年5月一、嵌入式PLC简介1、开发背景工控系统有大系统和小系统,特别是小系统,范围广,几乎覆盖了全部行业,并且要求是千差万其余。
控制器件有DCS、IPC和PLC等。
广大工控设计人员在器件选型时十分疑惑。
在数据办理上要求像IPC,在靠谱性上要求达到或超出PLC,在价位上力求便宜,好像单片机;在二次开发(应用程序)方面要求语言普通化、易学易懂易掌握。
谁都梦想有一款新式的工控产品能代替、包括IPC、PLC和单片机。
经过艰辛的努力,嵌入式PLC在科威公司问世了。
嵌入式PLC已列入国家科技攻关计划项目的阶段成就。
项目代号为2005BA206C。
2、什么是嵌入式PLC?嵌入式PLC是将通用的PLC梯形图语言、CANbus现场总线协议嵌入到单片机中,使其更具个性化、差别化,应用更宽泛、更灵巧,对用户更方便。
中考数学解题大招复习讲义(全国通用)模型06 射影定理模型(解析版)

模型介绍1.射影定理定义①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.2.如图在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,有射影定理如下: 注意:直角三角形斜边上有高时,才能用射影定理!例题精讲【例1】.在矩形ABCD 中,BE ⊥AC 交AD 于点E ,G 为垂足.若CG =CD =1,则AC 的长是.①AD 2=BD •DC ;②AB 2=BD •BC ;AC 2=CD •BC .解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.【例2】.如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为()A.﹣B.﹣C.﹣1D.﹣2解:设A(x1,0)(x1<0),B(x2,0)(x2>0),C(0,t),∵二次函数y=ax2+bx+2的图象过点C(0,t),∴t=2;∵AC⊥BC,∴OC2=OA•OB(射影定理),即4=|x1x2|=﹣x1x2,根据韦达定理知x1x2=,∴a=﹣.故选:A.【例3】.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是()A.3B.8C.D.2解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.变式训练【变式1】.如图,在△ABC中,若=AC,BC=2BD=6,DE⊥AC,则AC•EC的值是9.解:如图,∵在△ABC中,若AB=AC,BC=2BD=6,∴AD⊥BC,CD=BD=3.又DE⊥AC,∴∠CED=∠CDA=90°.∵∠C=∠C,∴△CDE∽△CAD.∴=,即AC•EC=CD2=9.(射影定理)故答案是:9.【变式2】.如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于O,且BE:ED=1:3,AD=6cm,则AE=cm.解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x(3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.【变式3】.如图,若抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,若∠OAC=∠OCB.则ac的值为()A.﹣1B.﹣2C.D.解:设A(x1,0),B(x2,0),C(0,c),∵二次函数y=ax2+bx+c的图象过点C(0,c),∴OC=c,∵∠OAC=∠OCB,OC⊥AB,∴△OAC∽△OCB,∴,∴OC2=OA•OB(即射影定理)即|x1•x2|=c2=﹣x1•x2,令ax2+bx+c=0,根据根与系数的关系知x1•x2=,∴,故ac=﹣1,故选:A.【变式4】.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=____________.解:连接CF、GF,如图:在正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC,∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣【变式5】.如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC 交⊙O于点E、H,连AD、ED、EC.若BD=8,DC=6,则CE的长为2.解:∵AC为⊙O的直径,∴∠ADC=90°,∵BG⊥AC,∴∠BGC=∠ADC=90°,∵∠BCG=∠ACD,∴△ADC∽△BGC,∴=,∴CG•AC=DC•BC=6×14=84,连接AE,∵AC为⊙O的直径,∴∠AEC=90°,∴∠AEC=∠EGC=90°,∵∠ACE=∠ECG,∴△CEG∽△CAE,∴=,∴CE2=CG•AC=84,∴CE=2.故答案为2.【变式6】.如图,四边形ABCD是平行四边形,过点A作AE⊥BC交BC于点E,点F在实战演练BC 的延长线上,且CF =BE ,连接DF .(1)求证:四边形AEFD 是矩形;(2)连接AC ,若∠ACD =90°,AE =4,CF =2,求EC 和AC的长.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵CF =BE ∴BE +CE =CF +CE ,即BC =EF ,∴AD =EF ,∵AD ∥EF ,∴四边形AEFD 是平行四边形,∵AE ⊥BC ,∴∠AEF =90°,∴平行四边形AEFD 是矩形;(2)解:如图,∵CF =BE ,CF =2,∴BE =2,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAC =∠ACD =90°,∵AE ⊥BC ,∴AE 2=BE •EC (射影定理),∴EC ===8,∴AC ===4.1.如图,在矩形ABCD 中,DE ⊥AC ,垂足为点E .若sin ∠ADE =,AD =4,则AB 的长为()A .1B .2C .3D .4解:∵DE ⊥AC ,∴∠ADE+∠CAD=90°,∵∠ACD+∠CAD=90°,∴∠ACD=∠ADE,∵矩形ABCD的对边AB∥CD,∴∠BAC=∠ACD,∵sin∠ADE=,BC=AD=4,∴=,∴=,∴AC=5,由勾股定理得,AB==3,故选:C.2.如图,在矩形ABCD中,BD=2.对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E,AE=3CE.则DE2的值为()A.4B.2C.D.4解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=2,∵AE=3CE,∴AE=AC=,CE=AC=,∵∠ADC=90°,∴∠DAC+∠ACD=90°,∵DE⊥AC,∴∠AED=∠CED=90°,∴∠ADE+∠DAC=90°,∴∠ADE=∠ACD,∴△ADE∽△DCE,∴=,∴DE2=AE•CE=×=,故选:C.3.如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于()A.B.C.D.解:如图,设点S为BC的中点,连接DP,DS,DS与PC交于点W,作PE⊥BC于点E,PF⊥AB于点F,∴DP=CD=2,PS=CS=1,即DS是PC的中垂线,∴△DCS≌△DPS,∴∠DPS=∠DCB=90°,∴DS===,由三角形的面积公式可得PC=,∵BC为直径,∴∠CPB=90°,∴PB==,∴PE=FB==,∴PF=BE==,∴AF=AB﹣FB=,∴AP==故选:B.4.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④OA(CP﹣CD)=AP•CD,正确的结论有()个.A.1B.2C.3D.4解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P,∴△PBC∽△PCA,∴PC2=PA•PB;②∵OC⊥PC,∴PC•OC=OP•CD;③∵CD⊥AB,OC⊥PC,∴OC2=OD•OP,∵OA=OC,∴OA2=OD•OP;④∵AP•CD=OC•CP﹣OA•CD,OA=OC,∴OA(CP﹣CD)=AP•CD,所以正确的有①,②,③,④,共4个.故选:D.5.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长.解:作EH⊥BC于H,如图,∵∠A=90°,AB=AC=8,∴BC=AB=16,∠C=45°,∵点E为AC的中点,∴AE=CE=4,∵△CEH为等腰直角三角形,∴EH=CH==4,∴BH=12在Rt△ABE中,BE==4,在Rt△BEF中,∵EH⊥BF,∴BE2=BH•BF,即BF==,∴CF=BC﹣BF=16﹣=.故答案为.6.如图,在矩形ABCD中,点E在边AD上,把△ABE沿直线BE翻折,得到△GBE,BG 的延长线交CD于点F.F为CD的中点,连结CG,若点E,G,C在同一条直线上,FG=1,则CD的长为2+2,cos∠DEC的值为﹣1.解:∵四边形ABCD是矩形,∴AB=CD,AD∥BC,∠BCD=∠A=∠D=90°,∴∠AEB=∠EBC,∠BCG=∠DEC,由折叠的性质得:BG=BA,∠EGB=∠A=90°,∠GEB=∠AEB,∴CD=BG,∴∠EBC=∠GEB,∴BC=EC,∵点E,G,C在同一条直线上,∴∠CGF=90°,∠CGB=180°﹣∠EGB=90°,∵F为CD的中点,∴CF=DF,设CF=DF=x,则BG=CD=2x,∵∠CFG=∠BFC,∴△CFG∽△BFC,∴=,∴CF2=FG•BF,即x2=1×(1+2x),解得:x=1+或x=1﹣(舍去),∴CD=2x=2+2,∵∠DEC+∠ECD=90°,∠GFC+∠ECD=90°,∴∠DEC=∠GFC,∴cos∠DEC=cos∠GFC===﹣1,故答案为:2+2,﹣1.7.如图,在平面直角坐标系中,直线y=kx+1分别交x轴,y轴于点A,B,过点B作BC ⊥AB交x轴于点C,过点C作CD⊥BC交y轴于点D,过点D作DE⊥CD交x轴于点E,过点E作EF⊥DE交y轴于点F.已知点A恰好是线段EC的中点,那么线段EF的长是.解:因为AB的解析式为y=kx+1,所以B点坐标为(0,1),A点坐标为(﹣,0),由于图象过一、二、三象限,故k>0,又因为BC⊥AB,BO⊥AC,所以在Rt△ABC中,BO2=AO•CO,代入数值为:1=•CO,CO=k,同理,在Rt△BCD中,CO2=BO•DO,代入数值为:k2=1•DO,DO=k2又因为A恰好是线段EC的中点,所以B为FD的中点,OF=1+1+k2,Rt△FED中,根据射影定理,EO2=DO•OF,即(k++)2=k2•(1+k2+1),整理得(k﹣)(k+)(k2+2)(k2+1)=0,解得k=.根据中位线定理,EF=2GB=2DC,DC==,EF=2.8.如图,在菱形ABCD中,过点D作DE⊥CD交对角线AC于点E,连接BE,点P是线段BE上一动点,作P关于直线DE的对称点P',点Q是AC上一动点,连接P'Q,DQ.若AE=14,CE=18,则DQ﹣P'Q的最大值为.解:如图,连接BD交AC于点O,过点D作DK⊥BC于点K,延长DE交AB于点R,连接EP′并延长,延长线交AB于点J,作EJ关于AC的对称线段EJ′,则点P′的对应点P″在线段EJ′上.当点P是定点时,DQ﹣QP′=DQ﹣QP″,当D,P″,Q共线时,QD﹣QP′的值最大,最大值是线段DP″的长,当点P与B重合时,点P″与J′重合,此时DQ﹣QP′的值最大,最大值是线段DJ′的长,也就是线段BJ的长.∵四边形ABCD是菱形,∴AC⊥BD,AO=OC,∵AE=14.EC=18,∴AC=32,AO=OC=16,∴OE=AO﹣AE=16﹣14=2,∵DE⊥CD,∴∠DOE=∠EDC=90°,∵∠DEO=∠DEC,∴△EDO∽△ECD,∴DE2=EO•EC=36,∴DE=EB=EJ=6,∴CD===12,∴OD===4,∴BD=8,=×OC×BD=BC•DK,∵S△DCB∴DK==,∵∠BER=∠DCK,∴sin∠BER=sin∠DCK===,∴RB=BE×=,∵EJ=EB,ER⊥BJ,∴JR=BR=,∴JB=DJ′=,∴DQ﹣P'Q的最大值为.解法二:DQ﹣P'Q=BQ﹣P'Q≤BP',显然P'的轨迹EJ,故最大值为BJ.勾股得CD,OD.△BDJ∽△BAD,BD2=BJ*BA,可得BJ=.故答案为:.9.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.解:(1)①∵四边形ABCD是矩形,∴AD=BC,∠BAD=90°,∵BC=AB,∴AD=AB,∴tan∠ABD==,∴∠ABD=60°,由折叠的性质得:AF=AB,∴△ABF是等边三角形,∴∠AFB=60°,∴∠AFD=180°﹣∠AFB=120°;②由折叠的性质得:BF⊥AE,EF=EB,∵EF=EC,∴EF=EB=EC,∴BC=2BE,∵四边形ABCD是矩形,∴∠ABC=90°,AD=BC=2BE,AD∥BC,∴△ADG∽△EBG,∴==2,∴AG=2EG,设EG=x,则AG=2x,∴AE=3x,在△ABE中,BG⊥AE,∴AB2=AG•AE(射影定理),即42=2x•3x,解得:x=(负值已舍去),∴AE=3x=2,∴BE===2,∴BC=2BE=4,即BC的长为4;(2)当点E,C',D三点共线时,如图3,由②可知,BC=4,∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°,AD=BC=4,CD=AB=4,AD∥BC,∴∠DCE=90°,∠CED=∠B'DA,由折叠的性质得:AB'=AB=4,∠B'=∠ABC=90°,∴∠DCE=∠B',DC=AB',∴△CDE≌△B'AD(AAS),∴DE=AD=4,∴CE===4,∴BE=BC+CE=4+4.10.如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.(1)求证:PC是⊙O的切线;(2)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.解:(1)∵PA=OA=2,AM=OM=1,CM=,又∵∠CMP=∠OMC=90°,∴PC==2,∵OC=2,PO=4,∴PC2+OC2=PO2,∴∠PCO=90°,∴PC与⊙O相切;(2)GE•GF为定值,理由如下:如图2,连接GA、AF、GB,∵点G为弧ADB的中点,∴,∴∠BAG=∠AFG,∵∠AGE=∠FGA,∴△AGE∽△FGA,∴,∴GE•GF=AG2,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=2,∴GE•GF=AG2=8.11.如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠CBG=90,∵四边形ABCD是正方形,∴∠CBE=90°=∠A,BC=AB,∴∠FBA+∠CBG=90,∴∠GCB=∠FBA,∴△ABF≌△BCE(ASA);(2)证明:如图2,过点D作DH⊥CE于H,设AB=CD=BC=2a,∵点E是AB的中点,∴EA=EB=AB=a,∴CE=a,在Rt△CEB中,根据面积相等,得BG•CE=CB•EB,∴BG=a,∴CG==a,∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,∴∠DCE=∠CBF,∵CD=BC,∠CHD=∠CGB=90°,∴△CHD≌△BGC(AAS),∴CH=BG=a,∴GH=CG﹣CH=a=CH,∵DH=DH,∠CHD=∠GHD=90°,∴△DGH≌△DCH(SAS),∴CD=GD;(3)解:如图3,过点D作DQ⊥CE于Q,S△CDG=•DQ•CG=CH•DG,∴CH==a,在Rt△CQD中,CD=2a,∴DH==a,∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,∴∠MDH=∠HCD,∴△CHD∽△DHM,∴=,∴HM=a,在Rt△CHG中,CG=a,CH=a,∴GH==a,∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,∴∠CGH=∠CNG,∴△GHN∽△CHG,∴,∴HN==a,∴MN=HM﹣HN=a,∴=12.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.(1)求过A,B,C三点的抛物线的解析式;(2)求点D的坐标;(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.解:(1)令二次函数y=ax2+bx+c,则,∴,∴过A,B,C三点的抛物线的解析式为y=﹣x2﹣x+2.(2)以AB为直径的圆的圆心坐标为O′(﹣,0),∴O′C=,OO′=;∵CD为⊙O′切线∴O′C⊥CD,∴∠O′CO+∠OCD=90°,∠CO'O+∠O'CO=90°,∴∠CO'O=∠DCO,∴△O'CO∽△CDO,∴=,即=,∴OD=,∴D坐标为(,0).(3)存在,抛物线对称轴为x=﹣,设满足条件的圆的半径为r,则E的坐标为(﹣+r,|r|)或F(﹣﹣r,|r|),而E点在抛物线y=﹣x2﹣x+2上,∴|r|=﹣(﹣+r)2﹣(﹣+r)+2;∴r1=﹣1+,r2=﹣1﹣(舍去),r3=1+,r4=1﹣(舍去);故以EF为直径的圆,恰好与x轴相切,该圆的半径为或1+.。
2021-2022学年初中数学精品讲义-全等三角形模型方法课之公共角、边模型(教师版)

2021-2022学年初中数学精品讲义-全等三角形模型方法课之公共角、边模型(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,△ABC 的面积为9cm 2,BP 平分∠ABC ,AP ⊥BP 于P ,连接PC ,则△PBC 的面积为( )A .3cm 2B .4cm 2C .4.5cm 2D .5cm 2【答案】C【分析】 证△ABP ≌△EBP ,推出AP =PE ,得出S △ABP =S △EBP ,S △ACP =S △ECP ,推出12S PBC S ABC ∆=∆,代入求出即可. 【详解】∵BP 平分∠ABC ,∴∠ABP =∠EBP ,∵AP ⊥BP ,∴∠APB =∠EPB =90°,在△ABP 和△EBP 中,∠ABP =∠EBPBP =BP∠APB =∠EPB ,∴△ABP ≌△EBP (ASA ),∴AP =PE ,∴S △ABP =S △EBP ,S △ACP =S △ECP , ∴2119 4.522S PBC S ABC cm ∆=∆=⨯=, 故答案选:C .【点睛】本题考查了全等三角形的性质和判定,三角形的面积的应用,注意:等底等高的三角形的面积相等.2.如图,BN 为∠MBC 的平分线,P 为BN 上一点,且PD ⊥BC 于点D ,∠APC +∠ABC =180°,给出下列结论:①∠MAP =∠BCP ;②PA =PC ;③AB +BC =2BD ;④四边形BAPC 的面积是△PBD 面积的2倍,其中结论正确的个数有( )A .4个B .3个C .2个D .1个【答案】A【分析】 过点P 作PK ⊥AB ,垂足为点K .证明Rt △BPK ≌Rt △BPD ,△P AK ≌△PCD ,利用全等三角形的性质即可解决问题.【详解】解:过点P 作PK ⊥AB ,垂足为点K .∵PK ⊥AB ,PD ⊥BC ,∠ABP =∠CBP ,∴PK =PD ,在Rt △BPK 和Rt △BPD 中,BP BP PK PD=⎧⎨=⎩, ∴Rt △BPK ≌Rt △BPD (HL ),∴BK =BD ,∵∠APC +∠ABC =180°,且∠ABC +∠KPD =180°,∴∠KPD =∠APC ,∴∠APK =∠CPD ,故①正确,在△P AK 和△PCD 中,AKP PDC PK PDAPK CPD ∠=∠⎧⎪=⎨⎪∠∠⎩=,∴△P AK≌△PCD(ASA),∴AK=CD,P A=PC,故②正确,∴BK﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD,故③正确,∵Rt△BPK≌Rt△BPD,△P AK≌△PCD(ASA),∴S△BPK=S△BPD,S△APK=S△PDC,∴S=S四边形KBDP=2S△PBD.故④正确.四边形ABCP故选A.【点睛】本题考查全等三角形的判定和性质,角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.3.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是()A.1.5 B.2 C.22D.10【答案】B【分析】根据已知条件可以得出∠E=∠ADC=90︒,进而得出∆CEB≅∆ADC,就可以得出BE=DC,进而求出DE的值.【详解】∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90︒,∴∠EBC+∠BCE=90︒,∵∠BCE+∠ACD=90︒,∴∠EBC=∠DCA,在∆CEB和∆ADC中,∠E=∠ADC,∠EBC=∠DCA,BC=AC,∴∆CEB≅∆ADC(AAS),∴BE=DC=1,CE=AD=3,∴DE=EC-CD=3-1=2,故选:B .【点睛】本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解决问题的关键.二、解答题4.已知,△ABC 是边长为4cm 的等边三角形,点P ,Q 分别从顶点A ,B 同时出发,沿线段AB ,BC 运动,且它们的速度均为1cm/s .当点P 到达点B 时,P 、Q 两点停止运动.设点P 的运动时间为t (s ).(1)如图1,连接AQ 、CP ,相交于点M ,则点P ,Q 在运动的过程中,∠CMQ 会变化吗?若变化,则说明理由;若不变,请求出它的度数.(2)如图2,当t 为何值时,△PBQ 是直角三角形?(3)如图3,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 交点为M ,请直接写出∠CMQ 度数.【答案】(1)不变,60°;(2)第43秒或第83秒时;(3)120°. 【详解】试题分析:(1)通过证△ABQ ≌△CAP 得到∠BAQ=∠ACP ,所以由三角形外角定理得到∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;(2)需要分类讨论:分∠PQB=90°和∠BPQ=90°两种情况;(3)通过证△ABQ ≌△CAP 得到∠BAQ=∠ACP ,所以由三角形外角定理得到∠CMQ=∠BAQ+∠APC=∠ACP+∠APC=180°-∠BAC=120°.试题解析:(1)不变.在△ABQ 与△CAP 中,∵{60AB ACB CAP AP BQ=∠=∠=︒=,∴△ABQ ≌△CAP (SAS ), ∴∠BAQ=∠ACP ,∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°; (2)设时间为t ,则AP=BQ=t ,PB=4-t ,①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ , ∴4-t=2t ,43t =; ②当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP ,∴ t=2(4-t ),t=83; ∴当第43秒或第83秒时,△PBQ 为直角三角形;(3)在△ABQ 与△CAP 中,∵{60AB ACB CAP AP BQ=∠=∠=︒=,∴△ABQ ≌△CAP (SAS ),∴∠BAQ=∠ACP ,∴∠∠CMQ=∠BAQ+∠APC=∠ACP+∠APC=180°-∠BAC=120°. 考点:①等边三角形的性质;②全等三角形的判定与性质.5.如图,在四边形ABCD 中,BC >BA ,AD=CD ,BD 平分∠ABC ,求证:∠A+∠C=180°.【答案】见解析【分析】先在线段BC 上截取BE=BA ,连接DE ,根据BD 平分∠ABC ,可得∠ABD =∠EBD ,根据AB EB ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,可判定△ABD ≌△EBD ,根据全等三角形的性质可得:AD=ED ,∠A =∠BED .再根据AD=CD ,等量代换可得ED =CD ,根据等边对等角可得:∠DEC =∠C .由∠BED +∠DEC =180°,可得∠A +∠C =180°. 【详解】证明:在线段BC 上截取BE=BA ,连接DE ,如图所示,∵BD 平分∠ABC ,∴∠ABD =∠EBD ,在△ABD 和△EBD 中,AB EB ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△EBD (SAS ),∴AD=ED ,∠A =∠BED .∵AD=CD,∴ED =CD ,∴∠DEC =∠C .∵∠BED +∠DEC =180°,∴∠A +∠C =180°.【点睛】本题主要考查全等三角形的判定和性质,解决本题的关键是要熟练掌握全等三角形的判定和性质.6.如图,在四边形ABCD 中,已知BD 平分∠ABC ,∠BAD +∠C =180°,求证:AD =CD .【答案】见解析【详解】试题分析:在边BC 上截取BE =BA ,连接DE ,根据SAS 证△ABD ≌△EBD ,推出AD =ED ,∠A =∠BED ,求出∠DEC =∠C 即可.试题解析:证明:在边BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠CBD .在△ABD 和△EBD 中,BA BE ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD (SAS ),∴AD =ED ,∠A =∠BED .∵∠A +∠C =180°,∠BED +∠CED =180°,∴∠C =∠CED ,∴CD =ED ,∴AD =CD .点睛:本题考查了等腰三角形的判定,全等三角形的性质和判定等知识点的应用,解答此题的关键是正确作辅助线,又是难点,解题的思路是把AD 和CD 放到一个三角形中,根据等腰三角形的判定进行证明,题型较好,有一定的难度.7.如图,OC 平分∠MON ,A 、B 分别为OM 、ON 上的点,且BO >AO ,AC =BC ,求证:∠OAC +∠OBC =180°.【答案】见解析.【分析】如图,作CE ⊥ON 于E ,CF ⊥OM 于F .由Rt △CF A ≌Rt △CEB ,推出∠ACF =∠ECB ,推出∠ACB =∠ECF ,由∠ECF +∠MON =360°﹣90°﹣90°=180°,可得∠ACB +∠AOB =180°,推出∠OAC +∠OBC =180°.【详解】如图,作CE ⊥ON 于E ,CF ⊥OM 于F .∵OC 平分∠MON ,CE ⊥ON 于E ,CF ⊥OM 于F .∴CE =CF ,∵AC =BC ,∠CEB =∠CF A =90°,∴Rt △CF A ≌Rt △CEB (HL ),∴∠ACF =∠ECB ,∴∠ACB =∠ECF ,∵∠ECF +∠MON =360°﹣90°﹣90°=180°,∴∠ACB +∠AOB =180°,∴∠OAC +∠OBC =180°.【点睛】本题考查全等三角形的判定和性质,四边形内角和定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.8.已知,如图ABC ∆中,AB AC =,90A ∠=︒,ACB ∠的平分线CD 交AB 于点E ,90BDC ∠=︒,求证:2CE BD =.【答案】见解析.【分析】延长BD 交CA 的延长线于F ,先证得△ACE ≌△ABF ,得出CE=BF ;再证△CBD ≌△CFD ,得出BD=DF ;由此得出结论即可.【详解】证明:如图,延长BD 交CA 的延长线于F ,90BAC ︒∠=90,90BAF BAC ACE AEC ︒︒∴∠=∠=∠+∠=90BDC ︒∠=90BDC FDC ︒∴∠=∠=90ABF BED ︒∴∠+∠=AEC BED ∠=∠ACE ABF ∴∠=∠AB AC =()ACE ABF ASA ∴∆∆≌CE BF ∴= CD 平分ACB ∠ACD BCD ∴∠=∠CD CD =()CBD CFD ASA ∴∆∆≌12BD FD BF ∴== 12BD CE ∴= 2CE BD ∴=【点睛】此题考查三角形全等的判定与性质,角平分线的性质,根据已知条件,作出辅助线是解决问题的关键.9.如图,在△ABC 中,点D 为边BC 的中点,点E 在△ABC 内,AE 平分∠BAC ,CE ⊥AE 点F 在AB 上,且BF=DE(1)求证:四边形BDEF 是平行四边形(2)线段AB ,BF ,AC 之间具有怎样的数量关系?证明你所得到的结论【答案】(1)见解析;(2)1()2BF AB AC =-,理由见解析 【分析】(1)延长CE 交AB 于点G ,证明AEG ∆≅AEC ∆,得E 为中点,通过中位线证明DE //AB ,结合BF=DE ,证明BDEF 是平行四边形(2)通过BDEF 为平行四边形,证得BF=DE=12BG ,再根据AEG ∆≅AEC ∆,得AC=AG ,用AB-AG=BG ,可证1()2BF AB AC =- 【详解】(1)证明:延长CE 交AB 于点G∵AE ⊥CE∴90AEG AEC ︒∠=∠=在AEG ∆和AEC ∆GAE CAE AE AEAEG AEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AEG ∆≅AEC ∆∴GE=EC∵BD=CD∴DE 为CGB ∆的中位线∴DE //AB∵DE=BF∴四边形BDEF 是平行四边形(2)1()2BF AB AC =- 理由如下:∵四边形BDEF 是平行四边形∴BF=DE∵D ,E 分别是BC ,GC 的中点∴BF=DE=12BG∵AEG ∆≅AEC ∆∴AG=AC BF=12(AB-AG )=12(AB-AC ).【点睛】本题主要考查了平行四边形的证明,中位线的性质,全等三角形的证明等综合性内容,作好适当的辅助线,是解题的关键.10.如图1,在平面直角坐标系中,直线AB 分别交x 轴、y 轴于(,0) ,(0,)A a B b 两点,且,a b 满足2()|4|0a b a t ,且0,t t >是常数,直线BD 平分OBA ∠,交x 轴于点D .(1)若AB 的中点为M ,连接OM 交BD 于点N ,求证:ON OD =;(2)如图2,过点A 作AE BD ⊥,垂足为E ,猜想AE 与BD间的数量关系,并证明你的猜想.【答案】(1)见解析;(2)2BD AE =,证明见解析.【分析】(1)由已知条件可得AO BO =,进而得OBA OAB ∠=∠,由直线BD 平分OBA ∠及直角三角形斜边上中线的性质得BOM OAB ∠=∠,再由三角形的外角定理,分别求得,ODN OND ∠∠,根据角度的等量代换,即可得ODN OND ∠=∠,最后由等角对等边的性质即可得证;(2)如图,延长AE 交y 轴于点C ,先证明BCE BAE △≌△,得AE EC =,再证明DOB COA ∠≌△,即可得2BD AC AE ==.【详解】(1)2()|4|0a b a t ,4a b t ∴==,AO BO ∴=,∴OBA OAB ∠=∠,直线BD 平分OBA ∠,ABD OBD ∴∠=∠, M 为AB 的中点, ∴12OM AB BM AM ===, BOM OBA ∴∠=∠,OBA OAB ∠=∠,BOM OAB ∴∠=∠,OND OBD BOM ∠=∠+∠,ODN OAB ABD ∠=∠+∠,OND ODN ∴∠=∠,ON OD ∴=.(2)2BD AE =,证明:如图,延长AE 交y 轴于点C ,直线BD 平分OBA ∠,AE BD ⊥,ABD OBD ∴∠=∠,AEB CEB ∠=∠, 又BE BE =,∴BCE BAE △≌△(ASA ),∴AE CE =1=2AC , AO BC ⊥,∴DOB COA ∠=∠,即90OAC OCA OCA CBE ∠+∠=∠+∠=︒,OAC OBD ∴∠=∠,又OB OA =,∴DOB COA ∠≌△(ASA ),2BD AC AE ∴==,即2BD AE =.【点睛】本题考查了平面直角坐标系的定义,非负数之和为零,三角形角平分线的定义,三角形中线的性质,三角形外角定理,三角形全等的性质与判定,等角对等边,熟练掌握以上知识,添加辅助线是解题的关键.11.如图,在ABC 中,BE 是ABC ∠的平分线,AD BE ⊥,垂足为D ,求证:21C ∠=∠+∠.【答案】见解析【分析】∠=∠,根据三角形的一个外角等于与它不相邻的两根据角平分线的定义可得ABE CBE个内角的和可得AED CBE C∠=∠+∠,然后根据直角三角形两锐角互余列出等式解答即可.【详解】∠的平分线,证明:BE是ABC∴∠=∠,ABE CBE由三角形的外角性质得,AED CBE C∠=∠+∠,AD BE⊥,∴∠+∠=︒,290ABE∴1190∠+∠=∠+∠+∠=︒,AED CBE C∴∠+∠=︒-∠,190C CBE∠=∠∠=︒-∠,ABE CBE ABE,290∴∠=∠+∠.21C【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记性质并准确识图是解题的关键.12.如图,我们把对角线互相垂直的四边形叫做“垂美四边形”.(1)性质探究:如图1.己知四边形ABCD中,AC⊥BD.垂足为O,求证:AB2+CD2=AD2+BC2;(2)解决问题:已知AB=BC=△ABC的边BC和AB向外作等腰Rt△BCE和等腰Rt△ABD;①如图2,当∠ACB=90°,连接DE,求DE的长;②如图3.当∠ACB≠90°,点G、H分别是AD、AC中点,连接GH.若GH=,则S△ABC=.【答案】(1)见解析;(2)②7 2【分析】(1)根据AC⊥BD可以得到∠AOB =∠COD=90°即可得到AB²=AO²+OB²,CD²=DO²+OC²即AB²+CD²=AO²+OB²+DO²+OC²同理可以得到AD²+BC²=AO²+OB²+DO²+OC²即可得到答案;(2)连DC、AE相交于点F,先证明△ABE≌△DBC得到∠CDB=∠BAE 从而证得AE⊥CD再利用勾股定理和(1)中的结论求解即可得到答案;(3)连DC、AE相交于点F,作CP⊥BD交DB延长线于点P,BP²+CP²=BC²=(²=32,DP²+PC²=DC²=(²=96,(DP²+PC²)-(BP²+CP²)=96-32=64,DP²-BP²=64 从而求出BP AB∥PC则S△ABC=12AB×BP.【详解】解:(1)证明:∵AC⊥BD∴∠AOB=90°在Rt△AOB中AB²=AO²+OB²∴∠COD=90°在Rt△COD中CD² =DO²+OC²∴AB²+CD²=AO²+OB²+DO²+OC²同理AD²+BC²=AO²+OB²+DO²+OC²∴AB2+CD2=AD2+BC ²(2) ①解:连DC、AE相交于点F∵Rt△BCE和Rt△ABD是等腰三角形∴BE=BC AB=BD∠CBE=∠ABD=90°∴∠ABE=∠DBC=90°+∠ABC∴△ABE≌△DBC∴∠CDB=∠BAE∵∠ABD=90°∴∠CDB+∠CDA+∠DAB=90°∴∠BAE+∠CDA+∠DAB=90°∴∠AFD=90°∴AE⊥CD∵AB BC∠ACB=90°∴AC=∵AB BD∠ABD=90°∴AD10=∵BC,BE∠CBE=90°∴CE8=由(1)中结论AD²+EC²=AC²+DE²∴(10)²+(8)²=(²+DE²∴DE②连DC、AE相交于点F∵点G、H分别是AD、AC中点,GH=∴DC=2GH =作CP⊥BD交DB延长线于点PBP²+CP²=BC²=(²=32²=96DP²+PC²=DC²=(∴(DP²+PC²)-(BP²+CP²)=96-32=64∴DP²-BP²=64∴(BD+BP)²-BP²=64∴(BP )²-BP ²=64∴BP ∵∠PBA =90°,∠P =90°,∴∠PBA +∠P =90°+90°=180°∴AB ∥PC则S △ABC =12AB ×BP =12×72【点睛】本题主要考查了四边形的综合问题,等腰直角三角形的性质,全等三角形的性质与判定,勾股定理,垂直的定义,解题的关键在于能够熟练掌握相关知识进行求解.。
全等三角形的讲义整理讲义

全等三角形专题一 全等三角形的性质【知识点1】能够完全重合的两个三角形叫做全等三角形。
(两个三角形全等是指两个三角形的大小和形状完全一样,与他们的位置没有关系。
)【知识点2】两个三角形重合在一起,重合的顶点叫做对应顶点;重合的边叫做 对应边;重合的角叫做对应角。
【例题1】如图,已知图中的两个三角形全等,填空:(1)AB 与 是对应边,BC 与 是对应边, CA 与 是对应边;(2)∠A 与 是对应角,∠ABC 与 是对应角, ∠BAC 与 是对应角【方法总结】在两个全等三角形中找对应边和对应角的方法。
(1)有公共边的,公 共边一定是对应边;(2)有公共角的,公共角一定是对应角;(3)有对顶角的,对顶角是对应角;(4)在两个全等三角形中,最长的边对最长的边,最短的边对最短的边,最大的角对最大的角,最小的角对最小的角。
【练习1】 如图,图中有两对三角形全等,填空: (1)△BOD ≌ ; (2)△ACD ≌ .【知识点3】 全等三角形的对应边相等,对应角相等。
(由定义还可知道,全等三角形的周长相等,面积相等,对应边上的中线和高相DABCOE ABCD等,对应角的角平分线相等)【例题2】 (海南省中考卷第5题) 已知图2中的两个三角形全等,则∠α度数是( )A.72°B.60°C.58°D.50°【例题3】(清远)如图,若111ABC A B C △≌△,且11040A B ∠=∠=°,°,则1C ∠= .【练习2】 如图,ACB A C B '''△≌△,BCB ∠'=30°,则ACA '∠的度数为( )A 20° B.30° C .35° D .40°【练习3】如图,△ABD 绕着点B 沿顺时针方向旋转90°到△EBC , 且∠ABD=90°。
EBC初级课件4

BEC初级精讲班第4讲讲义Company activitiesObjectives: To learn to describe company activities学习描述公司的商务活动To practise reading for specific information练习阅读重要信息To raise awareness of cohesion and connectors of addition and contrast提高对篇章衔接、表示递进与对照连接词的意识To review the present continuous复习现在进行时态Investing in central EuropeReading 1 Look at the diagram showing car company investment in central Europe. Answer the questions.vocabulary$1.8bn bn = billion van assembly plantFord Opel Daewoo Fiat Skoda $17m m = million plantKey:1 Fiat ( $1.8bn)2 Volkswagen ( in Mosel )3 Volkswagen ( in the former East Germany, Hungary, Czech republic, Slovakia, Poland)4 Poland ($3.52bn)5 Slovakia ($120m)Grammar 2Could you tell me the different uses of the present tenses.KeyPresentsimple Present continuousGeneral facts ( Volkswagen Something happening now (Daewoo is nowmanufactures cars ) building a new plant.)Routines ( I work for Audi.) Temporary situations ( Manyfirms are investingStates ( VW now owns 70% of Skoda.) a lot of money in central Europe.)Changing situations ( Costs are rising slowly.)Speaking 3 Why are companies investing so much in central Europe?Reasons given in the test:Cheap workforceGenerous government inward investment grantsSlow economic growth at homeStrong growth in central/eastern European car marketsPossible to take over existing facilities/companies cheaplyGood locations for exporting to the former Soviet UnionOther possible reasons not mentioned in the text:By manufacturing in Europe, Asian and US companies avoid restrictions on imports into EuropeInvesting in the area boosts local economies and adds to market growthHigher returns on investments due to low costsShareholder pressure to increase performanceDrivingeastwardsReading 1 Put the five extracts below into the correct order to complete thenewspaper article.vocabularyengineer earn attractionhuge profitgenerous state investment grants (subsidy/subsidise)car-maker modernise acquireSuggested answers:2 In addition to the cheap labour, …3 Volkswagen, for example, …4 Companies such as VW and Fiat…5 However, in spite of all these advantages…2 Say whether the following sentences are 'Right' or 'Wrong'. If there is not enough information to answer, choose 'Doesn't say'.Read through all the questions before scanning through the text. You should check carefully whether there is enough evidence in the text to declare the statements either 'Right' or 'Wrong'. If there is not, you should choose 'Doesn't say'.vocabulary:inward investment be equivalent toKey :1 B2 A3 A4 C5 B6 BVocabulary 3 Look at the words in italics in the text. Write the words in the correct group below.2 Key:AdditionContrastandbutinaddition howeverfurthermorealthoughmoreoverin spite ofalsonot only … but alsoIf not only … is used before the verb,λ the verb needs to be inverted. However, if it is used after the verb, there is no problem.I wish to point out that both in spite of and despite areλ followed by:1) a noun, 2) -ing or 3) the fact that; they are not followed by the infinitive. 4.Now use the words in italics in the text. Write the words in the correct group below.2 Opel is opening a new car plant in Poland. Moreover/Furthermore/In addition, it isopening a plant in Hungary.Opel is not only opening a new car plant in Poland but also a plant in Hungary.3 Wages are lower in central Europe. Moreover/Furthermore/In addition, workersare more flexible.Wages are not only lower in central Europe but workers are also more flexible.4 Wages are increasing in eastern Germany but they are 15-25% lower than in the west.Although wages are increasing in eastern Germany, they are 15-25% lower than in the west.In spite of an increase, wages in eastern Germany are 15-25% lower than in the west.5 VW has bought companies in central Europe. Moreover/Furthermore/In addition, it hasbuilt new factories there.VW has not only bought companies in central Europe but also built new factories there.6 Wages are lower in central Europe but this is not the only reason companies are investing there.Although wages are lower in central Europe, this is not the only reason companies are investing there.Speaking 5 Work in pairs. Draw a map showing your company's markets. Explain to your partner what is happening in these places at the moment.You can draw a map showing your company's markets and activities. The map can only be diagrams and need not be works of art. Then you can mark on important locations and exchange maps with a partner. Finally, you can take it in turns to ask each other what the locations are and what activities take place there.Essential vocabularyAddition Contrast ActivitiesGeneralalso although assembly to attractfurthermore however tobuild attractionmoreover in spite of todevelop to climbnot only … but also togrow coststo invest to earninvestment flexibleto modernise lowmodelto receivevanwagesExamfocus:VocabularyObjectives: To learn to use useful strategies for coping with unknown vocabulary学习处理生词的有用的策略To know useful ways of organsing and storing new vocabulary了解整理和积累词汇的有用方法词汇在我们学习和使用英语中十分重要。
《全等三角形》讲义(完整版)

全等三角形讲义一、知识点总结全等三角形定义:形状大小相同,并且能够完全重合的两个三角形叫做全等形三角形。
:形状大小相同,并且能够完全重合的两个三角形叫做全等形三角形。
补充说明:重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
:重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等:全等三角形的对应边相等,全等三角形的对应角相等 全等三角形判定定理:(1)边边边定理:三边对应相等的两个三角形全等。
(简称SSS ) (2)边角边定理:两边和它们的夹角对应相等的两个三角形全等。
)边角边定理:两边和它们的夹角对应相等的两个三角形全等。
((简称SAS) (3)角边角定理:两角和它们的夹边对应相等的两个三角形全等。
(简称ASA ASA)) (4)角角边定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(简称AAS AAS)) (5)斜边、直角边定理:斜边和一条直角边对应相等的两个直角三角形全等。
(简称HL HL)) 角平分线的性质:在角平分线上的点到角的两边的距离相等在角平分线上的点到角的两边的距离相等. .∵OP 平分∠平分∠AOB AOB AOB,,PM PM⊥⊥OA 于M ,PN PN⊥⊥OB 于N ,∴PM=PN 角平分线的判定:到角的两边距离相等的点在角的平分线上到角的两边距离相等的点在角的平分线上. .∵PM PM⊥⊥OA 于M ,PN PN⊥⊥OB 于N ,PM=PN ∴OP 平分∠平分∠AOB AOB三角形的角平分线的性质:三角形三个内角的平分线交于一点,并且这一点到三边的距离等。
二、典型例题举例A BC PMNO A BCPMN O例1、如图,△ABN ≌△ACM,∠B 和∠C 是对应角,AB 与AC 是对应边,写出其他对应边和对应角.例2、如图,△、如图,△ABC ABC 是一个钢架,是一个钢架,AB=AC AB=AC AB=AC,,AD 是连结点A 与BC 中点D 的支架.的支架.求证:△求证:△ABD ABD ABD≌△≌△≌△ACD ACD ACD..例3、已知:点A 、F 、E 、C 在同一条直线上,AF =CE ,BE ∥DF ,BE =DF . 求证:△ABE ≌△CDF .例4、如图:、如图:D D 在AB 上,上,E E 在AC 上,上,AB AB AB==AC AC,∠,∠,∠B B =∠=∠C C .求证AD AD==AE AE..例5、如图:∠、如图:∠1=1=1=∠∠2,∠,∠3=3=3=∠∠4 求证:求证:AC=AD AC=AD例6、如图,B 、E 、F 、C 在同一直线上,AF ⊥BC 于F ,DE ⊥BC 于E ,AB=DC ,BE=CF ,你认为AB 平行于CD 吗?说说你的理由吗?说说你的理由D CB ACADB123 4例7、如图1,△ABC 的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断△ABC 与△AEG 面积之间的关系,并说明理由.例8、如图,OC 是∠AOB 的平分线,P 是OC 上的一点,PD ⊥OA 交OA 于D ,PE ⊥OB 交OB 于E ,F 是OC 上的另一点,连接DF ,EF ,求证DF =EF例9、如图,△ABC 中,AD 是它的角平分线,P 是AD 上的一点,PE ∥AB 交BC 于E ,PF ∥AC 交BC 于F ,求证:D 到PE 的距离与D 到PF 的距离相等的距离相等例10、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是282cm ,AB =20cm ,AC =8cm,求DE 的长.AGF CBDE图1AEB DCFAB CDED C EF BA 例10、已知:BE ⊥CD ,BE =DE ,BC =DA ,求证:①,求证:① △BEC ≌△DAE ;②DF ⊥BC .例11、如图,已知:E 是∠AOB 的平分线上一点,EC ⊥OB ,ED ⊥OA ,C ,D 是垂足,连接CD ,求证:(1)∠ECD=∠EDC ;(2)OD=OC ;(3)OE 是CD 的中垂线.三、专题版块三、专题版块 专题一:专题一: 全等三角形的判定和性质的应用全等三角形的判定和性质的应用例1、如图,在△ABC 中,AB=AC , BAC=40°,分别以AB AB、AC 为边作两个等腰三角形ABD 和ACE ACE,使∠,使∠BAD=∠CAE=90°.(1)求∠DBC 的度数.(2)求证:BD=CE.例2、如图,A B ∥CD,AF CD,AF∥∥DE,BE=CF,DE,BE=CF,求证:求证:求证:AB=CD. AB=CD.例3、如图在△ABC 中,BE 、CF 分别是AC 、AB 边上的高,在BE 延长线上截取BM =AC ,在CF 延长线上截到CN =AB ,求证:AM =AN 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BEC初级精讲班第6讲讲义InternalcommunicationObjectives: To practise writing memos and e-mails练习写备忘录和电子邮件To review making requests and talking about obligation复习如何提要求和谈论职责Memo, notes and noticesReading 1Danos is a manufacturer of office furniture and supplies. Look at the examples of the company’s internal communication below and find the following information:the company’s marketsυsome of the company’sυ activitieswhere it is based.υPlease quickly scan the various forms of communication to get some general information about the company, its markets and activities. You are free to interpret the information as you wish (e.g. the name Veronique Leboeuf suggests the company has activities in the French market).请大家仔细阅读课本29页并回答问题。
Suggested answers:Markets: Britain ( Manchester Head office), Italy ( Rome conference), Spain ( Madrid office), France ( Veronique Leboeuf ).Activities: Manufacturer of office supplies and furniture ( given in rubric ), sells products directly in Europe.Location: Manchester ( Head Office ).2 Answer the questions below.Please scan through the texts once more and find the relevant information. Then you can close your books and answer the six questions from memory.Key:1. 30 Oct to 1 Nov2. A holiday in Florida3. Thursday 23 July4. Henry Wallace5. Henry and Paula ( but not Veronique Leboeuf)6. The name and telephone number of customer who phoned about the new seatingrange3 Read the documents on the opposite page again. What are the differences between memos, notes and notices?Suggested answers:Memo: Addressed to groups or individuals. More formal status than a note. Formal style, no omission of words, no abbreviations, formal style of address, use of job titles. Notes: Addressed to an individual. Informal, short, abbreviations ( tel no. ),contractions ( you’ve), omission of subjects, auxiliaries and articles ([I] Can’t find …), use of first names.Notices: Not addressed to anyone in particular. Formal style, no cont ractions, no ellipsis, no abbreviations.Functions 4Look at the memos and notes again. Find phrases to express requests andobligation/necessity. Put them in the groups below.Requests Obligation / necessityplease (send … )please ( go ahead …)could you ( give …)you need to ( arrive … )could we (meet …)it is essential that ( everybody books …)( salary sheets ) should ( arrive …) Writing memosListening 1Sarah Longman calls Henry Wallace to talk about expenses. Listen and take notes.Writing 2Now use your notes to write the memo Henry needs to send his salespeop le.请听录音两遍。
Suggested answer:To: All salespeopleFrom: Henry WallacePlease note that you need to enclose receipts with expenses claims.Vocabulary: Accounts expenses remind enclose receiptPage 135Writing e-mailSpeaking 1 slash = strokeMy E-mail address is Johnkin@Writing 3Suggested answer:To: SueFrom: HenryThanks for your e-mail reminding me about Mike going to Helsinki tomorrow. I spoke to him and we arranged a pricing strategies meeting on Monday morning. Can you let me know if you can come?Regards.Listening 2请你听两遍录音Page 135Suggested answer:To: stevecooper@danos .comFrom: karenmitchell@Hi SteveJohn and I are going to have a meeting next Tuesday lunchtime. Are you able to come? Could you let me know ASAP.RegardsEssentialvocabularyPage 152补充:短篇写作讲解第一部分短篇写作λ便函的格式"便函写作应试技巧"第二部分书信写作导读λ第一部分短篇写作I. 便函的格式一、什么是便函简单地说,便函就是指在同一家机构内从一个人或一个部门传递到另一个人或部门的书面信息,内容是要在当天或近期内所要办理的事情。
二、便函写作的格式便函通常包含以下几个部分:1. 公司名称;2. 公司的电话号码或传真号码;3. 收函人姓名(和职位)To:4. 留言人姓名(和职位)From:5. 留言日期Date:6. 便函主题Subject:7. 正文下面我们选择两则便函为例,结合我们刚刚讲到的有关便函的知识,给大家做一个具体的讲解。
II. 便函写作应试技巧一、题目要求在阅读写作考试的第46题,即写作考试的第一部分,考生需要完成一则便函的写作。
请看下面这个题目:A new designer, Mary Watts, has just joined your company.λWrite a memoλ to all staff:Telling them who the new employee isλSaying what herλ responsibilities will beExplaining where her office is located.λWriteλ 30-40 words.Write on your Answer Sheet.λ………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………在考试时,题目中会给你一个特定的情景,同时会告诉给你要完成三项写作任务;题目中会有清楚的字数限制,即30-40字,超出或少于这个字数限制都会影响你的成绩。
在便函写作中,你会碰到的写作文体有note、message、 memo或者e-mail。
这些都是非正式的文体,所以在语气和选词时都可以用不正式的语言完成。
同时,题目中还会给你要完成的写作文体的格式。
如上面这个例子就把便函的格式告诉给你了。
你在把答案写在答题卡上时不用抄写这个格式。
大家可以参看上面的例子再次来理解一下便函的结构。
不过,你并不需要把这个格式抄写到答题卡上。
此外,考试当中你还会碰到写便条(note)、留言(message)和电子邮件(e-mail)。
便条和留言的格式是直接写正文,然后在正文的最后签上自己的姓名。
而电子邮件的格式是大家经常在网上可以看到的,下面就是一个中文版的电子邮件的界面。
To: Johnkin@From: Alicetian@CC:Subject: Cash Flow不过考试时题目中都会给你格式,你不用抄写这些格式,只要从正文开始写起就可以了。
