2019春九年级数学下册第三章圆3.2圆的对称性课时作业新版北师大版
2019春九年级数学下册第三章圆3.1圆课时作业新版北师大版20190313362

第三章圆3.1圆知识要点基础练知识点1圆中有关的概念1.下列说法正确的有(C)①半径相等的两个圆是等圆;②半径相等的两个半圆的弧是等弧;③能够互相重合的弧是等弧; ④分别在两个等圆上的两条弧是等弧.A.1个B.2个C.3个D.4个2.如图,点A,B,P在☉O上,则图中弦的条数为(C)A.1B.2C.3D.43.已知☉O中最长的弦为16 cm,则☉O的半径为8cm.知识点2点与圆的位置关系4.☉O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与☉O的位置关系是(A)A.点P在☉O内B.点P在☉O上C.点P在☉O外D.点P在☉O上或☉O外【变式拓展】在数轴上,点A所表示的实数为3,点B所表示的实数为a,☉A的半径为2.下列说法中不正确的是(A)A.当a<5时,点B在☉A内B.当1<a<5时,点B在☉A内C.当a<1时,点B在☉A外1D.当a>5时,点B在☉A外5.在直角坐标系中,以点O(0,0)为圆心,以10为半径画圆,则点(-6,8)的位置在(B)A.☉O内B.☉O上C.☉O外D.不能确定6.如图,已知矩形ABCD中AC交BD于点O.求证:A,B,C,D4个点在以O为圆心,OA为半径的圆上.证明:∵四边形ABCD是矩形,O是对角线的交点,∴OA=OC=OB=OD,∴A,B,C,D4个点在以O为圆心,OA为半径的圆上.7.如图,△ABC1,△ABC2,△ABC3,…,△ABC n是n个以AB为斜边的直角三角形,试判断点C1,C2,C3,…,C n是否在同一个圆上?并说明理由.解:点C1,C2,C3,…,C n在以AB为直径的圆上.理由:取AB的中点D,分别连接C1D,C2D,C3D,…,C n D,则C1D,C2D,C3D,…,C n D分别表示对应的直角三角形斜边上的中线.根据直角三角形斜边上的中线等于斜边的一半,可知1C1D=C2D=C3D=…=C n D=AB,所以点C1,C2,C3,…,C n都在以AB为直径的圆上.2综合能力提升练8.圆的半径增加了一倍,那么圆的面积增加了(C)A.一倍B.二倍C.三倍D.四倍9.P为☉O内与点O不重合的一点,则下列说法正确的是(B)2A.点P到点O的距离都不小于☉O的半径B.☉O上有两点到点P的距离之和等于☉O的直径C.☉O上有两点到点P的距离之和最小D.☉O上有两点到点P的距离之和最大10.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为(C)A.4πB.9πC.16πD.25π11.若☉O所在平面内一点P到☉O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为(C)a +b a - bA. B.2 2a +b a - bC. D.a+b或a-b或2212.(枣庄中考)如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为(B)A.2 2<r< 17B. 17<r≤3 2C. 17<r<5D.5<r< 2913.如图,矩形ABCD的边AB=3,AD=4,若以点A为圆心画☉A.(1)使点B在☉A内,点D在☉A外,则☉A的半径r的取值范围是3<r<4.3(2)使点B,C,D中至少有一点在☉A内,且至少有一点在☉A外,则☉A的半径r的取值范围是3<r<5.14.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,求∠ACD的度数.解:∵∠ACB=90°,∠A=40°,∴∠B=50°.又∵CD=CB,∴∠CDB=∠B=50°,∴∠ACD=∠CDB-∠A=50°-40°=10°.15.如图,在△ABC中,D是∠BAC的平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E. 求证:点E是过A,B,D三点的圆的圆心.证明:∵点D在∠BAC的平分线上,∴∠BAD=∠CAD.又∵DE∥AC,∴∠ADE=∠CAD,∴∠BAD=∠ADE,∴AE=DE.又∵BD⊥AD于点D,∴AE=BE=DE.∵过A,B,D三点确定一个圆,且∠ADB=90°,∴AB是点A,B,D所在圆的直径,∴点E是过A,B,D三点的圆的圆心.拓展探究突破练16.如图,等边△ABC的边长为2,E是边BC上的动点,EF∥AC交边AB于点F,在边AC上取一点P,使PE=EB,连接FP.4(1)请直接回答:①写出图中与线段EF相等的线段;(不再另外添加辅助线)②当点E在什么位置时,四边形EFPC是平行四边形?并判断四边形EFPC是什么特殊的平行四边形.(2)在(1)的条件下,以点E为圆心,r为半径作圆,根据☉E与平行四边形EFPC四条边交点的总个数,求相应的r的取值范围.解:(1)①EF=BE=PE=BF.②当E是BC的中点时,四边形EFPC是平行四边形;四边形EFPC是菱形.(2)如图,过点E作EN⊥AC于点N.3当E是BC的中点时,EC=1,则NE=EC cos 30°=,23当0<r<时,有两个交点;23当r=时,有四个交点;23当<r<1时,有六个交点;2当r=1时,有三个交点;当r>1时,没有交点.5。
九年级数学下册第三章圆3.2圆的对称性练习北师大版(2021年整理)

2018-2019学年九年级数学下册第三章圆3.2 圆的对称性同步练习(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第三章圆3.2 圆的对称性同步练习(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第三章圆3.2 圆的对称性同步练习(新版)北师大版的全部内容。
课时作业(二十)[第三章 2 圆的对称性]一、选择题1.下列说法中,正确的是( )A.等弦所对的弧相等B.等弧所对的弦相等C.相等的圆心角所对的弦也相等D.相等的弦所对的圆心角也相等2.如图K-20-1,在⊙O中,错误!=错误!,∠AOB=40°,则∠COD的度数为( )链接听课例2归纳总结图K-20-1A.20°B.40°C.50°D.60°3.在⊙O中,已知错误!=5错误!,那么下列结论正确的是()A.AB>5CD B.AB=5CDC.AB<5CD D.以上均不正确4.把一张圆形纸片按图K-20-2所示方式折叠两次后展开,图中的虚线表示折痕,则错误!的度数是()图K-20-2A.120° B.135° C.150° D.165°5.如图K-20-3所示,在⊙O中,A,C,D,B是⊙O上的四点,OC,OD分别交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④错误!=错误!。
其中正确的有()图K-20-3A.4个 B.3个 C.2个 D.1个二、填空题6.如图K-20-4所示,在⊙O中,若错误!=错误!,则AB=______,∠AOB=∠______;若OE⊥AB于点E,OF⊥CD于点F,则OE______OF.图K-20-47.如图K-20-5,在⊙O中,AB∥CD,错误!所对的圆心角的度数为45°,则∠COD的度数为________.图K-20-58.如图K-20-6,三圆同心于点O,AB=4 cm,CD⊥AB于点O,则图中阴影部分的面积为________cm2.图K-20-69.如图K-20-7,AD是⊙O的直径,且AD=6,点B,C在⊙O上,错误!=错误!,∠AOB=120°,E是线段CD的中点,则OE=________。
初三九年级数学北师版 第3章 圆3.2 圆的对称性课后作业
∵四边形ABCD是平行四边形, ∴AD∥BC. ∴∠EAF=∠AFB,∠GAE=∠ABF.∴∠GAE=
∠EAF. ∴ GE=EF.
(2)若BF的度数为50°,求∠C的度数.
解:∵BF的度数为50°,∴∠BAF=50°. ∴∠ABF=∠AFB=65°. ∵四边形ABCD为平行四边形, ∴AB∥CD.∴∠ABF+∠C=180°. ∴∠C=180°-∠ABF=115°.
C. AB<2CD
D.不能确定
返回
知识点 3 相等圆心角、弧、弦之间的关
7 . 在 同 圆 或 等 圆 中 , 如 果 两 个 __圆__心__角__ 、 两 条
__弧____、两条____弦____中有一组量___相__等___,那么
它 们 所 对 应 的 其 余 各 组 量 都 分 别 ________ ; 其 依
∴AE=AC.同1 理可得BF=BD.∴AE=BF=CD. 2
(2)在(1)题中,如果∠AOB=120°,其他条件不变,如 图②所示,那么(1)中的结论还成立吗?若成立,请 证明;若不成立,请说明理由.
【思路点拨】(1)连接AC,BD,先证明AC=CD=BD, 再利用角的关系证明AE=AC,BF=BD;(2)类比(1) 进行证明.
返回
5.如图,AB,CD分别为⊙O的两条弦,OM⊥AB于M,
ON⊥CD于N,且∠AOB=∠COD,则下列结论中,
正确的有( )
①AB=CD;D ②OM=ON;③AB=CD.
A.0个
B.1个
C.2个
D.3个
返回
6.在⊙O中,∠AOB=2∠COD,则下列关系正确的
是( A ) A. AB=2CD
B.AB=2CD
为( ) A.5Dπ cm
2019春九年级数学下册第三章圆章末小结与提升课时作业新版北师大版20190313350
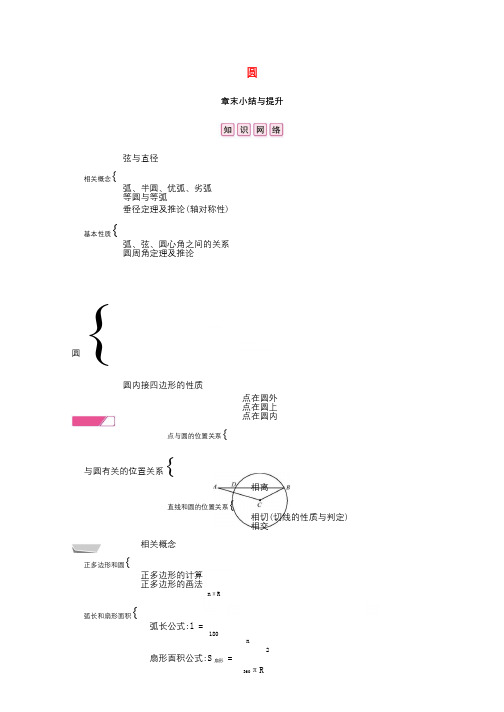
圆章末小结与提升弦与直径相关概念{弧、半圆、优弧、劣弧等圆与等弧垂径定理及推论(轴对称性)基本性质{弧、弦、圆心角之间的关系圆周角定理及推论圆{圆内接四边形的性质点在圆外点在圆上 点在圆内点与圆的位置关系{与圆有关的位置关系{相离 直线和圆的位置关系{相切(切线的性质与判定)相交相关概念正多边形和圆{正多边形的计算 正多边形的画法n πR弧长和扇形面积{弧长公式:l =180 n2扇形面积公式:S 扇形 = 360πR类型1垂径定理及其推论典例1如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为.【解析】作CE⊥AB于点E,∠B=180°-∠BAC-∠ACB=180°-20°-130°=30°,在Rt△BCE中,∵3∠CEB=90°,∠B=30°,BC=2,∴BE= BC= 3,∵CE⊥BD,∴DE=BE,∴BD=2BE=2 3.21【答案】2 3【针对训练】1.如图,设☉O的半径为r,弦的长为a,弦与圆心的距离为d,弦的中点到所对劣弧中点的距离为h,则下列结论:①r=d+h;②4r2=4d2+a2;③已知r,a,d,h中任意两个,可求其他两个.其中正确结论的序号是(C)A.①B.②③C.①②③D.①③2.(南通中考)已知∠AOB,作图.步骤1:在OB上任取一点M,以M为圆心,MO长为半径画半圆,分别交OA,OB于点P,Q;步骤2:过点M作PQ的垂线交PQ于点C;步骤3:画射线OC.则下列判断:①PC = CQ;②MC∥OA;③OP=PQ;④OC平分∠AOB.其中正确的个数为(C) A.1 B.2 C.3 D.43.如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm,求圆的半径.解:∵弦AB的垂直平分线交弧AB于点C,交弦AB于点D,2∴圆心在直线CD上.如图,设圆形轮片圆心为O,连接OA,设圆的半径为R,1由垂径定理知AD=AB=12.2在Rt△OAD中,OA2=OD2+AD2,∴R2=122+(R-8)2,解得R=13.∴圆的半径为13 cm.类型2圆心角定理、圆周角定理及其推论典例2如图,点A,B,C是☉O上的三点,且四边形ABCO是平行四边形,OF⊥OC交☉O于点F,则∠BAF等于() A.12.5° B.15°C.20°D.22.5°【解析】连接OB,∵四边形ABCO是平行四边形,∴OCAB,又OA=OB=OC,∴OA=OB=AB,∴△AOB1为等边三角形.∵OF⊥OC,OC∥AB,∴OF⊥AB,∴∠BOF=∠AOF=30°,由圆周角定理得∠BAF=∠2 BOF=15°.【答案】B【针对训练】31.(贺州中考)如图,在☉O中,AB是☉O的直径,AB=10,AC = CD = DB,点E是点D关于AB的对1称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小2值是10.其中正确的个数是(C)A.1B.2C.3D.42.(永州中考)如图,四边形ABCD是☉O的内接四边形,点D是AC的中点,点E是BC上的一点.若∠CED=40°,则∠ADC=100°.类型3切线的性质与判定典例3如图,△ABC内接于☉O,AC为☉O的直径,PB是☉O的切线,B为切点,OP⊥BC,垂足为E,交☉O于点D,连接BD.(1)求证:BD平分∠PBC;(2)若☉O的半径为1,PD=3DE,求OE及AB的长.【解析】(1)连接OB.∵PB是☉O的切线,∴OB⊥PB,∴∠PBO=90°,∴∠PBD+∠OBD=90°,4∵OB=OD,∴∠OBD=∠ODB,∵OP⊥BC,∴∠BED=90°,∴∠DBE+∠BDE=90°,∴∠PBD=∠EBD,∴BD平分∠PBC.(2)作DK⊥PB于点K.12BE·EDS △BDE DE∵= ,S △BDP =1PD2PB·DK又∵BD平分∠PBE,DE⊥BE,DK⊥PB,BE DE 1∴DK=DE,∴PB = PD = .3∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,∴∠OBE=∠P.∵∠OEB=∠BEP=90°,∴△BEO∽△PEB,BO OE OE BE 1∴,∴.= BO = PB =PBBE 31∵BO=1,∴OE=.3∵OE⊥BC,∴BE=EC.2∵AO=OC,∴AB=2OE=.3【针对训练】1.如图,已知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于点D,以D为圆心,DA为半径作圆,与射线交于点E,F.有下列结论:①△ABC是直角三角形;②☉D与直线BC相切;③点E是线段BF的黄金分割点;④tan ∠CDF=2.其中正确的结论有(A)5A.4个B.3个C.2个D.1个2.(天水中考)如图,点D为☉O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)判断直线CD和☉O的位置关系,并说明理由;(2)过点B作☉O的切线BE交直线CD于点E,若AC=2,☉O的半径是3,求BE的长.解:(1)直线CD和☉O的位置关系是相切.理由:连接OD.∵AB是☉O的直径,∴∠ADB=90°,∴∠DAB+∠DBA=90°.∵∠CDA=∠CBD,∴∠DAB+∠CDA=90°.∵OD=OA,∴∠DAB=∠ADO,∴∠CDA+∠ADO=90°,即OD⊥CE.∴直线CD是☉O的切线,即直线CD和☉O的位置关系是相切.(2)∵AC=2,☉O的半径是3,∴OC=2+3=5,OD=3.∴CD=4.∵CE切☉O于点D,EB切☉O于点B,∴DE=EB,∠CBE=90°.设DE=EB=x,在Rt△CBE中,由勾股定理,得CE2=BE2+BC2,则(4+x)2=x2+(5+3)2.解得x=6,即BE=6.类型4正多边形与圆的有关计算EF1.如图,正方形ABCD和正△AEF都内接于☉O,EF与BC,CD分别相交于点G,H,则的值是(C)GH66A. B. 2 C. 3 D.222.正三角形的高、外接圆半径、边心距之比为(A)A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶33.等腰直角三角形的外接圆的半径为(B)2A.腰长B.腰长的倍22C.底边长的倍D.腰上的高2类型5弧长与扇形面积的相关计算1.如图,在△ABC中,AB=AC.分别以B,C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB,AC的延长线分别交于点E,F,连接AD,BD,CD.若BC=6,∠BAC=50°,则DE,DF的长度之和为11 3π.2.(德州中考)如图,AB是☉O的直径,直线CD与☉O相切于点C,且与AB的延长线交于点E,C是BF的中点.(1)求证:AD⊥CD;7(2)若∠CAD=30°,☉O的半径为3,一只蚂蚁从点B出发,沿着BE-EC-CB爬回至点B,求蚂蚁爬过的路程.(π≈3.14, 3≈1.73,结果保留一位小数)解:(1)连接OC.∵直线CD与☉O相切,∴OC⊥CD,∵点C是BF的中点,∴∠DAC=∠EAC,∵OA=OC,∴∠OCA=∠EAC,∴∠DAC=∠OCA,∴OC∥AD,∴AD⊥CD.(2)∵∠CAD=30°,∴∠CAE=∠CAD=30°,由圆周角定理,得∠COE=60°,60°×π× 3∴OE=2OC=6,BE=6-3=3,BC的长为==π.180°在Rt△OCE中,EC=OE2 - OC2 = 62 - 32=3 3,∴蚂蚁爬过的路程=3+3 3+π≈11.3.8。
(版)北师版九年级下册第三章圆知识点及习题

九年级下册第三章圆【知识梳理】一、圆的认识1. 圆的定义:描述性定义:在一个平面内,线段OA绕它固定的一个端点的圆形叫做圆;固定的端点O叫做圆心;线段...O旋转一周,另一个端点A随之旋转所形成OA叫做半径;以点O为圆心的圆,记作⊙..O,读作“圆O〞集合性定义:圆是平面内到定点距离等于定长的点的集合。
其中定点叫做圆心,定长叫做圆的半径,圆......心定圆的位置,半径定圆的大小,圆心和半径确定的圆叫做定圆..。
对圆的定义的理解:①圆是一条封闭曲线,不是圆面;②圆由两个条件唯一确定:一是圆心〔即定点〕,二是半径〔即定长〕。
2、与圆相关的概念①弦和直径:弦:连接圆上任意两点的线段叫做弦.。
直径:经过圆心的弦叫做直径。
..②弧、半圆、优弧、劣弧:弧:圆上任意两点间的局部叫做圆弧..,简称弧.,用符号“⌒〞表示,以CD为端点的弧记为“〞,读作“圆弧CD〞或“弧CD〞。
半圆:直径的两个端点分圆成两条弧,每一条弧叫做半圆..。
优弧:大于半圆的弧叫做优弧。
..劣弧:小于半圆的弧叫做劣弧。
(为了区别优弧和劣弧,优弧用三个字母表示。
)..③弓形:弦及所对的弧组成的图形叫做弓形..。
④同心圆:圆心相同,半径不等的两个圆叫做同心圆...。
⑤等圆:能够完全重合的两个圆叫做等圆,半径相等的两个圆是等圆。
⑥等弧:在同圆或等圆中,能够互相重合的弧叫做等弧..。
⑦圆心角:顶点在圆心的角叫做圆心角....⑧弦心距:从圆心到弦的距离叫做弦心距....3、点与圆的位置关系及其数量特征:如果圆的半径为r,点到圆心的距离为 d,那么①点在圆上<===>d=r;②点在圆内<===>d<r;③点在圆外<===>d>r.其中点在圆上的数量特征是重点,它可用来证明假设干个点共圆,方法就是证明这几个点与一个定点、的距离相等。
二. 圆的对称性:1、圆是轴对称图形,直径所在的直线是它的对称轴,圆有无数条对称轴。
2019年秋北师大版九年级数学:下册 第3章 第2课时 圆的对称性作业本

A.32° C.68°
B.60° D.64°
︵︵︵
3.如图,AB 是⊙O 的直径,BC=CD=DE,∠BOC=40°, 则∠AOE 的度数是 60 度.
4.在⊙O 中,弦 AB 的长恰好等于半径,弦 AB 所对的圆心 角为 60°.
二、解答题(每题20分,共60分)
︵︵
5.如图,在⊙O中, AB = AC ,若∠B=70°,求∠A的度 数.
∴四边形AOBC是菱形,∴AB平分∠OAC.
∵CO=BO,∴△OBC是等边三角形,
∴OB=BC.
同理,△OCA是等边三角形,∴OA=AC.
又∵OA=OB,∴OA=AC=BC=BO, ∴四边形 OACB是菱形.
7.(2019黄石模拟节选)如图,A,B是⊙O上的两点,∠AOB
=120°,C是弧AB的中点.求证:AB平分∠OAC.
证明:连接OC, ∵∠AOB=120°, C是弧AB的中点, ∴∠AOC=∠BOC=60°, ∵OA=OC,∴△ACO是等边三角形, ∴OA=AC, 同理OB=BC,∴OA=AC=BC=OB,
︵︵ 解:∵在⊙O中,AB=AC,∠B=70°,∴∠C=∠B=70°,
∴∠A=180°-∠B-∠C=180°-70°-70°=40°.
6.如图,A,B,C是⊙O上三点,∠AOB=120°,C是弧AB 的中点,试判断四边形OACB的形状,并说明理由.
证明:如图,连接OC. ︵
∵C是AB的中点,
∴∠AOC=∠BOC=12×120°=60°.
一、选择或填空题(每题 10 分,共 40 分) 1.如果两个圆心角相等,那么( D ) A.这两个圆心角所对的弦相等 B.这两个圆心角所对的弧相等 C.这两个圆心角所对的弦的弦心距相等 D.以上说法都不对
北师大版九年级数学下册 第三章2 圆的对称性(含答案)
北师大版九年级数学下第三章2 圆的对称性(含答案)一、选择题1.下列说法中,正确的是( ) A .等弦所对的弧相等 B .等弧所对的弦相等C .相等的圆心角所对的弦也相等D .相等的弦所对的圆心角也相等2.如图1,在⊙O 中,AC ︵=BD ︵,∠AOB =40°,则∠COD 的度数为( )图1A .20°B .40°C .50°D .60°3.如图2,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD =34°,则∠AOE 的度数是( )图2A .51°B .56°C .68°D .78°4.如图3,在⊙O 中,AB ︵=2CD ︵,则下列结论正确的是( )图3A .AB>2CDB .AB =2CDC .AB<2CDD .以上都不正确5.如图4,已知A ,B ,C ,D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有( ) ①AB ︵=CD ︵;②BD ︵=AC ︵;③AC =BD ; ④∠BOD =∠AOC.图4A .1个B .2个C .3个D .4个二、填空题6.如图5所示,在⊙O 中,若AB ︵=CD ︵,则AB =________,∠AOB =∠________;若OE ⊥AB 于点E ,OF ⊥CD 于点F ,则OE______OF.图57.如图6,在⊙O 中,AB ∥CD ,AC ︵所对的圆心角的度数为45°,则∠COD 的度数为________.图68.如图7,三圆同心于点O ,AB =4 cm ,CD ⊥AB 于点O ,则图中阴影部分的面积为________cm 2.图79.如图8所示,AB 是半圆O 的直径,E 是OA 的中点,F 是OB 的中点,ME ⊥AB 于点E ,NF ⊥AB 于点F.有下列结论:①AM ︵=MN ︵=BN ︵;②ME =NF ;③AE =BF ;④ME =2AE.其中正确的有________.(填序号)图810.如图9,AB 是⊙O 的直径,AB =10,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA ,若P 是直径AB 上的一动点,则PD +PC 的最小值为________.图9三、解答题11.如图10,在⊙O 中,AB ︵=CD ︵. 求证:∠B =∠C.图1012.如图11所示,以▱ABCD 的顶点A 为圆心,AB 的长为半径作圆,与AD ,BC 分别交于点E ,F ,延长BA 交⊙A 于点G.求证:GE ︵=EF ︵.图1113.如图12,在⊙O 中,弦AB 与CD 相交于点E ,AB =CD ,连接AD ,BC. 求证:(1)AD ︵=BC ︵; (2)AE =CE.图1214.如图13,A ,B ,C 为⊙O 的三等分点. (1)求∠BOC 的度数;(2)若AB =3,求⊙O 的半径及S △ABC .图13附加题我们学习了弧、弦、圆心角之间的关系,实际上我们还可以得到圆心角、弧、弦、弦心距之间的关系如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等[弦心距指从圆心到弦的距离(如图14①中的OC,OC′),弦心距也可以说成圆心到弦的垂线段的长度].请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:如图②,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B和C,D.(1)求证:AB=CD.(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.图14参考答案1.[解析] B “在同圆或等圆中”是弧、弦、圆心角的关系定理成立的前提条件,不可忽视.以上选项中只有“等弧”满足该条件,所以B 正确.2.[解析] B ∵AC ︵=BD ︵,∴AB ︵=CD ︵,∴∠AOB =∠COD .∵∠AOB =40°,∴∠COD =40°.故选B. 3.[解析] D ∵BC ︵=CD ︵=DE ︵,∠COD =34°,∴∠BOC =∠EOD =∠COD =34°,∴∠AOE =180°-∠EOD -∠COD -∠BOC =78°.4.[解析] C 如图,取AB ︵的中点E ,连接AE ,BE . ∵在⊙O 中,AB ︵=2CD ︵, ∴AE ︵=BE ︵=CD ︵, ∴AE =BE =CD . ∵AE +BE >AB , ∴2CD >AB .故选C.5.[答案] D6.[答案] CD COD = 7.[答案] 90° 8.[答案] π[解析] AB =4 cm ,CO ⊥AB 于点O ,则OA =2 cm.根据圆的旋转不变性,把最小的圆逆时针旋转90°,把中间圆旋转180°,则阴影部分就合成了扇形OAC ,即圆的14,∴阴影部分的面积为14×π×22=π(cm 2).9.[答案] ①②③ 10.[答案] 10[解析] 如图,作点C 关于AB 的对称点C ′,连接OC ,OD ,OC ′,BC ′.∵BC =CD =DA ,∴∠AOD =∠COD =∠BOC =60°.∵点C 与点C ′关于AB 对称,∴BC ′=BC ,∴∠BOC ′=60°,∴点D ,O ,C ′在同一条直线上,∴DC ′=AB =10,即PD +PC 的最小值为10.11.证明:∵在⊙O 中,AB ︵=CD ︵, ∴∠AOB =∠COD . ∵OA =OB ,OC =OD ,∴在△AOB 中,∠B =90°-12∠AOB ,在△COD 中,∠C =90°-12∠COD ,∴∠B =∠C .12.证明:如图,连接AF . ∵AB =AF , ∴∠ABF =∠AFB .∵四边形ABCD 是平行四边形, ∴AD ∥BC ,∴∠EAF =∠AFB ,∠GAE =∠ABF , ∴∠GAE =∠EAF , ∴GE ︵=EF ︵.13.证明:(1)∵AB =CD ,∴AB ︵=CD ︵, ∴AB ︵-AC ︵=CD ︵-AC ︵, ∴AD ︵=BC ︵. (2)如图,连接AC . ∵AD ︵=BC ︵, ∴AD =BC .在△ABC 和△CDA 中,∵AB =CD ,BC =DA ,AC =CA , ∴△ABC ≌△CDA ,∴∠BAC =∠DCA , ∴AE =CE .14.解:(1)∵A ,B ,C 为⊙O 的三等分点, ∴AB ︵=BC ︵=AC ︵, ∴∠BOC =13×360°=120°.(2)过点O 作OD ⊥AB 于点D . ∵A ,B ,C 为⊙O 的三等分点, ∴AB =AC =BC =3, 即△ABC 是等边三角形, ∴∠BAO =∠OBA =30°,则AD =32,故OD =32,OA =3,即⊙O 的半径为 3.S △ABC =3S △ABO =3×12OD ·AB =9 34.附加题解:(1)证明:如图,过点O 作OM ⊥AB 于点M ,ON ⊥CD 于点N ,则∠OMP =∠ONP =90°. ∵PO 平分∠EPF , ∴OM =ON .∵OM ,ON 分别是弦AB ,CD 的弦心距, ∴AB =CD . (2)上述结论成立.证明:若点P 在⊙O 上,过点O 作OM ⊥AB 于点M ,ON ⊥CD 于点N .同(1)可得OM =ON . ∵OM ,ON 分别是弦AB ,CD 的弦心距, ∴AB =CD .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2圆的对称性
知识要点基础练
知识点1圆的对称性
1.(泰安中考)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是(C) A.1 B.2
C.3
D.4
2.如图,在☉O中,=2,则下列结论正确的是(C)
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.以上都不正确
3.一条弦把圆分成1∶3两部分,则劣弧所对的圆心角的度数为90°.
知识点2圆心角、弧、弦之间关系的应用
4.(贵港中考)如图,AB是☉O的直径,,∠COD=34°,则∠AEO的度数是(A)
A.51°
B.56°
C.68°
D.78°
5.如图,已知☉O中,AB=CD,连接AC,BD.求证:AC=BD.
证明:∵AB=CD,∴,
∴,∴,∴AC=BD.
6.如图,AB,CD是☉O的直径,弦CE∥AB,的度数为70°,求∠EOC的度数.
解:∵的度数为70°,CE∥AB,
∴∠C=∠AOC=70°,
∵OE=OC,∴∠E=∠C=70°,
∴∠EOC=180°-70°-70°=40°.
7.如图,已知D,E分别为半径OA,OB的中点,C为的中点.试问CD与CE是否相等?说明你的理由.解:相等.
理由:连接OC.
∵D,E分别为☉O半径OA,OB的中点,
∴OD=AO,OE=BO.
∵OA=OB,∴OD=OE.
∵C是的中点,∴,∴∠AOC=∠BOC.
又∵OC=OC,∴△DCO≌△ECO(SAS),
∴CD=CE.
综合能力提升练
8.在半径为2 cm的☉O中有长为2 cm的弦AB,则弦AB所对的圆心角的度数为(C)
A.60°
B.90°
C.120°
D.150°
9.(兰州中考)如图,在☉O中,若C是的中点,∠A=50°,则∠BOC=(A)
A.40°
B.45°
C.50°
D.60°
10.在同圆或等圆中,下列说法错误的是(A)
A.相等弦所对的弧相等
B.相等弦所对的圆心角相等
C.相等圆心角所对的弧相等
D.相等圆心角所对的弦相等
11.如图,☉O经过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则的度数为(B)
A.25°
B.40°
C.50°
D.55°
12.如图,已知A,B,C,D是☉O上的点,∠1=∠2,则下列结论中正确的有(D)
①;②;③AC=BD;④∠BOD=∠AOC.
A.1个
B.2个
C.3个
D.4个
【变式拓展】如图,O是∠EPF的平分线上一点,以O为圆心的圆与角的两边分别相交于点A,B和C,D,角平分线PO和☉O相交于点G,H.下列结论:①AB=CD;②;③PB=PD;④PA=PC.其中正确的有(D)
A.1个
B.2个
C.3个
D.4个
13.如图,AB是☉O的直径,BC,CD,DA是圆O的弦,且BC=CD=DA,则∠BCD等于(C)
A.100°
B.110°
C.120°
D.135°
14.如图,☉O中,已知,且=3∶4,则∠AOC=144° .
15.如图,已知C,D是以AB为直径的☉O上的两点,且OD∥BC.求证:AD=DC.
证明:连接OC.
∵OD∥BC,
∴∠AOD=∠B,∠COD=∠OCB,
又∵OB=OC,∴∠B=∠OCB,
∴∠AOD=∠COD,∴AD=DC.
16.如图,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,交AD,BC于点E,F,延长BA交☉A于点G,判断是否相等,并说明理由.
解:相等.
理由:连接AF.
∵A为圆心,∴AB=AF,∴∠ABF=∠AFB.
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,∴相等.
拓展探究突破练
17.如图,弦AB和CD相交于☉O内一点P,且∠OPB=∠OPD,求证:
(1);
(2)PA=PC.
证明:(1)作OE⊥AB于点E,OF⊥CD于点F.由角平分线的性质知OE=OF.
连接OA,OB,OC,OD.由HL知△OBE≌△ODF,则BE=DF.
∵△OAB和△OCD都是等腰三角形,OE⊥AB,OF⊥CD,
∴根据等腰三角形三线合一的性质知,AB=2BE,CD=2DF, ∴AB=CD,则.
(2)由(1)易证△OPB≌△OPD,∴PB=PD,
∵AB=CD,∴PA=PC.。
