小学奥数辅导与练习21三角形的分割(一)
四年级上册数学试题 奥数第21讲 图形的切拼一 全国用含答案

第21讲图形的切拼(一)把一个几何图形剪成几块形状相同的图形,或是把一个几何图形剪开后拼成另一种满足某种条件的图形,完成这样的图形剪拼,需要考虑图形剪开后各部分的形状、大小以及它们之间的位置关系。
这一讲,我们一起来研究这类问题。
例1如下图所示:是由三个正方形组成的图形,请你把它分成大小、形状都相同的四个图形。
)1(就要求把原来如果我们不考虑分成的四个图形的形状,只考虑它的面积,分析与解答:个正方每部分面积应是正方形面积的,再把三个三个正方形分成四个面积相等的部分。
)的分法。
形合成一个与个正方形形状相同的图形,于是我们就有了如图(2)2(块形状、大小都一样的小三角形。
块和9请把一个等边三角形分别分成例28个大小、48分析与解答:①分成块的方法是:先取各边的中点并把它们连接起来,得到形状相同的三角形,然后再把每一个三角形平均分成两份,得到如下左图所示的图形。
得到下右图所示然后再把分点彼此连接起来,9块的方法是:先把每边三等分,②分成的符合条件的图形。
将下图中的图形分成形状相同、面积相等的两部分,想一想,应该怎么分?例3的小正方形(请你在“坐标纸”上画11×分析与解答:为了方便,可先将图分成许多个面个面积单位,每一部分的面积应为16一画),如下左图:由此可知,图形的面积为32,以及原图形的形,其次为7积单位。
为了保证分成的两个图形形状相同,根据最长边为8下面继续进行类似的推理,,用两种阴影分别表示出来。
状,可知每一部分的最长边只能为7可以找到答案。
面积相等的两部分。
具体分法见下右图,图中的阴影和空白部分将上图分成了形状相同、形状都相同的两部4厘米,请你先把它剪成大小、例4长方形的长和宽分别是9厘米和分,然后再把它们拼成一个正方形。
厘4=36×(平方厘米),所以正方形的边长应为6分析与解答:已知长方形面积是:9合起来正3厘米,分成相等的两块,米,因此可以把长方形上半部剪下6厘米,下半部剪下厘米的正方形,如下图所示:好拼成一个边长为6请你把下图中的两个图形中的某一个分成三块,然后再把它们拼成一个正方形。
小学四年级奥数配套课件 图形的分割与剪拼

例题(九)(★★★★★)
然后把乙剪成三块(如右下图所示)拼成的正方形,即可。
本讲重点知识
重要入手点:规则图形的中心 等底等高的两个三角形面积相等 注:特殊三角形——正三角形和等腰直角三角形的面积都相同,所以六边形面积等于13平方米。
例题(七)(★ ★ ★ )
用同样大小的四块等腰直角三角板,能否拼出一个三角形、一个正方形、 一个长方形、一个梯形、一个平行四边形五种图形?若能,画出示意图。
例题(八)(★ ★ ★ )
试将一个4×9的长方形分割成两个大小相等、形状相同的 图形,然后拼成一个正方形。
知识链接
桌子上放着m根火柴,甲、乙二人轮流每次取走1—n根。规定谁 取走最后一根火柴谁获胜。如果双方都采用最佳方法,甲先取, 那么谁将获胜? (1)若m÷(1+n)=P
则乙有必胜策略。甲取几根,乙就取(n+1)减几根。 (2)若m÷(1+n)=P …r
则甲先取r根,然后乙取几根,甲就取(n+1)减几根。
例题(四)(★ ★ ★ ★)
怎样把一个等边三角形分别分成8块和9块形状、大 小都一样的三角形。
(2)分成9块的方法:先把每边三等分,然后再把分点连接起来
知识链接
等边三角形的等分方法 ——各边等分再连线
例题(五)(★ ★ ★ ★)
下图是一个被挖去了为总面积四分之一小正方形的大正方形,请你将它分成 大小形状完全一样的两部分。如果分三部分呢?如果分成四部分呢?
知识链接
层层倒推,步步必胜。
例题一(★★)
用一条线段把一个长方形分成形状大小都相同的两块,一共有多少种不同的分 割法?
长方形的最重要之处是哪里呢? (1)做长方形的两条对甬线,设交点为O
(小学奥数)图形的分割

幾何面積問題除了利用常規的五大模型、各種公式求得之外,還可以用圖形分割的思想來做。
我們發現,在迎春杯幾何問題中,這類題目很多。
掌握好這種思想方法,可以幫助我們解決很多幾何難題。
解題關鍵:分割其實就是運用特殊的三角形(等角直角三角形、等邊三角形等)、正方形、等邊圖形的特殊性質進行分割而得,所以分割的關鍵是利用了特殊圖形的關係解題。
解題思想:這其實就是一種化整為零的思想,各位同學不僅要學會幾何題中的這種方法,更要細細體味這種思想在解決各種問題中的妙用。
模組一、簡單分割【例 1】 3個相同的正方形紙片按相同的方向疊放在一起(如圖),頂點A 和B 分別與正方形中心點重合,如果所構成圖形的周長是48釐米,那麼這個圖形覆蓋的面積是__________平方釐米.【例 2】 正方形ABCD 的面積是1平方米,將四條邊分別向兩端各延長一倍,連結八個端點得到一個正方形(如圖),求大正方形的面積. D CB A例題精講知識點撥4-2-4.圖形的分割【例 3】 將邊長為a 的正方形各邊的中點連結成第二個正方形,再將第二個正方形各邊的中點連結成第三個正方形,依此規律,繼續下去,得到下圖那麼,邊長為a 的正方形面積是圖中陰影部分面積的________ 倍.【例 4】 正三角形ABC 的面積是1平方米,將三條邊分別向兩端各延長一倍,連結六個端點得到一個六邊形(如右圖),求六邊形的面積.CB A【例 5】 正六邊形ABCDEF 的面積是1平方米,將六條邊分別向兩端各延長一倍,交於六個點,組成如下圖的圖形,求這個圖形的面積.FE D C B AF A B CD E【例 6】 長方形ABCD 的面積是40平方釐米,E 、F 、G 、H 分別為AC 、AH 、DH 、BC 的中點。
三角形EFG 的面積是 平方釐米。
A【例 7】把同一個三角形的三條邊分別5等分、7等分(如圖1,圖2),然後適當連接這些等分點,便得到了若干個面積相等的小三角形.已知圖1中陰影部分面積是294平方分米,那麼圖2中陰影部分的面積是______平方分米.【例 8】右圖中的大正方形ABCD的面積是1,其他點都是它所在的邊的中點。
小学图形分割的方法请扩散学习

1、划分成相等的 (1)把正方形分成大小相等的9个、16个小正方形。
(2)把等边三角形切成4、9 个形状、大小都一样的三角形。
2、可不相等 (1)把一张正方形纸片分割成6个、7个、8个、11个小正方形,请在图上画出分割线。
(2)把下面的等边三角形分割成6个、7个、8个、11个小等边三角形。
(3)把一个等边三角形切成8、 12 个形状、大小都一样的三角形。 练习1、将下图分成形状、大小都一样的两部分。 12格平均分2份,每份6格 练习2、如图,长方形长7厘米,宽6厘米,把它分割成边长恰好是整厘米数的小正方形,(大小可不同)最
小学奥数中常见的辅助线的添加技巧3-等形分割(三角形面积、正方形面积、圆的面积等图形问题)
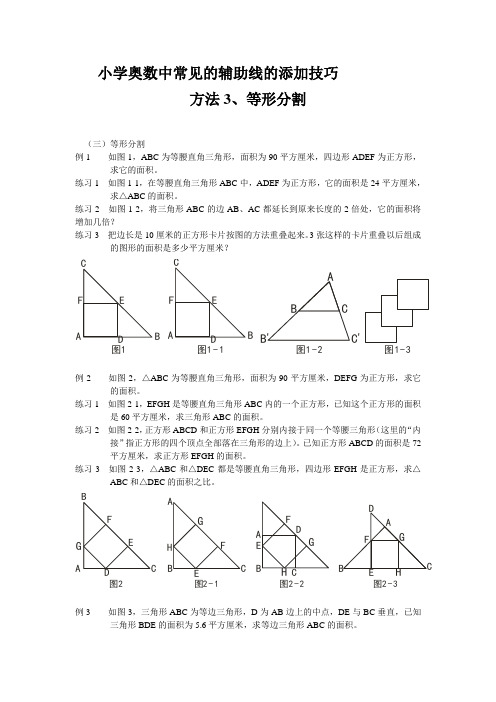
小学奥数中常见的辅助线的添加技巧方法3、等形分割(三)等形分割例1 如图1,ABC 为等腰直角三角形,面积为90平方厘米,四边形ADEF 为正方形,求它的面积。
练习1 如图1-1,在等腰直角三角形ABC 中,ADEF 为正方形,它的面积是24平方厘米,求△ABC 的面积。
练习2 如图1-2,将三角形ABC 的边AB 、AC 都延长到原来长度的2倍处,它的面积将增加几倍?练习3 把边长是10厘米的正方形卡片按图的方法重叠起来。
3张这样的卡片重叠以后组成的图形的面积是多少平方厘米?AB C EF DAB CEF DABC B 'C'图1-1图1-2图1-3图1例2 如图2,△ABC 为等腰直角三角形,面积为90平方厘米,DEFG 为正方形,求它的面积。
练习1 如图2-1,EFGH 是等腰直角三角形ABC 内的一个正方形,已知这个正方形的面积是60平方厘米,求三角形ABC 的面积。
练习2 如图2-2,正方形ABCD 和正方形EFGH 分别内接于同一个等腰三角形(这里的“内接”指正方形的四个顶点全部落在三角形的边上)。
已知正方形ABCD 的面积是72平方厘米,求正方形EFGH 的面积。
练习3 如图2-3,△ABC 和△DEC 都是等腰直角三角形,四边形EFGH 是正方形,求△ABC 和△DEC 的面积之比。
ABCEFDGA BE FDG H ABCEF DG H图2图2-1图2-2图2-3ABC FGH例3 如图3,三角形ABC 为等边三角形,D 为AB 边上的中点,DE 与BC 垂直,已知三角形BDE 的面积为5.6平方厘米,求等边三角形ABC 的面积。
练习1 如图3-1,D 为等腰直角三角形ABC 的腰AB 的中点, DE 与BC 垂直,已知三角形ABC 的面积为48平方厘米,求三角形BDE 的面积。
练习2 如图3-2,把一块面积为108平方厘米的正方形铁皮,做成一个无盖的正方体盒子。
分割图形小学三年级奥数题

分割图形小学三年级奥数题
亲爱的小朋友们,小学频道为你准备了小学三年级奥数——分割图形,希望大家开动脑筋,交出一份满意的答卷。
加油啊!
分割图形是使我们的头脑灵活,增强观察能力的一种有趣的游戏。
我们先来看一个简单的分割图形的题目──分割正方形。
在正方形内用4条线段作“井”字形分割,可以把正方形分成大小相等的9块,这种图形我们常称为九宫格。
用4条线段还可以把一个正方形分成10块,只是和九宫格不同的是,每块的大小不一定都相等。
那么,怎样才能用4条线段把正方形分成10块呢?请你先动脑筋想想,在动脑的同时还要动手画一画,手和脑同时参与活动,才能互相弥补缺乏,更快地寻找出答案。
其实,正方形是不难分割成10块的,下面就是其中两种分割方法。
想一想,用4条线段能将正方形分成11块吗?应该怎样分?请你画一画。
奥数试题 多边形的三角分割

三年级奥数题及答案:多边形的三角分割(1)由二十边形的一个顶点能画出多少条对角线?(2)四边形、五边形、…n边形,各有多少条对角线?(3)对角线如不相交,在五边形、六边形、七边形内最多能画出几条对角线?所谓“三角测量”,就是将多边形分割成一些三角形,这是一种相当重要的基本测量方法.但在这里,我们主要是讨论将多边形分割成三角形的各种不同方式,以及记录结果的方法.图2中的多边形ABCDEF,可以用3条对角线AC、AD与DF分成三角形.试找出其他两种用3条对角线将它分割成三角形的不同方法.图3中的七边形则是被4条对角线分割成三角形.你还能找出多少种其他的方法?有一种办法可以很清楚地记录不同的分割方法,那就是计算各顶点的三角形数目.因此这个多边形的分割方法可以记录为:1 4 1 3 1 3 2不论自哪个顶点开始,不论是顺时针或逆时针方向,都会得到相同的数字.1+4+1+3+1+3+2=15以不同方式分割七边形是否会得到相同的数字和?请解释你的结果.取各种不同边数的多边形,并记录下不同的分割方法;然后试试自己是否能不用绘图,就预测出十边形会有多少种不同的分割方法.带状模式把多边形分割成三角形所形成的数列,可以用来形成一些相当有趣的模式.第一行是只有1的数列.第二行是将多边形分割为三角形时所产生的数列.第三行的形成方式如下:第二行中两个相邻项的乘积为pq,减去1得(pq-1).将pq-1除以r,r为第一行的数字,就得到第三行在p与q之间的s:所有其他行的数字也是按上述方法从上两行的数字求出的.例如:试着自己作出类似的数字模式.你所取的多边形的边数愈多,分割后得到的第二行数列就愈长,而这条“带子”也就会愈宽.图4是另一个例子,形成的带状模式如下所示.除了水平方向之外,也要注意对角线方向的数字模式.。
解三角形中分割三角形问题专题训练

解三角形中分割三角形问题(含答案)该类问题在近年高考中比较常见題型,一本粘界生在高考中该类型题得分率相对较低。
对于这类问题, 由于多出一条分割线就多出三角形,因此,未知数变多,方程变多,方法也变多.但不同方法的运算难易 程度不一样,学生往往由于选择复杂路径,增加解方程运算难度,导致在考试中无法拿下.解决这类问题 关键是:(1)抓住多个三角形的公共角、公共边以及角平分线性质等了方程(组)解题。
(2)紧紧抓住“知 三可解”一三角形三边三角夭个元素中已知其中的三个元素,且至少有一个元素是边,则该三角形其他 边角都可以求解•由“可解三角形”出发寻找解题思路•熟练掌握每种可解条件求边求角的运算特点,选择 最佳解题路径•下面就全国卷在对这类问题的考察进行归纳总结,并配相应练习,让学生通过举一反三的 练习突破该难点。
类型一:利用公共边、角,角平分线性质列方程求解例1: (2016年3卷8)在8BC 中,B=^ BC 边上的高等于;BC ,则CoSA=(4 3(A)巫 (B)逅 (C) ■逅 (D)・10 10 10 10点评:本题以分割出的两个直角三角形的公共边Aih 快速的得出3C 三边的比,再用余弦定理求出角 A 的余弦值.例2: (2015年2卷17) ΔABC 中,D 是BC 上的点,AD 平分ZBAC, AABD 是AADC 面积的2倍。
点评^本题由AD 平分ZBAC 易得AB:Ae=BD:DG 这是角平分线常考的一个性质。
第(U)问抓住两个解:设EC 边上的高线为AD,则BC = 3AD,所以 AC = X ∕A D Γ+DC 2=√5AD> AB = JLXD ∙由余弦定理, 知 COS A= AB? +AC? _ BL 2 AB ∙ AC2AD'+5AD'-9AD' 2×>∕2AD× V5AD 一浮故选c ・ B D C (I)求 Sin ZB Sin ZCDC=-2,求BD 和AC 的长 解:(I )S AABD = — AB ∙ ADSinZB AD,SzkWC= 一 ACADSinZCAD,2 2因为 S .^B D =2S .>ZBAD=ZCAD^以 AB=2AC.由正弦定理可疇駅(∏)因为 SAABD : S ΔAD C=BD : DC ,所以 BD=√2.设 AC=X,由(1)知 AB=2AC=2x,在AABC 和AABD 中,f 解得x=l,所以AC=I.由余弦定理知,COS B 2(2x)2+Q-F2∙2x ∙√2三角形的公共角B f 当然也可以抓住在AABC 和厶ACD 的公共角C 列方程,还可抓住在AABD 和2∖ACD 的ZADB 和ZADC 列方程.强化训练(一)1.如图,在ΔABC 中,D 为BC 边上一点,ΔABD 为等边三角形,AB = 2CD.(I )若AACD 的面积为2√5,求AB ;(∏)若AC = √y.求SinZBAC ∙ 1 •解:(I)因为 SMID = 2^3 9 AB = BD = 2CD > 所以 S AA BD = 2S AACD = 4√5 > 另—方面 >S ΔABD = ^AB 2sin60o , ^f^AB 2sin60o = 4√31 AB =4. (∏)设CD=X,则AD=AB = 2x, BC = 3x.在AADC 中,ZADC = 180β -60β = 120β ,由余弦定理得,AC 2 = AD 2 + CD 2 - 2AD ∙ CDCOSZADC,即7 = (2X )2+X 2-2∙2X ∙X O S 12 O o> 解得 X= 1»所以 BC = DB + DC = 3x = 3.在ΔABC 中,由正弦定得;=石去?2.在AABC 中.已知ZABC 的平分线BD 交AC 于点D. BA=2BC. (I )^∆BDC 与ZkBDA 的面积之比; ⑵若ZABC=I20β , BC=3,求 AD 和 DC ・2.解:(I)设ZiBDC 与ABDA 的面积分别为S- S 2,则Sl=扌BC BD SinZCBD, S 2 = ^BA BD-SinZABD,因为BD 平分ZABC,所以ZABD = ZCBD,又因为BA = 2BC,所以S 2 = 2S 1,即孑=扌・(U)在厶ABC 中.由余弦定理可得:AC 2 = AB 2 + BC 2 - 2AB ∙ BCcOSI20o=36 + 9+2×3×6×i=63,ΛAC = 3√7,由(1)可得:^ = 2, ΛDC= √7, AD = 2√7. 3∙ ΔABC 的内角AB,C 所对的边分别是a,b f c 9 fib = 3(acosB + bcosA), b + c = 8. (I)求b5(∏ )若BC 边上的中线AD = P 求AABC 的面积・ 3∙解:(I)由正弦定理得SinB = 3(SillACOSB + SinBCOsA)9所以SinB = 3sin(A + B)t 因为A + B + C = π,所以Sill(A + B) = sin(π- C) = sinC> 即SinB = 3sinC t 所以b = 3c f 又因为b + c = 8,所以b =6, c = 2.(∏)在AABD 和AACD 中P 由余弦定理得所以SinZBAC =竺弊 3√21 14c2= AD2 + BD2一2AD ∙ BD COSZADB f b2= AD2+ CD2一2AD CD cos ZADG因为b = 6, c = 2, BD=DC=务AD =P 又因为ZADB + ZADC = ιr,即COSZADB = -COSZADC, 所以a2=31» 所以COSZBAC = L^ZS=害,又因为ZBACE(Om),所以SinZBAC =所以△ ABC 的面^S AABC = -bcsinZBAC =—.2 4类型二:从可解三角形出发,寻找解题思路,选择最佳路径例3:(2017年 3 卷17)∆ABC 的内角AB,C 的对边分别为a,b,c ,已知SiIiA+ √3cosA= 0, a =2√7 , b = 2・(I)求c;(∏)设D为BC边上一点,且AD丄Ac ,求A ABD的面积.解:(I)由SIn A+ 5/3 COS A= 0 > 得2sm(A+亍) = 0,即A+扌= kπ(keZ), 又A∈(0,π),所以A+^ = π,得A=y.由余弦定理得a2 =b2 +c2 -2bc cos A.又因为a = 2√7,b = 2,cosA=-∙∣代入并整理得(c +1)2 =25 ,解得c = 4.(U)解法1:因为AC = 2,BC = 2√7,AB = 4,由余弦定理得COSC = HL = 0因为M丄AD,即3ΓD为直角三2ab 7角形,则M = CD∙8sC,得CD = √7∙从而点D为BC的中点,S Z∖ABD =FS ABC = —X —×∣AB∣×∣AC∣×siιι A= •解法2:过B作BE丄AD于点E,因为M'丄AD,所以,ZBAE=30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的分割(一)
同学们大家好!三角形的面积的计算方法大家已经知道了,今天我再告诉大家一个规律:等底等高的三角形面积相等。
这是一个非常重要的规律,在解决多边形面积的许多问题中都要用到它。
今天,我们就一起来研究应用这一规律可以解决哪些问题。
【典型例题】
一. 阅读思考:
例1. 有一个三角形花坛,想把它平均分成两个相等的三角形,可以怎样分?
分析与解答:因为“等底等高的三角形面积相等”,所以要把这个三角形花坛平均分成两个相等的三角形,就是把这个三角形花坛分成两个等底等高的三角形就可以了。
而三角形的每条边都可以作三角形的底,所以我们只要把这三条边分别二等分,再把中点与这条边相对的顶点连接起来就可以了。
例2. 将任一三角形分成面积相等的六个三角形,应怎么分?
分析与解:根据等底等高的三角形面积相等这一结论,只要把原三角形分成六个等底等高的小三角形,它们的面积就必然相等。
而要找这六个等底等高的小三角形,只需把三角形的某一边六等分,再将各分点与这边相对的顶点连结起来即可。
如图(1)
图(1)
又因为,所以,如果我们把每一个小三角形的面积看成1,即
而可以看成是先把原三角形等分两份,再把每一份分别等分成三份。
C
图(2)
同理,可以看成是先把原三角形等分成三份,然后再把每一份等分成两份。
即
A A A
B C B C B C
图(3)
类似于这样的分法,我们还可以画出许多,这里就不一一列举了。
这两道例题有一个共同的思路,就是想办法找出等底等高的三角形,而找这种三角形,就要几等分某一条线段。
如果两个三角形的底相等,高不相等,它们的面积有什么关系呢?
如果两个三角形底的长度相等,高的长度不相等,那么它们的面积之比正好等于这两个三角形高的长度比。
同样的道理,我们还可以推出,如果两个三角形高的长度相等,底的长度不相等,那么这两个三角形的面积之比正好等于它们的底的长度比,因此我们有下面的结论:
如果甲、乙两个三角形的底(高)的长度相等,那么甲、乙两个三角形的面积之比等于它们的高(底)的长度之比。
例3. 把三角形ABC分成甲、乙、丙三部分,使甲的面积是乙的面积的3倍,丙的面积是乙的面积的4倍。
分析与解:要想使三角形甲的面积是三角形乙的面积的3倍,可以使这两个三角形的高相同,而三角形甲的底是三角形乙的底的3倍,同样使三角形丙的高和三角形乙的高相同,而三角形丙的底是三角形乙的底的4倍,这样一来,我们将三角形ABC的一条边8等分,使乙占其中的一份,甲占其中的3份,丙占其中的4份,即可达到目的。
B C
例4. 三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
(如图)
B D C
分析与解:根据如果两个三角形的高相等,那么这两个三角形的面积比等于它们底的比的结论,即可求出三角形ABC的面积。
三角形ADE和三角形DCE中,因为CE=3AE,所以三角形DCE 的底是三角形ADE的底的3倍,又因为这两个三角形的高相同,所以三角形DCE的面积是三角形ADE的面积的3倍,即
三角形DCE面积=三角形ADE面积×3
=20×3=60(平方厘米)
同理,在三角形ABD和三角形ADC中,因为DC=2BD,且这两个三角形有相同的高,所以三角形ADB的面积是三角形ADC的面积的,即
三角形ADB面积=三角形ADC面积×
=(三角形ADE面积+三角形DCE面积)×
=(20+60)
=80
=40(平方厘米)
所以三角形ABC面积=40+80=120(平方厘米)
【模拟试题】(答题时间:40分钟)
二. 尝试练习:
1. 将任意一个三角形的面积五等分,你能找到三种以上的方法吗?
2. 将任意一个三角形的面积四等分,你有几种方法?
3. 见图,在三角形ABC 中,CD 是AC 的,E 是BC 的中点,你能在原图形的基础上将三角形ABC 的面积5等份吗?
A
D
B E C
4.
见图ABCD 平行四边形,E 是BC 的中点,平行四边形ABCD
的面积比三角形ABE 的面积多多少倍?
D 5. 如图,把大三角形分成了甲、乙两部分,乙由A 、B 两部分组
成,求甲与乙两部分面积的比值。
C 9 A B
3 A 4.5 D 4.5 B
E
乙甲。
