2010 大方坯两相区综合应变的理论推导与计算

合集下载

材料力学公式总结

材料力学公式总结材料力学是研究材料在外力作用下的力学性能和变形规律的学科，它是材料科学的基础和核心。

在材料力学中，有许多重要的公式，它们可以帮助我们理解材料的性能和行为。

本文将对材料力学中的一些重要公式进行总结，希望能对大家的学习和工作有所帮助。

1. 应力和应变的关系公式。

在材料力学中，应力和应变是两个非常重要的概念。

应力是单位面积上的力，通常用σ表示，而应变是材料单位长度的变形量，通常用ε表示。

它们之间的关系可以用胡克定律来描述，即σ = Eε，其中E为杨氏模量，是描述材料抵抗变形能力的一个重要参数。

2. 弹性模量的计算公式。

弹性模量是描述材料在受力后能够恢复原状的能力的一个重要参数。

对于各向同性材料，弹性模量E可以用杨氏模量和泊松比来表示，即E = 2G(1+μ)，其中G 为剪切模量，μ为泊松比。

3. 应力-应变曲线的公式。

材料在受力时，应力和应变之间的关系通常通过应力-应变曲线来描述。

对于线弹性材料来说，应力-应变曲线是一条直线，其斜率就是杨氏模量E。

而对于非线性材料来说，应力-应变曲线通常是一条曲线，可以用一些复杂的数学公式来描述。

4. 塑性变形的公式。

当材料受到超过其屈服强度的应力时，就会发生塑性变形。

塑性变形的特点是应力和应变不再呈线性关系，而是出现了一定的变形硬化。

塑性变形的公式通常比较复杂，需要根据具体的材料和加载条件来确定。

5. 断裂力学的公式。

材料在受到过大的应力时会发生断裂，断裂力学是研究材料断裂行为的学科。

在断裂力学中，有许多重要的公式，如格里菲斯断裂准则、弗兰克-雷迪公式等，它们可以帮助我们预测材料的断裂行为。

总结。

材料力学中的公式是我们理解材料性能和行为的重要工具，通过对这些公式的学习和掌握，我们可以更好地应用材料力学知识，解决工程实际问题。

希望本文对大家有所帮助，也希望大家能够深入学习材料力学，为材料科学的发展做出贡献。

任意方向线应变计算公式的两种推导方法

任意方向线应变计算公式的两种推导方法D主应变的大小。

由以上分析可知对平面应力状态下任意方向线应变计算公式的推导是有现实的意义的。

2任意方向线应变计算公式的两种推导方法2.1传统推导方法——叠加法假设已知某微元体在xoy 平面发生线应变εx , εy ,及切应变γxy ,那么距x 轴为任意角α方向的线应变εα可以更具叠加原理求解，即分别将εx , εy 和γxy 对εα的贡献求出，然后再叠加即可。

现在以求εx 的贡献为例，叙述推导过程。

如图1，只有εx 单独作用时，在x 方向产生位移增量的 εx dx ，则OP 线位移到OP ′。

2.2利用广义胡克定律进行推导的方法叠加法是大多数资料书中使用的方法，主要应用了几何知识进行推导，需要进行画图分析，有时感到较为繁琐。

在对材料力学的学习过程中，笔者发现一种利用广义胡克定律进行推导的方法，可以避免繁琐的几何分析。

其大体思路为：沿所求线应变方向建立一个新直角坐标，利用平面应力状态下任意斜截面上的应力计算公式计算出新坐标内的两个垂直方向的应力，最后用广义胡克定律计算出所求线应变的大小。

具体的推导过程如下：在平面应力状态下，根据广义胡克定律有图2εx=1E（σx-νσy）（5）εy=1E(σy-νσx) （6）γxy=τxyG（7）式中E为材料的弹性模量，G为材料的切变模量，ν为材料的泊松比。

新版孙训方版。材料力学公式总结大全-新版.pdf

材料力学重点及其公式材料力学的任务（1）强度要求；（2）刚度要求；（3）稳定性要求。

变形固体的基本假设（1）连续性假设；（2）均匀性假设；（3）各向同性假设；（4）小变形假设。

外力分类：表面力、体积力；静载荷、动载荷。

内力：构件在外力的作用下，内部相互作用力的变化量，即构件内部各部分之间的因外力作用而引起的附加相互作用力截面法：（1）欲求构件某一截面上的内力时，可沿该截面把构件切开成两部分，弃去任一部分，保留另一部分研究（2）在保留部分的截面上加上内力，以代替弃去部分对保留部分的作用。

（3）根据平衡条件，列平衡方程，求解截面上和内力。

应力：dAdP AP pAlim正应力、切应力。

变形与应变：线应变、切应变。

杆件变形的基本形式（1）拉伸或压缩；（2）剪切；（3）扭转；（4）弯曲；（5）组合变形。

静载荷：载荷从零开始平缓地增加到最终值，然后不再变化的载荷。

动载荷：载荷和速度随时间急剧变化的载荷为动载荷。

失效原因：脆性材料在其强度极限b破坏，塑性材料在其屈服极限s时失效。

二者统称为极限应力理想情形。

塑性材料、脆性材料的许用应力分别为：3n s，b bn ，强度条件：maxmaxAN，等截面杆AN max轴向拉伸或压缩时的变形：杆件在轴向方向的伸长为：l l l 1，沿轴线方向的应变和横截面上的应力分别为：ll ，AP AN 。

横向应变为：b bb bb 1'，横向应变与轴向应变的关系为：'。

胡克定律：当应力低于材料的比例极限时，应力与应变成正比，即E ，这就是胡克定律。

E 为弹性模量。

将应力与应变的表达式带入得：EANl l静不定：对于杆件的轴力，当未知力数目多于平衡方程的数目，仅利用静力平衡方程无法解出全部未知力。

圆轴扭转时的应力变形几何关系—圆轴扭转的平面假设dx d。

物理关系——胡克定律dxd GG 。

力学关系dA dxd G dx d G dATAAA22圆轴扭转时的应力：tpW T RI Tmax；圆轴扭转的强度条件：][maxtW T，可以进行强度校核、截面设计和确定许可载荷。

材料力学常用基本公式

材料力学常用基本公式材料力学是研究材料的力学性质和力学变形行为的学科，涉及到材料的强度、刚度、变形、破坏等方面。

在材料力学的研究中，常用到一些基本公式来描述材料的力学特性。

以下是一些材料力学中常用的基本公式。

1.应力和应变的关系：应力（stress）是单位面积上的力，通常用σ表示，其计算公式为：σ=F/A其中，F是作用在材料上的力，A是该力作用在材料上的面积。

应变（strain）是材料在力作用下发生的变形程度，通常用ε表示，其计算公式为：ε=ΔL/L其中，ΔL是材料受力后的长度变化，L是材料受力前的初始长度。

2.各向同性线弹性材料的胡克定律：胡克定律描述了各向同性线弹性材料在弹性阶段的应力和应变关系，即应力与应变成正比。

胡克定律的公式为：σ=E*ε其中，E是材料的弹性模量，是描述材料对力产生变形的能力大小的物理量。

3.杨氏模量和剪切模量：在胡克定律中，杨氏模量（Young's modulus）是描述材料沿着受力方向的应力和应变关系，剪切模量是描述材料在垂直于受力方向发生剪切变形时的应力和应变关系。

它们的关系公式为：E=2G*(1+μ)其中，E是杨氏模量，G是剪切模量，μ是泊松比，描述了材料的侧向收缩程度和拉伸程度之间的比例关系。

4.流变方程：在一些材料的力学特性中，材料的应力和应变关系不再满足胡克定律，而呈现出非线性特性。

这时可以使用流变方程来描述应力和应变的关系。

其中，最常用的是弹塑性流变方程：σ=K*ε^n其中，σ是应力，ε是应变，K是材料的流变模量，n是流变指数。

5.共轭滑移原理：用于描述材料在微观滑移中的位错模型和宏观弹性力学行为之间的关系。

根据共轭滑移原理，材料在滑移发生时，应变应能量密度在前后变形区是不变的，可以表示为：ε*σ=ε_s*σ_s+ε_d*σ_d其中，ε*和σ*表示综合应变和综合应力，ε_s和σ_s表示剪切滑移应变和剪切滑移应力，ε_d和σ_d表示剪切向应变和剪切向应力。

PPT课件08-第八讲-外力功-应变能-互等定理

第十三章能量法
本章主要介绍能量法的基本原理与分析方法，包括：
外力功、应变能与克拉比隆定理功与位移互等定理克罗第-恩格塞定理与卡氏定理变形体虚功原理与单位载荷法研究对象：直杆、曲杆、桁架与刚架，涉及线性与非线性问题
第十三章能量法
讲授内容
§1 外力功、应变能与克拉比隆定理 §2 互等定理 §3 卡氏定理 §4 变形体虚功原理 §5 单位载荷法
4F 2D3n Gd 4
F
2
8FD3n Gd 4
§2 互等定理
功的互等定理位移互等定理例题
功的互等定理功的互等定理（简单形式）
两种加载状态
D ij
引起位移的载荷发生位移的部位
D ij
引起位移的载荷
发生位移的部位
线性弹性体的两种加载方式与外力功：
总功与加载次序无关
W1 W2
先加 F1，后加 F2
外力功 W
能量守恒
变形能 V 能量法
特点：间接、抽象，免去了复杂的变形分析；适于求解复杂问题。
基本概念
相应位移载荷 F 作用点处
沿载荷作用方向的位移 D.
由所有载荷共同引起外力功载荷 F 在其相应
位移 D 上所作之功
应变能构件因变形而储存的能量（变形能）
广义载荷力，力偶，一对大小相等、方向相反的力或力偶等广义位移线位移，角位移，相对线位移，相对角位移等
Mel2 2EI
A
A,F
A,Me
Fl 2 2EI
Mel EI
W FwA Me A F 2l 3 FMel 2 Me2l
2
2 6EI 2EI 2EI
某载荷做功与其它载荷相关
外力所作之总功，不能利用叠加原理计算

坯二次冷却区域两相界应变的模拟计算

连铸大方坯二次冷却区域两相界应变的模拟计算盛义平!"张晓春!"金正瑞#$!%燕山大学"河北秦皇岛&’’&&()#%中国第一重型机械集团公司"黑龙江富拉尔基!’!&(#*摘要+以某钢厂,!-../(!&..的连铸大方坯为例"对其两相界的应变进行了模拟计算"计算结果与引进设计资料给定的应变曲线基本吻合0关键词+连铸)大方坯)应变)计算中图分类号+12333%#文献标识码+4文章编号+!&&!5!-’6$#&&#*&75&&#-5&,89:;<=><?@A B:B C<9<D B E F G F D<H?:B C<9<D><9B C9A<A I;J>:I B F GK;<<?C9I F><9G:H J><<;C9=L<9FM N O P Q R S5T S U V!"W N4P Q6S X Y5Z[\U!"]^P W[_U V5‘\S#$!%R X U a[X Ub U S c_‘a S d ef S U[\X U V g X Y&’’&&("h[S U X)#%h[S U X2S‘a d N_X c eiX Z[S U_‘eQ‘Y\Th Y%2\j X_‘k S!’!&(#"h[S U X*8K I B H:>B+1X l S U V,!-../(!&..Z Y U d S U\Y\a j eZ X a d_gm j Y Y.Y n X a d__j T j X U d X a X U_o X.T j_"d[_ X\d[Y‘a a S.\j X d_X U gZ X j Z\j X d_d[_g_n Y‘.X d S Y US Ua_Z Y U g X‘eZ Y Y j S U Vp Y U_q1[_‘_a\j d Y n d[_Z X j Z\j X d S Y U m X a S Z X j j eS U Y a\j X d_a r S d[d[_g_n Y‘.X d S Y UZ\‘c_V S c_US Ud[_n Y‘_S V U.X d_‘S X j qs F Jt<H G I+Z Y U d S U\Y\a Z X a d S U V)m j Y Y.)g_n Y‘.X d S Y U)Z X j Z\j X d S Y U!前言处于高温状态的连铸大方坯在向下运行的过程中两相界的总应变由三部分组成+u在内部钢水静压力作用下产生的鼓肚应变)v在矫直过程中产生的矫直应变)w支撑辊偏离正确弧线产生的错位应变0假设在理想状态下辊列中的辊子错位应变为零"鼓肚应变和矫直应变便决定了连铸大方坯两相界的总应变0本文以某钢厂,!-.. /(!&..的连铸坯为例"对大方坯两相界的应变进行了计算"计算结果与原设计资料给定的应变曲线基本吻合"证明本文建立的数学模型和采用的计算方法是正确的0#鼓肚应变计算与板坯的鼓肚变形不同"在计算大方坯的鼓基金项目+国家重点科技$攻关*项目$-757#x5&#5&!5&,y*收稿日期+#&&#5&75&x作者简介+盛义平"男"(x岁"教授"燕山大学$&’’&&(*肚应变时"必须考虑铸坯的窄边对宽边的约束作用0因此"可将两支承辊间的连铸大方坯坯壳看作为两对边固定支撑$有支撑辊侧*z两对边弹性支撑$无支撑辊侧*的矩形板0矩形板在横向压力钢水静压力的作用下发生鼓肚变形0由钢的高温力学性质可知"坯壳的鼓肚变形分为两部分+一是瞬时弹性变形"二是随时间增大的蠕变变形0{%|变形几何方程总应变等于弹性应变与蠕变应变之和}~!}"~#}$~}%!}"%#}$%&~%!}"~%#}$~’()%$!*总应变与鼓肚变形量的微分关系}~!*+~!,*-#.-#~}%!*+%!,*-#.-#%&~%!#+~%!,#*-#.’()-~-%$#*/-#/#&&#P Y%7重型机械!"#$%&"#$’%()*"()#!"+$%&"+$’%()*"()+,"#+$)&"#+$’%()*"-./(#(+012式中3!4!"4!5和,4,"4,5分别为线应变和剪应变6其中上角标"和5分别表示总应变的弹性部分和蠕变部分0下同26下脚标#4+和#+分别为坯壳在坐标轴方向及其坐标平面内中的分量0下同27&#4&+4&#+分别为坯壳的曲率和扭率7*4*"分别为坯壳的总鼓肚变形量和初始弹性鼓肚变形量89:9本构方程弹性应变与应力分量的关系!"#$;<0=#’>=+2!"+$;<0=+’>=#2,"#+$)0;?>2<@-./#+0A 2蠕变应变速率与应力偏量的关系B;6)C!D 5#$1!E)=F #!D 5+$1!E)=F +,D 5#+$1!E)=@-./#+0G 2式中3<4>分别为弹性模量和泊桑系数3=4@分别为正应力和剪应力7=4!E分别为有效应力和有效应变速度7F 为应力偏量89:H 平衡方程在钢水静压力作用下6矩形板0坯壳2横截面上的应力与内力的关系为I #$J %=#K %I +$J %=+K %I #+$J%@#+-./K %0L 2式中3I #4I +分别为横截面上的弯矩6I #+为横截面上的扭矩8由以上诸式6容易得到当坯壳在支撑辊间运行时6坯壳的总曲率&与初始弹性曲率4初始弹性鼓肚变形量*"以及在两支承辊间的运行时间M之间的关系&#$&"#?N <)0;’>)20)>’;2()*"()+?0)’>2()*"()B C #M O &+$&"+?N <)0;’>)20)>’;2()*"()#?0)’>2()*"()B C +MO&#+$&"#+?1N <A 0;?>2()*"(#(+M -./O0P 2式中3N 为蠕变常数7M $Q R为坯壳在两支撑辊间的运行时间6Q 为两支撑辊间辊距6R 为拉坯速度7O 为时间指数8由以上讨论可知6当求得了坯壳在钢水静压力作用下的弹性解后6便可由式0P 2得到坯壳在两辊距间的总曲率6进而由式0)2求得坯壳的总鼓肚应变81矫直应变文献B 1C 给出了连铸坯在矫直变形过程中的曲率速率和矫直应变速率的方程式&D*$S I D*T "’U I *T V W5X0Y 2!D*$’Z &D*$S Z I D*T "?U Z I*T V W5X0[2式中T "$\]<Z )K ]T 5$\]Z;?;X^_‘a 5V Wb c XK ]其中3&*4I *4!*分别为矫直变形时的曲率4矫直力矩和矫直应变7<4U 4X 4a 54b 4c 分别为坯壳的弹性模量4蠕变速度常数4蠕变应力指数4蠕变活化能4气体常数和坯壳的绝对温度7Z 为坯壳横截面上的点至铸坯横截面中性轴的距离8当I D*de 时6式0Y 2中的S I D*f T "取负号4当I D*ge 时6式0Y 2中S I D*f T "取正号8式0[2中的矫直力矩由下式计算B A 4G C0参见图;2I *$A\h ;?h )K I $A J i )i)’j KZJZ ?N ’i )eZ =k lZ ’0if )’j 2B Cj)K %?A J N )N )’jK %J%’N ’i)eZ =k l%’0N f )’j 2B Cj)K Z0;e 2me 1m 重型机械)e e )n o :G图!连铸坯壳式中"#$%为铸坯表面的屈服应力&’为坯壳的厚度(将式)*+在矫直区内积分,即可求得矫直应变-.(将矫直应变与鼓肚应变相加,即得到在二冷区坯壳的总应变(/计算实例模拟计算时首先计算坯壳的温度和厚度,然后才能计算出坯壳的变形(图0为某厂生产的1!*223/!422大方坯坯壳在二冷区中的总应变曲线,图中的三个尖峰应变值对应三个矫直点(其中实线为连铸机引进资料中给定的曲线,虚线为由以上数学模型模拟计算所得的结果,可见两者是基本吻合的(图0二冷区坯壳总应变!567458292:;056745<292:;参考文献"=!>?5@5A B C D E F ;G?5H I E J K E 5H L M N O OF ;F P Q O :OR S M T M N N U 5V W L L N M X S M L Y OZ!*815=0>[\]]C ^]\_H 5K M N N UF ;F P Q O :O Z ?B [J ‘a D E C bH B J HZ!*845=1>盛义平,郭普学5连铸坯的矫直与弯曲=>5重型机械,!**1,)1+5=/>盛义平,孙蓟泉5连铸坯连续矫直理论的初步探讨=?>5重型机械,!**4,)/+5=c >A 5K5鲁捷斯等著5连续铸钢原理=d >5上海人民出版社eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee,!*f f 5钢管!!次荣获部省优秀科技期刊奖欢迎订阅0441年期刊钢管gh i j k i i l j k国内发行代号"<0m!*c 国外发行代号"/f 84A d 双月刊定价"8544元全年"/8544元n钢管o 系全国性公开发行期刊,由攀钢集团成都钢铁有限责任公司主办,中国钢铁工业协会钢管分会p 中国金属学会轧钢学会钢管学术委员会协办精诚为冶金行业内外读者服务精美的大!<^广告创意新颖创新q 实用q 系统q 导向融技术q 经济于一体传播钢管技术促进钢管发展中国期刊方阵q 双效期刊n钢管o 纵揽国内外钢管)无缝r 焊接+生产p 科研p 设计中的新技术p 新工艺p 新设备p 新产品以及经营管理p 市场营销p 财经商情p 价格物流p 环保节能等经验成果与动态欢迎各界朋友订阅,本刊除邮局发行外,还可随时办理零星函购)另付邮资费!0544元+地址"四川省成都市牛市口r 攀钢集团成都钢铁有限责任公司内n 钢管o 杂志社邮编"<!44<<户名"钢管杂志社开户银行"工商行成都市双桥分理处帐号"//400!<44*40/*4<<80联系人"陈莉电话")408+8/c c 1!1<8//484*<传真")408+8/c c 1!1<r!1r 0440J S 5c重型机械。

包钢连铸大方坯传热凝固与内裂纹研究

ｓａａｅｉｔｉｅａｃｃｉｂｌｎｓａ．ｎｂｃｎｌｅｔｔｃｃｔｉｆｃｎｈｎｒｋｕｉｔｉＩｃａｏｏｃｄｄｔｒｋｒｎｔｇｔｌｒｓｇｎｔｌｅｕｈｈａｆｅｎａｇｒａｓａｅｓｃｔｉａａｌｍｓｍｎｚｎ．ｓｍｎｚｎｗｅｔｂｏｈｓｕｅｉｌｉｂｏｉｅｅｔｅＴｅｅｔｈｒｌｍｊｔｓｐｂｉｒｎｙｔｅｏｓｇｏｈｅｇｏｅｅｈｏａｕｅｓ
Ｋｙｒｓｂｏｓｌｉｃｔｎｂｌｎ，ｎｉｅａｃｃｅｗｄ：ｍｉｆａｏ，ｉｓａ，ｒｌｋｏｌｏｏｄｉｉｕｇｔｎｎｒｇｒｉｔａ
独创性说明
本人郑重声明：所呈交的论文是我个人在导师指导下进行的研究工作及取得研究成果。尽我所知，除了文中特别加以标注和致谢的地方外，论文中不包含其他人已经发表或撰写的研究成果，也不包含为获得北京科技大学或其他教育机构的学位或证书所使用过的材料。与我一同工作的同志对本研究所做的任何贡献均已在论文中做了明确的说明并表
ｃｎｉｎｅｎｌｅｔｏｔａｙｓｏｔｃｃｃａｃｒａｄｍｉｏｄｉｈｖｂｅａａｚｄｒｉｌｂｅｎｒｋｒｔｓｔａｔａｅｎｙｏｈｅｃｌａｄｈａｈａｅｎｈｅｅｅｎ
ｒｓｓｃｃｓｔｃｃ．ｈａｔｎｅｍｔｍｔａｍｄｌｂｅｓｕｔｅｏｗｉａｅｒｋＴｅｔｓｒｈａｃｏｅｈｓｎｐａｎｈｈｈａｈｅｒｆａｅｉｌａｅｅｏｕｅａｔｃｌｌｅｔｐｒｕｄｔｂｔｎｓｅｔｃｎｓａｎｔｃｔ．ｏｉｌｔａｕｔｔｅｅｔｅｒｕｏａｄｌｈｋｅｌｇａｅＡｃｒｎｙｈｃａｈｍａｒｉｉｉｎｈｌｓｈｓｒｃｄｇ，ｅｓｉｏｅｅｓｅｓａｃｌｌｉｍｄｌｌｍｌｉｉｐｃｓｈｓｎｅｐｄＢｓｏｈｌｔｉａｕｔｇｅｏｂｏｓｉｆｎｒｅａｂｅｄｖｌｅ．ｅｎｌｎｃａｎｏｆｒｏｏｄｙｇｓｅｅｏｏａｄｔｓｔｏｄｌａｄｐｄｈｐｏｅｉｐｒｅｒｃｔｅｕｐｄｔｅｈｅｍｅｎｃｕｌｗｔｔｒｓｎａｍｔａｄｅｑｉｅｆｕｓｅｗｏｓｏｅｉｈｃｓｇａｅｎａｒｐｅｒｅｓａｉｐｄｃｏ，ｉｒｕｏｏｂｌｎｓａ，ｇｔｓａ，ｏｒｌｉｍｎｎｕｔｎｔｄｔｔｎｕｉｔｉｓａｈｎｉｓｐｒｏｍｓｇｅｔｒｉｈｓｉｉｆｇｎｔｉｅｔｎｕｔｉｎｏｅｂｇｒｒｒｐｌａｌｓａａｄｌｉａｎｔｌｕｃｒｈｖｂｅｃｃｌｅ．ｒｒｅｗｔｔｔｉｎｔａｓａｌｇｉｉｏａｅｎｕｔＩｏｏｔｉｈｒｎｏｔｎｈｑｄｅｅａａｄｎｐａｄｈｔｒｏｅｌｃｅｃｔａｓａ，ｉｅａｃｃｃｂｐｄｔａｄｕｅ．ｒｕｓｓｎｅｒｉｌｉｔｎｒｋｅｉｅｎｒｃＴｅｌｃｒｐｄｄｉｃｔｎｈｔｎｒａｒｅｌａｎｒｃｄｅｄｈｅｔｏｏｅｄｓｅｒ

应变花计算公式

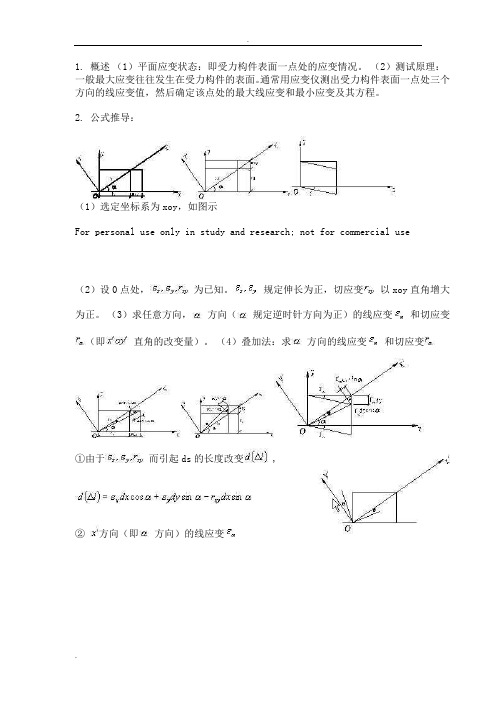
1. 概述（1）平面应变状态：即受力构件表面一点处的应变情况。

（2）测试原理：一般最大应变往往发生在受力构件的表面。

通常用应变仪测出受力构件表面一点处三个方向的线应变值，然后确定该点处的最大线应变和最小应变及其方程。

2. 公式推导：（1）选定坐标系为xoy，如图示For personal use only in study and research; not for commercial use（2）设0点处，为已知。

规定伸长为正，切应变以xoy直角增大为正。

（3）求任意方向，方向（规定逆时针方向为正）的线应变和切应变（即直角的改变量）。

（4）叠加法：求方向的线应变和切应变①由于而引起ds的长度改变 ,② 方向（即方向）的线应变③求的切应变即方向的直角改坐标轴偏转的角度以代替式（c）中的，求得坐标轴偏转角度：3. 结论（1）已知可求得任意方向的（2）已知 ,求得（3）主应变和主应变方向比较上述公式，可见故: 4. 应变圆5. 应变的实际测量①用解析法或图解法求一点处的主应变时，首先必须已知，然而用应变仪直接测量时，可以测试，但不易测量。

所以，一般是先测出任选三个方向的线应变。

②然后利用一般公式，将代入得出：联解三式，求出,于是再求出主应变的方向与数值④由③ 式求出，当时与二、四相限的角度相对应。

6. 直角应变花（45°应变花）测量为了简化计算，三个应变选定三个特殊方向测得：，代入一般公式求得：故讨论：若与二、四相限的角度相对应。

见P257、7.21题6. 等角应变花测量一般公式：测定值：代入式（a）得：主应变方向:故:于是由主应变公式：,穿过二,四相限.见P258，7.22题Example 1. 用直角应变花测得一点的三个方向的线应变Find：主应变及其方向Solution：故过二、四相限。

Example2. 若已测得等角应变花三个方向的线试求主应变及其方向Solution：即:应力测量 (measurement of stress)测量物体由于外因或内在缺陷而变形时，在它内部任一单位截面积上内外两方的相互作用力。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

收稿日期:2010-04-08;修订日期:2010-04-28作者简介:李武红(1979-),男,中国重型机械研究院有限公司工程师。

大方坯两相区综合应变的理论推导与计算李武红,杨拉道,路海波,薛松,李勤勇(中国重型机械研究院有限公司,陕西西安 710032)摘要:本文对大方坯两相区鼓肚应变、弯矫应变及辊子错位应变的计算公式做了详细的推导,可以为大方坯凝固计算提供一些有用的基础性数据。

关键词:大方坯;两相区;综合应变;鼓肚中图分类号:T F713 7 文献标识码:A 文章编号:1001-196X (2010)S1-0218-05Analog co m putation of co mprehensive strain in t wo -phase boundary on continuous casti n g billetLIW u -hong ,YANG La -dao ,L U H a-i bo ,XUE Song ,LI Q in -yong(Chi na N ationa lH eavy M achine ry Institute Co .,L td .,X i an 710032,China)Ab strac t :For m ulas deduced wh i ch re l a ted to bul g ing strain ,bend -stra i ghten i ng stra i n and d i slocati on stra i n i n t w o -phase boundary of conti nuous casti ng b illet are d i scussed i n this paper .T he resu lts could prov i de som e usefu l f unda m ental data f o r freezi ng calculati on of b illet .K ey words :bloo m;t w o -phase bounda ry ;co m prehensive strain ;bu l g i ng1 前言连铸坯两相区综合应变对铸坯质量影响很大,所以必须把两相区综合应变的数值控制在合理的范围内,同时,两相区综合应变的精确求解还可以作为旧连铸机改造和新连铸机总体设计的依据。

本文参照板坯两相区综合应变的求解公式,对大方坯进行了详细的推导和求解。

处于高温状态的连铸坯在向下运行的过程中两相区综合应变由三部分组成[1]: 在内部钢水静压力作用下产生的鼓肚应变 b(i); 在矫直过程中产生的矫直应变 u (i); 支撑辊偏离正确弧线产生的错位应变 r(i),即两相区综合应变 t(i)为: t(i)= b(i)+ u (i)+ r (i)。

2 两相区鼓肚应变的计算2 1 变形率计算公式的导出可以把铸坯鼓肚变形时贴近辊子一侧的凝固壳近似地看成是梁弯曲时发生的变形,如图1所示:图1 鼓肚变形示意图S =r +12S i rS (1)则鼓肚产生的变形率为:b(i)=S - SS100(%)(2)将(1)式代入(2)式得b(i)=S i /(2 r ) 100(%)(3)式中,r 为最大变形发生处坯壳变形曲线的曲率半径。

按照弹性理论,可以把铸坯向下弯曲时的鼓肚变形曲线表示成y =f (x ),参见图2,于是:1r =y(1+y 2)3/2可进一步近似地表示成:1r=y 代入(3)式得:b(i)=S i 2 1r100=50S i y |x =0(4)2 2 鼓肚变形曲线大方坯鼓肚变形可近似地看作两端固定梁,受均布载荷q 1(钢液静压力)和均布载荷q 2(考虑方坯形状系数的一个载荷)共同作用,如图2和图3所示两个模型:对于模型1:由材料力学知:y 1=q 1x 2(l i -x )224EJ图2 梁受均布1载荷示意图对于模型2:由材料力学知:图3 梁受均布载荷2示意图AC :y 2=q 2a 2x 224EJ (6-4a -4x a +x2a2)CD:y 2=q 2a 3l 1(4 R -a)24E J式中,E 为弹性系数;J 为材料惯性矩,J =bS3i12;l i ,x,y 为如图2,图3所示;q 1为均布载荷,q 1=pb ;q 2为均布载荷,q 2=P b ;P 为压力;P =[2(BD -2S i )+BB S i ] l ip 为单位面积上的载荷,即钢水静压力;b 为钢水静压力沿铸坯宽度上的分布长度,于是可写成:y =y 1+y 2整理后得:y=px 2(l i -x)22ES 3i +P 2E l 4i (4l i x-4x 2-S i l i )y max =y |x=12l i =pl 4i 32ES 3i +P 2E l 3i(l i -S i )(5)因此,第i 个辊子处的鼓肚变形量为:i =[p l 4i 32ES 3i +P 2E l 3i(l i -S i )]t s 2 3 鼓肚应变的计算公式对(5)式二次求导可得y ,将其代入(4)式,并令x =0得:b(i)=50S i (p l i ES 3i -4PE l 4i)(6)式中:P =[2(BD -2S i )+BB S i ] l i 因而得鼓肚应变的计算公式:b(i)=50S i (pl i ES 3i -4PE l 4i)(7)式中,S i 为第i 个辊子处的坯壳厚度,c m ;l i 为第i 个辊子处铸坯厚度中心线上的辊距,c m; i为第i 个辊子处的鼓肚量,c m;E,p i 为同前。

假设某台连铸机某流上共有N 对辊子,则根据以上各式,编写程序就可以计算出每个辊子处的鼓肚应变数值。

3 两相区弯矫应变的计算3 1 一点矫直应变公式的推导图4表示铸坯一点矫直前后的变形情况。

假设在此情况下铸坯上下侧温度相同,则中性轴与铸坯中心线重合。

假设一点矫直时内弧表面延伸量为AA ,外弧表面压缩量A A 。

根据应变定义,铸坯内弧侧表面AB 的矫直应变 s 为:s =AAAB因为 OAB 与 C AA 相似,所以:图4 铸坯矫直变形示意图(a)矫直前 (b)矫直后s =A C OB =0 5DR -D 100%由于R D ,所以可近似写成:s =0 5DR100%(8)在存在液芯的时候,设固/液相界面处的矫直应变为 t ,则按式(8):t =0 5D -SR 0100%(9)式中,S 为铸坯在矫直点的坯壳厚度;D 为铸坯厚度;R 0为铸机基本圆弧半径。

3 2 铸坯一点矫直应变模型设铸坯在某一弧形段的曲率半径为R 1,经过一次矫直后曲率半径变为R 2。

在这一过程中,铸坯外弧侧(下部)坯壳受压缩,而内弧侧(上部)坯壳受拉伸。

假设变形的中性轴与铸坯中心线重合,则内弧侧坯壳产生的拉伸应变 s ,x ,可按下式计算:s ,x =X (1R 1-1R 2) 100%(10)D /2-S X D /2式中,X 为该点到中性轴(中心线)的距离;R 1为矫直点前的圆弧半径;R 2为矫直点后的圆弧半径。

3 3 多点矫直的工程设计和应变计算3 3 1 多点矫直的基本思想多点矫直的实质就是将具有一定圆弧半径的铸坯矫直成水平直线时,不是靠一次(一个点矫直)完成,而是靠多次(多点处矫直)逐步完成,即把集中在一点的大幅度变形分散到若干点去逐步变形,使每一点的应变不致超过允许的极限应变[ ]。

中间要用若干过渡半径R 1 R 2 R 3 R 4 R n 。

按顺序分步达到目标。

多点矫直时铸坯的总矫直应变 s 与一点矫直时的应变相同,即:s = 1+ 2+ + i + + n 并要求i [ ]关于钢在固/液相区面处的许用应变[ ],如表1所示。

表1 许用应变[ ]的值%公司名称一般钢种要求严格的钢种备注新日铁0 10 1来华技术谈判资料(1979)西马克0 250 15宝钢访德代表团做讲座德马克0 20 21982年10月来华讲3 3 2 多点矫直的设计与应变公式推导1)己知前提条件己知的前提条件是:R 0为弧形连铸机的基本圆弧半径;D 为铸坯厚度;S 为计算点的凝固壳厚度,S =KLV;V 为拉坯速度;K 为凝固系数;L 为结晶器液面到计算点弧线距离。

在计算过程中,曲率半径均指铸机弧形半径(铸坯的外弧曲率半径)。

2)多点矫直的设计步骤根据已给定铸机的基本圆弧半径R 0和铸坯厚度D 等其它前提条件,计算出一点矫直时的总矫直应变量 s ,在考虑相应的矫直许用应变[ ]之后,初步估计出要用多少点矫直为宜,即确定矫直点数N 。

结合铸机的辊列布置,着手设计矫直点安排和布置方案,确定各矫直点的弧线长度L 和各个半径所占的弧角。

多点矫直时各不同曲率半径R 所占弧角之总和应等于90 ,即+ 0+ 1+ 2+ +n =90对各矫直点的铸坯固/液相界面处的矫直应变 i 和过渡曲率半径R i 进行计算、校核和选取,反复调整和复算,直至得到最佳结果为止。

计算各矫直点的应变速率。

3)矫直点数N 的确定先算出一点矫直时铸坯固/液相界面的总应变量 s :S =0 5D -SR 0=0 5D -kLVR 0使:SN[ ]于是得N i[ ]=0 5D -k L VR 0 [ ](11)4)多点矫直时铸坯固/液相界面拉伸应变计算公式根据一点矫直时,铸坯拉伸应变计算公式,可以推导出多点矫直时,任意一矫直点的铸坯固/液相界面处拉伸应变为:i =(0 5D -k L i V ) (1R i -1-1R i)(12)式中,R i -1为第i 矫直点前的铸坯曲率半径;R i 为第i 矫直点后的铸坯曲率半径;S i 为第i 矫直点后铸坯坯壳厚度;L i 为从结晶器液面到第i 矫直点的铸坯弧线长度。

4辊子错位应变的计算由于连铸机辊子偏离铸机弧线,在机内带液相的铸坯凝壳内表面上相对于辊子支撑位置处产生拉伸变形,称为辊子错位变形[2],如图5所示。

图5 辊子不对中受力示意图4 1 辊子错位变形曲线辊子不对中时的受力如图5所示,既有均布载荷,梁中间又有集中载荷,还有方坯形状系数对其作用。

1)均布载荷1时如图6:变形曲线为:y 1=qx 2(2l i -x )224EJ图6 梁受均布载荷1示意图2)集中载荷时的变形曲线如图7:图7 梁受集中载荷1示意图当0 x l i 1时y 2=P l 2i 2x 212EJ l i [3l i 12l i -(3l i 1+l i 2)x2l 2i]当l i 1=l i 2=l i 时y 2=Px 224EJ(3l i -4x )3)均布载荷2时的变形曲线(见图8):图8 梁受均布载荷2示意图AC 段:y 3=q 2a 2x 224EJ (6-4a -4x a +x2a2)CD 段:y 3=q 2a 3l i (4 R -a)24EJ 综合上列三个模型得:均布载荷与集中载荷共同作用时的变形曲线:y =y 1-y 2+y 3代入得:y =px 2(2l i -x )23ES i -Px 224EJ (3l i -4x )+P 132E l i(4l i x -2x 2-S i l i )(13)代入:P 1=[2(BD -2S i ) S i +BB S i ] l i ,当x =l i 时,y = rr =ql 4i 24EJ -P l 3i 24EJ +P 132E l 3i (2l i -S i )简化上式可求得: r =p l 4i 2ES 3i +P l 3i2EbS 3i-[2(BD -2S i ) S i +BB S i ] (2l i -S i )32E l 2iP =p bl i -2(BD -2S i ) S i +BB S i16l 5i(2l i -S i )bS 3i-2EbS 3i rl 3i代入(13)式得:y =px 2(2l i -x )22ES 3i -Px 22E bS 3i(3l i -4x )+[2(BD -2S i ) S i +BB S i ]32E l 3i(4l i x -4x 2-S i l i )(14)4 2 辊子不对中时坯壳内的变形率对(14)式进行二次求导可得:y |x =0=4p l 2i ES 3i -3P l iE bS 3i-[2(BD -2S i ) S i +BB S i ]8E l 3i将其代入(4)式可得辊子错位应变为: r(i)=50p l 2iES 2i-[2(BD -2S i ) S i +BB S i ] 25S i4E l 3i(2+3S i 2l i )+300S i rl 2i式中, r 为辊子错位量,一般取 r =0 05cm 。