2019-2020年中考数学专题复习新定义问题

合集下载

2019-2020年中考数学复习第二部分题型研究题型四新定义与阅读理解题类型二新概念学习型针对演练

2019-2020年中考数学复习第二部分题型研究题型四新定义与阅读理解题类型二新概念学习型针对演练针对演练1. 若x 1，x 2是关于x 的方程x 2＋bx ＋c ＝0的两个实数根，且|x 1|＋|x 2|＝2|k |(k 是整数)，则称方程x 2＋bx ＋c ＝0为“偶系二次方程”．如方程x 2－6x －27＝0，x 2－2x －8＝0，x 2＋3x －274＝0，x 2＋6x －27＝0, x 2＋4x ＋4＝0都是“偶系二次方程”.(1)判断方程x 2＋x －12＝0是否是“偶系二次方程”，并说明理由；(2)对于任意一个整数b ，是否存在实数c ，使得关于x 的方程x 2＋bx ＋c ＝0是“偶系二次方程”，并说明理由.2. 设二次函数y 1，y 2的图象的顶点分别为(a ，b )、(c ，d )，当a ＝－c ，b ＝2d ，且开口方向相同时，则称y 1是y 2的“反倍顶二次函数”．(1)请写出二次函数y ＝x 2＋x ＋1的一个“反倍顶二次函数”；(2)已知关于x 的二次函数y 1＝x 2＋nx 和二次函数y 2＝nx 2＋x ；函数y 1＋y 2恰是y 1－y 2的“反倍顶二次函数”，求n .3. 函数y ＝k x 和y ＝－k x (k ≠0)的图象关于y 轴对称，我们定义函数y ＝k x 和y ＝－k x(k ≠0)相互为“影像”函数：(1)请写出函数y ＝2x －3的“影像”函数：________；(2)函数________的“影像”函数是y ＝x 2－3x －5;(3)若一条直线与一对“影像”函数y ＝2x (x ＞0)和y ＝－2x(x ＜0)的图象分别交于点A 、B 、C (点A 、B 在第一象限)，如图，如果CB ∶BA ＝1∶2，点C 在函数y ＝－2x(x ＜0)的“影像”函数上的对应点的横坐标是1，求点B 的坐标．第3题图4. 如图，在平面直角坐标系中，已知点P 0的坐标为(1，0)，将线段OP 0按逆时针方向旋转45°，再将其长度伸长为OP 0的2倍，得到线段OP 1，又将线段OP 1按逆时针方向旋转45°，长度伸长为OP 1的2倍，得到线段OP 2，如此下去，得到线段OP 3，OP 4…，OP n (为正整数)．(1)求点P 3的坐标；(2)我们规定：把点P n (x n ，y n )(n ＝0，1，2，3…)的横坐标x n 、纵坐标y n 都取绝对值后得到的新坐标(|x n |，|y n |)称为点P n 的“绝对坐标”，根据图中P n 的分布规律，求出点P n的“绝对坐标”．第4题图考向2) 几何类(杭州：2015.19；台州：2016.23，2015、2013.24；绍兴：2017.22，2013.22，2012.21)针对训练1. (2017绍兴)定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．(1)如图①，等腰直角四边形ABCD，AB＝BC，∠ABC＝90°.①若AB＝CD＝1，AB∥CD，求对角线BD的长；②若AC⊥BD，求证：AD＝CD.(2)如图②，在矩形ABCD中，AB＝5，BC＝9，点P是对角线BD上一点，且BP＝2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形．求AE的长．第1题图2. 阅读下面的材料：如果一个三角形和一个平行四边形满足条件：三角形的一边与平行四边形的一边重合，三角形这边所对的顶点在平行四边形这边的对边上，则称这样的平行四边形为三角形的“友好平行四边形”，如图①，▱ABEF即为△ABC的“友好平行四边形”．请解决下列问题：(1)仿照以上叙述，说明什么是一个三角形的“友好矩形”；(2)若△ABC是钝角三角形，则△ABC显然只有一个“友好矩形”，若△ABC是直角三角形，其“友好矩形”有______个；(3)若△ABC是锐角三角形，且AB＜AC＜BC，如图②，请画出△ABC的所有“友好矩形”，指出其中周长最小的“友好矩形”，并说明理由．第2题图)3. (2017常州)如图①，在四边形ABCD中，如果对角线AC和BD相交并且相等，那么我们把这样的四边形称为等角线四边形．(1)①在“平行四边形、矩形、菱形”中，________一定是等角线四边形(填写图形名称)；②若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点，当对角线AC、BD还需要满足________时，四边形MNPQ是正方形；(2)如图②，已知△ABC中，∠ABC＝90°，AB＝4，BC＝3，D为平面内一点．①若四边形ABCD 是等角线四边形，且AD ＝BD ，则四边形ABCD 的面积是________； ②设点E 是以C 为圆心，1为半径的圆上的动点，若四边形ABED 是等角线四边形，写出四边形ABED 面积的最大值，并说明理由．第3题图4. (2017黄石)在现实生活中，我们经常会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为2∶1，我们不妨就把这样的矩形称为“标准矩形”．在“标准矩形”ABCD 中，P 为DC 边上一定点，且CP ＝BC ，如下图所示．(1)如图①，求证：BA ＝BP ；(2)如图②，点Q 在DC 上，且DQ ＝CP ，若G 为BC 边上一动点，当△AGQ 的周长最小时，求CG GB的值；(3)如图③，已知AD ＝1，在(2)的条件下，连接AG 并延长交DC 的延长线于点F ，连接BF ，T 为BF 的中点，M 、N 分别为线段PF 与AB 上的动点，且始终保持PM ＝BN ，请证明：△MNT 的面积S 为定值，并求出这个定值．第4题图5. 对于一个四边形给出如下定义：如一组对角相等且有一组邻边相等，则称这个四边形为奇特四边形，如图①中，∠B ＝∠D ，AB ＝AD ；如图②中，∠A ＝∠C ，AB ＝AD 则这样的四边形均为奇特四边形．(1)在图①中，若AB ＝AD ＝4，∠A ＝60°，∠C ＝120°，请求出四边形ABCD 的面积； (2)在图②中，若AB ＝AD ＝4，∠A ＝∠C ＝45°，请直接写出四边形ABCD 面积的最大值； (3)如图③，在正方形ABCD 中，E 为AB 边上一点，F 是AD 延长线上一点，且BE ＝DF ，连接EF ，取EF 的中点G ，连接CG 并延长交AD 于点H ，若EB ＋BC ＝m ，问四边形BCGE 的面积是否为定值？如果是，请求出这个定值(用含m 的代数式表示)；如果不是，请说明理由．第5题图6. 类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)如图①，在四边形ABCD 中，添加一个条件使得四边形A B CD 是“等邻边四边形”．请写出你添加的一个条件；(2)小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由；(3)如图②，小红作了一个Rt △ABC ，其中∠ABC ＝90°，AB ＝2，BC ＝1，并将Rt △ABC 沿∠ABC 的平分线BB ′方向平移得到△A′B′C′，连接AA ′，BC ′.小红要使平移后的四边形ABC ′A′是“等邻边四边形”，应平移多少距离(即线段BB ′的长)?第6题图7. (2017江西)我们定义：如图①，在△ABC 中，把AB 绕点A 顺时针旋转α(0°＜α＜180°)得到AB ′，把AC 绕点A 逆时针旋转β得到AC ′，连接B′C′.当α＋β＝180°时，我们称△AB′C ′是△ABC 的“旋补三角形”，△AB ′C ′边B′C′上的中线AD 叫做△ABC 的“旋补中线”，点A 叫做“旋补中心”．特例感知 (1)在图②，图③中，△AB′C′是△ABC 的“旋补三角形”，AD 是△ABC 的“旋补中线”． ①如图②，当△ABC 为等边三角形时，AD 与BC 的数量关系为AD ＝____BC ； ②如图③，当∠BAC ＝90°，BC ＝8时，则AD 长为________．猜想论证(2)在图①中，当△A B C 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用 (3)如图④，在四边形ABCD 中，∠C ＝90°，∠D ＝150°，BC ＝12，CD ＝23，DA ＝6.在四边形内部是否存在点P ，使△PDC 是△PAB 的“旋补三角形”？若存在，给予证明，并求△PAB 的“旋补中线”长；若不存在，说明理由．第7题图答案1. 解：(1)不是．理由如下：∵解方程x 2＋x －12＝0，得x 1＝－4，x 2＝3， ∴|x 1|＋|x 2|＝4＋3＝2×|3.5|， ∵3.5不是整数，∴方程x 2＋x －12＝0不是“偶系二次方程”； (2)存在．理由如下：∵方程x 2－6x －27＝0，x 2＋6x －27＝0是“偶系二次方程”，∴假设c ＝mb 2＋n ，当b ＝－6，c ＝－27时，有－27＝36m ＋n ， ∵x 2＝0是“偶系二次方程”，∴n ＝0，m ＝－34，∴c ＝－34b 2.又∵x 2＋3x －274＝0也是“偶系二次方程”，当b ＝3时，c ＝－274＝－34×32，∴可设c ＝－34b 2，对任意一个整数b ，当c ＝－34b 2时，b 2－4ac ＝b 2－4c ＝4b 2，∴x ＝－b±2|b|2，∴x 1＝－32b ，x 2＝12b ，∴|x 1|＋|x 2|＝32|b |＋12|b |＝2|b |.∵b 是整数，∴对于任意一个整数b ，存在实数c ，当且仅当c ＝－34b 2时，关于x 的方程，x 2＋bx ＋c＝0是“偶系二次方程”．2. 解：(1)∵y ＝x 2＋x ＋1，∴y ＝(x ＋12)2＋34，∴二次函数y ＝x 2＋x ＋1的顶点坐标为(－12，34)，∴二次函数y ＝x 2＋x ＋1的一个“反倍顶二次函数”的顶点坐标为(12，32)，∴反倍顶二次函数的解析式为y ＝(x －12)2＋32＝x 2－x ＋74；(2)y 1＋y 2＝x 2＋nx ＋nx 2＋x ＝(n ＋1)x 2＋(n ＋1)x ＝(n ＋1)(x 2＋x )＝(n ＋1)(x ＋12)2－n ＋14， ∴顶点的坐标为(－12，－n ＋14)，y 1－y 2＝x 2＋nx －nx 2－x ＝(1－n )x 2＋(n －1)x ＝(1－n )(x 2－x)＝(1－n)(x －12)2－1－n4， ∴顶点的坐标为(12，－1－n4)，由于函数y 1＋y 2恰是y 1－y 2的“反倍顶二次函数”，则－2×1－n 4＝－n ＋14，解得n ＝13.3. 解：(1)y ＝－2x －3；【解法提示】令－x ＝x 得y ＝－2x －3.(2)y ＝x 2＋3x －5；【解法提示】令－x ＝x 得y ＝x 2＋3x －5.(3) 如解图，作CC ′⊥x 轴，BB ′⊥x 轴，AA ′⊥x 轴垂足分别为C′、B′、A′，第3题解图设点B (m ，2m )，A (n ，2n)，其中m ＞0，n ＞0，由题意，将x ＝－1代入y ＝－2x中解得y ＝2，∴点C (－1，2)，∴CC ′＝2，BB ′＝ 2m ，AA ′＝2n，又∵A′B′＝n －m ，B ′C ′＝m ＋1，CC ′∥BB ′∥AA ′，CB ∶AB ＝1∶2, 则B′C′∶A′B′＝1∶2，则⎩⎪⎨⎪⎧n －m ＝2（m ＋1）2m －2n ＝23（2－2n ），消去n 化简得到3m 2－2m －3＝0,解得m ＝1＋103或1－103(舍弃)，∴2m ＝21＋103＝－2＋2103，∴点B 坐标为(1＋103，－2＋2103)．4. 解：(1)根据题意，得OP 3＝2OP 2＝4OP 1＝8OP 0＝8,根据等腰直角三角形的性质，得P 3(－42，42); (2)由题意知，旋转8次之后回到轴的正半轴，在这8次旋转中，点分别落在坐标象限的角平分线上或x 轴或y 轴上，但各点“绝对坐标”的横、纵坐标均为非负数，因此，各点的“绝对坐标”可分三种情况：①当P n 的n ＝0，4，8，12…，则点在x 轴上，则“绝对坐标”为(2n，0) ，②当P n 的n ＝2，6，10，14…，则点在y 轴上，则“绝对坐标”为(0，2n) ； ③当P n 的n ＝1，3，5，7，9…，则点在各象限的角平分线上，则“绝对坐标”为(2n －12，2n －12)．考向2 几何类针对演练1. 解：(1)①∵AB ＝CD ＝1，AB ∥CD ， ∴四边形ABCD 是平行四边形，又∵AB ＝BC ，∴▱ABCD 是菱形．又∵∠ABC ＝90°，∴四边形ABCD 为正方形， ∴BD ＝2；②如解图①，连接AC ，BD ，第1题解图①∵AB ＝BC ，AC ⊥BD ， ∴∠ABD ＝∠CBD ，又∵BD ＝BD ， ∴△ABD ≌△CBD ， ∴AD ＝CD ；(2)若EF 与BC 垂直，则AE ≠EF ，BF ≠EF ，∴四边形ABFE 不是等腰直角四边形，不符合条件；若EF 与BC 不垂直，①当AE ＝AB 时，如解图②，此时四边形ABFE 是等腰直角四边形，第1题解图②∴AE ＝AB ＝5；②当BF ＝AB 时，如解图③，此时四边形ABFE 是等腰直角四边形，第1题解图③∴BF ＝AB ＝5. ∵DE ∥BF ，∴△PED ∽△PFB ，∴ED FB ＝PD PB ＝12， ∴DE ＝2.5，∴AE ＝9－2.5＝6.5.综上所述，AE 的长为5或6.5. 2. 解：(1)三角形的一边与矩形的一边重合，三角形这边所对的顶点在矩形这边的对边上；(2)2；【解法提示】如解图①的矩形BCAF 、矩形ABED 为Rt △ABC 的两个“友好矩形”；第2题解图(3)此时共有3个“友好矩形”，如解图②的矩形BCDE 、矩形CAFG 及矩形ABHK ，其中的矩形ABHK 的周长最小．理由如下： ∵矩形BCDE 、矩形CAFG 及矩形ABHK 均为△ABC 的“友好矩形”，∴这三个矩形的面积相等，令其为S ，设矩形BCDE ，矩形CAFG 及矩形ABHK 的周长分别为L 1，L 2，L 3，△ABC 的边长BC ＝a ，CA ＝b ，AB ＝c ，则L 1＝2S a ＋2a ，L 2＝2S b ＋2b ，L 3＝2S c＋2c ，∴L 1－L 2＝(2S a ＋2a )－(2S b ＋2b )＝2S ab (b －a )＋2(a －b )＝2(a －b)·ab －S ab，而ab ＞S ，a ＞b ，∴L 1－L 2＞0，即L 1＞L 2，同理可得，L 2＞L 3，∴L 3最小，即矩形ABHK 的周长最小． 3. 解：(1)①矩形；【解法提示】平行四边形和菱形的对角线不相等，矩形的对角线相等，故矩形一定是等角线四边形．②垂直；【解法提示】∵四边形ABCD 是等角线四边形，∴AC ＝BD ，∵M 、N 、P 、Q 分别是边AB 、BC 、CD 、DA 的中点，∴MN ＝PQ ＝12AC ，PN ＝MQ ＝12BD ，∴MN ＝PQ ＝PN ＝MQ ，∴四边形MNPQ 是菱形，根据“有一个角是直角的菱形是正方形”可知需要四边形MNPQ 有一个角是直角，又易知MN ∥PQ ∥AC ，PN ∥QM ∥BD ，∴要使四边形MNPQ 是正方形需要AC ⊥BD .(2)①3＋221； ∵AD ＝BD ，∴D 在AB 的垂直平分线上，∵四边形ABCD 是等角线四边形， ∴AC ＝BD ，在Rt △ABC 中，∠ABC ＝90°，AB ＝4，BC ＝3， ∴AC ＝5， ∴BD ＝5，如解图①，取AB 的中点为M ，则DM ⊥AB ，第3题解图①在Rt △ADM 中，AD ＝BD ＝5，AM ＝BM ＝2，由勾股定理得DM ＝21；∴S 四边形ABCD ＝S △ABD ＋S △BCD ＝12AB ·DM ＋12BC ·BM＝12×4×21＋12×3×2＝3＋221； ②四边形ABED 面积最大值为18，理由如下：如解图②，设AE 与BD 交于点O ，夹角为α，则第3题解图②S 四边形ABED ＝S △AED ＋S △ABE ＝12AE ·ODsin α＋12AE ·OBsin α＝12AE ·BDsin α，∵AE ＝BD ，∴S 四边形ABED ＝12AE 2sin α，∴当AE 最大，且α＝90°时，四边形ABED 的面积最大，此时延长AC 交圆C 于E ，则AE 最大为5＋1＝6， ∴四边形ABED 的最大面积为12×62＝18.4. (1)证明：如解图①所示，第4题解图①∵PC ＝BC ，∠BCP ＝90°， ∴BP ＝2BC ，又∵矩形ABCD 为“标准矩形”，∴AB ＝2BC ， ∴AB ＝BP ；(2)解：如解图②，作点Q 关于直线BC 对称的点F ，连接AF 交BC 于点E ，连接QE 、GF ，第4题解图②∵DQ ＝CP ，∴CQ ＝DP ＝CF 且AQ 为定值， ∴EQ ＝EF ，GQ ＝GF ，∵AQ 为定值，要使△AGQ 的周长最小时， ∴只需AG ＋GQ ＝AG ＋GF 最小，显然AG ＋GF ≥AF ＝AE ＋EF ＝AE ＋EQ ，即当点G 与点E 重合时，△AGQ 的周长最小，此时CG GB ＝CE EB ＝CF AB ＝DPAB，∵DP AB ＝CD －CP AB ＝AB －BC AB ＝1－BC AB ＝1－22，∴当△AGQ 的周长最小时，CG GB ＝1－22； (3)证明：如解图③，MN 交AF 于点K ，连接KT ，第4题解图③由(2)可知，CF ＝DP ， ∴PF ＝AB 且PF∥AB ，∴四边形ABFP 为平行四边形，又由PM ＝BN ， ∴MF ＝AN ，∴△MFK ≌△NAK ，∴点K 为AF 与MN 的中点，又∵点T 为BF 的中点， ∴KT 为△FAB 的中位线， ∴S △FKT ＝S △TMK ＝S △TKN ，∴S △MNT ＝2S △FKT ＝12S △FAB ＝14S 平行四边形ABFP ＝14×2＝24，∴△MNT 的面积S 为定值，这个定值为24. 5. 解：(1)如解图①，设AC 与BD 交于点O ；第5题解图①∵AB ＝AD ，∠A ＝60°， ∴△ABD 是等边三角形，∴AB ＝AD ＝BD ＝4, ∠ABD ＝∠ADB ＝60°， ∵∠ABC ＝∠ADC ， ∴∠CBD ＝∠CDB ， ∵∠BCD ＝120°，∴∠CBD ＝∠CDB ＝30°， ∴CB ＝CD ， ∵AB ＝AD ， ∴AC ⊥BD ，∴BO ＝OD ＝2，OA ＝AB ·sin60°＝23，OC ＝OB ·tan30°＝233，∴S 四边形ABCD ＝12·BD ·OA ＋12·BD ·OC ＝12·BD ·(OA ＋OC )＝1633；(2)2；【解法提示】如解图②，作DH ⊥AB 于H ，过点B 、D 、C 作圆，连接BD ，第5题解图②∵∠C ′＝∠C ＝45°， ∴当C′B ＝C′D 时，△BDC ′的面积最大，此时四边形ABC ′D 的面积最大，易证四边形ABC′D 是菱形，在Rt △AHD 中，∵∠A ＝45 °，∠AHD ＝90°，AD ＝4， ∴AH ＝HD ＝22，∴四边形ABC′D 的面积＝AB·DH ＝82， ∴四边形ABCD 的面积的最大值为8 2. (3)四边形BCGE 的面积是定值，理由如下：如解图③，连接EC 、CF ，作FM ⊥BC 于M .第5题解图③在△BCE 和△DCF 中， ⎩⎪⎨⎪⎧BE ＝DF ∠EBC ＝∠FDC，BC ＝DC∴△BCE ≌△DCF (SAS)， ∴CE ＝CF ， ∵EG ＝GF ， ∴S △ECG ＝S △FCG ，∵四边形CDFM 是矩形，∴BC ＝DC ＝MF ，DF ＝BE ＝CM ， ∴BM ＝m ，BE ＋FM ＝m ，∴△FCM ，△DCF ，△BCE 的面积相等， ∴S 四边形BCGE ＝12·S 四边形BEFM ＝12·12·m ·m ＝14m 2.6. 解：(1)AB ＝BC 或BC ＝CD 或CD ＝AD 或AD ＝AB ； (2)解：小红的结论正确．理由如下：∵四边形的对角线互相平分， ∴这个四边形是平行四边形， ∵四边形是“等邻边四边形”， ∴这个四边形有一组邻边相等， ∴这个“等邻边四边形”是菱形；(3)由∠ABC ＝90°，AB ＝2，BC ＝1，得：AC ＝5， ∵将Rt △ABC 平移得到Rt △A ′B ′C ′，∴BB ′＝AA′，A′B′∥AB，A ′B ′＝AB ＝2，B ′C ′＝BC ＝1，A ′C ′＝AC ＝5， (Ⅰ)如解图①，当AA′＝AB 时，BB ′＝AA′＝AB ＝2；第6题解图①(Ⅱ)如解图②，当AA′＝A′C′时，BB ′＝AA′＝A′C′ ＝5；第6题解图②(Ⅲ)当A′C′＝BC′＝5时，如解图③，延长C′B′交AB 与点D ，则C′B ′⊥AB ，第6题解图③∵BB ′平分∠ABC ，∴∠ABB ′＝12∠ABC ＝45°，∴∠BB ′D ＝∠ABB′＝45°， ∴B ′D ＝BD ，设B′D＝BD ＝x ，则C′D ＝x ＋1，BB ′＝2x ，∵根据在Rt △BC ′D 中，BC ′2＝C′D 2＋BD 2即x 2＋(x ＋1)2＝5，解得：x ＝1或x ＝－2(不合题意，舍去)， ∴BB ′＝2x ＝2；第6题解图④(Ⅳ)当 BC′＝AB ＝2时，如解图④，与(Ⅲ)方法同理可得： x ＝－1＋72或x ＝－1－72(舍去)，∴BB ′＝2x ＝－2＋142.故应平移2或5或2或－2＋142的距离．7. 解：(1)①12，②4；【解法提示】①如解图①中，第7题解图①∵△ABC 是等边三角形，∴AB ＝BC ＝AC ＝AB′＝AC′， ∵DB ′＝DC′， ∴A D ⊥B ′C ′，∵∠BAC ＝60°，∠BAC ＋∠B′AC ′＝180°， ∴∠B ′AC ′＝120°， ∴∠B ′＝∠C′＝30°， ∴AD ＝12AB ′＝12BC .②如解图②中，第7题解图②∵∠BAC ＝90°，∠BAC ＋∠B′AC′＝180°， ∴∠B ′AC ′＝∠BAC ＝90°， ∵AB ＝AB′，AC ＝AC′， ∴△BAC ≌△B ′AC ′， ∴BC ＝B′C ′， ∵B ′D ＝DC′，∴AD ＝12B ′C ′＝12BC ＝4；(2)猜想：AD ＝12BC .理由：如解图③中，延长AD 到M ，使得AD ＝DM ，连接B′M，C ′M ，第7题解图③∵B ′D ＝DC ′，AD ＝DM ，∴四边形AC′MB′是平行四边形， ∴AC ′＝B′M＝AC ，∵∠BAC ＋∠B′AC′＝180°， ∠B ′AC ′＋∠AB′M ＝180°， ∴∠BAC ＝∠MB ′A, ∵AB ＝AB ′，∴△BAC ≌△AB ′M ， ∴BC ＝AM ， ∴AD ＝12BC ；(3)存在．理由：如解图④中，延长AD 交BC 的延长线于M ，作BE ⊥AD 于E ，作线段BC 的垂直平分线交BE 于P ，交BC 于F ，连接PA 、PD 、PC ，作△PCD 的中线PN ，连接DF 交PC 于O ，第7题解图④∵∠ADC ＝150°， ∴∠MDC ＝30°， ∴在Rt △DCM 中，∵CD ＝23，∠DCM ＝90°，∠MDC ＝30°， ∴CM ＝2，DM ＝4，∠M ＝60°，在Rt △BEM 中，∵∠BEM ＝90°，BM ＝BC ＋CM ＝14，∠MBE ＝30°， ∴EM ＝12BM ＝7，∴DE ＝EM －DM ＝3， ∵AD ＝6， ∴AE ＝DE , ∵BE ⊥AD ，∴PA ＝PD ，PB ＝PC ，在Rt △CDF 中，∵CD ＝23，CF ＝6， ∴∠CDF ＝∠CPE ＝60°，易证△FCP ≌△CFD ， ∴CD ＝PF ，∵CD ∥PF ， ∴四边形CDPF 是矩形， ∴∠CDP ＝90°，∴∠ADP ＝∠ADC－∠CDP ＝60°， ∴△ADP 是等边三角形， ∴∠APD ＝60°，∵∠BPF＝∠CPF＝60°，∴∠BPC＝120°，∴∠APD＋∠BPC＝180°，∴△PDC是△PAB的“旋补三角形”，在Rt△PDN中，∵∠PDN＝90°，PD＝AD＝6，DN＝3，∴PN＝DN2＋PD2＝（3）2＋62＝39.。

中考数学八大题型集训：专题复习(2)新定义运算

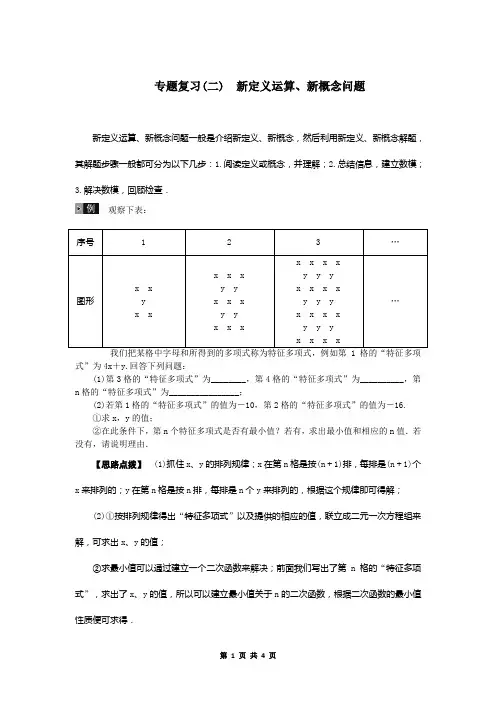
专题复习(二) 新定义运算、新概念问题新定义运算、新概念问题一般是介绍新定义、新概念，然后利用新定义、新概念解题，其解题步骤一般都可分为以下几步：1.阅读定义或概念，并理解；2.总结信息，建立数模；3.解决数模，回顾检查．观察下表：式”为4x＋y.回答下列问题：(1)第3格的“特征多项式”为________，第4格的“特征多项式”为__________，第n格的“特征多项式”为________________；(2)若第1格的“特征多项式”的值为－10，第2格的“特征多项式”的值为－16.①求x，y的值；②在此条件下，第n个特征多项式是否有最小值？若有，求出最小值和相应的n值．若没有，请说明理由．【思路点拨】(1)抓住x、y的排列规律；x在第n格是按(n＋1)排，每排是(n＋1)个x来排列的；y在第n格是按n排，每排是n个y来排列的，根据这个规律即可得解；(2)①按排列规律得出“特征多项式”以及提供的相应的值，联立成二元一次方程组来解，可求出x、y的值；②求最小值可以通过建立一个二次函数来解决；前面我们写出了第n格的“特征多项式”，求出了x、y的值，所以可以建立最小值关于n的二次函数，根据二次函数的最小值性质便可求得．【解答】 (1)16x ＋9y 25x ＋16y (n ＋1)2x ＋n 2y(n 为正整数)(2)①依题意，得⎩⎪⎨⎪⎧4x ＋y ＝－10，9x ＋4y ＝－16.解得⎩⎪⎨⎪⎧x ＝－247，y ＝267.②设最小值为W ，依题意得： W ＝(n ＋1)2x ＋n 2y ＝－247(n ＋1)2＋267n 2＝27n 2－487n －247＝27(n －12)2－3127. 即有最小值为－3127，相应的n 的值为12.这类题首先要读懂题目中的新概念或定义，然后将新概念的问题与原有的知识结合，利用原有的知识解决问题，其实就是“披了一件新外衣”，解决方法还是用原来的知识点．1．已知m ＝x ＋1，n ＝－x ＋2，若规定y ＝⎩⎪⎨⎪⎧1＋m －n （m≥n），1－m ＋n （m ＜n ），则y 的最小值为()A ．0B ．1C ．－1D ．22．在平面直角坐标系中，任意两点A(x 1，y 1)，B(x 2，y 2)规定运算：①A ○+B ＝(x 1＋x 2，y 1＋y 2)；②A ○⨯B ＝x 1x 2＋y 1y 2；③当x 1＝x 2且y 1＝y 2时，A ＝B. 有下列四个命题：(1)若A(1，2)，B(2，－1)，则A ○+B ＝(3，1)，A ○⨯B ＝0； (2)若A ○+B ＝B ○⨯C ，则A ＝C ； (3)若A ○⨯B ＝B ○⨯C ，则A ＝C ； (4)对任意点A 、B 、C ，均有(A ○+B)○+C ＝A ○+(B ○+C)成立．其中正确命题的个数为()A ．1个B ．2个C ．3个D ．4个3．对于实数a 、b ，定义一种运算“○⨯”为：a ○⨯b ＝a 2＋ab －2，有下列命题： ①1○⨯3＝2； ②方程x ○⨯1＝0的根为x 1＝－2，x 2＝1； ③不等式组⎩⎨⎧<-⊗<-⊗-031,04)2(x x 的解集为－1＜x ＜4；④点(12，52)在函数y ＝x ○⨯(－1)的图象上．其中正确的是()A ．①②③④B ．①③C ．①②③D ．③④4．对于任意实数m 、n ，定义一种运算m※n＝mn －m －n ＋3，等式的右边是通常的加减和乘法运算，例如：3※5＝3×5－3－5＋3＝10.请根据上述定义解决问题：若a ＜2※x＜7，且解集中有两个整数解，则a 的取值范围是________．5．在平面直角坐标系xOy 中，对于点P(x ，y)和Q(x ，y ′)，给出如下定义：若y′＝⎩⎪⎨⎪⎧y （x≥0），－y （x ＜0），则称点Q 为点P 的“可控变点”．例如：点(1，2)的“可控变点”为点(1，2)，点(－1，3)的“可控变点”为点(－1，－3)．(1)若点(－1，－2)是一次函数y ＝x ＋3图象上点M 的“可控变点”，则点M 的坐标为________；(2)若点P 在函数y ＝－x 2＋16(－5≤x≤a)的图象上，其“可控变点”Q 的纵坐标y′的取值范围是－16≤y ′≤16，则实数a 的取值范围是________．6．规定：sin(－x)＝－sinx ，cos(－x)＝cosx ，sin(x ＋y)＝sinx ·cosy ＋cosx ·siny.据此判断下列等式成立的是________(写出所有正确的序号)．①cos(－60°)＝－12；②sin75°＝6＋24； ③sin2x ＝2sinx ·cosx ；④sin(x －y)＝sinx ·cosy －cosx ·siny.7．对于平面直角坐标系中任意两点P 1(x 1，y 1)、P 2(x 2，y 2)，称|x 1－x 2|＋|y 1－y 2|为P 1、P 2两点的直角距离，记作：d(P 1，P 2)．若P 0(x 0，y 0)是一定点，Q(x ，y)是直线y ＝kx ＋b 上的一动点，称d(P 0，Q)的最小值为P 0到直线y ＝kx ＋b 的直角距离．令P 0(2，－3)．O 为坐标原点．则：(1)d(O ，P 0)＝________；(2)若P(a ，－3)到直线y ＝x ＋1的直角距离为6，则a ＝________．8．已知抛物线p ：y ＝ax 2＋bx ＋c 的顶点为C ，与x 轴相交于A 、B 两点(点A 在点B 左侧)，点C 关于x 轴的对称点为C′，我们称以A 为顶点且过点C′，对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线，直线AC′为抛物线p 的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y ＝x 2＋2x ＋1和y ＝2x ＋2，则这条抛物线的解析式为____________．9．对非负实数x“四舍五入”到个位的值记为<x>，即当n 为非负整数时，若n －12≤x<n ＋12，则<x>＝n ，如<0.46>＝0，<3.67>＝4，给出下列关于<x>的结论：①<1.493>＝1；②<2x>＝2<x>；③若<12x －1>＝4，则实数x 的取值范围是9≤x<11；④当x≥0，m 为非负整数时，有<m ＋2 013x>＝m ＋<2 013x>；⑤<x＋y>＝<x>＋<y>.其中，正确的结论有________(填写所有正确的序号)．10．若正整数n 使得在计算n ＋(n ＋1)＋(n ＋2)的过程中，各数位均不产生进位现象，则称n 为“本位数”．例如2和30是“本位数”，而5和91不是“本位数”．现从所有大于0且小于100的“本位数”中，随机抽取一个数，抽到偶数的概率为________．11．如果关于x 的一元二次方程ax 2＋bx ＋c ＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的是________．(写出所有正确说法的序号)①方程x 2－x －2＝0是倍根方程；②若(x －2)(mx ＋n)＝0是倍根方程，则4m 2＋5mn ＋n 2＝0；③若点(p ，q)在反比例函数y ＝2x 的图象上，则关于x 的方程px 2＋3x ＋q ＝0是倍根方程；④若方程ax 2＋bx ＋c ＝0是倍根方程，且相异两点M(1＋t ，s)，N(4－t ，s)都在抛物线y ＝ax 2＋bx ＋c 上，则方程ax 2＋bx ＋c ＝0的一个根为54.参考答案1．B 2.C 3.C 4.4≤a＜5 5.(1)(－1，2) (2)0≤a≤4 2 6.②③④7．(1)5 (2)2或－10 8.y ＝x 2－2x －3 9.①③④ 10.711 11.②③。

中考数学专题复习新定义问题(一)

中考数学专题复习新定义问题（一）学校:___________姓名：___________班级：___________考号：___________ 评卷人得分一、解答题1．在平面直角坐标系xOy 中，已知正方形ABCD ，其中2222,0,0,,,0,0,2222A B C D ⎛⎫⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，M ，N 为该正方形外两点，1MN =．给出如下定义：记线段MN 的中点为P ，平移线段MN 得到线段M N ''，使点,M N ''分别落在正方形ABCD 的相邻两边上，或线段M N ''与正方形的边重合（,,M N P '''分别为点M ，N ，P 的对应点），线段PP '长度的最小值称为线段MN 到正方形ABCD 的“平移距离”．（1）如下图，平移线段MN ，得到正方形ABCD 内两条长度为1的线段1122,M N M N ，则这两条线段的位置关系是_______；若12,P P 分别为1122,M N M N 的中点，在点12,P P 中，连接点P 与点_______的线段的长度等于线段MN 到正方形ABCD 的“平移距离”；（2）如图，已知点21,02E ⎛⎫+ ⎪ ⎪⎝⎭，若M ，N 都在直线BE 上，记线段MN 到正方形ABCD 的“平移距离”为1d ，求1d 的最小值；（3）若线段MN 的中点P 的坐标为(2)2，，记线段MN 到正方形ABCD 的“平移距离”为2d ，直接写出2d 的取值范围．2．对于平面直角坐标系xOy 中的线段PQ ，给出如下定义：若存在PQR 使得2PQRSPQ =，则称PQR 为线段PQ 的“等幂三角形”，点R 称为线段PQ 的“等幂点”．（1）已知(3,0)A ．①在点1234(1,3),(2,6),(5,1),(3,6)P P P P --中，是线段OA 的“等幂点”的是_____________； ①若存在等腰OAB 是线段OA 的“等幂三角形”，求点B 的坐标；（2）已知点C 的坐标为(2,1)C -，点D 在直线3y x =-上，记图形M 为以点(1,0)T 为圆心，2为半径的T 位于x 轴上方的部分，若图形M 上存在点E ，使得线段CD 的“等幂三角形”CDE △为锐角三角形，直接写出点D 的横坐标D x 的取值范围．3．对于平面直角坐标系xOy 中的图形M 和点P ，给出如下定义：将图形M 绕点P 顺时针旋转90︒得到图形N ，图形N 称为图形M 关于点P 的“垂直图形”．例如，图1中点D 为点C 关于点P 的“垂直图形”．（1）点A 关于原点O 的“垂直图形”为点B ． ①若点A 的坐标为(0,2)，则点B 的坐标为_______； ①若点B 的坐标为(2,1)，则点A 的坐标为_______．（2）(3,3),(2,3),(,0)E F G a --．线段EF 关于点G 的“垂直图形”记为E F ''，点E 的对应点为E '，点F 的对应点为F '． ①求点E '的坐标（用含a 的式子表示）；①若O 的半径为2，E F ''上任意一点都在O 内部或圆上，直接写出满足条件的EE '的长度的最大值．4．如图，直线l和直线l外一点P，过点P作PH l⊥于点H任取直线l上点Q，点H 关于直线PQ的对称点为点H'，标点H'为点P关于直线l的垂对点．在平面直角坐标系xOy中，（1）已知点(0,2)P，则点(0,0),(2,2),(0,4)O A B中是点P关于x轴的垂对点的是_______；（2）已知点(0,)M m，且0m>，直线443y x=-+上存在点M关于x轴的垂对点，求m的取值范围；（3）已知点(,2)N n，若直线y x n=+上存在两个点N关于x轴的垂对点，直接写出n 的取值范围，5．在平面直角坐标系xOy 中，对于点P 和线段ST ，我们定义点P 关于线段ST 的线段比()()PS PS PT ST k PT PS PT ST⎧<⎪⎪=⎨⎪≥⎪⎩（1）已知点(0,1),(1,0)A B ．①点(2,0)Q 关于线段AB 的线段比k =__________； ①点(0,)C c 关于线段AB 的线段比2k =，求c 的值．（2）已知点(,0)M m ，点(2,0)N m +，直线2y x =+与坐标轴分别交于,E F 两点，若线段EF 上存在点使得这一点关于线段MN 的线段比14k <，直接写出m 的取值范围．6．在平面直角坐标系xOy 中，对于点A 和线段MN ，如果点A ，O ，M ，N 按逆时针方向排列构成菱形AOMN ，且AOM α∠=，则称线段MN 是点A 的“α-相关线段”．例如，图1中线段MN 是点A 的“30-相关线段”．（1）已知点A 的坐标是(0,2)．①在图2中画出点A 的“30-相关线段”MN ，并直接写出点M 和点N 的坐标； ①若点A 的“α-相关线段”经过点(3,1)，求α的值；（2）若存在,()αβαβ≠使得点P 的“α-相关线段”和“β-相关线段”都经过点(0,4)，记PO t =，直接写出t 的取值范围．7．在平面直角坐标系xOy 中，O 的半径为1，点A 是平面内一点，过点A 的直线交O 于点 B 和点C （ABAC ），01BC ，我们把点 B 称为点A 关于O 的“斜射点”．（1）如图，在点12331(1,1),(0,),(,0)22A A A -中，存在关于 O 的“斜射点”的是_____________．（2）已知若(0,2)A ，点关于O 的“斜射点”为点B ，则点 B 的坐标可以是__________．（写出两个即可）（3）若点A 直线y kx k =+上，点A 关于O 的“斜射点”为(1,0)B -，画出示意图，直接写出 k 的取值范围．8．对于平面内的点P 和图形M ，给出如下定义：以点P 为圆心，r 为半径作圆，若P 与图形M 有交点，且半径r 存在最大值与最小值，则将半径r 的最大值与最小值的差称为点P 视角下图形M 的“宽度M d ”．（1）如图1.点(4,3)A ，(0,3)B ．①在点O 视角下，则线段AB 的“宽度AB d ”为_________； ①若B 半径为1.5，在点A 视角下，B 的“宽度Bd”为_________；（2）如图2，O 半径为2，点P 为直线1y x =-+上一点．求点P 视角下O “宽度Od”的取值范围；（3）已知点(,0),1C m CK =，直线333y x =+与x 轴，y 轴分别交于点D ，E ．若随着点C 位置的变化，使得在所有点K 的视角下，线段DE 的“宽度”均满足06DE d <<，直接写出m 的取值范围．9．在平面直角坐标系O x y 中，任意两点()11,P x y ，()22,Q x y ，定义线段PQ 的“直角长度”为2121PQ d x x y y =-+-．（1）已知点(3,2)A ． ① OA d =________；① 已知点(,0)B m ，若6AB d =，求m 的值；（2）在三角形中，若存在两条边“直角长度”之和等于第三条边的“直角长度”，则称该三角形为“和距三角形”．已知点(3,3)M ．① 点(0,)(0)D d d ≠．如果OMD 为“和距三角形”，求d 的取值范围；① 在平面直角坐标系xOy 中，点C 为直线4y x =--上一点，点K 是坐标系中的一点，且满足1CK =，当点C 在直线上运动时，点K 均满足使OMK △为“和距三角形”，请你直接写出点C 的横坐标C x 的取值范围．10．对于平面直角坐标系xOy 中的O 和图形N ，给出如下定义：如果O 平移m 个单位后，图形N 上的所有点在O 内或O 上，则称m 的最小值为O 对图形N 的“覆盖近距”．（1）当O 的半径为1时，①若点()3,0A ，则O 对点A 的“覆盖近距”为_________；①若O 对点B 的“覆盖近距”为1，写出一个满足条件的点B 的坐标_________； ①若直线2y x b =+上存在点C ，使O 对点C 的“覆盖近距”为1，求b 的取值范围；（2）当O 的半径为2时，(3,),(4,1)D t E t +，且12t -≤≤．记O 对以DE 为对角线的正方形的“覆盖近距”为d ，直接写出d 的取值范围．11．在平面直角坐标系xOy 中，对于任意两点()()1122,,,M x y N x y ，若1212x x y y k -+-=（k 为常数且0k ≠），则称点M 为点N 的k 倍直角点．根据以上定义，解决下列问题：（1）已知点(1,1)A①若点(2,3)B -是点A 的k 倍直角点，则k 的值是___________；①在点(2,3),(1,1),(0,2),(0,0)C D E O --中是点A 的2倍直角点的是_______； ①若直线2y x b =-+上存在点A 的2倍直角点，求b 的取值范围；（2）T 的圆心T 的坐标为(1,0)，半径为r ，若T 上存在点O 的2倍直角点，直接写出r 的取值范围．12．已知点P 、Q 分别为图形M 和图形N 上的任意点，若存在点P 、Q 使得PQ =1,我们就称图形M 、N 为友好图形，P 、Q 为关于图形M 、N 的一对友好点．（1）已知点 (1,0)A ,1(0,)2B ,C (-1,1)中, 与点O 为一对友好点，（2）已知O 半径r =1，若直线y x b =+与O 有且只有一对友好点，求b 的值；（3）已知点,D(m,2), D 半径r =1，若直线y=x+m 与D 是友好图形，求m 的取值范围．13．规定如下：图形M 与图形N 恰有两个公共点（这两个公共点不重合），则称图形M 与图形N 是和谐图形．（1）在平面直角坐标系xOy 中，已知O 的半径为2，若直线x k =与O 是和谐图形，请你写出一个满足条件的k 值，即k =______；（2）在平面直角坐标系xOy 中，已知点(),0A t ，直线3:33l y x =+与x 轴、y 轴分别交于B ，C 两点（其中点A 不与点B 重合），则线段AB 与直线l 组成的图形我们称为图形V ；①3t =时，以A 为圆心，r 为半径的A 与图形V 是和谐图形，求r 的取值范围；①以点A 为圆心，23为半径的A 与图形V 均组成和谐图形，求t 的取值范围．参考答案：1．（1）平行，P 1；（2）1d 的最小值为24；（3）21332222d -≤≤．【解析】【分析】（1）根据图形，比较PP 1，PP 2的长度即可求解；（2）根据已知条件求得①P 1BE =45︒，过P 1作P 1Q ①BE 于Q ，则△P 1QB 为等腰直角三角形，利用特殊角三角函数值即可求解；（3）先找到最值点，再利用两点之间的距离公式即可求解．【详解】（1）解：由图可得MN ①M 1N 1，MN ①M 2N 2， ①M 1N 1①M 2N 2，而PP 1<PP 2，故线段MN 到正方形ABCD 的“平移距离”为PP 1；故答案为：平行，P 1；（2）①B (0，22)，C (22，0)，四边形ABCD 为正方形， ①BC =2222122⎛⎫⎛⎫+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，①BCA =45︒， ①E (212+，0)， ①CE =221122+-==BC ， ①①1=①2，则①1+①2=①BCA =45︒， ①①1=①2=22.5︒，在Rt △BMN 中，BP 1为斜边上的中线，则BP 1=12MN =12=NP 1，①①P 1BN =①P 1NB ，又MN ①BE ， ①①2=①P 1NB ，①①2=①P 1NB =45︒，①P 1BE =①2+①P 1BN =45︒，过P 1作P 1Q ①BE 于Q ，则△P 1QB 为等腰直角三角形，在Rt△P1QB中，P1Q=P1B sin45︒=122224⨯=，①1d的最小值为24；（3）解：根据题意，P1、P2分别是AB、BC的中点，则线段MN到正方形ABCD的“平移距离”最大为PP1，最小为PP2，此时，P1 (24-，24)，P2 (24，24)，①PP1=22223322442⎛⎫⎛⎫++-=⎪ ⎪⎪ ⎪⎝⎭⎝⎭，PP2=22222112222224422⎛⎫⎛⎫⎛⎫-+-=-=-⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，①2d的取值范围是21332222d-≤≤．【点睛】本题考查正方形的性质、等腰直角三角形的判定和性质、坐标与图形的性质、锐角三角函数等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考压轴题．2．（1）①24,P P：①362⎛⎫⎪⎝⎭，或362⎛⎫⎪⎝⎭，-；（2）3212Dx-<<或5232Dx+<<【解析】【分析】（1）①根据定义求出三角形面积与OA 2进行比较即可确定线段OA 的“等幂点”；①如图，由OAB 是线段OA 的“等幂三角形”，可得2OAB S OA =．由点A 的坐标为()3,0A ，若记OAB 中OA 边上的高为h ，可得392OAB S h ==，求出6h =．由OAB 是等腰三角形，点B 在线段OA 的垂直平分线上即可求点B 的坐标为（32，6）或（32，-6）；（2）设半圆与x 轴交于G ，H 两点，过T 作CH 的平行线与半圆交于R ，作CH 的垂线交半圆于Q ，直线y =x -3与y 轴交于N ，设D （x ，x -3），过D 作y 轴平行线，与过C 作x 轴平行线交于F ，求出N (0，-3), H (3，0)，可证△ONH 为等腰直角三角形，①OHN =①ONH =45°，点D 运动分两种情况，第一种情况点D 在射线CH ，去掉线段CH 部分运动，在Rt △TCH 中TH =2，TC =CH =TH ×sin45°=22=22⨯，QC=2+2，又因为△ECD 为锐角三角形，点E 在QR 上运动，点E 到CD 的距离h 的范围是222h ≤≤+，可求h =2CD =22(x-2)，5232D x +<<；第二种情况点D 在射线CU 上，去掉线段CU 部分运动，点E 在QG 上运动，求出GU =GH ×cos45°=22，可得2222h ≤≤+，可求()2222222x ≤-≤+，解不等式即可得3212D x -<<．【详解】（1）①1OP A S=1211933222P OA y OA ⨯⋅=⨯⨯=<，P 1不是线段OA 的“等幂点”． 2OP A S=2211369=22P OA y OA ⨯⋅=⨯⨯=， P 2是线段OA 的“等幂点”． 3OP A S=3211331222P OA y OA ⨯⋅=⨯⨯=<，P 3不是线段OA 的“等幂点”． 4OP AS =421136922P OA y OA ⨯⋅=⨯⨯==， P 4是线段OA 的“等幂点”．是线段OA 的“等幂点”的是24,P P ，故答案为：24,P P ：①如图，①OAB 是线段OA 的“等幂三角形”，①2OAB S OA =．①点A 的坐标为()3,0A ，若记OAB 中OA 边上的高为h ，则有13922OAB S OA h h =⨯⨯==．解得6h =．①点B 在直线6y =或6y =-上．①OAB 是等腰三角形，①点B 在线段OA 的垂直平分线上．OA 的垂直平分线为x =32,与直线6y =或6y =-的交点为B 1（32，6），B 2（32，-6），综上所述，点B 的坐标为（32，6）或（32，-6），（2）设半圆与x 轴交于G ，H 两点，过T 作CH 的平行线与半圆交于R ，作CH 的垂线交半圆于Q ，直线y =x -3与y 轴交于N ，设D （x ，x -3），过D 作y 轴平行线，与过C 作x 轴平行线交于F ，当x =0时，y =-3,N (0，-3),当y =0时，x -3=0，x =3，H (3，0)，①ON =3=OH ，①ONH 为等腰直角三角形，①OHN =①ONH =45°，点D 运动分两种情况，第一种情况点D 在射线CH ，去掉线段CH 部分运动，①TC ①NH ，①OHN =45°，①①TCH 为等腰直角三角形，在Rt ①TCH 中TH =2，TC =CH =TH ×sin45°=22=22⨯，QC=2+2，又因为①ECD 为锐角三角形，点E 在QR 上运动，点E 到CD 的距离h 的范围是222h ≤≤+，CD=CF÷cos45°=2CF=2(x-2)，①线段CD 的“等幂三角形”， S △CDE =12h CD ⋅=CD 2， ①h =2CD =22(x -2)，①()222222x <-<+，解得55222x+<<，点D在H右侧，x>3，①5232Dx+<<；第二种情况点D在射线CU上，去掉线段CU部分运动，点E在QG上运动，又因为①ECD为锐角三角形，GU=GH×cos45°=22，①2222h≤≤+，①线段CD的“等幂三角形”，S△CDE=12h CD⋅=CD2，①h=2CD=22(2-x)，则()2222222x≤-≤+，解得3212Dx-<<，D 的横坐标D x 的取值范围为3212D x -<<或5232D x +<<．【点睛】本题考查新定义问题，仔细阅读新定义，抓住三角形的高为底的二倍，涉及三角形面积，等腰三角形，等腰直角三角形，线段垂直平分线，一次函数的性质，圆的性质，直线与圆的位置关系，锐角三角函数，锐角三角形，列双边不等式，解不等式等知识，难度较大，综合较强，熟练掌握多方面知识才是解题关键．3．（1）①()2,0；①()1,2-；（2）①(3,3)+'+E a a ；①22【解析】【分析】（1）①点A 在y 轴上，则点B 在x 轴上，且OB =OA =2，从而易得点B 的坐标；①由OA =OB ，过A 、B 分别作x 轴的垂线于N 、 M ，则可得①ANO ①①OMB ，故有AN =OM =2，ON =BM =1，再由点在第二象限，从而可得点A 的坐标；（2）①分别过点E 、E E '作x 轴的垂线，垂足分别为H 、Q ，则由OE OE '=，可得EHG GQE '△≌△,由此可得E '点的坐标；①由①知，点E '的两个坐标相等，表明E '点在第一、三象限的角平分线上，当E '点位于第一象限的圆上时，EE '最大,此时2OE '=，从而可得E '点坐标为(2,2)，这样可求得EE '的最大值．【详解】解：（1）①因点A 在y 轴上，故点B 必在x 轴正半轴上，又OB =OA =2，所以点A 坐标为()2,0；故答案为：()2,0．①如图，过A 、B 分别作x 轴的垂线于N 、 M ．则①ANO =①OMB =90，①①AON +①A =90°①①AOB =90°，①①AON +①BOM =90°，①①A =①BOM ，①OA =OB ，①①ANO ①①OMB ，①AN =OM =2，ON =BM =1，根据题意，点A 必在第二象限，①A ()1,2-．故答案为：()1,2-．（2）①如图，过点E 作EH x ⊥轴于点H ，过点E '作'⊥E Q x 轴于点Q ．由题意可知，,'90EG E G EGE '=∠=︒．①EHG GQE '△≌△．①,'==EH GQ HG QE ．①(3,3),(,0)-E G a ，①()3,0-H ．①．|3|3,3HG QE a a EH GQ ==+=+=='①|3|3OQ a a =+=+．①(3,3)+'+E a a ．①①EF ①x 轴①E F x ''⊥轴连接OE '，延长E F ''交x 轴于点H ，则E H x '⊥轴；过点E '作x 轴的平行线，过点E 作y 轴的平行线，两线交于点D ，则ED E D '⊥，如图所示；由①知，点E '的两个坐标相等，①|3|OH E H a '==+，表明E '点在第一、三象限的角平分线上，且位于与圆相交的圆内的一条线段上运动，当点E '位于第一象限上的圆上时，即2OE '=时，EE '最大，①①E HO '是等腰直角三角形，①22OH OE '==，①2OH E H '==，①(2,2)E '，①32DE '=+，32DE =-，在Rt EDE '中，由勾股定理得：2222(32)(32)22EE DE DE =+=-++=''，即EE '的最大值为：22．【点睛】本题考查了新定义，对于新定义这类问题，关键是弄清楚新定义的含义，抓住问题的实质，本题新定义的实质是旋转，通过作x 轴的垂线，构造两个全等的直角三角形，问题便容易解决．4．（1）O 和A ；（2）3m 2≥；（3）-2n 1+21＜＜且n≠2 【解析】【分析】（1）根据垂对点的定义即可得出答案；（2）先得出点M 关于x 轴的垂对点在以M 为圆心MO 即m 为半径的圆上，点(0,2)m 除外，再根据当直线443y x =-+与①M 相切时，m 的值最小，利用相似三角形的判定和性质得出m 的值即可；（3）先得出点N 关于x 轴的垂对点在以N 为圆心2为半径的圆上，点(n,4)除外，再分n =0、n ＜0 、n ＞0三种情况进行分类讨论即可．【详解】解：（1）①点(0,2)P ，①根据垂对点的定义可得点P 关于x 轴的垂对点为(0,0),(2,2)O A ；（2）①点(0,)M m ，且0m >，①由垂对点的定义可知，点M 关于x 轴的垂对点在以M 为圆心MO 即m 为半径的圆上，点(0,2)m 除外，则OM =m ；设直线443y x =-+与x 轴和y 轴的交点分别为G 、H ，①G（3，0），H（0，4），①22345GH=+=，①直线443y x=-+上存在点M关于x轴的垂对点，①当直线443y x=-+与①M相切时，m的值最小，此时切点为N,连接MN，则①HOG=①MNH=90°，①①OHG=①NHM①①OHG①①NHM①=MN MHOG GH①m4-m35=①3m=2①m的取值范围是：3m2≥；（3）①(,2)N n，点N关于x轴的垂对点在以N为圆心2为半径的圆上，点(n,4)除外，当n=0时，①N与y=x有两个交点，则直线y x n=+上存在两个点N关于x轴的垂对点，当n＞0时，相当于①N向右平移，y=x向上平移，当y=x+n与①N相切于①N左侧时是临界点，设切点为E，连接NE，①DEN=90°，过点E作EF①x轴于F，直线y=x+n与x轴y轴的交点分别为W、K，则W（-n，0），K （0，n），①OK=OW，①①OWK为等腰直角三角形，设过点(,2)N n且平行于x轴的直线与直线y=x+n相交于点D，则①DEN为等腰直角三角形，22DE=，设EF交DN于点I，在直角三角形ENI中，NE=2，①END=45°，①NI=EI=2，①E（n-2，2+2），①点E在y=x+n上，①2+2=n-2+n①n=1+2当n=2时，直线与圆交于点（0，2）、（2，4），此时只有一个垂对点，故n≠2．当n＜0时，相当于①N向左平移，y=x向下平移，同理得出n=1-2，①-2n1+21＜＜且n≠2 ．【点睛】本题属于新定义题型，涉及到了三角形的判定和性质、切线的性质，解题的关键在于读懂题目信息，并注意数形结合思想的应用．5．（1）①22；①C点为(0,3)或(0,3)-；（2）92422m-<<-+或52222m-<<-+．【解析】【分析】（1）①利用两点之间的距离公式和线段比k的定义即可得；①分若AC BC<时和AC BC≥时，两种情况讨论，根据线段比k的定义计算即可；（2）分①当点N 在E 点或在其左侧时，①当点N 在E 点右侧,M 点在E 点左侧时，①当M 点在E 点或在E 点右侧时三种情况讨论，结合图形和线段比k 的定义分析即可．【详解】解：（1）①22112AB =+=，22215AQ =+=，1BQ =， ①BQ AQ <， ①1222BQ k AB ===，故答案为：22； ①①(0,)C c ，①|1|AC c =-，21BC c =+，若AC BC <时， |1|22c k -==，解得3c =或1c =-（不满足2|1|1c c -<+舍去）；若AC BC ≥时，2122c k +==，解得3c =（不满足2|1|1c c -≥+舍去）或3c =-；综上所述，C 点为(0,3)或(0,3)-；（2）①直线2y x =+与坐标轴分别交于,E F 两点， ①(2,0)E -,(0,2)F ，①点(,0)M m ，点(2,0)N m +， ①MN =2，①如下图，当点N 在E 点或在其左侧时，22m +≤-，即4m ≤-， M 、N 到线段EF 的最短距离为ME 、NE ，此时ME >NE ，即2(2)124m --+<，解得92m >-，即942m -<≤-；①如下图，当点N在E点右侧,M点在E点左侧时，42m-<<-，M、N到线段EF的最短距离为ME、NG（N到EF的垂线段），()222,422ME m NG EN m=--==+，若2(4)22m m+<--，即22m<-，2(414)22m+<，解得242m<-+，此时2442m-<<-+，若2(4)22m m+>--，即22m>-，4212m--<，解得52m>-，此时522m-<<-；①如下图，当M点在E点，或在E点右侧时，2m≥-M 到线段EF 的距离近，为MG （M 到EF 的垂线段），2(2)1224m +<，解得222m <-+，即2222m -≤<-+ 综上所述，92422m -<<-+或52222m -<<-+．【点睛】本题是新定义的题目．注意考查一次函数与坐标轴交点问题，两点之间的距离公式．理解题中线段比的定义，能分类讨论结合图形分析是解题关键．6．（1）① 作图见解析；点M 的坐标是(1,3)，点N 的坐标是(1,32)+；①α的值为60︒或120︒ ；（2） 224t <≤．【解析】【分析】（1）①根据“ α− 相关线段”的定义求解；①由题意点M 必在直线x =3上，记MH ①x 轴于H ，则可得MH =1，①MOH =30°，然后分点M 在x 轴上方和点M 在x 轴下方两种情况分别求出α的值即可；（2）根据题意分0<t ≤22、22<t ≤4、t >4三种情况讨论．【详解】（1）①如图，MN 即为所求．过点M 作BM ①x 轴于点B ， ①四边形AOMN 为菱形， ①AO ①MN ，AO =MO =MN ， ①点A 在y 轴上， ①AO ①x 轴，①MN ①x 轴，即N 、M 、B 三点共线， ①①AOM =30°， ①①MOB =90°-30°=60°，在RT ①MOB 中，BO =12MO =1，MB =332MO =， ①点M 的坐标是(1,3)，点N 的坐标是(1,32)+． ①解：①点A 的“α-相关线段”MN 经过点(3,1)， ①点M 必在直线3x =上．记直线3x =与x 轴交于点(3,0)H ， ①2,3OM OA OH ===，①221MH OM OH =-=，30MOH ∠=︒．分两种情况：a ）如图，当点M 在x 轴上方时，点M 恰为(3,1)，符合题意，此时60,60AOMα︒∠==︒；b）如图，当点M在x轴下方时，点M为(3,1)-，由2MN=知点N为(3,1)，也符合题意，此时120,120AOMα︒∠==︒．综上，α的值为60︒或120︒．（2）当0<t≤22时，任意菱形的边MN都不经过点(0，4)；当22<t≤4且N为（0，4）时，点P的“α-相关线段”过(0，4)，当22<t≤4且M为（0，4）时，点P的“β-相关线段”过(0，4)；当t>4时,只有一种情况使P的“α-相关线段”或“β-相关线段”过(0，4)，此时(0，4)在线段OM上，①不符合题意综上所述，224t<≤【点睛】本题考查一次函数的应用，熟练掌握一次函数的图象与性质、菱形的性质是解题关键．7．（1）1A，2A；（2）（32-，12），（35，45）；（3）3k>或3k<-．【解析】【分析】（1）过点1(1,1)A -作直线交O 于点1B ，1C ，过点2()30,2A 作22B C y 轴交O 于点2B ，2C ，过点3()1,02A 作33B C x 轴交O 于点3B ，3C ，连接2OB ，3OC ，分别求出22B C ，33B C ，根据“斜射点”的判别条件ABAC ，01BC，分别进行判别即可；（2）过点A 作O 的切线AD ，交O 于点 D ，根据Rt ADO 中，1OD =， 2AO =，可求得点 D 的坐标是（32-，12），可知，满足 AB AC ，01BC，点D 是 O 的“斜射点”；在 OD 上取13=2OD ，并过 1D 作 144OD B C 交O 于点 4B ，4C ，可求得 4C 的坐标是（-1，0），设过A ，4C 两点的直线是 y kx b =+，并交 O 于点5B ，可求出点5B 的坐标是（35， 45），根据（1）中2A 的求法可知，55<1B C ，可得 5B 是O 的“斜射点”；（3）当0k >时，一次函数y kx k =+图像向上，过点B （-1，0）交O 于点5C ，并51BC ，可得5OBC 是等边三角形，根据（1）中 2A 的求法可知，点5C 的坐标是（12-， 32），可求出得： 3k =，则有当满足过点B 并且是O 的“斜射点”时，3k >，同理可得，当 0k >时，点5C 的坐标是（12-， 32-），可得满足过点 B 并且是O 的“斜射点”时，3k <-．【详解】解：（1）过点1(1,1)A -作直线交O 于点 1B ，1C , 过点2()30,2A 作 22BC y 轴交O 于点2B ，2C ，过点3()1,02A 作33BC x 轴交O 于点3B ，3C ，连接2OB ，3OC ，O 的半径为1，即231OB OC ，①22B C y 轴，2A 的坐标是 3(0,)2①y 轴垂直平分22B C ， ①由勾股定理可得：2222222231=11222B C OB OA ， ①22=1B C ，满足AB AC ，01BC ， ①点2A 是O 的“斜射点”； ①33B C x 轴，3A 的坐标是 1(,0)2①x 轴垂直平分33B C ，①由勾股定理可得：22223323132212=1B C OC OA ，①3331B C ，根据O 中，过点3A 的所有弦中，垂直半径的弦最短可知，过点3A 的所有弦都大于 3，因此点3A 不满足题意， ①点3A 不是是O 的“斜射点”；由图中图像可知1122B C B C ，即有：1122=1B C B C故满足AB AC ，01BC ， ①点1A 是O 的“斜射点”；综上所述，点1A ，2A 是O 的“斜射点”；（2）如图示，过点A 作O 的切线AD ，交O 于点 D ，在Rt ADO 中，1OD =，2AO =， ①2222=213AD AO D O ,设点D 的坐标是（D x ，D y ），则有：11··22ADOD S OD AD AO x ==， ①11··22ADOD S OD AD AO x == ①32D x （点D 在第二象限，取负值）， ①221D D x y ，①12Dy （点D 在第二象限，取正值），①点D 的坐标是（32-，12），满足AB AC ，01BC ，①点D 是O 的“斜射点”，即点B 的坐标可以是（32-，12）；在OD 上取13=2OD ，并过 1D 作144OD B C 交O 于点 4B ，4C ，根据（1）中2A 的求法可知，44=1B C ， 4C 的坐标是（-1，0），设过A ，4C 两点的直线是y kx b =+，并交O 于点5B①20b k b =⎧⎨-+=⎩，解之得 22b k ，①过A ，4C 两点的直线是22y x =+，设点5B 的坐标是（5B x ，5B y ），则有555522122B B B B x y y x ，解之得5510B Bx y或553545B B x y ，即点5B 的坐标是（35，45），根据（1）中2A 的求法可知，55<1B C ，即满足AB AC ，01BC ，①点5B 是O 的“斜射点”，即点B 的坐标可以是（35， 45）；综上所述，即点B 的坐标可以是（32-，12），（ 35，45）；（3）如图示，当0k >时，一次函数y kx k =+图像向上，过点B （-1，0）交O 于点 5C ，并51BC ，①51OB OC ，①5OBC 是等边三角形，根据（1）中2A 的求法可知，点5C 的坐标是（12-，32），①1322k k，解之得：3k =，当满足过点B 并且是O 的“斜射点”时，3k >，同理可得，当0k >时，点5C 的坐标是（12-， 32-），①满足过点B 并且是O 的“斜射点”时，3k <-，【点睛】本题是圆的综合题，主要考查了圆的切线的性质，勾股定理，等边三角形的判定与性质，弦长的性质，点与坐标的关系，方程组的解法，“斜射点”的定义的理解等知识点，熟悉相关性质是解题的关键． 8．（1）①2；①3；（2）24Od ≤≤；（3）332m <--或331m >-+．【解析】【分析】（1）①根据题意易得当线段AB 与以点O 为圆心的圆相切时半径最小，经过点B 时半径最大，由此问题可得解；①由题意可得当以点A 为圆心的圆与B 外切时半径最小，内切时半径最大，由此问题可得解；（2）设直线1y x =-+与O 的交点分别为M 和N ，与x 轴、y 轴交于点A 、B ，由题意易得点()()1,0,0,1A B ，即OA =1，OB =1，则可分当点P 在点M 上方、点N 下方时和当点P 在线段MN 上时，然后进行分类求解即可；（3）由直线333y x =+可得33,3OD OE ==，则6DE =，30EDO ∠=︒，由(),0,1C m CK =可知点K 在以点C 为圆心，半径为1的圆上，进而可分当C 经过点D 时和当C 与直线DE 相切于点K 时，然后求解即可．【详解】解：（1）①由题意得：当以点O 为圆心的圆与线段AB 相切于点B 时，半径为最小，经过点A 时半径最大，连接OA ，如图所示：①()4,3A，()0,3B，①3OB=，()()2240305OA=-+-=，①在点O视角下，则线段AB的“宽度ABd”为532-=，故答案为2；①由题意得：以点A为圆心的圆与B外切时半径最小，内切时半径最大，如图所示：①B半径为1.5，①半径最大为1.54 5.5+=，半径最小为4 1.5 2.5-=，①在点A视角下，B的“宽度Bd”为5.5-2.5=3，故答案为3；（2）设直线1y x =-+与O 的交点分别为M 和N ，与x 轴、y 轴交于点A 、B ，如图所示：当点P 在点M 上方时，则以点P 为圆心的圆与O 内切时半径最大，外切时半径最小，如图，设P 的半径最小为r ，由圆与圆的位置关系可得半径最大时为4r +， ①在点P 视角下O “宽度Od”为44r r +-=，同理可得当点P 在点N 下方时，与点P 在点M 外时相同；当点P 在线段MN 上时，则根据点到直线垂线段最短可得当点P 在AB 的中点时，此时在点P 视角下O “宽度Od ”取最小，即：以点P 为圆心的圆与O 内切时半径最大，外切时半径最小，如图所示：①由直线1y x =-+可得点()()1,0,0,1A B ，即OA =1，OB =1， ①①AOB 是等腰直角三角形， ①2AB =， ①点P 是AB 的中点， ①22OP =， ①P 的半径最小为222-，半径最大为222+， ①在点P 视角下O “宽度O d”为2222222⎛⎫+--= ⎪ ⎪⎝⎭，综上所述：在点P 视角下O “宽度Od ”的取值范围为24Od ≤≤；（3）由题意可得如图所示：由直线333y x =+可得当y =0时，则3033x =+，解得33x =-，当x =0时，则有y =3， ①()()33,0,0,3D E -， ①33,3OD OE ==， ①6DE =， ①30EDO ∠=︒， ①(),0,1C m CK =，①点K 在以点C 为圆心，半径为1的圆上，①由在所有点K 的视角下，线段DE 的“宽度”均满足06DE d <<，则有：当C 经过点D 时，如图所示：①DC =1， ①331OC =-， ①331m =-+，①当点K 与点D 重合时，以点K 为圆心的圆与线段DE 有交点时，半径最小为0，最大为6，所以在点K 的视角下，线段DE 的“宽度”为6DE d =，而点K 在C 的其他地方时，根据三角形三边关系可知始终满足题意， ①331m >-+；当C 与直线DE 相切于点K 时，如图所示：①CK =1，30EDO ∠=︒，①30CDK ∠=︒， ①22CD CK ==，①332OC =+，即332m =--，此时在点K 的视角下，线段DE 的“宽度”为6DE d =，故不符合题意， ①332m <--，综上所述：当随着点C 位置的变化，使得在所有点K 的视角下，线段DE 的“宽度”均满足06DE d <<，则m 的取值范围为332m <--或331m >-+．【点睛】本题主要考查直线与圆的位置关系、圆与圆的位置关系及一次函数的综合，熟练掌握直线与圆的位置关系、圆与圆的位置关系及一次函数的性质是解题的关键．9．（1）① 5；①1m =-或7；（2）①3d 且0d ≠；①3C x -＜222--或2212C x -+<【解析】【分析】（1）①根据题意把(0,0)O ，(3,2)A 代入2121PQ d x x y y =-+-计算即可；①把(3,2)A ，(,0)B m 代入公式，求得34m -=，去绝对值求得m 的值即可；（2）①据题意，锐角三角形不可能为 “和距三角形”，结合图像求出d 的取值范围；①结合图形画出所有可能情况即可求出C x 的取值范围．【详解】解：（1）① ①(3,2)A①212130205OA d x x y y =-+-=-+-=；故答案为：5① 知点(,0)B m ，(3,2)A 若6AB d =， ①21213206AB d x x y y m =-+-=-+-= ①34m -=，34m ∴-=或34,m -=-①1m =-或7；（2）① ()()()0,,0,0,3,3,D d O M,6,33,OD MO MDd d d d d∴===+-∴当d＞3时，不存在“和距三角形”，①当3d=时，构成直角三角形如图，符合要求，当3d<时，构成钝角三角形如图，符合要求，①3d且0d≠① 据题意，点K的轨迹是以点C为圆心，半径为1的圆，且锐角三角形不可能为“和距三角形”，如图：①综上所述：3C x -＜222--或2212C x -+<【点睛】本题考查了新定义，类比法，点与圆的位置关系，圆的切线等，解题的关键是有较强的理解能力及自学能力等．10．(1) ①2, ①(2,0)（答案不唯一）, ①2525b -≤≤ (2) 15432d -≤≤ 【解析】【分析】(1) ① 根据OA =3，可确定“覆盖近距”为3-1=2；①确定OB =2，写出坐标即可；①确定当OC ①GH 时的“覆盖近距”，以此确定b 的取值范围；(2)确定O 对以DE 为对角线的正方形的“覆盖近距”的最大值和最小值即可．【详解】解:(1) ①因为OA =3，圆的半径是1，故O 对点A 的“覆盖近距”为3-1=2；故答案为：2，①O 对点B 的“覆盖近距”为1，圆的半径是1，则OB =2，B 点坐标可以为（2，0）（答案不唯一）；故答案为：（2，0）（答案不唯一）；①设直线2y x b =+与x 轴、y 轴交于点G 、H ，当x =0时，y =b ，OH =b ；当y =0时，x =2b -，OG =2b ，tan①OHG =12，O 对点C 的“覆盖近距”为1，即OC =2,当OC ①GH 时，刚好存在“覆盖近距”为1，此时，OC =2，CH =4，222425OH =+=，同理，OI =25, 故b 的取值范围为：2525b -≤≤（2）根据题意可知以DE为对角线的正方形边长为1，如图所示，当t=-0.5时，“覆盖近距”最小，此时平移后的F经过E、G两点，EG交x轴于点H,连接FG,221520.52FH=-=，d=4-152；当t=2时，“覆盖近距”最大，如图所示，此时，EH=3,22345OE=+=,d=5-2=3；故d的取值范围为：15432d-≤≤【点睛】本题考查了新定义问题和与圆的位置关系，解题关键是准确理解题意，熟练运用圆的相关知识和解直角三角形，利用数形结合思想，正确推理计算．11．（1）①5；①D 、O ；①b 的取值范围为：17b -≤≤；（2）r 的取值范围为232r ≤≤．【解析】【分析】（1）①根据k 倍直角点的定义计算即可求解； ①根据“2倍直角点”的定义分别计算，即可判断；①根据“2倍直角点”的定义得到如图所示有正方形的边界即为点A 的2倍直角点存在的区域，列式计算，即可求解；（2）若T 上存在点O 的2倍直角点，即T 与如图的正方形有交点(正方形的边界为点O 的2倍直角点存在的区域)，根据切线的性质以及特殊角的三角函数值即可求解．【详解】（1）①根据k 倍直角点的定义得：121221315k x x y y =-+-=--+-=，故答案为：5；①点C (2，3)，121221313k x x y y =-+-=-+-=，点D (−1，1)，121211112k x x y y =-+-=--+-=，点E (0，−2)，121201214k x x y y =-+-=-+--=，点O (0，0)，121201012k x x y y =-+-=-+-=，①是点A 的2倍直角点的是D (−1，1)，O (0，0)，故答案为：D 、O ；①如图，正方形的边界即为点A 的2倍直角点存在的区域，若直线2y x b =-+与其有交点，则过点(-1，1)时，b 值最小，即()121b =-⨯-+，解得：1b =-，当过点(3，1)时，b 值最大，即123b =-⨯+，解得：7b =， ①b 的取值范围为：17b -≤≤；（2）若T 上存在点O 的2倍直角点，即T 与如图的正方形有交点(正方形的边界为点O 的2倍直角点存在的区域)，由图可知，当①T 与正方形有交点为H (0，0)时，①T 的半径最大，即3r =；当①T 与直线MN 相切时，①T 的半径最小，过T 作TQ ①MN 于Q ，即r TQ =，根据正方形的性质知①MNO =45︒， ①2sin sin 452TQ QNT TN ∠=︒==, ①1TN =，①22TQ =， ①r 的取值范围为232r ≤≤．【点睛】本题属于新定义与一次函数相结合的综合压轴题，考查了正方形的性质，特殊角的三角函数值，切线的性质等知识，读懂定义，紧扣定义解题，熟练掌握“k 倍直角点”的定义是解答此题的关键．12．（1）A ；（2）22b =或b=-22；（3）22m -≤≤322．【解析】【分析】（1）根据友好点的定义去计算判断，只要满足到原点的距离为1即可；（2）根据直线与圆O 相切时，只有一个公共点，再根据友好点的定义，将直线向外平移1各单位，后确定b 的值即可；（3）确定直线y =x +m 与直线y =2的交点，分交点在点D 左边和右边两种情形求解即可．【详解】解：（1）①(1,0)A ,1(0,)2B ,C (-1,1)，①OA =22(10)(00)-+-=1，OB =221(0)(00)2-+-=12，OC =22(10)(10)--+-=2，①符合新定义的点是（1,0），故答案为：A ；（2）如图，直线y x b =+与圆O 相切是时，直线与圆有一个公共点，此时OG =OD =1，根据直线的特点，知道直线与坐标轴构成等腰直角三角形，根据友好点的定义，只需将相切的直线沿着OD 或OG 向外平移一个单位长即可，分别到达E 或H 点，此时OE =2或OH =2，根据平移的性质，OE =EF =2，或OH =HM =2，根据勾股定理，得OM =OF =22， ①b =22或b =-22；。

九年级数学中考复习新定义专题练习

九年级数学中考复习新定义专题练习1.用“☆”定义一种新运算：对于任意有理数a 和b ，规定a ☆b = ab 2 + a .如：1☆3=1×32+1=10.则（-2）☆3的值为 .2.（2019•德州）已知：[x ]表示不超过x 的最大整数．例：[4.8]＝4，[﹣0.8]＝﹣1．现定义：{x }＝x ﹣[x ]，例：{1.5}＝1.5﹣[1.5]＝0.5，则{3.9}+{﹣1.8}﹣{1}＝．3. 用“△”定义新运算：对于任意有理数a ，b ，当a ≤b 时，都有2a b a b ∆=；当a ＞b 时，都有2a b ab ∆=．那么，2△6 = ，2()3-△(3)-= ． 4. 如图,在平面内，两条直线l 1，l 2相交于点O ，对于平面内任意一点M ，若p 、q 分别是点M 到直线l 1，l 2的距离，则称(p ，q )为点M 的“距离坐标”．根据上述规定，“距离坐标”是(2，1)的点共有______个．5. 定义：圆中有公共端点的两条弦组成的折线称为圆的一条折弦．阿基米德折弦定理：如图1，AB 和BC 组成圆的折弦，AB BC >，M 是弧ABC 的中点，MF AB ⊥于F ，则AF FB BC =+．如图2，△ABC 中，60ABC ∠=︒，8AB =，6BC =，D 是AB 上一点，1BD =，作DE AB ⊥交△ABC 的外接圆于E ，连接EA ，则EAC ∠=________°6.（2019•枣庄）对于实数a 、b ，定义关于“⊗”的一种运算：a ⊗b ＝2a +b ，例如3⊗4＝2×3+4＝10．（1）求4⊗（﹣3）的值；（2）若x ⊗（﹣y ）＝2，（2y ）⊗x ＝﹣1，求x +y 的值．7. 阅读材料：规定一种新的运算：a c =b ad bc d -．例如：1214-23=-2.34××= （1）按照这个规定，请你计算5624的值．（2）按照这个规定，当5212242=-+-x x 时求x 的值．8. 对于平面直角坐标系xOy 中的点M 和图形G ，若在图形G 上存在一点N ，使M ，N 两点间的距离等于1，则称M 为图形G 的和睦点．（1）当⊙O 的半径为3时，在点P 1（1,0），P 2,1），P 3（72,0），P 4（5,0）中，⊙O 的和睦点是________；（2）若点P （4,3）为⊙O 的和睦点，求⊙O 的半径r 的取值范围；（3）点A 在直线y =﹣1上，将点A 向上平移4个单位长度得到点B ，以AB 为边构造正方形ABCD ，且C ，D 两点都在AB 右侧．已知点E，若线段OE 上的所有点都是正方形ABCD 的和睦点，直接写出点A 的横坐标A x 的取值范围．9. 对于任意四个有理数a ，b ，c ，d ，可以组成两个有理数对（a ，b ）与（c ，d ）.我们规定：（a ，b ）★（c ，d ）=bc －ad .例如：（1，2）★（3，4）=2×3－1×4=2．根据上述规定解决下列问题：（1）有理数对（2，－3）★（3，－2）= ;（2）若有理数对（－3，2x －1）★（1，x +1）=7，则x = ;（3）当满足等式（－3，2x －1）★（k ，x ＋k ）=5＋2k 的x 是整数时，求整数k 的值．10. 对于任意有理数a ，b ，定义运算：a ⊙b =()1a a b +-，等式右边是通常的加法、减法、乘法运算，例如，2⊙5=2×（2+5）－1=13；(3)-⊙(5)-＝-3×（-3-5）-1=23．（1）求（-2）⊙312的值；（2）对于任意有理数m ，n ，请你重新定义一种运算“⊕”，使得5⊕3＝20，写出你定义的运算：m ⊕n ＝（用含m ，n 的式子表示）．11. （2019•衢州）定义：在平面直角坐标系中，对于任意两点A （a ，b ），B （c ，d ），若点T （x ，y ）满足x ＝，y ＝那么称点T 是点A ，B 的融合点．例如：A （﹣1，8），B （4，﹣2），当点T （x ，y ）满足x ＝＝1，y ＝＝2时，则点T （1，2）是点A ，B 的融合点．（1）已知点A （﹣1，5），B （7，7），C （2，4），请说明其中一个点是另外两个点的融合点．（2）如图，点D （3，0），点E （t ，2t +3）是直线l 上任意一点，点T （x ，y ）是点D ，E 的融合点．①试确定y 与x 的关系式．②若直线ET 交x 轴于点H ．当△DTH 为直角三角形时，求点E 的坐标．12. 已知在平面直角坐标系xOy 中的点P 和图形G,给出如下的定义：若在图形G 上存在一点Q ,使得Q P 、之间的距离等于1，则称P 为图形G 的关联点.（1）当圆O 的半径为1时，①点11(,0)2P ,2P,3(0,3)P 中，圆O 的关联点有_____________________. ②直线经过（0，1）点，且与y 轴垂直，点P 在直线上.若P 是圆O 的关联点，求点P 的横坐标x 的取值范围.（2）已知正方形ABCD 的边长为4，中心为原点，正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点，求圆的半径r 的取值范围.备用图备用图参考答案：1. -202. 1.13. 24 -64. 45. 60°6. (1) 5 (2) 137. （1）8 （2）x=18. （1）P2，P3；（2）4≤r≤6(3) -5+√2≤x A≤3 或√2-1≤x A≤19. （1）﹣5 （2）1 （3）k=1，﹣1，﹣2，﹣410. （1）-4（2）答案不唯一，例如：m⊕n＝m(n+1)11. （1）x＝（﹣1+7）＝2，y＝（5+7）＝4，故点C是点A、B的融合点；（2）①y＝2x﹣1；②点E（，6）或（6，15）．12. （1）P1 P2（2）-√3≤x≤√3（3）2√2-1≤r≤3。

中考数学专题复习新定义问题

中考数学专题复习新定义问题学校:___________姓名：___________班级：___________考号：___________ 评卷人得分一、解答题1．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（,B C ''分别是,B C 的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233,,,,,,A B C B C B C 的横､纵坐标都是整数．在线段112233,,B C B C B C 中，O 的以点A 为中心的“关联线段”是______________；（2）ABC 是边长为1的等边三角形，点()0,A t ，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，1,2AB AC ==．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．2．在平面直角坐标系xOy 中，⊙O 的半径为1，A ，B 为⊙O 外两点，AB=1．给出如下定义：平移线段AB ，得到⊙O 的弦A B ''（,A B ''分别为点A ，B 的对应点），线段AA '长度的最小值称为线段AB 到⊙O 的“平移距离”．（1）如图，平移线段AB 到⊙O 的长度为1的弦12PP 和34P P ，则这两条弦的位置关系是；在点1234,,,P P P P 中，连接点A 与点的线段的长度等于线段AB 到⊙O 的“平移距离”；（2）若点A ，B 都在直线323y x =+上，记线段AB 到⊙O 的“平移距离”为1d ，求1d 的最小值；（3）若点A 的坐标为32,2⎛⎫⎪⎝⎭，记线段AB 到⊙O 的“平移距离”为2d ，直接写出2d 的取值范围．3．在⊙ABC 中，D ，E 分别是ABC 两边的中点，如果DE 上的所有点都在⊙ABC 的内部或边上，则称DE 为⊙ABC 的中内弧．例如，下图中DE 是⊙ABC 的一条中内弧．（1）如图，在Rt⊙ABC 中，22AB AC D E ==，，分别是AB AC ，的中点．画出⊙ABC 的最长的中内弧DE ，并直接写出此时DE 的长；（2）在平面直角坐标系中，已知点()()()()0,20,04,00A B C t t >，，，在⊙ABC 中，D E ，分别是AB AC ，的中点． ⊙若12t =，求⊙ABC 的中内弧DE 所在圆的圆心P 的纵坐标的取值范围； ⊙若在⊙ABC 中存在一条中内弧DE ，使得DE 所在圆的圆心P 在⊙ABC 的内部或边上，直接写出t 的取值范围．4．对于平面直角坐标系xOy 中的图形M ，N ，给出如下定义：P 为图形M 上任意一点，Q 为图形N 上任意一点，如果P ，Q 两点间的距离有最小值，那么称这个最小值为图形M ，N 间的“闭距离”，记作d （M ，N ）．已知点A （2-，6），B （2-，2-），C （6，2-）．（1）求d （点O ，ABC ）；（2）记函数y kx =（11x -≤≤，0k ≠）的图象为图形G ，若d （G ，ABC ）1=，直接写出k 的取值范围；（3）T 的圆心为T （t ，0），半径为1．若d （T ，ABC ）1=，直接写出t 的取值范围．5．在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 存在一点Q ，使得P 、Q 两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当⊙O 的半径为2时，⊙在点1231135,0,,,,02222P P P ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 中，⊙O 的关联点是_______________． ⊙点P 在直线y=-x 上，若P 为⊙O 的关联点，求点P 的横坐标的取值范围．（2）⊙C 的圆心在x 轴上，半径为2，直线y=-x+1与x 轴、y 轴交于点A 、B ．若线段AB 上的所有点都是⊙C 的关联点，直接写出圆心C 的横坐标的取值范围．6．在平面直角坐标系xOy 中，点P 的坐标为（1x ，1y ），点Q 的坐标为（2x ，2y ），且12x x ≠，12y y ≠，若P ，Q 为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P ，Q 的“相关矩形”．下图为点P ，Q 的“相关矩形”的示意图．（1）已知点A 的坐标为（1，0）．⊙若点B 的坐标为（3，1）求点A ，B 的“相关矩形”的面积；⊙点C 在直线x=3上，若点A ，C 的“相关矩形”为正方形，求直线AC 的表达式；（2）⊙O 的半径为，点M 的坐标为（m ，3）．若在⊙O 上存在一点N ，使得点M ，N 的“相关矩形”为正方形，求m 的取值范围．7．在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的反称点的定义如下：若在射线CP上存在一点P′，满足CP+CP′=2r，则称P′为点P关于⊙C的反称点，如图为点P及其关于⊙C的反称点P′的示意图．特别地，当点P′与圆心C重合时，规定CP′=0．（1）当⊙O的半径为1时．①分别判断点M（2，1），N（32，0），T（1，3）关于⊙O的反称点是否存在？若存在，求其坐标；②点P在直线y=﹣x+2上，若点P关于⊙O的反称点P′存在，且点P′不在x轴上，求点P的横坐标的取值范围；（2）⊙C的圆心在x轴上，半径为1，直线y=﹣33x+23与x轴、y轴分别交于点A，B，若线段AB上存在点P，使得点P关于⊙C的反称点P′在⊙C的内部，求圆心C 的横坐标的取值范围．参考答案：1．（1）22B C ；（2）3t =±；（3）当min 1OA =时，此时3BC =；当max 2OA =时，此时62BC =．【解析】【分析】（1）以点A 为圆心，分别以112233,,,,,AB AC AB AC AB AC 为半径画圆，进而观察是否与O 有交点即可；（2）由旋转的性质可得AB C ''△是等边三角形，且B C ''是O 的弦，进而画出图象，则根据等边三角形的性质可进行求解；（3）由BC 是O 的以点A 为中心的“关联线段”，则可知,B C ''都在O 上，且1,2AB AB AC AC ''====，然后由题意可根据图象来进行求解即可．【详解】解：（1）由题意得：通过观察图象可得：线段22B C 能绕点A 旋转90°得到O 的“关联线段”，1133,B C B C 都不能绕点A 进行旋转得到；故答案为22B C ；（2）由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C ''△是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C''与y轴的交点为D，连接OB'，易得B C y''⊥轴，⊙12B D DC''==，⊙2232OD OB B D''=-=，2232AD AB B D''=-=，⊙3OA=，⊙3t=；当点A在y轴的正半轴上时，如图所示：同理可得此时的3OA=，⊙t3=-；（3）由BC是O的以点A为中心的“关联线段”，则可知,B C''都在O上，且1,2AB AB AC AC''====，则有当以B'为圆心，1为半径作圆，然后以点A为圆心，2为半径作圆，即可得到点A的运动轨迹，如图所示：由运动轨迹可得当点A也在O上时为最小，最小值为1，此时AC'为O的直径，⊙90AB C''∠=︒，⊙30AC B''∠=︒，⊙cos303BC B C AC'''==⋅︒=；由以上情况可知当点,,A B O'三点共线时，OA的值为最大，最大值为2，如图所示：连接,OC B C'''，过点C'作C P OA'⊥于点P，⊙1,2OC AC OA''===，设OP x=，则有2AP x=-，⊙由勾股定理可得：22222C P AC AP OC OP'''=-=-，即()222221x x--=-，解得：14x=，⊙154C P'=，⊙34B P OB OP ''=-=，在Rt B PC ''中，2262B C B P C P ''''=+=， ⊙62BC =；综上所述：当min 1OA =时，此时3BC =；当max 2OA =时，此时62BC =．【点睛】本题主要考查旋转的综合、圆的基本性质、三角函数及等边三角形的性质，熟练掌握旋转的性质、圆的基本性质、三角函数及等边三角形的性质是解题的关键． 2．（1）平行，P 3；（2）32；（3）233922d ≤≤【解析】【分析】（1）根据圆的性质及“平移距离”的定义填空即可；（2）过点O 作OE⊙AB 于点E ，交弦CD 于点F ，分别求出OE 、OF 的长，由1d OE OF =-得到1d 的最小值；（3）线段AB 的位置变换，可以看作是以点A 32,2⎛⎫⎪⎝⎭为圆心，半径为1的圆，只需在⊙O内找到与之平行，且长度为1的弦即可．平移距离2d 的最大值即点A ，B 点的位置，由此得出2d 的取值范围．【详解】解：（1）平行；P 3；（2）如图，线段AB 在直线323y x =+上，平移之后与圆相交，得到的弦为CD ，CD⊙AB ，过点O 作OE⊙AB 于点E ，交弦CD 于点F ，OF⊙CD ，令0y =，直线与x 轴交点为（-2，0），直线与x 轴夹角为60°，⊙2sin 603OE ︒==．由垂径定理得：221322OF OC CD ⎛⎫=-= ⎪⎝⎭，⊙132d OE OF =-=；（3）线段AB的位置变换，可以看作是以点A32,2⎛⎫⎪⎝⎭为圆心，半径为1的圆，只需在⊙O 内找到与之平行，且长度为1的弦即可；点A到O的距离为2235222AO⎛⎫=+=⎪⎝⎭．如图，平移距离2d的最小值即点A到⊙O的最小值：53122-=；平移距离2d的最大值线段是下图AB的情况，即当A1,A2关于OA对称，且A1B2⊙A1A2且A1B2=1时.⊙B2A2A1=60°，则⊙OA2A1=30°,⊙OA2=1,⊙OM=12, A2M=32,⊙MA=3,AA2=22339 322⎛⎫+=⎪⎪⎝⎭,⊙2d的取值范围为：233922d≤≤．【点睛】本题考查圆的基本性质及与一次函数的综合运用，熟练掌握圆的基本性质、点与圆的位置关系、直线与圆的位置关系是解题的关键．3．（1）π；（2）⊙P的纵坐标1py≥或12Py≤；⊙02t<≤.【解析】【分析】（1）由三角函数值及等腰直角三角形性质可求得DE=2，最长中内弧即以DE为直径的半圆，DE的长即以DE为直径的圆周长的一半；（2）根据三角形中内弧定义可知，圆心一定在DE的中垂线上，，⊙当12t=时，要注意圆心P在DE上方的中垂线上均符合要求，在DE下方时必须AC与半径PE的夹角⊙AEP满足90°≤⊙AEP＜135°；⊙根据题意，t的最大值即圆心P在AC上时求得的t值．【详解】解：（1）如图2，以DE 为直径的半圆弧DE ，就是△ABC 的最长的中内弧DE ，连接DE ，⊙⊙A=90°，AB=AC=22，D ，E 分别是AB ，AC 的中点，22114,42sin sin 4522︒∴=====⨯=AC BC DE BC B ， ⊙弧DE 122ππ=⨯=；（2）如图3，由垂径定理可知，圆心一定在线段DE 的垂直平分线上，连接DE ，作DE 垂直平分线FP ，作EG⊙AC 交FP 于G ，⊙当12t =时，C （2，0），⊙D （0，1），E （1，1），1,12⎛⎫ ⎪⎝⎭F ，设1,2P m ⎛⎫ ⎪⎝⎭由三角形中内弧定义可知，圆心线段DE 上方射线FP 上均可，⊙m≥1， ⊙OA=OC ，⊙AOC=90°⊙⊙ACO=45°，⊙DE⊙OC⊙⊙AED=⊙ACO=45°作EG⊙AC 交直线FP 于G ，FG=EF=12根据三角形中内弧的定义可知，圆心在点G 的下方（含点G ）直线FP 上时也符合要求； 12∴m 综上所述，12m或m≥1． ⊙图4，设圆心P 在AC 上，⊙P 在DE 中垂线上，⊙P 为AE 中点，作PM⊙OC 于M ，则PM=323,2⎛⎫∴ ⎪⎝⎭P t ， ⊙DE⊙BC⊙⊙ADE=⊙AOB=90°，222221(2)41∴=+=+=+AE AD DE t t⊙PD=PE ，⊙⊙AED=⊙PDE⊙⊙AED+⊙DAE=⊙PDE+⊙ADP=90°，⊙⊙DAE=⊙ADP12∴===AP PD PE AE 由三角形中内弧定义知，PD≤PM1322∴AE ，AE≤3，即2413+t ，解得：2t02>∴<t t【点睛】此题是一道圆的综合题，考查了圆的性质，弧长计算，直角三角形性质等，给出了“三角形中内弧”新定义，要求学生能够正确理解新概念，并应用新概念解题．4．（1）2；（2）10k -≤<或01k <≤；（3）4t =-或0422t -≤≤或422t =+．【解析】【详解】分析：（1）画出图形，根据“闭距离”的概念结合图形进行求解即可.（2）分0k <和0k >两种情况，画出示意图，即可解决问题.（3）画出图形，直接写出t的取值范围．详解：（1）如下图所示：⊙B（2-，2-），C（6，2-）⊙D（0，2-）⊙d（O，ABC）2OD==（2）10k-≤<或01k<≤（3）4t=-或0422t≤≤-或422t=+．点睛：属于新定义问题，考查点到直线的距离，圆的切线的性质，认真分析材料，读懂“闭距离”的概念是解题的关键.5．（1）⊙P 2、P 3，⊙－322≤x≤－22或22 ≤x≤322；（2）－2≤x≤1或2≤x≤22 . 【解析】【详解】试题分析：（1）⊙由题意得，P 只需在以O 为圆心，半径为1和3两圆之间即可，由23,OP OP 的值可知23,P P 为⊙O 的关联点；⊙满足条件的P 只需在以O 为圆心，半径为1和3两圆之间即可，所以P 横坐标范围是－322 ≤x≤－22 或22 ≤x≤322；（2）.分四种情况讨论即可，当圆过点A ， CA=3时；当圆与小圆相切时；当圆过点 A ，AC=1时；当圆过点 B 时，即可得出.试题解析：（1）12315,01,22OP P OP ===，点1P 与⊙的最小距离为32，点2P 与⊙的最小距离为1，点3P 与⊙的最小距离为12， ⊙⊙的关联点为2P 和3P ．⊙根据定义分析，可得当直线y=-x 上的点P 到原点的距离在1到3之间时符合题意； ⊙ 设点P 的坐标为P (x ，-x) ，当OP=1时，由距离公式可得，OP=22(0)(0)1x x -+--= ，解得22x =± ，当OP=3时，由距离公式可得，OP=22(0)(0)3x x -+--= ，229x x +=，解得322x =±， ⊙ 点的横坐标的取值范围为－322 ≤x≤－22 或22 ≤x≤322（2）⊙y=-x+1与轴、轴的交点分别为A、B两点，⊙ 令y=0得，-x+1=0，解得x=1，令得x=0得，y=0，⊙A(1，0) ，B (0，1) ，分析得：如图1，当圆过点A时，此时CA=3，⊙ 点C坐标为，C ( -2，0)如图2，当圆与小圆相切时，切点为D，⊙CD=1 ，又⊙直线AB所在的函数解析式为y=-x+1，⊙ 直线AB与x轴形成的夹角是45°，⊙ RT⊙ACD中，CA=2，⊙ C点坐标为(1-2，0)⊙C点的横坐标的取值范围为；-2≤cx≤1-2，如图3，当圆过点A时，AC=1，C点坐标为(2，0)如图4，当圆过点B 时，连接BC ，此时BC =3，在Rt⊙OCB中，由勾股定理得OC=23122-=，C点坐标为(22，0)．⊙ C点的横坐标的取值范围为2≤cx≤22；⊙综上所述点C的横坐标的取值范围为－322≤cx≤－22或22≤cx≤322．【点睛】本题考查了新定义题，涉及到的知识点有切线，同心圆，一次函数等，能正确地理解新定义，正确地进行分类讨论是解题的关键.6．（1）⊙2；⊙1y x =- 或1y x =-+；（2）1≤m≤5 或者51m -≤≤-．【解析】【详解】试题分析：（1）⊙易得S=2；⊙得到C 的坐标可以为（3，2）或者（3，-2），设AC 的表达式为y=kx+b ，将A 、C 分别代入AC 的表达式即可得出结论；（2）若⊙O 上存在点N ，使MN 的相关矩形为正方形，则直线MN 的斜率k=±1，即过M 点作k=±1的直线，与⊙O 相切，求出M 的坐标，即可得出结论．试题解析：（1）⊙S=2×1=2；⊙C 的坐标可以为（3，2）或者（3，-2），设AC 的表达式为y=kx+b ，将A 、C分别代入AC 的表达式得到：0{23k b k b =+=+或0{23k b k b=+-=+，解得：1{1k b ==-或1{1k b =-=，则直线AC 的表达式为1y x =- 或1y x =-+；（2）若⊙O 上存在点N ，使MN 的相关矩形为正方形，则直线MN 的斜率k=±1，即过M 点作k=±1的直线，与⊙O 有交点，即存在N ，当k=－1时，极限位置是直线与⊙O 相切，如图1l 与2l ，直线1l 与⊙O 切于点N ，ON=2，⊙ONM=90°，⊙1l 与y 交于1P （0，-2）．1M （1m ，3），⊙13(2)0m --=-，⊙1m =-5，⊙1M （-5，3）；同理可得2M （-1，3）；当k=1时，极限位置是直线3l 与4l （与⊙O 相切），可得3M （1，3）， 4M （5，3）．因此m 的取值范围为1≤m≤5或者51m -≤≤-．考点：一次函数，函数图象，应用数学知识解决问题的能力．7．（1）①见解析；②0＜x ＜2；（2）圆心C 的横坐标的取值范围是2≤x≤8．【解析】【详解】试题分析：（1） ⊙根据反称点的定义画图得出结论；⊙⊙CP≤2r ＝2 CP 2≤4， P （x ，－x ＋2）， CP 2＝x 2＋（－x ＋2）2＝2x 2－4x ＋4≤，2x 2－4x≤0， x （x －2）≤0，⊙0≤x≤2，把x ＝2和x=0代入验证即可得出，P （2，0），P′（2，0）不符合题意P （0，2），P′（0，0）不符合题意，⊙0＜x ＜2（2）求出A ，B 的坐标，得出OA 与OB 的比值，从而求出⊙OAB=30°，设C （x ，0） ⊙当C 在OA 上时，作CH⊙AB 于H ，则CH≤CP≤2r ＝2，⊙AC≤4，得出 C 点横坐标x≥2．（当x ＝2时，C 点坐标（2，0），H 点的反称点H′（2，0）在圆的内部）；⊙当C 在A 点右侧时，C 到线段AB 的距离为AC 长，AC 最大值为2，⊙C 点横坐标x≤8，得出结论.试题解析：（1）解：⊙M （2，1）不存在，3,02N ⎛⎫ ⎪⎝⎭存在，反称点1,02N ⎛⎫' ⎪⎝⎭(1,3)T 存在，反称点T′（0，0）⊙⊙CP≤2r ＝2 CP 2≤4， P （x ，－x ＋2）， CP 2＝x 2＋（－x ＋2）2＝2x 2－4x ＋4≤4 2x 2－4x≤0， x （x －2）≤0，⊙0≤x≤2，当x ＝2时，P （2，0），P′（2，0）不符合题意当x ＝0时，P （0，2），P′（0，0）不符合题意，⊙0＜x ＜2 （2）解：由题意得：A （6，0），()0,23B ，⊙3OA OB=，⊙⊙OAB ＝30°，设C （x ，0）⊙当C 在OA 上时，作CH⊙AB 于H ，则CH≤CP≤2r ＝2，⊙AC≤4， C 点横坐标x≥2．（当x ＝2时，C 点坐标（2，0），H 点的反称点H′（2，0）在圆的内部）⊙当C 在A 点右侧时，C 到线段AB 的距离为AC 长，AC 最大值为2，⊙C 点横坐标x≤8 综上所述：圆心C 的横坐标的取值范围2≤x≤8．考点：定义新运算；一次函数的图象和性质；二次函数的图象和性质；圆的有关性质，解直角三角形；答案第15页，共15页。

中考数学专题复习--新定义型问题课件

中考数学专题复习 “新定义”型问题
知识概述
“新定义”型问题
定义新运算
“定义新运算”是指用一个符号和已知运算表达式表示一种新的运算．解决这类问题的关键是理解新运算规定的规则，明白其中的算理算法．运算时，要严格按照新定义的运算规则，转化为已学过的运算形式，然后按正确的运算顺序进行计算．
定义新概念
例 3．在平面直角坐标系中，将一点(横坐标与纵坐标不相等) 的横坐标与纵坐标互换后得到的点叫这一点的“互换点”，如(－3，5)与(5，－3)是一对“互换点”．（2）M，N 是一对“互换点”，若点 M 的坐标为(m，n)，求直线 MN 的表达式(用含 m，n 的代数式表示)；
定义新概念（2）M，N 是一对“互换点”，若点 M 的坐标为(m，n)，求直线 MN 的表达式(用含 m，n 的代数式表示)；【简析】（2）设直线 MN 的表达式为 y = kx + b( k≠ 0) ．把 M( m,n) ，N( n，m) 代入 y = kx + b，解得 k=-1，b=m + n，∴ 直线 MN 的表达式为 y=-x+m+n．
“定义新图形”试题呈现的一般结构为: 给出新图形定义→了解新图形结构→理解和运用新图形性质．而理解新图形性质特征是解题的关键.
定义新图形例 4．定义：数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”. 理解：（1）如图 1，已知 A、B 是⊙O 上两点，请在圆上找出满足条件的点 C，使△ABC 为“智慧三角形”（画出点 C 的位置，保留作图痕迹）；
（1）填空：①- =
；
②若x=-2，则 x 的取值范围是
．

2019年中考数学专题知识突破(二)新定义型问题

专题知识突破二新定义型问题一、中考专题诠释所谓“新定义”型问题，主要是指在问题中定义了中学数学中没有学过的一些概念、新运算、新符号，要求学生读懂题意并结合已有知识、能力进行理解，根据新定义进行运算、推理、迁移的一种题型.“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力二、解题策略和解法精讲“新定义型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法；二是根据问题情景的变化，通过认真思考，合理进行思想方法的迁移．三、中考典例剖析考点一：规律题型中的新定义例1 （2019•济南）现定义一种变换：对于一个由有限个数组成的序列S0，将其中的每个数换成该数在S0中出现的次数，可得到一个新序列S1，例如序列S0：（4，2，3，4，2），通过变换可生成新序列S1：（2，2，1，2，2），若S0可以为任意序列，则下面的序列可作为S1的是（）A．（1，2，1，2，2）B．（2，2，2，3，3）C．（1，1，2，2，3）D．（1，2，1，1，2）思路分析：根据题意可知，S1中2有2的倍数个，3有3的倍数个，据此即可作出选择．考点二：运算题型中的新定义例2 （2019•铜仁）定义一种新运算：a⊗b=b2-ab，如：1⊗2=22-1×2=2，则（-1⊗2）⊗3=_______.思路分析：先根据新定义计算出-1⊗2=6，然后计算再根据新定义计算6⊗3即可．考点三：探索题型中的新定义例3 （2019•钦州）定义：直线l1与l2相交于点O，对于平面内任意一点M，点M到直线l1、l2的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是（）A．2 B．3 C．4 D．5思路分析：“距离坐标”是（1，2）的点表示的含义是该点到直线l1、l2的距离分别为1、2．由于到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上，到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上，它们有4个交点，即为所求．考点四：开放题型中的新定义例4 （2019•北京）对某一个函数给出如下定义：若存在实数M＞0，对于任意考点五：阅读材料题型中的新定义例5 （2019•乐山）对于平面直角坐标系中任意两点P1（x1，y1）、P2（x2，y2），称|x1-x2|+|y1-y2|为P1、P2两点的直角距离，记作：d（P1，P2）．若P0（x0，y0）是一定点，Q（x，y）是直线y=kx+b上的一动点，称d（P0，Q）的最小值为P0到直线y=kx+b的直角距离．令P0（2，-3），O为坐标原点．则：（1）d（O，P0）=_________；（2）若P（a，-3）到直线y=x+1的直角距离为6，则a=__________．思路分析：（1）根据题中所给出的两点的直角距离公式即可得出结论；（2）先根据题意得出关于x的式子，再由绝对值的几何意义即可得出结论．四、中考真题演练一、选择题1．（2019•大庆）对坐标平面内不同两点A（x1，y1）、B（x2，y2），用|AB|表示A、B两点间的距离（即线段AB的长度），用‖AB‖表示A、B两点间的格距，定义A、B两点间的格距为‖AB‖=|x1-x2|+|y1-y2|，则|AB|与‖AB‖的大小关系为（）A．|AB|≥‖AB‖ B．|AB|＞‖AB‖ C．|AB|≤‖AB‖ D．|AB|＜‖AB‖2．（2019•龙岩）定义符号min{a，b}的含义为：当a≥b时min{a，b}=b；当a ＜b时min{a，b}=a．如：min{1，-3}=-3，min{-4，-2}=-4．则min{-x2+1，-x}的最大值是（）A ．12B ．12C ．1D ．0 3．（2019•泰州）如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）A ．1，2，3B ．1，1C ．1，1D ．1，24．（2019•常德）阅读理解：如图1，在平面内选一定点O ，引一条有方向的射线Ox ，再选定一个单位长度，那么平面上任一点M 的位置可由∠MOx 的度数θ与OM 的长度m 确定，有序数对（θ，m ）称为M 点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA 在射线Ox 上，则正六边形的顶点C 的极坐标应记为（）A ．（60°，4）B ．（45°，4）C ．（50°，５．（2019•绍兴）若圆锥的轴截图为等边三角形，则称此圆锥为正圆锥，则正圆锥的侧面展开图的圆心角是（）A ．90°B ．120°C ．150°D ．180°6．4．（2019•乌鲁木齐）对平面上任意一点（a ，b ），定义f ，g 两种变换：f （a ，b ）=（a ，-b ）．如f （1，2）=（1，-2）；g （a ，b ）=（b ，a ）．如g （1，2）=（2，1）．据此得g （f （5，-9））=（）A ．（5，-9）B ．（-9，-5）C ．（5，9）D ．（9，5）7．5．（2019•常德）连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何图形的直径，根据此定义，图（扇形、菱形、直角梯形、红十字图标）中“直径”最小的是（）A ．B ．C ．D ．二、填空题8．（2019•临沂）一般地，我们把研究对象统称为元素，把一些元素组成的总体称为集合．一个给定集合中的元素是互不相同的，也就是说，集合中的元素是不重复出现的．如一组数1，1，2，3，4就可以构成一个集合，记为A={1，2，3，4}．类比实数有加法运算，集合也可以“相加”．定义：集合A 与集合B 中的所有元素组成的集合称为集合A 与集合B 的和，记为A+B ．若A={-2，0，1，5，7}，B={-3，0，1，3，5}，则A+B=___________．910．（2019•北京）在平面直角坐标系xOy 中，对于点P （x ，y ），我们把点P （-y+1，x+1）叫做点P ′伴随点．已知点A 1的伴随点为A 2，点A 2的伴随点为A 3，点A 3的伴随点为A 4，…，这样依次得到点A 1，A 2，A 3，…，A n ，…．若点A 1的坐标为（3，1），则点A 3的坐标为______，点A 2019的坐标为_______；若点A 1的坐标为（a ，b ），对于任意的正整数n ，点A n 均在x 轴上方，则a ，b 应满足的条件为 __________．11．（2019•荆州）我们知道，无限循环小数都可以转化为分数．例如：将0.3∙12．（2019•塘沽区二模）如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸、…，已知标准纸的短边长为a ．（说明：①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸、…都是矩形；②本题中所求边长或面积都用含a 的代数式表示．）（Ⅰ）如图2，把上面对开得到的“16开”纸按如下步骤折叠：第一步：将矩形的短边AB 与长边AD 对齐折叠，点B 落在AD 上的点B ′处，铺平后得折痕AE ；第二步：将长边AD 与折痕AE 对齐折叠，点D 正好与点E 重合，铺平后得折痕AF ．则AD ：AB 的值是；（Ⅱ）求“2开”纸长与宽的比；（Ⅲ）如图3，由8个大小相等的小正方形构成“L ”型图案，它的四个顶点E ，F ，G ，H 分别在“16开”纸的边AB ，BC ，CD ，DA 上，则DG 的长 .13．（2019•连云港）如图1，折线段AOB 将面积为S 的⊙O 分成两个扇形，大扇形、小扇形的面积分别为S 1、S 2，若 121S S S S ==0.618，则称分成的小扇形为“黄金扇形”．生活中的折扇（如图2）大致是“黄金扇形”，则“黄金扇形”的圆心角约为 _______．（精确到0.1）14．（2019•上海）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为．三、解答题15．（2019•厦门）当m，n是正实数，且满足m+n=mn时，就称点P（m，mn）为“完美点”，已知点A（0，5）与点M都在直线y=-x+b上，点B，C是“完美点”，且点B在线段AM上，若，求△MBC的面积．16．（2019•白银）阅读理解：17．（2019•漳州）如图，△ABC中，AB=AC，∠A=36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC）（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是_____度和______度；（2）在图2中画2条线段，使图中有4个等腰三角形；（3）继续按以上操作发现：在△ABC中画n条线段，则图中有____个等腰三角形，其中有________个黄金等腰三角形．18．（2019•北京）对于平面直角坐标系xOy中的点P和⊙C，给出如下的定义：若⊙C上存在两个点A、B，使得∠APB=60°，则称P为⊙C的关联点．已知点D（12，12），E（0，-2），F（0）．（1）当⊙O的半径为1时，①在点D、E、F中，⊙O的关联点是．②过点F作直线l交y轴正半轴于点G，使∠GFO=30°，若直线l上的点P（m，n）是⊙O 的关联点，求m的取值范围；（2）若线段EF上的所有点都是某个圆的关联点，求这个圆的半径r的取值范围．（1）请说出筝形和菱形的相同点和不同点各两条；（2）请仿照图1的画法，在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案，具体要求如下：①顶点都在格点上；②所涉及的图案既是轴对称图形又是中心对称图形；③将新图案中的四个筝形都图上阴影（建议用一系列平行斜线表示阴影）．20．（2019•黔西南州）已知点P （x 0，y 0）和直线y=kx+b ，则点P 到直线y=kx+b 例如：求点P （-2，1）到直线y=x+1的距离．解：因为直线y=x+1可变形为x-y+1=0，其中k=1，b=1．根据以上材料，求：（1）点P（1，1）到直线y=3x-2的距离，并说明点P与直线的位置关系；（2）点P（2，-1）到直线y=2x-1的距离；（3）已知直线y=-x+1与y=-x+3平行，求这两条直线的距离．21．（2019•抚州）【试题背景】已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3，且d1=d3=1，d2=2．我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”．【探究1】（1）如图1，正方形ABCD为“格线四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F，求正方形ABCD的边长．【探究2】（2）矩形ABCD为“格线四边形”，其长：宽=2：1，则矩形ABCD的宽为．（直接写出结果即可）【探究3】如图2，菱形ABCD为“格线四边形”且∠ADC=60°，△AEF是等边三角形，AE⊥k于点E，∠AFD=90°，直线DF分别交直线l、k于点G、点M．求证：EC=DF．【拓展】（4）如图3，l∥k，等边△ABC的顶点A、B分别落在直线l、k上，AB⊥k于点B，且AB=4，∠ACD=90°，直线CD分别交直线l、k于点G、点M、点D、点E分别是线段GM、BM上的动点，且始终保持AD=AE，DH⊥l于点H．猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．22．（2019•顺义区一模）设p，q都是实数，且p＜q．我们规定：满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间，表示为[p，q]．对于一个函数，如果它的自变量x 与函数值y满足：当p≤x≤q时，有p≤y≤q，我们就称此函数是闭区间[p，q]上的“闭函数”．（1）反比例函数y=2014x是闭区间[1，2019]上的“闭函数”吗？请判断并说明理由；（2）若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此函数的解析式；（3）若实数c，d满足c＜d，且d＞2，当二次函数y=12x2-2x是闭区间[c，d]上的“闭函数”时，求c，d的值．23．（2019•佛山）我们把“按照某种理想化的要求（或实际可能应用的标准）来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”（我国著名数学家徐利治）．如图是一个典型的图形模式，用它可测底部可能达不到的建筑物的高度，用它可测河宽，用它可解决数学中的一些问题．等等．（1）如图，若B1B=30米，∠B1=22°，∠ABC=30°，求AC（精确到1）；（2）如图2，若∠ABC=30°，B 1B=AB ，计算tan15°的值（保留准确值）；24．（2019•安徽）若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．（1）请写出两个为“同簇二次函数”的函数；（2）已知关于x 的二次函数y 1=2x 2-4mx+2m 2+1和y 2=ax 2+bx+5，其中y 1的图象经过点A （1，1），若y 1+y 2与y 1为“同簇二次函数”，求函数y 2的表达式，并求出当0≤x ≤3时，y 2的最大值．25．（2019•绵阳）我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题．请你利用重心的概念完成如下问题：（1）若O 是△ABC 的重心（如图1），连结AO 并延长交BC 于D ，证明：23AO AD =；（2）若AD 是△ABC 的一条中线（如图2），O 是AD 上一点，且满足23AO AD =，试判断O 是△ABC 的重心吗？如果是，请证明；如果不是，请说明理由；（3）若O 是△ABC 的重心，过O 的一条直线分别与AB 、AC 相交于G 、H （均不与△ABC 的顶点重合）（如图3），S 四边形BCHG ，S △AGH 分别表示四边形BCHG 和△AGH 的面积，试探究 BCHG AGHS S V 四边形的最大值．专题二新定义型问题参考答案三、中考典例剖析考点一：规律题型中的新定义例1解：A 、∵2有3个，∴不可以作为S 1，故选项错误；B 、∵2有3个，∴不可以作为S 1，故选项错误；C 、3只有1个，∴不可以作为S 1，故选项错误D 、符合定义的一种变换，故选项正确．故选：D ．考点二：运算题型中的新定义例2解：-1⊗2=22-（-1）×2=6，6⊗3=32-6×3=-9．所以（-1⊗2）⊗3=-9．故答案为-9．考点三：探索题型中的新定义例3解：如图，∵到直线l 1的距离是1的点在与直线l 1平行且与l 1的距离是1的两条平行线a 1、a 2上，到直线l 2的距离是2的点在与直线l 2平行且与l 2的距离是2的两条平行线b 1、b 2上， ∴“距离坐标”是（1，2）的点是M 1、M 2、M 3、M 4，一共4个．故选C ．当x=b 时，y=-b+1．则2b 12b a a 1-≤-+≤⎧⎪⎨⎪-⎩＞＝，∴-1＜b ≤3；（3）若m ＞1，函数向下平移m 个单位后，x=0时，函数值小于-1，此时函数的边界t ≥1，与题意不符，故m ≤1．当x=-1时，y=1 即过点（-1，1）四、中考真题演练一、选择题1．C2．A3．D4．A5．D6．D7．C二、填空题8. {-3，-2，0，1，3，5，7}9．２10．（-3，1），（0，4）；-1＜a＜1且0＜b＜211．45 9912：113．137.5 14．30°三、解答题15．解：∵m+n=mn且m，n是正实数，∴mn+1=m，即mn=m-1，∴P（m，m-1），即“完美点”P在直线y=x-1上，∵点A（0，5）在直线y=-x+b上，∴b=5，∴直线AM：y=-x+5，∵“完美点”B在直线AM上，∴由y x1 y x5＝＝-⎧⎨-+⎩解得x3y2＝＝⎧⎨⎩，∴B（3，2），∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=-x，而直线y=x-1与直线y=x 平行，直线y=-x+5与直线y=-x平行，∴直线AM与直线y=x-1垂直，∵点B是直线y=x-1与直线AM的交点，∴垂足是点B，∵点C是“完美点”，∴点C在直线y=x-1上，∴△MBC是直角三角形，∵B（3，2），A（0，5），∴，∵，∴，又∵∴BC=1，∴S △MBC =12 16．解：由题意得2x-（3-x ）＞0，去括号得：2x-3+x ＞0，移项合并同类项得：3x ＞3，把x 的系数化为1得：x ＞1．17．解：（1）如图1所示：∵AB=AC ，∠A=36°，∴当AE=BE ，则∠A=∠ABE=36°，则∠AEB=108°，则∠EBC=36°，∴这2个等腰三角形的顶角度数分别是108度和36度；故答案为：108，36；（2）如图2所示：（3）如图3所示：当1条直线可得到2个等腰三角形；当2条直线可得到4个等腰三角形；当3条直线可得到6个等腰三角形；…∴在△ABC 中画n 条线段，则图中有2n 个等腰三角形，其中有n 个黄金等腰三角形．故答案为：2n ，n ．18．解：（1）①如图1所示，过点E 作⊙O 的切线设切点为R ，∵⊙O 的半径为1，∴RO=1，∵EO=2，∴∠OER=30°，根据切线长定理得出⊙O 的左侧还有一个切点，使得组成的角等于30°，∴E 点是⊙O 的关联点，∵D （12，12），E （0，-2），F （0）， ∴OF ＞EO ，DO ＜EO ，∴D 点一定是⊙O 的关联点，而在⊙O 上不可能找到两点使得组成的角度等于60°，故在点D 、E 、F 中，⊙O 的关联点是D ，E ；故答案为：D ，E ；②由题意可知，若P 要刚好是⊙C 的关联点，需要点P 到⊙C 的两条切线PA 和PB 之间所夹的角为60°，由图2可知∠APB=60°，则∠CPB=30°，连接BC ，则PC=sin BC CPB∠=2BC=2r ， ∴若P 点为⊙C 的关联点，则需点P 到圆心的距离d 满足0≤d≤2r ；由上述证明可知，考虑临界点位置的P 点，如图3，点P 到原点的距离OP=2×1=2，过点O 作l 轴的垂线OH ，垂足为H ，tan ∠OGF=FO OG = ∴∠OGF=60°，∴OH=OGsin60°sin ∠OPH=OH OP = ∴∠OPH=60°，可得点P 1与点G 重合，过点P 2作P 2M ⊥x 轴于点M ，可得∠P 2OM=30°，∴OM=OP 2cos30°从而若点P 为⊙O 的关联点，则P 点必在线段P 1P 2上，∴（2）若线段EF上的所有点都是某个圆的关联点，欲使这个圆的半径最小，则这个圆的圆心应在线段EF的中点；考虑临界情况，如图4，即恰好E、F点为⊙K的关联时，则KF=2KN=12EF=2，此时，r=1，故若线段EF上的所有点都是某个圆的关联点，这个圆的半径r的取值范围为r≥1．19．解：（1）相同点：①两组邻边分别相等；②有一组对角相等；③一条对角线垂直平分另一条对角线；④一条对角线平分一组对角；⑤都是轴对称图形；⑥面积等于对角线乘积的一半；不同点：①菱形的对角线互相平分，筝形的对角线不互相平分；②菱形的四边都相等，筝形只有两组邻边分别相等；③菱形的两组对边分别平行，筝形的对边不平行；④菱形的两组对角分别相等，筝形只有一组对角相等；⑤菱形的邻角互补，筝形的邻角不互补；⑥菱形的既是轴对称图形又是中心对称图形，筝形是轴对称图形不是中心对称图形；（2）如图所示：．（3）在直线y=-x+1任意取一点P，当x=0时，y=1．∴P（0，1）．∵直线y=-x+3，∴k=-1，b=3，21．解：（1）∵l∥k，BE⊥l，∴∠BFC=∠BEA=90°，∴∠ABE+∠BAE=90°，∵四边形ABCD是正方形，∴∠ABC=90°，AB=BC．∴∠ABE+∠CBF=90°，∴∠BAE=∠CBF，∴△ABE≌△BCF，∴AE=BF，∵d1=d3=1，d2=2，∴BE=3，AE=1，在直角△ABE中，AB=＝，；（2）过B作BE⊥l于点E，交k于点F．则BE=1，BF=3，∵四边形ABCD是矩形，∴∠ABC=90°，∴∠ABE+∠FBC=90°，又∵直角△ABE中，∠ABE+∠EAB=90°，∴∠FBC=∠EAB，∴△AEB∽△BFC，当AB是较短的边时，如图（a），AB=12BC，则AE=12BF=32，在直角△ABE中，=当AB是长边时，如图（b），同理可得：；故答案为：（3）证明：如解答图1，连接AC，∵四边形ABCD是菱形，且∠ADC=60°，∴AC=AD，∵△AEF是等边三角形，∴AE=AF，∵AE⊥k，∠AFD=90°，∴∠AEC=∠AFD=90°，∴直角△AEC≌直角△AFD，∴EC=DF；（4）当2＜DH＜4时，BC∥DE．理由如下：如图2，当2＜DH＜4时，点D在线段CM上，连接AM．∵∠ABM=∠ACM=90°，AB=AC，AM=AM，∴Rt△ABM≌Rt△ACM，∴∠BAM=∠CAM，∴AM⊥BC，又∵AD=AE，AB=AC，∴Rt△ABE≌Rt△ACD，∴∠BAE=∠CAD，∴∠EAM=∠DAM，∴AM⊥ED．∴BC∥DE．22．解：（1）反比例函数y=2014x是闭区间[1，2019]上的“闭函数”，理由如下：反比例函数y=2014x在第一象限，y随x的增大而减小，当x=1时，y=2019；当x=2019时，y=1，所以，当1≤x≤2019时，有1≤y≤2019，符合闭函数的定义，故反比例函数y=2014x是闭区间[1，2019]上的“闭函数”；（2）分两种情况：k＞0或k＜0．①当k＞0时，一次函数y=kx+b（k≠0）的图象是y随x的增大而增大，故根据“闭函数”的定义知，km b m? kn b n＝＝+⎧⎨+⎩，解得k1b0＝＝⎧⎨⎩．∴此函数的解析式是y=x；②当k＜0时，一次函数y=kx+b（k≠0）的图象是y随x的增大而减小，故根据“闭函数”的定义知，km b n? k n b m＝＝+⎧⎨+⎩，解得k1b m n ＝＝-⎧⎨+⎩．∴此函数的解析式是y=-x+m+n；（3）∵y=12x2-2x=12(x2-4x+4)-2=12(x-2)2-2，∴该二次函数的图象开口方向向上，最小值是-2，且当x＜2时，y随x的增大而减小；当x ＞2时，y随x的增大而增大．①当c＜2＜d时，此时二次函数y=12x2-2x的最小值是-2=c，根据“闭函数”的定义知，d=12c2-2c或d=12d2-2d；Ⅰ）当d=12c2-2c时，由于d=12×（-2）2-2×（-2）=6＞2，符合题意；Ⅱ）当d=12d 2-2d 时，解得d=0或6，由于d ＞2，所以d=6；②当c≥2时，此二次函数y 随x 的增大而增大，则根据“闭函数”的定义知，22122122c c cd d d ⎧-=⎪⎪⎨⎪-=⎪⎩，解得，66c d =⎧⎨=⎩， ∵c ＜d ，∴66c d =⎧⎨=⎩不合题意，舍去．综上所述，c ，d 的值分别为-2，6．24.解：（1）设顶点为（h，k）的二次函数的关系式为y=a（x-h）2+k，当a=2，h=3，k=4时，二次函数的关系式为y=2（x-3）2+4．∵2＞0，∴该二次函数图象的开口向上．当a=3，h=3，k=4时，二次函数的关系式为y=3（x-3）2+4．∵3＞0，∴该二次函数图象的开口向上．∵两个函数y=2（x-3）2+4与y=3（x-3）2+4顶点相同，开口都向上，∴两个函数y=2（x-3）2+4与y=3（x-3）2+4是“同簇二次函数”．∴符合要求的两个“同簇二次函数”可以为：y=2（x-3）2+4与y=3（x-3）2+4．（2）∵y1的图象经过点A（1，1），∴2×12-4×m×1+2m2+1=1．整理得：m2-2m+1=0．解得：m1=m2=1．∴y1=2x2-4x+3=2（x-1）2+1．∴y1+y2=2x2-4x+3+ax2+bx+5=（a+2）x2+（b-4）x+8∵y1+y2与y1为“同簇二次函数”，∴y1+y2=（a+2）（x-1）2+1=（a+2）x2-2（a+2）x+（a+2）+1．其中a+2＞0，即a＞-2．∴b42(a2) 8(a2)1--+⎧⎨++⎩＝＝．解得：a5b10⎧⎨-⎩＝＝．∴函数y2的表达式为：y2=5x2-10x+5．∴y2=5x2-10x+5=5（x-1）2．∴函数y2的图象的对称轴为x=1．∵5＞0，∴函数y2的图象开口向上．①当0≤x≤1时，∵函数y2的图象开口向上，∴y2随x的增大而减小．∴当x=0时，y2取最大值，最大值为5（0-1）2=5．②当1＜x≤3时，∵函数y2的图象开口向上，∴y2随x的增大而增大．∴当x=3时，y2取最大值，最大值为5（3-1）2=20．综上所述：当0≤x≤3时，y2的最大值为20．25．解：（1）证明：如答图1所示，连接CO并延长，交AB于点E．∵点O是△ABC的重心，∴CE是中线，点E是AB的中点．∴DE是中位线，∴DE∥AC，且DE=12 AC．∵DE∥AC，∴△AOC∽△DOE，∴AO ACOD DE=2，∵AD=AO+OD，∴AOAD=23．（2）答：点O是△ABC的重心．证明：如答图2，作△ABC的中线CE，与AD交于点Q，则点Q为△ABC的重心．由（1）可知，AOAD=23，而AOAD=23，∴点Q与点O重合（是同一个点），∴点O是△ABC的重心．（3）如答图3所示，连接DG．设S△GOD=S，由（1）知AOAD=23，即OA=2OD，∴S△AOG=2S，S△AGD=S△GOD+S△AGO=3S．为简便起见，不妨设AG=1，BG=x，则S△BGD=3xS．∴S△ABD=S△AGD+S△BGD=3S+3xS=（3x+3）S，∴S△ABC=2S△ABD=（6x+6）S．设OH=k•OG，由S△AGO=2S，得S△AOH=2kS，∴S△AGH=S△AGO+S△AOH=（2k+2）S．∴S 四边形BCHG =S △ABC -S △AGH =（6x+6）S-（2k+2）S=（6x-2k+4）S ． ∴BCHG AGHS S V 四边形=(6-24)(22)x k S k S ++=3-21x k k ++ ① 如答图3，过点O 作OF ∥BC 交AC 于点F ，过点G 作GE ∥BC 交AC 于点E ，则OF ∥GE ． ∵OF ∥BC ， ∴23OF AO CD AD ==， ∴OF=23CD=13BC ； ∵GE ∥BC ， ∴11GE AG BC AB x ==+， ∴GE=1BC x +； ∴131BC OF BC GEx =+=13x +， ∴13(1)OF x GE OF x +=--+=12x x+-． ∵OF ∥GE ， ∴OH OF GH GE=， ∴1-2-OH OF x OG GE OF x+==， ∴k=12-x x+，代入①式得： BCHG AGH S S V 四边形=13-23-22-1112-x x x k x x k x +++=+++=-x 2+x+1=-（x-12）2+54， ∴当x=12时，BCHG AGHS S V 四边形有最大值，最大值为54．。

2019新定义题型中考专题复习课

►
类型之四
定义一种新函数
►
类型之四
定义一种新函数
课堂小结：
解题策略和解法总结：“新定义型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法；二是根据问题情景的变化，通过认真思考合理进行思想方法的迁移．
（三）定义一种新图形
（2013•台州）如果三角形有一边上的中线长恰好等于
这边的长，那么称这个三角形为“好玩三角形”．
如图在Rt△ABC中，∠C=90°，tanA=
求证：△ABC是“好玩三角形”；
3 2
C
B
A
专题突破二
弄清新概念图形的定义，把新概念图形分解转化，化为熟悉的图形或条件，运用熟悉的知识加以解决.
►
类型之四
定义一种新函数
请参考小明的方法解决下面的问题： (1)写出函数 y＝－x2＋3x2)若函数 y＝－x ＋3mx－2 与 y＝x2－2nx＋n 互为“旋转函数”，求(m＋ n)2015 的值；
1 (3)已知函数 y＝－2(x＋1)(x－4)的图象与 x 轴交于 A，B 两点，与 y 轴交于 1 C1 的二次函数与函数 y＝－ (x＋1)(x－4)互为“旋转函数”． 2
[解析] (1001)2＝1×23＋0×22＋0×21＋1×20＝9.
解答此类问题时，要弄清楚新数的定义，在新定义下进行运算.
·新课标
（一）定义一种新数
任给a、b 两数，按规则c = a + b + ab 扩充一个新数c，称这样的新数c 为“吉祥数”．又在a、 b、c 三个数中任取两数，按规则又可扩充一个“吉祥数”，…，每扩充一个“吉祥数”称为一次操作．现有数1和4，按上述规则操作三次得到的最大 “吉祥数”是多少？．

中考数学复习《新定义问题》

【解析】根据题意可知，S1中2有2的倍数个，3有3的倍数个，据此即可作出
选择．A.∵2有3个，∴不可以作为S1，故选项错误；B.∵2有3个，∴不可以
作为S1，故选项错误；C.3只有1个，∴不可以作为S1，故选项错误；D.符合定义的一种变换，故选项正确．故选D.
13．对于钝角α，定义它的三角函数值如下： sinα＝sin(180°－α)，cosα＝－cos(180°－α)．
11．任意一个正整数 n 都可以分解：n＝p×q(p，q 是正整数，且 p≤q)，在 n 的所有这种分解中，如果|p－q|最小，则称 p×q 是 n 的最佳分解． p 并规定：F(n)＝q.
(1)求F(12)；
(2)如果一个两位正整数t，t＝10x＋y(1≤x≤y≤9，x，y为自然数)，交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
15．定义：点 P 是△ABC 内部或边上的点(顶点除外)，在△PAB，△PBC， △PCA 中，若至少有一个三角形与△ABC 相似，则称点 P 是△ABC 的自相似 3 3 点．在平面直角坐标系中，点 M 是曲线 y＝ x (x＞0)上的任意一点，点 N 在 x 轴正半轴上． (1)如图 1，MN⊥x 轴，点 N( 3，0)，若 OM 上点 P 是△MON 的自相似点，求点 P 的坐标； (2)如图 2，当点 M(3， 3)，点 N(2，0)时，求△MON 的自相似点的坐标．
3．定义[a，b，c]为函数 y＝ax2＋bx＋c 的特征数，下面给出特征数为[2m，1－m ，－1－m]的函数的一些结论： 1 8 ①当 m＝－3 时，函数图象的顶点坐标是(3，3)； 3 ②当 m>0 时，函数图象截 x 轴所得的线段长度大于2； 1 ③当 m<0 时，函数在 x>4时，y 随 x 的增大而减小； ④当 m≠0 时，函数图象经过同一个点．其中正确的结论有( B ) A．①②③④ B．①②④ C．①③④ D．②④

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020年中考数学专题复习新定义问题【专题点拨】新定义运算、新概念问题一般是介绍新定义、新概念，然后利用新定义、新概念解题，其解题步骤一般都可分为以下几步：1.阅读定义或概念，并理解；2.总结信息，建立数模；3.解决数模，回顾检查．“新概念”试题，其设计新颖，构思独特，思维容量大，既能考查学生的阅读、分析、推理、概括等能力，又能考查学生知识迁移的能力和数学素养，同时还兼具了区分选拔的功能 .【解题策略】具体分析新颖问题→弄清问题题意→向已知知识点转化→利用相关联知识查验→转化问题思路解决【典例解析】类型一：规律题型中的新定义例题1：（2015•永州，第10题3分）定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x，下列式子中错误的是（）A．[x]=x（x为整数） B．0≤x﹣[x]＜1C．[x+y]≤[x]+[y]D．[n+x]=n+[x]（n为整数）【解析】：根据“定义[x]为不超过x的最大整数”进行计算【解答】：解：A、∵[x]为不超过x的最大整数，∴当x是整数时，[x]=x，成立；B、∵[x]为不超过x的最大整数，∴0≤x﹣[x]＜1，成立；C、例如，[﹣5.4﹣3.2]=[﹣8.6]=﹣9，[﹣5.4]+[﹣3.2]=﹣6+（﹣4）=﹣10，∵﹣9＞﹣10，∴[﹣5.4﹣3.2]＞[﹣5.4]+[﹣3.2]，∴[x+y]≤[x]+[y]不成立，D、[n+x]=n+[x]（n为整数），成立；故选：C．【点评】本题考查了一元一次不等式组的应用，解决本题的关键是理解新定义．新定义解题是近几年中考常考的题型．变式训练1：（2015•山东潍坊，第12题3分）如图，已知正方形ABCD，顶点A(1，3)、B(1,1)、C(3,1)．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为( )A．(—2012,2) B．（一2012，一2）C. (—2013,—2)D. (—2013,2)类型二：运算题型中的新定义例题2：（2016·四川宜宾）规定：log a b（a＞0，a≠1，b＞0）表示a，b之间的一种运算．现有如下的运算法则：log n a n=n．log N M=（a＞0，a≠1，N＞0，N≠1，M＞0）．例如：log223=3，log25=，则log1001000= ．【解析】实数的运算．先根据log N M=（a＞0，a≠1，N＞0，N≠1，M＞0）将所求式子化成以10为底的对数形式，再利用公式进行计算．【解答】解：log1001000===．故答案为：．变式训练2：(2016四川省乐山市第16题)在直角坐标系xOy 中，对于点P （x ，y ）和Q （x ，y′），给出如下定义：若(0)(0)y x y y x ≥⎧'=⎨-<⎩，则称点Q 为点P 的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．（1）若点（﹣1，﹣2）是一次函数3y x =+图象上点M 的“可控变点”，则点M 的坐标为；（2）若点P 在函数216y x =-+（5x a -≤≤）的图象上，其“可控变点”Q 的纵坐标y′的取值范围是1616y '-≤≤，则实数a 的取值范围是．类型三：探索题型中的新定义例题3：(2016山西省第10题)宽与长的比是21-5（约为0．618）的矩形叫做黄金矩形．黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD ，分别取AD ，BC 的中点E ，F ，连接EF ；以点F 为圆心，以FD 为半径画弧，交BC 的延长线与点G ；作AD GH ⊥，交AD 的延长线于点H ．则图中下列矩形是黄金矩形的是（）A ．矩形ABFEB ．矩形EFCDC ．矩形EFGHD ．矩形DCGH【解析】考点：黄金分割的识别【解答】：由作图方法可知DF=5CF ，所以CG=CF )15(-，且GH=CD=2CF ，从而得出黄金矩形CG=CF )15(-，GH=2CF ∴2152)15(-=-=CF CF GH CG ∴矩形DCGH 是黄金矩形。

变式训练3：（2014•山东济南，第14题，3分）现定义一种变换：对于一个由有限个数组成的序列S 0，将其中的每个数换成该数在S 0中出现的次数，可得到一个新序列S 1，例如序列S 0：（4，2，3，4，2），通过变换可生成新序列S 1：（2，2，1，2，2），若S 0可以为任意序列，则下面的序列可作为S 1的是（）A ．（1，2，1，2，2）B ．（2，2，2，3，3）C ．（1，1，2，2，3）D ．（1，2，1，1，2）类型四：开放题型中的新定义例题4：(2016山西省第19题)（本题7分）请阅读下列材料，并完成相应的任务：阿基米德折弦定理阿基米德（Archimedes ，公元前287~公元212年，古希腊）是有史以来最伟大的数学家之一．他与牛顿、高斯并称为三大数子．阿拉伯Al-Biruni （973年~1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Biruni 译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理．阿基米德折弦定理：如图1，AB 和BC 是O 的两条弦（即折线ABC 是圆的一条折弦），BC>AB ，M 是ABC 的中点，则从M 向BC 所作垂线的垂足D 是折弦ABC 的中点，即CD=AB+BD ．下面是运用“截长法”证明CD=AB+BD 的部分证明过程．证明：如图2，在CB 上截取CG=AB ，连接MA ，MB ，MC 和MG ．∵M 是ABC 的中点， ∴MA=MC ．．．任务：（1）请按照上面的证明思路，写出该证明的剩余部分；（2）填空：如图（3），已知等边△ABC内接于O，AB=2，D为O上一点，︒ABD，∠45=AE⊥BD与点E，则△BDC的长是．【答案】(1)、证明过程见解析；(2)、2+22【解析】考查了圆的证明。

（1）已截取CG=AB ∴只需证明BD=DG且MD⊥BC，所以需证明MB=MG故证明△MBA≌△MGC即可（2）AB=2，利用三角函数可得BE= 2由阿基米德折弦定理可得BE=DE+DC则△BDC周长=BC+CD+BD=BC+DC+DE+BE=BC+（DC+DE）+BE=BC+BE+BE=BC+2BE然后代入计算可得答案∠=∠，【解答】：(1)证明：又∵A C∴△MBA≌△MGC．∴MB=MG．又∵MD⊥BC，∵BD=GD．∴CD=CG+GD=AB+BD．+．(2)、222变式训练4：（2015•浙江嘉兴，第24题14分）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.（1）概念理解如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.（2）问题探究①小红猜想：对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗？请说明理由。

②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC 沿∠ABC的平分线BB＇方向平移得到△A＇B＇C＇，连结AA＇，BC＇.小红要是平移后的四边形ABC＇A＇是“等邻边四边形”，应平移多少距离（即线段BB＇的长）？（3）应用拓展如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD==90°，AC，BD为对角线，AC=AB.试探究BC，CD，BD的数量关系.类型五：阅读材料题型中的新定义例题5：（2016·浙江省湖州市·3分）定义：若点P（a，b）在函数y=的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”．例如：点（2，）在函数y=的图象上，则函数y=2x2+称为函数y=的一个“派生函数”．现给出以下两个命题：（1）存在函数y=的一个“派生函数”，其图象的对称轴在y轴的右侧（2）函数y=的所有“派生函数”，的图象都进过同一点，下列判断正确的是（）A．命题（1）与命题（2）都是真命题B．命题（1）与命题（2）都是假命题C．命题（1）是假命题，命题（2）是真命题D．命题（1）是真命题，命题（2）是假命题【解析】命题与定理．（1）根据二次函数y=ax2+bx的性质a、b同号对称轴在y轴左侧，a、b异号对称轴在y轴右侧即可判断．（2）根据“派生函数”y=ax2+bx，x=0时，y=0，经过原点，不能得出结论．【解答】解：（1）∵P（a，b）在y=上，∴a和b同号，所以对称轴在y轴左侧，∴存在函数y=的一个“派生函数”，其图象的对称轴在y轴的右侧是假命题．（2）∵函数y=的所有“派生函数”为y=ax2+bx，∴x=0时，y=0，∴所有“派生函数”为y=ax2+bx经过原点，∴函数y=的所有“派生函数”，的图象都进过同一点，是真命题．故选C．变式训练5：（2016·重庆市A卷·10分）我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=．例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所有3×4是12的最佳分解，所以F（12）=．（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数．求证：对任意一个完全平方数m，总有F（m）=1；（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值．【能力检测】1.（2015•甘肃天水，第10题，4分）定义运算：a⊗b=a（1﹣b）．下面给出了关于这种运算的几种结论：①2⊗（﹣2）=6，②a⊗b=b⊗a，③若a+b=0，则（a⊗a）+（b⊗b）=2ab，④若a⊗b=0，则a=0或b=1，其中结论正确的序号是（）A．①④ B．①③ C．②③④ D．①②④2.（2013浙江台州，16，5分）任何实数a，可用[]a表示不超过a的最大整数，如[]4=4，[]3=1，现对72进行如下操作：72 第1次[]72=8第2次[]8=2第3次[]2=1，这样对72只需进行3次操作后变为1，类似地，①对81只需进行次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是．3.（2016·重庆市B卷·10分）我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=．例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所有3×4是12的最佳分解，所以F（12）=．（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数．求证：对任意一个完全平方数m，总有F（m）=1；（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值．4.（2015•江苏盐城，第27题12分）知识迁移我们知道，函数y=a（x﹣m）2+n（a≠0，m＞0，n＞0）的图象是由二次函数y=ax2的图象向右平移m个单位，再向上平移n个单位得到；类似地，函数y=+n（k≠0，m＞0，n ＞0）的图象是由反比例函数y=的图象向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）．理解应用函数y=+1的图象可由函数y=的图象向右平移个单位，再向上平移个单位得到，其对称中心坐标为．灵活应用如图，在平面直角坐标系xOy中，请根据所给的y=的图象画出函数y=﹣2的图象，并根据该图象指出，当x在什么范围内变化时，y≥﹣1？实际应用某老师对一位学生的学习情况进行跟踪研究，假设刚学完新知识时的记忆存留量为1，新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为y1=；若在x=t（t≥4）时进行第一次复习，发现他复习后的记忆存留量是复习前的2倍（复习的时间忽略不计），且复习后的记忆存留量随x变化的函数关系为y2=，如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？5.（2014•吉林，第26题10分）如图①，直线l：y=mx+n（m＞0，n＜0）与x，y轴分别相交于A，B两点，将△AOB绕点O逆时针旋转90°，得到△COD，过点A，B，D的抛物线P叫做l的关联抛物线，而l叫做P的关联直线．（1）若l：y=﹣2x+2，则P表示的函数解析式为；若P：y=﹣x2﹣3x+4，则l表示的函数解析式为．（2）求P的对称轴（用含m，n的代数式表示）；（3）如图②，若l：y=﹣2x+4，P的对称轴与CD相交于点E，点F在l上，点Q在P的对称轴上．当以点C，E，Q，F为顶点的四边形是以CE为一边的平行四边形时，求点Q的坐标；（4）如图③，若l：y=mx﹣4m，G为AB中点，H为CD中点，连接GH，M为GH中点，连接OM．若OM=，直接写出l，P表示的函数解析式．【参考答案】变式训练1：（2015•山东潍坊，第12题3分）如图，已知正方形ABCD，顶点A(1，3)、B(1,1)、C(3,1)．规定“把正方形ABCD 先沿x 轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD 的对角线交点M 的坐标变为( )A ．(—2012,2)B ．（一2012，一2） C. (—2013,—2) D. (—2013,2)【解答】：∵正方形ABCD ，点A(1，3)、B(1,1)、C(3,1)．∴M 的坐标变为(2,2) ∴根据题意得：第1次变换后的点M 的对应点的坐标为（2－1，－2），即（1，－2），第2次变换后的点M 的对应点的坐标为：（2－2，2），即（0，2），第3次变换后的点M 的对应点的坐标为（2－3，－2），即（－1，－2），第2014次变换后的点M 的对应点的为坐标为（2－2014， 2），即（－2012， 2）故答案为A ．变式训练2：(2016四川省乐山市第16题)在直角坐标系xOy 中，对于点P （x ，y ）和Q （x ，y′），给出如下定义：若(0)(0)y x y y x ≥⎧'=⎨-<⎩，则称点Q 为点P 的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．（1）若点（﹣1，﹣2）是一次函数3y x =+图象上点M 的“可控变点”，则点M 的坐标为；（2）若点P 在函数216y x =-+（5x a -≤≤）的图象上，其“可控变点”Q 的纵坐标y′的取值范围是1616y '-≤≤，则实数a 的取值范围是．【答案】（1）（﹣1，2）；（2） 0≤a≤2．【解析】考查的考点：1．二次函数图象上点的坐标特征；2．一次函数图象上点的坐标特征；3．新定义．【解答】（1）根据“可控变点”的定义可知点M 的坐标为（﹣1，2）；（2）依题意，216y x =-+图象上的点P 的“可控变点”必在函数2216 (0)16 (50)x x y x x ⎧-+≥⎪=⎨--≤<⎪⎩的图象上，如图所示，∵1616y '-≤≤，当y′=16时，21616x =-+或21616x =-，∴x=0或x=42，当y′=﹣16时， 21616x -=-+或21616x -=-，∴x=42或x=0，∴a 的取值范围是0≤a≤42．故答案为：（1）（﹣1，2）；（2）0≤a≤42．变式训练3：（2014•山东济南，第14题，3分）现定义一种变换：对于一个由有限个数组成的序列S 0，将其中的每个数换成该数在S 0中出现的次数，可得到一个新序列S 1，例如序列S 0：（4，2，3，4，2），通过变换可生成新序列S 1：（2，2，1，2，2），若S 0可以为任意序列，则下面的序列可作为S 1的是（）A ．（1，2，1，2，2）B ．（2，2，2，3，3）C ．（1，1，2，2，3）D ．（1，2，1，1，2）【解答】：A 、∵2有3个，∴不可以作为S 1，故选项错误；B、∵2有3个，∴不可以作为S1，故选项错误；C、3只有1个，∴不可以作为S1，故选项错误D、符合定义的一种变换，故选项正确．故选：D．变式训练4：（2015•浙江嘉兴，第24题14分）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.（1）概念理解如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.（2）问题探究①小红猜想：对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗？请说明理由。