最新高中数学知识点汇总(表格格式)
最新高中数学知识点汇总(表格格式)
高中数学知识汇总先要进行分母实数化（分母乘以自己的共轭复数），在进行四则运算时，可以把i 看作成一个独立的字母，按照实数的四则运算律直接进行运算，并随时把i 2换成-1圆的方程圆心半径x 2+ y 2= r 2（0，0）r 标准方程(x – a ) 2 + ( y – b ) 2 =r 2（a ，b ）r一般方程x 2 + y 2 +D x + E y + F = 0⎪⎭⎫ ⎝⎛--22E ,D F E D 42122-+注：表中均为正整数两个平面与平面平行时，一个平面内任一点到另一个平面的距离。
离面面距【注：标准根据上下文理解为圆心到直线的距离与两圆的圆心距】注：1.表中两种形式的双曲线方程对应的渐近线方程分别为， 。
y x a =±y x b =± 2.表中四种形式的抛物线方程对应的准线方程分别是。
,,,2222p p p px x y y =-==-=计算公式()A P A =构成事件的测度试验全部结果所构成的测度离散型随机变量的所有取值及取值的概率列成的表格。
1n p =以数助形根据数与形之间的对应关系，通过把形转化为数，通过数的计算、式子的变换等解决数学问题的数学方法。
心中有图，见数想图，以开拓自己的思维视野.双曲线12222=-by a x （为参数）⎩⎨⎧==θθtan sec b y a x θ抛物线22y px= （为参数）222x pt y pt⎧=⎨=⎩t数学归纳法证明与正整数有关的不等式。
27.二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：。
高中数学必背知识点总结(最新最全)
高中数学必背知识点总结(最新最全) 1. 代数部分
- 多项式的基本概念和运算法则
- 指数与对数的运算规律
- 一次函数、二次函数及其图像性质
- 幂函数、对数函数及其图像性质
- 三角函数的基本概念和图像性质
- 等差数列与等比数列的基本概念和求和公式
- 排列与组合的基本概念和计算方法
2. 几何部分
- 直线、角、三角形及其性质
- 平行线和平行四边形的性质
- 相似三角形的判定和性质
- 圆的基本概念和性质
- 圆锥曲线（抛物线、双曲线、椭圆）的基本概念和性质- 空间几何体的表面积和体积计算公式
3. 概率与统计部分
- 随机事件的概念和性质
- 概率的定义和计算方法
- 二项分布的基本概念和应用
- 正态分布的基本概念和应用
- 统计图表的基本绘制和分析
4. 函数部分
- 函数的基本概念和性质
- 函数的图像和性质
- 函数的极限和连续性
- 导数的定义和计算方法
- 函数的求导法则和应用
- 积分的定义和计算方法
- 函数的微分方程和解法
以上是高中数学必背知识点的一个概要总结，希望对你有帮助！。
新课标高中数学知识点总结汇总表
新课标高中数学知识点总结汇总表一、函数与导数1. 函数基础- 函数的概念与表示法- 函数的性质：定义域、值域、单调性、奇偶性、周期性- 函数的运算：四则运算、复合函数、反函数、基本初等函数（幂函数、指数函数、对数函数、三角函数）2. 极限与连续- 极限的定义与性质- 无穷小与无穷大- 极限的运算法则- 函数的连续性与间断点3. 导数与微分- 导数的定义与几何意义- 导数的运算法则- 高阶导数- 隐函数与参数方程的导数- 微分的概念与应用4. 导数的应用- 函数的极值与最值问题- 曲线的切线与法线- 罗尔定理、拉格朗日中值定理、柯西中值定理- 泰勒公式与麦克劳林公式5. 不定积分- 积分的概念与性质- 基本积分表- 积分的运算法则- 特殊积分技巧：换元法、分部积分法二、平面向量与立体几何1. 平面向量- 向量的基本概念与运算- 向量的几何意义与线性运算- 向量的数量积与向量积- 平面向量的坐标表示与运算2. 立体几何- 空间几何体的性质与计算- 直线与平面的方程- 空间向量及其运算- 立体图形的表面积与体积三、解析几何1. 圆锥曲线- 圆的方程- 椭圆、双曲线、抛物线的方程与性质 - 圆锥曲线的切线与法线- 圆锥曲线的应用问题2. 参数方程与极坐标- 参数方程的概念与应用- 极坐标系与直角坐标系的转换- 简单曲线的极坐标方程四、概率与统计1. 概率论基础- 随机事件与概率的定义- 条件概率与独立事件- 全概率公式与贝叶斯公式- 随机变量与分布函数2. 统计学基础- 统计量的概念：均值、方差、标准差、中位数、众数 - 抽样与估计- 假设检验- 线性回归分析五、数学分析进阶1. 定积分- 定积分的概念与性质- 微积分基本定理- 定积分的计算方法- 定积分的应用：面积、体积、弧长、工作量2. 级数- 数项级数的概念与性质- 正项级数与收敛性判别法- 交错级数与绝对收敛- 幂级数与泰勒级数3. 多元函数微分学- 多元函数的偏导数与全微分- 多元函数的极值与最优化问题- 多重积分的概念与计算4. 常微分方程- 微分方程的基本概念- 可分离变量的微分方程- 一阶线性微分方程- 二阶常系数线性微分方程以上是新课标高中数学的主要知识点汇总，涵盖了函数、几何、概率统计以及数学分析等领域的核心内容。
高中数学知识点汇总(表格格式)
高中数学知识汇总9. 导数及其应用,n k【注：标准d 根据上下文理解为圆心到直线的距离与两圆的圆心距】注：1.表中两种形式的双曲线方程对应的渐近线方程分别为y x a =±， y x b=±。
2.表中四种形式的抛物线方程对应的准线方程分别是,,,2222p p p px x y y =-==-=。
型随机变量及其分布及其分布列分布列离散型随机变量的所有取值及取值的概率列成的表格。
性质（1）0(12)ip i n=≥L，，，；（2）121np p p+++=L。
事件的独立性条件概率概念：事件A发生的条件下，事件B发生的概率，()()()P ABP B AP A=|。
性质：0()1P B A|≤≤．,B C互斥，()()()P B C A P B A P C A=+U|||．独立事件事件A与事件B满足()()()P AB P A P B=，事件A与事件B相互独立。
n次独立重复试验每次试验中事件A发生的概率为p，在n次独立重复试验中，事件A恰好发生k次的概率为()(1)(012)k k n knP X k C p p k n-==-=L，，，，，。
典型分布超几何分布()012k n kM N MnNC CP X k kC--===L，，，，，m，其中{}minm M n=，，且n N≤，且,,,n N M N n M N*∈≤≤N，．＂二项分布分布列为：()(1)(012)k k n knP X k C p p k n-==-=L，，，，，，~()X B n p，。
数学期望EX np=、方差(1)DX np p=-【1n=时为两点分布】正态分布22()21()2πxax eμϕσ--=图象称为正态密度曲线，随机变量X满足()()baP a X b x dxϕ<=⎰≤，则称X的分布为正态分布．正态密度曲线的特点。
数字特征数学期望1122i i n nEX x p x p x p x p=+++++L L()E aX b aEX b+=+方差和标准差方差：21()ni iiDX x EX p==-∑，标准差：X DXσ=2()D aX b a DX+=23. 函数与方程思想,数学结合思想排序不等式设1212,n n a a a b b b ≤≤≤≤≤≤L L 为两组实数，12,,,n c c c L 是12,,,n b b b L 的任意排列， 则121111221122n n n n n n n a b a b a b a c a c a c a b a b a b -+++≤+++≤+++L L L 14444244443144424443144424443反序和乱序和顺序和， 当且仅当12n a a a ===L 或12n b b b ===L 时反序和等于顺序和。
高中数学知识点(表格格式)
高考数学回归知识必备*1 集合与常用逻辑用语)()()U U B C A C B = )U A A ={|x B x ={|U x x A =2.平面向量平行向量方向相同或者相反的两个非零向量叫做平行向量，也叫共线b θ>=，cos b 【注意：投影是数一般表示坐标表示（向量坐标上下文0a b a b ⊥⇔=。
a b +的平行四边形法则、三角形法则。
与加法运算有同样的坐标a b -的三角形法则。
a -MN ON OM =-(N MN x x =-a λ⋅为向量，0λ>(,a x λλ=a aλ=。
cosa b=⋅2a=b a b≤⋅。
2a x y=+ *3.不等式、线性规划*4.函数﹑基本初等函数I的图像与性质*5. 函数与方程﹑函数模型及其应用**6. 三角函数的图像与性质*7. 三角恒等变换与解三角形sin sin αβtan tan 1tan tan αβα±sin c C=。
*8. 等差数列﹑等比数列)n型*9. 数列求和及其数列的简单应用=(136==2⎢⎣。
knn n kC C ++++。
注：表中,n k均为正整数*10.空间几何体（其中r为半径、h为高、l为母线等）S hS h''S S ++*11.空间点、直线、平面位置关系（大写字母表点、小写字母表直线、希腊字母表平面）：个公共点。
α∥β，αβ公共点。
bαβ=⇒线线平行a b P=⎫⇒⎬⎭面面平行,//a b a αγβ==⇒⇒线线平行m n P=⎫⇒⎬⎭线面垂直,l aαβ=⊂面面垂直⇒线面垂直*12. 空间向量与立体几何存在唯一实数λ，aλ=p与,a b、（,a b存在实数对xa b c不共面，空间任意向量,,=++。
p xa yb zc所在直线与已知直线平行或者重合的非零向量线l的方向向量。
叫做平面α的b 。
a ，平面的法向量为n ，sin n θ。
两平面的法向量分别为1n 和12cos n θ=。
高中数学新课标必背
高中数学新课标必背高中数学新课标必背的内容涵盖了高中数学的基础知识和核心概念，这些内容是学生必须掌握的，以便于在高考中取得良好的成绩。
以下是一些重要的必背知识点：1. 集合与简易逻辑：- 集合的概念、表示法、子集、并集、交集、补集。
- 逻辑联结词：非、且、或、蕴含。
- 命题的真假判断。
2. 函数：- 函数的概念、定义域、值域、函数的单调性、奇偶性。
- 一次函数、二次函数、指数函数、对数函数、三角函数的图像和性质。
- 函数的复合、反函数。
3. 导数与微分：- 导数的概念、几何意义、物理意义。
- 基本初等函数的求导公式。
- 导数的应用：求切线方程、单调区间、极值、最值。
4. 积分：- 不定积分和定积分的概念、性质、计算方法。
- 定积分在几何和物理中的应用。
5. 三角函数与三角恒等变换：- 三角函数的定义、图像、性质。
- 三角恒等式：和差公式、倍角公式、半角公式、和差化积、积化和差。
6. 平面向量：- 向量的概念、表示法、向量的加减、数乘、点积、叉积。
- 向量的应用：表示平面几何问题、解决物理问题。
7. 数列：- 数列的概念、通项公式、求和公式。
- 等差数列和等比数列的性质和求和公式。
- 数列的极限概念。
8. 不等式：- 不等式的性质、解法。
- 绝对值不等式、一元二次不等式的解法。
- 基本不等式：算术平均数-几何平均数不等式、柯西不等式。
9. 解析几何：- 直线的方程、圆的方程、椭圆、双曲线、抛物线的标准方程。
- 直线与圆的位置关系、圆与圆的位置关系。
- 圆锥曲线的应用。
10. 立体几何：- 空间直线、平面的位置关系。
- 多面体、旋转体的体积和表面积的计算。
- 空间向量在立体几何中的应用。
11. 概率与统计：- 随机事件、概率的计算。
- 离散型随机变量和连续型随机变量的概率分布。
- 统计图表、数据的描述性统计。
12. 复数：- 复数的概念、表示法、复数的四则运算。
- 复数的几何意义、复数的模和辐角。
高中数学考点归纳(表格版)
高中数学知识汇总6.计数原理与二项式定理16. 空间向量与立体几何注：1.表中两种形式的双曲线方程对应的渐近线方程分别为y x a =±， y x b=±。
2.表中四种形式的抛物线方程对应的准线方程分别是,,,2222p p p p x x y y =-==-=。
21.离散型随机变量及其分布等式柯西不等式二维形式()()()()22222,,,ab c d ac bd a b c d ++≥+∈R ，等号当且仅当ad bc =时成立。
向量形式α,β是两个向量，则⋅≤αβαβ，当且仅当β是零向量或存在实数k ，使k =αβ时，等号成立。
一般形式()22211n n b a b a b a +++Λ()()222221222221n n b b b a a a ++++++≤ΛΛ()n i R b a i i Λ2,1,=∈等号当且仅当021====n a a a Λ或i i ka b =时成立（k 为常数，n i Λ2,1=）。
排序不等式 设1212,n n a a a b b b ≤≤≤≤≤≤L L 为两组实数，12,,,n c c c L 是12,,,n b b b L 的任意排列，则121111221122n n n n n n n a b a b a b a c a c a c a b a b a b -+++≤+++≤+++L L L 14444244443144424443144424443反序和乱序和顺序和，当且仅当12n a a a ===L 或12n b b b ===L 时反序和等于顺序和。
证明方法比较法 作差和作商比较综合法 根据已知条件、不等式的性质、基本不等式，通过逻辑推理导出结论 分析法 执果索因的证明方法 反证法 反设结论，导出矛盾放缩法通过把不等式中的部分值放大或缩小的证明方法数学归纳法 证明与正整数有关的不等式。
27.二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：判别式24b ac ∆=-0∆> 0∆= 0∆<二次函数2y ax bx c =++()0a >的图象一元二次方程20ax bx c ++=()0a >的根有两个相异实数根1,22b x a-±∆=()12x x <有两个相等实数根122b x x a==-没有实数根。
高中数学知识点总结最新全
高中数学知识点总结最新全一、代数1. 集合与函数- 集合的概念、运算及其性质- 函数的定义、性质和常见类型（如一次函数、二次函数、指数函数、对数函数、三角函数等）- 函数的图像和变换（平移、伸缩、对称等）2. 代数式- 整式、分式和根式的基本概念和运算法则- 二次根式的化简和求解- 多项式的因式分解（提公因式、公式法、配方法等）3. 方程与不等式- 一元一次方程、一元二次方程的解法- 不等式的性质和解集表示- 系统方程组的解法（代入法、消元法等）4. 序列与数列- 等差数列和等比数列的通项公式、求和公式- 数列的极限概念及其计算二、几何1. 平面几何- 点、线、面的基本性质- 三角形、四边形的性质和计算（包括特殊四边形如矩形、菱形、梯形等）- 圆的性质和相关定理（如切线、弦、切线长定理等）2. 空间几何- 空间直线和平面的方程- 空间图形的体积和表面积计算- 空间向量及其在几何中的应用（如向量积、数量积等）三、概率与统计1. 概率- 随机事件的概率定义和计算- 条件概率、独立事件的概念- 排列组合的基本原理和公式2. 统计- 数据的收集、整理和描述- 均值、中位数、众数、方差、标准差等统计量的计算 - 概率分布（如二项分布、正态分布等）及其应用四、数学分析1. 极限与连续- 数列极限的概念、性质和计算方法- 函数极限的定义、性质和计算- 连续函数的概念和基本性质2. 微积分- 导数的定义、几何意义和物理意义- 常见函数的导数和求导法则- 微分的应用（如相关率、极值问题等）- 积分的概念、基本定理和计算方法- 不定积分和定积分的求解五、数学思维与方法1. 逻辑推理- 命题逻辑的基本概念和推理规则- 直接证明和间接证明的方法2. 问题解决策略- 分类讨论、归纳总结、化归与转化等策略- 数学建模的基本思想和方法以上总结了高中数学的主要知识点，这些知识点构成了高中数学教育的核心内容，旨在培养学生的逻辑思维能力、抽象思维能力以及解决实际问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
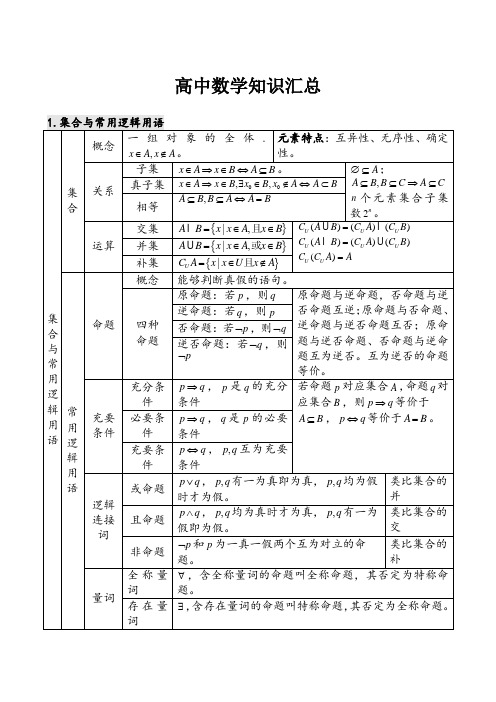
高中数学知识汇总
n 个元素集合子集数2)()()U U B C A C B =
)U A A =
{|x B x ={|U x x A =能够判断真假的语句。
原命题：若p 原命题与逆命题，否命题与逆否命题互逆；原命题与否命题、逆命题与逆否命逆命题：若q 否命题：若⌝←−−−
→一一对应向量OZ 向量OZ 的模叫做复数的模，di
+，则首先要进行分母实数化（分母乘以自己的共轭复数），在进行四则运算时，可以把字母，按照实数的四则运算律直接进行运算，并随时把
投影
cos b 在a 方向上的投影。
2,e 为,x y 轴上
一般表示,a b （0b ≠12(,)(,)x y x y x y x λ=⇔=a b +的平行四边形法则、三角形法则。
()(a b c a ++=+a b -的三角形法则。
MN (N M MN x x =-a λ⋅为向量，0λ>与a 方向相同， 与a 方向相反，a a λ=。
(,a x λλ=a )λμ，a a λμλ=+)(b a λλ++(
cos ,a b a b a b =⋅<>
2
a a =，a
b a b ≤⋅。
2a x y =+2121y y x ≤+
b a =，()a
c a c +=+()()()a b a b a b λλλ==。
与上面的数量积、数乘等具有同样
4.算法、推理与证明
圆的方程 圆心x 2+ y 2= r 2
（0，
6.计数原理与二项式定理
n m 种不同的方法
个元素的组合，所有不同组合的个数，叫做从!m 11n n a C a b -+1
1++；n n n C C C C 210++++ 8. 函数与方程﹑函数模型及其应用
9. 导数及其应用
)()g x ⎦
⎣复合函数求导法则[](())''(())'()y f g x f g x g x ==()
10. 三角函数的图像与性质
11. 三角恒等变换与解三角形
sin sin αβ
tan tan 1tan tan αβα±sin c C
=。
2sin R B =
12. 等差数列﹑等比数列
13. 数列求和及其数列的简单应用
=
1)(21)
(13
6
n ++=
=
32(1)(12)2n n n n +⎡⎤
=++
+=⎢⎥⎣。
22,3n n a n a =+=。
k n n
n
kC C +
++
+。
基本特征是均匀增加或者减少。
14.空间几何体（其中r 为半径、h 为高、l 为母线等）
S h
')S S h +
'0S = S h
h 底高
')S S h +
15.空间点、直线、平面位置关系（大写字母表点、小写字母表直线、希腊字母表平面）：
∥c ⇒a ∥共面和异面。
共面为相交和平行。
不同在任何一个平面的两条直线称为异面直线。
,B αα∉。
.α⊂。
分别对应线面无公共点、一个公共点、无数个公共点。
α∥β，αβ=判定定理,,//a b a αα⊄⊂线线平行⇒线面平行b αβ=⇒⇒线线平行
,a b P β⊂=⎫
⇒⎬⎭
⇒面面平行,//a b a αγβ==⇒面面平行⇒线线平行
m n P =⎫
⇒⎬⎭
⇒线面垂直a a b αα⊥⎫
⇒⎬⊥⎭
∥b ααβ⇒⊥⇒面面垂直,l a α
β=⊂面面垂直⇒特殊情况
两直线平行时角为0︒ 90︒时称两直
不共线）共面⇔存在实数对,,a b c 不共面，空间任意向量存在唯一的(,,)x y z ，使所在直线与已知直线l 平行或者重合的非零向量叫做直线l 的方向向量。
所在直线与已知平面垂直的非零向量的法向量。
,a b 。
,a n 。
2。
sin ,MN MN a 。
两平行线距离n ，平面αcos MN n MN MN n n
⋅=。
17.直线与圆的方程
18.圆锥曲线的定义、方程与性质
注：1.表中两种形式的双曲线方程对应的渐近线方程分别为y x a =±
， y x b =±。
2.表中四种形式的抛物线方程对应的准线方程分别是,,,2222
p p p p
x x y y =-==-=。
19. 圆锥曲线的热点问题
21.离散型随机变量及其分布
离散型随机变量及其分布随机变
量及其
分布列
概念
随着试验结果变化而变化的量叫做随机变量，所有取值可以一一列出的随机叫做
离散型随机变量。
分布列离散型随机变量的所有取值及取值的概率列成的表格。
性质（1）
0(12)
i
p i n
=
≥，，，；（2）
12
1
n
p p p
+++=。
事件的
独立性
条件概率
概念：事件A发生的条件下，事件B发生的概率，
()
()
()
P AB
P B A
P A
=
|。
性质：0()1
P B A
|
≤≤．,B C互斥，()()()
P B C A P B A P C A
=+
|||．独立事件事件A与事件B满足()()()
P AB P A P B
=，事件A与事件B相互独立。
n次独立
重复试验
每次试验中事件A发生的概率为p，在n次独立重复试验中，事件A恰好发生k
次的概率为()(1)(012)
k k n k
n
P X k C p p k n
-
==-=
，，，，，。
典型
分布
超几何
分布
()012
k n k
M N M
n
N
C C
P X k k
C
-
-
===
，，，，，m，其中{}
min
m M n
=，，且n N
≤，且,,,
n N M N n M N*
∈
≤≤N
，．＂
二项分布
分布列为：()(1)(012)
k k n k
n
P X k C p p k n
-
==-=
，，，，，，~()
X B n p
，。
数学期望EX np
=、方差(1)
DX np p
=-【1
n=时为两点分布】正态分布
2
2
()
2
1
()
2π
x
a
x e
μ
ϕ
σ
-
-
=图象称为正态密度曲线，随机变量X满足()()
b
a
P a X b x dx
ϕ
<=⎰
≤，则称X的分布为正态分布．正态密度曲线的特点。
数字
特征
数学期望1122i i n n
EX x p x p x p x p
=+++++()
E aX b aEX b
+=+
方差和
标准差
方差：2
1
()
n
i i
i
DX x EX p
=
=-
∑，标准差：X DX
σ=2
()
D aX b a DX
+=
22. 统计与统计案例
1(
i
i x x
n=-
∑24. 分类与整合思想,化归与转化思想
25.坐标系与参数方程
26. 不等式选讲
(n
n n
≥
()a b +时成立。
反序和
乱序和
顺序和
作差和作商比较
根据已知条件、不等式的性质、基本不等式，通过逻辑推理导出结论
27.二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：
28.三角函数的图象与性质：。