北约自主招生数学试题及答案
北约自主招生文科数学试题
北约自主招生文科数学试题X-1与Y=-5X^2+2X+3的交点的直线方程。
3、（数列）在等差数列｛an（n下标）｝中，a3=-13，a7=3，Sn（n下标）为其前n项和。
问数列｛Sn（n下标）｝的哪一项最小？并求出最小项值。
4、（三函\不等式）在三角形ABC中，若a+b》=（大于等于）2c，证明：C《=（小于等于）60度。
5、（数论）是否存在四个正实数，使得两两之积分别为2、3、5、6、10、16？参考思路：1、可以用余弦定理：先利用已知三边求出平行四边形一角的余弦值，则另一角的余弦值可知（互为相反数），再求未知对角线；也可以利用解几中的重要结论：平行四边形的两对角线平方和等于四边平方和（不过要先建立坐标系证明该结论）。
2、最容易想到的方法自然是联立两抛物线方程，解出交点坐标，用两点式或点斜式表示……好吧，我承认这样做有点难算，不过其实也不算太难啦（最后化简结果似乎是不含根式的）。
当然，也可以先设直线方程Y=kX+b，与两抛物线分别联立，再对比所得交点的系数，从而得解（我的一位同学就是这样做的）。
3、常规题。
先求公差，再求通项，再求前n项和，最后利用二次函数的性质解之（注意n 为正整数），或利用an《=0且a（n+1）>=0解之（n和n+1下标）。
4、可以考虑反证法；不然就用余弦定理表示出cosC，把式子分子中的a、b利用原题中的不等式换成c，再用基本不等式，中间经过若干步转换，最后化简为cosC》=0.5，于是得证。
5、尚未解出。
数论问题对高中文科生来说还是难了一点……1、最刁钻的问题：火车开车前为什么会先退一步然后再前进？在采访了物理老师之后，得出的结论是：通常情况下,火车各节车厢之间的挂钩拉得很紧,牵引力必须克服整列火车与铁轨的最大静摩擦力才能启动。
只有尽量减小这种摩擦力对启动的影响,才能使火车顺利地开出车站。
火车先倒车,就是为了使车厢间挂钩松弛,再向前启动,使车厢逐节启动。
2、最文乎的考题：对“人之所以异于禽兽者几希”的看法。
2014年3月北约自主招生数学试卷
2014北约理科数学试题1、圆心角为3π的扇形面积为6,π求它围成圆锥的表面积. 2、将10个人分成3组，一组4人，两组各3人，求共有几种分法.3、()()()()22,11,47,33f a f b a b f f f ++⎛⎫=== ⎪⎝⎭求()2014f . 4、()()2lg 2f x x ax a =-+的值域为,R 求a 的取值范围. 5、已知1,x y +=-且,x y 都为负实数，求1xy xy+的取值范围. 6、()22arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 7、求证：tan3.Q ︒∉8、已知实系数二次函数()f x 与()()(),g x f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.9、1213......a a a 是等差数列，{}|113,i j k M a a a i j k =++≤<<≤问：7160,,23是否可以同时在M中，并证明你的结论.10、()01,2,...,i x i n >=11.n i i x ==∏求证：))11.nni i x =≥∏2014北约文科数学试题1、圆心角为3π的扇形面积为6,π求它围成圆锥的表面积. 2、将10个人分成3组，一组4人，两组各3人，求共有几种分法.3、()()()()22,11,47,33f a f b a b f f f ++⎛⎫=== ⎪⎝⎭求()2014f . 4、()()2lg 2f x x ax a =-+的值域为,R 求a 的取值范围. 5、已知1,x y +=-且,x y 都为负实数，求1xy xy+的取值范围. 6、()22arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 7、等比数列{}(){}()411200,631200n n m m +≤≤-≤≤的公共项之和.8、梯形的对角线长分别为5和7，高是3,求梯形的面积.9、求证：tan3.Q ︒∉10、已知实系数二次函数()f x 与()()(),g x f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.2014北约理科数学试题（参考答案）1、圆心角为3π的扇形面积为6,π求它围成圆锥的表面积. 【解析】21,6,2,2S R R l R ααπ=⇒===扇从而圆锥底面周长为222,,67.r S r S πππππππ=⇒===+=底2、将10个人分成3组，一组4人，两组各3人，求共有几种分法.【解析】平均分堆问题.10634332100.2!C C C ⋅⋅=3、()()()()22,11,47,33f a f b a b f f f ++⎛⎫=== ⎪⎝⎭求()2014f . 【解析】观察等式可知，函数显然为线性一次函数，可设(),f x kx m =+()()11,47f f ==代入求得2,1,k m ==-从而()20144027.f =4、()()2lg 2f x x ax a =-+的值域为,R 求a 的取值范围. 【解析】值域问题.2440,1a a a ∆=-≥⇒≥或0.a ≤5、已知1,x y +=-且,x y 都为负实数，求1xy xy+的取值范围. 【解析】均值不等式，对勾函数性质.()()110,4x y xy =-+-≥⇒<≤从而117.4xy xy +≥FEDBA6、()22arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 【解析】()00,arctan 2.f C =⇒=-下面证明：()()22224arctanarctan 2arctan 2arctan 20.14143x x f x f x C x x +-⎛⎫+-=++=--= ⎪-+⎝⎭7、求证：tan3.Q ︒∉【解析】反证法.假设tan3,Q ︒∈则tan6,tan12,tan 24,Q Q Q ︒∈⇒︒∈⇒︒∈从而tan30,Q ︒∈矛盾.tan3.Q ∴︒∉8、已知实系数二次函数()f x 与()()(),g x f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.【解析】设()2,f x ax bx c =++()2,g x dx ex f =++则由()()f x g x =，可得()()()()()()220,40.a d x b e x c f b e a d c f -+-+-=∆=----=由()()30f x g x +=可得()()()()()()223330,34330.a d x b e x c f b e a d c f +++++=∆=+-++=化简得223124,b e ac df +=+即()22434e df ac b -=-又240.b ac ->240.e df ∴-<()g x ∴没有实根.9、1213......a a a 是等差数列，{}|113,i j k M a a a i j k =++≤<<≤问：7160,,23是否可以同时在M中，并证明你的结论.【解析】数列中的项.分析M 中项的构成，若按照从小到大的顺序排列，最小的项为123a a a ++，第二项为124a a a ++，最大的项为111213,a a a ++设n a 公差为,d 则M 中项的公差也为d ，所以M 中共有111213123131++---+=项，假设7160,,23均为M 中的项，不妨设212121217167110,,,,030,23221k k d k d k k Z k k k -=-=⇒=∈<≤、、且1231,k k +≤这样的k 不存在，矛盾.所以7160,,23不可以同时在M 中.10、()01,2,...,i x i n >=11.n i i x ==∏求证：))11.nni i x =≥∏【解析】不等式；柯西不等式或AM GM -平均不等式. 法一：AM GM -不等式.调和平均值n n ni n H G =≤=⎛⎫∑≤n i n ≤=⎛⎫∑n i ≤∑n i ⎛⎫≤∑1n n i i n n ⎛⎫⎛⎫≤+=∑∑，即)1≤，即))1nni ix ≤∏法二：由11.n i ix ==∏及要证的结论分析，由柯西不等式得))211i i x x ⎫≥⎪⎭，从而可设1i i y x =，且1111.n nii i iy x ====∏∏从而本题也即证))11.n ni i y =≥∏从而))211nni ii x x⎫≥⎪⎭∏，即))21nnii ix y ≥∏，假设原式不成立，即))11,nni i x =<∏则))11.nni i y =<∏从而))21nnii ix y <∏，矛盾.得证.2014北约文科数学试题（参考答案）1、圆心角为3π的扇形面积为6,π求它围成圆锥的表面积. 【解析】21,6,2,2S R R l R ααπ=⇒===扇从而圆锥底面周长为222,,67.r S r S πππππππ=⇒===+=底2、将10个人分成3组，一组4人，两组各3人，求共有几种分法.【解析】平均分堆问题.10634332100.2!C C C ⋅⋅=3、()()()()22,11,47,33f a f b a b f f f ++⎛⎫=== ⎪⎝⎭求()2014f . 【解析】观察等式可知，函数显然为线性一次函数，可设(),f x kx m =+()()11,47f f ==代入求得2,1,k m ==-从而()20144027.f =4、()()2lg 2f x x ax a =-+的值域为,R 求a 的取值范围. 【解析】值域问题.2440,1a a a ∆=-≥⇒≥或0.a ≤5、已知1,x y +=-且,x y 都为负实数，求1xy xy+的取值范围. 【解析】均值不等式，对勾函数性质.()()110,4x y xy =-+-≥⇒<≤从而117.4xy xy +≥6、()22arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 【解析】()00,arctan 2.f C =⇒=-下面证明：()()22224arctanarctan 2arctan 2arctan 20.14143x x f x f x C x x +-⎛⎫+-=++=--= ⎪-+⎝⎭7、等比数列{}(){}()411200,631200n n m m +≤≤-≤≤的公共项之和. 【解析】此题考察数的同余问题；设公共项为a ，1mod(4),3mod(6).a a ≡≡易得a 最小的数为9.4和6的最小公倍数为12,则912,.a k k N =+∈91242001,66.k k +=⨯+⇒=∴公共项之和为()67980127135.2S +==8、梯形的对角线长分别为5和7，高是3,求梯形的面积.【解析】如图，梯形面积为()()1122S AB CD h DF EC h =+=+，易求得4,DF EC == ()(1143622S DF EC h =+=+=+9、求证：tan3.Q ︒∉【解析】反证法.假设tan3,Q ︒∈则tan6,tan12,tan 24,Q Q Q ︒∈⇒︒∈⇒︒∈从而tan30,Q ︒∈矛盾.tan3.Q ∴︒∉10、已知实系数二次函数()f x 与()()(),g x f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.【解析】设()2,f x ax bx c =++()2,g x dx ex f =++则由()()f x g x =，可得()()()()()()220,40.a d x b e x c f b e a d c f -+-+-=∆=----=由()()30f x g x +=可得()()()()()()223330,34330.a d x b e x c f b e a d c f +++++=∆=+-++=化简得223124,b e ac df +=+即()22434e df ac b -=-又240.b ac ->240.e df ∴-<()g x ∴没有实根.FEDBA。
2012年北约自主招生文科试题及答案
北京大学自主招生数学（文科）解答24. 解法一：（4分）（6分）（6分）（2分）说明1. 直接猜出取中点时取得最小值43，得2分.解答二：建立坐标系，设)0,(a A ，)3,(b b B ，))1(3,(c c C -222CA BC AB ++6126422882222+--+--++=c c bc ca ab c b a （4分）61263215215)2(2222+--++++-=c b bc c b c b a （6分） 4343)43(536)1563(215)2(2222≥+-+-+++-=c c b c b a （6分）当43 =c ，41 =b ，21 =a 时，222CA BC AB ++取到最小值43 (2分)说明1. 原点取在别处（比如某边中点），可相应给分解答三：建立坐标系，设)0,(x A ，))21(3,(y y B -，))21(3,(z z C +222CA BC AB ++2333422882222++-+--++=z y yz xz xy z y x （4分） 4343)41(536)51(215)2(2222≥+++-+++-=z z y z y x （6分）4343)43(536)1563(215)2(2222≥+-+-+++-=c c b c b a （6分）当且仅当41- =z ，41 =y ，0 =x 时，222CA BC AB ++取到最小值43 (2分)25. 证明：内角相等的圆内接五边形必为正五边形。
解法一：证明: 假设圆内接五边形每条边所对应的弧长分别是x ， y ， z ，u ，v . 利用等角对等弧这一结论 我们有x + y + z = y + z + u （5分）同理 x + y + z = y + z + u =z + u + v = u + v + x = v + x + y (10 分)由此可知 x = y = z = u = v (15 分)再利用等弧对等弦，所以圆内接五边形的五条边都相等. (20分)解法二：证明: 假设圆内接五边形每条边所对应的弧长分别是x ， y ， z ，u ，v . 利用等角对等弧这一结论我们有 x + y + z = y + z + u （5分）x = u (10 分)同理 x = y = z = u = v (15 分)再利用等弧对等弦，所以圆内接五边形的五条边都相等. (20分) 解法三：证明: 连接CE∵ ABCE 是圆内接四边形∴ ∠A+∠1=180° ∠B+∠2=180°∵ ∠A=∠B∴ ∠1=∠2 （5分） ∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 （10分） ∴ DE = CD （15分） 同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法四： 连接CE∵ ABCE 是圆内接四边形 ∴ ∠A+∠1=180° ∵ ∠A=108°∴ ∠1= 72° (5分)∴ ∠BOE=2∠1= 144° (10分) 同理 ∠BOD=144°∴ ∠EOD=360°-144°-144°=72° (15分) 同理 ∠AOB=∠BOC=∠COD=∠DOE=∠EOA=72°∴ AB=BC=CD=DE=EA∴圆内接五边形的五条边都相等. (20分)解法五：证明: ∵∠BAE=∠ABC ∠1=∠2∴∠3=∠10 (5分)∵∠3=∠4 ∠9=∠10∴∠4=∠9∵∠BCD=∠AED∴∠5=∠8∵∠5=∠6 ∠7=∠8∴∠6=∠7 (或∠6=∠7= 54°) (10分) ∴∠5+∠6=∠7+∠8∴∠COD=∠DOE∴ CD=DE (15分)同理 AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法六：∵半径相等∴∠1=∠2 ∠3=∠4 ∠5=∠6 ∠7=∠8 ∠9=∠10∵∠1+∠2+∠3+… +∠9+∠10 =540°∴（∠1+∠10）+（∠4+∠5）+∠8=270°∵∠1+∠10=108°∠4+∠5=108°∴∠8= 54°（5分）∴∠9+∠8 = 108°∴∠9= 54°∴∠8=∠9 （10分）∵∠9+∠10=∠7+∠8∴∠AOE=∠DOE∴ AE=DE (15分)同理AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法七：∵同弧AB所对的角相等∴∠1=∠2 (5分)∵∠BAE=∠ABC AB=AB∴△ABC ≌△ABE (10分)∴ BC=AE (15分)同理AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法八：∵∠B=∠E∴ AC=AD （5分）∴∠1=∠2∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 (10分) ∴ A B=AE (15分)同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法九：∵ ∠B=∠E ∴ AC=AD （5分） ∴ ∠1=∠2 ∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 (10分) ∵ ∠B=∠E AC=AD∴ △ABC ≌ △ADE （15分） ∴ BC=AE同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法十： 设AB=a, AE= b2 ，BC= b 1,∵ ∠BAE=∠ABC= 108° ∴ AC=BE （5分）设 AC=BE=c 由余弦定理，得在△ABC 中 c 2= a 2+ b 12 －2 a b cos 108° ①在△ABE 中 c 2= a 2 +b 22 －2 a b cos 108° ② （10分） ①-②,得 （b 1－b 2）(b 1+b 2－2 a b cos 108°）= 0 ∵ cos 108°＜0∴ b 1+b 2－ 2 a b cos 108°＞0 （若同学没有这一步，则这道题只得10分） ∴ b 1= b 2 即BC=AE (15分) 同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法十一：∵ 圆内接五边形的各内角相等 ∴ AC=BD∴∠A0C=∠BOD (5分) ∴∠A0B+∠B0C=∠COD+∠BOC∴∠A0B =∠COD (10分) ∴ AB=CD (15分)同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)阅卷说明：1、只画图，没有证明，记0分。
2008-2011北京大学(北约)自主招生数学试题(全附答案)
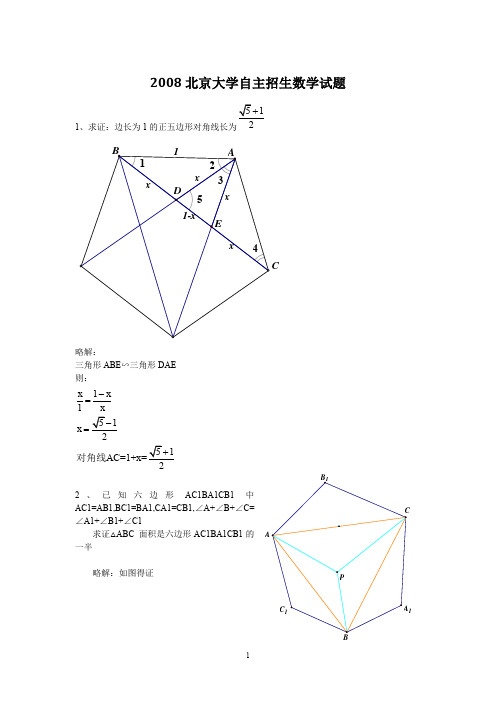
5
答案： 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号（9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号（55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的，因为 (m+499(k+m-2n))可能是负的，也就是当这是递减的等差数列的时候，那么 2009 就不在这个 数列中了。 3、 挺简单，设 a=tanx+（根 3）,b=cotx+(根号 3）,假设均为有理数。 那么由(a-（根号 3） ） （b-（根号 3） ）=1 可得（a+b）根号 3=ab+2.若 a+b 非零，除过来就矛盾了。 所以必有 a+b=0，此时 ab+2 也是 0. 显然与 a，b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)（必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内，则可得 a^2≤8（b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤（a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况，显然 2 是 a+b 的最大值， 5、设优秀有 a 人，及格 b 人，不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000（这里都取各层次里的最少人，故用小于等于） 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题，矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数
大学自主招生测评题真题及答案解析——数学一
大学自主招生测评题真题及答案解析——数学一一、选择题1、（北约2014年）设扇形的圆心角为3π，面积为6π，将它围成一个圆锥，求圆锥的表面积______（A ）132π （B ）7π （C ）152π （D ）8π答案：B6/660360ππ=，扇形弧长为60262360ππ=，故圆锥底面半径为1，圆锥的表面积等于67πππ+=2、（北约2013和为两根的有理系数多项式的最高次数最小为( )A. 2B.C. D. 答案：C解析：由,可知,同理由可知; 所以方程的次数最小,其次数为5,故选C.3、（华约2012年）红蓝两色车、马、炮棋子各一枚，将这6枚棋子排成一列，其中对对同字的棋子中，均为红棋子在前，蓝棋子在后，满足这种条件的不同的排列方式共有（ ）(A) 36种 (B) 60种 (C) 90种 (D)120种 答案：C4、（华约2010年）设向量,a b ，满足||||1,==⋅=a b a b m ，则||+a tb ()t R ∈的最小值为（ ）（A ）2 （B （C ）1 （D 答案：D5、（华约2010年）设复数2()1a i w i+=+，其中a 为实数，若w 的实部为2，则w 的虚部为（ ）（A ）32- （B ）12- （C ）12 （D ）32答案：A二、填空题6、（卓越2014年）不等式32210x x -+<的解集为_____________。
13561x =22x =1x 3(1)2x -=23(2)[(1)2]0x x ---=答案：1515112⎛⎫⎛++-, ⎪ ⎪ ⎝⎭⎝⎭解析：22x x =，把原式视作x 的三次多项式分解因式即可。
7、（卓越2013年）如图，AE 是圆O 的切线，A 是切点，AD 与OE 垂直，垂足是D ，割线EC 交圆O 于,B C ，且,ODC DBC αβ∠=∠=，则OEC ∠= （用,αβ表示）。
答案：βα-三、综合题8、（北约2014年）证明：tan 3是无理数。
2015年自主招生数学试卷(北约)
2015年自主招生试卷（北约）1． 已知等腰直角△PQR 的三个顶点分别在等腰直角△ABC 的三条边上，记△PQR ，△ABC 的面积分别为S △PQR ，S △ABC ，则PQR ABCS S ∆∆的最小值为 ．解答：如图5-1所示，图5-1 图5-2（1）当PQR ∆的直角顶点在ABC ∆的斜边上，则,,,P C Q R 四点共圆，180,APR CQR BQR ∠=∠=-∠所以sin sin .APR BQR ∠=∠在,APR BQR ∆∆中分别应用正弦定理得,sin sin sin sin PR AR QR BRA APRB BQR==.又45,A B ∠=∠=故PR QR =,故AR BR =即R 为AB 的中点.过R 作RH AC ⊥于H ，则12PR RH BC ≥=,所以22221()124PQR ABC BC S PR S BC BC ∆∆=≥=,此时PQR ABCS S ∆∆的最大值为14. （2）当PQR ∆的直角顶点在ABC ∆的直角边上，如图5-2所示，设1,(01),(0)2BC CR x x BRQ παα==≤≤∠=<<,则90.CPR PRC BRQ α∠=-∠=∠=在Rt CPR ∆中，,sin sin CR xPR αα== 在BRQ ∆中，31,,sin 4x BR x RQ PR RQB QRB B ππαα=-==∠=-∠-∠=+, AB P H由正弦定理, 1sin 3sin sin sin sin()44xPQ RB xB PQB αππα-=⇔=⇔∠+1sin cos 2sin x ααα=+，因此2221111()()22sin 2cos 2sin PQR x S PR ααα∆===+.这样，PQR ABCS S ∆∆2222111()cos 2sin (12)(cos sin )5αααα=≥=+++，当且仅当arctan 2α=取等号，此时PQR ABCS S ∆∆的最小值为15.2. 若集合{}2015*(,)(1)(2)()10,,A m n m m m n m Z n N =++++++=∈∈，则集合A中的元素个数为 ． 解答：由已知得20162015(21)25n n m ++=，因为,21n n m ++一奇一偶，所以,21n n m ++两者之一为偶数，即为2016201620162201620152,25,25,,25共有2016种情况，交换顺序又得到2016种情形，所以集合A 共有4032个元素. 3．若数列{}n a 的前n 项和nS =32n n -，*n N ∈，则20151182i i a i =+-∑= ．答案：20156048. 解答：1211352,nn n i i i i a a a n n -===-=-+∑∑又10a =，故2*352()n a n n n N =-+∈, 20152015201511111111()823(1)31i i i i a i i i i i =====-=+-++∑∑∑20156048. 4．若22sin cos 161610xx +=，则cos4x = .答案：12-. 解答:设2sin 16,116xt t =≤≤，则22cos 1sin 161616x x t-==，代入方程得16102,t t t +=⇒=或8t =，即21sin 4x =或34，所以cos4x =12-。
北京大学(北约)2010~2014自主招生试题及答案(全)
2014年北京大学自主招生数学试题1. 圆心角为3π的扇形面积为6π，求它围成圆锥的表面积. 2. 将10个人分成3组，一组4人，两组每组3人，共有几种分法. 3. 2()2()(),(1)1,(4)733a b f a f b f f f ++===,求()2014f . 4.2()lg(2)f x x ax a =-+的值域为R ，求a 的取值范围.5. 已知1x y +=-，且,x y 都为负实数，求1xy xy+的取值范围. 6. 22()arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 一、求证：tan3Q ∉二、已知实系数二次函数()f x 与()g x ，()()f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.三、1213,a a a 是等差数列，{}113i j k M a a a i j k =++≤<<≤，问：7160,,23是否同在M 中，并证明你的结论.四、()01,2,,i x i n >=，且11n i i x ==∏，求证1)1)nn i i x =≥∏.答案1．π7； 2．2100； 3．4027)2024(12)(=⇒-=f x x f ； 4．1 00≥≤⇒≥∆a or a ；5．⎪⎭⎫⎢⎣⎡+∞,417；6．2arctan 0)0(-=⇒=C f 一、求证：Q ∉︒3tan解：若Q aab Q a ∈-=︒=⇒∈=︒2126tan 3tan ，Q ab b a c ∈-+=︒=⇒19tan Q bc cb d ∈-+=︒=⇒115tan 52518tan 41518sin 2-=︒⇒-=︒ 于是Q d d ∈-=⇒=-=︒233215tan ，从而矛盾。
二．实系数二次函数)(),(x g x f ，)()(x g x f =和0)()(3=+x g x f 有两重根，)(x f 有两相异根，求证：)(x g 无实数根。
2013年北约自主招生数学试题与答案解析
2013年北约自主招生数学试题与答案2013-03-16（时间90分钟，满分120分）(1(7)(232(630g a b c d e a b c d a b c =-+----+++++702320a b c d e a b c d +---=⎧⇒⎨+++=⎩即方程组：420(1)20(2)70(3)2320(4)630(5)a c e b d a b c d e a b c d a b c ++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩，有非0有理数解.由（1）+（3）得：110a b c d ++-= （6） 由（6）+（2）得：1130a b c ++= （7） 由（6）+（4）得：13430a b c ++= （8） 由（7）-（5）得：0a =，代入（7）、（8）得：0b c ==，代入（1）、（2）知：0d e ==.于是知0a b c d e =====，与,,,,abcd e不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x和11为两根的有理系数多项式的次数最小为5.2.在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车，每一行每一列只有一辆车，每辆车占一格，共有几种停放方法？A. 720B. 20C. 518400D. 14400解析：先从6行中选取3行停放红色车，有36C 种选择.最上面一行的红色车位置有6种选择；最上面一行的红色车位置选定后，中间一行的红色车位置有5种选择；上面两行的红色车位置选定后，最下面一行的红色车位置有4种选择。
三辆红色车的位置选定后，黑色车的位置有3！=6种选择。
所以共有36654614400C ⨯⨯⨯⨯=种停放汽车的方法. 3.已知2225,25x y y x =+=+，求32232x x y y -+的值. A. 10 B. 12 C. 14 D. 16 解析：根据条件知：32232(25)2(25)(25)(25)x x y y x y y x y x -+=+-++++1515450x y xy =---由2225,25x y y x =+=+两式相减得()()22x y x y y x -+=-故y x =或2x y +=-①若x y =则225x x =+，解得1x =±于是知1x y ==+1x y ==当1x y ==+3223222415()50430504(25)3870x x y y xy x y x x x x x -+=-++-=---=-----3870108x =--=--.当1x y ==-3223222415()50430504(25)3870x x y y xy x y x x x x -+=--+-=---=-+---22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-3870108x =--=-+.（2）若x y ≠，则根据条件知：22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-，于是22(25)(25)2()106x y y x x y +=+-+=++=，进而知222()()12x y x y xy +-+==-. 于是知：32232415()5016x x y y xy x y -+=-+-=-.综上所述知，32232x x y y -+的值为108-±或16-.4.数列{}n a 满足11a =，前n 项和为1,42n n n S S a +=+，求2013a . A. 3019⨯22012B. 3019⨯22013C. 3018⨯22012D.无法确定解析：根据条件知：1221221424244n n n n n n n n n a S a S a a a a a ++++++++==+=++⇒=-.又根据条件知：1212121,425a S a a a a ==+=+⇒=.所以数列{}1221:1,5,44n n n n a a a a a a ++===-.又212114422(2)n n n n n n n a a a a a a a +++++=-⇔-=-.令12n n n b a a +=-， 则11212,23n n b b b a a +==-=，所以132n n b -=⋅.即11232n n n a a -+-=⋅.对11232n n n a a -+-=⋅，两边同除以12n +，有113224n n n n a a ++-=，即113224n n n n a a ++=+.令2n nn a c =，则134n n c c +=+，11122a c ==，于是知1331(1)244n n c n -=+-=.所以231,2(31)24nn n n a n --==-⋅.于是知：201120122013(320131)230192a =⨯-⋅=⋅.5．如图，ABC ∆中，AD 为BC 边上中线，,DM DN 分别,ADB ADC ∠∠的角平分线，试比较BM CN +与MN 的大小关系，并说明理由. A. BM+CN>MNB. MN +CN <MNC. BM+CN =MND.无法确定解析：如图，延长ND 到E ，使得DE DN =，连接BE ME 、.易知BDE CDN ∆≅∆，所以CN BE =.又因为,DM DN 分别为,ADB ADC ∠∠的角平分线，所以90MDN ∠=︒，知MD 为线段EN 的垂直平分线，所以MN ME =.所以B M C N B M B E +=+>=.6.模长为1的复数A B C 、、，满足0A B C ++≠，求AB BC CAA B C++++的模长.A. -1/2B. 1C. 2D.无法确定解析：根据公式z =1,1,1A A B B C C ⋅=⋅=⋅=.于是知：AB BC CAA B C ++=++=1==.所以AB BC CAA B C++++的模长为1.7．最多能取多少个两两不等的正整数，使得其中任意三个数之和都为素数. 解析：所有正整数按取模3可分为三类：3k 型、31k +型、32k +型.首先，我们可以证明，所取的数最多只能取到两类.否则，若三类数都有取到，设所取3k 型数为3a ，31k +型数为31b +，32k +型数为32c +，则3(31)(32)3(1)a b c a b c ++++=+++，不可能为素数.所以三类数中，最多能取到两类.其次，我们容易知道，每类数最多只能取两个.否则，若某一类3(012)k r r +=、、型的数至少取到三个，设其中三个分别为333a r b r c r +++、、，则(3)(3)(3)3()a r b r c r a b c r +++++=+++，不可能为素数.所以每类数最多只能取两个.结合上述两条，我们知道最多只能取224⨯=个数，才有可能满足题设条件. 另一方面，设所取的四个数为1、7、5、11，即满足题设条件. 综上所述，若要满足题设条件，最多能取四个两两不同的正整数.8．已知1232a a a a R ∈ 、、、、，满足12320130a a a a ++++= ，且122334201220132013122222a a a a a a a aa a -=-=-==-=- ，求证：12320130a a a a ===== .解析：根据条件知:122334************(2)(2)(2)(2)()0a a a a a a a a a a a a -+-+-++-=-++++= ，（1）另一方面，令12233421312222a a a a a a a a m -=-=-==-= ，则1223342222a a a a a a a a ---- 、、、、中每个数或为m ，或为m -.设其中有k 个m ，(2013)k -个m -，则：12233420131(2)(2)(2)(2)(2013)()(22013)a a a a a a a a k m k m k m-+-+-++-=⨯+-⨯-=- （2）由（1）、（2）知：(22013)0k m -= （3）而22013k -为奇数，不可能为0，所以0m =.于是知：12233420122013201312,2,2,,2,2a a a a a a a a a a ===== .从而知：2013112a a =⋅，即得10a =.同理可知：2320130a a a ==== .命题得证.9．对任意的θ，求632cos cos66cos 415cos 2θθθθ---的值. 解析：根据二倍角和三倍角公式知：632cos cos66cos 415cos 2θθθθ---622232cos (2cos 31)6(2cos 21)15(2cos 1)θθθθ=------63222232cos 2(4cos 3cos )162(2cos 1)115(2cos 1)θθθθθ⎡⎤⎡⎤=--------⎣⎦⎣⎦664242232cos (32cos 48cos 18cos 1)(48cos 48cos 6)(30cos 15)θθθθθθθ=--+---+--10=.10．已知有mn 个实数，排列成m n ⨯阶数阵，记作{}mxnija ，使得数阵中的每一行从左到右都是递增的，即对任意的123i m = 、、、、，当12j j <时，都有12ij ij a a ≤.现将{}mxnija 的每一列原有的各数按照从上到下递增的顺序排列，形成一个新的m n ⨯阶数阵，记作{}mxnija '，即对任意的123j n = 、、、、，当12i i <时，都有12i j i j a a ''≤.试判断{}mxnija '中每一行的n 个数的大小关系，并说明理由.解析：数阵{}mxnija '中每一行的n 个数从左到右都是递增的，理由如下：显然，我们要证数阵{}mxnija '中每一行的n 个数从左到右都是递增的，我们只需证明，对于任意123i m = 、、、、，都有(1)iji j a a +''≤，其中1231j n =- 、、、、. 若存在一组(1p qp qa a +''>.令(1)(1)k k q i q a a ++'=，其中123k m = 、、、、，{}{}123,,,,1,2,3,,m i i i i m = .则当t p ≤时，都有(1)(1)(1)tti q i q t q p q pq a a a a a +++'''≤=≤<.也即在(123iq a i = 、、、、m)中，至少有p 个数小于pq a '，也即pq a '在数阵{}mxnij a '的第q 列中，至少排在第1p +行，与pq a '排在第p 行矛盾.所以对于任意123i m = 、、、、，都有(1)iji j a a +''≤，即数阵{}mxnij a '中每一行的n 个数从左到右都是递增的.。