2019-2020学年第一学期江苏省南京市秦淮一中八年级上册期中考试题(含答案)
2019-2020学年江苏省南京市秦淮区四校联考八年级(上)期中语文试卷

2019-2020学年江苏省南京市秦淮区四校联考八年级(上)期中语文试卷一、基础(26分)1.(10分)用诗文原句或文学常识填空。
(1)树树皆秋色,。
(《野望》王绩)(2)日暮乡关何处是?。
(《黄鹤楼》崔颢)(3)庭中有奇树,。
(《庭中有奇树》《古诗十九首》)(4),壮心不已。
(《龟虽寿》曹操)(5)何夜无月?何处无竹柏?。
(《记承天寺夜游》苏轼)(6)岂不罹凝寒?。
(《赠从弟》刘桢)(7)香菱说:“《使至塞上》颈联中‘直’字似无理,‘圆’字似太俗,合上书一想,倒像是见了这景似的。
”她说的是哪一句?“,。
”(8)秋天,既有秋高气爽的舒畅也有悲悲戚戚的愁思,请写出两句“秋”相关的古诗词。
(出处不相同)2.(2分)为加点字注音,根据拼音写汉字。
溃.退yǎo无消息3.(3分)下列各句中加点成语使用错误的一项是()A.人的一生,有艰难困苦的逆境,也有峰回路转....的风景。
B.小王同学在学校辩论会上引经据典、断章取义....,赢得了大家的阵阵掌声。
C.他们两人的爱好、处事方法迥然不同....,谁也没法理解谁,谁也没法改变谁。
D.我市上下齐心协力,掀起“创卫”高潮,经过外璃粉刷、护栏改造、路面平整等系列改造,城市面貌焕然一...新。
..4.(3分)下列句子中,标点符号使用有误..的一项是()A.反腐不仅要惩治于后,更应预防于先;不仅需达到“不敢腐”“不能腐”的效果,更需激发“不想腐”“不愿腐”的自觉B.中央电视台5月1日推出的政论片《劳动铸就中国梦》,起到了鼓舞士气的宣传作用,传递出中国人民实现伟大民族复兴的中国梦的劳动情怀C.NBA总决赛正如火如荼地进行,球迷们都在纷纷竞猜骑士队和勇士队谁能夺得总冠军?D.当下新媒体以自己强大的冲击力,推出了众多的引入注目的明星﹣﹣歌星、舞星、体坛明星、政坛风云人物…5.(8分)请你阅读下面的文字,并回答问题。
2012年11月2日,江苏省扬州市某中学的一位同学,在放学骑车回家途中,不慎撞坏了一辆停在路边的轿车。
2019-2020学年八年级数学上学期期中原创卷A卷(江苏)(参考答案)

2⎨⎩⎪ 2019-2020 学年上学期期中原创卷A 卷八年级数学·参考答案7.E63958.69.910.62°11.在角的内部,到角两边距离相等的点在角的平分线上12.10 13.3 14.22.5° 15.18016.2m17. 【解析】∵AB ∥DE ,∴∠B =∠EDF ,(3 分)在△ABC 与△DEF 中,AB =DF ,∠B =∠EDF ,BC =DE ,∴△ABC ≌△FDE (SAS ),∴AC =FE .(7 分)18. 【解析】由折叠的性质,得:CD =C ′D =AB =8,∠C =∠C ′=90°.(2 分)设 DE =x ,则 AE =16–x .⎧∠A = ∠C' = 90︒ 在△ABE 和△C ′DE 中, ∠AEB = ∠C'ED, ⎪ AB = C'D ∴△ABE ≌△C ′DE ,∴BE =DE =x ,(5 分) 在 Rt △ABE 中,由勾股定理得AB 2+AE 2=BE 2,即 82+(16–x )2=x 2, 解得 x =10,即 DE =10.(7 分)19. 【解析】如图,(7 分)20. 【解析】 将长方形 ABCD 沿 EF ,GH 同时折叠, B 、C 两点恰好都落在 AD 边的 P 点处, ∴ BF = PF , PH = CH ,(2 分)∆PFH 的周长为10cm ,⎨⎩∴ PF + FH + HP = 10cm ,∴ BC = BF + FH + HC = 10cm .(6 分)又 AB = 2cm ,∴长方形 ABCD 的面积为: 2 ⨯10 = 20 (cm 2 ).(8 分)21. 【解析】(1)根据分析,水厂的位置 M 为:(3 分)(2)如图 2,在直角三角形 BEF 中,EF =CD =30(千米),BF =BD +DF =30+10=40(千米),∴BE === 50 (千米),(6 分)∴铺设水管长度的最小值为 50 千米,∴铺设水管所需费用的最小值为:50×3=150(万元).答:最低费用为 150 万元.(8 分)⎧ AB = AD22.【解析】(1)在△ABC 与△ADC 中, ⎪BC = DC , ⎪ AC =AC⎨ ⎩⎪ ∴△ABC ≌△ADC ,∴∠B =∠D ;(4 分)(2)∵△ABC ≌△ADC ,∴∠ACB =∠ACD ,∵AE ⊥BC ,AF ⊥CD ,∴AE =AF .(7 分)23. 【解析】(1)∵AF 平分∠DAC ,∴∠DAF =∠CAF ,∵AF ∥BC ,∴∠DAF =∠B ,∠CAF =∠ACB ,∴∠B =∠ACB ,∴△ABC 是等腰三角形;(4 分)(2)∵AB =AC ,∠B =40°,∴∠ACB =∠B =40°,∴∠BAC =100°,∴∠ACE =∠BAC +∠B =140°,(6 分) ∵CG 平分∠ACE ,∴ ∠ACG = 1∠ACE =70°,2∵AF ∥BC ,∴∠AGC =180°﹣∠BCG =70°.(8 分)24. 【解析】(1)∵AE ⊥AB ,AF ⊥AC ,∴∠BAE =∠CAF =90°,∴∠BAE +∠BAC =∠CAF +∠BAC ,即∠EAC =∠BAF ,⎧ AE = AB在△ABF 和△AEC 中, ∠EAC = ∠BAF , ⎪ AF = AC ∴△ABF ≌△AEC (SAS ),∴EC =BF ;(4 分)(2)如图,根据(1),△ABF ≌△AEC ,∴∠AEC =∠ABF ,∵AE ⊥AB ,∴∠BAE =90°,∴∠AEC +∠ADE =90°,∵∠ADE =∠BDM (对顶角相等),∴∠ABF +∠BDM =90°,在△BDM 中,∠BMD =180°﹣∠ABF ﹣∠BDM =180°﹣90°=90°,所以 EC ⊥BF .(8 分)25. 【解析】∵CD ⊥AC ,∴∠ACD =90°,∵∠ABD =135°,∴∠DBC =45°,(4 分)2 2 7 2 14 ∴∠D =45°,∴CB =CD ,(6 分)在 Rt △DCB 中:CD 2+BC 2=BD 2,2CD 2=8002,CD =400 ≈566(米),答:直线 l 上距离 D 点 566 米的 C 处开挖.(8 分)26. 【解析】(1)∵AD 平分∠BAC ,DE ⊥AB 于点 E ,DF ⊥AC 于点 F ,∴DE =DF ,(2 分)又∵DE ⊥AB 于点 E ,DF ⊥AC 于点 F ,∴∠AED =∠AFD =90°, 又∵AD =AD ,∴Rt △ADE ≌Rt △ADF (HL ),∴AE =AF ;(4 分)(2)∵∠MDN +∠BAC =180°,∴∠AMD +∠AND =180°,又∵∠DNF +∠AND =180°,∴∠EMD =∠FND ,(6 分) 又∵∠DEM =∠DFN ,DE =DF ,∴△DEM ≌△DFN , ∴S △DEM =S △DFN ,∴S 四边形 AMDN =S 四边形 AEDF ,(8 分)∵AD =6,DF =2 ,∴Rt △ADF 中,AF= 2 ,∴ S △ADF= 1 AF ⨯ DF = 1⨯ 2 7 ⨯ 2 = 2 , 2 2∴S 四边形 AMDN =S 四边形 AEDF = 2⨯ S △ADF = 4 .(9 分)27.【解析】(1)∵∠BAC =∠DAE =90°,∴∠BAE +∠CAE =∠BAE +∠BAD ,∴∠CAE =∠BAD ,又∵AB =AC ,AD =AE ,∴△ADB ≌△AEC (SAS );(4 分)(2) 由(1)得△ADB ≌△AEC ,∴∠C =∠ABD ,又∵∠ABC +∠C =90°,∴∠ABC +∠ABD =90°,∴DB ⊥BC ;(7 分)(3) 作 BE ⊥BD ,交 DC 的延长线于点 E ,14∵BE ⊥BD ,∴∠CBE +∠DBC =90°,又∵∠ABD +∠DBC =90°,∴∠ABD =∠EBC ,(9 分)∵∠BAD +∠BCD =180°,∠BCE +∠BCD =180°,∴∠BAD =∠BCE ,又∵BA =BC ,∴△BAD ≌△BCE (ASA ),∴BD =BE ,且 S △BAD =S △BCE , 1 ∴S 四边形 ABCD =S △ABD +S △DBC =S △BCE +S △BCD =S △BDE =2×7×7=24.5(cm 2).(11 分)。
江苏省南京市秦淮区(四校联考)2019-2020学年上学期初二数学期中试卷(PDF 有答案)
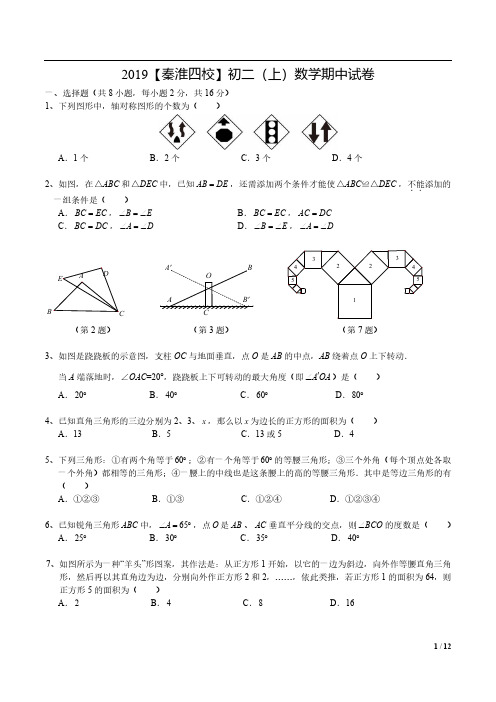
2019【秦淮四校】初二(上)数学期中试卷一、选择题(共8小题,每小题2分,共16分) 1、下列图形中,轴对称图形的个数为( )A .1个B .2个C .3个D .4个2、如图,在ABC △和DEC △中,已知AB DE =,还需添加两个条件才能使ABC DEC △≌△,不能..添加的一组条件是( )A .BC EC =,B E ∠=∠ B .BC EC =,AC DC = C .BC DC =,AD ∠=∠ D .BE ∠=∠,A D ∠=∠(第2题) (第3题) (第7题)3、如图是跷跷板的示意图,支柱OC 与地面垂直,点O 是AB 的中点,AB 绕着点O 上下转动. 当A 端落地时,∠OAC =20°,跷跷板上下可转动的最大角度(即A OA '∠)是( )A .20︒B .40︒C .60︒D .80︒4、已知直角三角形的三边分别为2、3、x ,那么以x 为边长的正方形的面积为( ) A .13 B .5 C .13或5 D .45、下列三角形:①有两个角等于60︒;②有一个角等于60︒的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A .①②③B .①③C .①②④D .①②③④6、已知锐角三角形ABC 中,65A ∠=︒,点O 是AB 、AC 垂直平分线的交点,则BCO ∠的度数是( )A .25︒B .30︒C .35︒D .40︒7、如图所示为一种“羊头”形图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2和2,……,依此类推,若正方形1的面积为64,则正方形5的面积为( )A .2B .4C .8D .168、如图,在Rt ABC △中,90ACB ∠=︒,6AC =,8BC =,AD 是BAC ∠的平分线.若P 、Q 分别是AD 和AC 上的动点,则PC PQ +的最小值为( ) A .245 B .4 C .125D .5(第8题) (第9题) (第13题)二、填空题(共10小题,每小题2分,共20分)9、如图,若ABE ACD △≌△,且65A ∠=︒,20C ∠=︒,则AEB ∠=_____________︒.10、若等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为_____________.11、若ABC △的三边长分别为a ,b ,c .下列条件:①A B C ∠=∠-∠;②()()2a b c b c =+-;③::3:4:5A B C ∠∠∠=;④::5:12:13a b c =.其中能判断ABC △是直角三角形的是_____________(填序号).12、若直角三角形的两直角边的长分别为5和12,则斜边上的中线是_____________.13、如图,在ABC △中,AB AC =,D 为BC 中点,且=20BAD ∠︒,则C ∠的度数是_____________°.14、在Rt ABC △中,90C ∠=︒,30B ∠=︒,4AB =cm ,则AC 的长度是_____________cm .15、如图,在Rt △ABC 中,90BCA ∠=︒,点D 是BC 上一点,AD =BD ,若AB =8,BD =5,则CD 的长是_____________.(第15题) (第17题)16、在ABC △中,60ABC ∠=︒,70ACB ∠=︒,若点O 到三边的距离相等,则BOC ∠=_____________°.17、在ABC △中,5AB AC ==,6BC =,若点P 在边AB 上移动,则CP 的最小值是_____________.18、在ABC △中,AB =5,AC =4,BC =3.若点P 在ABC △内部(含边界)且满足PC PA PB ≤≤,则所有点P 组成的区域的面积为_____________.AB三、解答题(共9小题,共64分)19、(6分)如图,点C、D在AB上,且AC=BD,AE=FB,AE∥BF,求证:△AED≌△BFC.20、(6分)如图,4 5的方格纸中,请你用三种不同的方法在除阴影之外的方格中任意选择一个涂黑,使得图中阴影部分构成的图形是轴对称图形.21、(6分)∠BAC为钝角,CD⊥AB,BE⊥AC,垂足分别为D、E,M是BC中点,求证:ME=MD.AB ED22、(8分)如图,在△ABC 中,AB =AC ,∠A =48°,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE =CF ,BD =CE ,求∠EDF 的度数.23、(7分)如图,在△ABC 中,∠ACB =90°,用直尺和圆规在斜边AB 上作一点P ,使得点P 到点B 的距离与点P到边AC 的距离相等.(保留作图痕迹,不写作法)AB24、(9分)如图,在ABC △中,∠C =90°,点P 在AC 上运动,点D 在AB 上,PD 始终保持与P A 相等,BD 的垂直平分线交BC 于点E ,交BD 于点F ,连接DE . ⑴判断DE 与DP 的位置关系,并说明理由;⑵若6AC =,8BC =,2PA =,求线段DE 的长.25、(10分)在△ABC 中,AB 、AC 边的垂直平分线分别交BC 边于点M 、N .⑴如图① ,若222BM CN MN ,则∠BAC = °;⑵如图②,∠ABC 的平分线BP 和AC 边的垂直平分线相交于点P ,过点P 作PH 垂直BA 的延长线于点H ,若AB =4,CB =10,求AH 的长.图① 图②FADB26、(12分) 【引例】 如图1,点A 、B 、D 在同一条直线上,在直线同侧作两个等腰直角三角形△ABC 和△BDE ,BA =BC ,BE =BD ,连接AE 、CD .则AE 与CD 的关系是_____________.图1【模型建立】如图2,在△ABC 和△BDE 中,BA =BC ,BE =BD ,∠ABC =∠DBE =α,连接AE 、CD 相交于点H . 求证:①AE =CD ;②∠AHC =α.图2【拓展应用】如图3,在四边形ABCD 中,对角线AC 与BD 交于点O ,∠BDC =90°,BD =CD ,∠BAD =45°.若AB =3,AD =4,求2AC 的值.图3AB2019【秦淮四校】初二(上)数学期中试卷一、选择题(共8小题,每小题2分,共16分)题号 1 2 3 4 5 6 7 8 答案BCBCDABA二、填空题(共10小题,每小题2分,共20分)【备注】第16题:若考虑点O 在三角形外,则另有3种情况,感兴趣的同学可自行研究,分别是25°,65°,115°. 第18题:先证明一个引例:当P 点在线段AB 垂直平分线左侧,则P A <PB , 证明如下:延长AP 交线段AB 的垂直平分线l 于点D ,连接DB ∵D 在线段AB 的垂直平分线上 ∴DA =DB∴AP =AD -PD =DB -PD在△PDB 中,两边之差小于第三边 ∴DB -PD <PB ∴P A <PB解:由18题题意得,P 点在如图所示的阴影三角形内设CF =x ,则AF =BF =4x -,在△BCF 中由勾股定理列方程,可得CF =78,则DF =98,S △DEF =1932728232⨯⨯=.三、解答题(共9小题,共64分) 19、(6分)证明:∵AE ∥BF ,∴∠A =∠B . 又∵AC =BD ,∴AC +CD =BD +CD ,即AD =BC . 在△AED 和△BFC 中,AE BF A B AD BC =⎧⎪∠=∠⎨⎪=⎩∴△AED ≌△BFC (SAS ).A F解:如图所示,共有4种情况(任选3个即可):21、(6分)证明:∵CD ⊥AB ,BE ⊥AC ,∴∠BEC =90°,∠BDC =90°,∵在Rt △EBC 和Rt △DBC 中,M 为斜边BC 中点;∴ME =12BC ,MD =12BC ,∴ME =MD . 22、(8分)解:∵AB =AC ,∠A =48°∴∠B =∠C =66°在△BED 和△CFE 中BD CE B C BE CF⎧=⎪⎪∠=∠⎨⎪=⎪⎩ ∴△BED ≌△CFE (SAS )∴∠BDE =∠CEF ,∠DEB =∠EFC ,ED =FE ∴∠EDF =∠EFD∵∠B +∠BDE +∠DEB =180° ∠DEF +∠CEF +∠DEB =180° ∴∠DEF =∠B =66°在△EDF 中,∠DEF +∠EDF +∠EFD =180° ∴∠EDF =()118066572︒-︒=︒. 23、(7分)方法一:①作∠B 的平分线交AC 于点D ,②过点D 作AC 的垂线交AB 于点P 或作BD ∴点P 即为所求.(右图为示意图,作图痕迹略)方法二:①过点B 作AB 的垂线交AC 的延长线于点D ,②作∠ADB 的平分线交AB 于点P , ∴点P 即为所求.(右图为示意图,作图痕迹略)⑴ DP DE ⊥,理由如下:∵PA PD =∴PAD PDA ∠=∠ ∵EF 垂直平分BD ∴ED EB =∴EDB EBD ∠=∠在ABC △中,90C ∠=︒,180C PAD EBD ∠+∠+∠=︒, ∴90PAD EBD ∠+∠=︒ ∴90PDA EDB ∠+∠=︒∵180PDE PDA EDB ∠+∠+∠=︒ ∴90PDE ∠=︒,即DP DE ⊥. ⑵ 解:连接PE∵2PA =,6AC = ∴4PC = ∵PA PD = ∴2PD = 设DE x = ∵DE BE = ∴BE x = ∵8BC =∴8CE BC BE x =-=-Rt PCE △中,90C ∠=︒,则()2222=168PE PC CE x =++-Rt PDE △中,90PDE ∠=︒,则2222=4PE PD DE x =++∴()221684x x +-=+,解得194x =,即194DE =.25、(10分)⑴ 解:连接MA 、NA ∵AB 、AC 边的垂直平分线分别交BC 于点M 、N∴BM=AM ,CN=AN∴∠B =∠BAM ,∠C =∠CAN ∵222BM CN MN ∴222AM AN MN += ∴△AMN 是直角三角形又∵∠AMN =∠B+∠BAM , ∠ANM=∠C +∠CANFABCMN∴∠AMN =2∠B ,∠ANM=2∠C∴∠AMN+∠ANM=2(∠B +∠C )=90° ∴∠B +∠C=45°∴∠BAC=180°-(∠B +∠C )=180°-45°=135°.⑵ 解:如图,连接P A 、PC ,过点P 作PQ ⊥BC 于点Q , ∵PN 垂直平分AC ∴P A =PC∵BP 平分∠ABC ∴∠HBP =∠QBP ∵PH ⊥BH ,PQ ⊥BC ∴∠BHP =∠BQP =90° 在△BHP 和△BQP 中HBP QBP BHP BQP BP BP ∠=∠∠=∠=⎧⎪⎨⎪⎩∴△BHP ≌△BQP (AAS) ∴PH =PQ ,BH =BQ在Rt △AHP 和Rt △CQP 中PA PCPH PQ =⎧⎨=⎩∴Rt △AHP 和Rt △CQP (HL)∴AH =CQ设AH =x ,则QC = x ∵AB=4,BC=10∴BH=4+x ,BQ=10-x ∴4+x =10-x ,解得x=3,即AH=3.26、(12分)【引例】AE =CD ,AE ⊥CD ; 【模型建立】① ∵∠ABC =∠DBE∴∠ABC +∠CBE =∠DBE +∠CBE 即∠ABE =∠CBD , 在△ABE 和△CBD 中,AB CB ABE CBD EB DB =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CBD (SAS ) ∴AE =CD .② 设AE 与BC 交于点O ,A11 / 12 ∵△ABE ≌△CBD ,∴∠EAB =∠DCB ,在△AOB 和△COH 中,∠OAB +∠AOB +∠ABO =180°,∠OCH +∠COH +∠OHC =180°,∵∠AOB =∠COH∴∠OHC =∠OBA ,即∠AHC =α.【拓展应用】如图,作DE ⊥AD ,截取DE =AD ,连接AE 、BE ,则∠ADE =90°,∠DAE =45°,∴∠EDA +∠ADB =∠BDC +∠ADB即∠EDB =∠ADC ,在△EDB 和△ADC 中,∴△EDB ≌△ADC (SAS )∴EB =AC∵∠BAD =45°∴∠EAB =∠EAD +∠DAB =90°在Rt △EAB 中,由勾股定理得222AE AB BE +=,在Rt △ADE 中,由勾股定理得222AD DE AE +=,∵AD =4,AB =3∴232AE =∴241BE =∴241AC =.ED AD EDB ADCBD CD=⎧⎪∠=∠⎨⎪=⎩。
2019-2020学年第一学期江苏省南京市秦淮一中八年级上册期中考试题(PDF版)

2019-2020八上期中考试秦淮区(一中)一、基础部分(27分)1.从下面两幅字中任选一幅临写。
(3分)和颜悦色锐不可当2.下列加点字注音完全正确的一项是( )(3分)A. 篡.(cuàn)改畸.形(qí)教诲.(huì)杳.无消息(yǎo)B. 镌.(juān)刻粗糙.(zào)悄.(qiǎo)然深恶.(wù)痛疾C. 解剖.(pōu)绯.红(fēi)咆.(páo)哮抑.扬顿挫(yì)D. 诘.(jié)责匿.名(nì)翘.(qiáo)首锐不可当.(dǎng)3.下列词语书写全都正确的一项是( )(3分)A.泄气浩翰由衷一丝不苟B.遁形杀戮娴熟诚惶诚恐C.落弟黝黑崎岖任劳任怨D.呓语躁热窒息筋疲力尽4.下列划线词语运用不恰当的一项是( )(3分)A.他们白手起家,在荒滩上盖起了厂房。
B.工程师和设计师们殚精竭虑,耗费了四年时间,终于实现了这个目标。
C.看了这封信,他才如梦初醒,方知自己上当受骗。
D.摇滚乐那强烈快速的节奏和迷离闪烁的灯光效果,让人眼花缭乱。
5.下列文学常识中表述错误的一项是( )(3分)A.三峡是瞿塘峡、巫峡和虎跳峡的总称,在长江上游重庆奉节和湖北宜昌之间。
B.苏轼,字子瞻,号东坡居士,眉山人,北宋文学家。
《记承天寺夜游》一文写于作者贬官黄州期间。
C.消息正文的结构通常是按照重要性递减的原则安排的,即所谓“倒金字塔结构”。
D.居里夫人是法国物理学家、化学家,原籍波兰,先后获1903年诺贝尔物理学奖和1911年诺贝尔化学奖。
6.用诗文原句填空。
(12分)(1)庭中有奇树,________________。
(《庭中有奇树•古诗十九首》)(2)________________,志在千里。
(曹操《龟虽寿》)(3)冰霜正惨凄,________________。
(刘桢《赠从弟》)(4)________________,狐兔翔我宇。
2023学年南京市秦淮区八年级语文(上)期中考试卷附答案解析

2023学年南京市秦淮区八年级语文(上)期中考试卷一、基础知识综合1.阅读下面的语段,回答问题。
今年亚运会女子10米台决赛中,全红婵第二跳407C的动作表现十分完美。
当全红婵高高跃起时,现场的中国观众一齐翘()首而望、屏()息liǎn()声,砰地一声落水,完美展示了何为“水花消失术”,现场7名栽判一致打出了10分的满分。
为了这一天,多少人dān()精竭虑啊。
(1)给加点字注音或根据拼音写汉字。
翘首而望屏息liǎn声dān 精竭虑(2)语段中有个错别字。
应将改为。
二、名句名篇默写2.根据要求默写。
漫步于古诗文的殿堂,我们观赏钱塘湖“几处早莺争暖树,(1)”的初春美景;欣赏东皋“树树皆秋色,(2)”的山野秋景;看到了三峡“(3),回清倒影”的春冬之水;听到了富春江“(4),猿则百叫无绝”的天籁之音;感受到刘桢借松树的刚劲,明志向之坚贞的“(5)?(6)”(《赠从弟》),而老当益壮的曹操则借物喻人向我们传递积极进取的人生态度“(7),(8)”(《龟虽寿》)。
三、综合性学习3.小淮同学参加主题为“诚信做人”的综合性活动,请你和他一起完成任务。
诚信是中华民族的传统美德之一,也是社会主义核心价值观之一。
在古人眼中,“信”是立信之本,交友之道、经商之魂、为政之要;在现代社会,诚信是公民的第二张身份证。
(1)【探诚信之义】为了探究诚信的传统内涵,小淮同学搜集了关于“信”的名言和故事,请你选出不符合要求的一项()A.贞信以昭,其乃得人。
B.一言既出,驷马难追。
C.商鞅立木。
D.韦编三绝。
(2)【报诚信之事】请你帮小淮同学用简洁的语言概括新闻的主要内容。
受到共享单车的启发,中国传媒大学经管学部学生开展了“共享雨伞”活动,把印有“诚信”图标的黑色长柄雨伞放置在教学楼大厅供同学们自由取用、自觉归还。
近日,在该校“培育和践行社会主义核心价值观系列活动”总结表彰会上,“共享雨伞”获评“诚信主题教育年特色项目”。
(3)【办诚信之赛】小秦为本次活动拟写了一则通知,通知中内容和形式上各有一处错误,请你指出来。
苏科版江苏省南京市八年级(上)期中数学试卷含答案解析版

2019-2020学年苏科版江苏省南京市八年级(上)期中数学试卷一.填空题(每题3分,共30分)1.下列图形中:①平行四边形;②有一个角是30°的直角三角形;③长方形;④等腰三角形.其中是轴对称图形有()个.A.1个B.2个C.3个D.4个2.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,若∠A+∠C=90°,则下列等式中成立的是()A.a2+b2=c2B.b2+c2=a2C.a2+c2=b2D.c2﹣a2=b23.下列四个数中,是负数的是()A.|﹣2|B.(﹣2)2C.﹣D.4.如果a、b、c是一个直角三角形的三边,则a:b:c等于()A.1:2:4B.1:3:5C.3:4:7D.5:12:135.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是()A.40°B.35°C.25°D.20°6.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于()A.4B.3C.2D.17.已知,则的值是()A.457.3B.45.73C.1449D.144.98.等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的底长为()A.3cm或5cmB.3cm或7cmC.3cmD.5cm9.在Rt△ABC中,AC=6,BC=8,分别以它的三边为直径向上作三个半圆,则阴影部分面积为()A.24B.24πC.D.10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为()A.90B.100C.110D.121二、填空题(每空3分,共30分)11.的平方根是.12.已知一个正数的两个不同的平方根是3x﹣2和4﹣x,则x=.13.已知x<1,则化简的结果是.14.黑板上写着在正对着黑板的镜子里的像是.15.在平面直角坐标系中,若点M(﹣2,6)与点N(x,6)之间的距离是3,则x的值是.16.若直角三角形的两直角边之和为7,面积为6,则斜边长为.17.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=25°,则∠ADE=°.18.如图,在△ABC中,AB=AC=5cm,AB的垂直平分线交AB于点D,交BC于点E,若△ACE的周长是12cm,则△ABC的周长是.19.直角三角形三角形两直角边长为5和12,三角形内一点到各边距离相等,那么这个距离为.20.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q 分别是AD和AE上的动点,则DQ+PQ的最小值是.三.解答题21.计算:(1)﹣|1﹣|+()2﹣(2)﹣32+(﹣1)2016+(﹣π)0﹣﹣(﹣)﹣2.22.求下列各式中的x的值:(1)4(2x﹣1)2=(2)8(x3+1)=﹣56.23.如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;(2)五边形ACBB′C′的周长为;(3)四边形ACBB′的面积为;(4)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为.24.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.25.如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D 为AB边上的一点,若AB=17,BD=12,(1)求证:△BCD≌△ACE;(2)求DE的长度.26.如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.27.如图,△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,且ME=MF.(1)求证:BE⊥AC;(2)若∠A=50°,求∠FME的度数.28.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为线段BC上的一动点,当BP为何值时,△DEP为等腰三角形.请求出所有BP的值.29.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.(1)求三角形ABC的面积.(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.2019-2020学年苏科版江苏省南京市八年级(上)期中数学试卷参考答案与试题解析一.填空题(每题3分,共30分)1.下列图形中:①平行四边形;②有一个角是30°的直角三角形;③长方形;④等腰三角形.其中是轴对称图形有()个.A.1个B.2个C.3个D.4个考点:轴对称图形.分析:根据轴对称图形的概念求解.解答:解:①、②不是轴对称图形;③长方形是轴对称图形;④等腰三角形是轴对称图形.共2个.故选B.点评:轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.2.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,若∠A+∠C=90°,则下列等式中成立的是()A.a2+b2=c2B.b2+c2=a2C.a2+c2=b2D.c2﹣a2=b2考点:勾股定理.专题:计算题.分析:由已知两角之和为90度,利用三角形内角和定理得到三角形为直角三角形,利用勾股定理即可得到结果.解答:解:∵在△ABC中,∠A+∠C=90°,∴∠B=90°,∴△ABC为直角三角形,则根据勾股定理得:a2+c2=b2.故选C点评:此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.3.下列四个数中,是负数的是()A.|﹣2|B.(﹣2)2C.﹣D.考点:实数的运算;正数和负数.专题:计算题.分析:根据绝对值的性质,有理数的乘方的定义,算术平方根对各选项分析判断后利用排除法求解.解答:解:A、|﹣2|=2,是正数,故本选项错误;B、(﹣2)2=4,是正数,故本选项错误;C、﹣<0,是负数,故本选项正确;D、==2,是正数,故本选项错误.故选C.点评:本题考查了实数的运用,主要利用了绝对值的性质,有理数的乘方,以及算术平方根的定义,先化简是判断正、负数的关键.4.如果a、b、c是一个直角三角形的三边,则a:b:c等于()A.1:2:4B.1:3:5C.3:4:7D.5:12:13考点:勾股定理.专题:计算题.分析:将四个选项的数字按照勾股定理进行计算,符合a2+b2=c2的即为正确答案.解答:解:A、∵12+22≠42,∴1:2:4不是直角三角形的三条边;故本选项错误;B、∵12+32≠42,∴1:3:5不是直角三角形的三条边;故本选项错误;C、∵32+42≠72,∴3:4:7不是直角三角形的三条边;故本选项错误;D、∵52+122=132,∴1:2:4是直角三角形的三条边;故本选项正确.故选D.点评:本题考查了勾股定理,符合a2+b2=c2的三条边才能构成直角三角形.5.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是()A.40°B.35°C.25°D.20°考点:等腰三角形的性质.分析:先根据等腰三角形的性质及三角形内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可.解答:解:∵△ABC中,AC=AD,∠DAC=80°,∴∠ADC==50°,∵AD=BD,∠ADC=∠B+∠BAD=50°,∴∠B=∠BAD=()°=25°.故选C.点评:此题比较简单,考查的是等腰三角形的性质及三角形内角和定理.6.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于()A.4B.3C.2D.1考点:菱形的判定与性质;含30度角的直角三角形.专题:几何图形问题.分析:过点P做PM∥CO交AO于M,可得∠CPO=∠POD,再结合题目推出四边形P为菱形,即可得PM=4,又由CO∥PM可得∠PMD=30°,由直角三角形性质即可得PD.解答:解:如图:过点P做PM∥CO交AO于M,PM∥CO∴∠CPO=∠POD,∠AOP=∠BOP=15°,PC∥OA∴四边形P为菱形,PM=4PM∥CO⇒∠PMD=∠AOP+∠BOP=30°,又∵PD⊥OA∴PD=PC=2.令解:作CN⊥OA.∴CN=OC=2,又∵∠CNO=∠PDO,∴CN∥PD,∵PC∥OD,∴四边形CNDP是长方形,∴PD=CN=2故选:C.点评:本题运用了平行线和直角三角形的性质,并且需通过辅助线求解,难度中等偏上.7.已知,则的值是()A.457.3B.45.73C.1449D.144.9考点:算术平方根.分析:把的被开方的小数点向右移动4位,则其平方根的小数点向右移动2位,即可得到=144.9.解答:解:∵==100,而=1.449,∴=1.449×100=144.9.故选D.点评:本题考查了算术平方根:若一个正数的平方等于a,那么这个数叫a的算术平方根,记作(a≥0).8.等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的底长为()A.3cm或5cmB.3cm或7cmC.3cmD.5cm考点:等腰三角形的性质;三角形三边关系.分析:已知的边可能是腰,也可能是底边,应分两种情况进行讨论.解答:解:当腰是3cm时,则另两边是3cm,9cm.而3+3<9,不满足三边关系定理,因而应舍去.当底边是3cm时,另两边长是6cm,6cm.则该等腰三角形的底边为3cm.故选:C.点评:本题从边的方面考查三角形,涉及分类讨论的思想方法.9.在Rt△ABC中,AC=6,BC=8,分别以它的三边为直径向上作三个半圆,则阴影部分面积为()A.24B.24πC.D.考点:勾股定理.专题:数形结合.分析:先求出直角三角形的斜边,再利用:阴影部分面积=两个小半圆面积+直角三角形面积﹣以斜边为直径的大半圆面积.解答:解:在Rt△ABC中,AC=6,BC=8,AB===10,S阴影=π()2+π()2+×6×8﹣π()2=+8π+24﹣=24.故选A.点评:本题考查勾股定理的知识,难度一般,解答本题的关键是利用勾股定理得出AB的长及找出阴影部分面积的表示,另外本题也进一步验证了勾股定理.10.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为()A.90B.100C.110D.121考点:勾股定理的证明.专题:常规题型;压轴题.分析:延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.解答:解:如图,延长AB交KF于点O,延长AC交GM于点P,所以四边形AOLP是正方形,边长AO=AB+AC=3+4=7,所以KL=3+7=10,LM=4+7=11,因此矩形KLMJ的面积为10×11=110.故选:C.点评:本题考查了勾股定理的证明,作出辅助线构造出正方形是解题的关键.二、填空题(每空3分,共30分)11.的平方根是.【考点】平方根.【分析】根据平方根,即可解答.【解答】解:=5,5的平方根是,故答案为:.12.已知一个正数的两个不同的平方根是3x﹣2和4﹣x,则x=﹣1.【考点】平方根.【分析】根据一个正数的平方根互为相反数,可得平方根的和为0,可得一元一次方程,根据解方程,可得x的值.【解答】解:已知一个正数的两个不同的平方根是3x﹣2和4﹣x,(3x﹣2)+(4﹣x)=0,解得x=﹣1,故答案为:﹣1.13.已知x<1,则化简的结果是1﹣x.【考点】二次根式的性质与化简.【分析】根据二次根式的性质化简得=|x﹣1|,由于x<1,然后根据绝对值的意义去绝对值即可.【解答】解:==|x﹣1|,∵x<1,∴=1﹣x.故答案为1﹣x.14.黑板上写着在正对着黑板的镜子里的像是50281.【考点】镜面对称.【分析】根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.【解答】解:根据镜面对称的性质,因此18502的真实图象应该是50281.故答案为:50281.15.在平面直角坐标系中,若点M(﹣2,6)与点N(x,6)之间的距离是3,则x的值是1或﹣5.【考点】坐标与图形性质.【分析】根据两点间的距离公式,可得答案.【解答】解:由MN==3,得|2+x|=3,解得x=1或x=﹣5,故答案为:1或﹣5.16.若直角三角形的两直角边之和为7,面积为6,则斜边长为5.【考点】勾股定理.【分析】可设直角三角形一直角边为x,则另一直角边为7﹣x,由面积为6作为相等关系列方程求得x的值,进而求得斜边的长.【解答】解:设直角三角形一直角边为x,则另一直角边为7﹣x,根据题意得x(7﹣x)=6,解得x=3或x=4,所以斜边长为=5,故答案为:5.17.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=25°,则∠ADE=40°.【考点】三角形内角和定理.【分析】根据三角形内角和定理可得∠B=65°,再由折叠可得∠CED的度数,再根据三角形外角的性质可得∠EDA的度数.【解答】解:∵在△ABC中,∠ACB=90°,∠A=25°,∴∠B=180°﹣90°﹣25°=65°,根据折叠可得∠CED=65°,∴∠EDA=65°﹣65°﹣25°=40°,故答案为:40.18.如图,在△ABC中,AB=AC=5cm,AB的垂直平分线交AB于点D,交BC于点E,若△ACE的周长是12cm,则△ABC的周长是17cm.【考点】线段垂直平分线的性质;等腰三角形的性质.【分析】由AB的垂直平分线交AB于点D,交BC于点E,易得AE=BE,又由△ACE的周长是12cm,可求得AC+BC=12cm,继而求得答案.【解答】解:∵DE是AB的垂直平分线,∴AE=BE,∵△ACE的周长是12cm,∴AC+AE+CE=AC+BE+CE=AC+BC=12cm,∵AB=AC=5cm,∴△ABC的周长是:AB+AC+BC=5+12=17(cm).故答案为:17cm.19.直角三角形三角形两直角边长为5和12,三角形内一点到各边距离相等,那么这个距离为2.【考点】角平分线的性质.【分析】连接OA,OB,OC利用小三角形的面积和等于大三角形的面积即可解答.【解答】解:由勾股定理得:AB=13,连接OA,OB,OC,则点O到三边的距离就是△AOC,△BOC,△AOB的高线,设到三边的距离是x,则三个三角形的面积的和是:AC•x+BC•x+AB•x=AC•BC,就可以得到x=2,故答案为:2.20.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q 分别是AD和AE上的动点,则DQ+PQ的最小值是2.【考点】轴对称-最短路线问题;正方形的性质.【分析】过D作AE的垂线交AE于F,交AC于D′,再过D′作AP′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.【解答】解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,∴D′是D关于AE的对称点,AD′=AD=4,∴D′P′即为DQ+PQ的最小值,∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,P′D′2+AP′2=AD′2,AD′2=16,∵AP′=P′D',2P′D′2=AD′2,即2P′D′2=16,∴P′D′=2,即DQ+PQ的最小值为2,故答案为:2.三.解答题21.计算:(1)﹣|1﹣|+()2﹣(2)﹣32+(﹣1)2016+(﹣π)0﹣﹣(﹣)﹣2.【考点】实数的运算;零指数幂;负整数指数幂.【分析】(1)原式利用平方根、立方根定义,以及绝对值的代数意义化简,计算即可得到结果;(2)原式利用乘方的意义,零指数幂、负整数指数幂法则,以及立方根定义计算即可得到结果.【解答】解:(1)原式=2﹣+1+9+=13.5﹣;(2)原式=﹣9+1+1﹣4﹣4=﹣15.22.求下列各式中的x的值:(1)4(2x﹣1)2=(2)8(x3+1)=﹣56.【考点】立方根;平方根.【分析】(1)先算算术平方根,再系数化为1,再根据平方根即可解答;(2)先系数化为1,再根据立方根即可解答.【解答】解:(1)4(2x﹣1)2=,4(2x﹣1)2=9,(2x﹣1)2=,2x﹣1=±,解得x1=﹣,x2=;(2)8(x3+1)=﹣56,x3+1=﹣7,x3=﹣8,x=﹣2.23.如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;(2)五边形ACBB′C′的周长为4+2+2;(3)四边形ACBB′的面积为7;(4)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为.【考点】作图-轴对称变换;轴对称-最短路线问题.【分析】(1)根据轴对称的性质,可作出△ABC关于直线l成轴对称的△AB′C′;(2)由勾股定理即可求得AC与BC的长,由对称性,可求得其它边长,继而求得答案;(3)由S△ABC =S梯形AEFB﹣S△AEC﹣S△BCF,可求得△ABC的面积,易求得△ABB′的面积,继而求得答案;(4)由点B′是点B关于l的对称点,连接B′C,交l于点P,然后由B′C的长即可.【解答】解:(1)如图:△AB′C′即为所求;(2)∵AC′=AC==2,BC=BC′==,BB′=2,∴五边形ACBB′C′的周长为:2×2+2×+2=4+2+2;故答案为:4+2+2;(3)如图,S△ABC =S梯形AEFB﹣S△AEC﹣S△BCF=×(1+2)×4﹣×2×2﹣×2×1=3,S△ABB′=×2×4=4,∴S四边形ACBB′=S△ABC+S△ABB′=3+4=7.故答案为:7;(4)如图,点B′是点B关于l的对称点,连接B′C,交l于点P,此时PB+PC的长最短,∴PB=PB′,∴PB+PC=PB′+PC=B′C==.故答案为:.24.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.【考点】全等三角形的判定与性质;等腰三角形的判定与性质.【分析】由已知条件,根据等腰三角形三线合一这一性质,CE=FE,再证明△ABD ≌△ACF,证得BD=CF,从而证得BD=2CE.【解答】证明:∵BE平分∠FBC,BE⊥CF,∴BF=BC,∴CE=EF,∴CF=2CE,∵∠BAC=90°,且AB=AC,∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,∴∠FBE=∠CBE=22.5°,∴∠F=∠ADB=67.5°,在△ABD和△ACF中,∵,∴△ABD≌△ACF(AAS),∴BD=CF,∴BD=2CE.25.如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D 为AB边上的一点,若AB=17,BD=12,(1)求证:△BCD≌△ACE;(2)求DE的长度.【考点】全等三角形的判定与性质;等腰直角三角形.【分析】(1)根据等腰直角三角形得出AC=BC,CE=CD,∠ACB=∠ECD=90°,求出∠BCD=∠ACE,根据SAS推出△BCD≌△ACE即可.(2)求出AD=5,根据全等得出AE=BD=12,在Rt△AED中,由勾股定理求出DE 即可.【解答】(1)证明:∵△ACB与△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∵∠ACB=∠ECD=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,∴∠BCD=∠ACE,在△BCD和△ACE中∴△BCD≌△ACE(SAS).(2)解:由(1)知△BCD≌△ACE,则∠DBC=∠EAC,∵∠CAD+∠DBC=90°,∴∠EAC+∠CAD=90°,即∠EAD=90°∵AB=17,BD=12,∴AD=17﹣12=5,∵△BCD≌△ACE,∴AE=BD=12,在Rt△AED中,由勾股定理得:DE===13.26.如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.【考点】翻折变换(折叠问题).【分析】利用勾股定理逆定理求出∠ACB=90°,根据翻转变换的性质可得AB′=AB,B′D=BD,然后求出B′C,设CD=x,表示出B′D,再利用勾股定理列方程求出x,最后根据三角形的面积公式列式计算即可得解.【解答】解:∵AC2+BC2=62+82=100,AB2=102=100,∴AC2+BC2=AB2,∴△ABC是直角三角形,∠ACB=90°,∵△ABC折叠AB落在直线AC上,∴AB′=AB=10,B′D=BD,∴B′C=AB′﹣AC=10﹣6=4,设CD=x,则B′D=BD=BC﹣CD=8﹣x,在Rt△B′CD中,由勾股定理得,B′C2+CD2=B′D2,即42+x2=(8﹣x)2,解得x=3,即CD=3,所以,阴影部分的面积=AC×CD=×6×3=9.27.如图,△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,且ME=MF.(1)求证:BE⊥AC;(2)若∠A=50°,求∠FME的度数.【考点】直角三角形斜边上的中线;等腰三角形的判定与性质.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得MF=BM=CM= BC,再求出ME=BM=CM=BC,再根据直角三角形斜边上的中线等于斜边的一半证明;(2)根据三角形的内角和定理求出∠ABC+∠ACB,再根据等腰三角形两底角相等求出∠BMF+∠CME,然后根据平角等于180°列式计算即可得解.【解答】(1)证明:∵CF⊥AB,垂足为F,M为BC的中点,∴MF=BM=CM=BC,∵ME=MF,∴ME=BM=CM=BC,∴BE⊥AC;(2)解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣50°=130°,∵ME=MF=BM=CM,∴∠BMF+∠CME=+=360°﹣2(∠ABC+∠ACB)=360°﹣2×130°=100°,在△MEF中,∠FME=180°﹣100°=80°.28.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为线段BC上的一动点,当BP为何值时,△DEP为等腰三角形.请求出所有BP的值.【考点】直角三角形斜边上的中线;平行线的判定;等腰三角形的判定.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得BD=AD=AC,再根据等腰三角形三线合一的性质可得DE⊥AB,再根据垂直于同一直线的两直线平行证明;(2)利用勾股定理列式求出DE的长,根据等腰三角形三线合一的性质求出BE=AE,然后分DE=EP、DP=EP、DE=DP三种情况讨论求解.【解答】(1)证明:∵∠ABC=90°,点D是AC的中点,∴BD=AD=AC,∵DE是∠ADB的角平分线,∴DE⊥AB,又∵∠ABC=90°,∴DE∥BC;(2)解:∵AE=3,AD=5,DE⊥AB,∴DE==4,∵DE⊥AB,AD=BD,∴BE=AE=3,①DE=EP时,BP==,②DP=EP时,BP=DE=×4=2,③DE=DP时,过点D作DF⊥BC于F,则DF=BE=3,由勾股定理得,FP==,点P在F下边时,BP=4﹣,点P在F上边时,BP=4+,综上所述,BP的值为,2,4﹣,4+.29.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.(1)求三角形ABC的面积.(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.【考点】坐标与图形性质;平行线的性质;三角形的面积.【分析】(1)根据非负数的性质得a+2=0,b﹣2=0,解得a=﹣2,b=2,则A(﹣2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;(2)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用三角形面积公式和S△PAC =S△APQ+S△CPQ=S△ABC得到•|t﹣1|•2+•|t﹣1|•2=4,然后解方程求出t即可得到P点坐标;(3)作EM∥AC,如图②,则AC∥EM∥BD,根据平行线的性质得∠CAE=∠AEM,∠BDE=∠DEM,则∠AED=∠CAE+∠BDE,而∠CAE=∠CAB,∠BDE=∠ODB,所以∠AED=(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.【解答】解:(1)∵(a+2)2+=0,∴a+2=0,b﹣2=0,解得a=﹣2,b=2,∴A(﹣2,0),C(2,2),∵CB⊥x轴,∴B(2,0),∴S△ABC=×(2+2)×2=4;(2)存在.如图③,AC交y轴于Q,则Q(0,1),设P(0,t),∵S△PAC=S△APQ+S△CPQ=S△ABC,∴•|t﹣1|•2+•|t﹣1|•2=4,解得t=3或t=﹣1,∴P点坐标为(0,3),(0,﹣1);(3)作EM∥AC,如图②,∵AC∥BD,∴AC∥EM∥BD,∴∠CAE=∠AEM,∠BDE=∠DEM,∴∠AED=∠CAE+∠BDE,∵AE,DE分别平分∠CAB,∠ODB,∴∠CAE=∠CAB,∠BDE=∠ODB,∴∠AED=(∠CAB+∠ODB),∵AC∥BD,∴∠CAB=∠OBD,∴∠CAB+∠ODB=∠OBD+∠ODB=90°,∴∠AED=×90°=45°.。
江苏省南京市2019-2020学年秦淮外国语学校八上英语期中试卷

【秦外英语】2019年八上期中试卷+答案一、听力部分(共15小题;每小题1分,计15分)略二、单项填空(共15小题;每小题1分,满分15分)从A、B、C和D四个选项中,选出可以填入空白处的最佳选项。
16.---Do you know________man on TV?---Yes,he is________honest person.A.a;anB.an;theC.the;anD.a;the17.People in the UK say“lorry”while people in the USA say“________”.A.yardB.vacationC.truckD.soccer18.---What’s your best friend like?---He________.A.likes playing footballB.is like tall and thinC.is like to help me a lotD.is helpful and kind19.Jimmy and Timmy are both50kg.That is to say,Jimmy is________Timmy.A.so heavy asB.as heavy asC.so heavier asD.as heavier as20.They decided to________the picture on the wall together.A.put inB.put outC.put awayD.put up21.---Would you please not smoke here?Look at the sign.---________.A.No.I willB.Yes.I willC.Sorry,I willD.Sorry,I won’t22.They live20kilometers________the school,but they still walk to school everyday.A.awayB.farC.far fromD.away from23.The flowers in Nancy’s room are as beautiful as________in Suzy’s.A.theyB.the onesC.theseD.them24.---Who is that girl sitting there________?---Well,her name is Jenny.A.friendlyB.happyC.lovelyD.quietly25.Jacky always thinks________a brave boy.But in fact,he is afraid of smallanimals.A.himB.heC.himselfD.him is26.Look!A number of people at Renmin Square________something.The numberof them________about1000.A.are discussing about;isB.is discussing;isC.are discussing about;areD.are discussing;is27.I hope you’d better________in the street.A.to not play footballB.not play footballC.don’t play footballD.not to play football28.Of the two American students,Amy is________one.I think you can find hereasily.A.tallestB.the tallerC.tallerD.the tallest29.What a great time we have________with each other during lunchtime!A.to chatB.chattingC.chatD.chatted30.---Shall I give you a ride as you look so tired?---Thank you.________.A.Don’t mention itB.It is your dutyC.Do as you likeD.It couldn’t be better三、完型填空(共10小题、每小题1分,共10分)Once,in a small village lived a family with eight children.Two of the children loved ___31___very much,but the family was so poor that it was impossible to send___32___of them to study at the art college at the same time.After many discussions the two boys finally___33___ a plan.They would toss(抛)a coin.The loser would go___34___into the mines(煤矿)and,with his money,___35___his brother’s study at the college.Then when the brother who won the toss finished his studies,after four years he would support the other brother studying at the___36___.James won the toss and Jack went down into the mines.James worked with all his heart and his paintings were much___37___than those of most of his teachers and by the time he___38___ his study,he was beginning to make a lot of money for his paintings.James returned.When he told Jack he could go to the art college,Jack said___39___:“The four years in the mines has done too much to my hands so it is too___40___.Now I can’t even hold a glass.”To show his great love,James drew his brother’s hands with fingers towards the sky.He called his drawing“The Praying Hands”which became very famous years later.31.A.school B.books C.painting D.money32.A.both B.all C.any D.neither33.A.looked out B.got out C.took out D.worked out34.A.off B.down C.up D.away35.A.pay B.follow C.agree D.let(原题有误,无正答,应该为pay for或者support)36.A.college B.mine C.home D.factory37.A.cheaper B.worse C.better D.older38.A.waited B.finished C.walked D.arrived39.A.happily B.bravely C.softly D.angrilyte B.early C.good D.helpful四、阅读理解(共15小题,每小题1分。
2019-20学年11.05南京秦淮区一中(单考)八上期中数学期中试卷 +答案

B
图1
图2
⑵如图 2 点 P 即为所求
8
22、⑴解:∵DE 是 AB 的垂直平分线 ∴DA=DB ∵△ACD 周长=AC+CD+DA ∴△ACD 周长=AC+CD+DB=AC+BC ∵AC=6,BC=10 ∴△ACD 周长为:AC+CD+DB=AC+BC=16
⑵解:∵AB=AC ∴∠B=∠C=25° ∴∠BAC=130° 由⑴得:DA=DB ∴∠B=∠DAB=25°
∴A、D 均在 EF 的垂直平分线上
∴AD 为 EF 的垂直平分线
即 AD 垂直平分 EF
24、证明:连接 BD,
∵AB=AC,AD⊥BC
∴AD 平分∠BAC
又∵∠BAC=120°
1 ∴∠BAD= BAC=60
2
又∵AB=AD
E
∴△ABD 为等腰三角形
又∵∠BAD=60°
B
∴△ABD 为等边三角形
F A
C
N
B E
图1
C
A
M
B
图2
3
22、(6 分)如图,在△ABC 中,AB=AC=6,BC=10,AB 的垂直平分线分别交 BC、AB 于点
D、E.
⑴求△ACD 的周长; ⑵若∠C= 25 ,求∠CAD 的度数.
A E
B
D
C
23、(6 分)如图,AD 为△ABC 的角平分线,DE⊥AB 于点 E,DF⊥AC 于点 F,连接 EF 交 AD 于点 O,求证:AD 垂直平分 EF.
D.无法确定
3、 如图,AB//DC,AB=DC,要使 A= C,直接利用三角形全等的判定方法是( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020八上期中考试秦淮区(一中)一、基础部分(27分)1.从下面两幅字中任选一幅临写。
(3分)和颜悦色锐不可当2.下列加点字注音完全正确的一项是( )(3分)A. 篡.(cuàn)改畸.形(qí)教诲.(huì)杳.无消息(yǎo)B. 镌.(juān)刻粗糙.(zào)悄.(qiǎo)然深恶.(wù)痛疾C. 解剖.(pōu)绯.红(fēi)咆.(páo)哮抑.扬顿挫(yì)D. 诘.(jié)责匿.名(nì)翘.(qiáo)首锐不可当.(dǎng)3.下列词语书写全都正确的一项是( )(3分)A.泄气浩翰由衷一丝不苟B.遁形杀戮娴熟诚惶诚恐C.落弟黝黑崎岖任劳任怨D.呓语躁热窒息筋疲力尽4.下列划线词语运用不恰当的一项是( )(3分)A.他们白手起家,在荒滩上盖起了厂房。
B.工程师和设计师们殚精竭虑,耗费了四年时间,终于实现了这个目标。
C.看了这封信,他才如梦初醒,方知自己上当受骗。
D.摇滚乐那强烈快速的节奏和迷离闪烁的灯光效果,让人眼花缭乱。
5.下列文学常识中表述错误的一项是( )(3分)A.三峡是瞿塘峡、巫峡和虎跳峡的总称,在长江上游重庆奉节和湖北宜昌之间。
B.苏轼,字子瞻,号东坡居士,眉山人,北宋文学家。
《记承天寺夜游》一文写于作者贬官黄州期间。
C.消息正文的结构通常是按照重要性递减的原则安排的,即所谓“倒金字塔结构”。
D.居里夫人是法国物理学家、化学家,原籍波兰,先后获1903年诺贝尔物理学奖和1911年诺贝尔化学奖。
6.用诗文原句填空。
(12分)(1)庭中有奇树,________________。
(《庭中有奇树•古诗十九首》)(2)________________,志在千里。
(曹操《龟虽寿》)(3)冰霜正惨凄,________________。
(刘桢《赠从弟》)(4)________________,狐兔翔我宇。
(曹植《梁甫行》)(5)东皋薄暮望,________________。
(王绩《野望》)(6)________________?烟波江上使人愁。
(崔颢《黄鹤楼》)(7)征蓬出汉塞,________________。
(王维《______》)(8)________________,云生结海楼。
(李白《渡荆门送别》)(9)几处早莺争暖树,________________。
(______《钱塘湖春行》)(10)________________,窥谷忘反。
(吴均《与朱元思书》)二、阅读理解(43分)(一)古诗阅读,完成7-8题。
(4分)与夏十二登岳阳楼李白楼观岳阳尽,川迥洞庭开。
雁引愁心去,山衔好月来。
云间连下榻,天上接行杯。
醉后凉风起,吹人舞袖回。
7.这首诗是李白由江夏南游洞庭时登岳阳楼而作,表达了_________的心情。
(1分)8.颔联中的“引”“衔”二字历来为人称赞,请任选一个字进行赏析。
(3分)_______________________________________________________________________________ (二)阅读下面两段文字,回答9-12题。
(13分)【甲】元丰六年十月十二日夜,解衣欲睡,月色入户,欣然起行。
念无与为乐者,遂至承天寺寻张怀民。
怀民亦未寝,相与步于中庭。
庭下如积水空明,水中藻、荇交横,盖竹柏影也。
何夜无月?何处无竹柏?但少闲人如吾两人者耳。
([宋]苏轼《记承天寺夜游》)【乙】过澎浪矶、小孤山,二山东西相望。
小孤属舒州宿松县,有戍兵。
凡江中独山,如金山、焦山、落星之类,皆名天下,然峭拔秀丽皆不可与小孤比。
自数十里外望之,碧峰巉①然孤起,(节选自[南宋]陆游《过小孤山大孤山》) [注] ①巉(chán):险峻陡峭。
②干:冲。
③信:果真9.解释句中加点字。
(4分)(1)念.无与为乐者( ) (2)但.少闲人( )(3)自.数十里外望之( ) (4)已非它山可拟.( )10.用“/”为乙文的画线句标出两处停顿。
(2分)愈近愈秀冬夏晴雨姿态万变11.用现代汉语翻译下面句子。
(4分)(1)水中藻、荇交横,盖竹柏影也。
______________________________________________________________________________ (2)碧峰巉然孤起,上干云霄。
_______________________________________________________________________________ 12.甲文末尾“闲人”二字,既有自嘲清闲之意,又有_________之情。
乙文作者以“__________"概括了小孤山的两大特点。
在写小孤山前先写金山、焦山,是用了_________的手法。
(3分) (三)阅读下面文章,回答13-15题.(12分)中国盲人足球队夺冠背后①三联生活周刊 2019年10月22日记者:刘畅10月6日,由业余运动员组成的中国盲人足球队第六次夺得亚锦赛冠军。
而比夺冠更重要的是,足球对盲人队员人格的完善。
“看不见”的夺冠没有欢呼,只有足球的撞击声,伴着一串铃响和不间断的“喂, 喂”的呼喊。
北京时间10月6日晚8点,泰国芭提雅青少年中心体育场的五人制足球场内,2019年盲人足球亚锦赛决赛正在中国队和伊朗队之间展开。
暮色中的观众稀稀拉拉,队员们却全不在意。
相比健全人的足球队,每队除守门员视力健全之外,其余四名队员均为全盲,他们要戴着眼罩比赛,甚至比赛时手触碰眼罩即是犯规。
指引他们的是声音——足球里放着铃铛,对方球员防守时,必须发出表达“我在这儿”的声音,队员们彼此的声音是确认方位的坐标,一旦球踢偏了,唯有靠教练在场边呼喊来定位。
纵然观众席上人山人海,比赛时也要保持绝对安静,让球员们沉浸在由声音和触感构筑的足球世界里。
中国队身着白色队服,伊朗队则是红色的。
在中国队员看来,这场“红白大战”是整个亚锦赛最为势均力敌的一场比赛。
中国队自2006年创立,已经五夺亚锦赛冠军,在2015年唯一没有夺得亚锦赛冠军的那次,冠军就是伊朗队。
比赛开始了。
中国队员在对方两三人之间闪转腾挪,如入无人之境。
中国队教练乐建昆告诉我,中国队的特点是带球技术独步天下,球不离脚。
上半场临近尾声时,比赛进入高潮。
中国队在右侧发角球,6号张家彬往场内带球,9号许观生扶着他在一侧护球,张家彬带了两步后,拉球就是一脚抽射,足球直入网窝。
决胜的下半场,教练组觉得“赢一个也是赢,赢两个也是赢”,提醒球员控制节奏,但球员们总觉得不保险,直到最后一刻都在疯狂进攻,最终将1比0的比分保持到终场,中国队卫冕,第六次登顶亚锦赛。
这是一场没有直播的亚锦赛决赛。
胜利的消息传来,网络上才有了中国队领奖时的视频,他们站成一排,骄傲地笑着。
这晚的辉煌过后,这支“看不见”的亚洲冠军队就将解散,业余身份的球员们将回到盲校学习和按摩推拿的日常里去。
训练“平常”乐建昆一边迈着大步,一步一停,一边扶着小队员的背,让他弯下腰,摸自己的小腿,用昆明话教导他感受正确运球时肌肉的变化。
在他们旁边,“喂,喂”声此起彼伏,四名高大些的队员在一起练习过人和抢圈。
他们接球的瞬间,双腿微微后撤,球碰到脚就【甲】(A.粘住了B.仿佛粘住了一般)。
而一旦带起球来,脚就像两把冰刀,球顺着刀锋【乙】(A.滑动 B.滚动)夺冠五日后,我在昆明的意象足球俱乐部,见到乐建昆带着云南省队的队员备战2021年全运会。
“很多父母可怜自己的盲人孩子,生怕他们磕碰,不让他们独自走动,导致有些孩子对独自行走非常恐惧,甚至上体育课的时候让他们走,他们也只能原地踏步。
我选拔苗子时,首先就是让他们从操场的一头一口气朝我跑过来,我就喜欢那种眼看就要撞上我也不减速的孩子。
”乐建昆说,若想踢球,敢于克服对独自奔跑的恐惧是最首要的任务。
我这才意识到,这里能甩开盲杖奔跑的队员,是盲人群体中的极少数,我在他们身上看到的“平常”反倒是一种“异常”。
要想正式踢盲人足球,还要学会带球。
盲人只能凭借声音判断球的位置,所以带球时往往原地倒脚,极大地影响效率,乐建昆最先雕琢的便是培养队员触球的角度,让他们行进间能把球带起来。
李海福刚接触盲人足球时,用一个月学会了带球,如今身为参加过西班牙亚锦赛的国家队队员,他面对两名防守队员的并排围堵,仿佛能够未卜先知,带球到禁区前一侧后立刻向旁边拉球,如此往复,趁防守人重心不稳之际,一脚抹过。
“一旦学会了带球,我就感觉获得了一种‘自由’,仿佛可以把球在脚上随意把玩,怎么也丢不了。
”李海福的眼睛外观上与常人无异, 唯有难以回应我的目光相对时,才让我意识到他是位盲人。
他们又是如何攀上亚洲之巅的?乐建昆告诉我,带球只是刚刚入门,虽然中国队带球技术好,对球员最大的考验还是在黑暗的奔跑中对抗,“中国队有冲劲儿”。
李海福记得起初面对冲击,本能地往后退,教练便让他防守时可以拉拽老队员,在不断的肢体接触中消除恐惧。
而完成最终的淬炼,仍然需要在正规比赛时,真正面对陌生人的冲击,并感知彼此在场上的位置,形成默契。
被足球改变的视力的缺失却永远也摆脱不了。
盲人球员无法做教练;参加省队、国家队的补贴,远抵不上他们的工资。
为何仍有队员甘愿为此停下工作?我站在宿舍区的空地上向乐建昆抛出这个问题,恰好两名队员撞个满怀,乐建昆张嘴就说“你瞎了吧!”,引得一片哄堂大笑。
他们的理由正在这一片欢笑之中。
球员代凯说,不仅在教练与队员之间,队员彼此也会拿自己的缺陷开玩笑,大家聚在一起要比其他地方轻松得多。
他记得自己4年前加入省队时感到不可思议:“盲人孩子普遍自卑,‘看不见’这件事,是不敢触碰的心结。
我在学校时,与同学之间说话小心翼翼,生怕伤害到彼此。
”“因为缺乏一种感官,盲人对事物的感知与健全人有差异,但他们普遍习惯于坚持自己的感受,不愿也不敢接受外界的意见。
”乐建昆记得有很多次,训练之余带着队员上街时,有路人见到他的队员会立刻闪开,队员们就觉得被冒犯了。
他反问队贞:“难道你希望他们撞上你吗?”可是单纯这样的解释往往是无力的,恰好是足球能够改变他们的认知。
乐建昆在训练中发现,很多孩子做错了动作,嘴上说着明白了,再做时错误依旧。
他们不是口是心非,而是确实感知不同。
比如踢球时,他们总觉得脚踢到球时越响,力量越大,球速越快。
事实却恰恰相反,正常人能看到球速的快慢,我为了说服他们,只能用秒表计时,让他们自己听哪一种踢法的球速快,主动改变自己的判断。
”一旦他们接受自己感官的偏差,他人的帮助便能照进他们心里,他们也能更加释然地面对这个社会。
代凯告诉我,他现在可以自如地坐高铁,坐飞机,往来各个城市之间,发现确实有好心人真心帮他。
遇到有人称他“瞎子”,他会认为那不过是人们的习惯叫法,不见得带有歧视,“即使真有歧视,又能把我怎么着呢?”“原本盲人只是视力有问题,若缺少运动,身体机能也会退化。
