Action potentials:动作电位 28页PPT
合集下载
Action potentials:动作电位28页PPT
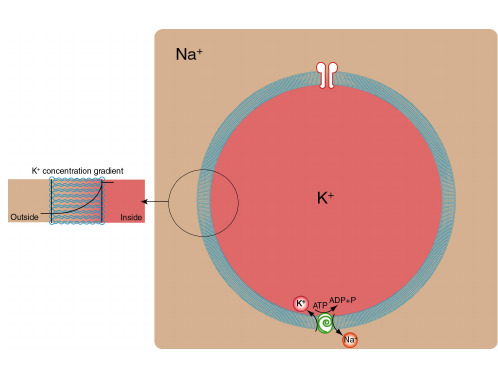
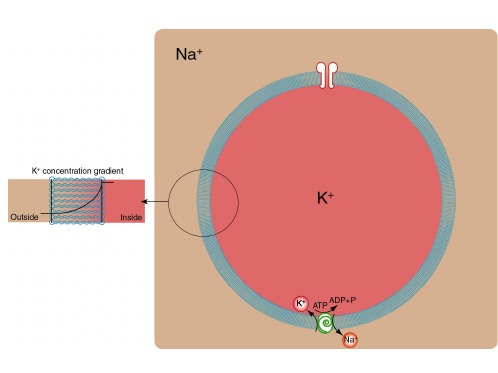
Diffusional forces acting on an ion
Given a mass of gas in thermal equilibrium we may measure its pressure (p) temperature (T) and volume (V). Boyle demonstrated that pV/T is a constant Volume occupied is proportional to the mass of gas, we can write the above constant as µR where µ is the mass in moles and R is a constant. R = 8.134 joule/mole K
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
Equation #4
At a constant temperature this may be written as Equation #5
Given a mass of gas in thermal equilibrium we may measure its pressure (p) temperature (T) and volume (V). Boyle demonstrated that pV/T is a constant Volume occupied is proportional to the mass of gas, we can write the above constant as µR where µ is the mass in moles and R is a constant. R = 8.134 joule/mole K
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
Equation #4
At a constant temperature this may be written as Equation #5
生理动作电位.PPT
29
组织兴奋后兴奋性的变化:
1. 绝 对 不 应 期 (absolute refractory period,ARP) 细胞 膜上的Na+通道处于失活状态 ,兴奋性降低到零。 2.相对不应期(relative refractory period),RRP)Na+通道开始逐 渐复活:但处于静息状态的 Na+ 通 道 数 目 及 其 开 放 能 力 尚未恢复到正常水平,兴奋 性低于正常。
膜内负电位增大——超极化
4
去极化: 细胞受刺激时,膜内电
位 短 时 内 由 -90mV 上 升 到 + 30mV,构成动作电位曲线的
+30mv 上升支。其中,超过零电位
至去极相顶端的电位数值称
0mv 为超射值。
-90mv
5
动作电位的形成机制
去极化
细胞受到有效刺激→Na+通道开 放→Na+顺电-化学梯度内流→膜外 电位↓、膜内电位↑(去极化) → 阈电 位→内负外正变成内正外负→电位差 成 为 Na+ 内 流 阻 力 →对 抗 Na+ 内 流 →Na+内流的动力 (浓度差)与阻力 (电位差)相等→Na+的平衡电位。
1 在正常海水中 2 在低Na+海水中 3 正常海水冲洗后
14
证实动作电位产生机制的依据
➢采用Na+通道特异性阻断剂河豚毒等后,动作电 位不再产生。 ➢用可膜片钳观察到动作电位与Na+通道开放高度 相关。
15
利用电压钳技术记录的枪乌 贼大神经轴突的膜电流及其
离子成分的分析
A:钳制电压 B:记录的内向电流和外向电流 C:河豚毒(TTX)阻断了Na+内向电 流 D:四乙铵(TEA)阻断了K+外向电流 (引自Kuffler等,1984)
组织兴奋后兴奋性的变化:
1. 绝 对 不 应 期 (absolute refractory period,ARP) 细胞 膜上的Na+通道处于失活状态 ,兴奋性降低到零。 2.相对不应期(relative refractory period),RRP)Na+通道开始逐 渐复活:但处于静息状态的 Na+ 通 道 数 目 及 其 开 放 能 力 尚未恢复到正常水平,兴奋 性低于正常。
膜内负电位增大——超极化
4
去极化: 细胞受刺激时,膜内电
位 短 时 内 由 -90mV 上 升 到 + 30mV,构成动作电位曲线的
+30mv 上升支。其中,超过零电位
至去极相顶端的电位数值称
0mv 为超射值。
-90mv
5
动作电位的形成机制
去极化
细胞受到有效刺激→Na+通道开 放→Na+顺电-化学梯度内流→膜外 电位↓、膜内电位↑(去极化) → 阈电 位→内负外正变成内正外负→电位差 成 为 Na+ 内 流 阻 力 →对 抗 Na+ 内 流 →Na+内流的动力 (浓度差)与阻力 (电位差)相等→Na+的平衡电位。
1 在正常海水中 2 在低Na+海水中 3 正常海水冲洗后
14
证实动作电位产生机制的依据
➢采用Na+通道特异性阻断剂河豚毒等后,动作电 位不再产生。 ➢用可膜片钳观察到动作电位与Na+通道开放高度 相关。
15
利用电压钳技术记录的枪乌 贼大神经轴突的膜电流及其
离子成分的分析
A:钳制电压 B:记录的内向电流和外向电流 C:河豚毒(TTX)阻断了Na+内向电 流 D:四乙铵(TEA)阻断了K+外向电流 (引自Kuffler等,1984)
action potential 动作电位

电鳗为什么能放电? 电鳗为什么能放电?
为了吃美味不要命!
河豚毒素( 河豚毒素(tetrodotoxin,TTX)
• 参考文献
• • Action Potential Energy Efficiency Varies Among Neuron Types in Vertebrates and Invertebrates Biswa Sengupta, Martin Stemmler, Simon B. Laughlin, and Jeremy E. Niven Sodium entry during action potentials of mammalian central neurons: incomplete inactivation and reduced metabolic efficiency in fast-spiking neurons Brett C. Carter and Bruce P. Bean Action potential initiation and propagation: upstream influences on neurotransmission Geraldine J. Kress and Steven Mennerick Simulation of developmental changes in action potentials with ventricular cell models Hitomi Itoh, Yasuhiro Naito, and Masaru Tomita Neuronal Competition for Action Potential Initiation Sites in a Circuit Controlling Simple Learning Georgina E. Cruz, Christie L. Sahley, and Kenneth J. Muller Action potential throughput in aged rat hippocampal neurons: regulation by selective forms of hyperpolarization John C. Gant and Olivier Thibault Differential regulation of action potential firing in adult murine thalamocortical neurons by Kv3.2, Kv1, and SK potassium and N-type calcium channels Michael R Kasten, Bernardo Rudy, and Matthew P Anderson
Action potentials:动作电位

Equation #7 G = Gdiff + Gelect = RTln(c) + zFE
(from #1 and #2)
The difference between free energy inside the cell and outside defines the free energy driving movement of the ion across the cell membrane which may be expressed as follows:
-t/v
deltaVm(t) = Im.R(1-e )
20
When we consider the passive electrical environment of axons or dendrites it is useful to
think of them as composite structures
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
(from #1 and #2)
The difference between free energy inside the cell and outside defines the free energy driving movement of the ion across the cell membrane which may be expressed as follows:
-t/v
deltaVm(t) = Im.R(1-e )
20
When we consider the passive electrical environment of axons or dendrites it is useful to
think of them as composite structures
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
动作电位Actionpotential

发放动作电位的速率是有限的,最大发放频率为?
动作电位Actionpotential
5
5
二、动作电位产生的理论模型 (AP in theory)
欧姆定律 I=V/R=gV
I电流与流过通道 的粒子数目和驱 动力有关。
g电导 与细胞膜上开放 的通道数目有关
动作电位Actionpotential
6
6
1、膜电流和膜电导
Iion = gion(Vm-Eion)
动作电位Actionpotential
9
9
2. 动作电位过程中的离子进出 (Ins and Outs of AP)
静息状态下,钠离子具有很大的驱动力 Vm-ENa=-80 -62=-142mV。 膜对离子的通透性由钾离子变为钠离子,膜电位可以在 极短的时间内逆转。
A、10mV去极化
B、60mV去极化,分别诱导出的漏电流Ileak 和电容电流Ic,内向电流,外向电流 C、去掉漏电流和电容电流后,在TTX和
TEA分别作用下,得到钾电流和钠电流。
动作电位Actionpotential
15 15
电压门控钠通道
(Voltage-gated sodium channel)
动作电位的下降相:
假如钠通道快速关闭,钾通道处于开放状态,膜对离子通透由钠离子 变为钾离子。钾离子流出胞外,膜内变负,直至钾离子平衡电位。
如果钾离子通道在动作电位下降相中钾电导增大,则动作电位的时程 就会缩短。
动作电位Actionpotential
12 12
综上所述,动作电位理论上可以认为:
膜电位去极化到阈值,gNa瞬时增大,钠离子进入膜内,神经元去极化; gNa增加时间短暂,在下降相中gK瞬时增加,钾离子快速外流,膜电位复 极化。
Action potentials:动作电位
Equation #6
Gdiff = RTln(c)
7
Electrical forces acting on an ion
According to Faraday the charge on a mole of material is 96483 z Coulombs where z is the charge of each atom or ion (the valency of an ion). This is the Faraday constant or F.
23
26
27
Diffusional forces acting on an ion
Given a mass of gas in thermal equilibrium we may measure its pressure (p) temperature (T) and volume (V). Boyle demonstrated that pV/T is a constant Volume occupied is proportional to the mass of gas, we can write the above constant as µR where µ is the mass in moles and R is a constant. R = 8.134 joule/mole K
Equation #4
At a constant temperature this may be written as Equation #5
We can use this result to describe the free energy of diffusion of a particular ion in our cell or outside of the cell as follows:
2.4-2.5 动作电位及产生机制-PPT

离子的电化学驱动力
电化学驱动力=Em-Ex
华中科技大学同济医学院生理学系
1
电压钳(voltage clamp)实验装置
细胞膜对离子通透性的定量研究和测量
细胞膜对离子通透性的定量研究和测量
内向电流是Na离子所介导
华中科技大学同济医学院生理学系
细胞膜对离子通透性的定量研究和测量
外向电流是由钾离子所介导
2
钠电导的电压和时间依赖性特点
钠通道的功能状态
钾电导的电压和时间依赖性特点
动作电位期间钠电导与钾电导的变化情况
华中科技大学同济医学院生理学系
3
动作电位与产生机制: 离子电化学驱动力的变化 离子通道电导的变化特点
动作电位(action potential)
概念: 细胞在静息电位基础上受到有效刺激后产 生的迅速的可向远处传播的膜电位波动。
动作电位(action potential)
动作电位
动作电位
锋电位(spike potential)
+30 超
射
mV)
位
升
降
支
支
-55
后去极化电位 阈电位
-70
时间(ms)
后电位 后超级化电位 (after potential)
动作电位的产生机制
动作电位期间的膜电位波动是由离子的跨膜移动形成的。 I= ⇒I=U×G 离子跨细胞膜流动的两个必要条件:
存在离子跨细胞膜移动的电化学驱动力 细胞膜对离子有通透性,即电导特性
动作电位

2011-2-28
J.Yang Dept.of Physiology YAUMC
4
2011-2-28
J.Yang Dept.of Physiology YAUMC
5
4.动作电位的特点 .
(1)全或无 ) 阈值: 阈值:最小刺激强度 (2)不衰减性传播 )
2011-2-28
J.Yang Dept.of Physiology YAUMC
25
(三)动作电位的传导
局部电流学说( 局部电流学说(local circuit theory) ) 跳跃式传导( 跳跃式传导(saltatory conduction) ) 所谓动作电位的传导, 所谓动作电位的传导,实际上是已兴奋的膜 部分通过局部电流“刺激” 部分通过局部电流“刺激”了相邻的未兴奋 的膜部分,使之出现动作电位,这样的过程 的膜部分,使之出现动作电位, 在膜表面连续进行下去, 在膜表面连续进行下去,就表现为兴奋在整 个细胞的传导。 个细胞的传导。 动作电位的传导速度是可以的测定的。 动作电位的传导速度是可以的测定的
三、动作电位(action potential,AP) 动作电位 ,
(一)细胞的动作电位 一 细胞的动作电位 1.动作电位的概念 指可兴奋细胞在受到 .动作电位的概念:指可兴奋细胞在受到 一定强度的刺激后, 一定强度的刺激后,膜两侧的电位在原 有静息电位的基础上发生的一次快速的 倒转和复原。 倒转和复原。 这种变化在受刺激部位产生后沿着细胞 膜向周围传播, 膜向周围传播 , 直至整个细胞膜都依次 经历这样一次膜电位的波动。 经历这样一次膜电位的波动。
J.Yang Dept.of Physiology YAUMC
15
2011-2-28
J.Yang Dept.of Physiology YAUMC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Equation #4
At a constant temperature this may be written as Equation #5
We can use this result to describe the free energy of diffusion of a particular ion in our cell or outside of the cell as follows:
Equation #8
(G)= (RTln(cout) +zFEout) —(RTln(cin) + zFEin)
Which simplifies to:
Equation #9)
(G) = R.T.ln(cout/cin) + z.F.δ(E)
By definition at equilibrium DG = 0 thus the equilibrium potential for any given ion is given by:
23
26
27
谢谢!
Diffusional forces acting on an ion
Given a mass of gas in thermal equilibrium we may measure its pressure (p) temperature (T) and volume (V). Boyle demonstrated that pV/T is a constant Volume occupied is proportional to the mass of gas, we can write the above constant as µR where µ is the mass in moles and R is a constant. R = 8.134 joule/mole K
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
Equation #7 G = Gdiff + Gelect = RTln(c) + zFE
(from #1 and #2)
The difference between free energy inside the cell and outside defines the free energy driving movement of the ion across the cell membrane which may be expressed as follows:
-t/v
deltaVm(t) = Im.R(1-e )
20
When we consider the passive electrical environment of axons or dendrites it is useful to
think of them as composite structures
Gelect = zFE or outside of the cell is the sum of these forces
So the free energy (G) inside or outside of the cell may be expressed as
21
We may usefully consider the path of current flow to determine the effect of neurite geometry on electrical characteristics
22
Models for channel gating
Equation #6
Gdiff = RTln(c)
7
Electrical forces acting on an ion
According to Faraday the charge on a mole of material is 96483 z Coulombs where z is the charge of each atom or ion (the valency of an ion). This is the Faraday constant or F.
If z =valency of ion E = electrical potential across the delimiting membrane.
Thus the electrical energy in a mole of an ion may be expressed as
Equation #1
Thus Equation #2
pV=µRT
Now the work done by an expanding gas can be calculated as follows: Equation #3
Where the gase expands from an initial volume Vi to a final volume Vf. Using equation #2, we can see that the work done per mole is
Equation #10 δ(E) = RT/ZF ln(cin/cout)
This is the Nernst-Einstein equation.
9
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
At a constant temperature this may be written as Equation #5
We can use this result to describe the free energy of diffusion of a particular ion in our cell or outside of the cell as follows:
Equation #8
(G)= (RTln(cout) +zFEout) —(RTln(cin) + zFEin)
Which simplifies to:
Equation #9)
(G) = R.T.ln(cout/cin) + z.F.δ(E)
By definition at equilibrium DG = 0 thus the equilibrium potential for any given ion is given by:
23
26
27
谢谢!
Diffusional forces acting on an ion
Given a mass of gas in thermal equilibrium we may measure its pressure (p) temperature (T) and volume (V). Boyle demonstrated that pV/T is a constant Volume occupied is proportional to the mass of gas, we can write the above constant as µR where µ is the mass in moles and R is a constant. R = 8.134 joule/mole K
15
16
17
Voltage clamp activated currents in axons
18
Na and K conductances that make the action potential
19
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
Equation #7 G = Gdiff + Gelect = RTln(c) + zFE
(from #1 and #2)
The difference between free energy inside the cell and outside defines the free energy driving movement of the ion across the cell membrane which may be expressed as follows:
-t/v
deltaVm(t) = Im.R(1-e )
20
When we consider the passive electrical environment of axons or dendrites it is useful to
think of them as composite structures
Gelect = zFE or outside of the cell is the sum of these forces
So the free energy (G) inside or outside of the cell may be expressed as
21
We may usefully consider the path of current flow to determine the effect of neurite geometry on electrical characteristics
22
Models for channel gating
Equation #6
Gdiff = RTln(c)
7
Electrical forces acting on an ion
According to Faraday the charge on a mole of material is 96483 z Coulombs where z is the charge of each atom or ion (the valency of an ion). This is the Faraday constant or F.
If z =valency of ion E = electrical potential across the delimiting membrane.
Thus the electrical energy in a mole of an ion may be expressed as
Equation #1
Thus Equation #2
pV=µRT
Now the work done by an expanding gas can be calculated as follows: Equation #3
Where the gase expands from an initial volume Vi to a final volume Vf. Using equation #2, we can see that the work done per mole is
Equation #10 δ(E) = RT/ZF ln(cin/cout)
This is the Nernst-Einstein equation.
9
Current flowing across the giant axon membrane may be represented by the sum of conductive components (What we now identify as ion channels) and capacitance (the cell membrane). The currents are described in the following circuit diagram.
