七年级第4章检测卷
初一七年级生物下册《第四章测试卷》(附答案)【人教版适用】

初一七年级生物下册《第四章测试卷》(附答案)【人教版适用】第四章检测卷时间:45分钟满分:100分一、选择题(每小题只有一个答案最符合题意,每小题2分,共50分)1.如图所示是血液分层实验,下列说法错误的是()A。
①是抗凝剂B。
②是血浆C。
③是白细胞D。
④是红细胞2.血液循环中,对运载血细胞,运输养料和废物起重要作用的是()A。
血浆B。
白细胞C。
红细胞D。
血小板3.如图是用显微镜观察到的人血涂片视野,下列表述中正确的是()A。
①个体最小,能穿透血管壁B。
②数量最多,能够吞噬病菌C。
③的数量最多,具有运输氧的功能D。
①②③三种细胞中只有③没有细胞核4.人们到医院看病时,有时需要做血常规化验。
医生判断患者是否贫血,是根据下列哪项的数值低于正常值而做出的()A。
血浆B。
白细胞C。
血小板D。
红细胞和血红蛋白5.下列对血小板功能的叙述中,正确的是()A。
具有运输氧气的作用B。
具有防御和保护的作用C。
具有运输二氧化碳的作用D。
具有止血和凝血的作用6.以下有关血液的说法正确的是()A。
B型血的病人可以接受AB型的血B。
人体出现炎症时血液中白细胞会比红细胞多一些C。
正常人的血液中血浆约占25%,是一种淡黄色液体D。
紧急时一个健康的O型血的成年人可以给A型血的病人献血200mL7.血液在哪种血管中流动速度最慢()A。
动脉B。
静脉C。
毛细血管D。
淋巴管8.下列哪一项不属于动脉血管的特征()A。
管壁厚B。
血流速度快C。
把血液从心脏送到身体各部分D。
是血液与组织细胞进行物质交换的场所9.输液时针刺入的是静脉,分析原因,错误的是()A。
静脉多数分布较浅B。
静脉内红细胞单行通过C。
静脉内血流速度较慢D。
静脉管壁较薄10.甲、乙、丙三人同行,丙受伤急需输大量血,已知丙的血型为B型,甲的血型为AB型,乙为B型,可以给丙输血的是()A。
甲B。
乙C。
甲、乙都可以D。
甲、乙都不可以11.足底的血液沿下肢静脉回流到心脏,而不倒流的主要原因是()A。
浙教版2024年《科学》七年级上册第4章第4节检测试卷与参考答案

浙教版2024年《科学》七年级上册第4章第4节检测试卷与参考答案1.发生热传递的条件是。
热传递的过程中,高温物体热量,温度;最终两个物体的相等()答案:两物体间有温度差;放出;小降;吸收;上升;温度2.热量指,用符号表示,国际单位为,符号为,比它大的单位还有。
答案:物体吸收或放出热的多少;Q;焦耳;J;千焦(kJ)3.在国际单位制中,比热的单位是;煤油的比热是2.1×103J/(kg·℃),它表示。
答案:J/(kg·℃);1kg的煤油,温度升高1℃需要吸收的热量是2.1×103J4.如图所示是一款冬季家庭常用的电暖气,在电暖气内部应充入比热较的液体,是为了使它通电后温度升高得更。
答案:小;快5.将质量相同、材料不同的三块金属甲、乙、丙加热到相同的温度后,放到表面平整的石蜡上,经过一段时间后,观察到如图所示的现象。
由此说明三块金属的比热()A.甲最大B.乙最大C.丙最大D.一样大答案:C6.新疆那拉提草原是闻名全国的旅游景区。
夏天,当你赤脚在烈日当空的小河边游玩时,你会发现:岸上的小石头热得烫脚,而河水却是冰凉的,这是因为()A.水比小石头的温度变化大B.水比小石头的比热大C.水比小石头吸收的热量小D.水比小石头的比热小答案:B7.水的比热比较大,人们往往利用它的这一特性为生产生活服务,下列事件与它的这一特性无关的是()A.让流动的热水流过散热器供暖B.汽车发动机用循环水冷却C.采用沸水多水量、短时间对蔬菜进行焯水处理,可减少营养素的损耗D.在较大的河流上建水电站,用水发电答案:D8.由于水的比热比沙石或干泥土的比热大,所以在沿海地区陆地表面的气温比海面的气温昼夜变化显著,因此()A.白天的海风多是从陆地吹向海面,夜晚的海风多是从海面吹向陆地B.白天的海风多是从海面吹向陆地,夜晚的海风多是从陆地吹向海面C.白天和夜晚的海风多是从陆地吹向海面D.白天和夜晚的海风多是从海面吹向陆地答案:B9.经常下厨的小关发现,同时用相同的燃气灶加热质量相等、初温相同的水和食用油,油的温度总是升高得快些。
七年级上册数学第4章质量评估试卷

第4章质量评估试卷一、选择题(每小题3分,共30分) 1.下列立体图形中是圆柱的为()图12.如图2所示,李老师办公桌上放着一个圆柱形茶叶盒和一个正方体的墨水盒,小芳从上面看,看到的图形是()图23.经过任意三点共可以画出的直线条数是( )A .一条或三条B .三条C .两条D .一条4.如图3所示,点A 、B 、C 、D 是直线l 上的四个点,图中共有线段条数是()图3A .3条B .4条C .5条D .6条5.甲、乙两地之间有四条路可走(如图所示),那么最短路线的序号是 ()图4A .①B .②C .③D .④6.如图5所示,已知线段AB =10 cm ,点N 在AB 上,NB =2 cm ,M 是AB 中点,那么线段MN 的长为()图5A .5 cmB .4 cmC .3 cmD .2 cm7.已知∠A =25°12′,∠B =25.12°,∠C =25.2°.下列结论正确的是 ( )A .∠A =∠B B .∠A =∠C C .∠B =∠CD .三个角互不相等8.一个正方体的相对的面上所标的数都是互为相反数的两个数,如图6所示是这个正方体的表面展开图,那么图中x 的值是()图6A .2B .8C .3D .-2 9.下列属于尺规作图的是( )A .用量角器画∠AOB 的平分线OP B .利用两块三角尺画15°的角C .用刻度尺测量后画线段AB =10 cmD .在射线OP 上截取OA =AB =BC =a 10.下列说法错误的是( )A .两个互余的角都是锐角B .锐角的补角大于这个角本身C .互为补角的两个角不可能都是锐角D .锐角大于它的余角二、填空题(每小题3分,共24分)11.有下列几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是________(填序号).12.我们在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为________. 13.如图7所示,延长线段AB 到C ,使BC =4,若AB =8,则线段AC 的长是线段BC 长的________倍.图714.图8中的直线表示方法中,正确的是________(填序号).图815.纸上有一个9°的角,如果用十倍放大镜观察这个角,就会得到一个________度的角. 16.一个角的余角是36°5′,这个角是________.17.如图9所示,O 是直线AB 上一点,∠COB =30°,则∠1=________.图918.计算:48°39′40″+67°41′35″=________,23°41′34″×3=_____ ___. 三、解答题(共66分)19.如图11,已知A 、B 、C 三点. (1)画直线AC ; (2)画射线BC ; (3)画线段AB ;(4)找出线段AB 的中点D ,连接CD ;(5)画出∠ABC 的平分线BE 与AC 相交于E ,BE 与CD 相交于点F.图1120.一个角的补角加上10°等于这个角的余角的3倍,求这个角.21.根据下列语句画图计算:作线段AB ,在AB 的延长线上取点C ,使BC =2AB ,M 是AC 的中点,若AB =30 cm ,求BM 的长.22.已知O 为直线AB 上一点,OE 平分∠AOC ,OF 平分∠COB ,求∠EOF 的大小.图1223.如图13所示,已知A 、O 、E 三点在同一条直线上,∠1=∠2,且∠1和∠4互为余角.图13(1)∠2和∠3互余吗?(2)∠3和∠4有什么关系,为什么? (3)∠3的补角是哪个?24.如图,BD 平分∠ABC ,BE 分∠ABC 为2:5两部分,∠DBE=21°,求∠ABC 的度数.。
七年级数学上册第四章《几何图形初步》测试卷-人教版(含答案)

七年级数学上册第四章《几何图形初步》测试卷-人教版(含答案)班级姓名(满分100分,限时60分钟)一、选择题(每小题3分,共30分)1.(2022独家原创)你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )A.点动成线B.线动成面C.面动成体D.面与面相交的地方是线2.(2021江苏镇江中考)如图所示,该几何体从上面看到的图形是( )A.正方形B.长方形C.三角形D.圆3.(2022甘肃白银期末)如图,观察图形,下列结论中不正确的是( )A.直线BA和直线AB是同一条直线B.图中有5条线段C.AB+BD>ADD.射线AC和射线AD是同一条射线4.如图所示,小于平角的角有( )A.9个B.8个C.7个D.6个5.(2022山东临沂沂水期末)如图,OA表示北偏东25°方向,OB表示南偏西50°方向,则∠AOB的度数是( )A.165°B.155°C.135°D.115°6.建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,这样做蕴含的数学原理是( )A.过一点有无数条直线B.两点确定一条直线C.两点之间线段最短D.线段是直线的一部分7.如图,下列各式中错误的是( )A.∠AOB<∠AODB.∠BOC<∠AOBC.∠COD>∠AODD.∠AOD>∠AOC8.(2022北京怀柔期末)如图是某个几何体的展开图,该几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点分别为D、E,则线段DE的长为( )A.5B.3C.1D.5或310.时钟显示为8:20时,时针与分针所夹的角是( )A.130°B.120°C.110°D.100°二、填空题(每小题3分,共30分)11.(2022独家原创)篮球运动员将篮球抛出后在空中形成一道弧线,这说明的数学原理是.12.如图所示,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC长的倍.13.(2022山东济南历下期末)计算:30°12'=°.14.如图,从A地到B地有①,②,③三条线路,其中最短的线路是(填“①”“②”或“③”),理由是.15.(2022北京通州期末)如图,棋盘上有黑、白两色棋子若干,若直线l经过3枚颜色相同的棋子,则这样的直线共有条.16.如图所示,O是直线AB上一点,OC是∠AOB的平分线.(1)图中互余的角是;(2)图中互补的角是.17.如图所示,图中有条直线, 条射线, 条线段.18.(2021湖北黄冈期末模拟)如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 度.19.如图,C,D是线段AB上两点,若BC=4cm,AD=7cm,且D是BC的中点,则AC的长等于cm.20.(2022安徽合肥蜀山期末)在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是.三、解答题(共40分)21.(5分)如图,已知不在同一直线上的四个点A、B、C、D.(1)画直线AD;(2)连接AB;(3)画射线CD;(4)延长线段BA至点E,使BE=2BA;(5)反向延长射线CD至点F,使DC=2CF.22.(2022北京东城期末)(5分)若一个角的补角是它的余角的6倍,求这个角的度数.23.(6分)如图,点O为直线AB上的一点,已知∠1=65°15',∠2=78°30',求∠1+∠2-∠3的大小.24.(2022广西玉林博白期末)(8分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.(1)射线OC的方向是;(2)若射线OE平分∠COD,求∠AOE的度数.25.(8分)如图,已知线段AC=12cm,点B在线段AC上,满足BC=1AB.2(1)求AB的长;(2)若D是AB的中点,E是AC的中点,求DE的长.26.(8分)点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠MOB.(1)如图(a),若∠AOM=30°,求∠CON的度数;(2)在图(a)中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);(3)将图(a)中的直角三角板OMN绕顶点O顺时针旋转至图(b)的位置,一边OM在直线AB上方,另一边ON在直线AB下方.①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;②当∠AOC=3∠BON时,求∠AOM的度数.图(a) 图(b)参考答案1.C 由平面图形变成立体图形的过程是面动成体.2.C 从上面看该几何体,所看到的图形是三角形.3.B 题图中有6条线段,故选B.4.C 符合条件的角中以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,共有1+2+1+1+2=7个,故选C.5.B 由题意得∠AOB=25°+90°+40°=155°.6.B 用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,依据是两点确定一条直线.7.C 因为OC在∠AOD的内部,所以∠COD<∠AOD,故C错误,符合题意.8.B 从展开图可知,该几何体有五个面,两个三角形的面,三个长方形的面,因此该几何体是三棱柱.9.D 如图1,DE=3;如图2,DE=5.故选D.图1 图210.A 8:20时,时针与分针之间有4+2060=133个大格,故8:20时,时针与分针所夹的角是30°×133=130°,故选A.11.点动成线解析将篮球看成一个点,这种现象说明的数学原理是点动成线.12.3解析因为AC=AB+BC=8+4=12,所以AC=3BC.13.30.2解析因为1°=60',所以12'=0.2°,所以30°12'=30.2°. 14.①;两点之间,线段最短解析从A地到B地最短的线路是①,依据是两点之间,线段最短.15.3解析如图所示:所以满足条件的直线共有3条.16.(1)∠AOD与∠DOC(2)∠AOD与∠BOD,∠AOC与∠BOC解析(1)因为O是直线AB上一点,OC是∠AOB的平分线,∠AOB=90°,所以∠AOC=∠BOC=12所以∠AOD+∠DOC=90°,即∠AOD与∠DOC互余.(2)∠AOD+∠BOD=180°,∠AOC+∠BOC=180°,即∠AOD与∠BOD互补,∠AOC与∠BOC互补.17.1;6;6解析题图中有1条直线,为直线AD;6条射线,分别为以A为端点的3条,以B为端点的1条,以D为端点的2条;6条线段,分别是AB、AC、AD、BC、CD、BD.18.180解析∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠DOB=90°+90°=180°.19.5解析因为D是线段BC的中点,BC=4cm,BC=2cm,所以CD=12因为AD=7cm,所以AC=7-2=5(cm).20.15°或65°解析①当OD与OC在OA的同侧时,如图,因为∠AOC=∠BOD=50°,∠AOB=20°,所以∠AOD=∠BOD+∠AOB=70°,因为OE平分∠AOD,∠AOD=35°,所以∠AOE=12所以∠COE=∠AOC-∠AOE=15°;②当OD与OC在OA的异侧时,如图,因为∠AOC=∠BOD=50°,∠AOB=20°,所以∠AOD=∠BOD-∠AOB=30°,因为OE平分∠AOD,所以∠AOE=1∠AOD=15°,2所以∠COE=∠AOC+∠AOE=65°.综上所述,∠COE的度数为15°或65°.21.解析如图所示.22.解析设这个角为x°,根据题意,得180-x=6(90-x),解得x=72.答:这个角是72°.23.解析∠1+∠2-∠3=65°15'+78°30'-(180°-65°15'-78°30')=143°45'-36°15'=107°30'.24.解析(1)北偏东70°.(2)因为∠AOB=40°+15°=55°,∠AOC=∠AOB,所以∠AOC=55°,∠BOC=110°.因为射线OD是OB的反向延长线,所以∠BOD=180°.所以∠COD=180°-110°=70°.因为OE 平分∠COD, 所以∠COE=35°. 又因为∠AOC=55°, 所以∠AOE=90°.25.解析 (1)因为BC=12AB,AC=AB+BC=12 cm, 所以AB+12AB=12 cm, 所以AB=8 cm.(2)因为D 是AB 的中点,AB=8 cm, 所以AD=12AB=4 cm,因为E 是AC 的中点,AC=12 cm, 所以AE=12AC=6 cm, 所以DE=AE-AD=6-4=2(cm).26.解析 (1)由已知得∠BOM=180°-∠AOM=150°, 因为∠MON 是直角,OC 平分∠BOM,所以∠CON=∠MON-12∠BOM=90°-12×150°=15°. (2)由已知得∠BOM=180°-∠AOM=180°-α, 因为∠MON 是直角,OC 平分∠BOM,所以∠CON=∠MON-12∠BOM=90°-12×(180°-α)=12α. (3)设∠AOM=β,则∠BOM=180°-β. ①∠AOM=2∠CON,理由如下: 因为OC 平分∠BOM,所以∠MOC=12∠BOM=12(180°-β)=90°-12β, 因为∠MON=90°,所以∠CON=∠MON-∠MOC=90°-(90°−12β)=12β,所以∠AOM=2∠CON.②由①可知∠BON=∠MON-∠BOM=90°-(180°-β)=β-90°,∠AOC=∠AOM+∠MOC=β+90°-12β=90°+12β,因为∠AOC=3∠BON,所以90°+12β=3(β-90°),解得β=144°, 所以∠AOM=144°.。
第四章 几何图形初步单元检测卷(含解析)
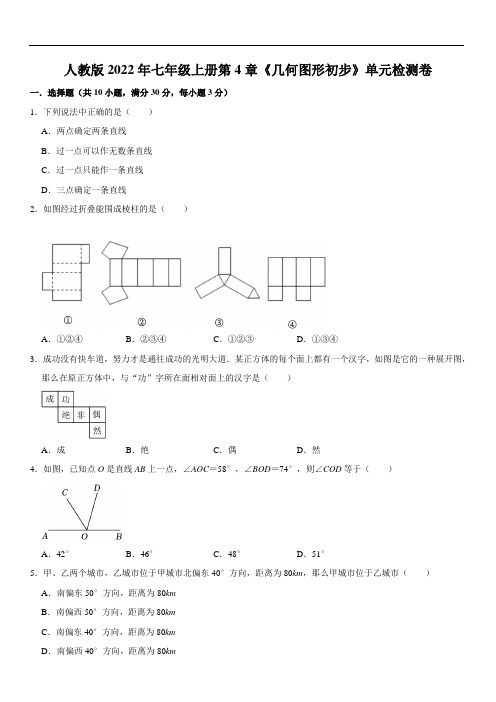
人教版2022年七年级上册第4章《几何图形初步》单元检测卷一.选择题(共10小题,满分30分,每小题3分)1.下列说法中正确的是()A.两点确定两条直线B.过一点可以作无数条直线C.过一点只能作一条直线D.三点确定一条直线2.如图经过折叠能围成棱柱的是()A.①②④B.②③④C.①②③D.①③④3.成功没有快车道,努力才是通往成功的光明大道.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“功”字所在面相对面上的汉字是()A.成B.绝C.偶D.然4.如图,已知点O是直线AB上一点,∠AOC=58°,∠BOD=74°,则∠COD等于()A.42°B.46°C.48°D.51°5.甲、乙两个城市,乙城市位于甲城市北偏东40°方向,距离为80km,那么甲城市位于乙城市()A.南偏东50°方向,距离为80kmB.南偏西50°方向,距离为80kmC.南偏东40°方向,距离为80kmD.南偏西40°方向,距离为80km6.如果一个角的余角等于这个角的补角的,那么这个角的度数是()A.30°B.45C.60°D.757.若∠α的补角为60°,∠β的余角为60°,则∠α和∠β的大小关系是()A.∠α<∠βB.∠α>∠βC.∠α=∠βD.无法确定8.钟表上,下午3:40时时针和分针之间形成的角(小于平角)的度数为()A.150°B.140°C.130°D.120°9.刘琪同学将一副三角板按如图所示位置摆放,摆放位置中∠α=∠β的图形是()A.B.C.D.10.如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BD=7cm,则BC的长为()A.2cm B.3cm C.4cm D.5cm二.填空题(共5小题,满分20分,每小题4分)11.计算90°﹣40°25′=.12.若∠α=53°23′17″,则∠α的补角的度数为.13.如图,经过刨平的木板上的两个点,能弹出一条笔直的直线,并且只有一条,其中蕴含的数学道理是.14.已知线段AB=8cm,在直线AB上有一点C,且BC=3cm,点M为线段AC的中点,则线段AM的长是多少.15.如图所示是一个几何体的表面展开图,则该几何体的体积为.(结果用含π式子表示)三.解答题(共8小题,满分70分)16.(6分)计算:180°﹣(35°54'+21°33').17.(6分)下面是一个正方体的平面展开图,请把10,,﹣,0.1,,﹣7分别填入六个正方形中,使得折成正方体后,相对面上的数互为倒数.18.(6分)一个角的补角加上20°后等于这个角的余角的3倍,求这个角.19.(8分)如图,在平面内有A,B,C三点.(1)画直线AB;画射线AC;画线段BC;(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至点E,使DE=AD;(3)数一数,此时图中共有多少条线段?多少条射线?20.(10分)(1)如图1,已知∠AOB=∠COD=90°,OE是∠AOC的角平分线,当∠BOD=42°时,求∠AOE 的度数;(2)如图2,已知∠AOB=80°,∠COD=110°,∠AOC=2∠BOD时,求∠BOD的度数;(3)如图3,当∠AOB=α,∠COD=β,且∠AOC=n∠BOD(n>1)时,请直接用含有α、β、n的式子表示∠BOD的值.21.(10分)如图,点B是线段AC上一点,且AB=28cm,.(1)求线段AC的长;(2)如果点O是线段AC的中点,求线段OB的长.22.(12分)已知∠AOB,过顶点O作射线OP,若∠BOP=∠AOP,则称射线OP为∠AOB的“好线”,因此∠AOB的“好线”有两条,如图1,射线OP1,OP2都是∠AOB的“好线”.(1)已知射线OP是∠AOB的“好线”,且∠BOP=30°,求∠AOB的度数.(2)如图2,O是直线MN上的一点,OB,OA分别是∠MOP和∠PON的平分线,已知∠MOB=30°,请通过计算说明射线OP是∠AOB的一条“好线”.(3)如图3,已知∠MON=120°,∠NOB=40°.射线OP和OA分别从OM和OB同时出发,绕点O按顺时针方向旋转,OP的速度为每秒12°,OA的速度为每秒4°,当射线OP旋转到ON上时,两条射线同时停止.在旋转过程中,射线OP能否成为∠AOB的“好线”.若不能,请说明理由;若能,请求出符合条件的所有的旋转时间.23.(12分)【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB 的中点表示的数为.【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t 秒(t>0).【综合运用】(1)填空:①A、B两点间的距离AB=,线段AB的中点表示的数为;②用含t的代数式表示:t秒后,点P表示的数为;点Q表示的数为.(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;(3)求当t为何值时,PQ=AB;(4)若点M为P A的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.人教版2022年七年级上册第4章《几何图形初步》单元检测卷参考答案一.选择题(共10小题,满分30分,每小题3分)1.【解答】解:A、应为两点确定一条直线,故本选项错误;B、过一点可以作无数条直线,故C选项错误,B选项正确;D、三点确定一条直线或三条直线,故D选项错误.故选:B.2.【解答】解:由题意知,①可以围成四棱柱,②可以围成五棱柱,③可以围成三棱柱,故选:C.3.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,与“功”字所在面相对面上的汉字是“然”.故选:D.4.【解答】解:根据题意可得,因为∠AOC+∠COD+∠BOD=180°,所以∠COD=180°﹣∠AOC﹣∠BOD=180°﹣58°﹣74°=48°.故选:C.5.【解答】解:如图:∵乙城市位于甲城市北偏东40°方向,距离为80km,∴甲城市位于乙城市南偏西40°方向,距离为80km,故选:D.6.【解答】解:设这个角为x°,则这个角的余角=90°﹣x°,补角=180°﹣x°,由题意得,90°﹣x°=(180°﹣x°),解得x=60.故选:C.7.【解答】解:∵∠α=180°﹣60°=120°,∠β=90°﹣60°=30°.∴∠α>∠β,故选:B.8.【解答】解:30°×(5﹣)=130°.所以3:40时,时针与分针所成的角度130°.故选:C.9.【解答】解:A、根据同角的余角相等可得∠α=∠β,符合题意;B、由三角板的性质可知,∠α>∠β,不符合题意;C、由三角形外角的性质可知,∠α<∠β,不符合题意;D、由平角的定义可知,∠α+∠β=180°,不符合题意.故选:A.10.【解答】解:∵AB=10cm,BD=7cm,∴AD=3cm,∵D是线段AC的中点,∴AC=6cm.∴BC=4cm.故选:C.二.填空题(共5小题,满分20分,每小题4分)11.【解答】解:90°﹣40°25′=89°60′﹣40°25′=49°35′,故答案为:49°35′.12.【解答】解:∵∠α=53°23′17″,∴∠α的补角的度数=180°﹣53°23′17″=126°36′43″,故答案为:126°36′43″.13.【解答】解:经过刨平的木板上的两个点,能弹出一条笔直的直线,并且只有一条,其中蕴含的数学道理是两点确定一条直线.故答案为:两点确定一条直线.14.【解答】解:①当点C在线段AB的延长线上时,此时AC=AB+BC=11cm,∵M是线段AC的中点,则AM=AC=5.5(cm);②当点C在线段AB上时,AC=AB﹣BC,=5cm,∵M是线段AC的中点,则AM=AC=2.5(cm).故答案为:5.5cm或2.5cm.15.【解答】解:V=Sh=π()2×6=24π,故答案为:24π.三.解答题(共8小题,满分70分)16.【解答】解:180°﹣(35°54'+21°33')=179°60'﹣57°27′=122°33'.17.【解答】解:如图所示:.18.【解答】解:设这个角为α,则这个角的补角为180°﹣α,余角为90°﹣α,根据题意可得,180°﹣α+20°=3(90°﹣α),解得:α=55°,所以这个角为55°.19.【解答】解:(1)如图,直线AB,线段BC,射线AC即为所求;(2)如图,线段AD和线段DE即为所求;(3)图中共有8条线段,6条射线.20.【解答】解:(1)如图1,∵∠AOB=∠COD=90°,∠BOD=42°,∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣42°=138°,∴∠AOE=∠AOC=×138°=69°答:∠AOE的度数为69°;(2)如图2,∵∠AOB=80°,∠COD=110°,∴∠AOC=∠AOB+∠COD﹣∠BOD=80°+110°﹣∠BOD,又∵∠AOC=2∠BOD,∴2∠BOD=80°+110°﹣∠BOD,∴∠BOD==,答:∠BOD的度数为°;(3)如图3,∵∠AOB=α,∠COD=β,∴∠AOC=∠AOB+∠COD﹣∠BOD=α+β﹣∠BOD,又∵∠AOC=n∠BOD,∴n∠BOD=α+β﹣∠BOD,∴∠BOD=,答:∠BOD=.21.【解答】解:(1)∵AB=28cm,BC=AB,∴BC=7cm.∴AC=AB+BC=28+7=35(cm);(2)∵点O是线段AC的中点,∴OC=AC=35=17.5(cm),∵BC=7cm,∴OB=OC﹣BC=17.5﹣7=10.5(cm).22.【解答】解:(1)∵OP是∠AOB的“好线”,且∠BOP=30°,∴∠AOP=2∠BOP=60°,①当OP在∠AOB的外部时,∠AOB=∠AOP﹣∠BOP=30°,②当OP在∠AOB的内部时,∠AOB=∠AOP+∠BOP=90°.(2)∵OB是∠MOP的平分线,且∠MOB=30°,∴∠BOP=∠MOB=30°,∠MOP=2∠MOB=60°,∴∠PON=120°,∵OA是∠PON的平分线,∴∠AOP=∠PON=60°,∴∠BOP=∠AOP,∴OP是∠AOB的一条“好线”;(3)设旋转的时间为t秒,①80﹣12t=4t,∴t=5,②3(12t﹣80)=4t,∴t=,综上所述,所有符合条件的旋转时间为5秒或秒.23.【解答】解:(1)①10,3;②﹣2+3t,8﹣2t;(2)∵当P、Q两点相遇时,P、Q表示的数相等∴﹣2+3t=8﹣2t,解得:t=2,∴当t=2时,P、Q相遇,此时,﹣2+3t=﹣2+3×2=4,∴相遇点表示的数为4;(3)∵t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,∴PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,又PQ=AB=×10=5,∴|5t﹣10|=5,解得:t=1或3,∴当:t=1或3时,PQ=AB;(4)∵点M表示的数为=﹣2,点N表示的数为=+3,∴MN=|(﹣2)﹣(+3)|=|﹣2﹣﹣3|=5.。
第4章 一元一次方程 章末检测卷(原卷版)

第4章 一元一次方程 章末检测卷(苏科版)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分120分,考试时间120分钟,试题共26题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022·仪征市七年级月考)下列方程中,是一元一次方程的是( ) A .24=1x x -B .110x-=C .=0xD .2=1x y +2.(2022·内蒙古)若关于x 的方程mx |m |﹣m +3=0是一元一次方程,则这个方程的解是( ) A .x =﹣2B .x =4C .x =﹣2或x =4D .x =23.(2022·重庆·垫江第八中学校七年级阶段练习)以下等式变形不正确的是( ) A .由x y =,得到22x y +=+ B .由233a b -=-,得到2a b = C .由m n =,得到am an =D .由am an =,得到m n =4.(2022·江苏·七年级专题练习)有8个球编号是①至①,其中有6个球一样重,另外两个都轻1克,为了找出这两个轻球,用天平称了三次:第一次①+①比①+①重,第二次①+①比①+①轻,第三次①+①+①和①+①+①一样重.那么,两个轻球的编号是( ) A .①①B .①①C .①①D .①①5.(2022·河南)若方程与关于的方程的解互为相反数,则的值为( ). A .B .C .D .6.(2022·河北·涿州市双语学校七年级期末)已知下列两个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?①甲乙两人从相距20km 的两地同时出发,背向而行,甲的速度是4km/h ,乙的速度是6km/h ,问经过几小时后两人相距60km ?其中可以用方程4x +6x +20=60表述题目中数量关系的应用题是( ) A .①B .①C .①①D .①①都不对7.(2022·江苏九年级专题练习)小明在解关于x 的一元一次方程332a xx -= 时,误将x -看成了x +,得到()2160x --=x 313a x-=a 13-13731-的解是x =1,则原方程的解是( ) A .1x =-B .57x =-C .57x =D .x =18.(2022·江苏南通市·七年级期末)在有理数范围内定义运算“☆”:12b b a a -=+☆,如:()1313112---=+=-☆.如果()21x x =-☆☆成立,则x 的值是( ) A .1- B .5 C .0 D .29.(2022·江苏七年级期中)如图,是由7块正方形组成的长方形,已知中间小正方形的边长为1,则这个长方形的面积为( )A .63B .72C .99D .11010.(2022·沙坪坝·重庆一中)已知关于x 的方程的解为偶数,则整数a 的所有可能的取值的和为( ) A .8B .4C .7D .-2二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在横线上) 11.(2022·江苏·太仓市七年级期中)如果关于x 的方程4231x m x -=+和23x x =-的解相同,那么m =__________.12.(2022·仪征市实验初中七年级月考)若关于x 的一元一次方程ax =b 的解满足x =b +a ,则称该方程为“和解方程”,例如:方程2x =−4的解为x =−2,而−2=−4+2,则方程2x =−4为“和解方程”.若关于x 的一元一次方程2x =b -1是“和解方程”,则b 的值为________________; 13.(2022·重庆实验外国语学校)若关于x 的方程无解,则a 的值为 14.(2022·仪征市实验初中七年级月考)下面是一个被墨水污染过的方程:2x ﹣1=3x +答案显示此方程的解是x =,被墨水遮盖的是一个常数,则这个常数是______________ 15.(2022·河南驻马店·七年级期中)已知关于x 的一元一次方程122022x x m +-=的解是71x =,那么关于1922ax x -=+6326a x x x -=-12-y 的一元一次方程13(1)2022y y m +-+=的解是_________.16.(2022·江苏盐城·七年级期末)某次篮球联赛共有十支队伍参赛,部分积分表如下表:根据表格提供的信息,可知胜一场积 _____分.17.(2022·山东济南·七年级专题练习)对于三个互不相等的有理数a ,b ,c ,我们规定符号max{,,}a b c 表示a ,b ,c 三个数中较大的数,例如max 2,3{,4}4=.按照这个规定则方程max{,,0}32x x x -=-的解为__________. 18.(2022·河南信阳·七年级期末)已知:方程3355x x +=+的解是5x =;方程()3333x x +=-+-的解是3x =-;方程()334433x x +++=+的解是1x =-(由43x +=得出).则方程()3111x x -+=的解是________. 三、解答题(本大题共8小题,共66分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(2022·江苏无锡·七年级期末)解方程:(1)()2157x x +=-; (2)11136x x -+-=.20.(2022·河南南阳·七年级期中)下面是小明同学解方程的过程,请认真阅读并完成相应任务.(1)任务一:填空:①以上求解步骤中,第一步进行的是______,这一步的依据是(填写具体内容)__________; ①以上求解步骤中,第________步开始出现错误,具体的错误是_____________﹔ ①请直接写出该方程正确的解为____________________.(2)任务二:①请你根据平时的学习经验,在解方程时还需注意的事项提一条合理化建议.21.(2022·河北沧州·七年级期末)某工厂有28名工人生产A 零件和B 零件,每人每天可生产A 零件18个或B 零件12个(每人每天只能生产一种零件),一个A 零件配两个B 零件.工厂将零件批发给商场时,每个A 零件可获利10元,每个B 零件可获利5元.(1)若每天生产的A 零件和B 零件恰好配套,求该工厂每天有多少工人生产A 零件?(2)因市场需求,该工厂每天在生产配套的零件外,还要多生产出一部分A 零件供商场零售.在(1)的人员分配情况下,现从生产B 零件的工人中调出多少名工人生产A 零件,才能使每天生产的零件全部批发给商场后总获利为3120元?22.(2022·上海市罗南中学八年级阶段练习)解关于x 的方程:(21)2(1)a x x +=+.23.(2022·四川成都实外七年级期末)为了丰富学生的课余生活、拓展学生的视野,学校小卖部准备购进甲、乙两类中学生书刊.若购买400本甲和300本乙共需要6400元.其中甲、乙两类书刊的进价和售价如下表:(1)求甲、乙两类书刊的进价各是多少元?(2)第一次小卖部购进的甲、乙两类书刊共800本,全部售完后总利润(利润=售价﹣进价)为5750元,求小卖部甲、乙两类书刊分别购进多少本?(3)第二次小卖部购进了与上次一样多的甲、乙两类书刊,由于两类书刊进价都比上次优惠了10%,小卖部准备对甲书刊进行打折出售,乙书刊价格不变,全部售完后总利润比上次还多赚10元,求甲书刊打了几折?24.(2022·江苏·扬州市梅岭中学七年级阶段练习)定义:若A﹣B=m,则称A与B是关于m的关联数.例如:若A﹣B=2,则称A与B是关于2的关联数;(1)若3与a是关于2的关联数,则a=______.(2)若2x﹣1与3x﹣5是关于2的关联数,求x的值.(3)若M与N是关于m的关联数,M=3mn+n+3,N的值与m无关,求N的值.25.(2022·福建福州七年级期中)随着互联网的普及和城市交通的多样化,人们的出行方式有了更多的选择.下图是某市两种网约车的收费标准,例:乘车里程为30公里,若选乘出租车,费用为:()()+⨯-+⨯-=(元);若选乘曹操出行(快选),费用为:14 2.23031301093.4()30+⨯+⨯-+⨯⨯=(元)10 2.4300.830100.46011640请回答以下问题:(1)小明家到学校的路程是10公里.如果选乘出租车,车费为元;如果选乘曹操出行(快选),车费为元.(2)周末小明有事外出,要选乘网约车,如果乘车费用预算为25元,他的行车里程数最大是多少公里?(3)元旦期间,小明外出游玩,约车时发现曹操出行(快选)有优惠活动:总费用打八折.于是小明决定选乘曹操出行(快选).付费后,细心的小明发现:相同的里程,享受优惠活动后的曹操出行(优选)的费用还是比出租车多了1.8元,求小明乘车的里程数.26.(2022·哈尔滨工业大学附属中学校开学考试)某小区建完之后,需要做内墙粉刷装饰,现有甲、乙两个工程队都想承包这项工程,已知甲工程队每天能粉刷160个房间,乙工程队每天能粉刷240个房间.且单独粉刷这些墙面甲工程队比乙工程队要多用20天,在粉刷的过程中,该开发商要付甲工程队每天费用1600元,付乙工程队每天费用2600元.(1)求这个小区共有多少间房间?(2)为了尽快完成这项工程,若先由甲、乙两个工程队按原粉刷速度合作一段时间后,甲工程队停工了,而乙工程队每天的粉刷速度提高25%,乙工程队单独完成剩余部分,且乙工程队的全部工作时间是甲工程队的工作时间的2倍还多4天,求乙工程队共粉刷多少天?(3)经开发商研究制定如下方案:方案一:由甲工程队单独完成;方案二:由乙工程队单独完成;方案三:按(3)问方式完成;请你通过计算帮开发商选择一种既省时又省钱的粉刷方案.。
湘教版数学七年级下册第4章 相交线与平行线 达标测试卷(含答案)

第4章相交线与平行线达标测试卷一、选择题(共6题,每题3分,共18分)1. 下列图形中,能将其中一个三角形平移得到另一个三角形的是()A B C D2. 如图,对于图中标记的各角,下列条件能够推理得到a∥b的是()A.∠1=∠2B.∠2=∠4C.∠3=∠4D.∠1+∠4=180°(第2题)(第3题)(第4题)3. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为()A.30°B.60°C.80°D.120°4. 在体育课上某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量的线段及理由是()A.BP,经过一点有且只有一条直线垂直于已知直线B.CP,垂线段最短C.DP,两点之间,线段最短D.BD,两平行线间的公垂线段相等5. 如图,已知正方形ABCD的面积为4,则三角形EBC的面积为()A.4 B.3 C.2 D.1(第5题)(第6题)(第7题)(第8题)6. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120°B.130°C.140°D.150°二、填空题(共6题,每题4分,共24分)7. 如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE=______°.8. 如图,a∥b,点P在直线a上,点A在直线b上,P A⊥b,P A=2 cm,则点A到直线a的距离为________cm.9. 如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=________.(第9题) (第10题)10. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________.11. 如图,若直线EF⊥MN于F,且∠1=140°,则当∠2=________时,AB∥CD.(第11题) (第12题)12. 如图,直线AB,CD交于点O,∠BOC=70°,现作射线OE⊥CD,则∠AOE的大小为__________.三、解答题(共6题,共58分)13. (8分)如图,要把水渠中的水引到C点,在渠岸AB的什么地方开沟,才能使沟最短?画出图形,并说明理由.14. (8分)如图,直线AB、CD相交于点O, OD垂直于OE,∠BOE=18°.求∠AOC的度数.15. (8分)如图,已知AD∥BC,AC=15 cm,BC=12 cm,BE⊥AC于点E,BE=10 cm,求AD与BC之间的距离.16. (10分)如图,已知∠ABC=180°-∠A,BD⊥CD于点D,EF⊥CD于点F.(1)试说明:AD∥BC.(2)若∠1=36°,求∠2的度数.317. (10分)如图,将周长为18 cm的三角形ABC沿BC方向平移得到三角形DEF.如果四边形ABFD的周长是21 cm,求平移的距离.18. (14分)问题情境:如图①,AB∥CD,∠P AB=130°,∠PCD=120°,求∠APC的度数.小明的解题思路:如图②,过P作PE∥AB,通过平行线的性质,可得∠APC =50°+60°=110°.问题迁移:(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A,B两点外侧运动(点P与A,B,O三点不重合),请你直接写出∠CPD,∠α,∠β之间的数量关系.答案一、1.A 2.D 3.A 4.B 5.C 6.C二、7.258.2【点拨】因为a∥b,P A⊥b,P A=2 cm,所以AP⊥a,所以点A到直线a 的距离=P A=2 cm.9.50°10.48°【点拨】如图,因为AC∥BD,∠1=48°,所以∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.11.50°【点拨】如图,因为AB∥CD,所以∠3=∠4(两直线平行,同位角相等).又因为∠1+∠3=180°,∠1=140°,所以∠3=∠4=40°.因为EF⊥MN,所以∠2+∠4=90°,所以∠2=50°.12.20°或160°【点拨】因为OE⊥DC,所以∠DOE=90°.因为∠AOD=∠BOC,∠BOC=70°,所以∠AOD=70°.①当OE在DC的左侧时,∠AOE=∠DOE-∠AOD=90°-70°=20°;②当OE在DC的右侧时,∠AOE=∠DOE+∠AOD=90°+70°=160°.综上,∠AOE=20°或160°.5三、13.解:图略.过C作CD⊥AB,垂足为D,在D处开沟,则沟最短.因为直线外一点与直线上各点连线的所有线段中,垂线段最短.14.解:因为OD⊥OE,所以∠BOD+∠EOB=90°.因为∠BOE=18°,所以∠BOD=90°-18°=72°,所以∠AOC=∠BOD=72°.15.解:过点A作BC的垂线,交BC于点P,三角形ABC的面积为12×AC×BE=12×15×10=75(cm2),又因为三角形ABC的面积为12×BC×AP=75(cm2),所以AP=12.5 cm,因此AD与BC之间的距离为12.5 cm.16.解:(1)因为∠ABC=180°-∠A,所以∠ABC+∠A=180°,所以AD∥BC.(2)因为AD∥BC,∠1=36°,所以∠3=∠1=36°.因为BD⊥CD,EF⊥CD,所以∠BDC=∠EFC=90°.所以BD∥EF.所以∠2=∠3=36°.17.解:因为三角形DEF是由三角形ABC沿BC方向平移得到的,所以AD=CF,AC=DF.所以四边形ABFD的周长为AD+AB+BF+DF=AD+AB+BC+AC+CF=2AD+(AB+BC+AC)=21 cm.因为AB+BC+AC=18 cm,所以2AD=3 cm,解得AD=1.5 cm.答:平移的距离为1.5 cm.18.解:(1)∠CPD=∠α+∠β.理由如下:如图①,过P作PE∥AD交CD于E,因为AD∥BC,所以AD∥PE∥BC.所以∠α=∠DPE,∠β=∠CPE.所以∠CPD=∠DPE+∠CPE=∠α+∠β.(2)当点P在线段BA的延长线上时,如图②.∠CPD=∠β-∠α.当点P在线段AB的延长线上时,如图③. ∠CPD=∠α-∠β.7。
沪科版七年级上《第4章直线与角》达标检测试卷含答案

第4章达标检测卷(120分,90分钟)题号一二三总分得分一、选择题(每题4分,共40分)1.下列几何图形中为圆柱体的是()2.如图,将长方形绕它的一条边MN所在的直线旋转一周而成的几何体是()(第2题)3.如图所示,能相交的图形有()(第3题) A.1个B.2个C.3个D.4个4.如图所示,C,D是线段AB上的两点,若BC=3 cm,DB=5 c m,且D是AC的中点,则AC的长等于()A.3 cm B.4 cm C.8 cm D.10 cm(第4题)(第6题) 5.下列说法中,正确的有()①如果∠1=∠2,∠3=∠4,那么∠1=∠3;②如果∠1=∠2,∠2=∠3,那么∠1=∠3;③如果∠1是∠2的补角,∠3是∠4的补角,且∠2=∠4,那么∠1=∠3;④如果∠1是∠2的余角,∠3+∠2=90°,那么∠1=∠3.A.1个B.2个C.3个D.4个6.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是()A.20°B.25°C.30°D.70°7.已知点A,B,C共线,如果线段AB=5 cm,BC=4 cm,那么A,C两点间的距离是()A.1 cm B.9 cm C.1 cm或9 cm D.2 cm或10 cm8.如图,由A测B的方向是()A.南偏东25°B.北偏西25°C.南偏东65°D.北偏西65°(第8题)(第10题) 9.在时刻8:30,时钟上的时针和分针之间的夹角为()A.85°B.75°C.70°D.60°10.如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;②图中有2对互补的角;③若∠BAE=100°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11.其中说法正确的有() A.1个B.2个C.3个D.4个二、填空题(每题5分,共20分)11.(中考·济南)如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释这一现象的原因:________________________.12.用度分秒表示:57.32°=________°________′________″.13.如图,从A到B的最短的路线是________.(第11题)(第13题)(第14题)14.如图,∠AOB=∠COD=90°,下列说法:①∠BOC=∠AOC=∠BOD;②∠AOC =∠BOD;③∠BOC与∠AOD互补;④∠BOC的余角只有∠AOC;⑤若∠AOD=2∠BOC,则∠BOC=60°,其中一定正确的序号是________.三、解答题(17、20题每题9分,21题8分,22题10分,其余每题6分,共60分)15.计算:(1)55°25′57″+27°37′24″-16°48′22″;(2)(58°47′25″+12°36′45″)÷5.16.如图,已知∠α和∠β(∠α>∠β),求作∠AOD,使得∠AOD=2∠α-∠β.(第16题)17.若第一个角的补角比第二个角的余角的3倍少20°,而第二个角的补角比第一个角的余角的3倍多20°,求这两个角的度数.18.下面是小马虎解的一道题.题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.解:根据题意画出图形,如图所示.∠AOC=∠BOA-∠BOC=70°-15°=55°.若你是老师,会给小马虎满分吗?若会,请说明理由;若不会,请指出小马虎的错误.(第18题)19.如图,线段AD上两点B,C将AD分成2∶3∶4三部分,M是AD的中点,若MC=2,求线段AD的长.(第19题)20.如图,OB,OC是∠AOD内任意两条不同的射线,OM平分∠AOB,ON平分∠COD,若∠MON=45°,∠BOC=20°,求∠AOD的度数.(第20题)21.已知直线AB上有一点C,且AB=10 cm,BC=4 cm,M是AB的中点,N是BC 的中点,求MN的长.22.(1)如图,已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;(2)若在(1)中,∠AOB=α,其他条件不变,求∠MON的度数;(3)若在(1)中,∠AOB=α,∠BOC=β,其他条件不变,求∠MON的度数;(4)你能从(1)(2)(3)中发现什么规律?(第22题)答案一、1.C 2.C 3.B 4.B 5.C 6.D 7.C 8.C 9.B 10.B 二、11.两点之间,线段最短 12.57;19;12 13.A -F -E -B14.②③⑤ 点拨:因为∠AOB =∠COD =90°,所以根据同角的余角相等,可得∠BOD =∠AOC ,但不能得到∠BOD 或∠AOC 与∠BOC 相等,故①错误,②正确;因为∠BOC +∠AOD =∠AOB +∠COD =180°,所以∠BOC 与∠AOD 互补,故③正确;∠BOC 的余角是∠BOD 或∠AOC ,故④错误;当∠AOD =2∠BOC 时,∠AOD +∠BOC =3∠BOC ,而∠AOD +∠BOC =∠AOB +∠COD =180°,所以3∠BOC =180°,即∠BOC =60°,故⑤正确.因此填②③⑤.三、15.解:(1)原式=(55°+27°-16°)+(25′+37′-48′)+(57″+24″-22″)=66°+14′+59″=66°14′59″.(2)原式=70°83′70″÷5=14°+16′+(180″+70″)÷5=14°+16′+50″=14°16′50″. 16.解:作法:如图.(1)作∠AOB =∠α;(2)以射线OB 为边,在∠AOB 的外部作∠BOC =∠α; (3)以射线OC 为边,在∠AOC 的内部作∠COD =∠β. 则∠AOD 就是所求作的角.(第16题)17.解:设第一个、第二个角的度数分别为x ,y ,则⎩⎪⎨⎪⎧180°-x =3(90°-y )-20°,180°-y =3(90°-x )+20°,解得⎩⎪⎨⎪⎧x =50°,y =40°. 所以这两个角的度数分别为50°和40°.18.解:不会给小马虎满分.小马虎只考虑了OC 落在∠AOB 内部的情况.当OC 落在∠AOB 的外部时,∠AOC =∠BOA +∠BOC =85°.19.解:设AB 的长为2k(k >0),则BC ,CD 的长分别为3k ,4k , 所以AD =2k +3k +4k =9k.因为M 是AD 的中点,所以MD =12AD =4.5k ,所以MC =MD -CD =4.5k -4k =0.5k =2,解得k =4. 所以AD =9k =9×4=36.20.解:因为OM 平分∠AOB ,ON 平分∠COD ,所以∠AOB =2∠BOM ,∠COD =2∠CON ,所以∠AOD =∠AOB +∠COD +∠BOC =2∠BOM +2∠CON +∠BOC =2(∠BOM +∠CON)+∠BOC =2(∠MON -∠BOC)+∠BOC =2×(45°-20°)+20°=70°.21.解:分两种情况:(1)当点C 在AB 的延长线上时,因为AB =10 cm ,M 是AB 的中点,所以BM =5 cm . 因为BC =4 cm ,N 是BC 的中点,所以BN =2 cm ,所以MN =5+2=7(cm ). (2)当点C 在线段AB 上时,因为AB =10 cm ,M 是AB 的中点,所以BM =5 cm . 因为BC =4 cm ,N 是线段BC 的中点,所以BN =2 cm ,所以MN =5-2=3(cm ). 综上所述,MN 的长为7 cm 或3 cm .22.解:(1)因为∠AOB 是直角,∠BOC =30°,所以∠AOC =∠AOB +∠BOC =90°+30°=120°.因为OM 平分∠AOC , 所以∠MOC =60°.因为∠BOC =30°,ON 平分∠BOC ,所以∠NOC =15°. 所以∠MON =∠MOC -∠NOC =60°-15°=45°. (2)因为∠AOB =α,所以∠AOC =∠AOB +∠BOC =α+30°.因为OM 平分∠AOC ,所以∠MOC =α+30°2=α2+15°.因为∠BOC =30°,ON 平分∠BOC ,所以∠NOC =15°. 所以∠MON =∠MOC -∠NOC =⎝⎛⎭⎫α2+15°-15°=α2. (3)因为∠AOB =α,∠BOC =β, 所以∠AOC =∠AOB +∠BOC =α+β. 因为OM 平分∠AOC ,所以∠MOC =α+β2.因为ON 平分∠BOC ,所以∠NOC =β2.所以∠MON =∠M OC -∠NOC =α+β2-β2=α2.(4)从(1)(2)(3)中发现:∠MON 的度数只与∠AOB 的度数有关,和∠BOC 的度数无关,∠MON 的度数等于∠AOB 的度数的一半.。
