概率论与数理统计2版(李书刚编)思维导图
概率论与数理统计知识网络图

概率论与数理统计知识网络图概率论与数理统计这一章可以分为概率论和数理统计两部分,基本思想是用随机的思想来研究随机现象的统计规律性。
其内容是学习随机事件和概率、随机变量及其概率分布、二维随机变量及其联合概率分布、随机变量的数字特征、大数定律和中心极限定理、数理统计的基本概念、参数估计、假设检验等知识。
在研究生入学考试中,本章是《高等数学一》、《高等数学三》和《高等数学四》的考试内容。
通过这一章的学习,我们认为应达到如下要求:1、对于随机事件,特别是随机变量及其分布函数、二维随机变量及其联合分布函数应该有清晰的概念。
2、对于随机性的方法能运用自如。
3、具备对实际问题理解能力,定性分析和定量计算相统一的能力和推理、演绎的逻辑思维能力。
知识网络图⎧⎪⎪⎨⎪⎪⎩⎧⎪⎨⎪⎩事件的运算和概率计算加法公式、乘法公式、条件概率公式随机事件和概率以及全概率公式和贝叶斯公式的应用事件独立性的判定,古典概型、几何概型问题概率分布和分布函数的性质和计算随机变量及其分布函数离散型和连续型随机变量的计算问题随机变量的函数的分布的求法二维离散型和连续型随机变量概率分布的计算二维随机变量取某范围值的概率概率论二维随机变量及其联合分布函数二维离散型随机变量函数的分布⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎪⎪⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎧⎪⎨⎪⎩⎩⎧⎧⎪⎨⎨⎩⎪⎩的求法二维连续型随机变量函数的分布的求法离散型和连续型随机变量的数字特征正态分布的数字特征的计算随机变量的数字特征随机变量的独立性、相关性和相关系数切比雪夫不等式数字特征的应用大数定律大数定律和中心极限定理中心极限定理数理统计的基本概念矩估计点估计数理统计参数估计最大似然估计区间估计⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩假设检验,主要是正态总体未知参数的假设检验。
高中数学课件-概率与统计思维导图

概率
求法
定义: (大量实验),频率的稳定值 对称性 概率模型
概率模型
古典概型 计算:基本事件数 几何概型 条件概型
计数 原理
分类加法、分布乘法 排列 组合
随机变量
独立事件概型
分布列模型
期望与方差
0-1分布 超几何分布:不放回地摸正、次品 二项分布:独立重复实验、量大
正态分布 定义
性质
3.回归效果分析 4.预测/决策
n
^2
y 残差平方和
( yi
)
i
残差平方和越小,拟合效果越好
残差图
i1
n
^
( yi yi )2 残差平方和
相关指数
R2
1
i 1 n
R2 1, 拟合效果越好
( yi y)2 总偏差平方和
i 1
与相关系数r正比,与残差平方和反比关系
独立性检验的一般性步骤Fra bibliotekX/Y
抽样方法
收集数据
简单随机抽样: 抽签法、随机数表
系统(等距)抽样
分层抽样
统计
统计图表
整理数据
统计指标
分析数据
函数拟合/独立性检验
预测/关联
茎叶图 频率分布直方图
折线图
平均数 中位数 集中趋势 众数
定 线性回归方程
量
拟
变 量
非线性回归方程
合
饼状图 条形图
标准差 离散程度
方差
极差 变化范围
分
类 独立性检验 变 (有关联分析) 量
y1
y2
总计
第1步:作2X2列联表
x1
a
b
a+b
x2
《概率导论 第2版修订版 》读书笔记PPT模板思维导图下载

《概率导论 第2版修订版 》
PPT书籍导读
读书笔记模板
最
新
版
本
01 献词
目录
02 译者序
03 第2版前言
04
第1章 样本空间与概 率
05 第2章 离散随机变量
06 第3章 一般随机变量
目录
07 第4章 随机变量的高 级主题
09
第6章 伯努利过程和 泊松过程
08 第5章 极限理论 010 第7章 马尔可夫链
目录
011 第8章 贝叶斯统计推 断
013 附表
012 第9章 经典统计推断
本书基于麻省理工学院开设的概率论入门课程编写,内容系统,例题和习题丰富,结构层 次性强,能够满 足不同读者的需求。书中介绍了概率模型、离散随机变量和连续随机变量、多元随机变量以及极限理论等概率论 基础知识,还介绍了矩母函数、条件概率的现代定义、独立随机变量的和、最小二乘估计等高级内容。
7.6 小结和讨论
7.5 连续时间的 马尔可夫链
7.7 习题
第8章 贝叶斯统计推断
0 1
8.1 贝叶 斯推断与 后验分布
0 2
8.2 点估 计、假设 检验、最 大后验概 率准...
0 3
8.3 贝叶 斯最小均 方估计
0 4
8.4 贝叶 斯线性最 小均方估 计
0 5
8.5 小结 和讨论
0 6
8.6 习题
0 4
2.4 期望、 均值和方 差
0 6
2.6 条件
0 5
2.5 多个 随机变量 的联合概 率质量函 数
2.8 小结和讨一般随机变量
3.1 连续随机变 量和概率密度函
概率统计思维导图初三

概率与统计(公式、定理、结论图表)
快 速 提 分
思维导图
事件
随机事件
确定事件
机会 必然事件 不可能事件
树状图
分析预测概率
列表
Байду номын сангаас
概率
用实物替代
用频率估计概率 模拟实验
用计算器模拟
收集数据
媒体调查
亲自调查
普查
抽样调查
抽样的基本要求 总体,个体,样本,样本容量
频数分布 频数,频率 整理数据
统计
频数分布直方图,频数折线图,扇形统计图
统计图表
集中程度 平均数,中位数,众数
分析数据
统计量
离散程度 极差,方差,标准差
加权平均数
用样本估计总体
作出决策
作出判断或预测
概率论与数理统计图文课件最新版-第3章-多维随机变量及其分布
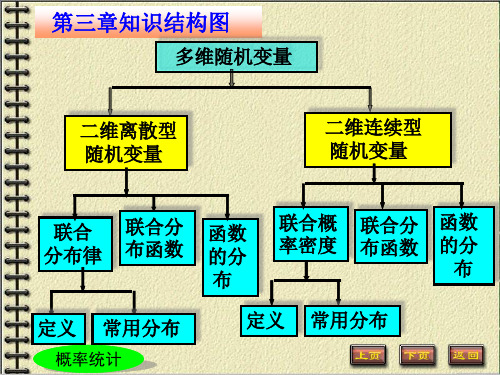
比如:
概率统计
比如:
1 x y 0
F( x, y) 0 x y 0
对这二元函数来验证第4条性质。
现找 4 个点如下:
( x2 , y2 ) (1, 1); ( x1, y2 ) (1, 1)
( x2 , y1 ) (1, 1); ( x1, y1 ) (1, 1)
F(1,1) F(1,1) F(1, 1) F(1, 1)
0
x 0, y 0 其它
求: (1) 分布函数 F( x, y)
(2) ( X ,Y )落在G内的概率
其中 G: x y 1 及 x 轴、y 轴所围区域
解: (1) Q
x
F(x, y)
y
f ( x, y)dxdy
当 x 0, y 0 时
xy
F( x, y)
0 dx 0
2,4,8,10,14,16,20这7个 数不能被3整除,但能
被2整除
6,12,18这3个数能被2 整除,又能被3整除
不难验证:
1 1
7473
pi j 0, 0 0 pi j 21 21 21 21 1
概率统计
故 得: (X,Y) 的 联合分布 律为:
XY
0 1
01
7
4
21 21
7
P( x1 X x2 , y1 Y y2 )
F ( x2 , y2 ) F ( x2 , y1 ) F ( x1, y1 ) F ( x1, y2 )
如图:
y
y2 L
y1 L M
M
x
0 x1
x2
概率统计
2. 二维随机变量分布函数 F(x,y) 的性质
性质1 F(x,y) 分别对 x 和 y 单调非减, 即:
