广东工业大学09-10学年线性代数试题A卷
(完整版)广东工业大学09-10学年线性代数试题A卷

(C) ;(D) .
5、设 、 为n阶实对称可逆矩阵,则下面命题错误的是()
(A)有可逆矩阵 、 使得 (B)有可逆矩阵 使得
(C)有可逆矩阵 使得 (D)有正交矩阵 使得
三、计算行列式(6分):
设 ,计算 的值,其中 是代数余子式.
四、(10分)设矩阵 满足关系 ,其中 ,求 .
1、(6分)若 为 阶幂等阵( ),求证: = .
2、(8分)设 是 实矩阵, 是 维实列向量,
证明:(1)秩 ; (2)非齐次线性方程组 有解.
五、(10分)设线性方程组为 ,问: 、 取何值时,方程组无解、有唯一解、有无穷多解? 在有无穷多解时求出其通解。
六、(10分)设 是 的一个基础解系, 不是 的解,即 ,
讨论:向量组 线性相关还是线性无关?.
七、(10分)设 ,问A能否对角化?若能对角化,则求出可逆矩阵 ,使得 为对角阵.
八、(共14分)证明题:
(C)若方阵 不可逆,则 都不可逆
(D)若 阶矩阵 或 不可逆,则 必不可逆
2、设 为 阶矩阵, 为其伴随矩阵,则 ( ).
(A) (B) (C) (D)
3、若非齐次线性方程组 中方程个数少于未知数个数,那么( ).
(A) 必有无穷多解;(B) 必有非零解;
(C) 仅有零解;(D) 一定无解.
4、设有向量组 , , , 与 ,则向量组的极大线性无关组是()
线性代数试题线性代数试卷及答案大全(173页大合集)

属于 对应的特征向量为 ,单位化: ,
属于 对应的特征向量为 ,单位化: ,
取 ,则有 。
八、(本题8分)证明:由
得 的特征值 ,
,
故 的最大特征值是 。
试卷2
闭卷考试时间:100分钟
一、填空题(本题15分,每小题3分)
1、若n阶行列式零元素的个数超过n(n-1)个,则行列式为。
三、(本题8分)解:从第一行开始,每行乘 后逐次往下一行加,再按最后一行展开得:
原式= 。
四、(本题12分)解:由 ,得: ,
可逆,故 ;
由于 , 。
五、(本题14分)解:(1)令 , ,
则 线性无关,故 是向量组 的一个极大无关组;
(2)由于4个3维向量 线性相关,
若 线性无关,则 可由 线性表示,与题设矛盾;
A:矩阵A必没有零行
B:矩阵A不一定是阶梯形矩阵
C:矩阵A必有零行
D:矩阵A的非零行中第一个不等于零的元素都是1
非齐次线性方程组Ax=b中,系数矩阵A和增广矩阵(A b)的秩都等于3,A是3×4矩阵,则▁▁▁。【A】
A:方程组有无穷多解
B:无法确定方程组是否有解
C:方程组有唯一解
D:方程组无解
试卷1
4、若 阶实方阵 , 为 阶单位矩阵,则( )。
(A) (B)
(C) (D)无法比较 与 的大小
5、设 , , , ,其中 为任意常数,则下列向量组线性相关的为( )。
(A) ( B) (C) (D)
三、(10分)计算 阶行列式 , 的主对角线上的元素都为 ,其余位置元素都为 ,且 。
四、(10分)设3阶矩阵 、 满足关系: ,且 ,求矩阵 。
B:Ax=0的基础解系中的解向量的个数不可能为n-r
广东工业大学华立学院 建筑学部 2009-2010学年第 2 学期课表
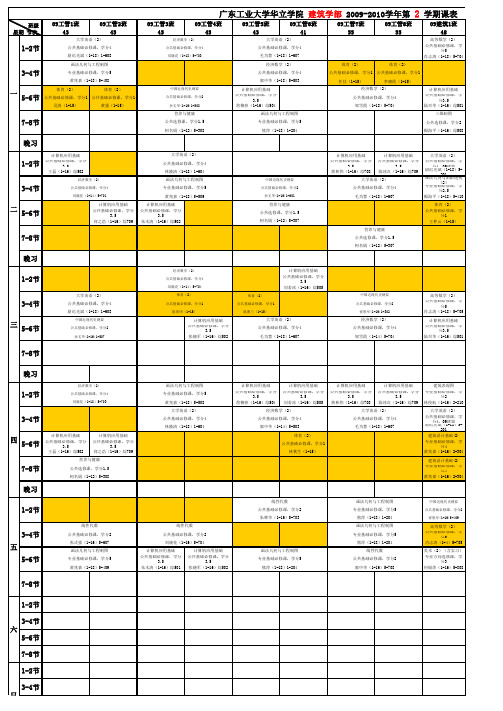
公共基础必修课,学分3.5 公共基础必修课,学分3.5
郑之浩(1-16)综709
朱木清(1-16)综502
王仲云(1-15)
经济数学(2)
计算机应用基础
公共基础必修课,学分3.5
1-2节
大学英语(2)
公共基础必修课,学分4 刘晓花(1-14)5-704 体育(2) 公共基础必修课,学分1 陈勇明(1-15) 体育(2) 公共基础必修课,学分1 陈燕兰(1-15)
刘若冰(1-16)综505
中国近现代史纲要 公共基础必修课,学分2 崔胜军(1-16)修课,学分5
3-4节 三 5-6节 7-8节 晚习
公共基础必修课,学分4 尉迟光斌(1-18)1-608
中国近现代史纲要 公共基础必修课,学分2 余文华(1-16)1-507
肖志涛(1-18)5-705 计算机应用基础
公共基础必修课,学分4 林隆清(1-18)1-604 计算机应用基础 计算机应用基础
尉迟光斌(1-18)5-201
建筑设计基础(2)
专业基础必修课,学分4
5-6节 7-8节 晚习
公共基础必修课,学分3.5 公共基础必修课,学分3.5
王磊(1-16)综502
郑之浩(1-16)综709
黄兆嘉(1-16)2-304 建筑设计基础(2)
大学英语(2) 公共基础必修课,学分4 李晓燕(1-18)1-510 经济数学(2) 公共基础必修课,学分4 胡杨慧(1-18)5-704 体育(2)
公共基础必修课,学分1
计算机应用基础
计算机应用基础
高等数学(2) 公共基础必修课,学分5 刘建辉(1-18)5-705 大学物理(1) 公共基础必修课,学分4 刘伟(1-16)1-402
广东工业大学电工学考试试卷A及答案

广东工业大学考试试卷 (A)一、单项选择题:在下列各题中,将唯一正确的答案代码填入括号内(本大题共 13 小题,每小题2分,总计 26分 )1、在 图 示 电 路 中,已 知:U S =1 V ,I S =1 A 。
电 流 I 为 ( )。
(a) 1 A (b) -1 A (c) 0 AI2、图 示 电 路 中,已 知:I S1 = 3 A ,I S2 = 6 A 。
当 理 想 电 流 源 I S1 单 独 作 用 时,流 过 电 阻 R 的 电 流 是 1 A ,那么,当 理 想 电 流 源 I S1 和 I S2 共 同 作 用 时,流 过 电 阻 R 的 电 流 I 值 为 ( )。
(a) -1 A (b) 1 A (c) -2 AI R3、在 图 示 的 电 路 中 ,已 知 :I S = 2 A ,U S = 4 V 。
当 开 关 S 闭 合 后 ,流 过 开 关 S 的 电 流 I 为 ( )。
(a) 1.6 A (b) -1.6 A(c) 0U S4、用 幅 值 ( 最 大 值 ) 相 量 表 示 正 弦 电 压 u = 537sin(ωt -90︒ ) V 时,可写 作mU ( )。
(a) V 90537m︒-∠=U(b) V 90537m︒∠=U (c) V )90(537m︒-∠=t U ω 5、 图 示 正 弦 交 流 电 路 中,A 01︒∠=I ,R =3 Ω,ωL = 4 Ω,则LI 为 ( )。
(a) 0.8∠36.9︒ A (b) 0.6∠36.9︒ A (c) 0.6∠-53.1︒AωLj I ..L6、 已 知 某 电 路 的 电 压 相 量 V 45141︒∠=U ,电 流 相 量A 455︒∠=I ,则 电路 的 有 功 功 率 P 为 ( )。
(a) 705 W (b) 500 W (c) 0 W7、 对 称 三 相 电 路 的 有 功 功 率 ϕcos 3l l I U P =,功 率 因 数 角 ϕ 为 ( )。
三、2009-6-15线性代数A卷

广东工业大学试卷用纸,共3页,第1页广东工业大学试卷用纸,共3页,第2页2、设行列式1534780311113152−−−==A D ,则2=+−+4443424135A A A A .(A )0(B )1(C )-1(D )-163、设A 、B 是n 阶方阵,下列等式正确的是.(A )AB=BA (B )))((22B A B A B A −+=−(C )22AA =(D )111)(−−−+=+B A B A 4、设0α是非齐次方程组b AX =的一个解,r ααα,,,21⋯是0=AX 的基础解系,则.(A)01,,,r ααα⋯线性相关。
(B )01,,,r ααα⋯线性无关。
(C )01,,,r ααα⋯的线性组合是b AX =的解。
(D )01,,,r ααα⋯的线性组合是0=AX 的解。
5、n 阶方阵A 与对角阵相似的充要条件是.(A)A 是实对称阵;(B)A 有n 个互异特征值;(C)A 的特征向量两两正交.(D)A 有n 个线性无关的特征向量;三、(10分)设na a a A +++=111111111||21⋯⋯⋯⋯⋯⋯⋯,021≠n a a a ⋯其中.求A .四、(10分)设4阶方阵C B A ,,满足方程11)2(−−=−C A B C E T ,试求矩阵A ,其中123212010*******,0012001200010001B C −−⎛⎞⎛⎞⎜⎟⎜⎟−⎜⎟⎜⎟==⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠五、(10分)讨论λ为何值时,方程组⎪⎩⎪⎨⎧=+++=+++=+++λλλλ321321321)1(3)1(0)1(x x x x x x x x x广东工业大学试卷用纸,共3页,第3页(1)有唯一解?(2)无解?(3)有无穷多解?并在此时求出其通解。
六、(10分)已知R 3中的向量组321,,ααα线性无关,向量组112223,b k b αααα=−=+,331b k αα=+线性相关,求k 值。
广州大学2009-2010(6)线性代数期末考试卷试题及解答2

广州大学2009-2010(6)线性代数期末考试卷试题及解答2第一篇:广州大学2009-2010 (6)线性代数期末考试卷试题及解答2 《线性代数》客观题100题一.填充题1456xx展开后,x2的系数为______.x321.行列式23A⎫⎪,则C=____.⎝BO⎭3.设α,β,γ为3维列向量,已知3阶行列式|4γ-α,β-2γ,2α|=40,则行列式2.设A是m阶方阵,B是n阶方阵,且A=a, B=b, C= ⎛O|α,β,γ|=______.12301bbbb23432-1-1cccc2344126dddd234 4.设|A|=415a,则4A41+3A42+2A43+A44=______.5.行列式aaa234=_______________________________________________.a000⎫⎛1-a⎪-11-aa00 ⎪-11-aa0⎪=____________________________.6.五阶行列式det 0 ⎪00-11-aa ⎪000-11-a⎪⎝⎭⎛a 0 7.n阶行列式det M0 b⎝b0Λ00⎫⎪abΛ00⎪MMMM⎪=____________.⎪00Λab⎪00Λ0a⎪⎭T8.设向量α=(1,2),β=(2,1),矩阵A=αβ,则An=____________.⎛1 9.设A=2 2⎝21-22⎫⎪-2,则A2n+1=____________.⎪1⎪⎭10.设A=⎛3⎝22⎫n+1n⎪,则A-5A=____________.3⎭⎛1 111.设矩阵A=0 ⎝0110000220⎫⎪0⎪,则An=____________________.0⎪⎪2⎭*-112.设A,B均为n阶矩阵,A=2,B=-3,则2AB⎛2 413.已知A*=6 ⎝800=______.0⎫⎪200⎪,则A-1=____________________.420⎪⎪641⎭⎛10⎫-1T-1*-114.设矩阵A的逆矩阵A=⎪,则(A)=_________,(A)=_________.⎝11⎭⎛1 15.设A=2 3⎝0240⎫⎪0,则(A*)-1=________________.⎪5⎪⎭1aαα,T16.设n 维向量α=(a,0,Λ,0,a)T,a<0,若A=E-ααT的逆矩阵为B=E+则a=______.17.设矩阵A满足A2+A-4E=O,则(A-E)-1=____________.⎛1 -218.设A=0 ⎝003-40005-60⎫⎪0⎪,且B=(E+A)-1(E-A),则(E+B)-1=________.0⎪⎪7⎭⎛1 *19.设矩阵A,B满足ABA=2BA-8E,其中A=0 0⎝0-200⎫⎪0,则B=______.⎪1⎪⎭20.设A,B为可逆矩阵,X=⎛1 21.若矩阵 0 -1⎝242⎛O⎝BA⎫-1⎪为分块矩阵,则X=____________.O⎭3⎫⎪4的秩为2,则a=______.⎪a⎪⎭22.设ai≠0, bi≠0(i=1,2,⎛a1b1 abΛ)n,矩阵A=21 Mab⎝n1a1b2a2b2M anb2ΛΛΛa1bn⎫a2bn⎪⎪,则矩阵A的秩M⎪anbn⎪⎭r(A)=______.⎛1 23.已知4⨯3矩阵A的秩R(A)=2,而B=0 4⎝0302⎫⎪0,则R(AB)=______.⎪5⎪⎭24.设A=⎛1⎝1-11⎫T⎪,则行列式AA=______.23⎭25.若α1,α2,α3都是线性方程组Ax=b的解向量,则A(2α1-5α2+3α3)=______.⎧x1+3x2+2x3=0⎪26.当a=______时, 齐次方程组⎨x1-2x2+3x3=0有非零解.⎪2x+x+ax=023⎩1⎛1 27.设A=4 3⎝2t-1-2⎫⎪3,B是3阶非零矩阵,且AB=O,则t=______.⎪1⎪⎭28.线性方程组x1+x2+x3+x4+x5=0的基础解系含有______个解向量.29.设n阶矩阵A的各行元素之和均为零,且A的秩为n-1,则线性方程组Ax=0的通解为____________________.⎧a11x1+a12x2+a13x3+a14x4=0T30.已知⎨的基础解系为(bi1,bi2,bi3,bi4)(i=1,2),则⎩a21x1+a22x2+a23x3+a24x4=0⎧b11x1+b12x2+b13x3+b14x4=0的基础解系为________________________.⎨⎩b21x1+b22x2+b23x3+b24x4=0⎛1 31.已知矩阵A=2 3⎝2353474595⎫⎪6,则秩R(A)=______,齐次线性方程组Ax=0⎪11⎪⎭的解空间的维数等于______.32.设向量组(1,1,1),(1,2,3),(2,3,a)线性相关,则a=______.TTT33.已知三维线性空间的一组基底为α1=(1,1,0),α2=(1,0,1),α3=(0,1,1),向量β=(2,0,0)在上述基底下的坐标是____________.34.从R2的基α1=⎪,α2=⎝0⎭⎛1⎫⎛1⎫⎛1⎫⎛1⎫β=,β=到基1⎪⎪2 ⎪的过渡矩阵为__________.-1⎝⎭⎝1⎭⎝2⎭T35.设向量α=(1,2,2)T,A为三阶正交矩阵,则长度||Aα||=______.36.已知向量α=(1,1,1)与β=(1,2,a)正交,则a=______.37.向量α=(1,2,2,3)与β=(3,1,5,1)的夹角θ=______.38.设A=(aij)3⨯3是实正交矩阵,且a11=1,b=(1,0,0)T,则线性方程组Ax=b的解是____________________.39.设A是3阶矩阵,它的3个特征值互不相等,并且矩阵A的行列式A=0,则矩阵A的秩R(A)=______.40.若2阶方阵A满足A2-5A+6E=O,且A的两个特征值不相等, 则|A|=____.41.设2阶方阵A≠O满足A2=3A,则A有一特征值λ=____,且(A-I)-1=____.42.设3阶方阵A的特征值为1,2,3,则|6E-A|=______.43.设3阶矩阵A的特征值为1,2,2,则行列式|4A-1-E|=______.44.设A为n阶矩阵,A≠0,若A有特征值λ,则(A*)2+E必有特征值______.45.设A为2阶矩阵,α1,α2为线性无关的2维列向量,Aα1=0,Aα2=2α1+α2,则A的非零特征值为______.⎛1 46.设矩阵A=2 3⎝210-2⎫⎪2,α=(a,1,1)T。
[VIP专享]广工10高数A(2)试卷及答案
![[VIP专享]广工10高数A(2)试卷及答案](https://img.taocdn.com/s3/m/9429543825c52cc58bd6bea3.png)
1.级数
n1
sin n
n2
的收敛性为(
A 绝对收敛 B 条件收敛 C 发散 D 敛散性不能确定
)
广东工业大学试卷用纸,共 7 页,第 0 页
88.8918÷1.2990÷.1=4214÷3922=.0034=1÷15251371=8535.78.208÷023.2173c00÷1*m=29030.3922c=.1÷20m3=2÷120252.=3535=42314c)*523m240341*31.252=31*.1.535.*031342.*9205221.04.455=+213*05*2022.02.854850.3150.*+58c12*5m1*202+.050+0.014*85.20*051000+0+03/8T.+0÷+=55+1*011+010+91÷01454050*0010200+5+0+080+400*+4**1*1510.3910%*C%-*6+÷M(=*M=5÷50)*30*31(÷3110*5+**÷4*1m243.%71e=78%n0)8=8s.5=77.93c.6c0mmc.4*m1*31,0w199o.k2.m4c-cem.5mn2csp26m659*.0.34-50.60c5*pm.3c85m9,c05g.m.05i0rp-l.s.85p6/c50bcm0.om7py.c.6spm5c+mc;0m..7.cmk ; 1+1k+12+1+k2234=1c+m1++4+4+2
五、(8 分)计算二重积分 x y 2 dxdy ,其中 D={ (x, y) | 0 x 1,0 y 1}。
(完整)线性代数习题集(带答案)

第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( )。
(A) 24315 (B ) 14325 (C ) 41523 (D )24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( )。
(A )k (B)k n - (C )k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A ) 0 (B )2-n (C ) )!2(-n (D) )!1(-n4.=001001001001000( )。
(A ) 0 (B)1- (C) 1 (D ) 25.=001100000100100( )。
(A) 0 (B )1- (C ) 1 (D) 26.在函数100323211112)(x x x x x f ----=中3x 项的系数是( ). (A) 0 (B)1- (C) 1 (D) 27。
若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B ) 4- (C) 2 (D) 2-8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A )ka (B)ka - (C )a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B )3- (C ) 3 (D ) 210。
若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ).(A )1- (B)2- (C )3- (D )011。
若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B )2- (C)3- (D )012。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
讨论:向量组 β , β + α 1 , β + α 2 ,, β + α k 线性相关还是线性无关?.
4 6 0 (10 设 则求出可逆矩阵 P , 七, 分) A = 3 5 0 , A 能否对角化?若能对角化, ( 问 3 6 1
(A) α1,α2,α3 ; (C) α1,α2,α5 ;
)
Байду номын сангаас
(B) α1,α2,α4 ; (D) α1,α2,α4,α5 .
5,设 A , B 为 n 阶实对称可逆矩阵,则下面命题错误 错误的是( 错误
)
(A)有可逆矩阵 P , Q 使得 PBQ = A (B)有可逆矩阵 P 使得 P 1 ABP = BA (C)有可逆矩阵 P 使得 P 1 B 2 P = A 2 (D)有正交矩阵 P 使得 P 1 AP = P T AP = B
广东工业大学试卷用纸,共
(C)若方阵 AB 不可逆,则 (D)若 n 阶矩阵
A , B 都不可逆
).
(D) k
n 1
A 或 B 不可逆,则 A B 必不可逆
2,设 A 为 n 阶矩阵, A * 为其伴随矩阵,则 kA* = (
(A) k n A (B) k A
n
(C) k
n
A
n 1
A
n
3,若非齐次线性方程组 Ax = b 中方程个数少于未知数个数,那么(
2x
1,函数 f ( x) = x
学
1
3
.
2
订
x 1 中, x 3 的系数为 1 x
1 0 2,设 A1 = 0 3 ,
A1 1 1 A2 = 1 0 , A = 0
0 ,则 A 1 = A2
.
业:
1 0 2 3,设 A 是 4 × 3 矩阵,且 R ( A) = 2 ,而 B = 0 2 0 ,则 R ( AB ) = 1 0 3 2 * 4,设矩阵 A 与 B = 3 相似,则 | A + E |= _________ . 3
三,计算行列式(6 分) 计算行列式( :
1 5 1 3 1 1 3 4 1 2 1 2 2 3 3 4
设 A =
,计算 A41 + A42 + A43 + A44 的值,其中 A4 i (i = 1,2,3,4) 是代数余子式.
4 2 3 四, 10 分)设矩阵 X 满足关系 AX = A + 2 X ,其中 A = 1 1 0 ,求 X . ( 1 2 3
(A) Ax = b 必有无穷多解; (C) Ax = 0 仅有零解; (B) Ax = 0 必有非零解; (D) Ax = 0 一定无解.
).
4 , 设 有 向 量 组 α1=(1, 1, 4) , α2=(0, 1, , α3=( 0, 14) , α4=(1, 2, 0) 与 - 2, 3, 2) 3, 7, - 2, α5=( 1, 10),则向量组的极大线性无关组是( 2, 5,
五, 10 分)设线性方程组为 (
x1 3 x 2 x3 = 0 x1 4 x 2 + a x3 = b ,问: a , b 取何值时,方程组无 2 x x + 3 x = 5 2 3 1
解,有唯一解,有无穷多解? 在有无穷多解时求出其通解. 设 即 六, 10 分) α 1 ,α 2 ,,α k 是 Ax = 0 的一个基础解系,β 不是 Ax = 0 的解, Aβ ≠ 0 , (
广东工业大学考试试卷 ( A
课程名称: 课程名称:
名:
)
线性代数
试卷满分 100 分
考试时间: 2010 考试时间: 2010 年 1 月 5 日 (第 19 周 星期 二 )
题 号 一 二 三 四 五 六 七 八 九 十 总分
姓
评卷得分
线
评卷签名 复核得分 号: 复核签名
填空题( 一, 填空题(每小题 4 分,共 20 分) :
1 5,若 λ = 2 为可逆阵 A 的特征值,则 A2 的一个特征值为 3
1
.
专
装
.
院:
选择题( 二, 选择题(每小题 4 分,共 20 分) :
1,下列命题正确 正确的是( 正确 (A) 若
) .
AB = E ,则 A 可逆且 A 1 = B
AB |=| BA |
3 页,第 1 页
学
(B) 方阵 AB 的行列式阶子式 |
使得 P -1AP 为对角阵.
( 证明题: 八, 共 14 分)证明题:
1, 分)若 A 为 n 阶幂等阵( A 2 = A ) , (6 ,求证: r ( A) + r ( A E n ) = n . ( 2, 分)设 A 是 m × n 实矩阵, β ≠ 0 是 m 维实列向量, , (8 ( 证明: (1)秩 r ( A) = r ( AT A) ; (2)非齐次线性方程组 AT Ax = AT β 有解.
广东工业大学试卷用纸,共
3
页,第
3 页
�
