电路分析基础(第四版第二章)
电路分析基础第四版课后答案 (2)
电路分析基础第四版课后答案第一章电路基本概念和定律1.1 电路基本概念1.什么是电路？2.什么是电流？3.什么是电压？4.什么是电阻？5.什么是电导？1.2 电路定律1.请简述欧姆定律的表达式及其在电路分析中的应用。
2.请简述基尔霍夫电流定律的表达式及其在电路分析中的应用。
3.请简述基尔霍夫电压定律的表达式及其在电路分析中的应用。
第二章电路分析方法2.1 参考方向和参考极性1.请简述参考方向在电路分析中的作用。
2.请说明电流方向和电压极性的确定方法。
2.2 串联与并联电路1.什么是串联电路？2.什么是并联电路？3.串联和并联电路的特点有哪些？2.3 电压分流和电流合并定律1.请简述电压分流定律的表达式及其在电路分析中的应用。
2.请简述电流合并定律的表达式及其在电路分析中的应用。
2.4 电阻网络简化1.什么是电阻网络简化？2.列举电阻网络简化的方法。
第三章基本电路3.1 电压源与电流源1.请简述理想电压源的特性及其在电路分析中的应用。
2.请简述理想电流源的特性及其在电路分析中的应用。
3.2 集总元件与非集总元件1.什么是集总元件？2.什么是非集总元件？3.请举例说明集总元件和非集总元件的特点。
3.3 电阻的平均功率和瞬时功率1.请简述电阻的平均功率和瞬时功率的计算方法。
3.4 等效电路和戴维南定理1.什么是等效电路？2.请简述戴维南定理及其在电路分析中的应用。
第四章变流电路4.1 正弦波电压和正弦波电流1.什么是正弦波电压？2.什么是正弦波电流？3.请简述正弦波电压和正弦波电流的特点。
4.2 交流电路中的电阻、电感和电容1.请简述交流电路中电阻、电感和电容的特性及其在电路分析中的应用。
4.3 相量法和复数法分析交流电路1.请简述相量法分析交流电路的基本原理。
2.请简述复数法分析交流电路的基本原理。
4.4 等效电路和史密斯图分析交流电路1.什么是等效电路？2.请简述史密斯图分析交流电路的基本原理。
第五章电流电压分析基础5.1 直流稳态分析1.什么是直流稳态？2.请简述直流稳态分析的基本步骤。
电路分析(第四版)(章 (2)
R1R2
R2 R3
R3R1
R12 R23 R31 R12 R23 R31
(2-22)
第2章 电路的等效变换
将式(2-22)分别除以式(2-20)、 (2-18)和式(2-19)， 可得
R12
R1
R2
R1R2 R3
(2-23)
R23
R2
R3
R3R2 R1
(2-24)
R31
R3
R1
R3R1 R2
(2-25)
电源作用下，通过各电阻的电流都相同，则称此连接方式为电 阻的串联。图2.1(a)所示为三个电阻串联。
设电压和电流的参考方向如图2.1(a)中所示，则根据KVL， 有
U＝U1+U2+U3
(2 - 1)
第2章 电路的等效变换
又由欧姆定律，可得
U1=R1I
U2=R2I
(2-2)
U3=R3I 由式(2-1)及式(2-2)可得
G2 G
I
I3
G3U
G3 G
I
(2-11)
第2章 电路的等效变换
式(2-11)为并联电导的分流公式， 由此可得
I１∶I２∶I３=G１∶G２∶G３ 上式说明，并联电导中电流的分配与电导大小成正比， 即与电 阻成反比。若给式(2-6)两边各乘以电压U，则得
UI=UI１+UI２+UI３
即
P=P１+P２+P３
可得
I=(G１+G２+G３)U
(2-8)
第2章 电路的等效变换
若用一个电导
G=G１+G２+G３
(2-9)
来替代图2.3(a)中三个电导并联之和，如图2.3(b)所示， 则在对
电路理论基础第四版第2章习题答案详解
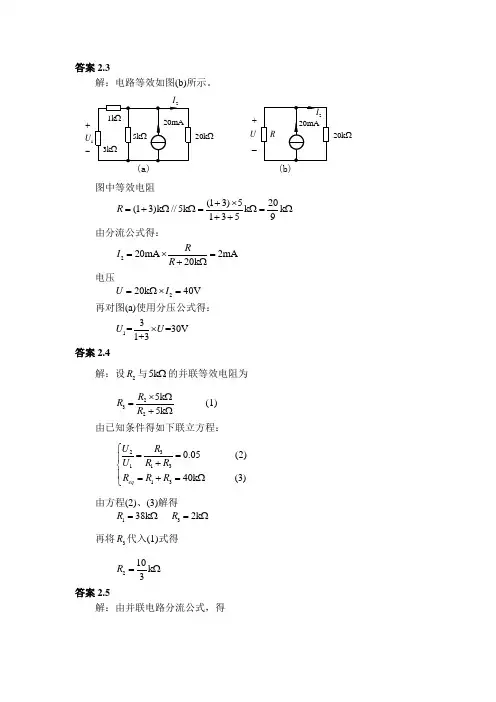
答案2.3解：电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得：13==30V 1+3U U ⨯ 答案2.4解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U U R R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω 答案2.5解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=- 答案2.6解：首先将电路化简成图(b)。
图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=- 答案2.7xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。
将22'-端x R 用始端11'-x R 替代，则变为4级再加x R ，如此替代下去，则变为无穷级。
从始端11'-看等效电阻为x R ,从33'-端看为1-∞级，也为x R , 则图(a)等效为图(a-1)。
电路分析基础课件第2章 电路分析中的等效变换
v
+
Seq
-
a+
v
-b a+ v -b
n
v v v v vSeq s1 s2 s3 sn vSk k 1
2 电压源的并联
只有电压相等且极性相同时， 电压源才能并联。
ai ++ + +
i
a +
+
v vS vS
vS
b
-
-
-
v vS b- -
3 电流源的并联
iS1 iS2
例8 求:I
I1 1
解： Δ—Y 转换 2.6 10
R1
R12 R13 R12 R13 R23
100 25
4
R2
R23R13 25
2
+ 9V
R2 22
4
R3
R23R12 25
2
-
b
R14 R1 (R2 R24 ) //( R3 R34 )
R110 5 R3
ia
ia
iSn
+
iS
++
v
vv
b
-b
n
i i i iS s1 s2 sn iSk k 1
4 电流源的串联
只有电流相等且参考方向相同时，
电流源才能串联。
iS iS ... iS
i
a+
v
-b
iS
i
a+ v -b
5 电压源与电流源的串联
a i+
N
电路课件 第二章(第四版 邱关源 高等教育出版社)
B
i
+ u -
等效 C
i
+ u -
对A电路中的电流、电压和功率而言，满足
B
A （1）电路等效变换的条件
C
A
两电路具有相同的VCR 未变化的外电路A中 的电压、电流和功率 化简电路，方便计算
明 确
（2）电路等效变换的对象 （3）电路等效变换的目的
2.3 电阻的串联、并联和串并联
1. 电阻串联( Series Connection of Resistors )
（4） 功率
p1=G1u2， p2=G2u2，， pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
总功率
p=Gequ2 = (G1+ G2+ …+Gn ) u2
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 表明
（1） 电阻并连时，各电阻消耗的功率与电阻大小成反比 （2） 等效电阻消耗的功率等于各串连电阻消耗功率的总和
第2章 电阻电路的等效变换
重点： 1. 电路等效的概念； 2. 电阻的串、并联； 3. Y— 变换; 4. 电压源和电流源的等效变换；
2.1 引言
电阻电路 分析方法 （1）欧姆定律和基尔霍夫定律是分 析电阻电路的依据； （2）等效变换的方法,也称化简的方法 仅由电源和线性电阻构成的电路
2. 电阻并联 (Parallel Connection)
(1) 电路特点
i + u _
R1
i1 R2
i2 Rk
ik Rn
in
(a) 各电阻两端分别接在一起，两端为同一电压 (KVL)； (b) 总电流等于流过各并联电阻的电流之和 (KCL)。
电路分析基础第2章简单电阻电路
(2-1)
2021/5/25
2
第2章 简单电阻电路
图2-1 电阻串联电路
2021/5/25
3
第2章 简单电阻电路
应用KVL，有
或 对于(2-2)
US=U1+U2=(R1+R2)I I US R1 R2
(2-2) (2-3)
即有
US=ReqI
(2-4)
Req=R1+R2
(2-5)
称为等效电阻，相应的等效电路如图2-1(b)所示。一般来
图2-12 例2-6的电路
2021/5/25
33
第2章 简单电阻电路
也可以从另一路径计算，有
Ua=35-25×1.2=5 V 自测题2-5 若把电路中原来为-3 V的点改为电位的参
考点，则其他各点的电位将
。
(Ａ) 变高 (Ｂ) 变低 (Ｃ) 不变 (Ｄ)
2021/5/25
34
第2章 简单电阻电路
第2章 简单电阻电路
2.1 串联电路 2.2 并联电路 2.3 串-并联电路 本章小结 思考题 习题2
2021/5/25
1
第2章 简单电阻电路
2.1 串联电路
2.1.1
两个元件连接在单节点上，称为串联。串联连接的电路
元件具有相同的电流。如图2-1(a)所示就是两个电阻串联的 电路。应用欧姆定律有
U1=R1I, U2=R2I
2021/5/25
7
第2章 简单电阻电路
图2-2 例2-1的电路
2021/5/25
8
第2章 简单电阻电路
解 可用线性电阻元件作为灯泡的近似模型。根据题意， 可以画出如图2-2所示电路。根据灯泡上标出的额定电压和功 率，各灯泡的电阻大小分别为
电路分析基础—第2章
2021年4月4日9时3信7分息学院
1
结束
(1-1)
第2章 运用独立电流、电压变量的分析方法 电路分析基础
2—1 网孔分析 1、网孔电流
是一个沿着网孔边界流动的假想电流，即设想每个网 孔里具有相同的电流。 2、网孔电流法
以网孔电流为未知量列写电路方程分析电路的方法。它仅 适用于平面电路。
基本思想
以网孔电流为未知量，各支路电流可用网孔电流的线 性组合表示，来求得电路的解。
第2章 运用独立电流、电压变量的分析方法 电路分析基础
第二章 网孔分析和节点分析
线性电路的一般分析方法
• 普遍性：对任何线性电路都适用。 • 系统性：计算方法有规律可循。
方法的基础 • 电路的连接关系—KCL，KVL定律。
• 元件的电压、电流关系特性。
复杂电路的一般分析法就是根据KCL、KVL及元 件电压和电流关系列方程、解方程。根据列方程时所 选变量的不同可分为支路电流法、网孔电流法和节点 电压法。
列写的方程
节点电压法列写的是节点上的KCL方程，独立方程数为：
注意
(n 1)
① 与支路电流法相比，方程数减少b-(n-1)个。
② 任意选择参考点。其它节点与参考点的电位差即为节点电 压(位)，方向为从独立节点指向参考节点。
2021年4月4日9时3信7分息学院
17
结束
(1-17)
第2章 运用独立电流、电压变量的分析方法 电路分析基础
结束
(1-23)
第2章 运用独立电流、电压变量的分析方法
1）一般情况
例1： P75 例2—8 试写电路的节点方程
电路分析基础
选5为参考点，其余4个节点的电压分别为Un1、Un2、Un3、Un4
电路分析基础第二章 电路元件及电路基本类型(完整)
5V
_
i
_
PR = Ri = 5 ×1 = 5W
2
满足：P（发）＝P（吸）
+
10V
+
_ +
解
uR
uR = (10 − 5) = 5V
i=
P10V
= 5 = 1A R 5 = uS i = 10 ×1 = 10W
uR
发出
P5V = u S i = 5 × 1 = 5W
吸收 吸收
上页
下页
2. 电流源
上页
下页
当t0=0时，上式可写成 1 t u = u (0) + ∫ i (τ )dτ C 0 分别写出在t和t+∆t两个瞬间的电压表达式，然后取其 差值∆u，得
1 t +Δt Δu = u (t + Δt ) − u (t ) = ∫ i (τ )dτ C t
如果在[t，t+∆t]内，i(t)均为有限值，那么当∆t→0时， 就有∆u→0，这说明只要电容电流是有界函数，电容电 压就是连续函数，不会跳变。
u=Ri Ψ=L i q=Cu R为电阻参数 L为电感参数 C为电容参数
元件参数表征了元件的物理特性。 为叙述方便，“电阻”可表示“电阻器”、 “电阻元件” 及“电阻参数”。可推广到 电感和电容。
1. 时不变(定常) & 时变元件
元件参数不随时间改变者为时不变元件， 否则为时变元件。 如 时不变元件：u ( t ) = 5 i ( t ) 时变元件： u(t ) = cos t ⋅ i(t ) 如滑线变阻器抽头由马达带动做 简谐运动时，阻值（cost）随t变。
i
0.5F
us (t ) C
电路分析基础第四版课后习题第一章第二章第三章第四章答案
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ，列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示，试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向，
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
《电路分析基础》_第2章-1
US1
+
i1
i2 R3
_
US2
_
_
R2 0 i1 U S1 U S 2 R1 R 2 R i U R R R 2 2 3 3 2 S2 R3 R3 R4 0 i3 US4
－
2 i1
1 + 10V
－
5 i3 3 i3 4A
i2 2 i 2
i1=2A
i2=－1A
b).若电路中存在电阻与电流源并联单口，则可先等效变 换为电压源和电阻串联单口，将电路变为仅由电压源和电
阻构成的电路，再建立网孔方程的一般形式。
2 i1 + 4V
－
4 + 10V
－
2 i1 + 4V
7 15 0 5 5 10 0 10 13 i2 ? 7 5 0 5 21 10 0 10 13
15 5 10 i1 7 5 0
5 0 21 10 10 13 ? 5 0 21 10 10 13
110 11 10 5 5 10 7 1 7 0 10 13 10 13 i2 7 5 0 122 7 5 0 11 10 122 7 1 7 5 21 10 0 10 10 13 7 0 10 13 0 10 13
R11 R21 R 31
R12 R22 R32
R13 i1 u S 11 R23 i2 u S 22 i u R33 3 S 33
其中：
RKK称为网孔K的自电阻，它们分别是各网孔内全部 电阻的总和，恒为正号。 例如 R11= R1+ R4+ R5 ,
电路分析基础第二章
- R2il1+ (R2 +R3) il2 =uS2
令
R11=R1+R2 — 回路1的自电阻。等于回路1中所有电阻之和。 R22=R2+R3 — 回路2的自电阻。等于回路2中所有电阻之和。
自电阻总为正。 R12= R21= –R2 — 回路1、回路2之间的互电阻。 当两个回路电流流过相关支路方向相同时，互电阻取正 号；否则为负号。
(2) 列 KVL 方程
(R1+R2)Ia
-R2Ib
= US1- US2
-R2Ia + (R2+R3)Ib
- R3Ic = US2
-R3Ib + (R3+R4)Ic = -US4
对称阵，且 互电阻为负
(3) 求解回路电流方程，得 Ia , Ib , Ic
(4) 求各支路电流： I1=Ia , I2=Ib-Ia , I3=Ic-Ib , I4=-Ic
0 : 无关
特例：不含受控源的线性网络 Rjk=Rkj , 系数矩阵为对称阵。 （平面电路， Rjk均为负(当回路电流均取顺(或逆)时针方向)）
回路法的一般步骤： (1) 选定l=b-(n-1)个独立回路，并确定其绕行方向； (2) 对l个独立回路，以回路电流为未知量，列写其 KVL方程； (3) 求解上述方程，得到l个回路电流； (4) 求各支路电流(用回路电流表示)；
-Ib+3Ic=3U2
增补方程: ② U2=3(Ib-Ia)
4Ia-3Ib=2
解得 Ia=1.19A
受控电压源
③ -12Ia+15Ib-Ic=0 9Ia-10Ib+3Ic=0
Ib=0.92A Ic=-0.51A
看作独立电 压源列方程
李瀚荪《电路分析基础》(第4版)课后习题详解-第2章 网孔分析和节点分析【圣才出品】
11 / 19
圣才电子书
十万种考研考证电子书、题库视频学习平
台
解：由图 2-15 可知，该电路有 3 个独立节点，计有 3 个节点电压
和 ，但
故得
解得
U1＝2 V
2-15 若节点方程为
试绘出最简单的电路。 解：由方程可知电路有 3 个节点和 1 个参考点，先画互电阻，再考虑自电阻，最后添 上电流源，画得电路如图 2-16 所示。
圣才电子书
十万种考研考证电子书、题库视频学习平 台
解得
未求解，对计算受控源功率无关。 受控源电压：
受控源功率： （24 V）（28 A）＝672 W
由于功率是按电压、电流的关联参考方向计算的，答案为正值，表明吸收功率，即受 控源吸收的功率 672 W。
§2-2 互易定理
解得
u＝2 V
2-12 电路如图 2-12 所示，试用节点分析求各支路电流。
9 / 19
圣才电子书
十万种考研考证电子书、题库视频学习平 台
图 2-12 解：标出节点编号，列出节点方程 整理得 解得 求得 后，各电阻的电流即可用欧姆定律求得。例如 2-13 电路如图 2-13 所示，试用节点分析求
求该电路的一种可能的形式。 解：题中 的表达式是用克莱姆法则求解联立方程未知量的算式，其分母为联立方程 组的系数，分子行列式第一列即联立方程等式右端数值，由此可列出方程
可知该电路应有三个网孔，由方程互电阻项可确定网孔 1 和 3、网孔 2 和 3 之间有 1 Ω 电阻，网孔和 2 之间没有公共电阻，但由等式右端可判定网孔 1 和 2 之间有 1 V 电 压源，一种可能的电路如图 2-3 所示。
4 / 19
李瀚荪编《电路分析基础》(第4版)第二章
§2-1 网孔分析法
网孔电流
若将电压源和电阻串联作为一条支路时，该电路共有6 条支路和4个节点。对①、②、③节点写出KCL方程。
i1 i3i1i4i30i4 0 i4 i1 i3
i1
i2i1i5i20i5
0i5
i1
i2
i2 i3i2i6i30i6 0 i6 i2 i3
电流i4、i5和i6是非独立电流，它们由独立电流i1、i2和i3 的线性组合确定。这种线性组合的关系，可以设想为电流i1、 i2和i3沿每个网孔边界闭合流动而形成，如图中箭头所示。 这种在网孔内闭合流动的电流，称为网孔电流。它是一组能
确定全部支路电流的独立电流变量。
§2-1 网孔分析法
思想： 以网孔电流为求解对象，列写KVL方程。
im1
R1 im2 R2
- US2+
im3
R3
R4im1 R4im2 U S U S 2 R4im1 (R1 R2 R4 )im2 R2im3 0 R2im2 (R2 R3 )im3 U S 2
iR2 im2 im3
含有电流源电路的网孔方程
本网孔中沿网孔电流方向所含电压源 电压升的代数和
§2-1 网孔分析法
网孔电流法的一般步骤：
(1) 选定m=b-(n-1)个网孔，确定其绕行方向； (2) 对m个网孔，以网孔电流为变量，列写
其KVL方程； (3) 求解上述方程，得到m个网孔电流； (4) 求各支路电流(用网孔电流表示)； (5) 求解其它参数。
图2-2
+ 10V -
(R1 R3 )im1 R3im2 20
（续）例2-1
《电路分析基础》第2章指导与解答
第2章电路的基本分析方法电路的基本分析方法贯穿了整个教材，只是在激励和响应的形式不同时，电路基本分析方法的应用形式也不同而已。
本章以欧姆定律和基尔霍夫定律为基础，寻求不同的电路分析方法，其中支路电流法是最基本的、直接应用基尔霍夫定律求解电路的方法；回路电流法和结点电压法是建立在欧姆定律和基尔霍夫定律之上的、根据电路结构特点总结出来的以减少方程式数目为目的的电路基本分析方法；叠加定理则阐明了线性电路的叠加性；戴维南定理在求解复杂网络中某一支路的电压或电流时则显得十分方便。
这些都是求解复杂电路问题的系统化方法。
本章的学习重点：●求解复杂电路的基本方法：支路电流法；●为减少方程式数目而寻求的回路电流法和结点电压法；●叠加定理及戴维南定理的理解和应用。
2．1 支路电流法1、学习指导支路电流法是以客观存在的支路电流为未知量，应用基尔霍夫定律列出与未知量个数相同的方程式，再联立求解的方法，是应用基尔霍夫定律的一种最直接的求解电路响应的方法。
学习支路电流法的关键是：要在理解独立结点和独立回路的基础上，在电路图中标示出各支路电流的参考方向及独立回路的绕行方向，正确应用KCL、KVL列写方程式联立求解。
支路电流法适用于支路数目不多的复杂电路。
2、学习检验结果解析（1）说说你对独立结点和独立回路的看法，你应用支路电流法求解电路时，根据什么原则选取独立结点和独立回路？解析：不能由其它结点电流方程（或回路电压方程）导出的结点（或回路）就是所谓的独立结点（或独立回路）。
应用支路电流法求解电路时，对于具有m条支路、n个结点的电路，独立结点较好选取，只需少取一个结点、即独立结点数是n－1个；独立回路选取的原则是其中至少有一条新的支路，独立回路数为m－n＋1个，对平面电路图而言，其网孔数即等于独立回路数。
2．图2.2所示电路，有几个结点？几条支路？几个回路？几个网孔？若对该电路应用支路电流法进行求解，最少要列出几个独立的方程式？应用支路电流法，列出相应的方程式。
电路分析基础章后习题答案及解析(第四版)
第1章习题解析一．填空题：1.电路通常由电源、负载和中间环节三个部分组成。
2.电力系统中，电路的功能是对发电厂发出的电能进行传输、分配和转换。
3. 电阻元件只具有单一耗能的电特性，电感元件只具有建立磁场储存磁能的电特性，电容元件只具有建立电场储存电能的电特性，它们都是理想电路元件。
4. 电路理论中，由理想电路元件构成的电路图称为与其相对应的实际电路的电路模型。
5. 电位的高低正负与参考点有关，是相对的量；电压是电路中产生电流的根本原因，其大小仅取决于电路中两点电位的差值，与参考点无关，是绝对的量6.串联电阻越多，串联等效电阻的数值越大，并联电阻越多，并联等效电阻的数值越小。
7.反映元件本身电压、电流约束关系的是欧姆定律；反映电路中任一结点上各电流之间约束关系的是KCL定律；反映电路中任一回路中各电压之间约束关系的是KVL定律。
8.负载上获得最大功率的条件是：负载电阻等于电源内阻。
9.电桥的平衡条件是：对臂电阻的乘积相等。
10.在没有独立源作用的电路中，受控源是无源元件；在受独立源产生的电量控制下，受控源是有源元件。
二．判断说法的正确与错误：1.电力系统的特点是高电压、大电流，电子技术电路的特点是低电压，小电流。
（错）2.理想电阻、理想电感和理想电容是电阻器、电感线圈和电容器的理想化和近似。
（对）3. 当实际电压源的内阻能视为零时，可按理想电压源处理。
（对）4.电压和电流都是既有大小又有方向的电量，因此它们都是矢量。
（错）5.压源模型处于开路状态时，其开路电压数值与它内部理想电压源的数值相等。
（对）6.电功率大的用电器，其消耗的电功也一定比电功率小的用电器多。
（错）7.两个电路等效，说明它们对其内部作用效果完全相同。
（错）8.对电路中的任意结点而言，流入结点的电流与流出该结点的电流必定相同。
（对）9．基尔霍夫电压定律仅适用于闭合回路中各电压之间的约束关系。
（错）10．当电桥电路中对臂电阻的乘积相等时，则该电桥电路的桥支路上电流必为零。
第2章 电路分析基础第4版
UOC U
1 R
aI
NA R U
b
当网络中含有受控源时，除源后，受控源仍保留在
网络中，这时不可以用上述方法的1计算等效电阻
[例题2.2.1] 已知图示电路及其参数，求流过
电阻R3的电流I3。
[解]
a R3 I3 c R5
a R3 I3 c
将a、b两端 左侧作戴维 宁等效
R0
R1 R2 R1 R2
参考点(即零电位点)，试求：⑴ 当Ui =3V时a点的 电位Va ；⑵ 当Va =-0.5V时的Ui 。
[解] ⑴ ⑵ 当应V用aK=V-L0列.5回V路时方程
R1 I
a
R1IR2IR2UI S U US abUi 0 0
I
I
U SUS R1
U iUab R22 (
2
解 ： 设 流 过 R1 电 流 的 参
b
考方向如图所示。
应用KCL可得 IR1=I2 - I1=1A
电流源I1的功率
P1
U
baI1
IR1
R1
I1
20W
吸收功率
电流源I2的功率 P2 = (Uca+Uab) I2
= (-I2R2 -IR1R1)I2= -80W
发出功率
[例题2.1.2]电路及参数如图所示，取b点为电位的
回路1 R1I1 R2I2 U S1 0 (3)
回路2 R2I2 R3I3 R4I4 0 (4)
回路3
I1 a I3 R3 b I5
R4 I4 R5 I5 U S 2 0
(5)
R1
⑷ 解联立方程组，求出
＋
各支路电流
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
节点分析法
仅含有电流源、电阻的电路
节点分析法
节点分析法
含有电压源、电阻的电路
节点分析法
例 试列写下图含理想电压源电路的节点电压方程。
选择合适的参考点（方程简洁）
+ Us
R2iM 2 R3iM 3
R5iM 2 R4iM 3
R5iM1 R6iM 2 R4iM1 R6iM 3
R6iM 3 R6iM 2
uS2 uS4
0 uS3
0
向一致时取“+”； 否则取“-”。
整理得
(R1 R4 R5 )iM1 R5iM 2 R4iM 3 uS1 uS 4
i+
理想运放的电路符号
运算放大器
含运放电路分析
节点分析法 两个理想运放条件
书中的例子：比例器、电压跟随器
电路对偶性
电路的对偶量
电压 电流 网孔电流
电阻 电导
电压源
短路 开路
电荷
KCL 串联
KVL 并联
电感
节点电压 电流源
磁链 电容
总结
• 网孔分析法，网孔电流 • 节点分析法，节点电压 • 互易定理 • 对偶性 • 含运放的电路分析
IS=I1-I3
互易定理
互易定理表明线性电路“因果互易”的性质。
互易定理
互易定理的证明
互易定理
互易定理的应用
由例题可以得到：互易定理可用于简化电路分 析过程。
节点分析法
例如图示电 路各支路电 压可表示为:
u1 u10 v1 u2 u20 v2 u3 u30 v3
u4 u10 u30 v1 v3 u5 u10 u20 v1 v2 u6 u20 u30 v2 v3
0
方程总数 b
b-(n-1) n-1
(2) 根据电路含有电流源或电压源选择分析方法。
(3) 网孔法、节点法易于编程。目前用计算机分析网络 (电网，集成电路设计等)采用节点法较多。
运算放大器
运算放大器(operational amplifier)：
一种有着十分广泛用途的电子器件。最早开始 应用于1940年，主要用于模拟计算机，可模拟加、 减、积分等运算，对电路进行模拟分析。1960年 后，随着集成电路技术的发展，运算放大器逐步 集成化，大大降低了成本，获得了越来越广泛的 应用。
R5iM1 (R2 R5 R6 )iM 2 R6iM 3 uS 2
R4iM1 R6iM 2 (R3 R4 R6 )iM 3 uS 4 uS3
网孔分析法
上面的式子经过观察可表示成如下
R11iM1 R12iM 2 R13iM 3 uS11
: 公共端(接地端)
º
+U
u-
_
u+
+
uo
-U
º
º
运算放大器
电路模型
uRi
u+
Ro
+ _A(u+-u-)
Ri ：运算放大器两输入端间的输入电阻 Ro：运算放大器的输出电阻
运算放大器
理想运算放大器
满足如下条件：
① A
u+=u-
② Ri , i+=i-=0
iu- _ _
ud
u+ + +
uo
G5uN1 G3uN 2 (G3 G4 G5 )uN3 0
节点分析法
观察一下，可得到这样一个标准的方程
G11u N1 G12u N 2 G13u N 3 iS11
G21u N1
G22u N 2
G23u N 3
iS
22
G31u N1
G32u N 2
网孔分析法
思想： 以网孔电流为求解对象，列写KVL方程。
b–n+1个网孔电流即是一组独立电流变量
网孔分析法
网孔电流法的独立方程数为b-(n-1)。与支路电流 法相比，方程数可减少n-1个。
R1iM1 R5iM1 R5iM 2 R4iM1 R4iM 3 uS4 uS1 0 电压与回路绕行方
R21iM 1
R22iM 2
R23iM 3
uS
22
R31iM 1
R32iM 2
R33iM 3
uS 33
自电阻、互电阻
网孔电压升的代数和
注意：适用于仅含独立电压源和电阻的电路
网孔分析法
自电阻
互电阻
R1 R4 R5
R4
R5
R11iM1 R12iM 2 R13iM 3 uS11 uS1 uS 4
( UR 降=E升 )
网孔分析法
R3
例3.
_ Ui+ I3 R4
+
US1_ R1
IS R_2
I1 US2 +
I2
R5
引入电流源电压为变量，增加网孔电流和电流源电流
的关系方程。
(R1+R2)I1-R2I2=US1+US2+Ui
-R2I1+(R2+R4+R5)I2-R4I3=-US2 -R4I2+(R3+R4)I3=-Ui
I3
Ib
R3 Ic
I4 R4
+ US4
_
求解网孔电流方程，得 Ia , Ib , Ic 求各支路电流： I1=Ia , I2=Ib-Ia , I3=Ic-Ib , I4=-Ic 校核： 选一新回路。
例2. I1+ 2V
_
网孔分析法
1
2
I2 I3
I4 1
I5
Ia 3
U2 +
Ib
+ –3U2
节点分析法
基本思想 (思考)：
能否假定一组变量，使之自动满足 KVL，从而 就不必列写KVL方程，减少联立方程的个数？
KVL恰说明了电位的单值性。如果选节点电压为 未知量，则KVL自动满足，就无需列写KVL方程。 当以节点电压为未知量列电路方程、求出节点电压 后，便可方便地得到各支路电压、电流。
节点分析法两个独立性约束网孔分析法网孔电流
若将电压源和电阻串联作为一条支路时，该电路共有6 条支路和4个结点。对①、②、③结点写出KCL方程。
i1 i3i1i4i30i4 0 i4 i1 i3
i1
i2i1i5i20i5
0i5
i1
i2
i2 i3i2i6i30i6 0 i6 i2 i3
基本思想 ：
以节点电压为求解对象，列写KCL方程。
节点分析法
节点电压法的独立方程数为(n-1)个。与支路电流法 相比，方程数可减少b-( n-1)个。
i1 i5 iS 0 i1 i2 i3 0 i3 i4 i5 0
i1 G1 (u N1 u N 2 )
其KVL方程； (3) 求解上述方程，得到m个网孔电流； (4) 求各支路电流(用网孔电流表示)； (5) 求解其它参数。
网孔分析法
仅含有电压源、电阻的电路
网孔分析法
含有电流源、电阻的电路
网孔分析法
含有受控源、电阻的电路
网孔分析法
例1. IaR I1
1 R1
US1
+
US1
_
网孔分析法
I2 R2
其中 Gii —自电导，等于接在节点i上所有支路的电导之 和(包括电压源与电阻串联支路)。总为正。
Gij = Gji—互电导，等于接在节点i与节点j之间的所 支路的电导之和，并冠以负号。
iSii — 流入节点i的所有电流源电流的代数和。
节点分析法
节点法的一般步骤：
(1) 选定参考节点，标定n-1个独立节点； (2) 对n-1个独立节点，以节点电压为未知
理想运放的条件 了解运放电路的分析方法
节点分析法
列写图中含VCCS电 iS1 路的节点电压方程。
1 R2
+ uR2 _
R1
R3
gmuR2
2
(1) 先把受控源当作独立源看列方程；
(2) 用节点电压表示控制量。
解：
un1 un2 R1
un1 R2
iS1
un2 un1 R1
支路电流i4、i5和i6可以用另外三个支路电流i1、i2和i3的 线性组合来表示。
网孔分析法
i1 i3 i4 0 i4 i1 i3
i1
i2
i5
0
i5
i1
i2
i2 i3 i6 0 i6 i2 i3
电流i4、i5和i6是非独立电流，它们由独立电流i1、i2和i3 的线性组合确定。这种线性组合的关系，可以设想为电流i1、 i2和i3沿每个网孔边界闭合流动而形成，如图中箭头所示。 这种在网孔内闭合流动的电流，称为网孔电流。它是一组能 确定全部支路电流的独立电流变量。
Rjk:互电阻
+ : 流过互阻两个网孔电流方向相同 - : 流过互阻两个网孔电流方向相反
特例：不含受控源的线性网络 Rjk=Rkj , 系数矩阵为对称阵。 （平面电路， Rjk均为负(当网孔电流均取顺(或逆)时针方向))
网孔分析法
网孔电流法的一般步骤：
(1) 选定m=b-(n-1)个网孔，确定其绕行方向； (2) 对m个网孔，以网孔电流为变量，列写