材料力学 重庆大学试题集
重庆大学 工程材料 考题 参考答案

参考答案一、名词解释(6分/小题,共30分)1. 塑性是指材料在外力作用下,产生永久残余变形而不断裂的能力,而韧性是指材料断裂时所需能量的度量。
2. 铁素体是碳溶解在体心立方晶格的α-Fe 中形成的间隙固溶体,而奥氏体是碳溶解在面心立方晶格的γ-Fe 中形成的间隙固溶体。
3. 调质处理是指淬火加高温回火的热处理工艺,而变质处理是指向合金液中加入某种用于控制合金相或非金属夹杂物生长形态的微量元素的熔体处理工艺方法。
4. 淬透性是指淬透性表示钢淬火后获得淬透层深度的能力,而淬硬性表示钢淬火后能达到的最高硬度。
5. 将亚共析钢加热至AC3以上20~30℃,保温足够时间奥氏体化后,随炉缓慢冷却,从而得到接近平衡的组织,这种热处理工艺称为完全退火。
将钢加热到Ac1以上20~30℃,保温一段时间,然后缓慢冷却到略低于Ar1的温度,并停留一段时间,使组织转变完成,得到在铁素体基体上均匀分布的球状或颗粒状碳化物的组织,这种热处理工艺称为球化退火。
二、绘图题(10分)1、请在立方晶系中绘制以下晶向: ]231[ ]012[ (4分,每个2分)2、立方晶系的{111}晶面族包含几个晶面?请绘制出所有晶面。
(6分) 答:4个(2分),绘图见下图(每个1分)。
三、铁碳相图知识(30分)1、叙述以下点或线的含义:P 、S 、E 、C 、N 、J 、A 、G 、GS 、EC 。
(5分,每个0.5分)2、上图中三条水平线上各发生什么相变反应?请分别写出其反应式,并给出反应温度、反应相和反应相的成分。
(6分)(每式2分,不写化学成分不扣分)3、含碳量为0.6%的碳钢的组织组成物是什么?相对含量各占多少?相组成物是什么?其相对含量又各占多少?(6分)组织组成物为F+P ,F%=(0.77-0.6)/(0.77-0.0218)≈23%,P%=1-F%=77 %; 相组成物为F+Fe 3C ,F%=(6.69-0.6)/(6.69-0.0218)≈91%,P%=1-F%=9%。
(NEW)重庆大学航空航天学院863材料力学二(含弹性力学的平面问题)历年考研真题汇编

2013年重庆大学863材料力学二(含基本变形、组合变形与弹性力学的 平面问题)考研真题
2009年重庆大学863材料力学(含基本变形、组合变形与弹性力学的平 面问题)考研真题
2008年重庆大学863材料力学(含基本变形、组合变形与弹性力学的平 面问题)考研真题
2006年重庆大学470材料力学(含基本变形、组合变形与弹性力学的平 面问题)考研真题
的平面问题)考研真题
2013年重庆Leabharlann 学863材料力学二 (含基本变形、组合变形与弹性
力学的平面问题)考研真题
2009年重庆大学863材料力学(含 基本变形、组合变形与弹性力学
的平面问题)考研真题
2008年重庆大学863材料力学(含 基本变形、组合变形与弹性力学
的平面问题)考研真题
2006年重庆大学470材料力学(含 基本变形、组合变形与弹性力学
大学材料力学习题及答案(题库)精选全文

可编辑修改精选全文完整版一.是非题:(正确的在括号中打“√”、错误的打“×”) (60小题) 1.材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
( √ )2.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。
( √ ) 3.在载荷作用下,构件截面上某点处分布内力的集度,称为该点的应力。
(√ ) 4.在载荷作用下,构件所发生的形状和尺寸改变,均称为变形。
( √ ) 5.截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ,它们的单位相同。
( √ )6.线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量,它们都是无量纲的量。
( √ )7.材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( ) 8.在强度计算中,塑性材料的极限应力是指比例极限p σ,而脆性材料的极限应力是指强度极限b σ。
( )9.低碳钢在常温静载下拉伸,若应力不超过屈服极限s σ,则正应力σ与线应变ε成正比,称这一关系为拉伸(或压缩)的虎克定律。
( )10.当应力不超过比例极限时,直杆的轴向变形与其轴力、杆的原长成正比,而与横截面面积成反比。
( √ )11.铸铁试件压缩时破坏断面与轴线大致成450,这是由压应力引起的缘故。
( )12.低碳钢拉伸时,当进入屈服阶段时,试件表面上出现与轴线成45o 的滑移线,这是由最大剪应力max τ引起的,但拉断时截面仍为横截面,这是由最大拉应力max σ引起的。
( √ )13.杆件在拉伸或压缩时,任意截面上的剪应力均为零。
( ) 14.EA 称为材料的截面抗拉(或抗压)刚度。
( √ ) 15.解决超静定问题的关键是建立补充方程,而要建立的补充方程就必须研究构件的变形几何关系,称这种关系为变形协调关系。
( √ ) 16.因截面的骤然改变而使最小横截面上的应力有局部陡增的现象,称为应力集中。
重庆大学材料力学习题解答

C 0.75m 1m
A
D 1.5m
B F
1、受力分析
C 0.75m A 1m F D 1.5m B F
FCD
Fx Fy
d=2cm,E=200GPa, []=160MPa
M
A
0
F AB FCD sin AD 0
57.6 kN
3、根据AB杆的强度条件,求许可载荷
查表得水平杆AB的面积为A2=2×12.74cm2
FN 2 A2
3F 2 3F
1 1 6 4 120 10 2 12 . 74 10 A2 1.732 F 3
176.7 kN
4、许可载荷
F min57.6 kN 176.7kN
F 57.6 kN
题8
图示吊环, 载荷F=1000kN,两边 的斜杆均由两个横截面为矩形的钢杆构 成,杆的厚度和宽度分别为b=25mm, h=90mm,斜杆的轴线与吊环对称,轴 线间的夹角为α=200 。钢的许用应力为 〔σ〕=120MPa。试校核斜杆的强度。 解:1、计算各杆件的轴力。研究 节点A为的平衡
第二章
题1:试作此杆的轴力图。 F l 解: FR 1 F F 2 1
q
F l
F
F
F
2l 2 q
l 3 F 3
FR
FR = F
F'=2ql F
F
1
FR = F
F
F
FN1 = F
2
q
3
F x
1
FR = F
2
FN 3 = F
3 F
F
FR = F
材料力学_考试题集(含答案)
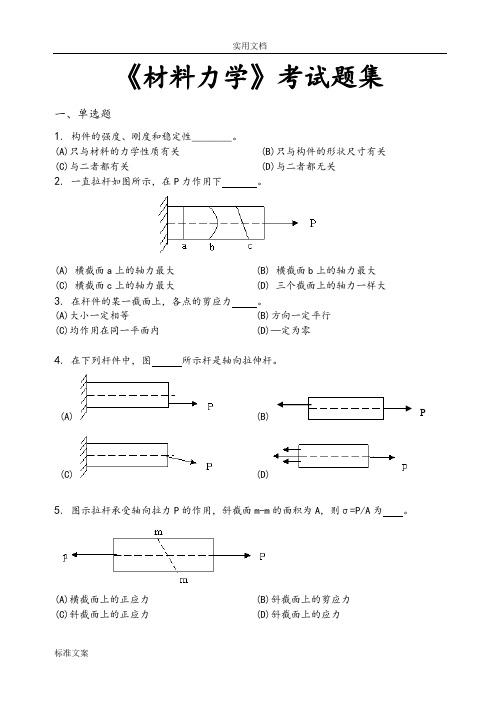
《材料力学》考试题集一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关 (B)只与构件的形状尺寸有关(C)与二者都有关 (D)与二者都无关2.一直拉杆如图所示,在P力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中,图所示杆是轴向拉伸杆。
(A)(C) (D)5.图示拉杆承受轴向拉力P的作用,斜截面m-m的面积为A,则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力P6.解除外力后,消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍,则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2 (B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等,正负号相同(B)绝对值相等,正负号不同(C)绝对值不等,正负号相同(D)绝对值不等,正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内;(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上,各个截面上的。
P(A)剪力相同,弯矩不同(B)剪力不同,弯矩相同(C)剪力和弯矩均相同(D)剪力和弯矩均不同13.当横向力作用于杆件的纵向对称面内时,关于杆件横截面上的内力与应力有以下四个结论。
重庆大学工程材料试卷及答案

材料专业01,02班〈〈材料科学与工程基础〉〉试题 (A 卷) (参考答案)一、填空题(每空1分,共24分)1、体心立方晶胞原子数是 2 ,原子半径是 √3 /4 a ,致密度为 0.68 ,配位数为 8 。
2、金属晶体中常见的点缺陷有 空位、间隙原子 ;线缺陷是 位错 ;最主要的面缺陷是 相界、晶界、亚晶界 。
3、结晶的进行是依靠两个密切联系的基本过程实现的,这两个过程是 形核 和 核长大 。
4、金属塑性变形的两种基本方式是 滑移 和 孪生 。
5、钢的奥氏体化分为 形核 、 核长大 、 非A 相溶解 和 均匀化 等四个基本过程。
6、钢铁材料中的马氏体常见组织形态有 M 板 和 M 针 ,其亚结构分别是 位错 和 孪晶 。
7、根据共析钢转变产物的不同,可将C 曲线分为 P 、 B 和 M 三个转变区。
8、钢中的硫和磷是有害杂质,硫的最大危害性是 热脆 ,磷的最大危害性是 冷脆 。
二、判断题(正确打“√”、错误打“×”。
每题1分,共10分)1、在立方晶系中,(111)⊥[110]。
(× )2、间隙相是溶质原子溶入溶剂晶格形成的固溶体。
(× )3、体心立方晶体可以沿()101-晶面上的[111]晶向滑移。
(√ )4、在铁碳合金中,只有共析成分的的合金才能发生共析反应。
(× )5、退火态铁碳合金室温下的组织均为铁素体加渗碳体。
(× )6、所谓本质细晶粒钢,就是一种在任何加热条件下晶粒均不粗化的钢。
(×)7、钢中合金元素含量越多,则淬火后钢的硬度越高。
(× )8、具有低温回火脆性的钢,从回火温度快冷至室温即可避免产生回火脆性。
(X) 9、表面淬火既能改变钢的表面化学成分和性能,又能改善其心部的组织与性能。
(X)10、在灰铸铁中,碳主要以石墨形式存在。
(√ )三、名词解释(每题4分,共16分) 固溶强化 过冷奥氏体 晶间腐蚀 滑移变形四、问答题(每题5分,共15分)1、晶粒大小对常温下金属的力学性能有何影响?试提出三种细化晶粒的方法,并简述其原理。
材料力学智慧树知到答案2024年重庆大学

材料力学重庆大学智慧树知到答案2024年第一章测试1.变形固体的基本假设是()。
A:连续、均匀性假设和线性弹性假设; B:线性弹性假设和小变形假设; C:连续、均匀性假设和各向同性假设; D:各向同性假设、小变形假设和线性弹性假设。
答案:C2.要使构件安全、正常地工作,必须满足()。
A:稳定性要求 B:强度要求、刚度要求、稳定性要求 C:强度要求 D:强度要求和稳定性要求答案:B第二章测试1.应力是指截面上每点处单位面积内的分布内力,即内力集度。
()A:错 B:对答案:B2.构件中不同点处的线应变及切应变一般是不同的,而且线应变与正应力相对应,切应变与切应力相对应。
()A:错 B:对答案:B3.等直杆发生拉(压)变形时,横截面上各点既有正应力,又有切应力。
()A:错 B:对答案:A4.等直杆受力如图,该杆的轴力最大值为()。
A:2kN B:4kN C:5kN D:3kN 答案:D5.等直杆受力如图,其上端截面的轴力为()。
A:F+ql B:-F+ql C:F D:ql答案:B第三章测试1.等直杆受力如图,该杆的扭矩最大值为()。
A:6kN.m B:2kN.m C:4kN.m D:8kN.m答案:C2.等截面圆轴配置四个皮带轮,各轮传递的力偶的力偶矩如图所示。
从抗扭的角度如何改变四个轮之间的相对位置,轴的受力最合理的是()。
A:将B轮与C轮对调 B:将B轮与D轮对调, 然后再将B轮与C轮对调 C:将C轮与D轮对调 D:将B轮与D轮对调答案:C3.内外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内圆周上各点的切应力为()。
A:τ B:零C:ατ D:答案:C4.一圆轴用普通碳素钢制成,受扭后发现单位长度扭转角超过了许用值,为提高刚度拟采用的合理措施是()A:用铸铁代替 B:改为优质合金钢 C:减少轴的长度 D:增大轴的直径答案:D5.下述结论中,正确的是()A:若物体内各点的应变均为零, 则物体无位移 B:应变分为线应变和切应变, 其量纲为长度 C:若物体的各部分均无变形, 则物体内各点的应变为零 D:受拉杆件全杆的轴向伸长,标志着杆件内各点的变形程度答案:C第四章测试1.悬臂梁受力如图,以下说法正确的是()。
重庆理工大学材料力学期末考试复习题及答案

一、填空题:1. 受力后几何形状和尺寸均保持不变的物体称为 。
2. ______________________ 构件抵抗 的能力称为强度。
3. 圆轴扭转时,横截面上各点的切应力与其到圆心的距离成 比。
4. 梁上作用着均布载荷,该段梁上的弯矩图为 。
5. 偏心压缩为 的组合变形。
6. 柔索的约束反力沿 离开物体。
7. 构件保持 的能力称为稳定性。
8. 力对轴之矢 情况下为零。
9. 梁的中性层与横截面的交线称为 。
10. 图所示点的应力状态,其最大切应力是 。
ICOMPa11. 物体在外力作用下产生两种效应分别是 。
12. 外力解除后可消失的变形,称为 。
13. 力偶对任意点之矩都 _______________________ 。
14. 阶梯杆受力如图所示,i― 横截面面积分别为 2A 和A,弹性模量为E,则杆中最大正应力为。
15. 梁上作用集中力处,其剪力图在该位置有 16. 光滑接触面约束的约束力沿 17. 外力解除后不能消失的变形,称为 。
18. 平面任意力系平衡方程的三矩式,只有满足三个矩心 的条件时,才能成为力系平衡的20.图所示点的应力状态,已知材料的许用正应力 [b ],其第三强度理论的强度条件是21. 物体相对于地球处于静止或匀速直线运动状态,称为 22. 在截面突变的位置存在 集中现象。
指向物体。
充要条件。
19.图所示,梁最大拉应力的位置在点处。
23. 梁上作用集中力偶位置处,其弯矩图在该位置有。
24. 图所示点的应力状态,已知材料的许用正应力[b ],其第三强度理论的强度条件是25. 临界应力的欧拉公式只适用于26. 只受两个力作用而处于平衡状态的构件,称为。
27. 作用力与反作用力的关系是。
28. 平面任意力系向一点简化的结果的三种情形是___________________________________________ 。
29. 阶梯杆受力如图所示,设AB和BC段的横截面―为E,则截面C的位移为30. 若一段梁上作用着均布载荷,则这段梁上的剪力图为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉压静不定 如图所示结构由刚性横梁AD、弹性杆1和2组成,梁的一端作用铅垂载荷F,两弹性杆均长l,拉压刚度为EA,试求D点的垂直位移。(图上有提示)
解:在力F作用下,刚性梁AD发
生微小转动,设点B和C的铅垂位移分别为和,则=设杆和杆的伸长量分别为 △l1和△l2,根据节点B和C处的变形关系,有
1113cos302l
2221cos602l
则△l1和△l2的关系为 1232ll (a) 由平衡条件,对A点取矩得 12sin60sin3023NNFaFaFa 即 12332llEAEAFll (b) 联立方程(a)和(b),解得 2127FllEA D点位移为 2233362227DaFllaEA
------------------------------------------------------------------------------------------------------ 一.摩尔积分 单位载荷法 直径80mmd的圆截面钢杆制成的钢架,在自由端C处受到集中力1kNF作用,钢杆的弹性模量为200GPaE,0.8mR,2.4mh,不计剪力和轴力的影响,试求自由端c处的水平位移。(提示:可采用莫尔积分方法求解) 题图 解:(1)求梁的内力方程
半圆弧BC段: cos)(FFN )(0
)cos()(1FRM )(0 直杆AB段: FxFN)( )(hx0 FRxM2)( )(hx0 (2)求自由端的水平位移 在自由端水平方向加单位载荷,如图)(b所示,由水平单位载荷产生的轴力和弯矩方程分别为: 半圆弧BC段: sin)(NF )(0
sin)(RM )(0
直杆AB段: 0)(xFN )(hx0 xxM)( )(hx0
由莫尔积分,可得自由端c处的水平位移为:
300032
()()()()cossin2(1cos)(sin)208.91mmNNCxllhFxFxMxMx
dxdxEAEIFFRFRdxdxdxEAEIEIFRFRhEIEI
------------------------------------------------------------------------------------------------------
ABC
R
Fh
------------------------------------------------------------------------------------------------------下一题有问题,M(x1,2,3)? ------------------------------------------------------------------------------------------------------ 二.应力应变分析 图2所示为一矩形截面铸铁梁,受两个横向力作用。 (1)从梁表面的A,B,C三点处取出的单元体上,用箭头表示出各个面上的应力。 (2)定性地绘出A,B,C三点的应力圆。 (3)在各点的单元体上,大致画出主应力单元体图。 (4)试根据第一强度理论,说明(画图表示)梁破坏时裂缝在B,C两点处的走向。
图2 解: (1)中间段是纯弯曲,故切应力为零。点C在中性层上,所以正应力为零。单元体受力如图2.1所示。
图2.1 (2)点B应力圆与轴相切,点C应力圆以原点为圆心,见图2.2。
图2.2 (3)主应力单元体如图2.3所示。 图2.3 (4)根据第一强度理论,物体是由最大拉应力造成破坏,故裂缝面应垂直于主应力1,如图2.4所示。
图2.4 ------------------------------------------------------------------------------------------------------ 图示矩形截面hb简支梁在集中载荷P作用下. 1 在y方向间距4ha的A、B、C、D、E五点取单元体,定性分析这五点的应力情况, 并指出单元体属于哪种应力状态.(C点位于中性层) 2 若测得梁上D点在x及y方向上的正应变为εx=4.0×10 - 4及εy= -1.2×10 – 4. 已知材料的弹性模量 E=200GPa,泊松比μ=0.3.试求D点x及y方向上的正应力.
解:1各点的应力状态[10分(每个单元体2分)] A、E点为单向应力状态;C点为纯剪切应力状态;B、D点为二向应力状态。
b h A B C E D P y x 2 求D点x及y方向上的正应力 )(1yxxE
)(1xyyE 解得: MPax80
0y
------------------------------------------------------------------------------------------------------
x
y xy yx
D ------------------------------------------------------------------------------------------------------ 图所示薄壁圆筒,未受力时两端与固定支座贴合,试问当内压为p时筒壁的应力。筒的长
度为l,内径为D,壁厚为,材料的泊松比为。(00.5)
解:首先,解除右端固定支座,并用约束力RF代替其作用。 在内压p作用下,筒壁的轴向和周向正应力分别为
,4xppD
,2ppD
根据胡克定律,并考虑到00.5,得到筒体的轴向变形为 ,,()(12)04pxpplpDllEE
在约束力RF作用下,筒体的轴向变形则为 ()RRRFFlFllEAED
利用叠加法,得到筒体的总轴向变形为 (12)4RRpFFlpDllllEED 根据筒的变形协调条件,由上式得补充方程为 0l
即 (12)04RFlpDlEED 由此可得约束力为 2(12)4RpDF
由上述分析可以得到筒壁的轴向和周向正应力分别为
42RxFpDpDD
2pD
-------------------------------------------------------------------------------------------------------------- 在一块厚钢块上挖了一条贯穿的槽,槽的宽度和深度都是1cm。在此槽内紧密无隙地嵌入了一铝质立方块,其尺寸是111cm,并受P=6kN压缩力如图示,试求铝立方块的三个主应力。假定厚钢块是不变形的,铝的E=71GPa,=0.33。
解 34162316100060111000.33601019.8MPaPa
==
------------------------------------------------------------------------------------------------------ 两端封闭的薄壁圆筒,长度为l,内径为D,壁厚为,如图所示。已知材料的弹性模量为E,泊松比为。筒内无内压时,两端用刚性壁夹住。筒内承受内压为p时,求此时圆筒作用于刚性壁上的力。
解:(1)静力关系 当圆筒受内压p时,圆筒受刚性支座的约束力NAF和NBF作用,由水平方向的平衡关
系可知: NNBNAFFF 是一次静不定问题
(2)几何关系 取圆筒的轴向、环向和径向分别为x,y和z向。 由约束条件可得: 0x (3)物理关系 由广义Hooke定律 )(zyxxE1
其中,DFpDNx4 2
pD
y
0z
故,011EEzyxx)(可得
pDFN4212)(
ABp
DlNAFNBF
A B p
Dl
