SPC控制图(X-R cpk)新
spc(xbar-r,xbar-s,中位数极差3合一控制图)

14 21
1.08 1.31 1.12 1.18 1.15 1.17 0.98 1.05 1.00 1.26 1.14 0.33 1.11 0.35 1.60 0.80 1.22 1.01 0.62 0.08 0.11
15 22
1.08 1.26 1.13 0.94 1.30 1.15 1.07 1.02 1.22 1.18 1.14 0.36 1.11 0.35 1.60 0.80 1.22 1.01 0.62 0.08 0.11
4 11
1.08 1.12 1.11 1.28 1.00 0.95 1.15 1.14 1.28 1.31 1.13 0.36 1.11 0.35 1.60 0.80 1.22 1.01 0.62 0.08 0.11
5 12
0.98 1.30 1.31 1.12 1.08 1.10 1.15 1.35 1.12 1.26 1.14 0.37 1.11 0.35 1.60 0.80 1.22 1.01 0.62 0.08 0.11
子组容量 D4 C4
3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78 0.80 0.89 0.92 0.94 0.95 0.96 0.97 0.97 0.97
B4
3.27 2.57 2.27 2.09 1.97 1.88 1.82 1.76 1.72
B3
0.00 0.00 0.00 0.00 0.03 0.12 0.19 0.24 0.28
2 9
1.01 1.10 1.15 0.97 1.25 1.12 1.10 0.90 1.04 1.08 1.09 0.35 1.11 0.35 1.60 0.80 1.22 1.01 0.62 0.08 0.11
SPC控制图简介

8.3:连续6点递增或递减
Six points in a row steadily increasing or
decreasing
过程均值偏移
9. 异常点原因分析的步骤
• 对于控制图所出现的异常点, 我们建议按下列順序 进行检查:
a. 取 Data 是否随机; b. 数字的读取是否准确、测试仪器是否符合
两种变异
过程预防 对过程采取行动 避免浪费、不生产
无用产品的 预防策略
偶因 始终存在 不易识别
异因 可查明特殊原因
归结为5M1E
1.3 统计过程控制的目的
• SPC的目的:建立并保持过程处于可接受的并且稳定的水平, 以确保产品和服务符合规定的要求
• 控制图。是实现上述目的所应用的主要统计工具
表征过程 当前样本 序列信息
LCL
UCL
Specification Limits (USL,LSL)
由顾客或管理层确定,表述过程的理想状态
Control Limits
(UCL,LCL)
由抽样数据计算确定,表述过程的实际状态
1.2 传统方法与过程预防策略
传统的质量检验策略
科学的过程预防策略
事后检验 浪费和不经济
未识別
识別
不控制 生产过程 控制
• 分析用控制图的目的是对收集到的一定数据进 行分析,寻找稳态。
• 控制用控制图是对实时数据进行分析,保持稳 态。
• 稳态,也称统计控制状态(state in statistical control),即过程中只有偶因没有异因的状态。
• 稳态是生产追求的目标。
4.1 稳态的统计解释(又称统计稳态)
8. 判异准则
SPC中控制图和CPK图应用培训课1

导致质量特性波动的因素根据来源的不同,可分为人(man)、机(machine)、料 (material)、法(method)、环(environment)、测(measurement)6个方面,简 称为5M1E。
14
百分比
百分比
拟合后P值都不大于0.05咋办,看峰度、偏度值
N 均值 标准差 中位数 最小值 最大值 偏度
峰度
58 0.946897 0.0221008 0.94 0.91 1
0.651317 -0.319062
对于偏度值和峰度值在-1到1之间都可以按照近似正态去做CPK图
挥发份 的过程能力
过程数据
3
记住开山鼻祖休哈特(1891-1967年) 及其贡献
第一张控制图在休哈特手中产生:
美国休哈特博士基于对西方电气公司所制造产品的特性变异的关注和对抽样结果的研 究,创立了统计过程控制(SPC)理论。1924年5月16日他绘制出了世界上第一张控 制图,1931年发表经典著作《制成品质量的经济控制》,并将控制图应用在西方电气 公司霍商工厂的保险丝、加热控制和电站装置的生产上。
13
0.95、0.94、0.93、0.94、0.96、0.98、0.92、0.93
拟合转换一下看看P值有超过0.05的没有
百分比
百分比
挥发份 的概率图
正态 - 95% 置信区间 99
正态 - 95% 置信区间 99
90
90
百分比
50
常用控制图

SPCSPC(Statistical Process Control,统计过程控制或统计制程控制)目录∙ 1 什么是SPC∙ 2 SPC起源与发展∙ 3 3σ原理简介∙ 4 SPC技术原理∙ 5 SPC控制图及计算∙ 6 SPC控制图(管制图)的实施∙7 SPC控制图(管制图)异常的判断及处理∙8 制程能力指数(参数)CPK∙9 SPC的发展特点∙10 SPC对企业带来的好处什么是SPCSPC即英文“Statistical Process Control”之缩写,意为“统计制程控制” SPC或称统计过程控制。
SPC主要是指应用统计分析技术对生产过程进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
在生产过程中,产品的加工尺寸的波动是不可避免的。
它是由人、机器、材料、方法和环境等基本因素的波动影响所致。
波动分为两种:正常波动和异常波动。
正常波动是偶然性原因(不可避免因素)造成的。
它对产品质量影响较小,在技术上难以消除,在经济上也不值得消除。
异常波动是由系统原因(异常因素)造成的。
它对产品质量影响很大,但能够采取措施避免和消除。
过程控制的目的就是消除、避免异常波动,使过程处于正常波动状态。
SPC起源与发展1. 1924年休哈特博士在贝尔实验室发明了品质控制图。
2. 1939年休哈特博士与戴明博士合写了《品质观点的统计方法》。
3.二战后美英将品质控制图方法引进制造业,并应用于生产过程。
4. 1950年,戴明到日本演讲,介绍了SQC的技术与观念。
5.SQC是在发生问题后才去解决问题,是一种浪费,所以发展出了SPC。
6.美国汽车制造商福特、通用汽车公司等对SPC很重视,所以SPC得以广泛应用。
7.ISO9000(2000)体系亦注重过程控制和统计技术的应用(如8.1,8.2.3)。
常用控制图

SPCSPC(Statistical Process Control,统计过程控制或统计制程控制)目录∙ 1 什么是SPC∙ 2 SPC起源与发展∙ 3 3σ原理简介∙ 4 SPC技术原理∙ 5 SPC控制图及计算∙ 6 SPC控制图(管制图)的实施∙7 SPC控制图(管制图)异常的判断及处理∙8 制程能力指数(参数)CPK∙9 SPC的发展特点∙10 SPC对企业带来的好处什么是SPCSPC即英文“Statistical Process Control”之缩写,意为“统计制程控制” SPC或称统计过程控制。
SPC主要是指应用统计分析技术对生产过程进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
在生产过程中,产品的加工尺寸的波动是不可避免的。
它是由人、机器、材料、方法和环境等基本因素的波动影响所致。
波动分为两种:正常波动和异常波动。
正常波动是偶然性原因(不可避免因素)造成的。
它对产品质量影响较小,在技术上难以消除,在经济上也不值得消除。
异常波动是由系统原因(异常因素)造成的。
它对产品质量影响很大,但能够采取措施避免和消除。
过程控制的目的就是消除、避免异常波动,使过程处于正常波动状态。
SPC起源与发展1. 1924年休哈特博士在贝尔实验室发明了品质控制图。
2. 1939年休哈特博士与戴明博士合写了《品质观点的统计方法》。
3.二战后美英将品质控制图方法引进制造业,并应用于生产过程。
4. 1950年,戴明到日本演讲,介绍了SQC的技术与观念。
5.SQC是在发生问题后才去解决问题,是一种浪费,所以发展出了SPC。
6.美国汽车制造商福特、通用汽车公司等对SPC很重视,所以SPC得以广泛应用。
7.ISO9000(2000)体系亦注重过程控制和统计技术的应用(如8.1,8.2.3)。
X-R控制图CPK

Ca
产品批号 工序名称 85度 片温 产品规格 加工设备/编号 产品性能: 测量工具 温度
测量项目/特性
####
下限值 单位
N0.
规格中心值 2012.03.16 数据制表
85.000 范琴琴
上限值 测量操作
90.000 范琴琴
80.000 mm
双金属测温台
测量日期
N
日期
时间/批次
1
2
6 4 2
0
79.685 80.700 81.715 82.730 83.745 84.760 85.775 86.790 87.805 88.820
1 82.2 85.1 异常 分析 85.5 87
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
尺寸值
判异方法说明:
1 81.100 83.000 83.700 81.600 85.400 82.300 84.800 81.900 84.800 82.200
1.606 0.71 1.038 85.133 81.711 6.239 0.000 83.422 2.950 87.800 80.700 7.100 50
检 查 件
1.任何超出控制界限的点; 2.连续7点全在中心线一侧 3.连续7点上升或下降; 4.任何其他明显非随机的图形
注: 上表中黄色单元格为填写项.其它会自动生成.每次采样为5个数据,
#### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### 样本数量N 直方图
SPC统计过程控制及CPK分析
管制图的类型
•计量值管制图
•平均值与全距管制图( X-R Chart ) •中位值与全距管制图( X-R Chart ) •个别值与移动全距管制图( X-Rm Chart ) •平均值与标准差管制图( X-σ Chart )
•计数值管制图
•不良率管制图 ( P Chart ) •不良数管制图 ( P-Chart or d Chart ) •缺点数管制图 ( C Chart ) •单位缺点数管制图 ( U Chart )
16 40%
14 35%
14
35%
12 30%
10
10 25%
9
25%
22.50%
8 20%
系列1
15% 6
10%
12.550%
4
5% 2 5%
2
0%
1
2
3
4
5
0
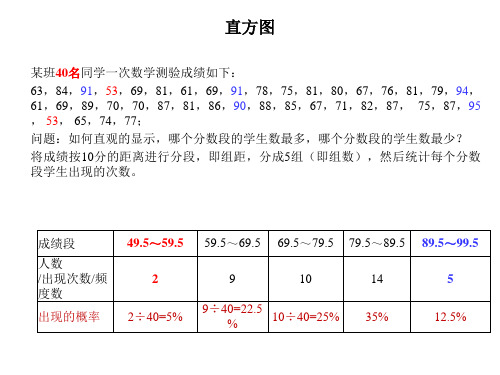
49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
5% 22.5% 25% 35% 12.5%
若某随机变量可以看作是有相互独立的大量随机变量综合作用的结果,每一个因 素在总的影响中的作用都很微小,则综合作用的结果服从正态分布
举例:
射击发射炮弹的落点与目标的偏差,就受着许多随机因素的影响
如瞄准时的误差
空气阻力所产生的误差,
炮弹、炮身结构所引起的误差等 测量中产生的误差都是服从正态分布的随机变量: 仪器偏差 温度变化偏差 估读误差造成的偏差 测试参数造成的偏差
•判定准则1:(2/3A) •3点中有2点在A区或A区以外
•UCL •A
•B
X •C •C
•B •LCL
现场SPC X-R控制图

数据重要趋势 点数最大长度 递增趋势 递 增 链 数 点数最大长度 递减趋势 19.093 递 减 链 数 0.000 超出控制线点数
X图 4 8 6 7 3
均值(X-图)
19.17 19.14 19.11 19.08 19.05 19.02 18.99 18.96 18.93
1 2 3
均值
Data Values UCLx LCLx Average X
11 5
14 3
1
0
0
4
5
6
7
8
9
10
11
12
13 极差值
14
15
16
17
18
19
20
21
22
23
24
25
正态分布曲线
数据区间
控制图表现: 过程能力分析:
注意!控制图中有点子出界,或出现7点链条情况!!!
过程能力充足! 11-19
2
19.1 19.11 19.12 19.12 19.12 19.114 0.020
4
5
6
7
8
9
10
11
12
13 数据点
14
15
16
17
18
19
20
21
22
23
24
25
极差(R-图)
频数
60
正态分布
0.240 0.200 0.160
极差
50 40 30 20 11 10 0 0 26
49
0.120 0.080 0.040 0.000
1 2 3
R Value UCLr LCLr Average R
