全等三角形及其判定习题课
全等三角形的判定-八年级数学上册同步精品课堂知识清单+例题讲解+课后练习(人教版)(原卷版)

第二课时——全等三角形的判定知识点一:全等三角形的判定:判定方法内容数学语言 图形表示 注意点边边边(SSS )三边分别相等的两个三角形全等。
可简写为“边边边”或“SSS ”在△ABC 与△DEF中:⎪⎩⎪⎨⎧===EF BC DF AC DE AB ∴△ABC ≌△DEF边角边(SAS )两边及其夹角分别对应相等的两个三角形全等。
可简写为“边角边”或“SAS ”在△ABC 与△DEF中:⎪⎩⎪⎨⎧=∠=∠=DF AC D A DEAB ∴△ABC ≌△DEF用“边角边(SAS )判定全等时,角一定是两边的夹角,否则不能判定全等。
在写条件的时候角必须写在中间。
角边角(ASA )两角及其夹边分别对应相等的两个三角形全等。
可简写为“角边角”或“ASA ”在△ABC 与△DEF中:⎪⎩⎪⎨⎧∠=∠=∠=∠E B DE AB DA ∴△ABC ≌△DEF用“角边角(ASA )判定全等时,边是两角的夹边,在书写的过程中需把边写在中间特别提示:在写全等三角形的数学语言时,等号左边写“≌”左边三角形的条件,等号右边写“≌”右边三角形的条件。
并且条件的顺序必须和判定条件顺序一致。
方法总结:【类型一:补充证全等条件】1.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF的是()A.BC=DE B.AE=DBC.∠A=∠DEF D.∠ABC=∠D2.如图,在△ABC和△BAD中,AC=BD,要使△ABC≌△BAD,则需要添加的条件是()第2题第3题A.∠BAD=∠ABC B.∠BAC=∠ABD C.∠DAC=∠CBD D.∠C=∠D3.如图,BC=BD,添加下列一个条件后,仍无法判定△ABC≌△ABD的是()A.AC=AD B.∠ABC=∠ABD C.∠CAB=∠DAB D.∠C=∠D=90°4.如图,已知点A,D,C,F在同一条直线上,AB=DE,AD=CF,要使△ABC≌△DEF,则下列条件可以添加的是()第4题第5题第7题A.∠B=∠E B.∠A=∠EDF C.AC=DF D.BC∥EF5.如图,已知AB=AE,∠EAB=∠DAC,添加一个条件后,仍无法判定△AED≌△ABC的是()A.AD=AC B.∠E=∠B C.ED=BC D.∠D=∠C6.下列条件,不能判定两个直角三角形全等的是()A.两个锐角对应相等B.一个锐角和斜边对应相等C.两条直角边对应相等D.一条直角边和斜边对应相等7.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,添加一个条件,不能使得Rt△ABC≌Rt△DCB 的是()A.AB=DC B.AC=DB C.∠ABC=∠DCB D.BC=BD8.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是()A.AD=CB B.∠A=∠CC.BD=DB D.AB=CD【类型二:证明三角形全等】9.请将以下推导过程补充完整.如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF平分∠DCE.求证:△DCF ≌△ECF 证明:∵AD ∥BE ∴∠A =∠B在△ACD 和△BEC 中()⎪⎩⎪⎨⎧=∠=∠BC AD B A ∴△ACD ≌△BEC ( )∴CD =CE ( ) ∵CF 平分∠DCE ∴ 在△DCF 和△ECF 中()⎪⎩⎪⎨⎧==CE CD CF CF ∴△DCF ≌△ECF (SAS )10.如图,点C 在BD 上,AB ⊥BD ,ED ⊥BD ,AC ⊥CE ,AB =CD .求证:△ABC ≌△CDE .11.如图,点A、D、B、E在一条直线上,AD=BE,AC=DF,AC∥DF,求证:△ABC≌△DEF.12.如图,点D在线段BC上,AB=AD,∠1=∠2,DA平分∠BDE:求证:△ABC≌△ADE.13.天使是美好的象征,她的翅膀就像一对全等三角形.如图AD与BC相交于点O,且AB=CD,AD=BC.求证:△ABO≌△CDO.14.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.15.如图,CA=CD,∠BCE=∠ACD,BC=EC.求证:△ABC≌△DEC.16.如图,D、C、F、B四点在一条直线上,AC=EF,AC⊥BD,EF⊥BD,垂足分别为点C、点F,BF=CD.试说明:△ABC≌△EDF.17.如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.18.如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE =BF.19.如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,求证:Rt△ADE≌Rt△CDF.【类型三:全等三角形的判定与性质】20.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠F AC =40°,则∠BFE=()第20题第21题A.35°B.40°C.45°D.50°21.如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为()A.21B.24C.27D.3022.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为()第22题第23题A.3B.5C.6D.723.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是()A.1B.2C.3D.424.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.(1)求证:AB=FE;(2)若ED⊥AC,AB∥CE,求∠A的度数.25.如图,四边形ABCD中,AD∥BC,E为CD的中点,连结BE并延长交AD的延长线于点F.(1)求证:△BCE≌△FDE;(2)连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.26.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.(1)求证:BC=DC;(2)若∠A=25°,∠D=15°,求∠ACB的度数.【类型四:全等三角形的应用】27.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.那么判定△ABC和△DEC全等的依据是()第27题第28题A.SSS B.SAS C.ASA D.AAS28.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是()A.带①②去B.带②③去C.带③④去D.带②④去29.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.第29题第30题30.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB =OC,测得AB=a,EF=b,圆形容器的壁厚是()A .aB .bC .b ﹣aD .21(b ﹣a )一、选择题(10题)1.如图为正方形网格,则∠1+∠2+∠3=( )第1题 第2题 第3题A .105°B .120°C .115°D .135°2.如图,已知∠C =∠D =90°,添加一个条件,可使用“HL ”判定Rt △ABC 与Rt △ABD 全等.以下给出的条件适合的是( )A .∠ABC =∠ABDB .∠BAC =∠BAD C .AC =AD D .AC =BC3.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.A .①B .②C .③D .①和②4.根据下列已知条件,能唯一画出△ABC 的是( )A.∠C=90°,AB=6B.AB=4,BC=3,∠A=30°C.AB=5,BC=3D.∠A=60°,∠B=45°,BC=45.如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是()A.ASA B.SSS C.AAS D.SAS6.如图,已知∠EAC=∠BAD,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠D.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个7.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离BD与CD的距离间的关系是()第7题第8题A.BD>CD B.BD<CD C.BD=CD D.不能确定8.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动()分钟后,△CAP与△PQB全等.A.2B.3C.4D.89.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为()第9题第10题A.4cm B.6cm C.8cm D.求不出来10.如图,在△AOB和△COD中,OA=OB,OC=OD(OA<OC),∠AOB=∠COD=α,直线AC,BD 交于点M,连接OM.下列结论:①AC=BD,②∠OAM=∠OBM,③∠AMB=α,④OM平分∠BOC,其中正确结论的个数是()A.4B.3C.2D.1二、填空题(6题)11.如图,线段AB,CD相交于点O,AO=BO,添加一个条件,能使△AOC≌△BOD,所添加的条件的是.12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=.第12题第14题13.在△ABC中,AB=3cm,AC=4cm,则BC边上的中线AD的取值范围是.14.在直角三角形中,存在斜边的平方等于两条直角边的平方的和。
八年级数学上册第十二章全等三角形12.2三角形全等的判定第4课时利用HL判定两个直角三角形全等习题名

11.如图1,已知点P的坐标为(2,2),点A在x轴正半轴上运动,点B在y轴负半轴上运动,且PA=PB.(1)求证:PA⊥PB;(2)求OA-OB的值;(3)如图2,若点B在y轴正半轴上运动时,求OA+OB的值.
(2)解:∵Rt△APE≌Rt△BPF,∴AE=BF.∵AE=OA-OE=OA-2,BF=OB+OF=OB+2,∴OA-2=OB+2,∴OA-OB=4.(3)解:过点P作PE⊥x轴于点E,作PF⊥y轴于点F.同(1)可得Rt△APE≌Rt△BPF,∴AE=BF.∵AE=OA-OE=OA-2,BF=OF-OB=2-OB,∴OA-2=2-OB,∴OA+OB=4.
谢谢大家
每一个成功者都有一个开始。勇于开始,才能找到成功的路成功源于不懈的努力,人生最大的敌人是自己怯懦每天只看目标,别老想障碍宁愿辛苦一阵子,不要辛苦一辈子积极向上的心态,是成功者的最基本要素生活总会给你另一个机会,人生就像骑单车,想保持平衡就得往前走21:19:48我们必须在失败中寻找胜利10、一个人的梦想也许不值钱,但一个人的努力很值钱。11、在真实的生命里,每桩伟业都由信心开始,并由信心跨出第一步。
易错点 混淆直角三角形全等的判定方法
5.要判定两个直角三角形全等,下列说法正确的有( )①有两条直角边对应相等;②有两个锐角对应相等;③有斜边和一条直角边对应相等;④有一条直角边和一个锐角相等;⑤有斜边和一个锐角对应相等;⑥有两条边相等. A.6个 B.5个 C.4个 D.3个
拔尖角度一 分类讨论与“HL”判定方法的综合
10.如图,在△ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC上和过点A且垂直于AC的射线AQ上运动,问点P运动到AC上什么位置时,△ABC才能和△APQ全等?
认识全等三角形-性质与判定(SAS-ASA)例题与配套习题-精校版

(1)全等三角形对应相等的角所对的边是对应边,两个对应角所夹的边是对应边.
(2)全等三角形对应相等的边所对的角是对应角,两条对应边所夹的角是对应角.
(3)两个全等三角形有公共边的,公共边一定是对应边.
(4)两个全等三角形有公共角的,公共角一定是对应角.
观察下图中的三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?
画一个三角形△ABC,使得∠A=30°,∠B=60°,AB=2cm.
二、同步题型分析
例10.已知:OP是∠MON的平分线,C是OP上一点,CA⊥OM,CB⊥ON,垂足分别是A、B,△AOC与△BOC全等吗?为什么?
例11.如图,O是AB的中点,∠A=∠B,△AOC和△BOD全等吗?
例7.如果把上题图拉开,成如右图所示形状,若要使得它们全等,还需要什么条件?
例8.如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么?
例9.已知:如图,点E、F 在CD上,且CE=D F,AE=BF,AE∥BF.求证:△AEC≌△BFD
例3.如图,△ABC≌△ADE,∠B=30°,∠C=60°,BC=3cm,你能确定△ADE中哪些角的大小,哪些边的长度?
例4.如图,△ABC≌△DEF,B与E、C与F是对应顶点,问进行怎样的图形变换可以使这两个三角形重合?
例5.如图是一个边长为4cm的正方形,需将它分成两个全等的图形,你有几种不同的分法?试一试.
供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
11.2三角形全等的判定(AAS-ASA)练习题及答案

11.2三角形全等的判定(AAS-ASA)◆随堂检测1.如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?2.已知如图,AB=AC,AD=AE,∠BAC=∠DAE,试说明BD=CE。
3.如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC。
试说明AD=CB。
4.如图,已知AC 、BD 相交于点0,∠A=∠B ,∠1=∠2,AD=BC. 试说明△AOD ≌△BOC.◆典例分析例:如图:已知AE 交BC 于点D ,∠1= AB=AD. 求证:DC=BE 。
证明:∵∠ADB=∠1+∠C , ∠ADB=∠3+∠E , 又∵∠1=∠3, ∴∠C=∠E 。
在△ABE 和△ADC 中, ∵∠E =∠C , ∠2 =∠1, AB =AD ,∴ △ABE ≌△ADC (AAS )。
∴DC=BE 。
解析:要证DC=BE,先观察DC 与BE 分别在可能全等的两个三角形中.根据所给条件选择方法◆课下作业●拓展提高5.玻璃三角板摔成三块如图,现在到玻璃店在配一块同样大小的三角板,最省事的方法( )A 、带①去B 、带②去C 、带③去D 、带①②③去6. 如图,有一块边长为4的正方形塑料摸板ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 .7.如图,已知AC 、BD 交于E ,∠A=∠B ,∠1=∠2.求证:AE=BE .8.如图,在△ABC 中,MN ⊥AC ,垂足为N ,,且MN 平分∠AMC ,△ABM 的周长为9cm,AN=2cm,求△ABC 的周长。
9.如图,在△ABC 中,∠B=∠C ,说明AB=ACABCDE10.已知:如图E 在△ABC 的边AC 上,且∠AEB=∠ABC 。
⑴求证:∠ABE=∠C ;⑵若∠BAE 的平分线AF 交BE 于F ,FD ∥BC 交AC 于D ,设AB=5,AC=8,求DC 的长。
小学八年级数学三角形全等的判定习题课教学设计

《三角形全等的判定习题课》教学设计一、关于教学内容和要求的试探本节的要紧内容是:通过判定三角形全等的三种题型温习全等三角形的判定方式,利用题中的已知条件、挖掘“隐含条件”、转化“间接条件”、合理添加“辅助线”来判定三角形全等,充分把握分析问题的方式,使所学的知识能灵活应用到解题当中。
要求慢慢培育学生观看、比较、分析、综合、抽象和归纳的能力,提高学生的空间想象能力和思维能力,这是《数学课程标准》中对中学数学的要求。
本节的课题是《三角形全等的判定习题课》是八年级数学的重点内容之一,在生活中有普遍的应用,同时三种题型中的条件的挖掘、转化与利用也是九年级的重点内容,在八年级学习中适当的安排相应的内容,关于九年级的学习起着渗透的踊跃作用,学会运用条件的直接与间接的利用、转化解决问题策略的思想方式,进展学生的创新意识,增强图形变换的爱好,也巩固了全等的知识。
二、学生情形的分析一、学生已有的知识基础:本节课是在学生已经学习完了全等三角形的判定方式,的基础上进一步来研究的。
二、八年级学生心理生理特点:中学生心理学研究指出:初中时期是智力进展的关键时期,学生逻辑思维从体会型慢慢向理论型进展,观看能力经历力和想象能力也随着迅速进展。
从学生年龄特点来看,初中生好动、好奇、好表现,抓住学生特点,踊跃采纳形象生动,形式多样的教学方式和学生普遍踊跃参与的教学形式,定能激发学生爱好,有效培育学生能力,增进学生个性进展。
生理上,青青年好动,注意力易分散,爱发表观点,希望取得教师的夸奖。
因此在教学中抓住学生的特点,一方面要运用直观形象,激发学生的爱好,使他们的注意力始终集中在课堂上;另一方面要制造条件和机遇,让学生发表观点,发挥学生学习的主动性。
三、学习目标的确信1、熟练把握全等三角形的判定方式。
2、能准确、灵活的运用三角形全等的判定方式解决问题。
3、通过变式练习提高分析问题和解决问题的能力。
训练学生解题的严谨性。
四、学习重、难点的分析重点:利用三角形全等的判定方式正确的解题。
三角形全等的判定习题课

知识回顾:
判断三角形 全等的方法:
1.定义(重合)法; 2.SSS; 3.ASA; 4.SAS; 5.AAS.
三角形全等的条件
• • • • • • (1)必须有三个元素对应相等; (2)至少有一条边相等. 全等的有: SSS,SAS,ASA,AAS. 不全等的有: AAA,SSA.
小试牛刀
1.如图1,若△ABE≌△ACD.且∠B=20°, ∠A=50°, CD=5cm, 则∠ADC= ,BE= . 2.已知:如图2,∠B=∠DEF,BC=EF,补充条件 求证: △ ABC≌ △ DEF. (1) 若要以“SAS”为依据,还缺条件 _____; (2) 若要以“ASA”为依据,还缺条件_____; (3) 若要以“AAS”为依据,还缺条件_____. A D B D O C E 图1 A
E
F
C
三角形全等的条件
例3:已知,如图,D在AB上,E在AC上,AB=AC, ∠B=∠C,求证:AD=AE 证明:在△ACD和△ABE中, A ∠A=∠A AC=AB ∠C= ∠B E D ∴ △ACD≌ △ABE(ASA) ∴ AD=AE C B
三角形全等的条件
例3变式:
已知,如图,D在AB上,E在AC上,AB=AC, ∠B=∠C, 求证:BD=CE A 证明:在△ACD和△ABE中, ∠A=∠A AC=AB ∠C= ∠B E D ∴ △ACD≌ △ABE(ASA) ∴ AE=AD ∴AB-AD=AC-AE C B 即BD=CE
三角形全等的判定
定义
能够完全重合的三角形
全 等 三 角 形
全等三角形对应边相等 性质 全等三角形对应角相等 SSS SAS ASA AAS 注意:AAA,SSA 不能判断一般三 角形全等
2.5 第4课时 全等三角形的判定3——AAS练习题 2021—2022学年湘教版八年级数学上册
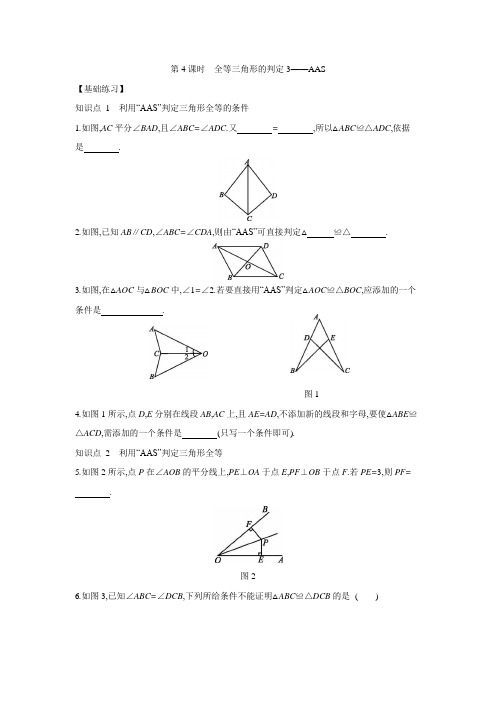
第4课时全等三角形的判定3——AAS【基础练习】知识点1利用“AAS”判定三角形全等的条件1.如图,AC平分∠BAD,且∠ABC=∠ADC.又=,所以△ABC≌△ADC,依据是.2.如图,已知AB∥CD,∠ABC=∠CDA,则由“AAS”可直接判定△≌△.3.如图,在△AOC与△BOC中,∠1=∠2.若要直接用“AAS”判定△AOC≌△BOC,应添加的一个条件是.图14.如图1所示,点D,E分别在线段AB,AC上,且AE=AD,不添加新的线段和字母,要使△ABE≌△ACD,需添加的一个条件是(只写一个条件即可).知识点2利用“AAS”判定三角形全等5.如图2所示,点P在∠AOB的平分线上,PE⊥OA于点E,PF⊥OB于点F.若PE=3,则PF=.图26.如图3,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()图3A.∠A=∠DB.AB=DCC.∠ACB=∠DBCD.AC=BD7.如图4所示,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.图48.[2020·昆明]如图5,AC是∠BAE的平分线,D是线段AC上的一点,∠C=∠E,AB=AD.求证:BC=DE.图59.已知:如图6,∠AOB=90°,OA=OB,直线l经过点O,分别过A,B两点作AC⊥l于点C,BD⊥l于点D.求证:△AOC≌△OBD.图6【能力提升】10.下列条件中,不能证明△ABC≌△DEF的是()A.AC=DF,BC=EF,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠EC.AC=DE,∠A=∠F,∠B=∠ED.AB=DE,∠C=∠F,∠B=∠E11.如图7所示,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段:.图712.如图8,已知∠1=∠2,AD=AE,则图中的全等三角形共有对.(不添加辅助线)图813.如图9,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE=CE.图914.如图10,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.求证:(1)△AEF≌△CEB;(2)AF=2CD.图1015.如图11,∠ABC=90°,AB=BC,D为AC上一点,分别过点A,C作BD的垂线,垂足分别为F,E.求证:EF=CE-AF.图1116.如图12,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=DF.求证:AD=CE.图12答案1.AC AC AAS2.ABC CDA3.∠A=∠B4.答案不唯一,如∠AEB=∠ADC 或∠B=∠C 等5.3 [解析] 由AAS 可证得△POF ≌△POE ,于是有PF=PE=3.6.D7.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC , 即∠BAC=∠EAD.在△ABC 和△AED 中,{∠C =∠D,∠BAC =∠EAD,AB =AE,∴△ABC ≌△AED (AAS). 8.证明:∵AC 是∠BAE 的平分线, ∴∠BAC=∠DAE.在△BAC 和△DAE 中,{∠C =∠E,∠BAC =∠DAE,AB =AD,∴△BAC ≌△DAE (AAS), ∴BC=DE.9.证明:∵∠AOB=90°, ∴∠AOC+∠BOD=90°. ∵AC ⊥l ,BD ⊥l , ∴∠ACO=∠ODB=90°, ∴∠A+∠AOC=90°, ∴∠A=∠BOD.在△AOC 和△OBD 中,{∠ACO =∠ODB,∠A =∠BOD,AO =OB,∴△AOC ≌△OBD (AAS). 10.C11.答案不唯一,如AC=BD 或BC=AD 或OD=OC 或OA=OB 12.2 [解析] ∵∠1=∠2, ∴∠ABE=∠ACD. 在△ABE 和△ACD 中,{∠ABE =∠ACD,∠A =∠A,AE =AD,∴△ABE ≌△ACD (AAS), ∴AB=AC ,∴AD-AB=AE-AC ,即BD=CE. 在△BOD 和△COE 中,{∠1=∠2,∠BOD =∠COE,BD =CE,∴△BOD ≌△COE (AAS). 13.证明:∵FC ∥AB ,∴∠DAE=∠FCE ,∠ADE=∠CFE. 在△ADE 和△CFE 中,{∠ADE =∠CFE,∠DAE =∠FCE,DE =FE,∴△ADE ≌△CFE (AAS), ∴AE=CE.14.证明:(1)∵AD ⊥BC ,CE ⊥AB ,∴∠BCE+∠CFD=90°,∠BCE+∠B=90°, ∴∠CFD=∠B. 又∵∠CFD=∠AFE , ∴∠AFE=∠B. 在△AEF 与△CEB 中,{∠AFE =∠B,∠AEF =∠CEB =90°,AE =CE,∴△AEF ≌△CEB (AAS). (2)∵AB=AC ,AD ⊥BC , ∴BC=2CD.由(1)知△AEF ≌△CEB , ∴AF=BC ,∴AF=2CD.15.证明:由题意知∠ABC=∠F=∠BEC=90°, ∴∠CBE+∠ABF=∠BAF+∠ABF=90°, ∴∠CBE=∠BAF. 在△ABF 和△BCE 中,{∠F =∠BEC,∠BAF =∠CBE,AB =BC,∴△ABF ≌△BCE (AAS), ∴AF=BE ,BF=CE. ∵BE+EF=BF , ∴EF=BF-BE=CE-AF.16.证明:如图,过点D 作DG ∥BC 交AC 于点G , 则∠DGF=∠ECF. 在△DFG 和△EFC 中,{∠DGF =∠ECF,∠DFG =∠EFC,DF =EF,∴△DFG ≌△EFC (AAS), ∴GD=CE.∵△ABC 是等边三角形, ∴∠A=∠B=∠ACB=60°. ∵DG ∥BC ,∴∠ADG=∠B ,∠AGD=∠ACB , ∴∠A=∠ADG=∠AGD=60°, ∴△ADG 是等边三角形, ∴AD=GD , ∴AD=CE.。
全等三角形的性质与判定 习题课

∠CAD.
∴△ABE≌△ACD(SAS).
(2)求证:DC⊥BE. (2)证明:由(1)知△ABE≌△ACD, ∴∠ACD=∠B=45°. 又∵∠ACB=45°, ∴∠BCD=∠ACB+∠ACD=90° .∴DC⊥BE.
9.如图,在Rt△ABC中,∠BAC=90°,点D、E在边BC上
,∠CAE=∠B,E是CD的中点,且AD平分∠BAE,试问
5.如图,点C,F在线段BE上,BF=EC,∠1=∠2.请你添
加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅
助线和字母)
答案不唯一,可以是∠E=∠B,∠D=∠A,FD=CA, AB∥ED 等. 以 DF=AC 加以证明.∵BF=EC, ∴BF-CF=EC-CF,即 BC=EF.
BC=EF, 在△ABC 和△DEF 中,∠1=∠2, CA=FD,
所以△AMN≌△CMN(ASA). 所以 AN=NC,AM=CM. 因为 AN=2 cm,所以 AC=2AN=4 cm. 又因为△ABM 的周长为 9 cm, 所以△ABC 的周长为 9+4=13(cm).
7.如图所示,要测量湖中小岛E距岸边A和D的距离,作
法如下:(1)任作线段AB,取中点O;(2)连接DO并延长使 DO=CO;(3)连接BC;(4)用仪器测量E,O在一条线上, 并交CB于点F,要测量AE,DE,只需测 量BF,CF即可,为什么? 由条件可知,△AOD≌△BOC,∴BC=AD. 又 ∠A = ∠B , ∠ AOE = ∠BOF , AO = BO , 故 △AOE≌△BOF.
∴△CBG≌△FEH(AAS). ∴CG=FH AC=DF, .在 Rt△ACG 和 Rt△DFH 中, CG=FH, ∴Rt△ACG≌Rt△DFH(HL). ∴∠A=∠D. ∠ABC=∠DEF, 在△ABC 和△DEF 中,∠A=∠D, AC=DF, ∴△ABC≌△DEF(AAS).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8分
2.如图,AC和BD相交于点O,AB=DC,∠A=∠D, (1)请写出符合条件的五个结论(对顶角除 外,且不添加辅助线) (2)从你写出的五个结论中任选一个说明你 的理由.
A
4分
D
C
E 思路:
已知两角: 找夹边 AB=AE (ASA)
找一角的对边
AC=AD 或DE=BC (AAS)
5.如图,AM=AN, BM=BN 请说明△AMB≌△ANB的理由 解:在△AMB和△ANB中 AN ____) 已知 AM _______(__ BM _______ BN (已知) _______ _________( AB 公共边) AB
1、①全等三角形的概念:
能完全重合的两个三角形叫做全等三角形。
②全等三角形的特征: 全等三角形的对应边相等,对应角相等。
4分
2、三角形全等的条件:
4分
三边 ①_________对应相等的两个三角形全等(简写成 “边边边”或“SSS”); 它们的夹边 ②两角和__________________对应相等的两个三 ASA 角边角 角形全等.(简写成__________或“_________”) 其中一个角的对边 ③ 两角和__________________对应相等的两个三 角形全等.(简写成________或“ASA”) 角角边 它们的的夹角 ④ 两边和_______________对应相等的两个三角 SAS 形全等(简写成“边角边”或“________”);
4分
2 1 3
5.在下列说法中,正确的有( B )个.并说明 判断的理由。 ①三角对应相等的两个三角形全等 ②三边对应相等的两个三角形全等 ③两角、一边对应相等的两个三角形全等 ④两边、一角对应相等的两个三角形全等 A.1 B.2 C.3 D.4
4分
1 2 3 4 5
1.如图,已知△ABC和△DCB中,AB=DC,请补 充一个条件 ,使△ABC≌ △DCB.
A D C 找夹角 找第三边 ∠ABC=∠DCB (SAS) AC=DB (SSS)
4分
B
思路: 已知两边:
2.如图,已知∠C=∠D,要识别△ABC≌△ABD, 需要添加的一个条件是 .
C
4分
A B D
思路
已知一边一角 (边与角相对)
∠CAB=∠DAB (AAS) 找任一角 或者 ∠CBA=∠DBA
A D
4分
M B N C
5.如图,AB=AC,∠B=∠C,你能证明 △ABD≌△ACE吗? A
E
证明:在△ABD≌△ACE中 ∠A=∠A, ∵ AB=AC, ∠B=∠C, ∴△ABD≌△ACE(ASA).
D
C
B
4分
1 2 3
1.已知:如图,BD=CD,∠ABD=∠ACD, DE、DF分别垂直于AB及AC交延长线于E、 F. 求证:DE=DF.
A O
D
10分
CBຫໍສະໝຸດ 解: (1)答:符合上述条件的五个结论为: △AOB≌△DOC,OA=OD,OB=OC, ∠ABO=∠DCO,∠OBC=∠OCB. (2) 证明如下: ∵AB=DC,∠A=∠D, 又有∠AOB=∠DOC ∴△AOB≌△DOC ∴OA=OD,OB=OC,∠ABO=∠DCO ∵OB=OC ∴∠OBC=∠OCB.
3.若△ABD≌△ACD,对应边是 对应角是 . A
AB和AC,AD和AD,BD和CD ∠ABD和∠ ACD, ∠ ADB和 ∠ ADC, ∠ BAD和∠ CAD
B
,
D
C
4分
4.如图,某同学把一块三角形的玻璃打碎成了 三块,现在要到玻璃店去配一块完全一样的玻 璃,那么最省事的方法是( C ),并说明理由。 A.带①去 B.带②去 C.带③去 D.带①和③去
2.如图, 已知AB=AD,∠BAE=∠DAC,要使 △ABC≌△ADE,可补充的条件是 _____________________(写出一个即可).
解:可补充的条件是: 当AC=AE,△ABC≌△ADE (SAS); 当∠C=∠E,△ABC≌△ADE (AAS); 当∠B=∠D,△ABC≌△ADE (ASA). 故答案为:AC=AE或∠C=∠E或 ∠B=∠D.
∴△ABM ≌
N B A
M
△ABN
(
SSS
)
4分
1.如图, 已知直线AD, BC交于点E, 且AE=BE, 欲说明△AEC≌△BED,需增加的条件可以 是______________________(只填一个即可).
4分
解: 根据“SAS”, 可添加CE=DE; 根据 “ASA”,可添加∠A=∠B; 根据“AAS”, 可添 加∠C=∠D. 故填CE=DE或∠A=∠B或∠C=∠D.
题目设置: 竞赛题由一、必答题;二、选答题;三、共答题; 四、抢答题四部分组成。 规则:共18道题。 1、必答题:每组必须完成此题,答对加分。答错 不加分,但此题分数由答对题组平分。 2、选答题:每组必须完成此题,答对加分,答错 不加分,但此题分数由答对题组平分。 3、共答题:各组共答一题,答错不加分,但此题 分数分别加给答对此题的组。 4、抢答题:此题采用抢答方式进行,优先抢到题 者优先作答。答对加分,答错扣分,扣除的分数 分别加给答对此题的组。
3.如图,已知∠1=∠2,要识别△ABC≌△CDA, 需要添加的一个条件是 .
D
2 1
C
4分
A 思路:
B 已知一边一角 (边与角相邻): AD=CB (SAS) ∠ACD=∠CAB (ASA)
找夹这个角的另一边
找夹这条边的另一角 找边的对角
∠D=∠B (AAS)
4.如图,已知∠B=∠E,要识别△ABC≌ △AED,需要添加的一个条件是 .
4分
3.如图,已知AC⊥BD于点P,AP=CP,请增 加一个条件,使△ABP≌△CDP (不能添加 辅助线),你增加的条件是 .
A B
4分
P D C
解:添加的条件为BP=DP或AB=CD或 ∠A=∠C或∠B=∠D或AB//CD.
4.如图,沿AM折叠,使D点落在BC上的N点 处,如果AD=7cm, DM=5cm,∠DAM=300,则 7 cm, NM=___cm, ∠NAM= 300 . AN= 5
3.已知:如图,AB=AE,AC=AD , BC=DE,
C , D在BE边上.
求证:∠CAE=∠DAB.
8分
3.证明:∵AB=AC, ∴∠ABC=∠ACB. ∴∠ABD=∠ACE. ∵CD=BE,CD=DB+BC, BE=CE+BC, ∴DB=CE. ∵AB=AC,∠ABD=∠ACE,DB=CE, ∴△ABD≌△ACE. ∴AD=AE.
