全等三角形判定练习题A4
全等三角形证明题专项练习题Word版

证明三角形全等专项练习姓名 号数1.如图,已知△ABC 为等边三角形,点D 、E 分别在BC 、AC 边上,且AE=CD ,AD 与BE 相交于点F . (1)求证:ABE ≌△CAD ; (2)求∠BFD 的度数.2.如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE .3.如图,在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M .(1)求证:△ABC≌△DCB ;(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN的数量关系,并证明你的结论.OCEBDAB CA DMN4.在⊿ABC 中,∠ACB 的平分线交AB 于E ,过E 点作BC 的平行线交AC 于F ,交外角∠ACD 的平分线于G 。
求证:F 为EG 的中点。
5.在⊿ABC 中,∠B =60。
,∠BAC 和∠BCA 的平分线AD 和CF 交于I 点。
试猜想:AF 、CD 、AC 三条线段之间有着怎样的数量关系,并加以证明。
6.在直角⊿ABC 中,CA =CB ,BD 为AC 上的中线,作∠ADF =∠CDB ,如图,连结CF 交BD于E ,求证:CF ⊥BD 。
(提示:作AC 的中线CO )GOEFDBCA7、以⊿ABC 的边AB 、AC 为边向形外作等边⊿ABM 、⊿CAN ,BN 和CM 交于一点P 。
试判断:第5题 第6题∠APM 、∠APN 的大小关系,并加以证明。
8. 在∆ABC 中,AB=AC ,DE∥BC.(1)试问∆ADE 是否是等腰三角形,说明理由.(2)若M 为DE 上的点,且BM 平分ABC ∠,CM 平分ACB ∠,若ADE ∆的周长20,BC=8.求ABC ∆的周长.9. 如图, 已知: 等腰Rt △OAB 中,∠AOB=900, 等腰Rt △EOF 中,∠EOF=900, 连结AE 、BF. 求证:(1) AE=BF; (2) AE ⊥BF.10. 如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于点F ,交AC 的平行线BG于点G ,DE ⊥GF 交AB 于点E ,连接EG 。
全等三角形经典题型50题(含答案)

全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延伸 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连结 BF 和 EF。
由于 BC=ED,CF=DF,∠ BCF=∠ EDF。
因此三角形 BCF 全等于三角形 EDF(边角边 )。
因此 BF=EF,∠ CBF=∠ DEF。
连结 BE。
在三角形BEF 中 ,BF=EF。
因此∠ EBF=∠ BEF。
又由于∠ ABC=∠AED。
因此∠ABE=∠AEB。
因此 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
因此三角形 ABF 和三角形 AEF全等。
因此∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延伸线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD均分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连结(SASED∵ AD)均分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 均分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连结 CF 由于 CE⊥AB 因此∠CEB=∠ CEF= 90 °由于 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 由于∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°因此∠ D=∠ CFA 由于AC 均分∠ BAD 因此∠ DAC=∠ FAC 又由于AC= AC因此△ ADC≌ △ AFC( SAS)因此 AD= AF 因此 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别均分∠ ABC、∠ BCD,且点 E 在 AD 上。
(完整版)全等三角形判定综合练习题
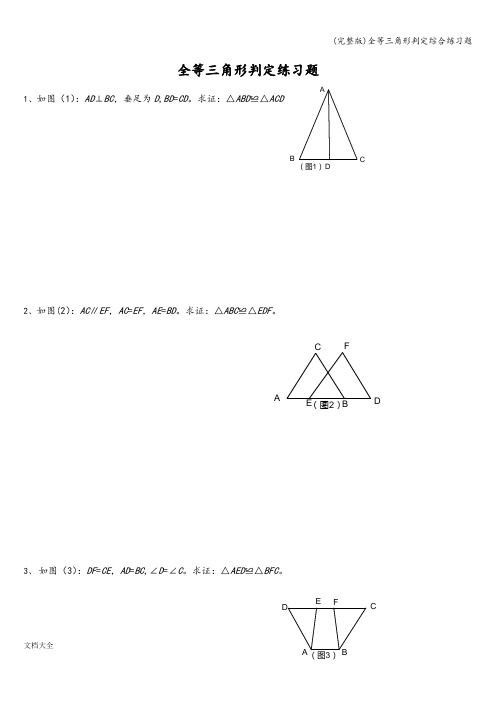
全等三角形判定练习题1、如图(1):AD ⊥BC ,垂足为D ,BD =CD 。
求证:△ABD ≌△ACD2、如图(2):AC ∥EF ,AC =EF ,AE =BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF =CE ,AD =BC ,∠D =∠C 。
求证:△AED ≌△BFC 。
FE (图2)DCBAFEDC(图1)DCBA4、 如图(4):AB =AC ,AD =AE ,AB ⊥AC ,AD ⊥AE .求证:(1)∠B =∠C ,(2)BD =CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE 。
求证:AC ⊥CE 。
E(图4)DCBAE(图5)DCBA6、如图(6):CG =CF ,BC =DC ,AB =ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF =EG ,(2)BF ∥DG .7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN =BC 。
求证:(1)MN 平分∠AMB ,(2)∠A =∠CBM 。
GFE(图6)DC BANM(图7)CBA8、如图(8):A 、B 、C 、D 四点在同一直线上,AC =DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE =CF 。
求证:AM 是△ABC 的中线。
FE(图8)DC B AMFE(图9)CBA10、如图(10)∠BAC =∠DAE ,∠ABD =∠ACE ,BD =CE . 求证:AB =AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA =PD .12、如图(12)AB ∥CD ,OA =OD ,点F 、D 、O 、A 、E 在同一直线上,AE =DF . 求证:EB ∥CF 。
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
全等三角形经典题型50题(含问题详解)

全等三角形经典题型50题(含问题详解)全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<ae<ad<2ad2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF 。
所以三角形BCF 全等于三角形EDF(边角边)。
所以BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以∠EBF=∠BEF 。
又因为∠ABC=∠AED 。
所以∠ABE=∠AEB 。
所以AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以三角形ABF 和三角形AEF 全等。
所以∠BAF=∠EAF (∠1=∠2)。
ADC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE ,所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS )所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
难点突破——三角形全等证明题练习50道(含详细解析)
难点突破——三角形全等证明题练习50道(含详细解析)1.如图所示,90A D ∠=∠=︒,AB DC =,AC ,BD 相交于点M ,求证:(1)ABC DCB ∠=∠;(2)AM DM =.2.如图,点C ,F ,B ,E 在同一条直线上,AC CE ⊥,DF CE ⊥,垂足分别为C ,F ,且AB DE =,CF BE =.求证:A D ∠=∠.3.如图,ABC ∆中,AD 是BC 边上的中线,E ,F 为直线AD 上的点,连接BE ,CF ,且//BE CF .(1)求证:DE DF =;(2)若在原有条件基础上再添加AB AC =,你还能得出什么结论.(不用证明)(写2个)4.如图,AB AC =,//CD AB ,点E 是AC 上一点,且ABE CAD ∠=∠,延长BE 交AD 于点F .(1)求证:ABE CAD ∆≅∆;(2)如果65ABC ∠=︒,25ABE ∠=︒,求D ∠的度数.5.如图,已知D 为BC 的中点,DE AB ⊥,DF AC ⊥,点E 、F 为垂足,且BE CF =.求证:ABC ∆是等腰三角形.6.已知:如图,AB AE =,C F ∠=∠,EAC BAF ∠=∠.求证:AC AF =.7.如图所示,AB AD =,12∠=∠,添加一个适当的条件,使ABC ADE ∆≅∆(不再添加其它线段,不再标注或使用其他字母).8.如图,BE ,AD 是ABC ∆的高且相交于点P ,点Q 是BE 延长线上的一点.(1)试说明:12∠=∠;(2)若AP BC =,BQ AC =,线段CP 与CQ 会相等吗?请说明理由.9.如图,AB CD =,DE AC ⊥,BF AC ⊥,点E ,F 是垂足,AE CF =,求证:(1)ABF CDE ∆≅∆;(2)//AB CD .10.如图,点C 在线段AB 上,//AD EB ,AC BE =,AD BC =,CF 平分DCE ∠. 求证:CF DE ⊥于点F .11.如图:已知在ABC ∆中,90ACB ∠=︒,1AC BC ==,点D 是AB 上任意一点,AE AB ⊥,且AE BD =,DE 与AC 相交于点F .(1)试判断CDE ∆的形状,并说明理由.(2)是否存在点D ,使AE AF =?如果存在,求出此时AD 的长,如果不存在,请说明理由.12.如图,在ABC ∆中,AB AC =,BD AC ⊥⊥于D ,CE AB ⊥于E .求证:AD AE =.13.如图,点A ,B ,C ,D 在一条直线上,且AC BD =,若12∠=∠,EC FB =. 求证:ACE DBF ∆≅∆.证明:14.已知:如图,点E 是ABC ∆外角CAF ∠平分线上的一点.(1)比大小:BE EC + A B A C+(填“>”、“ <”或“=” ) (2)证明(1)中的结论.15.如图,在ABC ∆中,BD 是边AC 上的中线,BD BC ⊥于点B ,AE BD ⊥交BD 的延长线于点E ,30ABD ∠=︒,求证:2AB BC =.16.如图所示,两个形状相同,大小不同的等腰三角形ABC 与ADE 如图放置,A 为它们共同的顶角顶点,B 、C 、D 在同一条直线上,连接CE .(1)你能在图中找到一对全等三角形吗?证明你的结论;(2)若35BAC ∠=︒,求ECD ∠的度数.17.已知,如图,直线AB BC ⊥,线段AB BC <,点D 在直线AB 上,且AD BC =,AE AB ⊥,且AE BD =,连接DE 、DC ,ADE α∠=.(1)请在下图中补全图形,并写出CDE ∠的度数 (用含α的代数式表示);(2)如图,当点D 在点B 下方,点F 在线段BC 的延长线上,且BD CF =,直线AF 与DC交于点P,试问APD∠的度数是否是定值?若是定值,求出并说明理由.18.已知等腰三角形ABC中,点D为BC中点,点E是BA延长线上一动点,点F是AC延长线上一动点连接DE、DF,且180∠+∠=︒.EDF BAC(1)如图1,若90+=;BAC∠=︒,求证:AE AC AF(2)如图2,若120∠=︒,AE、AC、AF三条线段还满足(1)中的结论吗?若满足,BAC则直接证明;若不满足,请写出结论并证明.19.已知D为ABC⊥,垂足分别为点∆所在平面内一点,且DB DC=,DE AB⊥,DF ACE、F,DE DF=.(1)如图1,当点D在BC边上时,判断ABC∆的形状;并证明你的结论;(2)如图2,当点D在ABC∆内部时,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请举出反例(画图说明,不需证明).20.如图,在Rt ABC∠=︒,点P为AC边上的一点,延长BP至点D,使得AD APC∆中,90=,当AD AB⊥于E.⊥时,过点D作DE AC(1)求证:CBP ABP∠=∠;(2)若4AB BC -=,8AC =.求AB 的长度和DE 的长度.21.如图(1),8A B c m =,AC AB ⊥,BD AB ⊥,6AC BD cm ==.点P 在线段AB 上以2/m s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.它们运动的时间为()t s(1)若点Q 的运动速度与点P 的运动速度相等,当1t =时,判断线段PC 与PQ 满足的关系,并说明理由.(2)如图(2),将图(1)中的AC AB ⊥,BD AB ⊥为改“CAB DBA a ∠=∠=︒”,其它条件不变.设点Q 的运动速度为/xcm s ,是否存在实数x ,使得ACP ∆与BPQ ∆全等?若存在,求出相应的x 、t 的值;若不存在,请说明理由.22.如图,AD AC =,1239∠=∠=︒,C D ∠=∠,点E 在线段BC 上.(1)求证:ABC AED ∆≅∆.(2)求AEC ∠的度数.23.已知:如图,点A 、D 、C 、B 在同一条直线上,AD BC =,AE BF =,//AE FB ,求证://CE DF .24.如图,点D 在ABC ∆外部,点C 在DE 边上,BC 与AD 交于点O ,若123∠=∠=∠,AC AE =.求证:(1)B D ∠=∠;(2)ABC ADE ∆≅∆.25.已知:如图,AB AC =,AE AF =,连结BF ,CE ,交于O ,连结AO .求证:(1)B C ∠=∠;(2)AO 平分BAC ∠.26.如图所示,已知ABC ∆中AB AC =,E 、D 、F 分别在AB ,BC 和AC 边上,且BE CD =,BD CF =,过D 作DG EF ⊥于G . 求证:12EG EF =.27.已知在ABC ∆中,AC BC =,分别过A ,B 两点作互相平行的直线AM ,BN ,过点C 的直线分别交直线AM ,BN 于点D ,E .(1)如图1,若AM AB ⊥,求证:CD CE =;(2)如图2,60ABC DEB ∠=∠=︒,判断线段AD ,DC 与BE 之间的关系,并说明理由.28.阅读下列材料,并完成任务.如图,四边形ABCD是一个筝形,其中AB AD=.对角线AC,BD相交于点O,=,BC CD过点O作0M AB⊥,垂足分别为M,N.⊥,ON AD求证:四边形AMON是筝形.29.如图,在ABC∠=∠,AC与BD交于点=,AED∆中AB AC∆中AE AD=,EAD BACO.(1)试确定ADC∠与AEB∠间的数量关系,并说明理由;(2)若65∠的度数.ACB∠=︒,求BDC30.如图,AD为ABC=.求=,FD CD ∆的高,E为AC上一点,BE交AD于F,且有BF AC证:(1)BFD ACD ∆≅∆;(2)BE AC ⊥.31.在等腰OAB ∆和等腰OCD ∆中,OA OB =,OC OD =,连接AC 、BD 交于点M .(1)如图1,若40:AOB COD ∠=∠=︒①AC 与BD 的数量关系为 ;②AMB ∠的度数为 .(2)如图2,若90:AOB COD ∠=∠=︒①判断AC 与BD 之间存在怎样的数量关系?并说明理由; ②求AMB ∠的度数.32.如图,点B 、F 、C 、E 在同一直线上,AC 、DF 相交于点G ,AB BE ⊥,垂足为B ,DE BE ⊥,垂足为E ,且AC DF =,BF CE =.(1)求证:ABC DEF ∆≅∆;(2)若65A ∠=︒,求AGF ∠的度数.33.如图,在ABC ∆中,B C ∠=∠,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE CF =,AD EC AB +=.(1)求证:DE EF =.(2)当36A ∠=︒时,求DEF ∠的度数.34.在ABC ∆中,45ACB ∠=︒,AD BC ⊥垂足为D ,点E 在AD 上,ED BD =,连接CE 并延长交AB 于点F ,连接DF .(1)求证:BAD ECD ∠=∠.(2)求证:45DFE ∠=︒.35.如图,在ABC ∆和BAD ∆中,AC 与BD 相交于点E ,AD BC =,DAB CBA ∠=∠,求证:12∠=∠.36.如图所示,AB AC =,AD AE =,BAC DAE ∠=∠,122∠=︒,228∠=︒, 求3∠的度数.37.如图,在直角坐标系中有一点(5,5)P ,(0,)M m 为y 轴上任意一点,N 为x 轴上任意一点,且90MPN ∠=︒.(1)当5m =时,OM ON +的值为 ;(2)当05m <<时,OM ON +的值是否改变?说明你的理由;(3)探索:当0m <时,OM 与ON 的数量关系为 .38.已知,如图,射线BD 平分锐角ABC ∠,且平分钝角ADC ∠,求证:CD AD =.39.如图所示,BF AC ⊥于点F ,CE AB ⊥于点E ,BF 与CE 交于D ,且BD CD =. 求证:D 在BAC ∠的平分线上.40.如图(1),7A B c m =,AC AB ⊥,BD AB ⊥垂足分别为A 、B ,5AC cm =.点P 在线段AB 上以2/cm s 的速度由点A 向点B 运动,同时,点Q 在射线BD 上运动.它们运动的时间为()t s (当点P 运动结束时,点Q 运动随之结束).(1)若点Q 的运动速度与点P 的运动速度相等,当1t =时,ACP ∆与BPQ ∆是否全等,并判断此时线段PC 和线段PQ 的位置关系,请分别说明理由;(2)如图(2),若“AC AB ⊥,BD AB ⊥”改为“60CAB DBA ∠=∠=︒”,点Q 的运动速度为/xcm s ,其他条件不变,当点P 、Q 运动到某处时,有ACP ∆与BPQ ∆全等,求出相应的x 、t 的值.41.如图,在ABC∠,CE平分BCA∠,AD、CE交于点F,B∆中,60∠=︒,AD平分BAC=,连结FG.CD CG(1)求证:FD FG=;(2)线段FG与FE之间有怎样的数量关系,请说明理由;(3)若60B∠≠︒,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.42.已知BF平分ABC∆的外角ABE∠,D为射线BF上一动点.(1)如图所示,若DA DC∠=∠;=,求证:ABC ADC(2)在D点运动的过程中,试比较BA BC+的大小,并说明你的理由.+与DC DA43.如图,在ABC=,∠=︒,BD AC⊥于点D,点E在DB的延长线上,DE BCABC∆中,90=.12∠=∠,求证:DF AB44.如图,在ABC ∆和ADE ∆中,点E 在BC 边上,BAC DAE ∠=∠,B D ∠=∠,AB AD =.求证:AEC C ∠=∠.45.如图,AB AC =,E 、D 分别是AB 、AC 的中点,AF BD ⊥,垂足为点F ,AG CE ⊥,垂足为点G ,试判断AF 与AG 的数量关系,并说明理由.46.如图,90ACB ∠=,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D 、E .(1)求证:ACD CBE ∆≅∆;(2)已知5AD =,3DE =,求BE 的长.47.如图,AE 、BD 是ABM ∆的高,AE ,BD 交于点C ,且A E B E =,BD 平分ABM ∠.(1)求证:2BC AD =;(2)求M DE ∠的度数.48.在ABC∠交AB于D,E,F在AC,BC∠=︒,CD平分ACBA∆中,AB AC=,36上,且108∠=︒.EDF(1)求ADC∠的度数;(2)求证:AE BF BC+=.49.已知:如图,90∠的角平分线上,且点A到点⊥于点E,点A在FOCF∠=︒,AE OC=.B、点C的距离相等.求证:BF EC50.已知:如图,点C、D、B、F在一条直线上,且AB BD=,⊥,AB CD⊥,DE BD =.CE AF求证:(1)ABF CDE∆≅∆;(2)CE AF⊥.难点突破——三角形全等证明题练习50道(含详细解析)参考答案与试题解析一.解答题(共50小题)1.如图所示,90A D ∠=∠=︒,AB DC =,AC ,BD 相交于点M ,求证:(1)ABC DCB ∠=∠;(2)AM DM =.【解答】证明:(1)90A D ∠=∠=︒,ABC ∴∆和DCB ∆都是直角三角形.在Rt ABC ∆和Rt DCB ∆中,BC CB AB DC =⎧⎨=⎩, Rt ABC Rt DCB(HL)∴∆≅∆,ABC DCB ∴∠=∠;(2)Rt ABC Rt DCB ∆≅∆,AC DB ∴=,ACB DBC ∠=∠,MC MB ∴=,AM DM ∴=.2.如图,点C ,F ,B ,E 在同一条直线上,AC CE ⊥,DF CE ⊥,垂足分别为C ,F ,且AB DE =,CF BE =.求证:A D ∠=∠.【解答】证明:AC CE ⊥,DF CE ⊥,90C DFE ∴∠=∠=︒,CF BE =,CB FE ∴=,AB DE =,Rt ACB Rt DFE(HL)∴∆≅∆,A D ∴∠=∠.3.如图,ABC ∆中,AD 是BC 边上的中线,E ,F 为直线AD 上的点,连接BE ,CF ,且//BE CF .(1)求证:DE DF =;(2)若在原有条件基础上再添加AB AC =,你还能得出什么结论.(不用证明)(写2个)【解答】(1)证明:AD 是ABC ∆的中线, BD CD ∴=,//BE CF ,FCD EBD ∴∠=∠,DFC DEB ∠=∠,在CDE ∆和BDF ∆中,FCD EBD DFC DEB CD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()CDF BDE AAS ∴∆≅∆,DE DF ∴=(2)可以得出AD BC ⊥,BAD CAD ∠=∠.(理由等腰三角形三线合一).4.如图,AB AC =,//CD AB ,点E 是AC 上一点,且ABE CAD ∠=∠,延长BE 交AD 于点F .(1)求证:ABE CAD ∆≅∆;(2)如果65ABC ∠=︒,25ABE ∠=︒,求D ∠的度数.【解答】(1)证明://CD AB ,BAE ACD ∴∠=∠,ABE CAD ∠=∠,AB AC =,()ABE CAD ASA ∴∆≅∆;(2)解:AB AC =,65ABC ACB ∴∠=∠=︒,180180656550BAC ABC ACB ∴∠=︒-∠-∠=︒-︒-︒=︒, 又25ABE CAD ∠=∠=︒,502575BAD BAC CAD ∴∠=∠+∠=︒+︒=︒, //AB CD ,180********D BAD ∴∠=︒-∠=︒-︒=︒.5.如图,已知D 为BC 的中点,DE AB ⊥,DF AC ⊥,点E 、F 为垂足,且BE CF =.求证:ABC ∆是等腰三角形.【解答】证明:D 为BC 的中点,BD CD ∴=,DE AB ⊥,DF AC ⊥,90BED CFD ∴∠=∠=︒,在Rt BED ∆和Rt CFD ∆中,BD CD BE CF =⎧⎨=⎩,Rt BED Rt CFD(HL)∴∆≅∆, B C ∴∠=∠,AB AC ∴=,ABC ∴∆是等腰三角形.6.已知:如图,AB AE =,C F ∠=∠,EAC BAF ∠=∠.求证:AC AF =.【解答】证明:EAC BAF ∠=∠, BAC EAF ∴∠=∠,在ABC ∆和AEF ∆中,BAC EAF C F AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABC AEF AAS ∴∆≅∆,AC AF ∴=.7.如图所示,AB AD =,12∠=∠,添加一个适当的条件,使ABC ADE ∆≅∆(不再添加其它线段,不再标注或使用其他字母).【解答】解:条件为AC AE =,理由是: 12∠=∠,12DAC DAC ∴∠+∠=∠+∠, BAC DAE ∴∠=∠,在ABC ∆和ADE ∆中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩()ABC ADE SAS ∴∆≅∆.8.如图,BE ,AD 是ABC ∆的高且相交于点P ,点Q 是BE 延长线上的一点.(1)试说明:12∠=∠;(2)若AP BC =,BQ AC =,线段CP 与CQ 会相等吗?请说明理由.【解答】证明:(1)BE ,AD 是ABC ∆的高 190BCA ∴∠+∠=︒,290BCA ∠+=︒, 12∴∠=∠,(2)AP BC =,12∠=∠,BQ AC =, ()APC BCQ SAS ∴∆≅∆CP CQ ∴=.9.如图,AB CD =,DE AC ⊥,BF AC ⊥,点E ,F 是垂足,AE CF =,求证:(1)ABF CDE ∆≅∆;(2)//AB CD .【解答】证明:(1)AE CF =, AE EF CF EF ∴+=+,即AF CE =. 又BF AC ⊥,DE AC ⊥, 90AFB CED ∴∠=∠=︒.在Rt ABF ∆与Rt CDE ∆中,AB CD AF CE =⎧⎨=⎩, Rt ABF Rt CDE(HL)∴∆≅∆;(2)Rt ABF Rt CDE ∆≅∆, C A ∴∠=∠,//AB CD ∴.10.如图,点C 在线段AB 上,//AD EB ,AC BE =,AD BC =,CF 平分DCE ∠. 求证:CF DE ⊥于点F .【解答】证明://AD BE , A B ∴∠=∠,在ACD ∆和BEC ∆中AD BC A B AC BE =⎧⎪∠=∠⎨⎪=⎩,()ACD BEC SAS ∴∆≅∆, DC CE ∴=, CF 平分DCE ∠,CF DE ∴⊥.11.如图:已知在ABC ∆中,90ACB ∠=︒,1AC BC ==,点D 是AB 上任意一点,AE AB ⊥,且AE BD =,DE 与AC 相交于点F .(1)试判断CDE ∆的形状,并说明理由.(2)是否存在点D ,使AE AF =?如果存在,求出此时AD 的长,如果不存在,请说明理由.【解答】解:(1)CDE ∆是等腰直角三角形.理由如下: 90ACB ∠=︒,AC BC =, 45B BAC ∴∠=∠=︒,AE AB ⊥,904545CAE ∴∠=︒-︒=︒,B CAE ∴∠=∠,在ACE ∆和BCD ∆中,AE BDB CAE AC BC=⎧⎪∠=∠⎨⎪=⎩,()ACE BCD SAS ∴∆≅∆,CD CE ∴=,ACE BCD ∠=∠,90ACD BCD ACB ∠+∠=∠=︒,90DCE ACD ACE ∴∠=∠+∠=︒,CDE ∴∆是等腰直角三角形;(2)存在1AD =.理由如下:AE AF =,45CAE ∠=︒,1(18045)67.52AEF AFE ∴∠=∠=︒-︒=︒,9067.522.5ADE ∴∠=︒-︒=︒,CDE ∆是等腰直角三角形,45CDE ∴∠=︒,22.54567.5ADC ∴∠=︒+︒=︒,在ACD ∆中,1804567.567.5ACD ∠=︒-︒-︒=︒, ACD ADC ∴∠=∠,1AD AC ∴==.12.如图,在ABC ∆中,AB AC =,BD AC ⊥⊥于D ,CE AB ⊥于E .求证:AD AE =.【解答】证明:AB AC =,ABC ACB ∴∠=∠,BD AC ⊥,CE AB ⊥,90BDC CEB ∴∠=∠=︒,在BCE ∆和CBD ∆中,BEC CDB EBC DCB BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()DBC ECB AAS ∴∆≅∆,CD BE ∴=,AB AC =,AD AE ∴=.13.如图,点A ,B ,C ,D 在一条直线上,且AC BD =,若12∠=∠,EC FB =. 求证:ACE DBF ∆≅∆.证明: 12∠=∠,FBD ECA ∴∠=∠,FB CE =,BD AC =,()DBF ACE SAS ∴∆≅∆.【解答】证明:12∠=∠,FBD ECA ∴∠=∠,FB CE =,BD AC =,()DBF ACE SAS ∴∆≅∆.故答案为:12∠=∠,FBD ECA ∴∠=∠,FB CE =,BD AC =,()DBF ACE SAS ∴∆≅∆.14.已知:如图,点E 是ABC ∆外角CAF ∠平分线上的一点.(1)比大小:BE EC+(填“>”、“<”或“=”)+>AB AC(2)证明(1)中的结论.【解答】解:(1)结论:BE EC AB AC+>+.故答案为>.(2)理由:在AF上截取AH,使得AH AC=.AC AE∠=∠,AE AE=,CAF HAE=,∴∆≅∆,EAC EAH SAS()∴=,EC EH+>,EB EH BH∴+>+.EB EC AB AC15.如图,在ABC⊥于点B,AE BD∆中,BD是边AC上的中线,BD BC⊥交BD的延长线于点E,30=.AB BCABD∠=︒,求证:2【解答】证明:BD是AC上的中线,∴=,AD DCBD BC⊥,AE BD⊥,EBC AEB∴∠=∠=︒,90又ADE CDB∠=∠,∴∆≅∆,ADE CDB AAS()AE CB ∴=,90AEB ∠=︒,30ABD ∠=︒,2AE AB ∴=,即2AB BC =.16.如图所示,两个形状相同,大小不同的等腰三角形ABC 与ADE 如图放置,A 为它们共同的顶角顶点,B 、C 、D 在同一条直线上,连接CE .(1)你能在图中找到一对全等三角形吗?证明你的结论;(2)若35BAC ∠=︒,求ECD ∠的度数.【解答】解:(1)能,ABD ACE ∆≅∆,理由如下: ABC ∆和ADE ∆是两个形状相同,大小不同的等腰三角形, BAC DAE ∴∠=∠,AB AC =,AD AE =,BAD CAE ∴∠=∠,在BAD ∆和CAE ∆中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴∆≅∆;(2)ABD ACE ∆≅∆,B ACE ∴∠=∠,ACE ECD B BAC ∠+∠=∠+∠,35ECD BAC ∴∠=∠=︒.17.已知,如图,直线AB BC ⊥,线段AB BC <,点D 在直线AB 上,且AD BC =,AE AB ⊥,且AE BD =,连接DE 、DC ,ADE α∠=.(1)请在下图中补全图形,并写出CDE ∠的度数 290α-︒或902α︒-或90︒ (用含α的代数式表示);(2)如图,当点D 在点B 下方,点F 在线段BC 的延长线上,且BD CF =,直线AF 与DC交于点P ,试问APD ∠的度数是否是定值?若是定值,求出并说明理由.【解答】解:(1)如图1,点D 在点B 上方时,点E 在点A 右侧,AD BC =,DAE DBC ∠=∠,AE BD =, ()ADE BCD SAS ∴∆≅∆ADE BCD α∴∠==∠,90BDC AED α∠=∠=︒-, 290CDE ADE BDC α∴∠=∠-∠=-︒, 点D 在点B 上方时,点E 在点A 左侧, 90CDE ADE BDC ∠=∠+∠=︒;如图11-,点D 在点B 下方时,点E 在点A 右侧,AD BC =,DAE DBC ∠=∠,AE BD =, ()ADE BCD SAS ∴∆≅∆ADE BCD α∴∠==∠,90BDC AED α∠=∠=︒-, 902EDC BDC ADE α∴∠=∠-∠=︒-,点D 在点B 下方时,点E 在点A 左侧, 90CDE ADE BDC ∴∠=∠+∠=︒;故答案为:290α-︒或902α︒-或90︒;(2)APD ∠的度数是45︒,理由是:如图2,过F 作FM x ⊥轴于F ,使FM BC =,连接CM ,DM ,AD BC =,AD FM ∴=,AD x ⊥轴,//AD FM ∴,∴四边形ADM F 是平行四边形,//AF DM ∴,PDM APD ∴∠=∠,FM BC =,90CFM DBC ∠=∠=︒,CF BD =, ()CFM DBC SAS ∴∆≅∆,BCD CMF ∴∠=∠,DC CM =,90FCM CMF ∠+∠=︒,90FCM BCD ∴∠+∠=︒,90DCM ∴∠=︒,DCM ∴∆是等腰直角三角形,45CDM ∴∠=︒,45APD CDM ∴∠=∠=︒.18.已知等腰三角形ABC 中,点D 为BC 中点,点E 是BA 延长线上一动点,点F 是AC 延长线上一动点连接DE 、DF ,且180EDF BAC ∠+∠=︒.(1)如图1,若90BAC ∠=︒,求证:AE AC AF +=;(2)如图2,若120BAC ∠=︒,AE 、AC 、AF 三条线段还满足(1)中的结论吗?若满足,则直接证明;若不满足,请写出结论并证明.【解答】(1)证明:连接AD ,设AF 交DE 于G ,如图1所示: 90BAC ∠=︒,AB AC =,45B ∴∠=︒,点D 为BC 中点,12AD BC BD CD ∴===,45BAD CAD B ∠=∠=︒=∠,AD BC ⊥, 180EDF BAC ∠+∠=︒,180EAC BAC ∠+∠=︒, EDF EAC ∴∠=∠,AGE DGF ∠=∠,BED AFD ∴∠=∠,在BDE ∆和ADF ∆中,B CAD BED AFD BD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BDE ADF AAS ∴∆≅∆,BE AF ∴=,AB AC =,BE AE AB =+,AE AC AF ∴+=;(2)解:不满足(1)中的结论,12AC AE AF +=;理由如下: 连接AD ,取AC 的中点G ,连接DG ,如图2所示: 120BAC ∠=︒,AB AC =,30ACB ∴∠=︒,60EAC ∠=︒,点D 为BC 中点,AD BC ∴⊥,60CAD ∠=︒,12DG AC AG CG ∴===,120DAE ∠=︒, ADG ∴∆是等边三角形,AD DG ∴=,60AGD ADG EDF ∠=∠=︒=∠, 120DGF DAE ∴∠=︒=∠,ADE GDF ∠=∠, 同(1)得:AED GFD ∠=∠,在ADE ∆和GDF ∆中,DAE DGF AED GFD AD GD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADE GDF AAS ∴∆≅∆,AE GF ∴=,AG GF AF +=, ∴12AC AE AF +=;19.已知D 为ABC ∆所在平面内一点,且DB DC =,DE AB ⊥,DF AC ⊥,垂足分别为点E 、F ,DE DF =.(1)如图1,当点D 在BC 边上时,判断ABC ∆的形状;并证明你的结论;(2)如图2,当点D 在ABC ∆内部时,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请举出反例(画图说明,不需证明).【解答】解:(1)结论:ABC ∆是等腰三角形. 理由:DE AB ⊥,DF AC ⊥,90BED CFD ∴∠=∠=︒.在Rt EBD ∆与Rt FCD ∆中,DE DF DB DC =⎧⎨=⎩, Rt EBD Rt FCD(HL)∴∆≅∆,B C ∴∠=∠AB AC ∴=,ABC ∴∆是等腰三角形.(2)当点D 在ABC ∆内部时,(1)中的结论仍然成立. 理由:如图2,DE AB ⊥,DF AC ⊥, 90BED CFD ∴∠=∠=︒,在Rt EBD ∆与Rt FCD ∆中,DE DF DB DC =⎧⎨=⎩, Rt EBD Rt FCD(HL)∴∆≅∆,EBD FCD ∴∠=∠.DB DC =,DBC DCB ∴∠=∠,EBD DBC FCD DCB ∴∠+∠=∠+∠, 即ABC ACB ∠=∠,AB AC ∴=,ABC ∴∆是等腰三角形.20.如图,在Rt ABC ∆中,90C ∠=︒,点P 为AC 边上的一点,延长BP 至点D ,使得AD AP =,当AD AB ⊥时,过点D 作DE AC ⊥于E .(1)求证:CBP ABP ∠=∠;(2)若4AB BC -=,8AC =.求AB 的长度和DE 的长度.【解答】(1)证明:90C ∠=︒, 90CBP BPC ∴∠+∠=︒, AD AB ⊥,90PBA BDA ∴∠+∠=︒, AD AP =,BDA DPA BPC ∴∠=∠=∠, CBP ABP ∴∠=∠;(2)解:设AB x =,4AB BC -=,4BC x ∴=-,在Rt ABC ∆中,由勾股定理得:222(4)8x x -+=, 解得:10x =,6BC ∴=,10AB =;作PF AB ⊥于F ,如图所示:在BCP ∆和BFP ∆中,90CBP ABP C BFP BP BP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()BCP BFP AAS ∴∆≅∆6BC BF ∴==,DE AC ⊥,90EAD ADE PAF EAD ∴∠+∠=︒=∠+∠,PAF ADE ∴∠=∠,在PAF ∆和ADE ∆中,PFA AED PAF ADE PA AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()PAF ADE AAS ∴∆≅∆,1064DE AF AB BF ∴==-=-=.21.如图(1),8A B c m =,AC AB ⊥,BD AB ⊥,6AC BD cm ==.点P 在线段AB 上以2/m s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.它们运动的时间为()t s(1)若点Q 的运动速度与点P 的运动速度相等,当1t =时,判断线段PC 与PQ 满足的关系,并说明理由.(2)如图(2),将图(1)中的AC AB ⊥,BD AB ⊥为改“CAB DBA a ∠=∠=︒”,其它条件不变.设点Q 的运动速度为/xcm s ,是否存在实数x ,使得ACP ∆与BPQ ∆全等?若存在,求出相应的x 、t 的值;若不存在,请说明理由.【解答】解:(1)ACP BPQ ∆≅∆,AC AB ⊥,BD AB ⊥90A B ∴∠=∠=︒2AP BQ ==6BP ∴=BP AC ∴=,在ACP ∆和BPQ ∆中,AP BQ A B AC BP =⎧⎪∠=∠⎨⎪=⎩,ACP BPQ ∴∆≅∆,C QPB ∴∠=∠,90APC C ∠+∠=︒,90APC QPB ∴∠+∠=︒,PC PQ ∴⊥;(2)存在x 的值,使得ACP ∆与BPQ ∆全等,①若ACP BPQ ∆≅∆,则AC BP =,AP BQ =,可得:682t =-,2t xt =解得:2x =,1t =;②若ACP BQP ∆≅∆,则AC BQ =,AP BP =,可得:6xt =,282t t =-解得:3x =,2t =.22.如图,AD AC =,1239∠=∠=︒,C D ∠=∠,点E 在线段BC 上.(1)求证:ABC AED ∆≅∆.(2)求AEC ∠的度数.【解答】(1)证明:1239∠=∠=︒,12CAE CAE ∴∠+∠=∠+∠,即BAC EAD ∠=∠,在ABC ∆和AED ∆中,BAC EAD AC AD C D ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ABC AED ASA ∴∆≅∆.(2)解:由(1)得::ABC AED ∆≅∆.AB AE ∴=,11(1801)(18039)70.522B AEB ∴∠=∠=︒-∠=︒-︒=︒, 13970.5109.5AEC B ∴∠=∠+∠=︒+︒=︒., 23.已知:如图,点A 、D 、C 、B 在同一条直线上,AD BC =,AE BF =,//AE FB ,求证://CE DF .【解答】证明:AD BC =,AD DC BC DC ∴+=+,AC BD ∴=,//AE BF ,A B ∴∠=∠,在ACE ∆和BDF ∆中,,,,AC BD A B AE BF =⎧⎪∠=∠⎨⎪=⎩()ACE BDF SAS ∴∆≅∆.ACE BDF ∴∠=∠.//CE DF ∴.24.如图,点D 在ABC ∆外部,点C 在DE 边上,BC 与AD 交于点O ,若123∠=∠=∠,AC AE =.求证:(1)B D ∠=∠;(2)ABC ADE ∆≅∆.【解答】证明:(1)13∠=∠,13DAC DAC ∴∠+∠=∠+∠,即BAC DAE ∠=∠,1803E ACE ∠=∠︒-∠-∠,1802ACB ACE ∠=︒-∠-∠,23∠=∠,ACE ACE ∠=∠,ACB E ∴∠=∠,在ABC ∆与ADE ∆中BAC DAE AC AEE ACB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ABC ADE ASA ∴∆≅∆,B D ∴∠=∠.(2)由(1)可得ABC ADE ∆≅∆.25.已知:如图,AB AC =,AE AF =,连结BF ,CE ,交于O ,连结AO .求证:(1)B C ∠=∠;(2)AO 平分BAC ∠.【解答】证明:(1)在ABF ∆和ACE ∆中,AB AC BAF CAE AF AE =⎧⎪∠=∠⎨⎪=⎩,()ABF ACE SAS ∴∆≅∆,B C ∴∠=∠;(2)AB AC =,AE AF =,BE CF ∴=,在BOE ∆和COF ∆中,B C BOE COF BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BOE COF AAS ∴∆≅∆,OB OC ∴=,在ABO ∆和ACO ∆中,AB AC B C OB OC =⎧⎪∠=∠⎨⎪=⎩,()ABO ACO SAS ∴∆≅∆,OAB OAC ∴∠=∠,即AO 平分BAC ∠.26.如图所示,已知ABC ∆中AB AC =,E 、D 、F 分别在AB ,BC 和AC 边上,且BE CD =,BD CF =,过D 作DG EF ⊥于G . 求证:12EG EF =.【解答】证明:连接DE 、DF ,如右图所示,AB AC =,B C ∴∠=∠,在EBD ∆和DCF ∆中,BE CD B C BD CF =⎧⎪∠=∠⎨⎪=⎩,()EBD DCF SAS ∴∆≅∆,DE DF ∴=,DG EF ⊥,DG ∴是等腰DEF ∆的中线,12EG EF ∴=.27.已知在ABC ∆中,AC BC =,分别过A ,B 两点作互相平行的直线AM ,BN ,过点C 的直线分别交直线AM ,BN 于点D ,E .(1)如图1,若AM AB ⊥,求证:CD CE =;(2)如图2,60ABC DEB ∠=∠=︒,判断线段AD ,DC 与BE 之间的关系,并说明理由.【解答】(1)证明:如图1,延长AC 交BN 于点F ,AC BC =,CAB CBA ∴∠=∠,又AB AM ⊥,90BAM ∴∠=︒,又//AM BN ,180BAM ABN ∴∠+∠=︒,90ABN ∴∠=︒,90BAF AFB ∴∠+∠=︒,90ABC CBF ∠+∠=︒,CBF AFB ∴∠=∠,BC CF ∴=,AC FC ∴=,又//AM BN ,DAF AFB ∴∠=∠,在ADC ∆和FEC ∆中,DAC EFC AC FC ACD FCE ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ADC FEC ASA ∴∆≅∆,DC EC ∴=;(2)解:AD DC BE +=;理由如下:如图2,在EB 上截取EH EC =,连接CH ,AC BC =,60ABC ∠=︒,ABC ∴∆为等边三角形,60DEB ∠=︒,CHE ∴∆是等边三角形,60CHE ∴∠=︒,60HCE ∠=︒,120BHC ∴∠=︒,//AM BN ,180ADC BEC ∴∠+∠=︒,120ADC ∴∠=︒,60DAC DCA ∴∠+∠=︒,又180DCA ACB BCH HCE ∠+∠+∠+∠=︒,60DCA BCH ∴∠+∠=︒,DAC BCH ∴∠=∠,在DAC ∆与HCB ∆中,DAC HCB ADC CHB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()DAC HCB AAS ∴∆≅∆,AD CH ∴=,DC BH =,又CH CE HE==,∴=+=+,BE BH HE DC AD即AD DC BE+=.28.阅读下列材料,并完成任务.如图,四边形ABCD是一个筝形,其中AB AD=.对角线AC,BD相交于点O,=,BC CD过点O作0M AB⊥,ON AD⊥,垂足分别为M,N.求证:四边形AMON是筝形.【解答】证明:在ABC ∆和ADC ∆中AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩,()ABC ADC SSS ∴∆≅∆,BAC DAC ∴∠=∠,又OM AB ⊥,ON AD ⊥,垂足分别为M ,N ,OM ON ∴=;90AMO ANO ∠=∠=︒,9090BAC DAC ∴︒-∠=︒-∠,AOM AON ∴∠=∠,即OA 平分MON ∠,又AM OM ⊥,AN ON ⊥,AM AN ∴=∴四边形AMON 是筝形.29.如图,在ABC ∆中AB AC =,AED ∆中AE AD =,EAD BAC ∠=∠,AC 与BD 交于点O .(1)试确定ADC ∠与AEB ∠间的数量关系,并说明理由;(2)若65ACB ∠=︒,求BDC ∠的度数.【解答】解:(1)ADC AEB ∠=∠,理由如下:BAC EAD ∠=∠BAC EAC EAD EAC ∴∠-∠=∠-∠即:BAE CAD ∠=∠在ABE ∆和ACD ∆中AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩()ABE ACD SAS ∴∆≅∆ADC AEB ∴∠=∠(2)BOC ∠是ABO ∆和DCO ∆的外角BOC ABD BAC ∴∠=∠+∠,BOC ACD BDC ∠=∠+∠ABD BAC ACD BDC ∴∠+∠=∠+∠ABD ACD ∠=∠BAC BDC ∴∠=∠65ACB ∠=︒,AB AC =65ABC ACB ∴∠=∠=︒180180656550BAC ABC ACB ∴∠=︒-∠-∠=︒-︒-︒=︒50BDC BAC ∴∠=∠=︒30.如图,AD 为ABC ∆的高,E 为AC 上一点,BE 交AD 于F ,且有BF AC =,FD CD =.求证:(1)BFD ACD ∆≅∆;(2)BE AC ⊥.【解答】证明:(1)AD 为ABC ∆的边BC 上的高,BDF ∴∆和ADC ∆为直角三角形.90BDF ADC ∴∠=∠=︒.在Rt BFD ∆和Rt ACD ∆中,BF AC FD CD=⎧⎨=⎩, Rt ∴△Rt ACD(HL)BFD ∆≅∆;(2)BDF ADC ∆≅∆,DBF DAC ∴∠=∠.AFE ∠与BFD ∠是对顶角,90BDF AEF ∴∠=∠=︒,BE AC ∴⊥.31.在等腰OAB ∆和等腰OCD ∆中,OA OB =,OC OD =,连接AC 、BD 交于点M .(1)如图1,若40:AOB COD ∠=∠=︒①AC 与BD 的数量关系为 AC BD = ;②AMB ∠的度数为 .(2)如图2,若90:AOB COD ∠=∠=︒①判断AC 与BD 之间存在怎样的数量关系?并说明理由;②求AMB ∠的度数.【解答】解:(1)①AOB COD ∠=∠,AOB AOD COD AOD ∴∠+∠=∠+∠,BOD AOC ∴∠=∠,在BOD ∆和AOC ∆中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩,()BOD AOC SAS ∴∆≅∆,AC BD ∴=;故答案为:AC BD =,②BOD AOC ∆≅∆,OBD OAC ∴∠=∠,40AOB ∠=︒,180********OAB OBA AOB ∴∠+∠=︒-∠=︒-︒=︒,又OAB OBA OAB ABD OBD ∠+∠=∠+∠+∠140OAB OBA OAB ABD OAC ∴∠+∠=∠+∠+∠=︒,140MAB ABM ∴∠+=︒,在ABM ∆中,180AMB MAB ABM ∠+∠+=︒,40AMB ∴∠=︒;故答案为:40︒;(2)①AC BD =,理由如下:90AOB COD ∠=∠=︒,AOB AOD COD AOD ∴∠+∠=∠+∠,BOD AOC ∴∠=∠,在BOD ∆和AOC ∆中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩,()BOD AOC SAS ∴∆≅∆,BD AC ∴=;②BOD AOC ∆≅∆,OBD OAC ∴∠=∠,又90OAB OBA ∠+∠=︒,ABO ABM OBD ∠=∠+∠,MAB MAO OAB ∠=∠+∠,90MAB MBA ∴∠+∠=︒, 又在AMB ∆中,180AMB ABM BAM ∠+∠+∠=︒,180()1809090AMB ABM BAM ∴∠=︒-∠+∠=︒-︒=︒.32.如图,点B 、F 、C 、E 在同一直线上,AC 、DF 相交于点G ,AB BE ⊥,垂足为B ,DE BE ⊥,垂足为E ,且AC DF =,BF CE =.(1)求证:ABC DEF ∆≅∆;(2)若65A ∠=︒,求AGF ∠的度数.【解答】(1)证明:AB BE ⊥,90B ∴∠=︒,DE BE ⊥,90E ∴∠=︒,BF CE =,BF CF CE CF ∴+=+,即CB EF =,在Rt ABC ∆和Rt DEF ∆中,AC DF BC EF=⎧⎨=⎩, Rt ABC Rt DEF(HL)∴∆≅∆(2)解:65A ∠=︒,AB BE ⊥,906525ACB ∴∠=︒-︒=︒,由(1)知Rt ABC Rt DEF ∆≅∆,25ACB DFE ∴∠=∠=︒,50AGF ACB DFE ∴∠=∠+∠=︒33.如图,在ABC ∆中,B C ∠=∠,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE CF =,AD EC AB +=.(1)求证:DE EF =.(2)当36A ∠=︒时,求DEF ∠的度数.【解答】(1)证明:AD EC AB +=,AD BD AB +=BD EC ∴=,在BDE ∆和CEF ∆中BD EC B C BE CF =⎧⎪∠=∠⎨⎪=⎩,()BDE CEF SAS ∴∆≅∆,DE EF ∴=;(2)解:ABC ∆中,36A ∠=︒,1(18036)722B C ∴∠=∠=︒-︒=︒,由(1)知:BDE CEF ∆≅∆BDE CEF ∴∠=∠,又DEF CEF B BDE ∠+∠=∠+∠,72DEF B ∴∠=∠=︒.34.在ABC ∆中,45ACB ∠=︒,AD BC ⊥垂足为D ,点E 在AD 上,ED BD =,连接CE 并延长交AB 于点F ,连接DF .(1)求证:BAD ECD ∠=∠.(2)求证:45DFE ∠=︒.【解答】证明:(1)AD 是ABC ∆的高,45ACB ∠=︒,90ADB CDE ∴∠=∠=︒,ACD ∆是等腰直角三角形,AD CD ∴=,在ABD ∆和CED ∆中,AD CD ADB CDE DE DB =⎧⎪∠=∠⎨⎪=⎩,()ABD CED SAS ∴∆≅∆,BAD ECD ∴∠=∠;(2)如图,在EC 上截取EG BF =,ABD CED ∆≅∆,B CED ∴∠=∠,在BDF ∆和EDG ∆中,EG BF B CED DE DB =⎧⎪∠=∠⎨⎪=⎩,()BDF EDG SAS ∴∆≅∆,DF DG ∴=,BDF EDG ∠=∠,90FDG FDE EDG FDE BDF ADB ∴∠=∠+∠=∠+∠=∠=︒,DFG ∴∆是等腰直角三角形,45DFE ∴∠=︒.35.如图,在ABC ∆和BAD ∆中,AC 与BD 相交于点E ,AD BC =,DAB CBA ∠=∠,求证:12∠=∠.【解答】证明:在ABD ∆和BAC ∆中,AD BC DAB CBA AB BA =⎧⎪∠=∠⎨⎪=⎩,ABD BAC ∴∆≅∆()SAS ,34∴∠=∠,DAB CBA ∠=∠,12∴∠=∠.36.如图所示,AB AC =,AD AE =,BAC DAE ∠=∠,122∠=︒,228∠=︒, 求3∠的度数.【解答】解:BAC DAE ∠=∠,BAD CAE ∴∠=∠,在ABD ∆与ACE ∆中,1AD AE CAE AB AC =⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴∆≅∆;228ABD ∴∠=∠=︒;31ABD ∠=∠+∠,122∠=︒,350∴∠=︒.37.如图,在直角坐标系中有一点(5,5)P ,(0,)M m 为y 轴上任意一点,N 为x 轴上任意一点,且90MPN ∠=︒.(1)当5m =时,OM ON +的值为 10 ;(2)当05m <<时,OM ON +的值是否改变?说明你的理由;(3)探索:当0m <时,OM 与ON 的数量关系为 .【解答】解:(1)作PA y ⊥轴于A ,PB x ⊥轴于B ,如图1所示:(5,5)P ,5PA PB OA OB ∴====,(0,5)A ∴,当5m =时,(0,5)M ,A ∴与M 重合,B 与N 重合,5ON OH ∴==,10OM ON ∴+=;故答案为:10;(2)当05m <<时,OM ON +的值不改变,理由如下:作PA y ⊥轴于A ,PB x ⊥轴于B ,如图2所示:则90APB ∠=︒,5PA PB ==,90MPN ∠=︒,APM BPN ∴∠=∠,在APM ∆和BPN ∆中,90PAM PBN PA PB APM BPN∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,()APM BPN ASA ∴∆≅∆,AM BN ∴=,10OM ON OA AM OB BN OA OB ∴+=-++=+=;(3)当0m <时,OM 与ON 的数量关系为10OM ON =-,理由如下: 作PA y ⊥轴于A ,PB x ⊥轴于B ,如图3所示: 同(2)得:()APM BPN ASA ∆≅∆,AM BN ∴=,10OM AM OA BN OA ON OB OA ON ∴=-=-=--=-; 故答案为:10OM ON =-.38.已知,如图,射线BD 平分锐角ABC ∠,且平分钝角ADC ∠,求证:CD AD =.【解答】证明:射线BD 平分锐角ABC ∠,且平分钝角ADC ∠, 12∴∠=∠,34∠=∠,ADB CDB ∴∠=∠,在CBD ∆和ABD ∆中,21BD BD CDB ADB ∠=∠⎧⎪=⎨⎪∠=∠⎩,()CBD ADB ASA ∴∆≅∆,CD AD ∴=.39.如图所示,BF AC ⊥于点F ,CE AB ⊥于点E ,BF 与CE 交于D ,且BD CD =. 求证:D 在BAC ∠的平分线上.【解答】证明:BF AC ⊥于点F ,CE AB ⊥于点E , 90BED CFD ∴∠=∠=︒,在BDE ∆和CDF ∆中,BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BDE CDF AAS ∴∆≅∆,DE DF ∴=,D ∴在BAC ∠的平分线上.40.如图(1),7A B c m =,AC AB ⊥,BD AB ⊥垂足分别为A 、B ,5AC cm =.点P 在线段AB 上以2/cm s 的速度由点A 向点B 运动,同时,点Q 在射线BD 上运动.它们运动的时间为()t s (当点P 运动结束时,点Q 运动随之结束).(1)若点Q 的运动速度与点P 的运动速度相等,当1t =时,ACP ∆与BPQ ∆是否全等,并判断此时线段PC 和线段PQ 的位置关系,请分别说明理由;(2)如图(2),若“AC AB ⊥,BD AB ⊥”改为“60CAB DBA ∠=∠=︒”,点Q 的运动速度为/xcm s ,其他条件不变,当点P 、Q 运动到某处时,有ACP ∆与BPQ ∆全等,求出相应的x 、t 的值.【解答】解:(1)ACP BPQ ∆≅∆, AC AB ⊥,BD AB ⊥90A B ∴∠=∠=︒2AP BQ ==,5BP ∴=,BP AC ∴=,在ACP ∆和BPQ ∆中,AP BQ A B AC BP =⎧⎪∠=∠⎨⎪=⎩,ACP BPQ ∴∆≅∆;C BPQ ∴∠=∠,90C APC ∠+∠=︒,90APC BPQ ∴∠+∠=︒,90CPQ ∴∠=︒,PC PQ ∴⊥;(2)存在x 的值,使得ACP ∆与BPQ ∆全等, ①若ACP BPQ ∆≅∆,则AC BP =,AP BQ =,可得:572t =-,2t xt = 解得:2x =,1t =;②若ACP BQP ∆≅∆,则AC BQ =,AP BP =,可得:5xt =,272t t =- 解得:207x =,74t =.41.如图,在ABC ∆中,60B ∠=︒,AD 平分BAC ∠,CE 平分BCA ∠,AD 、CE 交于点F ,CD CG =,连结FG .(1)求证:FD FG =;(2)线段FG 与FE 之间有怎样的数量关系,请说明理由;(3)若60B ∠≠︒,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.【解答】(1)证明:EC 平分ACB ∠, FCD FCG ∴∠=∠,CG CD =,CF CF =,()CFD CFG SAS ∴∆≅∆,FD FG ∴=.(2)解:结论:FG FE =.理由:60B ∠=︒,120BAC BCA ∴∠+∠=︒, AD 平分BAC ∠,CE 平分BCA ∠,1()602ACF FAC BCA BAC ∴∠+∠=∠+∠=︒, 120AFC ∴∠=︒,60CFD AFE ∠=∠=︒, CFD CFG ∆≅∆,60CFD CFG ∴∠=∠=︒,60AFG AFE ∴∠=∠=︒,。
全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)B ACDF21 E∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形的判定练习
全等三角形的判定专项练习一.填空题(每题4分,共24分)1.如图,△ABD ≌△ACE,对应角是_______________________,对应边是__________________.2. 已知:如图,△ABC ≌△FED,且BC=DE.则∠A=__________,A D=_______.3. 如图,△ABD ≌△ACE,则AB 的对应边是_________,∠BAD 的对应角是______. 4.如图,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是____________.1 2 3 45.如图, 已知:∠1=∠2 , ∠3=∠4 , 要证BD=CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△______ , 根据是__________.6.如图,ABC △中,∠B =∠C ,D ,E ,F 分别在AB ,BC ,AC 上,且BD CE ,=DEF B ∠∠ 求证:=ED EF .证明:∵∠DEC =∠B +∠BDE ( ),又∵∠DEF =∠B (已知),∴∠______=∠______(等式性质).在△EBD 与△FCE 中,∠______=∠______(已证), ______=______(已知),∠B =∠C (已知), ∴EBD FCE △≌△( ).∴ED =EF ( ). 5 6 二.选择题(每题5分,共40分)7. 下列各条件中,不能作出惟一三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边8. 如图,已知:△ABE ≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是 ( )A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE8 99. 图中全等的三角形是 ( )A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ10. AD=AE , AB=AC , BE 、CD 交于F , 则图中相等的角共有(除去∠DFE=∠BFC )A.5对B.4对C.3对D.2对 ( ) 11.如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数是 ( )A.70°B. 85°C. 65°D. 以上都不对A B CD12AD EC B F 4321E D C BA12. 已知:如图,△ABC ≌△DEF,AC ∥DF,BC ∥EF.则不正确的等式是 ( )A.AC=DFB.AD=BEC.DF=EFD.BC=EF10 11 12 13 14 13.如图 , ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC 的度数为 ( )A.50°B.30°C.45°D.25° 14. 如图 , ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC= ( )A.70°B.80°C.100°D.90° 三.解答题(每题9分,共36分)15. 已知:如图 , 四边形ABCD 中 , AB ∥CD , AD ∥BC .求证:△ABD ≌△CDB.16. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .17.如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF .18.如图,工人师傅要检查人字梁的∠B 和∠C 是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA 和CA 上取BE CG =; ②在BC 上取BD CF =;③量出DE 的长a 米,FG 的长b 米.如果a b =,则说明∠B 和∠C 是相等的.他的这种做法合理吗?为什么?七年级全等三角形判定专题训练 (查找隐含着的三角形全等的条件)(一)公共边1、已知:如图,AD ∥BC ,AD =CB ,你能说明△ADC ≌△CBA 吗? 证明:FG E D C B A AD E CBFG CEDBO A∵AD ∥BC (已知)∴∠=∠(两直线平行,内错角相等)在 中⎪⎪⎩⎪⎪⎨⎧∠=∠(公共边)=(已证)(已知)= ∴ ≌ ( )2、如图,∠B =∠C ,AD 平分∠BAC ,求证:△ABD ≌△ACD 证明: ∵AD 平分∠BAC ( )∴∠ =∠ (角平分线的定义) 在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∠∠∠=∠(公共边)=(已证)=(已知) ∴△ABD △ACD ( )3、如图,已知AB =AC ,AD 是BC 边上的中线,求证:AD 是角平分线吗 证明:∵AD 是BC 边上的中线(已知)∴ = (中线的定义) 在 中∴ ≌ ( ).∴ = (全等三角形的对应角相等) ∴AD 是角平分线( )4、如图,已知21∠=∠,AD=AB ,求证:ADC ABC ∆≅∆。
全等三角形判定基础练习(有答案)
全等三角形判定基础练习(有答案)一.选择题(共3小题)1.如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是()A.AB=AC B.∠ADC=∠AEB C.∠B=∠C D.BE=CD2.判定两个三角形全等,给出如下四组条件:①两边和一角对应相等;②两角和一边对应相等;③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是()A.①和②B.①和④C.②和③D.③和④3.如图,下列各组条件中,不能得到△ABC≌△BAD的是()A.BC=AD,∠ABC=∠BAD B.BC=AD,AC=BDC.AC=BD,∠CAB=∠DBA D.BC=AD,∠CAB=∠DBA二.解答题(共6小题)4.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.5.如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.6.如图,BE⊥AC于E,CF⊥AB于F,CF、BE相交于点D,且BD=CD.求证:AD平分∠BAC.7.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.8.如图,在△ABC中,AB=AC,点D、E在BC上,且BD=CE.求证:△ABE≌△ACD.9.如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:△ABE≌△ACD.全等三角形判定(孙雨欣)初中数学组卷参考答案与试题解析一.选择题(共3小题)1.如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是()A.AB=AC B.∠ADC=∠AEB C.∠B=∠C D.BE=CD【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,看看条件是否符合判定定理即可.【解答】解:A、∵在△ABE和△ACD中,,∴△ABE≌△ACD(SAS),正确,故本选项错误;B、∵在△ABE和△ACD中,,∴△ABE≌△ACD(ASA),正确,故本选项错误;C、∵在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),正确,故本选项错误;D、根据AE=AD,BE=CD和∠A=∠A不能推出△ABE和△ACD全等,错误,故本选项正确;故选D.【点评】本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.2.判定两个三角形全等,给出如下四组条件:①两边和一角对应相等;②两角和一边对应相等;③两个直角三角形中斜边和一条直角边对应相等;④三个角对应相等;其中能判定这两个三角形全等的条件是()A.①和②B.①和④C.②和③D.③和④【分析】认真分析各选项提供的已知条件,结合全等三角形判定方法对选项提供的已知条件逐一判断.【解答】解:①两边和一角对应相等不正确,应该是两边的夹角,故本选项错误,②两角和一边对应相等,符合AAS,故本选项正确,③两个直角三角形中斜边和一条直角边对应相等,符合SAS,故本选项正确,④三个角对应相等,可以相似不全等,故本选项错误,故选C.【点评】本题主要考查了对全等三角形的判定方法的理解及运用.常用的判定方法有AAS,SSS,SAS 等,难度适中.3.如图,下列各组条件中,不能得到△ABC≌△BAD的是()A.BC=AD,∠ABC=∠BAD B.BC=AD,AC=BDC.AC=BD,∠CAB=∠DBA D.BC=AD,∠CAB=∠DBA【分析】根据图形可得公共边AB=AB,再加上选项所给条件,利用判定定理SSS、SAS、ASA、AAS分别进行分析即可.【解答】解:根据图形可得公共边:AB=AB,A、BC=AD,∠ABC=∠BAD可利用SAS证明△ABC≌△BAD,故此选项不合题意;B、BC=AD,AC=BD可利用SSS证明△ABC≌△BAD,故此选项不合题意;C、AC=BD,∠CAB=∠DBA可利用SAS证明△ABC≌△BAD,故此选项不合题意;D、BC=AD,∠CAB=∠DBA不能证明△ABC≌△BAD,故此选项符合题意;故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.二.解答题(共7小题)4.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.【分析】利用∠1=∠2,即可得出∠ABE=∠CBF,再利用全等三角形的判定SAS得出即可.【解答】证明:∵∠1=∠2,∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,在△ABE与△CBF中,,∴△ABE≌△CBF(SAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.5.如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.【分析】首先根据∠QAP=90°,AB⊥PQ可证出∠PQA=∠BAC,在加上条件BC=AP,∠C=∠QAP=90°,可利用AAS定理证明△ABC和△QPA全等.【解答】△ABC能和△QPA全等;证明:∵∠QAP=90°,∴∠PQA+∠QPA=90°,∵QP⊥AB,∴∠BAC+∠APQ=90°,∴∠PQA=∠BAC,在△ABC和△QPA中,,∴△ABC≌△QPA(AAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.6.如图,BE⊥AC于E,CF⊥AB于F,CF、BE相交于点D,且BD=CD.求证:AD平分∠BAC.【分析】要证AD平分∠BAC,只需证DF=DE.可通过证△BDF≌△CDE(AAS)来实现.根据已知条件,利用AAS可直接证明△BDF≌△CDE,从而可得出AD平分∠BAC.【解答】证明:∵BE⊥AC,CF⊥AB,∴∠BFD=∠CED=90°.在△BDF与△CDE中,,∴Rt△BDF≌Rt△CDE(AAS).∴DF=DE,∴AD是∠BAC的平分线.【点评】本题考查了全等三角形的判定和性质,以及到角两边距离相等的点在角平分线上等知识.发现并利用△BDF≌△CDE是正确解答本题的关键.7.如图AB,CD相交于点O,AD=CB,AB⊥DA,CD⊥CB,求证:△ABD≌△CDB.【分析】首先根据AB⊥DA,CD⊥CB,可得∠A=∠C=90°,再利用HL定理证明Rt△ABD≌Rt△CBD即可.【解答】证明:∵AB⊥DA,CD⊥CB,∴∠A=∠C=90°,在Rt△ABD和Rt△CBD中,∴Rt△ABD≌Rt△CBD(HL).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.8.如图,在△ABC中,AB=AC,点D、E在BC上,且BD=CE.求证:△ABE≌△ACD.【分析】由AB=AC可得∠B=∠C,然后根据BD=CE可证BE=CD,根据SAS即可判定三角形的全等.【解答】证明∵AB=AC,∴∠B=∠C,∵BD=EC,∴BE=CD,在△ABE与△ACD中,,∴△ABE≌△ACD(SAS).【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.9.如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:△ABE≌△ACD.【分析】根据全等三角形的判定定理ASA推出即可.【解答】证明:∵在△ABE和△ACD中,∴△ABE≌△ACD(ASA).【点评】本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.10.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.【分析】利用已知得出∠A=∠DBE,进而利用ASA得出△ABC≌△BDE即可.【解答】证明:在Rt△ABC中,∵∠ABC=90°,∴∠ABE+∠DBE=90°,∵BE⊥AC,∴∠ABE+∠A=90°,∴∠A=∠DBE,∵DE是BD的垂线,∴∠D=90°,在△ABC和△BDE中,∵,∴△ABC≌△BDE(ASA).【点评】此题主要考查了全等三角形的判定,三角形内角和定理的应用,正确发现图形中等量关系∠A=∠DBE是解题关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形判定练习题1、如图(1):AD ⊥BC ,垂足为D ,BD =CD 。
求证:△ABD ≌△ACD2、如图(2):AC ∥EF ,AC =EF ,AE =BD 。
求证:△ABC ≌△EDF 。
3、如图(3):DF =CE ,AD =BC ,∠D =∠C 。
求证:△AED ≌△BFC 。
FE 图图2图DCBAFEDC图图1图DCBA4、如图(4):AB =AC ,AD =AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B =∠C ,(2)BD =CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE 。
求证:AC ⊥CE 。
E图图4图D CBAE图图5图DCBA6、如图(6):CG =CF ,BC =DC ,AB =ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF =EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN =BC 。
求证:(1)MN 平分∠AMB ,(2)∠A =∠CBM 。
GFE图图6图D C BANM图图7图CBA8、如图(8):A 、B 、C 、D 四点在同一直线上,AC =DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE =CF 。
求证:AM 是△ABC 的中线。
F E图图8图DC B AM F E图图9图CBA10、如图(10)∠BAC =∠DAE ,∠ABD =∠ACE ,BD =CE 。
求证:AB =AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA =PD 。
12、如图(12)AB ∥CD ,OA =OD ,点F 、D 、O 、A 、E 在同一直线上,AE =DF 。
求证:EB ∥CF 。
E图图10图D CBAP4321图图11图D B AF13、如图(13)△ABC ≌△EDC 。
求证:BE =AD 。
14、如图(14)在△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 的中线,过点C 作CF ⊥AE 于F ,过B 作BD ⊥CB 交CF 的延长线于点D 。
(1)求证:AE =CD ,(2)若BD =5㎝,求AC 的长。
E图图13图DCBAFE图图14图DCBA15、如图(15),△ABC 中,AB =2AC ,∠BAC =90°,延长BA 到D ,使AD =AB ,延长AC 到E ,使12CE =AC 。
求证:△ABC ≌△AED 。
16、如图(16)AD ∥BC ,AD =BC ,AE =CF 。
求证:(1)DE =DF ,(2)AB ∥CD 。
图图15图E DCBAF图图16图EDCBA17、如图:在△ABC 中,AD ⊥BC 于D ,AD =BD ,CD =DE ,E 是AD 上一点,连结BE 并延长交AC 于点F 。
求证:(1)BE =AC ,(2)BF ⊥AC 。
18、如图:在△ABC 中,∠ACB =90°,AC =BC ,D 是AB 上一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F 。
求证:AE =EF +BF 。
F图图17图EDCBAF图图18图E D CBA19、如图:AB=DC,BE=CF,AF=DE。
求证:△ABE≌△DCF。
20、如图;AB=AC,BF=CF。
求证:∠B=∠C。
21、如图:AB∥CD,∠B=∠D,求证:AD∥BC。
F图图19图EDCBAFEDC BA22、如图:AB=CD,AE=DF,CE=FB。
求证:AF=DE。
23、如图:AB=DC,∠A=∠D。
求证:∠B=∠C。
F图图22图EDCB ADA24、如图:AD=BC,DE⊥AC于E,BF⊥AC于F,DE=BF。
求证:(1)AF=CE,(2)AB∥CD。
25、如图:CD⊥AB于D,BE⊥AC于E,OD=OE。
求证:AB=AC。
F图图24图ED CB AO 图图25图EDC BA26、如图:在△ABC 中,AB =AC ,AD 和BE 都是高,它们相交于点H ,且AH =2BD 。
求证:AE =BE 。
27、如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD =AC ,在CF 的延长线上截取CG =AB ,连结AD 、AG 。
求证:(1)AD =AG ,(2)AD ⊥AG 。
H图图26图E DCBAGH F图图27图E DCBA28、如图:AB =AC ,EB =EC ,AE 的延长线交BC 于D 。
求证:BD =DC 。
29、如图:△ABC 和△DBC 的顶点A 和D 在BC 的同旁,AB =DC ,AC =DB ,AC 和DB 相交于O 。
求证:OA =OD 。
E DCBA ODCBA30、如图:AB =AC ,DB =DC ,F 是AD 的延长线上的一点。
求证:BF =CF 。
31、如图:AB =AC ,AD =AE ,AB 、DC 相交于点M ,AC 、BE 相交于点N ,∠DAB=∠EAC 。
求证:AM =AN 。
32、如图:AD =CB ,AE ⊥BD ,CF ⊥BD ,E 、F 是垂足,AE =CF 。
求证:AB =CD 。
FDCBANME DCBAA33、如图:在△ABC中,AD是它的角平分线,且BD=CD,DE,DF分别垂直AB,AC,垂足为E,F。
求证:EB=FC。
34、如图:CD⊥AB,BE⊥AC,垂足分别为D、E,BE,CD相交于点O。
求证:(1)当∠BOA=∠COA时,OB=OC。
(2)当OB=OC时,∠BOA=∠COA。
F EDCBAO EDC BA35、如图:在△ABC 中,∠BAC =90°,∠ABD =∠ABC ,BC ⊥DF ,垂足为F ,AF 交BD 于E 。
求证:12AE =EF 。
36、如图:在△ABC 中,O 是∠ABC 与∠ACB 的平分线的交点。
求证:点O 在∠A 的平分线上。
FED CBAOCBA37、如图:在△ABC 中,∠B ,∠C 相邻的外角的平分线交于点D 。
求证:点D 在∠A 的平分线上。
38、如图:AD 是△AB C 中∠BAC 的平分线,过AD 的中点E 作EF ⊥AD 交BC 的延长线于F ,连结AF 。
求证:∠B =∠CAF 。
DCBAFE DCBA39、如图:AD 是△ABC 的中线,DE ⊥AC 于E ,DF ⊥AB 于F ,且BF =CE ,点P 是AD 上一点,PM ⊥AC 于M ,PN ⊥AB 于N 。
求证:(1)DE =DF ,(2)PM =PN 。
40、如图:在△ABC 中,∠A =60°,∠B ,∠C 的平分线BE ,CF 相交于点O 。
求证:OE =OF 。
41、如图:E 是∠AOB 的平分线上一点,EC ⊥OA ,ED ⊥OB ,垂足为C ,D 。
求证:(1)OC=OD ,(2)DF=CF 。
PN MFE DCBAFOECBACA42、如图:在△ABC 中,∠C=90°,AC =BC ,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,且AE =BD ,DF ⊥AB 于F 。
求证:CD =DF 。
1243、如图:AB =FE ,BD =EC ,AB ∥EF 。
求证:(1)AC =FD ,(2)AC ∥EF ,(3)∠ADC =∠FCD 。
FE D CBA FEDCBA44、如图:AD=AE,∠DAB=∠EAC,AM=AN。
求证:AB=AC。
45、如图:AB=AC,BD=CE。
求证:OA平分∠BAC。
NME DC BAOEDC BA- 21 -46、如图:AD 是△ABC 的BC 边上的中线,BE 是AC 边上的高,OC 平分∠ACB ,OB =OC 。
求证:△ABC 是等边三角形。
47、如图:在△ABC 中,∠C =90°,AC =BC ,过点C 在△ABC 外作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N 。
(1)求证:MN =AM +BN 。
(2)若过点C 在△ABC 内作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N ,则AM 、BN 与MN 之间有什么关系?请说明理由。
O ED CBAN MCBANMC BA。
