稳恒磁场小结与习题课
稳恒磁场习题课选讲例题
霍耳效应
2.对载流导线
— 安培力：
df Idl B
f Idl B
l
电流单位 A (安培)旳定义
3.对载流线圈 — 磁力矩：
M
m B
m NIS
第十一章 恒定磁场
恒定磁场习题课选讲例题
物理学教程 （第二版）
例 一无限长载流 I 旳导线，中部弯成如图所示旳
四分之一圆周 AB，圆心为O，半径为R，则在O点处旳
设电流都是均匀旳分布在导体旳横截面上，求：（1）
导体圆柱内（r < a）；（2）两导体之间（a < r < b）；
（3）导体圆管内（b < r < c）以及（4）电缆外（r > c）
各点处磁感应强度旳大小.
解 电流如图所示
作半径为 r 旳同心圆回路,
并以逆时针方向为回路正向.
b a +I
c
I
第十一章 恒定磁场
BD
E
第十一章 恒定磁场
恒定磁场习题课选讲例题
物理学教程 （第二版）
例 边长为0.2 m旳正方形线圈，共有50 匝 ，通
以电流 2 A ，把线圈放在磁感应强度为 0.05 T 旳均匀
磁场中. 问在什么方位时， 线圈所受旳磁力矩最大？
磁力矩等于多少？
解 M NBIS sin
得
π 2
,
M
M max
2
+
I
B2
B1
o
I
4
l
+I
3
解 能够用安培环路定理和 叠加原理计算。
每一无限长直线电流在 O 点
旳磁感强度 B B1 B2 B3 B4
大学物理稳恒磁场习题课
S
当 S 很小时，可得
B2S B1S 0
B1
B2
B
有 B2 B1 ，即同一条磁感应线上的
B
相等
如再在该磁场中做一有向矩形安培环路 abcda ， ☆ bc 、 让 ab 、cd 与磁感应线平行， da 与磁感应线垂直。 / 设沿 ab 段磁感应强度为 B ，沿 cd 段磁感应强度为 B ， 由磁感应线疏密不均匀可知 ， 磁感应强度沿该回路的线积分为 / B d l B ab B cd 0
也就不能推出 H d S 0
S
r 都相等，
。
因此，一般说来，不能得出 通过以闭合曲线 L 为边界的各曲面的通量均相等的结论
例如，一永磁棒，设棒内 M 为一常值，
对以 L 为边界的二曲面 S1 和S2 ，有
☆
S1
B dS B dS
S2
M 的方向与外磁场方向相反
Pm 为无矩分子在外磁场中出则的附加磁矩，
磁场强度 引入磁场强度辅助矢量 H
H
B
☆
在各向同性均匀介质中 M m H
m 称为磁化率，是一个纯数。
0
M
顺磁质中
m 1，抗磁质中 m 1 。 H 和 B 的关系为
T
)
2．毕奥一萨伐尔定律
电流元
电流元
☆
Idl
是矢量， 与
大小等于电流 I
导线元长度 dl 的乘积，
方向沿电流正方向。
毕奥一萨伐尔定律 电流元 Idl 在
P 点产生的磁感应强度为
0 4 107 N A2
0 Idl r 0 Idl r ˆ dB 3 2 4 r 4 r
第7章稳恒磁场及答案教学总结
第7 章稳恒磁场及答
案
第七章稳恒电流
1、在磁感强度为B 的均匀磁场中作一半径为r 的半球面S , S 边线所在平面的法
线方向单位矢量n 与B 的夹角为
，则通过半球面 S 的磁通量(取弯面向外为正)
(C) o I /4 . (D) 2 o I/3 .
4、如图，在一固定的载流大平板附近有一载流小线框能自由转 动或平
动.线框平面与大平板垂直.大平板的电流与线框中电流 方向如图所示，
则通电线框的运动情况对着从大平板看是：
(A)靠近大平板.
(B)顺时针转动. (C)逆时针转动. (D)离开大平板向外运动.
(A) r 2B . . (B) 2 r 2B . 2 2
(C) - r Bsin . (D) - r Bcos . 2、磁场由沿空心长圆筒形导体的均匀分布的 \ B 电流产生，圆筒半径为 R , x 坐标轴垂直圆筒 轴线，原点在中心轴线上.图(A)〜(E)哪一条 曲线表示B -x 的关系？ AB (A) (D) 『(C) )R x O R x n 3、如图，两根直导线ab 和cd 沿半径方向被 接到一个截面处处相等的铁环上，稳恒电流
I 从a 端流入 而从d 端流出，则磁感强度 B 沿图中闭合路径L 的积分 B dl 等于 L
1 (A) 。
1 .
(B)-。
丨. 3 L。
大学物理-磁学习题课和答案解析
2． 均匀磁场的磁感应强度 B 垂直于半径为r的圆面．今
4． 如图，在面电流线密度为 j 的均匀载流无限大平板附近， 有一载流为 I 半径为 R的半圆形刚性线圈，其线圈平面与载流 大平板垂直．线圈所受磁力矩为 ，受力 0 0 为 ．
μ
5、（本题3分） 长直电缆由一个圆柱导体和一共轴圆筒状导体组成，两导体 中有等值反向均匀电流I通过，其间充满磁导率为μ的均匀磁介 质．介质中离中心轴距离为r的某点处的磁场强度的大小H I =________________ ，磁感强度的大小B =__________ ． I 2 r 2 r
B (A) B (B) √ R B x (D) O 圆筒 电流 O x
B
0 I (r R) 2r
(r R)
O B
R
x O (C) x O
B
(E)
B0
O
R
R
x
R
x
2、（本题3分）一匀强磁场，其磁感强度方向垂直于纸面(指 向如图)，两带电粒子在该磁场中的运动轨迹如图所示，则 (A) 两粒子的电荷必然同号． (B) 粒子的电荷可以同号也可以异号． (C) 两粒子的动量大小必然不同． (D) 两粒子的运动周期必然不同．
（C） B dl B dl , BP BP 1 2
（D） B dl B dl , BP1 BP2
L1 L2
L1
L2
L1
L2
[ ]
5．有一矩形线圈 AOCD ，通以如图示方向的电流 I，将它置 于均匀磁场 B 中，B 的方向与X轴正方向一致，线圈平面与X 轴之间的夹角为 , 90 ．若AO边在OY轴上，且线圈可 绕OY轴自由转动，则线圈 （A）作使 角减小的转动． （B）作使 角增大的转动． （C）不会发生转动． （D）如何转动尚不能判定．
大学物理第8章 稳恒磁场 课后习题及答案
*作品编号：DG13485201600078972981* 创作者： 玫霸*第8章 稳恒磁场 习题及答案6. 如图所示，AB 、CD 为长直导线，C B为圆心在O 点的一段圆弧形导线，其半径为R 。
若通以电流I ，求O 点的磁感应强度。
解：O 点磁场由AB 、C B、CD 三部分电流产生，应用磁场叠加原理。
AB 在O 点产生的磁感应强度为01=BC B在O 点产生的磁感应强度大小为θπμR I B 402=RIR I 123400μππμ=⨯=，方向垂直纸面向里CD 在O 点产生的磁感应强度大小为)cos (cos 421003θθπμ-=r IB)180cos 150(cos 60cos 400︒︒-=R Iπμ)231(20-=R I πμ，方向垂直纸面向里 故 )6231(203210ππμ+-=++=R I B B B B ，方向垂直纸面向里 7. 如图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连。
已知圆环的粗细均匀，求环中心O 的磁感应强度。
解：圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。
且θπθ-==21221R R I I 电阻电阻 1I 产生的磁感应强度大小为）（θππμ-=24101RI B ，方向垂直纸面向外2I 产生的磁感应强度大小为θπμRIB 4202=，方向垂直纸面向里 所以， 1)2(2121=-=θθπI I B B 环中心O 的磁感应强度为0210=+=B B B8. 如图所示，一无限长载流平板宽度为a ，沿长度方向通过均匀电流I ，求与平板共面且距平板一边为b 的任意点P 的磁感应强度。
解：将载流平板看成许多无限长的载流直导线，应用叠加原理求解。
以P 点为坐标原点，垂直载流平板向左为x 轴正方向建立坐标系。
在载流平板上取dx aIdI =，dI 在P 点产生的磁感应强度大小为 x dI dB πμ20=dx axIπμ20=，方向垂直纸面向里P 点的磁感应强度大小为⎰⎰+==a b b x dx a I dB B πμ20bab a I +=ln 20πμ 方向垂直纸面向里。
第7章 (稳恒磁场)习题课
二．载流导线和运动电荷所受磁场力
1． 洛伦兹力: 特征:方向垂直于v和B所构成的平 面；不作功，不改变电荷的速率和动能．
方向沿x方向 （若F为正值，则合力的方向与x轴正向一致）。
例5 半径分别为R1和R2的两个半圆弧与直径的两小段
构成的通电线圈abcda (如图所示)，放在磁感强度
为B的均匀磁场中，平行线圈所在平面．则 线圈的磁矩大小为
1 2 I ( R2 R12 ) 2 ___________ ，
R2 a b
2r
0
2
R o r
dr
B
0
2
dr
0
R
0R
2
dr
例4. 均匀带电细直线AB, 电荷线密度为λ, 绕垂直于 直线通过O 点的轴以角速度ω 匀速转动( 线形状不 变, O 点在A B 延长线上) , 求: r dr (1 ) O点的磁感应强度B; O B a A (2 ) 磁矩m ; b （1）解 ：在带电细线离O点r处取线元dr，其带 电量 dq dr，旋转时相当于一圆电流
2 r 2 R2 I 1 H 2 2 2r R R 3 2
1.解: 圆电流在O点产生的磁场 0 I 2 B1 方向× 2R 长直导线电流在O点产生的磁场 0 I 2 方向× B2 2R 导体管在O点产生的磁场由安培环路定理求得，
B3
0 I1
2 (d R)
方向×
圆心O点处的磁感应强度
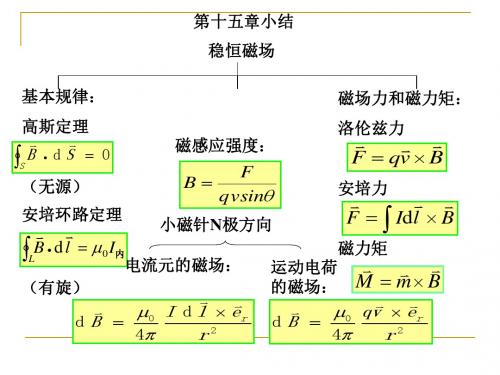
稳恒磁场小结与习题课共33页文档
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢！
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
稳恒磁场小结与习题课 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。
稳恒磁场习题课
———杜甫 《曲江二首 》
稳恒磁场习题课
物理教研室 戴占海
基本要求：
一、掌握毕奥—萨伐尔定律及计算载流导 线磁场的方法；
二、掌握安培环路定理，并会利用该定理 计算具有对称性电流分布的磁场。
三、掌握安培定律及计算载流导线（或载 流线圈）在磁场中受力（或力矩）的方法；
四、掌握洛伦兹力公式及计算运动电荷在 磁场中受力问题。
B轴线 2
0 IS
R2 x2
3 / 2 (不必记)
例题1、如图在半径为R的圆周上，a、b、
c三点依次相隔90°，
a、c两处有垂直纸面
向里的电流元 Idl
b
求：b点磁感应强度 Id l
Idl
解: dBIdl
dBIdl
0 4
Idl 2R2
dB 2 0
Idl
2
0 Idl
4 2R 2 2
I
Ib2 R2
0 I 2R2
(a
b2 )
2a
例题4、 载流方线圈边长2a,通电流I, 求：中心o处磁感应强度
解：O点B为四段有限长直载流导线产生的
磁感应强度的叠加，方向相同，所以
B0 4
40 IB1sin445o40aIsi[ns(in452 0)sin
1
]
4a
a
2 0I a
方向： ⊙
例题5、如图在无限长直电流I1的磁场中， 有一通有电流I2,边长为a的正三角形回路 （回路与直电流共面）。求回路所受合力
证明：
Bo
0ni tg( ) 2a n
并求证当Bn时0i，Bo简化为
O
2a
证明：n边多边形、每边对中心张角为 2/n，
稳恒磁场
稳 恒 磁 场 习 题 课(数学表达式中字母为黑体者表示矢量)壹 内容提要一、磁感强度B 的定义 1. 用运动的试验电荷q 0在磁场中受力定义： 大小B=F max /(q 0v )，方向与q 0受力为零时的速度方向平行，且矢量F 、v 、B 满足右手螺旋法则。
2. 用磁矩为m (题库为P m ) 的试验线圈在磁场中受力矩定义：大小B=M max /m ，方向与试验线圈处于稳定平衡时m 的方向相同。
二、毕奥—沙伐尔定律 1.电流元I d l 激发磁场的磁感强度 d B =[μ0 /( 4π)]I d l ×r /r 3； 2. 运动点电荷q 激发磁场的磁感强度 B =[μ0 /( 4π)]q v ×r /r 3。
三、磁场的高斯定理 1. 磁感线(略)；2. 磁通量 Φm =⎰⋅Sd S B (计算磁通量时注意曲面S 的法线正方向)；3. 高斯定理0d =⋅⎰SS B ；4. 稳恒磁场是无源场。
四、安培环路定理 1. 表达式 ：真空中⎰∑=⋅l i I 0 d μl B ,介质中⎰∑=⋅li I 0d l H ； 2. 稳恒磁场是非保守场，是涡旋场或有旋场。
五、磁矩 m (题库为P m )： 1. 定义 m =I ⎰S d S (任何载流线圈均可定义磁矩 m )；2. 磁偶极子激发的磁场：延长线上 B=[μ0/(4π)](2 m /r 3)；中垂线上B=[μ0/(4π)](－m /r 3)；3. 载流线圈在均匀磁场中受力矩 M= m ×B 。
六、洛伦兹力 1. 表达式 F m = q v ×B , F = q (E ＋v ×B )；2. 带电粒子在均匀磁场中运动(设v 与B 的夹角为α)：回旋半径 R =mv sin α / (qB ), 回旋周期 T =2πm / (qB ), 回旋频率 ν= qB / (2πm ),螺距 d =2π mv cos α / (qB )；3.霍耳效应：(1).定义(略), (2).在磁场方向与电流方向不变的情况下正载流子与负载流子受磁场力方向相同, (3).霍耳电压U H =R H IB/d , (4)霍耳系数R H =1/(nq )。
大学物理学-稳恒磁场习题课
⑶电子进入均匀磁场B中，如图所示，当电子位于 A点的时刻，具有与磁场方向成 角的速度v，它绕螺旋 线一周后到达B点，求AB的长度，并画出电子的螺旋轨 道，顺着磁场方向看去，它是顺时针旋进还是逆时针旋 进？如果是正离子（如质子），结果有何不同？
1、均匀磁场的磁感应强度B垂直于半径为r的圆面，今以该圆面
其中 直电流 ab和cd的延长线
o dc
fI
R1 R2
eI
过o
b
电流bc是以o为圆心、以 R2为半径的1/4圆弧
I
电流de也是以o为圆心、
但，是以R1为半径的1/4 圆弧
a
直电流ef与圆弧电流de在
e点相切
求：场点o处的磁感强度 B
解：
场点o处的磁感强度是由五段
特殊形状电流产生的场的叠加，f I
o dc
磁场力的大小相等方向相反； (3)质量为m，电量为q的带电粒子，受洛仑兹力作用，
其动能和动量都不变； (4)洛仑兹力总与速度方向垂直，所以带电粒子运动的
轨迹必定是圆。
习题课 1 一电子束以速度v沿X轴方向射出，在Y轴上 有电场强度为E的电场，为了使电子束不发生偏 转，假设只能提供磁感应强度大小为B=2E/v的
df
2ds
n
2 0
2 0
i dl 单位面积受力
da
df Idl B其余
da dl 0i
B总 0i
2 其余 0i
2
df
0i 2
n
dadl 2
表三 作用力
4.应用
静电场
稳恒磁场
类比总结
电偶极子 pe
fi 0
i M pE
三
磁偶极子 pm
fi 0
电磁学第5讲——稳恒磁场小结与习题课ppt课件
O b 2
但B3≠ 0．
I
(D) B ≠ 0，因为虽然B3= 0，但 B1 B2 0
．
4、在真空中，将一根无限长载流导线在一平面内 弯成如图所示的形状，并通以电流I，则圆心O点 的磁感强度B的值为
0 I /(4a)
图 35 I
I
a
I
O
5、两个同心圆线圈，大圆半径为R，通有电流I1；小 圆半径为r，通有电流I2，方向如图．若r << R (大线 圈在小线圈处产生的磁场近似为均匀磁场)，当它们 处在同一平面内时小线圈所受磁力矩的大小为
0
I1 O r
I2
R
例题
例1：一根长直圆柱形铜导体载有电流 I ，均匀分布
于截面上，在导体内部，通过圆柱中心轴线作一平面
S ，如右图所示，
计算通过每米长导线内 S 平面
的磁通量。
S
解：如图所示，设电流垂直纸面向外.
在垂直于铜导体中轴线的平面
上，作一半径为 r , 圆心位于中轴
线上的圆，应用安培回路定理：
0I
0
4
例2、一半径为 4.0 cm的圆环放在磁场中，磁场的方 向对环而言是对称发散的，如图所示．圆环所在处 的磁感强度的大小为0.10 T，磁场的方向与环面法向 成60°角．求当圆环中通有电流I =15.8A时，圆环所 受磁力的大小和方向．
60° B
I
例3、一根同轴线由半径为R1的长导线和套在它外面 的 内 半 径 为 R2 、 外 半 径 为 R3 的 同 轴 导 体 圆 筒 组
导线1、2的延长线均通过O点)．设载流导线1、2和 正方形
线框中的电流在框中心O点产生的磁感强度分别用 表示，则O点的磁感强度大小［ A］
高中物理稳恒电流技巧小结及练习题
高中物理稳恒电流技巧小结及练习题一、稳恒电流专项训练1．材料的电阻随磁场的增强而增大的现象称为磁阻效应，利用这种效应可以测量磁感应强度．如图所示为某磁敏电阻在室温下的电阻—磁感应强度特性曲线，其中R B、R0分别表示有、无磁场时磁敏电阻的阻值．为了测量磁感应强度B，需先测量磁敏电阻处于磁场中的电阻值R B.请按要求完成下列实验．(1)设计一个可以测量磁场中该磁敏电阻阻值的电路，并在图中的虚线框内画出实验电路原理图(磁敏电阻及所处磁场已给出，待测磁场磁感应强度大小约为0.6～1.0 T，不考虑磁场对电路其他部分的影响)．要求误差较小．提供的器材如下：A．磁敏电阻，无磁场时阻值R0＝150 ΩB．滑动变阻器R，总电阻约为20 ΩC．电流表A，量程2.5 mA，内阻约30 ΩD．电压表V，量程3 V，内阻约3 kΩE．直流电源E，电动势3 V，内阻不计F．开关S，导线若干(2)正确接线后，将磁敏电阻置入待测磁场中，测量数据如下表：123456U(V)0.000.450.91 1.50 1.79 2.71I(mA)0.000.300.60 1.00 1.20 1.80根据上表可求出磁敏电阻的测量值R B＝______Ω.结合题图可知待测磁场的磁感应强度B＝______T.(3)试结合题图简要回答，磁感应强度B在0～0.2 T和0.4～1.0 T范围内磁敏电阻阻值的变化规律有何不同？________________________________________________________________________.(4)某同学在查阅相关资料时看到了图所示的磁敏电阻在一定温度下的电阻—磁感应强度特性曲线(关于纵轴对称)，由图线可以得到什么结论？___________________________________________________________________________.【答案】（1）见解析图（2）1500；0.90（3）在0～0.2T范围内，磁敏电阻的阻值随磁感应强度非线性变化（或不均匀变化）；在2．要描绘某电学元件（最大电流不超过６mＡ，最大电压不超过７Ｖ）的伏安特性曲线，设计电路如图，图中定值电阻Ｒ为１ＫΩ，用于限流；电流表量程为１０mＡ，内阻约为５Ω；电压表（未画出）量程为１０Ｖ，内阻约为１０ＫΩ；电源电动势Ｅ为１２Ｖ，内阻不计。
稳恒磁场习题课
y
p (0, a)
I
对于导线1:
B1
0 I
p
0 I
p
a
O
I
1
x
2
4 π a sin a
4 π a p
0 I
1 cosa
2
1 sin 垂直向外 4 π a cos
垂直向里
0 I
B2
0 I
p
sin ada
0 I
4πa
B B1 B2
0 I 0 I p Bb （cos cos p） 4πa 2 4πa
方向垂直向里
P a b c d
稳恒磁场一
第九章 稳恒磁场
5 ．一质点带电 q=8.0×10-10C ，以速度 u=3.0×105m/s 在 半 径 为 R=6.00×10-3m 的 圆 周 上 ， 作 匀 速 圆 周 运 动．该带电质点在轨道中心所产生的磁感强度B=___， 该带电质点轨道运动的磁矩pm =_______．
2 πd R
向外为正时，
O R
0 I 2 1 0 I1 B B1 B2 B3 1 2 R p 2 πd R
I1 d
I2
稳恒磁场一
第九章 稳恒磁场
3．半径为R的导体球壳表面流有沿同一绕向均匀分布 的面电流，通过垂直于电流方向的每单位长度的电流为 K．求球心处的磁感强度大小．
I
稳恒磁场一
第九章 稳恒磁场
4．一条无限长载流导线折成如图示形状，导线上通有 电流I=10A．P点在cd的延长线上，它到折点的距离a = 2 cm，则P点的磁感强度B =_________ 5.0×10-5T．
稳恒磁场复习总结-PPT
(1)r R1;
(2)R1 r R2; (3)R2 r R3;
R1 R2
R3
(4)r R3.
11
解：电流分布具有轴对称性，磁场分布也具 有轴对称性：即磁感强度的方向与电流成右 手螺旋关系，而且凡是到轴距离相等的点磁 感强度大小相等。
(1)r R1
Bdl
l
B 0
2π
B
Ir R12
2、载流导体所受磁力——安培力 3、载流线圈在均匀磁场中的磁力矩
4
三、重要结论 1、无限长载流直导线
B 0I ,方向与电流成右手螺旋关系。 2r
半无限长载流直导线 B 0I ,方向与电流成右手螺旋关系。
4r 2、载流圆环圆心
B 0I ,方向与电流成右手螺旋关系。
2R
5
载流圆弧圆心
B 0I ,方向与电流成右手螺旋关系。 2R 2
2r
0I
r2 R12
B 的方向与
I
成右螺旋
12
(2)R1 r R2Biblioteka Bdl lB 2r
0I
B 0I
B 的方向与 I 成右螺旋
2π r
(3)R2 r R3
l
B
d
l
B
2r
0
I
I
(r 2 R32
R22 ) R22
13
B dl
L
0
Ii
2
(二)、磁力
1、运动电荷所受磁力——洛仑兹力 F qv B
2、载流导体所受磁力——安培力
dF Idl B F LdF LIdl B
3、载流线圈在均匀磁场中的磁力矩
M m B, m IS ISen
3
二、基本题型 (一)、求磁感强度
06 稳恒磁场复习+习题课(优教课堂)
内
圆
柱 体
外
电荷均匀分布
E
2 0r
E0
E
2 0r
E
r 2 0 R2
E
2
0
课堂教育
r
电流均匀分布
B 0I 2r
B0
B 0I 2r
B
0 Ir 2R 2
B 0I
9
2r
? 静电场
比较
磁场
E dl 0
B dl 0 Ii
i
电场有保守性，它是
磁场没有保守性，它是
保守场，或有势场
非保守场，或无势场
0 4
q r
r3
3.磁场方程 1)磁场高斯定理 2)安培环路定理
S B dS 0 (稳恒磁场无源)
lB dl 0 Ii (稳恒磁场有旋)
课堂教育
3
4.载流线圈的磁矩
Pm NISn
5.电磁相互作用
1)安培定律 df Idl B 2)磁场对载流导线的安培力 3)磁场对载流线圈的作用力矩
二.典型例题
例1. 一无限长直导线通有电流I,求通过矩形线框
abcd(与直导线共面)的磁通量. 解:在abcd内任取一面积元dS=l1dx,
l2
a
b
I 在此面积元内磁感应强度可看作常
量.
a l1
方向垂直于纸面向里 B 0 I
d
c
d m
B dS
2x
BdS cos 00 0I 2x
l1dx
x
dx
I2l2
课堂教育
19
设为导线电阻率,S为截面积
B0
0 2Rl
I1l1
I2l2
0 2Rl
【精选】稳恒磁场习题课43
4
磁力矩M的方向由
mB
确定，
为垂直于B的方向向上。即从上往
下俯视，线圈是逆时针旋轉。
B
60o
m
一.本章主要内容回顾
1.磁场的计算 1)毕奥---萨伐尔定律
dB
0 4
Idl
r
r3
2)电流产生磁场
B
0 4
Idl
r
r3
B dB
I
半径B为1 R21的0RI半2圆在4R圆0I1 心产生的磁感应强度为：
半径为BR2 2的4半R0 I2圆在圆心产生的磁感应强度为：
R1
R2
I
又两直导线在圆心处的磁感应强度为0。
所以圆心处的磁感应强度为：
B
B2
B1
0I 4
1 R2
1 R1
（2）如果两个半圆面正交（图2），则圆心O点的磁感应强度的
大小为＿＿＿，方向与y轴的夹为＿＿＿＿。
半径为R1的半圆在圆心产生 的磁感应强度为：
B
z B2
B1
0I 2R
2
0I 4R1
半径为R2的半圆在圆心产
I
θ
B1
y
生的磁感应强度为：
I
B2
0I 4 R2
所以圆心O处的磁感应强度为：
x
方向：与y轴的夹角
B
B12
B22
0I 4 R1 R2
B
0 4
q r r3
dB
0 4
dqr r2
高中物理稳恒电流技巧小结及练习题含解析
高中物理稳恒电流技巧小结及练习题含解析一、稳恒电流专项训练1．如图10所示，P 、Q 为水平面内平行放置的光滑金属长直导轨，相距为L 1 ，处在竖直向下、磁感应强度大小为B 1的匀强磁场中．一导体杆ef 垂直于P 、Q 放在导轨上，在外力作用下向左做匀速直线运动．质量为m 、每边电阻均为r 、边长为L 2的正方形金属框abcd 置于倾斜角θ=30°的光滑绝缘斜面上(ad ∥MN ，bc ∥FG ，ab ∥MG, dc ∥FN)，两顶点a 、d 通过细软导线与导轨P 、Q 相连，磁感应强度大小为B 2的匀强磁场垂直斜面向下，金属框恰好处于静止状态．不计其余电阻和细导线对a 、d 点的作用力．（1）通过ad 边的电流I ad 是多大？（2）导体杆ef 的运动速度v 是多大？【答案】(1)238mg B L (2)1238mgr B B dL【解析】 试题分析：(1)设通过正方形金属框的总电流为I ，ab 边的电流为I ab ，dc 边的电流为I dc ， 有I ab ＝34I ① I dc ＝14I ② 金属框受重力和安培力，处于静止状态，有mg ＝B 2I ab L 2＋B 2I dc L 2 ③由①～③，解得I ab ＝2234mg B L ④ (2)由(1)可得I ＝22mg B L ⑤ 设导体杆切割磁感线产生的电动势为E ，有E ＝B 1L 1v ⑥设ad 、dc 、cb 三边电阻串联后与ab 边电阻并联的总电阻为R ，则R ＝34r ⑦ 根据闭合电路欧姆定律，有I ＝E R⑧ 由⑤～⑧，解得v ＝121234mgr B B L L ⑨ 考点：受力分析，安培力，感应电动势，欧姆定律等．2．为了测量一个阻值较大的末知电阻，某同学使用了干电池（1.5V ），毫安表（1mA ），电阻箱（0～9999W ），电键，导线等器材．该同学设计的实验电路如图甲所示，实验时，将电阻箱阻值置于最大，断开2K ，闭合1K ，减小电阻箱的阻值，使电流表的示数为1I ＝1.00mA ，记录电流强度值；然后保持电阻箱阻值不变，断开1K ，闭合2K ，此时电流表示数为1I ＝0.80mA ，记录电流强度值．由此可得被测电阻的阻值为____W ．经分析，该同学认为上述方案中电源电动势的值可能与标称值不一致，因此会造成误差．为避免电源对实验结果的影响，又设计了如图乙所示的实验电路，实验过程如下： 断开1K ，闭合2K ，此时电流表指针处于某一位置，记录相应的电流值，其大小为I ；断开2K ，闭合1K ，调节电阻箱的阻值，使电流表的示数为___ ，记录此时电阻箱的阻值，其大小为0R ．由此可测出x R ＝ ．【答案】0375,,I R【解析】解：方案一中根据闭合电路欧姆定律，有E=I 1（r+R 1+R 2） （其中r 为电源内阻，R 1为电阻箱电阻，R 2为电流表内阻）E=I 2（r+R 1+R 2+R ）由以上两式可解得R=375Ω方案二是利用电阻箱等效替代电阻R 0，故电流表读数不变，为I ，电阻箱的阻值为R 0． 故答案为375，I ，R 0．【点评】本题关键是根据闭合电路欧姆定律列方程，然后联立求解；第二方案是用等效替代法，要保证电流相等．3．一电路如图所示，电源电动势E=28v ，内阻r=2Ω，电阻R1=4Ω，R2=8Ω，R3=4Ω，C 为平行板电容器，其电容C=3.0pF ，虚线到两极板距离相等,极板长L=0.20m ，两极板的间距d=1.0×10-2m ．（1）闭合开关S 稳定后，求电容器所带的电荷量为多少?（2）当开关S 闭合后，有一未知的、待研究的带电粒子沿虚线方向以v0=2.0m/s 的初速度射入MN 的电场中，已知该带电粒子刚好从极板的右侧下边缘穿出电场，求该带电粒子的比荷q/m （不计粒子的重力，M 、N 板之间的电场看作匀强电场，g=10m/s 2）【答案】（1）114.810C -⨯ （2）46.2510/C kg -⨯【解析】【分析】【详解】（1）闭合开关S 稳定后，电路的电流：12282482E I A A R R r ===++++； 电容器两端电压：222816R U U IR V V ===⨯=；电容器带电量： 12112 3.01016 4.810R Q CU C C --==⨯⨯=⨯（2）粒子在电场中做类平抛运动，则：0L v t =21122Uq d t dm= 联立解得46.2510/q C kg m-=⨯4．四川省“十二五”水利发展规划指出，若按现有供水能力测算，我省供水缺口极大，蓄引提水是目前解决供水问题的重要手段之一。
大学物理习题课-稳恒电流的稳恒磁场-2011.6.10
e v v L m • 电子轨道角动量与磁矩的关系： = − 电子轨道角动量与磁矩的关系： 2me • 顺磁质的磁化机理 B = B0 + B′ > B0 顺磁质的磁化机理:
• 抗磁质的磁化机理（电子进动产生反向附加场）: 抗磁质的磁化机理（电子进动产生反向附加场）
v v m = ISen
82 µ0Iev fm = evB = 495 π r
方向向左
例3 试定性分析下列载流线圈所受的磁力及其从静 止开始的运动。 止开始的运动。 1）I1与I2 共面， I1为竖直的无限长电流，I2 为圆电流。 共面， 为竖直的无限长电流， 为圆电流。 ） 首先要明确载流 dF1 线圈所处的磁场, 线圈所处的磁场 y dF2 非均匀） （非均匀） I1 o I2 再分析电流元受的 安培力。 x 安培力。 y方向的合力抵消， 方向的合力抵消， 方向的合力抵消 x方向的合力不抵消， 方向的合力不抵消， 方向的合力不抵消 dF2’ 所以圆电流向左平动。 所以圆电流向左平动。 圆电流向左平动
P点处的磁感应强度 π µ0I (r − Rcosθ )dθ B = ∫ dB = 2∫ 0 4 2 (r2 + R2 − 2rRcosθ ) π π µ0I π dθ cosθdθ = 2 r∫ 2 2 − R∫ 2 2 0 r + R − 2rRcosθ 0 r + R − 2rRcosθ 2π
B= 2R
载流长直螺线管内的磁场： 载流长直螺线管内的磁场： B = µ nI r r0 运动电荷的磁场： 运动电荷的磁场：
r µ0qv ×er B= 4πr2
• 磁通量
r r 均匀场 Φm = BS⊥ BS cosθ = B⋅ S =
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2 BR 2
n
R
60°
B
任意曲面
S
12.一对同轴的无限长空心导体圆筒,内、外半 径分别为 R1 和 R2 ( 筒壁厚度可以忽略不计 ) , 电流 I 沿内筒流去,沿外筒流回,如图所示。 (1) 计算两圆筒间的磁感应强度； (2) 求通过长度为 l 的一段截面(图中的斜线部 分)的磁通量。
r R1
B dl
l
0 Ir 2
R1
2
0 I 2 l B dl R12 r
B
I
2 1
I
r
I
0 Ir
2π R
R1 r R2
B dl 0 I
l
0 I B 2πr
R 2 r R3 B dl 0 I i
(A) B dl B dl,
L1 L2
B P1 BP2 . B P1 BP2 .
B P1 BP2 . B P1 BP2 .
L2
(B)
(C)
B dl B dl,
L1 L2
L1 L2
L1
I1 I 2
P1
B dl B dl, (D) B dl B dl,
四、求磁通量的方法
1. 磁通量
B
dS
B
Φm B dS
S
2 1 Wb 1 T 1 m 单位
s
2. 磁场的高斯定理
B dS 0
S
——无源场
1.如图，两根直导线ab和cd沿半径方向被 接到一个截面处处相等的铁环上，稳恒电 流 I从a端流入而从d 端流出，则磁感强度 B 沿图中闭合路径L的积分 B d l 等于
c I R b
O
d
e
Bcd
0 I 2R
0 I
a
R
o点磁感应强度为：
0 I 0 I Bo 8R 8 R 2R
1 4
7. 将通有电流I = 5.0 A的无限长导线折成如图
形状，已知半圆环的半径为R =0.10 m．求
圆心O点的磁感强度．
R O I
R
L
r
B
载流长圆柱面：
B
0
(r < R) (r > R)
0 I 2r
(2) 载流长螺线管内部
B 0nI
(3) 环形螺线管内部
0 NI B 2r
三、求安培力与力矩的方法 1.安培力
电流元
dF Idl B
F d F Id l B 磁感应强度 B
F max B qv
定义：
B 的方向：正电荷定义为
的方向。 Fmax v
即：小磁针N极指向。
二、求磁感应强度B的两种方法 1.毕奥--萨伐尔定律
μ0 I dl r dB 3 4π r
P
磁场叠加原理：
一段导线
B dB
b
d
方向？
0 I1 0 I 2 I3 dx 2x 2 (3r x) 0 I 3 I1 I2 ( )dx 2 x 3r x
a
c
M
I1
o
I3
r
I2
N
r
r
x
0 I 3 2 r I1 I2 F dF ( )dx r 2 x 3r x MN 0 I 3 ( I1 I 2 ) ln 2 2
L1 L2
(a)
I1 I 2
(b )
P2 I3
[ C ]
3．两根长直导线通有电流I，图示有三种环 路；在每种情况下，等于： ______________________ (对环路a)． 0 I
0 _______________________( 对环路b)． _______________________(对环路c)．
L
结论：
(1) 载流直导线
y
2
B P
有限长：
μ0 I cos θ1 cos θ2 B 4r
无限长： B 0 I 2r
重要
I o
x
1
r
延长线上： B 0
(2) 载流圆环轴线上一点：
B
2x R
2
0 IR
2 2 3/2
I
R
o
x
x
环心处：
Bo
0 I
2R
y
b a 45° 45° O
I
B
x
16. 如图，载有电流I1和I2的长直导线ab和cd相互平 行，相距3r，今有载流电流I3的导线MN=r，水平放 置，且其两端MN分别与I1、 I2的距离都是r，ab、cd
和MN共面，求导线MN所受的磁力大小和方向。
解： dF I 3 ( B1 B2 )dx
重要
I
o
B
μ0 qv r (3) 运动电荷的磁场 B 3 4π r
2.安培环路定理 真空中：
I1 I1
L
I2 I 3
I1
B dl μ0 Ii
L i
——有旋场
电流正负的规定？
重要结果： (1) 载流长圆柱体
I
(r < R)
(r > R)
B
0 Ir 2 2R 0 I 2r
L L
2. 洛仑兹力 FL q v B
均匀磁场中任意形状载流导线受力：
F IL B
a
b
L
I
B
均匀磁场中闭合载流导线受力：
F dF 0
L
I
L
B
2.磁力矩 磁 矩
M m B
m NIS
I
S
en
m
方向：与电流满足右手定则。
l
2 I (r 2 R2 ) Ii I (R2 R2 ) 3 2
r
I I I
r
0 I ( R32 r 2 ) B 2 2r ( R32 R2 )
B0
r R3
B dl 0
l
14. 如图，一根载流导线被弯成半径为R的1/4 圆弧，放在磁感强度为B的均匀磁场中，则载 流导线ab所受磁场的作用力的大小为 y ____________ ． 2RBI ，方向_________________
b c c a I⊙ I
2 0 I
4. 如图所示，磁感强度沿闭合曲线L的环流 B dl _________________．
L
I1
L
I1
I2
0 ( I 2 2I1 ）
5．一载有电流 I 的细导线分别均匀密绕在半径 为 R 和 r 的长直圆筒上形成两个螺线管 ( R=2r )，两螺线管单位长度上的匝数相等．两 螺线管中的磁感应强度大小 BR 和 Br 应满足：
(A) BR 2Br .
( B)BR Br . (C)2BR Br . ( D)BR 4 Br .
[ B ]
6. 如图所示组合载流导线，求 o 点的磁 感应强度 B 。
c
I a b R
O
d R
e
c
解：
I R
1
d
2
e
a
b
O
1 0 I 0 I 方向垂直向里 Bbc 4 2R 8R 0 I Bcd (cos1 cos 2 ) 4a 0 I [cos( / 4 ) cos(3 / 4 )] 4R sin( / 4 )
0 I B , 4R
C O 2 B A I 1
10. 有一无限长通电流的扁平铜片，宽度为 l，厚 度不计，电流 I 在铜片上均匀分布，在铜片外与 铜片共面，求 P 点的 B 的大小？
0 l r ln 2l r
I l r P
11. 在匀强磁场 中，取一半径为R的圆，圆 B 面的法线 与 成60°角，如图所示，求 n B 通过以该圆周为边线的如图所示的任意曲面 S的磁通量 。 正负？
L
(A) 0 I
1 (B) 0 I 3
120°
I b
a L
(C) 0 I 4
20 I (D) 3
I
c d
[ D ]
2. 在图 (a) 和 (b) 中各有一半径相同的圆形回路 L1、L2，圆周内有电流 I1、I2，其分布相同，且 均在真空中，但在 (b) 图中L2 回路外有电流 I3, P1、P2 为两圆形回路上的对应点，则：
解: (1)由安培环路定理 B dl B 2r 0 I
L
0 I B 2r
(R1< r < R2)
l
I
(2)在截面上 r 处,取宽为 dr ,长 l 的窄条,其面 积
则 d B dS m
0 I ldr 2r
dm
( μ0 4π 10 H m )
7 1
0 I 0 I B , 4R 4 R
8．如图，两根导线沿半径方向引到铁环的 上A、A′两点，并在很远处与电源相连，则 环中心的磁感强度为____________．
0
O
A A′
I
+ I
9. 如图所示，用均匀细金属丝构成一半径为R的圆 环C，电流I由导线1流入圆环A点，并由圆环B点 流入导线2．设导线1和导线2与圆环共面，则环 心O处的磁感强度大小为 ________________________，（分成几段考虑？ ） 方向___________________．