《管理运筹学》(第二版)课后习题参考答案,DOC
《管理运筹学》复习题及参考答案

《管理运筹学》复习题及参考答案第一章运筹学概念一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心主要是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,“s·t”表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
18. 1940年8月,英国管理部门成立了一个跨学科的11人的运筹学小组,该小组简称为OR。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是( A )A.销售数量 B.销售价格 C.顾客的需求 D.竞争价格2.我们可以通过(C)来验证模型最优解。
A.观察 B.应用 C.实验 D.调查3.建立运筹学模型的过程不包括(A )阶段。
A.观察环境 B.数据分析 C.模型设计 D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的( B )A数量B变量 C 约束条件 D 目标函数5.模型中要求变量取值(D )A可正B可负C非正D非负6.运筹学研究和解决问题的效果具有( A )A 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
《管理运筹学》复习题及参考答案

《管理运筹学》复习题及参考答案一、选择题1. 管理运筹学的研究对象是()A. 生产过程B. 管理活动C. 经济活动D. 运筹问题参考答案:D2. 以下哪个不属于管理运筹学的基本方法?()A. 线性规划B. 整数规划C. 非线性规划D. 人力资源规划参考答案:D3. 在线性规划中,约束条件是()A. 等式B. 不等式C. 方程组D. 矩阵参考答案:B4. 以下哪种方法不属于线性规划的对偶问题求解方法?()A. 单纯形法B. 对偶单纯形法C. 拉格朗日乘数法D. 牛顿法参考答案:D5. 在目标规划中,以下哪个不是目标约束的类型?()A. 等式约束B. 不等式约束C. 目标函数约束D. 线性约束参考答案:C二、填空题1. 管理运筹学的核心思想是______。
参考答案:最优化2. 在线性规划中,最优解存在的条件是______。
参考答案:可行性、有界性3. 整数规划的求解方法主要有______和______。
参考答案:分支定界法、动态规划法4. 在目标规划中,目标函数的求解方法有______、______和______。
参考答案:单纯形法、拉格朗日乘数法、动态规划法5. 非线性规划问题可以分为______、______和______。
参考答案:无约束非线性规划、约束非线性规划、非线性规划的对偶问题三、判断题1. 管理运筹学的研究对象是管理活动。
()参考答案:正确2. 在线性规划中,最优解一定存在。
()参考答案:错误3. 整数规划的求解方法比线性规划复杂。
()参考答案:正确4. 目标规划的求解方法与线性规划相同。
()参考答案:错误5. 非线性规划问题一定比线性规划问题复杂。
()参考答案:错误四、计算题1. 某工厂生产甲、乙两种产品,甲产品每件利润为10元,乙产品每件利润为8元。
生产甲产品每件需消耗2小时机器工作时间,3小时人工工作时间;生产乙产品每件需消耗1小时机器工作时间,2小时人工工作时间。
工厂每周最多可利用机器工作时间100小时,人工工作时间150小时。
管理运筹学(本科)(参考答案)学习版.doc

上交作业课程题目可以打印,答案必须手写,否则该门成绩0分。
管理运筹学 作业题一、名词解释(每题3分,共15分)1. 可行解:满足某线性规划所有的约束条件(指全部前约束条件和后约束条件)的任意一组决策变量的取值,都称为该线性规划的一个可行解,所有可行解构成的集合称为该线性规划的可行域(类似函数的定义域),记为K 。
2. 最优解:使某线性规划的目标函数达到最优值(最大值或最小值)的任一可行解,都称为该线性规划的一个最优解。
线性规划的最优解不一定唯一,若其有多个最优解,则所有最优解所构成的集合称为该线性规划的最优解域。
3. 状态:指每个阶段开始时所处的自然状态或客观条件。
4. 决策树:决策树(Decision Tree )是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
5. 最大最小准则:最大最小准则又称小中取大法或悲观法。
为不确定型决策的决策准则之一,其决策的原则是“小中取大”。
这种决策方法的思想是对事物抱有悲观和保守的态度,在各种最坏的可能结果中选择最好的。
决策时从决策表中各方案对各个状态的结果选出最小值,即在表的最右列,再从该列中选出最大者。
这种方法的基本态度是悲观与保守。
其基本思路是首先找出最不利情况下的最大收益。
二、 简答题(每题6分,共24分) 1. 简述单纯形法的基本步骤。
答:(1)把一般线形规划模型转换成标准型;(2)确定初始基可行解;(3)利用检验数j σ对初始基可行解进行最优性检验,若0≤j σ ,则求得最优解,否则,进行基变换;(4)基变换找新的可行基,通过确定入基变量和出基变量,求得新的基本可行解;(5)重复步骤(3)、(4)直至0≤j σ,求得最优解为止。
2. 简述动态规划的基本方程。
答:对于n 阶段的动态规划问题,在求子过程上的最优指标函数时,k 子过程与k+1过程有如下递推关系:对于可加性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =+=++∈终端条件:f n+1 (s n+1) = 0对于可乘性指标函数,基本方程可以写为n k s f x s r s f k k k k k s D x k k opt k k k ,,2,1)}(),({)(11)( =⨯=++∈终端条件:f n+1 (s n+1) = 13. 简述破圈法求最小生成树的步骤。
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为:,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
管理运筹学第二章课后答案

管理运筹学(谢家平)第二章课后答案1 解maxZ=200x1+240x260x1+50x2≤420030x1+40x2≤300060x1+50x2≤4500化成标准型为:maxZ=200x1+240x2+0x3+0x4+0x560x1+50x2+x3=420030x1+40x2+x4=300060x1+50x2+x5=4500**********************最优解如下*************************目标函数最优值为: 18400变量最优解相差值------- -------- --------x1 20 0x2 60 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .8892 0 4.8893 300 0目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 180 200 288x2 166.667 240266.667常数项数范围:约束下限当前值上限------- -------- -------- --------1 3750 4200 45002 2100 3000 33603 4200 4500 无上限最优生产方案是生产甲产品20,生产乙产品60。
x3=0,x4=0,x5=300说明:生产甲乙产品的材料为瓶颈材料增加材料会增加甲乙二设备D为富余设备。
因为甲产品上升100大于88所以甲需要调整,而乙产品下降的60小于73.33所以不需要调整。
由表可知非紧缺资源最多可以减少300,紧缺资源分别可以增加300,360。
2 设项目第一二三年年初投资为x1,x5x6;项目I第一年年初投资x2项目III第二年年初投资为x3项目IV第三年年初投资为x4MaxZ=0.2x1+0.5x2+0.6x3+0.4x4+0.2x5+0.2x6+30X1+X2≤30X2≤20X5+x3≤30—(x1+x2)+1.2x1X3≤15X6+x4≤30-(x1+x2)+1.2x1-x5-x3+1.5x2X4≤10X1,x2,x3,x4,x5,x6≥0**********************最优解如下*************************目标函数最优值为: 27.5变量最优解相差值------- -------- --------x1 12.5 0x2 17.5 0x3 15 0x4 10 0x5 0 .3x6 16.25 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .32 2.5 03 0 .34 0 .15 0 .26 0 .2目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 .08 .2 .56x2 .14 .5 .62x3 .5 .6 无上限x4 .2 .4 无上限x5 无下限.2 .5x6 0 .2 .28常数项数范围:约束下限当前值上限------- -------- -------- --------1 15 30 452 17.5 20 无上限3 9 30 334 12 15 285 13.75 30 无上限6 0 10 26.25项目一一二三年年初投资为12.5, 0,16.25项目二第一年初投资为17.5项目三第二年年初投资为15项目四年初投资为10 万元3设五种家具分别为x1,x2,x3,x4,x5。
《管理运筹学》习题1解答
《管理运筹学》习题11.永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B工序。
Ⅰ可在A、B 的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工。
加工单位产品所需的工序时间及其他各项数据如表所示。
问:为使该厂获得最大利润,应如何制定产品加工方案?(只建模,不求解。
)表12.某快餐店坐落在一个旅游景点中,雇佣了两名正式职工,两人都是每天工作8小时。
其余工作由临时工来担任。
在星期六,该快餐店从上午11时开始营业到夜晚10时关门。
根据游客就餐情况,在星期六每个营业小时所需职工数(包括正式工和临时工)如表2所示。
已知一名正式职工11点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时;另一名正式职工13点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时。
临时工每班连续工作时间存在3小时、4小时两种情况,前者每小时工资为4元但每班人数不超过5人,后者每小时工资为5元但每班人数不受限制。
那么应如何安排临时工的班次,使得使用临时工的总成本最小?(只建模,不求解。
)3.某公司生产Ⅰ,Ⅱ两种产品,市场对Ⅰ,Ⅱ两种产品的需求量为:产品Ⅰ在1—4月每月需10000件,5—9月每月30000件,10—12月每月需100000件;产品Ⅱ在3—9月每月15000件,其他月每月50000件。
该公司生产这两种产品成本为:产品Ⅰ在1—5月内生产每件5元,6—12月内生产每件4.5元;产品Ⅱ在1—5月内生产每件8元,6—12月内生产每件7元。
该公司每月生产这两种产品的总和不超过120000件。
产品Ⅰ容积为每件0.2立方米,产品Ⅱ容积为每件0.4立方米,该公司仓库容积为15000立方米,占用公司每月每立方米库容需1元,如该公司仓库不足时,可从外面仓库租借,租用外面仓库每月没立方米库容需1.5元。
《管理运筹学》习题1解答

《管理运筹学》习题11.永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B工序。
Ⅰ可在A、B 的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工。
加工单位产品所需的工序时间及其他各项数据如表所示。
问:为使该厂获得最大利润,应如何制定产品加工方案?(只建模,不求解。
)表12.某快餐店坐落在一个旅游景点中,雇佣了两名正式职工,两人都是每天工作8小时。
其余工作由临时工来担任。
在星期六,该快餐店从上午11时开始营业到夜晚10时关门。
根据游客就餐情况,在星期六每个营业小时所需职工数(包括正式工和临时工)如表2所示。
已知一名正式职工11点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时;另一名正式职工13点开始上班,工作4个小时后,休息1个小时,而后再工作4个小时。
临时工每班连续工作时间存在3小时、4小时两种情况,前者每小时工资为4元但每班人数不超过5人,后者每小时工资为5元但每班人数不受限制。
那么应如何安排临时工的班次,使得使用临时工的总成本最小?(只建模,不求解。
)3.某公司生产Ⅰ,Ⅱ两种产品,市场对Ⅰ,Ⅱ两种产品的需求量为:产品Ⅰ在1—4月每月需10000件,5—9月每月30000件,10—12月每月需100000件;产品Ⅱ在3—9月每月15000件,其他月每月50000件。
该公司生产这两种产品成本为:产品Ⅰ在1—5月内生产每件5元,6—12月内生产每件4.5元;产品Ⅱ在1—5月内生产每件8元,6—12月内生产每件7元。
该公司每月生产这两种产品的总和不超过120000件。
产品Ⅰ容积为每件0.2立方米,产品Ⅱ容积为每件0.4立方米,该公司仓库容积为15000立方米,占用公司每月每立方米库容需1元,如该公司仓库不足时,可从外面仓库租借,租用外面仓库每月没立方米库容需1.5元。
管理运筹学课后答案-----韩伯裳
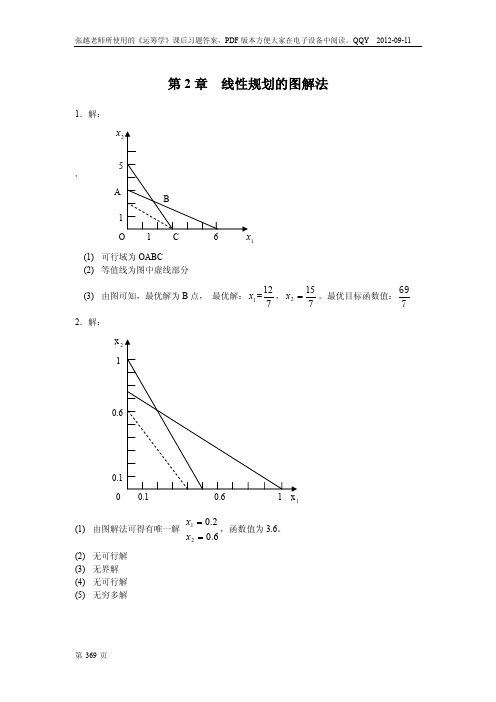
12 15 69 , x2 。最优目标函数值: 7 7 7
0.6
0.1 0 0.1 0.6 1 x1
(1) 由图解法可得有唯一解 (2) (3) (4) (5) 无可行解 无界解 无可行解 无穷多解
x1 0.2 x 2 0 .6
,函数值为 3.6。
第 369 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
从上午11时到下午10时分成11个班次设xi表示第i班次安排的临时工的人数模型如minf16x1x2x3x4x5x6x7x8x9x10x11x1x2x2x3x1x2x3x4x3x4x5x4x5x6x5x6x7x6x7x8x6x7x8x9x8x9x10x9x10x11在满足对职工需求的条件下在11时安排8个临时工13时新安排1个临时工14时新安排1个临时工16时新安排4个临时工18时新安排6个临时工可使临时工的总成本最小
' '' 3 x1 5 x 2 5x2 s1 70 ' '' 2 x1' 5 x 2 5x2 50 ' '' 3 x1' 2 x 2 2 x2 s 2 30 ' '' x1' , x 2 , x2 , s1 , s 2 0
4.解: 标准形式:
max z 10 x1 5 x2 0s1 0s 2
3 x1 4 x 2 s1 9 5 x1 2 x 2 s 2 8 x1 , x 2 , s1 , s 2 0
松弛变量(0,0) 最优解为 x1 =1,x 2 =3/2.
第 370 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海量资源,欢迎共阅 《管理运筹学》(第二版)课后习题参考答案 第1章线性规划(复习思考题) 1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(LinearProgramming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0ib,
决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 海量资源,欢迎共阅 2 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件0XbAX,的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示: 5.用表格单纯形法求解如下线性规划。
s.t.0,,86238321321321xxxxxxxxx
解:标准化32124maxxxxZ
s.t.0,,,,862385432153214321xxxxxxxxxxxxx
列出单纯形表 jc 4 1 2 0 0 i
BC BX b 1x 2x 3x 4x
5x
0 4x 2 [8] 3 1 1 0 2/8
0 5x 8 6 1 1 0 1 8/6
j 4 1 2 0 0 4 1x 1/4 1 3/8 [1/8] 1/8 0 (1/4)/(1/8)
0 5x 13/2 6 -5/4 1/4 -3/4 1 (13/2)/(1/4)
j 0 -1/2 3/2 -1/2 0 2 3x 2 8 3 1 1 0 海量资源,欢迎共阅 0 5x 6 -2 -2 0 -1 1
j -12 -5 0 -2 0 故最优解为TX)6,0,2,0,0(*,即2,0,0321xxx,此时最优值为4*)(XZ.
6.表1—15中给出了求极大化问题的单纯形表,问表中dccaa,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x代替基变量5x;(4)该线性规划问题具有无界解;(5)该线性规划问
题无可行解。 表1—15某极大化问题的单纯形表
jc 1c
2c
0 0 0
i
BC BX b 1x 2x 3x 4x
5x
0 3x d
4 1a 1 0 0
0 4x 2 -1 -5 0 1 0
0 5x 3 2a -3 0 0 1
j 1c
2c
0 0 0
解:(1)0,0,0
21ccd;
(2)中至少有一个为零)(
2121,0,0,0ccccd;
(3)221
34,0,0ad
ac;
(4)0,012ac;
(5)1x为人工变量,且1c为包含M的大于零的数,234ad;或者2x为人工变量,
且2c为包含M的大于零的数,0,01da.
7.用大M法求解如下线性规划。 海量资源,欢迎共阅 4 s.t.0,,101632182321321321321xxxxxxxxxxxx
解:加入人工变量,进行人造基后的数学模型如下: s.t.)6,,2,1(0101632182632153214321ixxxxxxxxxxxxxi
列出单纯形表 jc 5 3 6 0 0 -M i
BC BX b 1x 2x 3x 4x
5x
6x
0 4x 18 1 2 1 1 0 0 18/1
0 5x 16 2 1 [3] 0 1 0 16/3
-M 6x 10 1 1 1 0 0 1 10/1
j 5+M 3+M 6+M 0 0 0 0 4x 38/3 1/3 5/3 0 1 -1/3 0 38/5
6 3x 16/3 2/3 1/3 1 0 1/3 0 16
-M 6x 14/3 1/3 [2/3] 0 0 -1/3 1 14/2
j M311 M321 0 0 M312 0
0 4x 1 -1/2 0 0 1 1/2 -5/2 -
6 3x 3 [1/2] 0 1 0 1/2 -1/2 6
3 2x 7 1/2 1 0 0 -1/2 3/2 14
j 1/2 0 0 0 -3/2 M23 0 4x 4 0 0 1 1 1 -3
5 1x 6 1 0 2 0 1 -1 海量资源,欢迎共阅 3 2x 4 0 1 -1 0 -1 2
j 0 0 -1 0 -2 -1-M 故最优解为TX)0,0,4,0,4,6(*,即0,4,6321xxx,此时最优值为42*)(XZ.
8.A,B,C三个城市每年需分别供应电力320,250和350单位,由I,II两个电站提供,它们的最大可供电量分别为400单位和450单位,单位费用如表1—16所示。由于需要量大于可供量,决定城市A的供应量可减少0~30单位,城市B的供应量不变,城市C的供应量不能少于270单位。试建立线性规划模型,求将可供电量用完的最低总费用分配方案。 表1—16单位电力输电费(单位:元) 电站城市 A B C
I 15 18 22 II 21 25 16 解:设ijx为“第i电站向第j城市分配的电量”(i=1,2;j=1,2,3),建立模型如下:
s.t.3,2,1;2,1,035027025032029045040023132313221221112111232221131211jixxxxxxxxxxxxxxxxxij
9.某公司在3年的计划期内,有4个建设项目可以投资:项目I从第一年到第三年年初都可以投资。预计每年年初投资,年末可收回本利120%,每年又可以重新将所获本利纳入投资计划;项目II需要在第一年初投资,经过两年可收回本利150%,又可以重新将所获本利纳入投资计划,但用于该项目的最大投资不得超过20万元;项目III需要在第二年年初投资,经过两年可收回本利160%,但用于该项目的最大投资不得超海量资源,欢迎共阅 6 过15万元;项目IV需要在第三年年初投资,年末可收回本利140%,但用于该项目的最大投资不得超过10万元。在这个计划期内,该公司第一年可供投资的资金有30万元。问怎样的投资方案,才能使该公司在这个计划期获得最大利润? 解:设)1(
ix表示第一次投资项目i,设)2(ix表示第二次投资项目i,设)3(ix表示第三次
投资项目i,(i=1,2,3,4),则建立的线性规划模型为
s.t.4,3,2,1,0,,101520302.15.12.1302.130)3()2()1()1(4)1(3)1(2)1(3)2(1)1(2)1(1)1(1)1(2)2(1)1(4)3(1)1(2)1(1)1(1)1(3)2(1)1(2)1(1ixxxxxxxxxxxxxxxxxxxxxxiii
通过LINGO软件计算得:44,12,0,20,10
)2(1)2(1)1(3)1(2)1(
1xxxxx.
10.某家具制造厂生产五种不同规格的家具。每种家具都要经过机械成型、打磨、上漆几道重要工序。每种家具的每道工序所用的时间、每道工序的可用时间、每种家具的利润由表1—17给出。问工厂应如何安排生产,使总利润最大? 表1—17家具生产工艺耗时和利润表
生产工序 所需时间(小时) 每道工序可用
时间(小时) 1 2 3 4 5
成型 3 4 6 2 3 3600 打磨 4 3 5 6 4 3950 上漆 2 3 3 4 3 2800 利润(百元) 2.7 3 4.5 2.5 3 解:设ix表示第i种规格的家具的生产量(i=1,2,…,5),则
