匝道超高值计算表
超高值计算与加宽值算

Lc
高次抛物线过渡:bx = (4k3 - 3k4)b
(5)旋转断面: (x≥x0)
x ix ih 旋转阶段横坡度ix: Lc
ih iG 当双坡阶段的渐变率p1小于0.3%时: ix iG ( x x0 ) Lc x0
h'cx iG h" cx bx b bJ B iJ bJ ih ix iG h cx
(3)标注路拱横坡度。向前进方向右侧倾斜的路拱坡度为正,向左 倾斜为负。
二、平曲线路面加宽及其过渡
平曲线加宽原因: (1)汽车在曲线上行驶时,前后轮轨迹不重合, 占路面宽度大。 (2)由于横向力影响,汽车出现横向摆动。 汽车行驶在曲线上,各轮迹半径不同,其中以后 内轮轨迹半径最小,且偏向曲线内侧,故曲线内侧 应增路面宽度,以确保曲线上行车的顺适与安全。 全加宽:是圆曲线上固定不变的定值。
2i1 x0 Lc i1 ih
2i1b1 2i1b1 660i1b1 当p1 0.003 时,x0 p1 x0
hi1 (b1 bx )i1 ,
x ho1 (2 1)b1i1 x0
hi 2 hi1 b2i2 ,
hi3 hi 2 b3i3
ho 2 (2
超高渐变率
超高过渡段计算
绕边线时: Lc b ic
p
绕中线时:
b (ic ig ) Lc 2 p
多车道公路的超高缓和段长度,视车道数按上式 计算之值乘以下列系数: 从旋转轴到行车带边缘的距离 系数 2车道 1.5 3车道 2.0
(五)横断面上超高值的计算
1. 超高形成过程: (1)绕路面内边缘线旋转
超高计算——精选推荐

1.超高的过渡方式由于本设计的道路等级为高速公路,所以超高的过渡为有中间带道路的超高过渡。
有中间带的道路行车道,在直线路段的横断面均为以中间带为脊向两侧倾斜的路拱。
路面要由双向倾斜的路拱形式过渡到具有超高的单向倾斜的超高形式,外侧逐渐抬高,在抬高过程中,行车道外侧是绕中间带旋转的,若超高横坡度等于路拱横坡,则直至与内侧横坡相等为止。
本设计采用的是绕中央分隔带边缘旋转。
2.超高过渡段长度的确定(1) 超高缓和段的长度按下式计算:p iL c∆=/ B式中:cL——超高缓和段长度(m);β——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);i∆——超高坡度与路拱坡度的代数差,%P ——超高渐变率,即旋转轴线与行车道(设路缘带时为路缘带)外侧边缘线之间的相对坡度;为了行车的舒适,超高过渡段应不小于按上式计算的长度。
但从利于排除路面降水而考虑,横坡度由2%过渡到0%路段的超高渐变率不得小于1/200,即超高不该设置的太长。
一般情况下,在确定缓和曲线长度时,已经考虑了超高过渡段所需的最短长度,故一般取超高过渡段长度L与缓和曲线长度s L相等。
c本设计中,圆曲线半径均小于不设超高的最小圆曲线半径,因此都设置了超高过渡段。
3、资料整理已知本路段在一般地区设计为高速四车道,设计速度为100km/h,R分别为1500m、1600m、转角左为29°46′53.9″,转角右为22°58′40.2″,缓和曲线Ls分别为250 m、220 m,路拱横坡度为2%。
3.1、公路超高渐变值3.2、圆曲线和超高值3.3、各公路等级路基宽度计算其超高过渡段长度。
平曲线半径R =1500m 。
高速公路该公路设计速度100km/h ,由R=1500 m ,s L =250 m 可知超高值为3%,故采用绕中央分隔带边缘旋转,超高渐变率取1/225,旋转轴边缘至行车道边缘(若有路缘带,至路缘带边缘)。
即据规范确定路拱横坡%2=g i ,土路肩坡度为%3=j i ,由此确定缓和段曲线长度:25.146225/1%)2%3(13'=+⨯=∆⨯=PiC B L 取150m缓和曲250=S L >150=C L 取250=S L 时,横坡从路拱坡度(-2%)过渡到超高横坡3%的超高渐变率:3841250%)2%3(131=+⨯=P <3301 又因为不设超高的半径为4000,此点距ZH 点距离为:L=75.934000250150040002=⨯=A 根据此条件确定的超高缓和段长度为:250-93.75=156m ,此时横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率: P= 2401156%)2%3(13=+⨯>3301(2) 计算各桩号处超高值:b j1j2b B1b b 1Bb j2j1b 图3.4 超高计算点位置图图中: B ——行车道宽度;1b ——内侧路缘带; 2b ——外侧路缘带;1j b ——硬路肩宽度; 2j b ——土路肩宽度; g i ——路拱横坡度; j i ——土路肩横坡度;c i ——超高横坡度。
高速公路曲线上超高值计算

超高值计算方法——设加宽的临界断面
高速公路曲线上超高值计算
超高值计算方法——设加宽的临界断面
hn ai2 (abjx)i1 b
hzhai2 2i1 h外a(i2 i1)(2ab)i1 (ab)i1ai2
b jx
x Lc
bj
高速公路曲线上超高值计算
超高值计算方法——旋转断面(X>L 1)
ix
x Lc
高速公路曲线上超高值计算
绕路面边缘旋转的超高值计算方法
在公路施工中,路面的超高横坡度及正常 路拱横坡度是不便用坡度控制的,而是用 路中线与路基、路面边缘相对于路基设计 高程的相对高差控制的。因此,在设计中 为便于施工,应计算出路线上任意位置的 路基设计高程于路肩及路中线的高差。
高速公路曲线上超高值计算
ib
h w ai 2 ( a b ) i x
h zh
ai 2
b 2 ix
h n ai 2 ( a b jx ) i x
b jx
x Lc
bj
高速公路曲线上超高值计算
超高值计算方法——圆曲线段的全超高断面
高速公路曲线上超高值计算
超高值计算方法——圆曲线段的全超高断面
hw ai 2 (a b )ib
准备 双坡
旋转
高速公路曲线上超高值计算
超高形成过程——准备阶段
准备阶段:(也称提肩阶段) 在进入超高缓和段之前的L0=1-2米范围内,
把路肩横坡度抬高到与路面相同的横坡, 即使路基顶面变成简单的双向横坡。
高速公路曲线上超高值计算
超高形成过程——双坡阶段
双坡阶段:
从进入超高缓和段开始,先保持路面内侧不 动,外侧绕路中线向上旋转到与内侧同坡,
曲线上的超高值计算
超高设置与计算说明
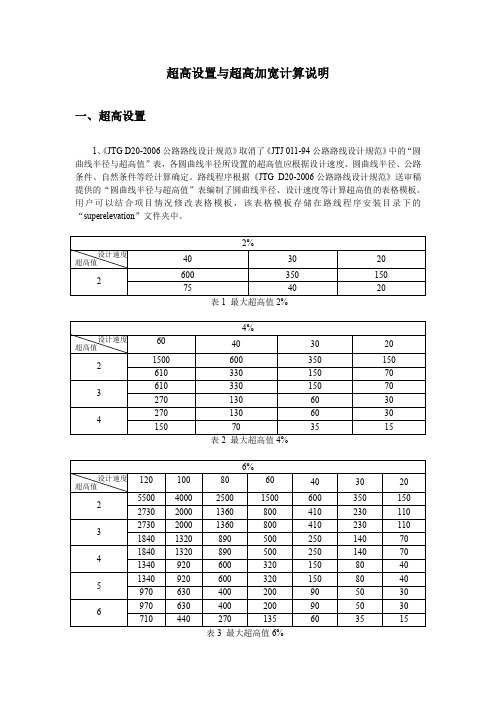
超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表,各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。
路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。
用户可以结合项目情况修改表格模板,该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。
表1 最大超高值2%表2 最大超高值4%表3 最大超高值6%表5 最大超高值10%2、在超高自动计算前,用户可以先进行超高设置,程序中的命令:[数据处理]→[超高分段] →[超高值设置],设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表,若用户需要修改表格模板可点击“浏览”按钮弹出表格模板,然后修改表格模板。
点击“确定”按钮后,程序就会把用户设置的超高值存入数据库,超高自计算就会以用户设置的超高值进行计算。
若用户不进行超高设置,程序会按程序内默认的超高值进行计算。
4、表格模板格式不能修改,只能修改模板中的数据。
二、超高计算命令:[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”,程序不考虑渐变率计算的超高缓和长度,默认超高在缓和曲线上完成;反之考虑渐变率计算的超高缓和长度。
1、2 当选中窗体中的“S型曲线YH(HY)全超高”,程序认为S型曲线YH(HY)刚好达到全超高,然后向GQ点推;反之由GQ点向YH(HY)推。
1.3 当选中窗体中的“S型曲线公切点横坡0%”,则公切点超高为0%,若未选中,则公切点为正常路拱。
2、超高自动计算时,线元划分成如下单元进行计算:2、1直线——圆曲线和圆曲线——直线(1)中间没有缓和曲线,超高缓和长度直线和圆曲线上各一半。
匝道的计算公式与认识

18.有时设计院没有给出匝道最后一段缓和曲线的结束半径,那么在积木法计算前就需要计算最后一段缓和曲线的结束半径。
公式如下:其中 A 是缓和曲线参数、R 是半径ls 是缓和曲线长度。
回旋线是公路路线设计中最常见的一种缓和曲线。
我国的标准规定缓和曲线采用回旋线。
它的基本公式为:A*A=r*l其中:A是回旋线参数。
r是回旋线上某点的曲率半径(m)l是回旋线上某点到原点的曲线长在回旋线上的任意点上,r是随着l 的变化而变化的。
但是在缓和曲线的终点处,l=Ls,r=R,则上式可写为A*A=R*Ls则 -------A=√R*Ls在设计上可以由已知R和Ls计算A,也可以按各种条件选择R和A,再计算Ls.至于用于计算坐标,你可以综合所有的已知条件进行计算,它只是提供一个计算和你进行复核的条件。
对互通立交端部的一点认识随着经济和交通运输事业的飞速发展,高等级公路的普遍修建,作为高等级公路车辆出入门户的互通式立交也开始大量修建。
立体交叉中主线与交叉线处于不同高程上,需用道路将其互相联系,便于各方向车流四通八达,这些起联系作用的道路通常称为匝道。
匝道两端与主线、交叉线连接区域称之为匝道端部。
匝道端部范围,包括匝道出入口,三角区,变速车道等部分。
匝道的端部形式,就其出入口位置不同,有左出入口和右出入口;就其主线或交叉线几何形状不同,有直线和曲线等。
匝道端部形式多样,几何关系以及设计都较繁琐,而且都应满足各自不同的技术要求,如设计不当,将造成对车辆行驶不利,容易引发事故阻碍交通。
本文就结合自己的设计经验,针对匝道端部设计做一些探讨。
一、匝道端部路线平、纵面要求1、路线平面要求从主线流出的车辆,在进入匝道的短暂运行过程中,其驾驶过程较为复杂,分流、转向、减速对司机都有一定的操作要求,同时司机产生心理压力也有影响。
因此,出口处应为车辆行驶创造良好条件,对路线平面应有较高要求,入口处一般也应如此。
我国公路《规范》规定,驶入匝道的分流点应具有较大的曲率半径,并使曲率变化适应行驶速度的变化。
速速超高计算

反算 p =
B[iG − (− ih )] 1 1 = < Lc 224 200
超高加宽设计如下表:
桩号 K53+994.101 K54+000 K54+020 K54+040 K54+060 K54+079.101 K54+08 K54+100 K54+120 K54+140 K54+157.118 K54+160 K54+180 K54+200 K54+220 K54+240 K54+242.118 路基加宽 x x=0<x0 x=5.899<x0 x=25.899<x0 x=45.899>x0 x=65.899>x0 x=85>x0 x=85.889>x0 x=105.889>x0 x=122.118>x0 x=102.118>x0 x=85>x0 x=82.118>x0 x=62.118>x0 x=42.118<x0 x=22.118<x0 x=2.118<x0 x=0<x0 (m) 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 外缘(%) -2.000 -1.445 0.438 2.320 4.202 6.000 6.000 6.000 6.000 6.000 6.000 5.729 3.846 1.964 0.082 -1.801 -2.000 中线(%) 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 内缘(%) -2.000 -2.000 -2.000 -2.320 -4.202 -6.000 -6.000 -6.000 -6.000 -6.000 -6.000 -5.729 -3.846 -2.000 -2.000 -2.000 -2.000 HZ YH HY 备注 ZH
超高计算实例(通用)

方法一:根据 路基设计表求 缓和段起点桩号(升坡说明:任意取的两点桩号差越大越接近真实值。
注:求得的起、终点桩号只是满足缓和段变化的最小桩号(或最大桩号),故此桩号不一定
L C有些图纸中直接取附近的整数,不一定是5的整数倍
L C有些图纸中直接取附近的整数,不一定是5的整数倍
L C有些图纸中直接取附近的整数,不一定是5的整数倍
方法二:根据 图纸变坡平面图 缓和段起点桩号(升说明:任意取的两点桩号差越大越接近真实值。
L C有些图纸中直接取附近的整数,不一定是5的整数倍
段起点桩号(升坡)
不一定等于图纸中的起点或终点桩号。
,不一定是5的整数倍
,不一定是5的整数倍
,不一定是5的整数倍
和段起点桩号(升坡)
,不一定是5的整数倍。
高速公路--匝道计算

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P(左转为“-”,右转为“+”)1求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
