现代控制理论大作业
现代控制理论大作业
现代控制理论大作业一、位置控制系统----双电位器位置控制系统由系统分析可知，系统的开环传递函数：2233.3s =s s 2*0.07s*s 205353G（）（+1）*（++1）另：该系统改进后的传递函数：223.331s =s s 2*0.07s*s 3455353G （）（+1）*（++1）1、时域数学模型<1>稳定性>> s=tf('s');>> G=33.3/(s*(s/20+1)*(s^2/53^2+2*0.07*s/53+1)); >>sys=feedback(G,1); >> sysTransfer function:9.915e007 -----------------------------------------------------------53 s^4 + 1453 s^3 + 1.567e005 s^2 + 2.978e006 s + 9.915e007>> pzmap(sys)由零极点图可知，该系统有四个极点，没有零点，其中两个在左半s 开平面上，两个在s 平面的虚轴处，则，四个极点的坐标分别是：>> p=pole(sys)p =0.0453 +45.2232i0.0453 -45.2232i-13.7553 +26.9359i-13.7553 -26.9359i系统的特征方程有的根中有两个处于s的右半平面，系统处于不稳定状态<2>稳态误差分析稳态误差分析只对稳定的系统有意义，系统（G）处于不稳定状态，所以不做分析。
改进后系统（G1）如下，求其特征方程的极点：>> s=tf('s');>> G1=3.33/(s*(s/345+1)*(s^2/53^2+2*0.07*s/53+1));>> sys2=feedback(G1,1);>>p=pole(sys2);p =1.0e+002 *-3.4492-0.0206 + 0.5258i-0.0206 - 0.5258i-0.0338可以看出，改进后的传递函数G1的四个极点都在s平面的右半开平面上，则系统G1是稳定的，故对此系统做稳态误差分析：由系统G1的开环传递函数在原点处有一个极点，故属于1型系统。
现代控制理论大作业课件
自适应控制设计需要建立合适的自适应算法和控制器结构。
详细描述
自适应控制设计需要建立合适的自适应算法和控制器结构， 以确保控制器能够实时地调整自身参数并保证系统的最优 性能。此外，还需要对算法和控制器结构进行充分的验证 和测试，以确保其在实际应用中的可靠性和有效性。
06
非线性系统理论
非线性系统的基本性质
齐次性
线性系统的输出与输入成正比，即当输入信 号乘以一个常数时，输出信号也乘以相同的 常数。
叠加性
对于线性系统的多个输入信号，其输出信号等于各 个输入信号单独作用于系统所产生的输出信号之和。
时不变性
线性系统的输出信号与输入信号在不同时刻 的比值保持恒定，即系统特性不随时间变化。
线性系统的状态空间表示
平衡点稳定性
分析非线性系统平衡点的稳定性，可以通过求 解系统的线性化方程来获得。
动态稳定性
动态稳定性是指非线性系统在受到扰动后恢复稳定的能力。
非线性系统的控制设计
状态反馈控制
通过测量系统的状态变量， 并使用状态反馈控制器来 控制非线性系统的输出。
滑模控制
滑模控制是一种变结构控 制方法，通过设计滑模面 和滑模控制器来实现对非
最优控制问题的描述
01
最优控制问题是在给定初始和终端状态约束下，寻找一个控制输 入，使得系统状态在满足约束条件下，某个性能指标达到最优。
02
性能指标通常包括系统状态和控制输入的能量、时间和成 本等。
03
约束条件可以是系统状态、控制输入或性能指标的限制。
极小值原理
极小值原理是求解最优控制问题的一种方法，它基于动态规划的思想，通 过求解一系列的子问题来找到最优解。
状态方程
描述系统内部状态变量随时间变化的数学方程，通常 表示为矩阵形式。
现代控制理论大作业
2019/11/21
2
课题背景
系统工作原理
Accelerometer gyroscope 遥控器
电源
左轮 软件编码
AD 采样
滤波
MCU
驱动器1 驱动器2
无线模块
软件编码 右轮
减速机构 左电机
右电机 减速机构
2019/11/21
3
系统工作原理 前进（后仰）
后退（前倾）
2019/11/21
课题背景
后退（纠正后仰） 前进（纠正前倾）
Matlab计算程序:
pole=[-1,-2,-3,-4]; K=place(A,B,pole) A1=A-B*K; pole=[-3,-4,-5,-6]; K=place(A,B,pole) A2=A-B*K; pole=[-8,-9,-10,-11]; K=place(A,B,pole) A3=A-B*K;
figure; hold on; plot(curve1(:,2),'color','blue'); plot(curve2(:,2),'color','red'); plot(curve3(:,2),'color','green'); xlabel(‘时间（s）'); ylabel(‘摆动角度（rad）'); hold off
2019/11/21
N C,CA,CA2 ,CA3
计算结果：
rankc = 4 ranko = 4
结论： k（M）=4 系统完全能控 Rank（N）=4 系统完全能观
稳定性分析
运用Matlab解出矩阵A的特征值如下：
现代控制理论大作业
现代控制理论大作业“现代控制理论”课本质上是一门工学理论基础课，它在电气工程领域众多研究工作中也有着广泛的应用，例如发电机励磁控制、发电机调速控制、电力电子装置控制等。
“现代控制理论”课立足于近年来控制理论与工程应用的最新进展，旨在实现以下两个目的：一是将控制与系统理论的前沿领域介绍给研究生，使之理解基本思想并掌握基本设计方法；二是在工程实践（主要是电力系统）与先进理论之间架设一座桥梁，使研究生能正确地运用有关理论和方法解决实际工程问题。
通过实现上述目标，本课程可拓宽研究生的专业基础知识，了解和掌握学科前沿动态，培养和提高研究生独立从事科研的能力。
课程内容本课程的教学理念是“用生动鲜活的例子诠释复杂的控制理论，用教师的研究经历点亮学生思考的火炬”。
“现代控制理论”立足于近年来控制理论与工程应用的最新进展，紧紧围绕鲁棒控制和非线性系统控制两个重点，主要讲述以下内容：①线性最优控制系统理论。
②非线性最优控制系统设计——微分几何方法。
③线性H∞控制设计原理。
④非线性控制系统H∞设计原理。
课程教学方式本课程采用教师讲授、学生课外阅读、习题练习和研究型大作业相结合的教学模式。
为加强理论联系实际，避免过分理论化，课程结合控制工程特别是电力系统工程实际，设置了下述专题研究：a. 汽轮机汽门开度系统非线性控制器设计b. 可控串联补偿鲁棒控制器设计c. 水轮机调速非线性鲁棒控制器设计d. 静止无功补偿器非线性控制器设计e. 直流输电系统非线性控制器设计f. 倒立摆控制器设计（购置2级和3级倒立摆各1台）g. 电力巡线机器人越障控制上述专题研究的目的是：在基本掌握现代控制理论主要设计方法的基础上，让研究生开展某一专题的研究，以培养学生的综合能力和素质。
这一部分内容可以代替课程的期末考试（笔试闭卷）。
教师事先就专题研究的要求、选题、难度等方面进行指导；专题研究一般由个人独立完成，内容较多的题目可以两个人作为一组来完成。
现代控制理论大题
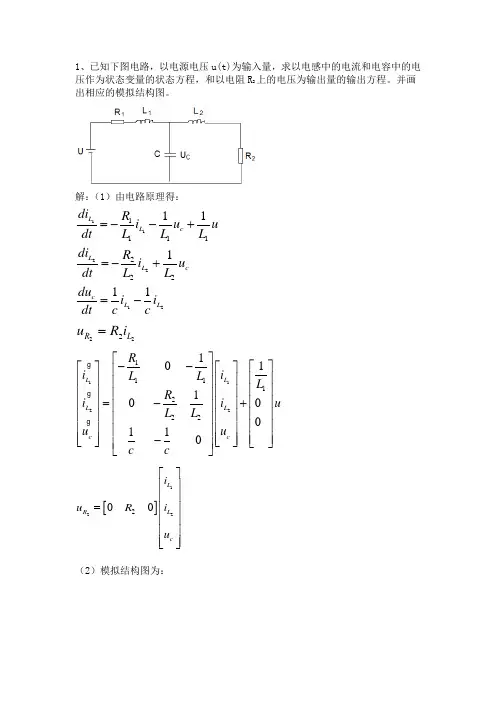
1、已知下图电路，以电源电压u(t)为输入量，求以电感中的电流和电容中的电压作为状态变量的状态方程，和以电阻R 2上的电压为输出量的输出方程。
并画出相应的模拟结构图。
解：（1）由电路原理得：112212111122211111L L c L L cc L L di R i u udt L L L di R i u dt L L du i i dtcc=--+=-+=-222R L u R i =112211112221011000110L L L L c c R ii L L L R i i u L L u u cc⎡⎤--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦[]12220L R L c i u R i u ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦（2）模拟结构图为：2、试从高阶微分方程385y y y u ++= 求得系统的状态方程和输出方程 解：1． 解：选取状态变量1x y =，2x y = ，3x y = ，可得12233131835x x xx x x x u y x ===--+=写成1000010835xx u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦[]10y x =3三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。
解112(1)(1)11()()()(1)(2)(1)(2)4s s s s g s g s g s s s s s s -+++==⋅=++---最小实现为[]010,10401xx u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥⎣⎦⎣⎦4、将下列状态方程u x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=11 4321 化为能控标准形。
解 []⎥⎦⎤⎢⎣⎡-==7111Ab bU C 11188P ⎡⎤=-⎢⎥⎣⎦. ⎥⎦⎤⎢⎣⎡=43412P 1314881148P-⎡⎤-⎢⎥=⎢⎥--⎢⎥⎣⎦. 101105C A PAP-⎡⎤==⎢⎥-⎣⎦⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==1011 43418181Pb b Cu x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=10 51010 . 5、利用李亚普诺夫第一方法判定系统1211xx -⎡⎤=⎢⎥--⎣⎦的稳定性。
现代控制理论课程设计方案书(大作业)
现代控制理论课程设计报告题目打印机皮带驱动系统能控能观和稳定性分析项目成员史旭东童振梁沈晓楠专业班级自动化112指导教师何小其分院信息分院完成日期 2014-5-28目录1. 课程设计目的 (4)2.课程设计题目描述和要求 (4)3.课程设计报告内容 (4)3.1 原理图 (4)3.2 系统参数取值情况 (5)3.3 打印机皮带驱动系统的状态空间方程 (5)4. 系统分析 (8)4.1 能控性分析 (8)4.2 能观性分析 (8)4.3 稳定性分析 (9)5. 总结 (11)项目组成员具体分工打印机皮带驱动系统能控能观和稳定性分析课程设计的内容如下：1.课程设计目的综合运用自控现代理论分析皮带驱动系统的能控性、能观性以及稳定性，融会贯通并扩展有关方面的知识。
加强大家对专业理论知识的理解和实际运用。
培养学生熟练运用有关的仿真软件及分析，解决实际问题的能力，学会应用标准、手册、查阅有关技术资料。
加强了大家的自学能力，为大家以后做毕业设计做很好的铺垫。
2.课程设计题目描述和要求(1)环节项目名称：能控能观判据及稳定性判据(2)环节目的：①利用MATLAB分析线性定常系统的可控性和客观性。
②利用MATLAB进行线性定常系统的李雅普诺夫稳定性判据。
(3)环节形式：课后上机仿真(4)环节考核方式：根据提交的仿真结果及分析报告确定成绩。
(5)环节内容、方法：①给定系统状态空间方程，对系统进行可控性、可观性分析。
②已知系统状态空间方程，判断其稳定性，并绘制出时间响应曲线验证上述判断。
3.课程设计报告内容3.1 原理图在计算机外围设备中，常用的低价位喷墨式或针式打印机都配有皮带驱动器。
它用于驱动打印头沿打印页面横向移动。
图1给出了一个装有直流电机的皮带驱动式打印机的例子。
其光传感器用来测定打印头的位置，皮带张力的变化用于调节皮带的实际弹性状态。
图1 打印机皮带驱动系统3.2 系统参数取值情况表1打印装置的参数3.3 打印机皮带驱动系统的状态空间方程图2 打印机皮带驱动模型状态空间建模及系统参数选择。
现代控制理论作业
现代控制理论大作业要求：（1）自选一实际物理对象进行研究，建立实际物理系统的状态空间模型；（2）进行原系统的定性分析，包括稳定性、能控性、能观性分析；（3）根据系统提出的性能指标要求（如超调量、超调时间、调节时间等动态 性能指标以及稳态误差等稳态性能指标），进行原系统的仿真分析，和要求的性能指标做对比；（4）对不稳定系统且能镇定的系统，进行镇定控制；（5）对未达到性能指标要求的系统进行状态反馈控制设计，满足系统性能指 标要求；（6）设计状态观测器观测所有状态；（7）设计降阶状态观测器；（可选）（8）最优控制；（9）体会及对课程建议。
1实际物理模型：如图1所示，为一交接车前后连接振动简化模型。
设计一个调节器系统使得在无扰动的情况下，系统保持在零位置上（y1=0）。
其中m1=1，m2=2，k=36，b=0.62系统的描述方程：)()(m )()(m 212122121211y y b y y k yu y y b y y k y-+-=+-+-= 其空间状态模型为：设：。
,,,24132211y x yx y x y x ====[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡432121432143210001u 01003.03.018186.06.0-3636-10000100x x x x y y x x x x x x x x 3分析与求解过程：由根轨迹和特征根（a = -0.4500 + 7.3347i -0.4500 - 7.3347i -0.000 0 ）知虽实根都为负数但都靠近零轴，是李雅普诺夫定义下的稳定，但存在震荡，所以把希望闭环极点配置在10-s ,10-s ，32-2-s ，322-s ===+=和把最小阶观测器希望极点配置在16-s ,15-s ==来改善系统的性能。
现代控制理论结课大作业
现代控制理论结课大作业一、引言现代控制理论是现代科学技术的重要组成部分，广泛应用于工程控制系统中。
在控制理论课程的学习过程中，结课大作业是一项重要的任务。
本文将介绍现代控制理论结课大作业的相关要求和设计思路。
二、研究背景现代控制理论是控制理论的一个重要分支，它主要研究控制系统的建模、分析和设计方法。
通过运用数学和工程技术知识，利用现代控制理论可以对各种系统进行精确的描述和控制。
因此，现代控制理论在自动控制领域具有广泛的应用。
三、大作业要求现代控制理论结课大作业要求学生能够独立选择一个控制系统并进行详细的研究和设计。
具体要求如下： 1. 选择一个真实的控制系统作为研究对象；2. 系统建模：根据实际情况，选择合适的建模方法，将系统转化为数学模型；3. 系统分析：通过分析系统模型，对系统的稳定性、鲁棒性等进行评估； 4. 系统设计：基于现代控制理论的设计思想，设计适合该系统的控制器； 5. 系统仿真：利用仿真软件对设计的控制系统进行验证和优化； 6. 结果分析和总结：对仿真结果进行分析，总结设计过程和经验教训。
四、设计思路在完成现代控制理论结课大作业时，需要有清晰的设计思路和步骤。
以下是一个可能的设计思路供参考： 1. 选择合适的控制系统：可以选择一个典型的工业控制系统，或者选择一个与个人兴趣相关的系统； 2. 进行系统建模：根据系统的实际情况，选择适合的建模方法，如状态空间法、传递函数法等；3. 系统分析：利用控制理论的知识和工具，分析系统的稳定性、鲁棒性，确定系统的可控性和可观性等性能指标；4. 系统设计：基于现代控制理论，设计一个合适的控制器结构，并选择适当的控制参数；5. 系统仿真：利用仿真软件，对设计的控制系统进行仿真验证，观察系统的响应特性和控制性能； 6.结果分析和总结：根据仿真结果，分析系统的优点和不足之处，并总结设计过程中的经验教训。
五、实例分析下面以一个简单的倒立摆系统为例，介绍如何完成现代控制理论结课大作业。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现代控制理论直流电动机模型的分析姓名：李志鑫班级：测控1003学号：20100203030921直流电动机的介绍1.1研究的意义直流电机是现今工业上应用最广的电机之一，直流电机具有良好的调速特性、较大的启动转矩、功率大及响应快等优点。
在伺服系统中应用的直流电机称为直流伺服电机，小功率的直流伺服电机往往应用在磁盘驱动器的驱动及打印机等计算机相关的设备中，大功率的伺服电机则往往应用在工业机器人系统和CNC铣床等大型工具上。
[1]1.2直流电动机的基本结构直流电动机具有良好的启动、制动和调速特性，可以方便地在宽范围内实现无级调速，故多采用在对电动机的调速性能要求较高的生产设备中。
直流伺服电机的电枢控制：直流伺服电机一般包含3个组成部分：-图1.1①磁极：电机的定子部分，由磁极N—S级组成，可以是永久磁铁（此类称为永磁式直流伺服电机），也可以是绕在磁极上的激励线圈构成。
②电枢：电机的转子部分，为表面上绕有线圈的圆形铁芯，线圈与换向片焊接在一起。
③电刷：电机定子的一部分，当电枢转动时，电刷交替地与换向片接触在一起。
直流电动机的启动电动机从静止状态过渡到稳速的过程叫启动过程。
电机的启动性能有以下几点要求：1）启动时电磁转矩要大，以利于克服启动时的阻转矩。
2）启动时电枢电流要尽可能的小。
3）电动机有较小的转动惯量和在加速过程中保持足够大的电磁转矩，以利于缩短启动时间。
直流电动机调速可以有：（1）改变电枢电源电压；（2）在电枢回路中串调节电阻；（3）改变磁通，即改变励磁回路的调节电阻Rf以改变励磁电流。
本文章所介绍的直流伺服电机，其中励磁电流保持常数，而有电枢电流进行控制。
这种利用电枢电流对直流伺服电机的输出速度的控制称为直流伺服电机的电枢控制。
如图1.2Bm电枢线路图1.2——定义为电枢电压（伏特）。
——定义为电枢电流（安培）。
——定义为电枢电阻（欧姆）。
——定义为电枢电感（亨利）。
——定义为反电动势（伏特）。
——定义为励磁电流（安培）。
——定义为电机产生的转矩（牛顿•米）——定义为电机和反射到电机轴上的负载的等效粘带摩擦系数（牛顿•米∕度•秒）—定义为电机和反射到电机轴上的负载的等效转动惯量（千克•米）。
1.3建立数学模型电机所产生的转矩，正比于电枢电流I与气隙磁通Φ的乘积，即：Φ (1-1) 而气隙磁通Φ又正比于激励电流，故式（1-1）改写为(1-2)对于激磁电流为常数，合并为一个常数K,称为电机力矩常数。
电枢电流I的正负即代表电机的正反转。
当电枢转动时，在电枢中感应出与电机转轴角速度成正比的电压，称为反电动势，即(1-3)其中称为反电动势常数。
电机的速度是由电枢电压E控制，应用基尔霍夫电压定律导出电枢电流I的微分方程式为：(1-4) 电枢电流I产生力矩，用来克服系统含负载的惯性和摩擦，可得(1-5) 由式（1-3）与式（1-4）合并移项后可得：(1-6) 式（1-5）移项后可得：(1-7)将式（1-6）与式（1-7）以状态方程式来表示如下：(1-8) 令R=1、L=0.2、1、=0.1、=5、K=0.5, ,代入式(1-8)可得：A=、B=、设，，则1-9 2.1对所建的模型进行分析A=; B=;C=]2.2求矩阵的特征值和特征向量(1)特征值对于线性定常系统则=det()=称为系统的特征多项式，令其等于零，即得到系统的特征方程=0式中的A为n*n的系统矩阵。
特征方程的根称为系统的特征值。
因为上述系统为线性定常系统，则=0所求的根为系统的特征值。
解得；-0.1125得到的系统特征根都为负，系统稳定。
(2)特征向量设是系统一个特征值，若存在一个n维非零向量,满足A=或则称为系统相对应于特征值的特征向量。
2.3 将状态方程化为对角标准型对于线性定常系统，若系统的特征值，，…，互异，必存在非奇异变换矩阵P，经过x=P或=x的变换，可将状态方程化为对角线标准型，即=+u和互异，必存在非奇异变换矩阵P，经过x=P的变换，将状态方程化对角为标准型。
由APi=求出矩阵P1=P2=P===+=CP=+U=[0.0205 -0.6983]X得到新的矩阵：A’=; B’=;C’=2.4从状态空间表达式求取传递函数阵线性定常系统的状态空间表达式为：对上式取拉氏变换，可得sX(s)-X(0)=AX(s)+BU(s)Y(s)=CX(s)+DU(s)设初始条件X(0)=0，则有sX(s)=AX(s)+BU(s)X(s)=Y(s)==得到传递函数：代入数值：得到根据传递函数可以写出新的能控标准型的状态空间：=x+uy=还可以写出标准型(能观型实现)=x+uy=2.5系统状态空间表达式的求解设线性定常系统的齐次状态方程为=Ax (2-1)在这里初始值为t=,初始状态为x()。
系统齐次状态方程在初始状态x()激励下的解x(t)(其中t)，称为系统的自由解或零输入解。
设齐次状态方程的解x(t)为t的向量幂级数形式即x(t)=+t++…+++… (2-2)式(2-2)代入式(2-1)，得+…=A+t++…+++…) (2-3) 由于式(2-2)是式(2-1)的解，所以式(2-3)对所有时间t均成立，故式(2-3)等号两边t的同次幂级数应相等，即A=……对式(2-2),若令t=0,可得(2-4)为状态向量x(t)的初始值，即定常系统的初始状态。
将(i=1,2,…)及代入式(2-2),得到x(t)=+A+++…=(I+At+)x(0) (2-5)仿照标量指数函数展开成幂级数形式=1+at+ (2-6)将式(2-5)括号内n*n矩阵的无穷项级数和称为矩阵指数函数，记为,即= I+At+ (2-7)则齐次状态方程的解可表示为x(t)=x(0)这里A=;求这里t=1s根据前面的分析，我们求出了系统的特征值和特征向量=P=2.6 Lyapunov第二法分析系统的开环稳定性线性定常连续系统=Ax在平衡状态Xe=0处，渐进稳定的充要条件是：对给定的一个正定对称矩阵Q,存在一个正定的对称矩阵P,且满足矩阵方程：而标量函数v(x)= 是这个系统的一个二次型形式的李雅普诺夫函数。
我们这里我们选定对称矩阵Q 时，常取Q=I ，于是得取I= 求出P==P11= ;=由此可知P ,正定。
系统在原点处的平衡状态是渐进稳定的。
而系统的李式函数及其导函数分别为 v(x)= 0 (s)= (-I)x 0 2.7 系统开环阶跃响应0510152025303540450.10.20.30.40.50.60.70.80.9Step ResponseTime (sec)A m p l i t u d e2.8 系统的能控性和能观性1状态的能控性设线性定常系统的状态方程为(t)=A(t)+Bu(t)如果存在一个分段连续的输入信u(t),能在有限时间区间[内，将系统的任一初始状态x()转移到终端状态x(),那么，称此系统的状态是完全能控的，或简称系统是能控的。
若系统n个状态变量中，至少有一个状态变量不能控时，则称此系统是状态不完全能控的，或简称系统是不可控的。
若n*nm能控性矩阵Uc=[B AB …]的秩是n构造系统的能控矩阵,系统为二阶Uc=[B AB]Uc=其秩rankUc=2=n;原系统能控。
2 状态的能观性如果对任意给定的输入信号u(t),在有限观测时间，能够根据输出量y(t)在内的测量值，唯一的确定系统在时刻的初始状态x()，则称次系统的状态是完全能观测的，或简称系统是能观测的。
若nm*n能观测性矩阵的秩是构造系统的能观性矩阵，系统为二阶Vo=Vo==2=n原系统能观2.9 闭环系统的极点配置控制系统的性能主要取决于系统极点在跟平面上的分布。
因此，在系统设计中，通常是根据对系统的品质要求，规定闭环系统极点应有的分布情况。
所谓的极点配置就是通过选择反馈矩阵，将闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的动态性能。
设受控系统的的状态空间表达式为：通过状态反馈u=r-Kx能使其闭环极点任意配置的充要条件是系统完全能控。
根据f(s)=和(s)=(s-)(s-)...(s-)使其s的多项式对应的系数相等，得到n个代数方程，即可求出K=[这里，用状态反馈将系统的闭环极点配置到合适的值，目标是使得闭环系统阶跃响应的上升时间比开环系统阶跃响应的上升时间缩短3倍左右。
通过大量仿真，我找到了期望极点值P=[-5 -0.5]所以得到K=[0.0960 -3.7808]2.10 状态观测器的设计设线性定常系统的状态空间表达式为将输出方程对t逐次求导，代以状态方程并整理可得y=Cx-CBu=CAx-CB-CABu=C x...-...-C Bu=C x即=x=写出观测器的特征多项式和期望的特征多项式使其s多项式对应项的系数相等，得到n个代数方程，即可求出反馈阵L=通过simulink 仿真，我找到了一组观测器的期望极点所以得到L=2.11 生成系统状态估计器A= ; B= ;C=2-12 求输出和观测的传递函数#100.51T o : O u t (1)-1-0.5T o : O u t (2)00.20.40.60.81 1.2 1.4 1.6 1.80.51T o : O u t (3)Step ResponseTime (sec)A m p l i t u d e#2#32-13 对输出函数进行分析写出状态空间表达式x=x+uy=因为上述系统为线性定常系统，则=0所求的根为系统的特征值。
解得；-5得到的系统特征根都为负，系统稳定。
2-14 跟踪正弦波T=1:300;plot(T/10,y(1:300,:));ylabel('y');l egend('系统','观测');5101520253000.050.10.150.20.250.30.350.40.450.5yT=1:300;plot(T/10,x1(1:300,:));ylabel('x1');legend('系统','观测');51015202530-1.5-1-0.500.51x 1T=1:300;plot(T/10,x2(1:300,:));ylabel('x2');legend('系统','观测');2-15 跟踪阶跃信号5101520253000.050.10.150.20.250.30.350.40.450.5x 2T=1:300;plot(T/10,y(1:300,:));ylabel('y');l egend('系统','观测');510152025300246810121416y;legend('系统','观测');51015202530-1001020304050607080x 1;legend('系统','观测');510152025300246810121416x 2源程序：%状态空间的四个矩阵a=[-5 -5;0.1 -0.02]b=[5 0]'c=[0 1]d=0;%矩阵特征值和特征向量[p,j]=eig(a)%状态方程的求解t=1a1=a*t[v,d1]=eig(a1)p1=expm(a1)%lyapunov第二法分析系统的开环稳定性a2=a'Q=[1 0;0 1]h=lyap(a2,Q)%对角矩阵和特征根验算inv(p)*a*pp*j*inv(p)%状态空间表达式g=ss(a,b,c,d)%状态空间表达式求传递函数：方法1 [num,den]=ss2tf(a,b,c,d)%状态空间表达式求传递函数：方法2 gc=tf(g)%构造能控性矩阵qc=ctrb(a,b)%求能控性矩阵的秩rank(qc)%构造能观性矩阵qo=obsv(a,c)%求能观性矩阵的秩rank(qo)%反馈控制期望闭环极点P=[-5 -0.5]k=acker(a,b,P)%验证配置结果eig(a-b*k)'%配置观测器期望极点po=[-4 -5]l=acker(a',c',po)'%验证配置结果eig(a-l*c)%开环阶跃响应step(num,den)pause%生成系统状态估计器est=estim(g,l)step(est)pause%分别得到输出和观测状态的传递函数tf(est)%跟踪正弦波T=1:300;plot(T/10,y(1:300,:));ylabel('y');legend('系统','观测');pauseT=1:300;plot(T/10,x1(1:300,:));ylabel('x1');legend('系统','观测');pauseT=1:300;plot(T/10,x2(1:300,:));ylabel('x2');legend('系统','观测');pause%跟踪阶跃信号T=1:300;plot(T/10,y(1:300,:));ylabel('y');legend('系统','观测');pauseT=1:300;plot(T/10,x1(1:300,:));ylabel('x1');legend('系统','观测');pauseT=1:300;plot(T/10,x2(1:300,:));ylabel('x2');legend('系统','观测');3 结束语这次的现代控制理论作业，我花费了十几天时间。