高考算法程序框图真题练习及答案详解
高中数学《算法---程序框图》典型例题练习(含答案)

高中数学《算法---程序框图》典型例题练习(含答案)算法与程序框图在高考中常以小题出现,难度不大,主要考察循环结构。
在处理这类问题时关键在于计算的准确。
一、基础知识:读框图时,要抓住“看头,审尾,记过程”这三点1、看头:观察框图中变量的个数,以及赋予的初始值2、审尾:强调细致的“审查”循环结束时,变量所取到的最后一个值,这也是易错点3、记过程:为了保证计算的准确,在读取框图的过程中,可详细记录循环体中每经过一个步骤,变量取值的变化情况,以便于在跳出循环时能快速准确得到输出变量的值二、典型例题:例1:执行下图所示的程序框图,若输入2x =,则输出y 的值为 .思路:通过框图的判断语句可知y 关于x 的函数为:2321,01,012,1x x y x x x x x −<⎧⎪=+≤<⎨⎪+≥⎩,所以当2x =时,322212y =+⋅=答案:12例2:阅读右边的程序框图,运行相应的程序,则输出的值为( )A .3B .4C .5D .6思路:循环的流程如下:① 1,2i a ==② 2,5i a ==③ 3,16i a ==④ 4,65i a ==i循环终止,所以4i =答案:B例3:某程序框图如图所示,若输出的57S =,则判断框内为( )A. 4?k >B. 5?k >C. 6?k >D. 7?k >思路:循环的流程如下:① 2,4k S ==② 3,11k S ==③ 4,26k S ==④ 5,57k S ==所以应该在此时终止,所以填入4?k >答案:A例4:执行右面的程序框图,如果输入的N 是6,那么输出的p 是( )A. 120B. 720C. 1440D. 5040思路:循环的流程如下:① 1p =② 2,2k p ==③ 3,6k p ==④ 4,24k p ==⑤ 5,120k p ==⑥ 6,720k p ==答案:B例5:右图是一个算法的流程图,则输出S 的值是______ 第4题思路:循环的流程如下: ① 1123S =+=② 22,327n S ==+=③ 33,7215n S ==+=④ 44,15231n S ==+=⑤ 55,31263n S ==+=循环结束,所以63S =答案:63S =例6:执行如图所示的程序框图,若输出i 的值为2,则输入x 的最大值是( )A .5B .6C .22D .33思路:因为输出的2i =,说明只经过了一次循环。
高三数学算法和程序框图试题
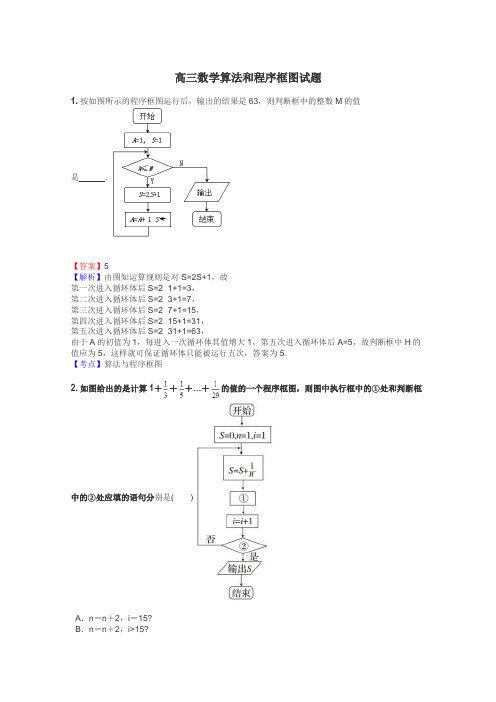
高三数学算法和程序框图试题1.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是.【答案】5【解析】由图知运算规则是对S=2S+1,故第一次进入循环体后S=2×1+1=3,第二次进入循环体后S=2×3+1=7,第三次进入循环体后S=2×7+1=15,第四次进入循环体后S=2×15+1=31,第五次进入循环体后S=2×31+1=63,由于A的初值为1,每进入一次循环体其值增大1,第五次进入循环体后A=5,故判断框中H的值应为5,这样就可保证循环体只能被运行五次,答案为5.【考点】算法与程序框图2.如图给出的是计算1+++…+的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句分别是()A.n=n+2,i=15?B.n=n+2,i>15?C.n=n+1,i=15?D.n=n+1,i>15?【答案】B【解析】①的意图为表示各项的分母,而分母相差2,∴n=n+2.②的意图是为直到型循环结构构造满足跳出循环的条件,而分母从1到29共15项,∴i>15,故选B.3.执行右侧的程序框图,若输入,则输出 .【答案】C【解析】第一次运行后y=5,第二次运行后y=,第三次运行后,此时,满足条件,故输出.【考点】程序框图.4.执行如图所描述的算法程序,记输出的一列的值依次为,其中且.(1)若输入,写出全部输出结果.(2)若输入,记,求与的关系().【答案】(1)输出结果共4个,依次是:.(2).【解析】(1)这是一个循环结构,依次写出每次循环的结果即可.(2)由框图中可得当时,.再由可得.将代入即可得与的关系.(1)这是一个循环结构,前4次输出的为:,第5次循环的结果为,与相等,故结束循环.所以输出的为:.(2)当时,..【考点】1、程序框图;2、递推数列.5.执行如图所示的程序框图,输出结果S= .【答案】-2013【解析】根据程序框图,,故输出的S为.【考点】程序框图.6.已知某程序框图如图所示,则该程序运行后输出的结果为( )A.B.C.D.【答案】A【解析】运行第一次:成立;运行第二次:成立;运行第三次:成立;运行第四次成立;运行第五次:成立;运行第2007次:成立;运行第2008次:不成立;输出A的值:故选A.【考点】循环结构.7.执行如图所示的程序框图,则输出的的值是______.【答案】【解析】程序在执行过程中,的值依次为:;;;;;故的值依次周期性的出现,而且周期为4,当时,,故输出的.【考点】程序框图.8.执行如图所示的程序框图,如果输入,,那么输出的a值为()A.B.C.D.【答案】C【解析】不成立,执行第一次循环,;不成立,执行第二次循环,;不成立,执行第三次循环,;成立,跳出循环体,输出的值为,故选C.【考点】算法与程序框图9.运行如图所示的程序框图,若输出的是,则①应为()A.n≤5B.n≤6C.n≤7D.n≤8【答案】C【解析】由程序框图算法可知,,由于输出,即,解得,故①应为“”,故选【考点】算法程序框图。
高一数学算法和程序框图试题答案及解析

高一数学算法和程序框图试题答案及解析1.如图所示,程序框图(算法流程图)的输出结果是()A.B.C.D.【答案】A【解析】条件成立,第一次执行循环体,条件成立,第二次执行循环体条件成立,第三次执行循环体;条件不成立,退出循环,输出.【考点】程序框图的识别和应用.2.若某程序图如图所示,则该程序运行后输出的k的值是()A.4B.5C.6D.7【答案】B【解析】第一次执行循环体,.第二次执行循环体,,.第三次执行循环体,【考点】理解程序框图的逻辑结构.3.如下图所示程序框图,已知集合是程序框图中输出的值},集合是程序框图中输出的值},全集U=Z,Z为整数集,当时,等于( )A.B.{-3. -1,5,7}C.{-3, -1,7}D.{-3, -1,7,9}【答案】D.【解析】依次执行程序框图中的语句:,;,;,;,;,;,;,;∴,,∴.【考点】读程序框图.4.在如图所示的程序框图中,输入A=192,B=22,则输出的结果是( ).A.0B.2C.4D.6【答案】B.【解析】本题要注意的是C是A除以B所得的余数,按程序框图可知有如下过程:原来:,第一次:C=16,A=22,B=16;第二次:C=6,A=16,B=6;第三次:C=4,A=6,B=4;第四次:C=2,A=4,B=2;第五次:C=0,A=2,B=0,此时B=0,则输出A=2,故选B.【考点】读懂程序框图的流程,赋值语句(如A=B,是把B的值赋值给A).5.如果执行右边的程序框图,那么输出的()A.22B.46C.94D.190【答案】C【解析】.运行第1次,=1,=1,=2,=4,=2>5,否,循环;运行第2次,=3,=10,=3>5,否,循环;运行第3次,=4,=22,=4>5,否,循环;运行第4次,=5,=46,=5>5,否,循环;运行第5次,=6,=94,=6>5,是,输出S=94,故选C【考点】程序框图6.按右边程序框图运算:若,则运算进行几次才停止?A.B.C.D.【答案】C【解析】第一次循环,第二次循环,第三次循环,第四次循环,第五次循环。
数学算法和程序框图试题答案及解析

数学算法和程序框图试题答案及解析1.运行如图所示的程序,若结束时输出的结果不小于3,则的取值范围为()A.B.C.D.【答案】D【解析】第一次运行后,第二次运行后,第三次运行后,此时,停止循环,则,即.2.一个算法的程序框图如右图所示,若该程序输出的P位于区间内,则判断框内应填入的条件是()A.B.C.D.【答案】C【解析】因为第一次循环,第二次循环,第三次循环,第四次循环,第五次循环,第六次循环,此时应结束循环,所以判断框中应填选C.【考点】程序框图3.执行如图所示的程序框图,输出的S值为时,则输入的的值为()A.B.C.D.【答案】D【解析】在程序执行过程中,的值依次为;;;,程序结束,输出的S值为.故,即.【命题意图】本题考查程序框图基础知识,意在考查学生基本运算能力和逻辑推理能力. 4.已知函数y=,写出求该函数函数值的算法及程序框图.【答案】见解析【解析】算法如下:第一步,输入x.第二步,如果x>0,则y=-2;如果x=0,则y=0;如果x<0,则y=2.第三步,输出函数值y.相应的程序框图如图所示.5.设计算法求+++…+的值,并画出程序框图.【答案】见解析【解析】算法如下:第一步,令S=0,i=1;第二步,若i≤2 011成立,则执行第三步;否则,输出S,结束算法;第三步,S=S+;第四步,i=i+1,返回第二步.程序框图:6.根据下列算法语句, 当输入x为60时, 输出y的值为()A.25B.30C.31D.61【答案】C【解析】,故选择C。
解答要注意条件的运用和判断。
【考点】本题考查算法程序,重点突出对条件语句的考查.是容易题。
7.如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则()A.A+B为a1,a2,…,aN的和B.为a1,a2,…,aN的算术平均数C.A和B分别是a1,a2,…,aN中最大的数和最小的数D.A和B分别是a1,a2,…,aN中最小的数和最大的数【答案】C【解析】由程序框图可知,当x>A时,A=x;当x≤A且x<B时,B=x,所以A是a1,a2,…,a N 中的最大数,B是a1,a2,…,aN中的最小数.故选C.8.执行如图所示的程序框图,则输出的S值是()A.-1B.C.D.4【答案】A【解析】本小题主要考查程序框图的应用.解题的突破口为分析i与6的关系.当i=1时,S==-1;当i=2时,S==;当i=3时,S==;当i=4时,S==4;当i=5时,S==-1;当i=6时程序终止,故而输出的结果为-1.9.程序框图如图所示,则该程序运行后输出的值是________.【答案】【解析】本题主要考查算法的程序框图及其应用.当i=1时,T==1,而i=1+1=2,不满足条件i>5;接下来,当i=2时,T=,而i=2+1=3,不满足条件i>5;接下来,当i=3时,T ==,而i=3+1=4,不满足条件i>5;接下来,当i=4时,T==,而i=4+1=5,不满足条件i>5;接下来,当i=5时,T==,而i=5+1=6,满足条件i>5;此时输出T =,故应填.10.某程序框图如图所示,现将输出值依次记为:若程序运行中输出的一个数组是则数组中的()A.32B.24C.18D.16【答案】A【解析】解:运行第一次,输出 , , ,运行第二次,输出运行第三次,输出运行第四次,输出运行第五次,输出运行第六次,输出所以选A.11.若如图所示的程序框图输出的S是30,则在判断框中M表示的“条件”应该是( ) A.B.C.D.【答案】B【解析】首先执行程序到,则应该填,故选B.12.某程序框图如图所示,若,则该程序运行后,输出的的值为()A.33B.31C.29D.27【答案】B【解析】若,,则;;满足条件继续,;不满足条件,输出,结束.13.执行程序框图,则输出的S是()A.5040B.4850C.2450D.2550【答案】C【解析】由程序框图分析可知:第一次循环:第二次循环:第三次循环:…,当时循环结束,此时,故输出的结果为2450,选C.14.某程序框图如图所示,该程序运行后输出的值是()A.63B.31C.27D.15【答案】A【解析】程序框图运行如下:15.某程序框图如图所示,则该程序运行后输出的值为.【答案】7【解析】开始时,,进入循环,;,继续循环,;,继续循环,;,跳出循环,故.16.执行如图所示的算法流程图,则最后输出的等于.【答案】63【解析】第一次循环,第二次循环,第三次循环,第四次循环,第六次循环,终止循环,输出.17.若某程序框图如右图所示,则该程序运行后输出的值为.【答案】8【解析】,不满足是奇数,,不满足;,不满足是奇数,,不满足;,满足是奇数,,不满足;,不满足是奇数,,不满足;,不满足是奇数,,不满足;,不满足是奇数,,不满足;,不满足是奇数,,满足,输出.18.在下图算法框图中,若输入,程序运行的结果那么判断框中应填入的关于的判断条件是()A.B.C.D.【答案】B.【解析】由,而输出,由程序框图使用列举法可得:,,结束算法,输出,因此判断框内条件应为“”故选B.【命题意图】本题考查定积分,算法框图中的顺序结构,条件结构、循环结构以及相应语句等基础知识,意在考查分析问题、解决问题的能力、基本运算能力及推理能力.19.对任意函数,,可按如图构造一个数列发生器,记由数列发生器产生数列{}.若定义函数,且输入,则数列{}的项构成的集合为()A.B.C.D.【答案】C【解析】∵的定义域,把代入可得,把代入可得,把代入可得,因为,所以数列只有三项:,,.【命题意图】本题考查程序框图基础知识,意在考查学生基本运算能力和运算能力.20.如图所示,程序框图(算法流程图)的输出结果是,那么判断框中应填入的关于的判断条件是()A.B.C.D.【答案】B【解析】经分析,此时满足题意,循环终止,故选B.【命题意图】本题主要考程序框图和循环结构等基础知识,意在考查学生是否理解和认识,并能利用程序框图解决问题的能力.。
高考常考基础题3 程序框图(答案版)
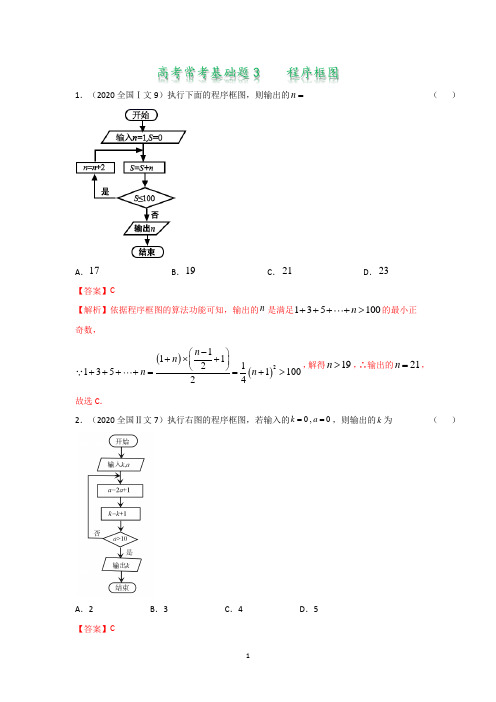
高考常考基础题3 程序框图1.(2020全国Ⅰ文9)执行下面的程序框图,则输出的 ( )A .B .C .D .【答案】C【解析】依据程序框图的算法功能可知,输出的是满足的最小正奇数,,解得,∴输出的,故选C .2.(2020全国Ⅱ文7)执行右图的程序框图,若输入的,则输出的为()A .2B .3C .4D .5【答案】Cn=17192123n 135100n ++++>()()211112135110024n n n n -⎛⎫+⨯+ ⎪⎝⎭++++==+>19n >21n =0,0k a ==k【解析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出的值,模拟程序的运行过程:,第1次循环,,为否; 第2次循环,,为否;第3次循环,,为否;第4次循环,,为是,退出循环,输出.故选C .3.(2019全国Ⅰ文理】如图是求的程序框图,图中空白框中应填入( )A .B .C .D . 【答案】A【解析】初始:,∵第一次应该计算=,=2; 执行第2次,,∵第二次应该计算=,=3, k 0,0k a ==2011a =⨯+=,011k =+=210>2113a =⨯+=,112k =+=310>2317a =⨯+=,213k =+=710>27115a =⨯+=,314k =+=1510>4k =112122++12A A =+12A A=+112A A =+112A A=+1,122A k ==≤1122+12A +1k k =+22k =≤112122++12A +1k k =+结束循环,故循环体为,故选A . 【秒杀速解】认真观察计算式子的结构特点,可知循环体为. 4.(2019全国Ⅲ文理】执行下边的程序框图,如果输入的为0.01,则输出的值等于A .B .C .D . 【答案】C【解析】输入的为,不满足条件; 不满足条件;满足条件,结束循环; 输出,故选C . 12A A=+12A A =+εs 4122-5122-6122-7122-ε0.0111,01,0.01?2x s x ==+=<1101,0.01?24s x =++=<⋅⋅⋅611101,0.00781250.01?22128S x =++++==<676111112(1)22222S =+++=⨯-=-5.(2018全国Ⅱ文理)为计算,设计了如图的程序框图,则在空白框中应填入 A . B . C . D .【答案】B 【解析】由程序框图的算法功能知执行框计算的是连续奇数的倒数和,而执行框计算的是连续偶数的倒数和,∴在空白执行框中应填入的命令是,故选B .11111123499100=-+-++-…S1=+i i 2=+i i 3=+i i 4=+i i 1=+N N i11=++T T i 2=+i i6.(2017新课标Ⅰ文理)下面程序框图是为了求出满足的最小偶数,那A.和B.和C.和D.和【答案】D【解析】由题意选择,则判定框内填,由∵选择偶数,∴矩形框内填,故选D.7.(2017新课标Ⅲ文理)执行下面的程序框图,为使输出的值小于91,则输入的正整数的最小值为A.5 B.4 C.3 D.2【答案】D【解析】若,第一次循环,成立,,,321000n n->n 1000A>1n n=+1000A>2n n=+1000A≤1n n=+1000A≤2n n=+321000n n->1000A≤2n n=+SN2N=12≤100S=10M=-22i=≤成立,第二次循环,此时,,不成立,∴输出成立,∴输入的正整数的最小值是2,故选D .8.(2015新课标II 文理)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入分别为14,18,则输出的=A .0B .2C .4D .14【答案】B 【解析】第一次执行,输入,,∵,∴; 第二次执行,输入,,∵,∴; 第三次执行,输入,,∵,∴; 第四次执行,输入,,∵,∴; 第五次执行,输入,,∵,∴;此时.9.(2013新课标I 文理)执行如图程序框图,如果输入的,则输出s 属于A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]【答案】A 【解析】有题意知,当时,,当时,90S =1M =32i =≤9091S =<N ,a ba 14a 18b a b 18144b =-=14a 4ba b >14410a =-=10a 4ba b >1046a =-=6a4b a b >642a =-=2a 4b a b <422b =-=2a b [1,3]t ∈-[1,1)t ∈-3s t =[3,3)∈-[1,3]t ∈24s t t =-,∴输出s 属于[3,4],故选.10.(2013江西文理)阅读如图程序框图,如果输出,那么在空白矩形框中应填入的语句为A .B .C .D .【答案】C 【解析】由题意,当时,空白的判断框中的语句应使;故选项A ,B 中,当 时,都有;故排除;假设空白的判断框中的语句是C 项中的,则第一次运行时,;第二次运行时,;第三次运行时,;第四次运行时,;此时不满足,故输出,满足题意,故选C .[3,4]∈-A 5i =2*2S i =-2*1S i =-2*S i =2*4S i =+5i =10S ≥5i =10S <2*S i =2,5i S ==3,6i S ==4,9i S ==5,10i S ==10S <5i =11.(2012新课标文理)如果执行如图的程序框图,输入正整数和实数,输出、,则A .为的和B .为的算术平均数 C .和分别是 中最大的数和最小的数D .和分别是 中最小的数和最大的数【答案】C 【解析】由当时可知应为中最大的数,由当时可知应为中最小的数.)2(≥N N N a a a ,,,21 A B B A +N a a a ,,,21 2B A +N a a a ,,,21 A B N a a a ,,,21 A B N a a a ,,,21 x A >A x =A 12,,,N a a a ⋅⋅⋅x B <B x =B 12,,,N a a a ⋅⋅⋅1+=k k xA =xB =11,,1a B a A k ===ka x =?A x >?B x <?N k ≥BA, 输出Na a a ,,,N,21 输入 开始结束是是是否否否。
高考数学算法初步与程序框图练习和答案
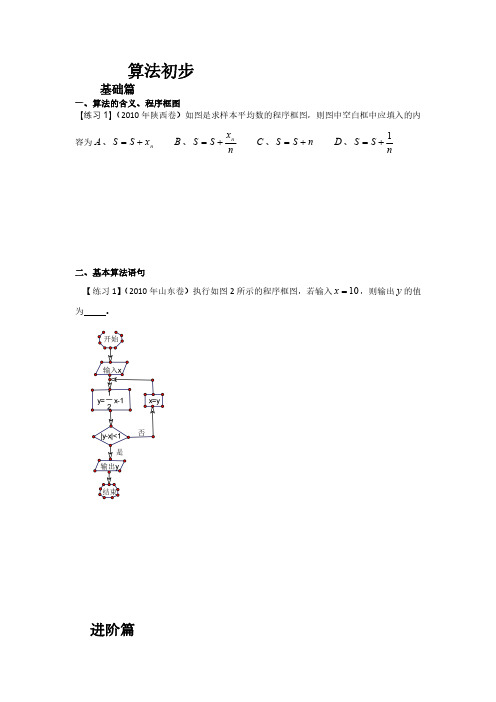
算法初步基础篇一、算法的含义、程序框图【练习1】(2010年陕西卷)如图是求样本平均数的程序框图,则图中空白框中应填入的内容为A 、n x S S +=B 、n x S S n +=C 、n S S +=D 、nS S 1+=二、基本算法语句【练习1】(2010年山东卷)执行如图2所示的程序框图,若输入10=x ,则输出y 的值为。
进阶篇一、求输出结果类【练习1】下图为某算法的程序框图,则程序运行后输出的结果是▲.x。
【练习2】(2010年安徽卷)如图所示,程序框图(算法流程图)的输出值【练习3】(2010年福建卷)阅读如图3所示的程序框图,运行相应的程序,输出的i 的值等于A 、2B 、3C 、4D 、5二、填条件类【练习1】(2010年浙江卷)某程序框图如图所示,若输出的57=S ,则判断框内为A 、?4>k B 、?5>k C 、?6>k D 、?7>k三、问它在干什么类【练习1】给出以下一个算法的程序框图,该程序框图的功能是()A.求出a、b、c三数中的最大数B.求出a、b、c三数中的最小数C.将a、b、c按从小到大排列D.将a、b、c按从大到小排列算法初步基础篇一、算法的含义、程序框图【练习1】【分析】:依据题中提供的框图可知,图中所示的算法功能是求样本平均数,故应先求和:【答案】:依据题设中框图的算法程序可知该框图的算法功能是求样本1021,,,x x x ⋅⋅⋅的平均数x ,因此可先求1021,,,x x x ⋅⋅⋅的和S ,按循环的程序n x S S +=,故应选正确答案A 。
二、基本算法语句【练习1】【解析】当10=x 时,4=y ,不满足1||<-x y ,执行y x =;当4=x 时,1=y ,不满足1||<-x y ,执行y x =;当1=x 时;21-=y ,不满足1||<-x y ,执行y x =;当4=x 时;当21-=x 时,45-=y ,满足1||<-x y ,故输出的y 的值是45-。
高中数学算法流程图试题与详细解析
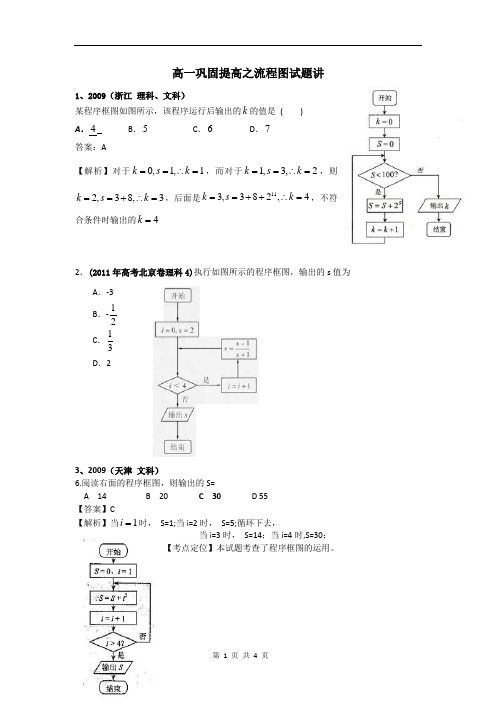
高一巩固提高之流程图试题讲1、2009(浙江 理科、文科)某程序框图如图所示,该程序运行后输出的k 的值是 ( ) A .4 B .5 C .6 D .7答案:A【解析】对于0,1,1k s k ==∴=,而对于1,3,2k s k ==∴=,则2,38,3k s k ==+∴=,后面是113,382,4k s k ==++∴=,不符合条件时输出的4k =2.(2011年高考北京卷理科4)执行如图所示的程序框图,输出的s 值为 A .-3B .-12C .13D .23、2009(天津 文科)6.阅读右面的程序框图,则输出的S=A 14B 20C 30D 55 【答案】C【解析】当1=i 时, S=1;当i=2时, S=5;循环下去,当i=3时, S=14;当i=4时,S=30;【考点定位】本试题考查了程序框图的运用。
4、2009(天津 理科)(5)阅读右图的程序框图,则输出的S=A. 26B. 35C. 40D. 57 【考点定位】本小考查框架图运算,基础题。
解:当1=i 时,2,2==S T ;当2=i 时,7,5==S T ;当3=i 时,15,8==S T ;当4=i 时,26,11==S T ;当5=i 时,40,14==S T ;当6=i ,i>5输出结果,故选择C 。
5、2009(广东 理科)随机抽取某产品n 件,测得其长度分别为12,,,n a a a ,则图3所示的程序框图输出的s = ,s 表示的样本的数字特征是 .(注:框图中的赋值符号“=”也可以写成“←”“:=”) 【解析】s =na a a n+⋅⋅⋅++21;平均数6、2009(上海 理科)某算法的程序框如右图所示,则输出量y 与输入量x 满足的关系式是____________________________ .开始输出S 结束i>5?是否S=0,i=1T=3i-1S=S+T i=i+1答案:2,12,1x x y x x ⎧≤=⎨->⎩7、2009(安徽 文科、理科)程序框图(即算法流程图)如图所示,其输出结果是_______。
高二数学算法和程序框图试题答案及解析

高二数学算法和程序框图试题答案及解析1.阅读如图所示的程序框图,如果输入的n的值为6,那么运行相应程序,输出的n的值为.【答案】5.【解析】进入循环前n=6.i=0,此时n为偶数,故=3,i=1,满足继续进行循环的条件;当n=3.i=1,此时n为奇数,故n=3n+1=10,i=2,满足继续进行循环的条件;n=10.i=2,此时n为偶数,故=5,i=3,不满足继续进行循环的条件;故输出的n值为5【考点】程序框图.2.下面框图所给的程序运行结果为S=28,那么判断框中应填入的关于k的条件是( )A.?B.k≤7?C.k<7?D.k>7?【答案】D【解析】运行第1次,k=10,S=1,不是输出结果,满足条件,循环,S=S+k=11,k=k-1=9;运行第2次,k=9,S=11,不是输出结果,满足条件,循环,S=S+k=20,k=k-1=8;运行第3次,k=8,S=20,不是输出结果,满足条件,循环,S=S+k=28,k=k-1=7;运行第4次,k=7,S=28,是输出结果,故不满足条件,故应填入关于k的条件为k>7?,故选D. 考点:程序框图3.如图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是()A.B.C.D.【答案】A【解析】由图可知,第一次循环之后值增加2,的值为3,然后在执行循环体,的值增加2,的值为5,此时循环下去最后变化到,当,判定框的条件成立,执行循环体因此选.【考点】程序框图的应用.4.读下面的流程图,若输入的值为-5时,输出的结果是_________【答案】2【解析】按程序流程计算即可.-5,-3,-1,1,2,输出A=2.【考点】程序推断.5.执行如图所示的程序框图,输出的值为()A.B.C.D.【答案】C【解析】由初始条件为:k=0,S=0;第一次运行:判断0<3是否成立?是,则;第二次运行:判断1<3是否成立?是,则;第三次运行:判断2<3是否成立?是,则;第四次运行:判断3<3是否成立?否,则输出;故选C.【考点】算法与程序框图.6.执行右侧的程序框图,若输入n=3,则输出T= .【答案】20【解析】输入n=3,则初始条件为:n=3,i=0,S=0,T=0,运行第一次:03,是,i=i+1=1,S=1,T=S=1;运行第二次:13,是,i=i+1=2,S=1+2=3,T=1+3=4;运行第三次:23,是,i=i+1=3,S=3+3=6,T=4+6=10;运行第四次:33,是,i=i+1=4,S=6+4=10,T=10+10=20;运行第五次:43,否,输出T=20.故应填入20.【考点】算法与程序框图.7.阅读如图的程序框图.若输入n=5,则输出k的值为( )A.B.C.D.【答案】B【解析】经过第一次循环得到的结果为,此时不满足退出循环的条件,经过第二次循环得到的结果为,此时不满足退出循环的条件,经过第三次循环得到的结果为,此时不满足退出循环的条件,经过第四次循环得到的结果为,满足判断框中的条件,执行“是”输出的k为3【考点】循环结构8.执行如图所示的程序框图,则输出的值为()A.3B.-6C.10D.-15【答案】C【解析】由已知可得该程序的功能是计算并输出的值,所以输出的值为=10,故选C.【考点】程序框图.9.根据如图所示的流程图,则输出的结果为___________.【答案】16【解析】由图知,起始数据为,,第一次执行循环体后,,满足条件;第二次执行循环体后,,满足条件;第三次执行循环体后,,不满足条件,退出循环体,故输出的结果为.【考点】直到型循环结构.10.按流程图的程序计算,若开始输入的值为,则输出的的值是【答案】231【解析】根据框图的循环结构,依次;;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中算法程序框图一.选择题(共18小题)
1.如图给出了一个算法程序框图,该算法程序框图的功能是()
8.阅读如图所示的程序框图,运行相应的程序,输出的结果为()
9.阅读如图所示的程序框图,运行相应的程序,输出的结果是()
10.(2014•福建)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()
11.(2014•北京)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()
12.(2013•辽宁)执行如图所示的程序框图,若输入n=10,则输出的S=()
.C D.
14.(2012•福建)阅读如图所示的程序框图,运行相应的程序,输出s值等于()
15.(2012•广东)执行如图所示的程序框图,若输入n的值为6,则输出s的值为()
16.(2012•辽宁)执行如图所示的程序框图,则输出的S的值是()
C D
17.(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()
18.(2011•北京)执行如图所示的程序框图,输出的s值为()
D
二.填空题(共9小题)
19.程序框图(如图所示),则该程序框图表示的算法的功能是:_________.
20.有如图程序框图,则该程序框图表示的算法功能是_________.
21.如图所示的程序框图,其算法功能是_________.
22.(2014•许昌三模)如图所示,程序框图(算法流程图)的输出结果是_________.
23.如图所示的程序框图表示的算法的结果是_________.
24.某算法的程序框图如图所示,则程序输出y的值是_________.
25.(2011•江西)下图是某算法的程序框图,则程序运行后所输出的结果是_________.
26.(2014•惠州模拟)如图所示,程序框图(算法流程图)的输出结果为_________.
27.阅读如图所示的程序框图,运行相应的程序,则输出的s值等于_________.
三.解答题(共1小题)
28.如图所示,程序框图(算法流程图)的输出结果是_________.
参考答案与试题解析
一.选择题(共18小题)
1.如图给出了一个算法程序框图,该算法程序框图的功能是()
2.如图给出一个算法的程序框图,该程序框图的功能是()
3.(2012•三明模拟)如图给出一个算法的程序框图,该程序框图的功能是()
4.程序框图表示的算法的运行结果是()
5.程序框图中所表示的算法是()
y=
6.(2014•泉州一模)运行图中所示程序框图所表达的算法,输出的结果是()
7.(2013•合肥二模)如图所示,程序框图(算法流程图)的输出结果是()
8.阅读如图所示的程序框图,运行相应的程序,输出的结果为()
9.阅读如图所示的程序框图,运行相应的程序,输出的结果是()
10.(2014•福建)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()
11.(2014•北京)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()
12.(2013•辽宁)执行如图所示的程序框图,若输入n=10,则输出的S=()
.C D.
,
,
,
的值为.
13.(2012•天津)阅读程序框图,运行相应的程序,当输入x的值为﹣25时,输出x的值为()
x=
x=
14.(2012•福建)阅读如图所示的程序框图,运行相应的程序,输出s值等于()
15.(2012•广东)执行如图所示的程序框图,若输入n的值为6,则输出s的值为()
16.(2012•辽宁)执行如图所示的程序框图,则输出的S的值是()
C D
S=
S=
17.(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()
=
S=1++=
S=1+++
18.(2011•北京)执行如图所示的程序框图,输出的s值为()
D
﹣
二.填空题(共9小题)
19.程序框图(如图所示),则该程序框图表示的算法的功能是:计算并输出使1×3×5×7×…>10000成立的最小整数.
20.有如图程序框图,则该程序框图表示的算法功能是求使不等式1×3×5×…×i≥10000成立的最小i值.
21.如图所示的程序框图,其算法功能是计算并输出使1×3×5×7×…>1000成立的最小整数.
22.(2014•许昌三模)如图所示,程序框图(算法流程图)的输出结果是﹣2.
23.如图所示的程序框图表示的算法的结果是127.
24.某算法的程序框图如图所示,则程序输出y的值是﹣1.
25.(2011•江西)下图是某算法的程序框图,则程序运行后所输出的结果是27.
26.(2014•惠州模拟)如图所示,程序框图(算法流程图)的输出结果为.
,
+=
+=
.
故答案为:
27.阅读如图所示的程序框图,运行相应的程序,则输出的s值等于46.
三.解答题(共1小题)
28.如图所示,程序框图(算法流程图)的输出结果是.
由此可得结论.解:根据程序框图,程序的功能是求和
故答案为:。
