江西省四校2011-2012学年高二数学零班期中联考试题 理
江西省四校2011-2012学年高二数学零班期中联考试题 理
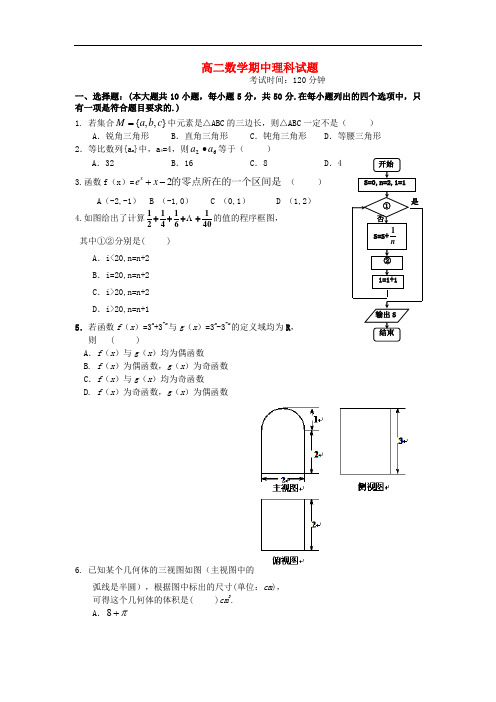
高二数学期中理科试题考试时间:120分钟一、选择题:(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.)1. 若集合},,{c b a M =中元素是△ABC 的三边长,则△ABC 一定不是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形 2.等比数列{a n }中,a 4=4,则62a a ∙等于( )A .32B .16C .8D .43.函数f (x )=2xe x +-的零点所在的一个区间是 ( ) A (-2,-1) B (-1,0) C (0,1) D (1,2)4.如图给出了计算401614121++++ 的值的程序框图,其中①②分别是( ) A .i<20,n=n+2 B .i=20,n=n+2 C .i>20,n=n+2 D .i>20,n=n+15.若函数f (x )=3x+3-x与g (x )=3x-3-x的定义域均为R ,则 ( )A .f (x )与g (x )均为偶函数 B. f (x )为偶函数,g (x )为奇函数C .f (x )与g (x )均为奇函数 D. f (x )为奇函数,g (x )为偶函数6. 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )cm 3.A .π+8B .328π+C .π+12D .3212π+7.“|x|<2”是“x 2-x-6<0”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件8.若21nx x ⎛⎫- ⎪⎝⎭的展开式中含x 的项为第6项,设nn n x a x a x a a x ++++=- 2210)31(,则n a a a +++ 21的值为 ( )A .255B . 32C .-225D .- 329.设=(1,-2),OB =(a,-1),OC =(-b ,0),a>0,b>0,O 为坐标原点,若A 、B 、C三点共线,则ba 21+的最小值是( )A .2B .4C .6D .810.已知函数)2,0(sin cos )(π∈-=x x x m x f 在单调递增,则实数m 的取值范围为( )A .)0,(-∞B .]1,(-∞YC Y C .]0,(-∞D .)1,(-∞二、填空题(本大题共5小题,每小题5分,共25分,请将正确答案填写在横线上) 11. 高二某班甲、乙两名学生在本学期的其中5次数学考试 成绩的茎叶图如图所示,甲、乙两人5次数学考试成绩 的中位数分别为 ; 平均数分别为 .12.已知函数0()sin ,af a xdx =⎰则[()]2f f π= . 13.已知数列{a n }中,a 1=21,a n+1=a n +1412-n ,则a n =________.14.已知M={(x,y )|x+y ≤6,x ≥0,y ≥0},N={(x,y )|x ≤4,y ≥0,x-2y ≥0},若向区域M 随机投一点P ,则P 落入区域N 的概率为15.如图,四边形OABC 是边长为1的正方形,OD =3,点P 为△BCD 内(含边界)的动点,设(,)OP OC OD R αβαβ=+∈,则αβ+的最大值等于 .第11题图甲乙7 4 2 87899016 3 0三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)16.( 12分)已知函数2()22sin f x x x =-. (1)求函数()f x 的最大值; (2)求函数()f x 的零点的集合.17.( 12分)横峰中学将在四月份举行安全知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为32. (Ⅰ)求选手甲可进入决赛的概率;(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.18.( 12分)直四棱柱1111ABCD A BC D -中,底面ABCD 为菱形,且 160,,BAD A A AB E ∠==为1BB 延长线上的一点,1D E ⊥面1D AC .(Ⅰ)求二面角1E AC D --的大小;(Ⅱ)在1D E 上是否存在一点P ,使1//A P 面EAC ?若存在,求1:D P PE 的值;不存在,说明理由.19. ( 12分)已知函数xf (x )ln(e a )=+(a 为常数)是R 上的奇函数,函数x x f x g sin )()(+=λ是区间[-1,1]上的减函数.(1)求a 的值;(2)若]1,1[1)(2-∈++<x t t x g 在λ上恒成立,求t 的取值范围20.(13分)设数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有0n a >,n S =(1)求1a ,2a 的值;(2)求数列{}n a 的通项公式n a ;21.( 14分)已知圆O :122=+y x ,点O 为坐标原点,一条直线l :)0(>+=b b kx y 与圆O 相切并与椭圆1222=+y x 交于不同的两点A 、B (1)设)(k f b =,求)(k f 的表达式;(2)若32=⋅OB OA ,求直线l 的方程;(3)若)4332(≤≤=⋅m m OB OA ,求三角形OAB 面积的取值范围.高二数学 (理) (期中)参考答案1. D2.B3. C4. C5. B6. A7.C8. A9. D 10. B 11. 84,82, 84,84 12. 1cos1- 13.2434--n n 14. 9215. 4317.【解】 (Ⅰ) 选手甲答3道题进入决赛的概率为278)32(3=; ……………1分选手甲答4道题进入决赛的概率为2783231)32(223=⋅⋅C ;…………………………3分选手甲答5道题进入决赛的概率为811632)31()32(2224=⋅⋅C ; …………………5分∴选手甲可进入决赛的概率278=p +278+81168164=. …………………7分(Ⅱ)依题意,ξ的可能取值为3,4,5.则有31)31()32()3(22=+==ξP ,27103132)31(3231)32()4(223223=⋅⋅+⋅⋅==C C p ξ,27831)31()32(32)31()32()5(22242224=⋅⋅+⋅⋅==C C p ξ, …………………………10分因此,有ξ 345P31 2710 2782732727527433==⋅+⋅+⋅=∴ξE . (12)分18.解:(Ⅰ)设AC 与BD 交于O ,如图所示建立空间直角坐标系O xyz -,设2AB =, 则1(3,0,0),(0,1,0),(3,0,0),(0,1,0),(0,1,2),A B C D D ---设(0,1,2),E h +则11(0,2,),(23,0,0),(3,1,2),D E h CA D A ===-1D E ⊥平面1111,,,D AC D E AC D E D A ∴⊥⊥220,1,h h ∴-=∴=即(0,1,3)E ……………………2分1(0,2,1),(3,1,3)D E AE ∴==-设平面EAC 的法向量为(,,)m x y z =则由,,m CA m AE ⊥⊥得30x y z =-++= 令1z =-∴平面EAC 的一个法向量为(0,3,1)m =-又平面1D AC 的法向量为11112(0,2,1),cos ,m D E D E m D E m D E ⋅=∴<>==⋅||||∴二面角1E AC D --大小为45…………………………………………………6分19.解:(1)x f (x)ln(e )a =+是奇函数,x x ln(e )ln(e )a a -∴+=-+,1))((=++∴-a e a e x x0)(,112=++∴=+++∴--a e e a a ae ae x x x x ,故a=0. . ………………4分(2)由(I )知:x x x g x x f sin )(,)(+=∴=λ,]1,1[)(-在x g 上单调递减, 0cos )('≤+=∴x x g λx cos -≤∴λ在[-1,1]上恒成立,1-≤∴λ,1sin )1()]([max --=-=λg x g ,11sin 2++<--∴t t λλ只需 01sin )1(2>++++∴t t λ(其中1-≤λ)恒成立, ………………8分令)1(011sin )1()(2-≤>++++=λλλt t h ,则2t 10,t 1t sin110,+<⎧⎨--+++>⎩01sin ,01sin 122>+-⎩⎨⎧>+--<∴t t t t t 而恒成立, 1-<∴t ………………12分20.(1)解:当1n =时,有11a S ==0n a >,所以11a =.当2n =时,有2S =12a a +=将11a =代入上式,由于0n a >,所以22a =. …………………4分21.解 (1)(0)y kx b b =+>与圆221x y +=相切,1=,即221(0)b k k =+≠,所以.12+=k b ………………………………4分(2)设1122(,),(,),A x y B x y 则由2212y kx bx y =+⎧⎪⎨+=⎪⎩,消去y 得:222(21)4220k x kbx b +++-=又280(0)k k ∆=>≠,所以2121222422,.2121kb b x x x x k k -+=-=++ …………6分 则1212OA OB x x y y ⋅=+=221.21k k ++由23OA OB ⋅=, 所以21.k =所22.b=0,b b >∴=所以:l y x y x ∴==-……………………9分(3)由(2)知: 22123.,2134k m m k +=≤≤+所以22213,3214k k +≤≤+ 211,2k ∴≤≤由弦长公式得||AB =所以1||2S AB ==解得2.43S ≤≤ ……14分。
2011-2012学年第一学期期中考试高二数学科试题参考答案

1 / 22011-2012学年第一学期期中考试高二数学科试题参考答案一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置。
11.62 12. 13.14 14.55三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤。
15.解:由于方程无实根∴ ……………4分化简: ……………6分 解得∴实数的取值范围为. ……………10分 16.解(1) ……………2分= ……………6分所以. ……………8分 (2) ……………10分 . ……………14分 17.解:(1)⎪⎩⎪⎨⎧=⨯+=+410219202020911d a d a ……………4分 即……………7分……………8分 (2) ……………11分 得:……………14分 18.解:在中,,,, ……………6分为等腰三角形,,……………8分 作BD 垂直AC 交于D 在中,,,,……………12分……………13分故该船没有触礁的危险.……………14分19.解:设生产甲种棉纱x吨,乙种棉纱吨,…………2分又由题意知,…………6分由此作出可行域如图所示. ……9分把函数变形为,作出直线l:并平移,由图像知,当直线经过Mz能取到最大值,由,解得,即M(120,60)∴(元)…………13分∴生产甲种棉纱120吨,乙种棉纱元.…………14分20.解:(1) 当时, …………1分当时, …………3分∴当时也满足①式所以数列的通项公式为…………4分又且即∴…………6分∴…………7分(2)∵…………8分∴①…………9分① 得②…………10分由①-②得…………11分…………13分∴…………14分温馨提示-专业文档供参考,请仔细阅读后下载,最好找专业人士审核后使用!2 / 2。
江西省高二下学期数学期中联考试卷(含答案)

江西省高二下学期数学期中联考试卷姓名:________ 班级:________ 成绩:________一、单选题(共10题;共20分)1.设集合A={x|x2−5x+6>0},B={x|x−1<0},则A∩B=()A.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)2.已知实数a,b满足a2+b2=4,则ab的取值范围是()A.[0,2]B.[−2,0]C.(−∞,−2]∪[2,+∞)D.[−2,2]3.已知条件p:x>1,q:1x<1,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知0<θ<π4,则双曲线C1:x2sin2θ−y2cos2θ=1与C2:y2cos2θ−x2sin2θ=1的()A.实轴长相等B.虚轴长相等C.离心率相等D.焦距相等5.设变量x,y满足约束条件:{y≥xx+2y≤2x≥−2,则z=x−3y的最小值()A.-2B.-4C.-6D.-86.定义在R上的奇函数y=f(x)满足 f(3)=0,且不等式f(x)>−xf′(x)在(0,+∞)上恒成立,则函数g(x)= xf(x)+lg|x+1|的零点的个数为()A.4B.3C.2D.17.已知函数f(x)=e x, g(x)=ln x2+12,对任意a∈R,存在b∈(0,+∞),使得f(a)=f(b),则b−a的最小值为()A.2√3−1B. e28.若仅存在一个实数t∈(0,π2),使得曲线C:y=sin(ωx−π6)关于直线x=t对称,则ω的取值范围是()A.[13,73) B. [43,103) C.(13,73] D. (43,103]2=2px(p>0)的交点为A,B,直线AB经过抛物线的焦点F,且线段AB的长度等于双曲线的虚轴长,则双曲线的离心率为()A.√2+1B.3C.10.定义平面向量之间的一种运算“⊙”如下:对任意的a⃗=(m,n),b⃗⃗=(p,q),令a⃗⊙b⃗⃗=mq−np,下面说法错误的是()A.若a⃗与b⃗⃗共线,则a⃗⊙b⃗⃗=0B.a⃗⊙b⃗⃗=b⃗⃗⊙a⃗C.对任意的λ∈R,有(λa⃗)⊙b⃗⃗=(λa⃗⊙b⃗⃗)D.(a⃗⊙b⃗⃗)2+(a⃗∙b⃗⃗)2=|a⃗|2|b⃗⃗|2二、填空题(共7题;共8分)11.已知函数f(x)={3|x|−1,−1≤x≤1−32x2+6x−4,x>1,实数a,b,c,d∈[−1,+∞)且a<b<c<d,满足f(a)=f(b)=f(c)=f(d),则lg(−a)−lgb+4c+26−d的取值范围是________.12.若不等式组{x 2−x −2>02x 2+(5+2k )x +5k <0的整数解只有-2,则k 的取值范围是________.13.如图,五边形ABCDE 由两部分组成,∆ABE 是以角B 为直角的直角三角形,四边形BCDE 为正方形,现将该图形以AC 为轴旋转一周,构成一个新的几何体。
江西省四校2011-2012学年高二下学期第三次月考数学(理)试题
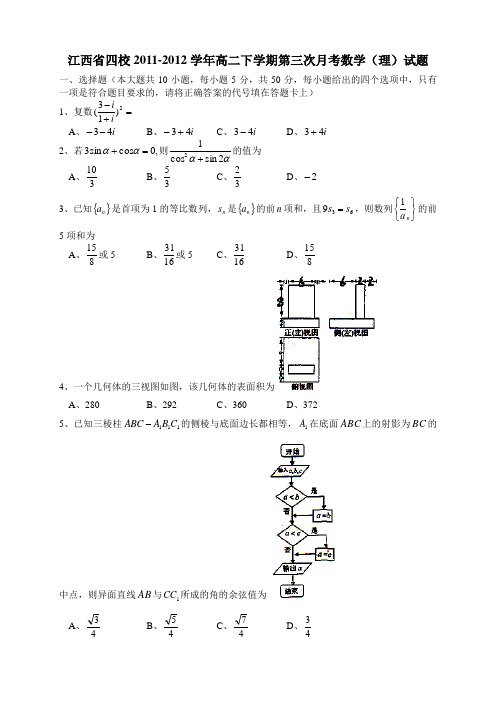
江西省四校2011-2012学年高二下学期第三次月考数学(理)试题一、选择题(本大题共10小题,每小题5分,共50分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答题卡上)1、复数=+-2)13(i iA 、i 43--B 、i 43+-C 、i 43-D 、i 43+2、若,0cos sin 3=+αα则αα2sin cos 12+的值为A 、310B 、35C 、32D 、2-3、已知{}n a 是首项为1的等比数列,n s 是{}n a 的前n 项和,且639s s =,则数列⎭⎬⎫⎩⎨⎧n a 1的前5项和为A 、815或5B 、1631或5 C 、1631 D 、815 4、一个几何体的三视图如图,该几何体的表面积为A 、280B 、292C 、360D 、3725、已知三棱柱111C B A ABC -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为A 、43 B 、45 C 、47D 、436、由曲线32,x y x y ==围成的封闭图形面积为 A 、121 B 、41C 、31D 、127 7、若,3,3log ),18sin 18(cos 222121==-=c b a 执行如图所示的程序框图,则输出的结果是A 、)18sin 18(cos 22- B 、3log 21C 、213D 、)18sin 18(cos 22-或213 8、设y x ,满足约束条件,0,002063⎪⎩⎪⎨⎧≥≥≥+-≤--y x y x y x 若目标函数)0,0(>>+=b a by ax z 的最大值为12,则ba 32+的最小值为 A 、625 B 、38C 、311D 、49、已知椭圆)0(1:2222>>=+b a b y a x C 的离心率为23,过右焦点F 且斜率为)0(>k k 的直线与C 相交于A 、B 两点,若3=,则k = A 、1B 、2C 、3D 、210、用},min{b a 表示b a ,两数中的最小值,若函数{}|||,|m in )(t x x x f +=的图象关于直线21-=x 对称,则t 的值为A 、2-B 、2C 、1-D 、1 二、填空题(本大题共5小题,每小题5分,共25分)11、已知点P 在曲线14+=x e y 上,α为曲线在点p 处的切线的倾斜角,则α的取值范围是 。
2011—2012学年度第一学期南昌市期中形成性测试卷高二数学答案

2011—2012学年度第一学期南昌市期中形成性测试卷高二数学(理科甲卷)参考答案及评分意见一、选择题(本大题共10小题,每小题3分,共30分)二、填空题(本大题共5小题,每小题4分,共20分,请将正确答案填写在横线上) 11.2637; 12.25)2()1(22=-+-y x ; 13.3; 14. 4; 15.181622=+yx。
三、解答题(本大题共5小题,共50分.解答应写出文字说明、证明过程或演算步骤) 16.解:圆014222=++-+y x y x 的圆心为(1,-2)………………………………3分 圆心到切线的距离为半径,既r ==6分所以要求圆的方程为22(1)(2)5x y -++=…………………………………………………8分 17.解:设直线l 的方程为1y kx -=或0x =,……………………………………………2分17310031y kx x x y k =+⎧⇒=⎨-+=-⎩; ……………………………………………………………4分 172802y kx x x y k =+⎧⇒=⎨+-=+⎩, ………………………………………………………………6分 由770312k k +=-+,得14k =-, (8)分又直线0x =不合题意. ………………………………………………………………………9分 ∴所求直线方程为440x y +-=. …………………………………………………………10分18.解:原方程可变形为322++m m ymx=1,因为m >0,所以焦点在x 轴,………………2分即32,3,2++=+==m m m c m m b m a ,所以23==ac e , (5)分将c .a 代入解得m =1………………7分 所以椭圆的标准方程为14122=+yx ,所以长轴长为2,短轴长为1,…………………9分焦点为(23,0),(-23,0)……………………………………………………………10分19.解:依抛物线定义可得到焦点与到准线的距离相等,所以有A 点到准线的距离为8714,由抛物线方程可知准线为:x =87,由此可知A 点的横坐标为-14,………………………4分代入抛物线方程可解得纵坐标为±7,所以A 点坐标为(-14,±7)…………6分因为直线l 与直线OA 垂直,所以2±=l k ,…………………………………………………8分又因为经过焦点(0,87-),所以直线l 的方程为)87(2+=x y ,)87(2+-=x y化简得472+=x y 472--=x y ……10分20.解:(1)由22141y kx x y =+⎧⎨-=⎩消去y 得22(4)220k x kx ---=(*), (1)分当2400k ⎧-≠⎨∆>⎩,解得k -<<(2k≠±)时,l 与C 有两个交点A 、B (2)分设A (1x ,1y ),B (2x ,2y ),因OA OB ⊥ ,故0OA OB ⋅=。
江西省四校-高二数学零班期中联考试题 理
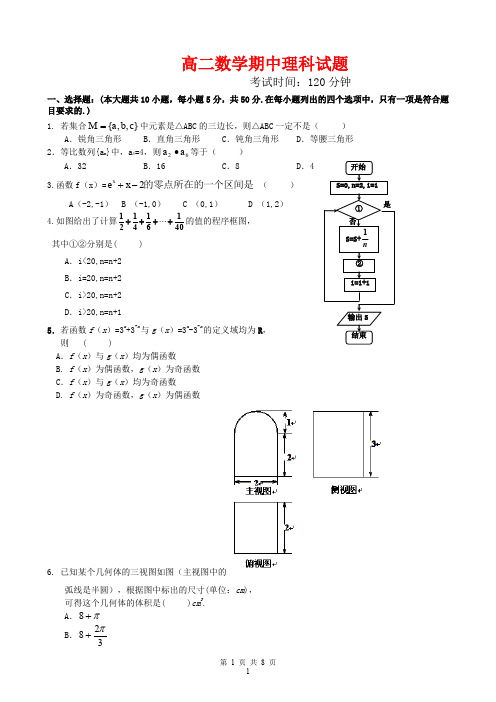
高二数学期中理科试题考试时间:120分钟一、选择题:(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.)1. 若集合},,{c b a M =中元素是△ABC 的三边长,则△ABC 一定不是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形 2.等比数列{a n }中,a 4=4,则62a a ∙等于( )A .32B .16C .8D .43.函数f (x )=2xe x +-的零点所在的一个区间是 ( ) A (-2,-1) B (-1,0) C (0,1) D (1,2) 4.如图给出了计算401614121++++的值的程序框图, 其中①②分别是( ) A .i<20,n=n+2 B .i=20,n=n+2 C .i>20,n=n+2 D .i>20,n=n+15.若函数f (x )=3x+3-x与g (x )=3x-3-x的定义域均为R ,则 ( )A .f (x )与g (x )均为偶函数 B. f (x )为偶函数,g (x )为奇函数C .f (x )与g (x )均为奇函数 D. f (x )为奇函数,g (x )为偶函数6. 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )cm 3. A .π+8B .328π+C .π+12D .3212π+7.“|x|<2”是“x 2-x-6<0”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件8.若21nx x ⎛⎫- ⎪⎝⎭的展开式中含x 的项为第6项,设nn n x a x a x a a x ++++=- 2210)31(,则n a a a +++ 21的值为 ( )A .255B . 32C .-225D .- 329.设OA =(1,-2),OB =(a,-1),OC =(-b ,0),a>0,b>0,O 为坐标原点,若A 、B 、C 三点共线,则ba 21+的最小值是( )A .2B .4C .6D .810.已知函数)2,0(sin cos )(π∈-=x x x m x f 在单调递增,则实数m 的取值范围为( ) A.)0,(-∞ B .]1,(-∞Y C Y C .]0,(-∞ D .)1,(-∞二、填空题(本大题共5小题,每小题5分,共25分,请将正确答案填写在横线上) 11. 高二某班甲、乙两名学生在本学期的其中5次数学考试 成绩的茎叶图如图所示,甲、乙两人5次数学考试成绩 的中位数分别为 ; 平均数分别为 . 12.已知函数0()sin ,af a xdx =⎰则[()]2f f π= .13.已知数列{a n }中,a 1=21,a n+1=a n +1412-n ,则a n =________. 14.已知M={(x,y )|x+y ≤6,x ≥0,y ≥0},N={(x,y )|x ≤4,y ≥0,x-2y ≥0},若向区域M 随机投一点P ,则P 落入区域N 的概率为15.如图,四边形OABC 是边长为1的正方形,OD =3,点P 为△BCD 内(含边界)的动点,设(,)OP OC OD R αβαβ=+∈,则αβ+的最大值等于 .三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)16.( 12分)已知函数2()22sin f x x x =-.(1)求函数()f x 的最大值;第11题图甲乙7 4 2 87899016 3 0(2)求函数()f x 的零点的集合.17.( 12分)横峰中学将在四月份举行安全知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为32. (Ⅰ)求选手甲可进入决赛的概率;(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.18.( 12分)直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,且160,,BAD A A AB E ∠==为1BB 延长线上的一点,1D E ⊥面1D AC .(Ⅰ)求二面角1E AC D --的大小;(Ⅱ)在1D E 上是否存在一点P ,使1//A P 面EAC ?若存在,求1:D P PE 的值;不存在,说明理由.19. ( 12分)已知函数xf (x)ln(e a)=+(a 为常数)是R 上的奇函数,函数x x f xg sin )()(+=λ是区间[-1,1]上的减函数.(1)求a 的值; (2)若]1,1[1)(2-∈++<x t t x g 在λ上恒成立,求t 的取值范围20.(13分)设数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有0n a >,n S =.(1)求1a ,2a 的值;(2)求数列{}n a 的通项公式n a ;21.( 14分)已知圆O :122=+y x ,点O 为坐标原点,一条直线l :)0(>+=b b kx y 与圆O 相切并与椭圆1222=+y x 交于不同的两点A 、B (1)设)(k f b =,求)(k f 的表达式;(2)若32=⋅OB OA ,求直线l 的方程; (3)若)4332(≤≤=⋅m m OB OA ,求三角形OAB 面积的取值范围.高二数学 (理) (期中)参考答案1. D2.B3. C4. C5. B6. A7.C8. A9. D 10. B 11. 84,82, 84,84 12. 1cos1- 13.2434--n n 14. 9215. 4317.【解】 (Ⅰ) 选手甲答3道题进入决赛的概率为278)32(3=; ……………1分选手甲答4道题进入决赛的概率为2783231)32(223=⋅⋅C ;…………………………3分选手甲答5道题进入决赛的概率为811632)31()32(2224=⋅⋅C ; …………………5分∴选手甲可进入决赛的概率278=p +278+81168164=. …………………7分 (Ⅱ)依题意,ξ的可能取值为3,4,5.则有31)31()32()3(22=+==ξP ,27103132)31(3231)32()4(223223=⋅⋅+⋅⋅==C C p ξ, 27831)31()32(32)31()32()5(22242224=⋅⋅+⋅⋅==C C p ξ, …………………………10分 因此,有ξ 345P31 2710 2782732727527433==⋅+⋅+⋅=∴ξE . ……………………………12分18.解:(Ⅰ)设AC 与BD 交于O ,如图所示建立空间直角坐标系O xyz -,设2AB =, 则1(3,0,0),(0,1,0),(3,0,0),(0,1,0),(0,1,2),A B C D D ---设(0,1,2),E h +则11(0,2,),(23,0,0),(3,1,2),D E h CA D A ===-1D E ⊥平面1111,,,D AC D E AC D E D A ∴⊥⊥220,1,h h ∴-=∴=即(0,1,3)E ……………………2分1(0,2,1),(3,1,3)D E AE ∴==-设平面EAC 的法向量为(,,)m x y z =则由,,m CA m AE ⊥⊥得30x y z =-++= 令1z =-∴平面EAC 的一个法向量为(0,3,1)m =-又平面1D AC 的法向量为11112(0,2,1),cos ,2m D E D E m D E m D E ⋅=∴<>==⋅||||∴二面角1E AC D --大小为45…………………………………………………6分19.解:(1)x f (x)ln(e )a =+是奇函数,x x ln(e )ln(e )a a -∴+=-+,1))((=++∴-a e a e x x0)(,112=++∴=+++∴--a e e a a ae ae x x x x ,故a=0. . ………………4分(2)由(I )知:x x x g x x f sin )(,)(+=∴=λ,]1,1[)(-在x g 上单调递减, 0cos )('≤+=∴x x g λx cos -≤∴λ在[-1,1]上恒成立,1-≤∴λ,1sin )1()]([max --=-=λg x g ,11sin 2++<--∴t t λλ只需 01sin )1(2>++++∴t t λ(其中1-≤λ)恒成立, ………………8分令)1(011sin )1()(2-≤>++++=λλλt t h ,则2t 10,t 1t sin110,+<⎧⎨--+++>⎩01sin ,01sin 122>+-⎩⎨⎧>+--<∴t t t t t 而恒成立, 1-<∴t ………………12分20.(1)解:当1n =时,有11a S ==0n a >,所以11a =.当2n =时,有2S =12a a +=,将11a =代入上式,由于0n a >,所以22a =. …………………4分21.解 (1)(0)y kx b b =+>与圆221x y +=相切,1=,即221(0)b k k =+≠,所以.12+=k b ………………………………4分(2)设1122(,),(,),A x y B x y 则由2212y kx bx y =+⎧⎪⎨+=⎪⎩,消去y 得:222(21)4220k x kbx b +++-=又280(0)k k ∆=>≠,所以2121222422,.2121kb b x x x x k k -+=-=++ …………6分 则1212OA OB x x y y ⋅=+=221.21k k ++由23OA OB ⋅=, 所以2 1.k =所22.b=0,b b >∴=所以:l y x y x ∴=+=-……………………9分(3)由(2)知: 22123.,2134k m m k +=≤≤+所以22213,3214k k +≤≤+ 211,2k ∴≤≤由弦长公式得2||21AB k =+所以1||2S AB ==解得2.3S ≤≤ ……14分。
江西省四校2011-2012学年高二理科零班联考数学试题
一、选择题(本大题共10小题,每小题5分,共50分)1.设02x π<<,则“2sin1x x <”是“sin 1x x < ( )A .充分而不必要条件B .充分必要条件C .必要而不充分条件D .既不充分也不必要条件2.设向量a 与b 的夹角为θ,定义a 与b 的“向量积":a b ⨯是一个向量,它的模sin a b a b θ⨯=⋅⋅若()()3,1,1,3a b =--=,则a b ⨯= ( )A .3B .2C .23D .43.现有四个函数①x x y sin ⋅= ②x x y cos ⋅= ③|cos |x x y ⋅= ④xx y 2⋅=的部分图象如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( (( )A. ①④②③ B。
①④③② C。
④①②③ D. ③④②① 4.某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两人至少有一人参加.当甲乙同时参加时,他们两人的发言不能相邻.那么不同的发言顺序的种数为( )A . 360B .520C .600D .7205.设A ={(x ,y )|(x -1)2+y 2≤25},B ={(x ,y )|(x +1)2+y 2≤25},C t ={(x ,y )||x |≤t ,|y |≤t ,t >0},则满足C t (A ∩B)时,t 的最大值是 ( )A.3B.4 C 。
5 D 。
66.某游戏中,一个珠子从如图所示的通道由上至下滑下,从最下面的六个出口出来,规定猜中出口者为胜。
如果你在该游戏中,猜得珠子从出口3出来,那么你取胜的概率为( )A.165 B 。
325C.61 D 。
以上都不对7.已知点1(,)40x x y x y ax by c ≥⎧⎪+≤⎨⎪++≥⎩是不等式组表示的平面区域内的一个动点,且目标函数2z x y =+的最大值为7,最小值为1,则a b c a++的值为( )A .2B .12C .-2D .-18.已知直线l 在平面α、β上的射影分别是直线a,b .有以下四个命题:①若α∥β,则a ∥b ; ②若α⊥β,则a ⊥b ;③若a 与b 相交,则直线l 垂直于α、β的交线;④ 若l 垂直于α、β的交线,则a 与b 相交; 则正确的命题是( )。
江西省南昌四校11-12学年高二上学期期中联考(数学理)
南昌四校11-12学年高二上学期期中联考试题数学理试卷一、选择题(每题5分 , 共50分)1、已知M (-2,0),N (2,0),|PM |-|PN|=4,则动点P 的轨迹是: ( )A 、双曲线B 、双曲线左支C 、一条射线D 、双曲线右支2“2k =”是“22cos sin 2y kx kx π=-的最小正周期为”的( )A .充分不必要条件B .必要不充分条件C .充分且必要条件D .既不充分也不必要条件3抛物线y=x 2上到直线2x-y=4距离最近的点的坐标是( )A)45,23( B (1,1) C)49,23( D (2,4)4有下列四个命题:①“若0x y +=,则,x y 互为相反数"的逆命题; ②“全等三角形的面积相等”的否命题;③“若1q ≤,则220x x q ++=有实根”的逆否命题;④“不等边三角形的三个内角相等”逆命题; 其中真命题为 ( )(A)①② (B)②③ (C )①③ (D )③④5椭圆1244922=+y x 上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直,则△21F PF 的面积为( )A .20B .22C .28D .246与曲线1492422=+y x 共焦点,而与曲线1643622=-y x 共渐近线的双曲线方程为( )A .191622=-x y B .191622=-y x C .116922=-x yD .116922=-y x7、、双曲线的虚轴长为4,离心率26=e ,F 1、F 2分别是它的左,右焦点,若过F 1的直线与双曲线的左支交于A 、B 两点,且|AB |是|AF 2|与|BF 2|的等差中项,则|AB |为( )。
A 、28 B 、24 C 、22 D 、88、已知点(x,y )在抛物线24yx =上,则22132z y x =++的最小值是( )A 。
2B 。
3 C. 4 D. 09已知c 是椭圆)0(12222>>=+b a by a x 的半焦距,则a c b +的取值范围是( )A (1, +∞) B),2(∞+C)2,1( D]2,1(10过椭圆左焦点F 且倾斜角为60的直线交椭圆于A 、B 两点,若FB FA 2=,则椭圆的离心率为 ( ) A .32 B.22 C. 21 D.32二、填空题(每题5分,共25分)11、抛物线22x y -=的焦点坐标为_________,12、在椭圆13422=+y x 内有一点P (1,-1),F 为椭圆右焦点,在椭圆上有一点M ,使|MP|+2|MF |的值最小,则M 的坐标____________ 13、已知平面内有一条线段AB ,4||=AB ,动点P 满足AB O PB PA 为,3||||=-的中点,则p 点的轨迹方程____________14、已知方程22152+x y m m+=-, m 为何值时 方程表示焦点在y 轴的椭圆.15在下列四个命题中,正确的序号有________.(填序号)①命题“存在一个三角形没有外接圆"的否定 ②“⎩⎨⎧≤-=∆>04,02ac b a ”是“一元二次不等式20axbx c ++≥的解集为R 的充要条件③ 存在2,0a R a∈≤使得④∈>若x R,sinx+cosx m 为真命题,则m 的范围为m 三、解答题(共75分)16 (1) 抛物线的顶点在原点,焦点在射线x -y +1=0(x ≥0)上求抛物线的标准方程;(2)求一条渐近线方程是043=+y x ,一个焦点是()5,0的双曲线标准方程,并求此双曲线的离心率.(本题满分12分)17、已知命题p :方程2210ax x ++=至少有一负根;命题q :任意实数x ∈R 满足不等式2210x ax ++≥,(1)求命题p 中a 的范围 (2)若命题“p 或q ” 为真,命题“p 且q "为假时,求实数a 的取值范围.(本题满分12分)18抛物线的顶点在原点,它的准线过双曲线2222-1,0,0)y x a b a b=>>的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的一个交点位3()2-分别求(1)抛物线的方程(2)双曲线的方程(本题满分12分)19,在平面直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F 交抛物线于A 、B 两点.(1) 若AB =8,求 直线l 的斜率 (2)若AF =m,BF =n.求证11mn+为定值(本题满分12分)20、设F1、F2分别为椭圆C:错误!+错误!=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2错误!.(1)求椭圆C的焦距;(2)如果错误!=2错误!,求椭圆C的方程.(本题满分13分)21、已知动点P与双曲线x2-y2=1的两个焦点F1,F2的距离之和为(1)求动点P的轨迹方程;(2)设M(0,-1),若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B,若要使|MA|=|MB|,试求k的取值范围.(本题满分14分)高二上学期数学联考(理科)答案一、选择题:本大题共10小题,每小题5分,满分50分.二、填空题:本大题共5小题,每小题5分,满分25分. 11.(0,—18)12.,-1)13.224431()972x y x -=≥ 14.352m15. ①②③16(1)射线x -y +1=0(x ≥0)与y 轴交点(0,1)为抛物线的焦点,∴抛物线方程为x 2=4y 。
江西省四校2011-2012学年高二理科零班联考物理试题
V 1~RV 2A 1A 2命题人:施国民 时间:100分钟 满分:100分一.选择题(本题共12小题,每小题4分,共48分.有的小题只有一个选项正确,有的小题有多个选项正确.全部选对的得4分,选不全的得2分.)1.两个完全相同的电热器,分别通有如图所示的交变电流i 1、i 2,它们的电功率之比为2:1,则I m1与I m2之比为A .1︰1B .2︰1C .2︰1D .4︰12。
如图,三只白炽灯泡L 1、L 2、L 3分别与线圈L 、电阻R 、电容器C 串联后接在同一个交流电源上,供电电压瞬时值为t U um ωsin 1=,此时三只灯泡的亮度相同.现换另一个电源供电,供电电压瞬时值为2sin2tU u m ω=,则三只灯泡的亮度变化是A .L 1变亮,L 2不变,L 3变暗B .L 1变暗,L 2不变,L 3变亮C .L 1变亮,L 2变亮,L 3变暗D .L 1变暗,L 2变亮,L 3变亮3.如图是街头变压器给用户供电的示意-I m1 0 ti 2I m2 -I m2T0 t i 1I m1 T图。
输入端接入的电压t22002=(V),输出电压通过输电线输uπ100sin送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是A.V2表的读数为2220VB.A1表的示数随A2表的示数的增大而增大,反之亦然C.副线圈中交流电的频率为100HzD.用户端闭合开关,则V2表读数不变,A1表读数变大,变压器的输入功率增大4.图示电路中R3是光敏电阻,当开关S闭合后,在没有光照射时,a、b两点等电势,当用光照射电阻R3时,则A.R3的电阻变小,a点的电势高于b点电势B.R3的电阻变小,a点的电势低于b点电势C.R3的电阻变大,a点的电势高于b点电势D.R3的电阻变大,a点的电势低于b点电势5。
图是一水平弹簧振子做简谐振动的振动的振动图像(x—t图),由图可推断,振动系统A.在t1和t3时刻具有相等的动能和相同的速度B.在t3和t4时刻具有相等的势能和相同的速度C.在t4和t6时刻具有相同的位移和回复力D.在t1和t6时刻具有相同的速度和加速度6。
江西高二高中数学期中考试带答案解析
江西高二高中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.复数的虚部是()A.B.C.D.2.下列命题正确的是()A.命题:若,则的否命题是:若,则.B.命题:,使得的否定是:,均有.C.命题:存在四边相等的四边形不是正方形,该命题是假命题.D.命题:,则的逆否命题是真命题.3.下面的各图中,散点图与相关系数r不符合的是()4.根据右边程序框图,当输入x=10时,输出的是()A.14.1B.19C.12D.-305.已知双曲线的一个焦点与抛物线的焦点重合,且双曲线的离心率等于,则该双曲线的方程为()A.B.C.D.6.设a,b是非零实数,且a<b,则下列不等式成立的是().A.a2<b2B.ab2<a2b C.<D.<7.函数(a>0)在(0,2)上不单调,则a的取值范围是()A.0<a<1B.0<a<C.a>1D.<a<18.在古希腊,毕达哥拉斯学派把1,3,6,10,15,……这些数叫做三角形数,因为这些数目的石子可以排成一个正三角形(如下图)则第10个三角形数是()A.35B.36C.45D.559.已知3x2+y2≤1,则3x+y的取值范围是().A.B.C.D.10.已知抛物线C,点满足,则直线,与抛物线公共点的个数是()A.B.C.D.或11.已知是椭圆的两个焦点,过且与椭圆长轴垂直的直线交椭圆于、两点,若是正三角形,则这个椭圆的离心率是()A.B.C.D.12.设函数是奇函数的导函数,f(-2)=0,当时,,则使得成立的x的取值范围是()A.(-,-2)(0, 2)B.(-,-2)(2, +)C.(-2,0)(2,+)D.(-2,0)(0,2)二、填空题1.已知的取值如下表:4.55.5从散点图分析,与线性相关,且回归方程为,则实数的值为_______2.已知复数满足,则的最大值是________3.已知直线过点,且与抛物线交于、两点,则________4.设函数满足,则 .三、解答题1.已知复数满足: 求的值.2.某单位为了调查员工喜欢体育运动是否与性别有关,决定从本单位中抽取50人进行问卷调查,得到了如下列联表:已知在全部50人中随机抽取一人,抽到喜爱打篮球的学生的概率为(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜欢体育运动与性别有关?并说明你的理由.下面的临界值表仅供参考:P(2≥k)0.150.100.050.0250.0100.0050.001k参考公式:2= ,其中n=a+b+c+d.3.设p:实数满足,q:实数满足.(1)若,且p∧q为真,求实数的取值范围;(2)若,且是的充分不必要条件,求实数的取值范围.4.已知函数.(1)试求使等式成立的的取值范围;(2)若关于的不等式的解集不是空集,求实数的取值范围.5.已知椭圆:()的离心率=,且过点.(1)求椭圆的方程;(2)椭圆长轴两端点分别为,,点为椭圆上异于,的动点,定直线与直线,分别交于,两点,又,求证:直线EM 直线EN6.已知函数(1)若求a的值;(2)若a>1,求函数f(x)的单调区间与极值点;(3)设函数是偶函数,若过点A(1,m)可作曲线y=f(x)的三条切线,求实数m的范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【精品资料】高2年级名校期中期末试卷及答案Word精排版高二数学期中理科试题考试时间:120分钟一、选择题:(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.)1. 若集合},,{c b a M =中元素是△ABC 的三边长,则△ABC 一定不是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形 2.等比数列{a n }中,a 4=4,则62a a ∙等于( )A .32B .16C .8D .43.函数f (x )=2xe x +-的零点所在的一个区间是 ( ) A (-2,-1) B (-1,0) C (0,1) D (1,2)4.如图给出了计算401614121++++ 的值的程序框图,其中①②分别是( ) A .i<20,n=n+2 B .i=20,n=n+2 C .i>20,n=n+2 D .i>20,n=n+15.若函数f (x )=3x+3-x与g (x )=3x-3-x的定义域均为R ,则 ( )A .f (x )与g (x )均为偶函数 B. f (x )为偶函数,g (x )为奇函数C .f (x )与g (x )均为奇函数 D. f (x )为奇函数,g (x )为偶函数6. 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )cm 3. A .π+8B .328π+C .π+12D .3212π+7.“|x|<2”是“x 2-x-6<0”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件8.若21nx x ⎛⎫- ⎪⎝⎭的展开式中含x 的项为第6项,设n n n x a x a x a a x ++++=- 2210)31(,则n a a a +++ 21的值为 ( )A .255B . 32C .-225D .- 329.设OA =(1,-2),OB =(a,-1),OC =(-b ,0),a>0,b>0,O 为坐标原点,若A 、B 、C 三点共线,则ba 21+的最小值是( )A .2B .4C .6D .810.已知函数)2,0(sin cos )(π∈-=x x x m x f 在单调递增,则实数m 的取值范围为( ) A.)0,(-∞ B .]1,(-∞Y C Y C .]0,(-∞ D .)1,(-∞二、填空题(本大题共5小题,每小题5分,共25分,请将正确答案填写在横线上) 11. 高二某班甲、乙两名学生在本学期的其中5次数学考试 成绩的茎叶图如图所示,甲、乙两人5次数学考试成绩 的中位数分别为 ; 平均数分别为 .12.已知函数0()sin ,af a xdx =⎰则[()]2f f π= . 13.已知数列{a n }中,a 1=21,a n+1=a n +1412-n ,则a n =________.14.已知M={(x,y )|x+y ≤6,x ≥0,y ≥0},N={(x,y )|x ≤4,y ≥0,x-2y ≥0},若向区域M 随机投一点P ,则P 落入区域N 的概率为15.如图,四边形OABC 是边长为1的正方形,OD =3,点P 为△BCD 内(含边界)的动点,设(,)OP OC OD R αβαβ=+∈,则αβ+的最大值等于 .三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤) 16.( 12分)已知函数2()22sin f x x x =-. (1)求函数()f x 的最大值;第11题图甲乙7 4 2 87899016 3 0(2)求函数()f x 的零点的集合.17.( 12分)横峰中学将在四月份举行安全知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为32. (Ⅰ)求选手甲可进入决赛的概率;(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.18.( 12分)直四棱柱1111ABCD A BC D -中,底面ABCD 为菱形,且 160,,BAD A A AB E ∠==为1BB 延长线上的一点,1D E ⊥面1D AC .(Ⅰ)求二面角1E AC D --的大小;(Ⅱ)在1D E 上是否存在一点P ,使1//A P 面EAC ?若存在,求1:D P PE 的值;不存在,说明理由.19. ( 12分)已知函数xf (x)ln(e a)=+(a 为常数)是R 上的奇函数,函数x x f xg sin )()(+=λ是区间[-1,1]上的减函数.(1)求a 的值; (2)若]1,1[1)(2-∈++<x t t x g 在λ上恒成立,求t 的取值范围20.(13分)设数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有0n a >,n S =(1)求1a ,2a 的值;(2)求数列{}n a 的通项公式n a ;21.( 14分)已知圆O :122=+y x ,点O 为坐标原点,一条直线l :)0(>+=b b kx y 与圆O 相切并与椭圆1222=+y x 交于不同的两点A 、B(1)设)(k f b =,求)(k f 的表达式;(2)若32=⋅OB OA ,求直线l 的方程;(3)若)4332(≤≤=⋅m m OB OA ,求三角形OAB 面积的取值范围.高二数学 (理) (期中)参考答案1. D2.B3. C4. C5. B6. A7.C8. A9. D 10. B 11. 84,82, 84,84 12. 1cos1- 13.2434--n n 14. 9215. 4317.【解】 (Ⅰ) 选手甲答3道题进入决赛的概率为278)32(3=; ……………1分选手甲答4道题进入决赛的概率为2783231)32(223=⋅⋅C ;…………………………3分选手甲答5道题进入决赛的概率为811632)31()32(2224=⋅⋅C ; …………………5分∴选手甲可进入决赛的概率278=p +278+81168164=. …………………7分(Ⅱ)依题意,ξ的可能取值为3,4,5.则有31)31()32()3(22=+==ξP ,27103132)31(3231)32()4(223223=⋅⋅+⋅⋅==C C p ξ,27831)31()32(32)31()32()5(22242224=⋅⋅+⋅⋅==C C p ξ, …………………………10分因此,有2732727527433==⋅+⋅+⋅=∴ξE . ……………………………12分18.解:(Ⅰ)设AC 与BD 交于O ,如图所示建立空间直角坐标系O xyz -,设2AB =,则1(0,1,0),((0,1,0),(0,1,2),A B C D D --设(0,1,2),E h +则11(0,2,),(23,0,0),(3,1,2),D E h CA D A ===-1D E ⊥平面1111,,,D AC D E AC D E D A ∴⊥⊥220,1,h h ∴-=∴=即(0,1,3)E ……………………2分1(0,2,1),(3,1,3)D E AE ∴==-设平面EAC 的法向量为(,,)m x y z =则由,,m CA m AE ⊥⊥得30x y z =-++= 令1z =-∴平面EAC 的一个法向量为(0,3,1)m =-又平面1D AC 的法向量为11112(0,2,1),cos ,2m D E D E m D E m D E ⋅=∴<>==⋅||||∴二面角1E AC D --大小为45…………………………………………………6分19.解:(1)x f (x)ln(e )a =+是奇函数,x x ln(e )ln(e )a a -∴+=-+,1))((=++∴-a e a e x x0)(,112=++∴=+++∴--a e e a a ae ae x x x x ,故a=0. . ………………4分(2)由(I )知:x x x g x x f sin )(,)(+=∴=λ,]1,1[)(-在x g 上单调递减, 0cos )('≤+=∴x x g λx cos -≤∴λ在[-1,1]上恒成立,1-≤∴λ,1sin )1()]([max --=-=λg x g ,11sin 2++<--∴t t λλ只需 01sin )1(2>++++∴t t λ(其中1-≤λ)恒成立, ………………8分令)1(011sin )1()(2-≤>++++=λλλt t h ,则2t 10,t 1t sin110,+<⎧⎨--+++>⎩01sin ,01sin 122>+-⎩⎨⎧>+--<∴t t t t t 而恒成立, 1-<∴t ………………12分20.(1)解:当1n =时,有11a S ==0n a >,所以11a =.当2n =时,有2S =12a a +=将11a =代入上式,由于0n a >,所以22a =. …………………4分21.解 (1)(0)y kx b b =+>与圆221x y +=相切,1=,即221(0)b k k =+≠,所以.12+=k b ………………………………4分(2)设1122(,),(,),A x y B x y 则由2212y kx bx y =+⎧⎪⎨+=⎪⎩,消去y 得:222(21)4220k x kbx b +++-=又280(0)k k ∆=>≠,所以2121222422,.2121kb b x x x x k k -+=-=++ …………6分 则1212OA OB x x y y ⋅=+=221.21k k ++由23OA OB ⋅=, 所以2 1.k =所22.b=0,b b >∴=所以:l y x y x ∴==-……………………9分(3)由(2)知: 22123.,2134k m m k +=≤≤+所以22213,3214k k +≤≤+ 211,2k ∴≤≤由弦长公式得||AB =所以1||2S AB ==解得2.43S ≤≤ ……14分。
