平面向量与空间向量知识点对比
最新平面向量与空间向量知识点对比
0≤< a,b >≤ π
0≤< a,b >≤ π
结合律、交换律
平面向量 a 与一个实数的乘积是一个向量,记作 λa.
空间向量 a 与一个实数的乘积是一个向量,记作 λa.
向量 a a 0 与 b 共线,当且仅当有唯一一个实数
,使 空间两个向量 a a 0 与 b 共线, 当且仅当有唯一一个实数
常用公式
AB x2 x1, y2 y1 .
AB x2 x1, y2 y1, z2 z1 .
(a+b)(a-b ) =a2-b2 = |a| 2- |b| 2, (a ?b) 2 =a2?2ab+b2
设 A x1, y1 , B x 2, y2 ,则:
(1)|a|= a a (2 )a⊥b a· b=0 (3) cos a, b a b (a 0,b 0)
| a || b |
=
x1 x2 y1 y2 z1z2
x12 y12 z12 x22 y22 z22
a xi y j zk x, y, z
设 a x1, y1, z1 ,b x2 , y2 , z2 ,则:
=
x1x2 y1 y2
x12 y12
x22 y22
a xi y j x, y
设 a x1, y1 , b x2 , y2 ,则:
a b x1 x2 , y1 y2 ,
坐标运算
a b x1 x2, y1 y2 , a x1, y1 ,
a / /b a b x1y2 x2 y1 0
ab
ab 0
x1 x2 y1 y 2 0
名师精编 优秀资料
内容
定义
表示方法
相同点 模的大小
平面向量和空间向量的知识点对比

平面向量和空间向量的知识点对比知识点平面向量空间向量。
---定义既有大小又有方向的量,在平面内既有大小又有方向的量,在空间中。
表示方法通常用有向线段表示,如→AB,也可以用坐标表示(x,y)通常用有向线段表示,如→AB,坐标表示为(x,y,z)向量的模对于平面向量→a=(x,y),|→a|=√(x^2)+y^{2}对于空间向量→a=(x,y,z),|→a|=√(x^2)+y^{2+z^2}相等向量大小相等且方向相同的向量,在平面内大小相等且方向相同的向量,在空间中。
平行向量(共线向量)方向相同或相反的非零向量,在平面内→a=k→b(k∈ R)表示→a∥→b方向相同或相反的非零向量,在空间中→a=k→b(k∈ R)表示→a∥→b加法运算三角形法则和平行四边形法则。
<br>若→a=(x_1,y_1),→b=(x_2,y_2),则→a+→b=(x_1+x_2,y_1+y_2)三角形法则和平行四边形法则。
<br>若→a=(x_1,y_1,z_1),→b=(x_2,y_2,z_2),则→a+→b=(x_1+x_2,y_1+y_2,z_1+z_2)减法运算三角形法则。
<br>若→a=(x_1,y_1),→b=(x_2,y_2),则→a-→b=(x_1-x_2,y_1-y_2)三角形法则。
<br>若→a=(x_1,y_1,z_1),→b=(x_2,y_2,z_2),则→a-→b=(x_1-x_2,y_1-y_2,z_1-z_2)数乘运算若→a=(x,y),k∈ R,则k→a=(kx,ky)若→a=(x,y,z),k∈ R,则k→a=(kx,ky,kz)数量积若→a=(x_1,y_1),→b=(x_2,y_2),则→a·→b=x_1x_2+y_1y_2,→a·→b=|→a||→b|cosθ(θ为→a与→b的夹角)若→a=(x_1,y_1,z_1),→b=(x_2,y_2,z_2),则→a·→b=x_1x_2+y_1y_2+z_1z_2,→a·→b=|→a||→b|cosθ(θ为→a与→b的夹角)向量的夹角设→a=(x_1,y_1),→b=(x_2,y_2),cosθ=frac{→a·→b}{|→a||→b|}=frac{x_1x_2+y_1y_2}{√(x_1)^2+y_{1^2}·√(x_2)^2+y_{2 ^2}},θ∈[0,π]设→a=(x_1,y_1,z_1),→b=(x_2,y_2,z_2),co sθ=frac{→a·→b}{|→a||→b|}=frac{x_1x_2+y_1y_2+z_1z_2}{√(x_1)^2+y_{1^2+z_1^2}·√(x_2)^2+y_{2^2+z_2^2}},θ∈[0,π]向量垂直若→a=(x_1,y_1),→b=(x_2,y_2),→a⊥→bLeftrightarrow→a·→b=0Leftrightarrow x_1x_2+y_1y_2=0若→a=(x_1,y_1,z_1),→b=(x_2,y_2,z_2),→a⊥→bLeftrightarrow→a·→b=0L eftrightarrow x_1x_2+y_1y_2+z_1z_2=0向量的应用在平面几何、物理(如力的合成与分解等)中有广泛应用在立体几何(如证明线面平行、垂直,求异面直线所成角、线面角、二面角等)、物理(如空间力的分析等)中有广泛应用。
高中数学第二章空间向量与立体几何1从平面向量到空间向量ppt课件

→ —→ (2)〈AB,C1A1〉; 解答 〈A→B,C—1→A1〉=π-〈A→B,A—1→C1〉=π-π4=34π.
→ —→ (3)〈AB,A1D1〉.
解答
〈A→B,A—1→D1〉=〈A→B,A→D〉=π2.
引申探求 →→
在本例中,求〈AB1,DA1〉. 解答
如图,衔接B1C,那么B1C∥A1D, →→
梳理
间向量的夹角
(1)文字表达:a,b是空间中两个非零向量,过空间恣意一点O,作
→ OA
=a,O→B=b,那么∠AOB 叫作向量a与向量b的夹角,记作〈a,b〉 .
(2)图形表示:
角度
表示
〈a,b〉=__0_
〈a,b〉是_锐__角__
〈a,b〉是_直__角__ 〈a,b〉是_钝__角__〈a,b〉 Nhomakorabea_π__
第二章 空间向量与立体几何
§1 从平面向量到空间向量
学习目的 1.了解空间向量的概念. 2.了解空间向量的表示法,了解自在向量的概 念. 3.了解空间向量的夹角. 4.了解直线的方向向量与平面的法向量的概念.
内容索引
问题导学 题型探求 当堂训练
问题导学
知识点一 空间向量的概念
思索1
类比平面向量的概念,给出空间向量的概念. 答案 在空间中,把具有大小和方向的量叫作空间向量.
答案 解析
研讨长方体的模型可知,一切顶点两两相连得到的线段中,长度为1 的线段只需4条,故模为1的向量有8个.
12345
5.在直三棱柱ABC-A1B1C1中,以下向量可以作为平面ABC法向量的 是②__③____.(填序号)答案
No Image
12345
规律与方法
在空间中,一个向量成为某直线的方向向量的条件包含两个方面:一是 该向量为非零向量;二是该向量与直线平行或重合.二者缺一不可. 给定空间中恣意一点A和非零向量a,就可以确定独一一条过点A且平行 于向量a的直线.
高中数学空间向量

高中数学空间向量
高中数学中,空间向量是一个重要的知识点。
空间向量是三维空间中的一个向量,由三个实数表示坐标。
它与平面向量不同,平面向量只有两个坐标。
空间向量有三个重要的基本运算:加法、减法和数量积。
加法和减法可以看做是两个向量的矢量和矢量差,表示向量之间的相对位置和方向。
数量积可以衡量两个向量之间的相似程度,比如两个向量垂直时数量积等于0,两个向量平行时数量积有最大值。
空间向量还有很多重要的应用,其中最重要的就是解决三维空间中的几何问题。
比如,计算线段、直线和平面之间的距离、角度和交点等。
此外,空间向量还能用于模拟物理系统、计算电场和磁场等方面,有着广泛的应用。
在学习空间向量时,需要掌握向量的基本概念和运算法则,理解向量的几何和代数表示,并且熟练掌握向量的应用技巧。
学习空间向量不仅可以帮助我们解决一些实际问题,在高考数学中也是一个非常重要的知识点。
6-2平面向量场与空间向量场_712106810

f ( x, y ) P ( x, y )dx g ( y ). 两边对y求导, 有 Q( x, y ) f y ( x, y ) P( x, y )dx g ( y ). y 于是g ( y ) Q( x, y ) P( x, y )dx, 解出g , 从而得f . y
Recall:有势场u : 无源场u : 无旋场u : 保守场u : 调和场u :
f , s.t., u f u 0 u 0 积分与路径无关 (有势场&无源场) f , f 0, s.t., u f
目标 : 一定条件下,保守场,有势场和无旋场三者相互等价. Remark:从定义上来看,保守场和有势场都不好验证,但 无旋场很容易验证.
Pdx Qdy
( x, y )
( x0 , y0 )
Pdx Qdy
因积分与路径无关, 对后一积分任意取定一条以 ( x0 , y0 )为起点,以( x, y )为终点的逐段光滑曲线L, 对前一积分,其积分曲线从( x0 , y0 )先沿L至( x, y ), 再沿平行于oy轴的直线段L1从( x, y )到( x, y y ). 于是
(1) (2),(1) (3)
L Pdx Qdy 0.
Proof : (1) (2) 任取D中逐段光滑的有向闭曲线 L,在L上任取两点A, B, 将L分成有相同起点A和相 同终点B的两条逐段光滑的有向曲线L1和L2 (如图). 因v是保 x, y y) (其中0 1) Q( x, y) (当y 0时.)
平面向量与空间解析几何

平面向量与空间解析几何平面向量和空间解析几何是数学中重要的概念,它们在几何学和物理学中扮演着重要的角色。
平面向量是一个有大小和方向的量,可以表示为有序对(x, y)。
在二维空间中,平面向量通常用于描述平面内的位置关系、运动方向等。
空间解析几何则是研究三维空间中点、直线、平面等几何对象的性质和关系的数学分支。
平面向量定义平面向量可以用有向线段表示,其大小为线段的长度,方向为线段的方向。
平面向量的加法、减法和数乘等运算可以通过坐标运算来实现。
两个平面向量(x1, y1)和(x2, y2)的加法为(x1+x2, y1+y2),减法为(x1-x2, y1-y2),数乘为k * (x, y) = (k*x, k*y)。
运算性质•交换律:a + b = b + a•结合律:a + (b + c) = (a + b) + c•分配律:k * (a + b) = k * a + k * b空间解析几何点和坐标在空间解析几何中,三维空间中的一个点可以用有序三元组(x, y, z)表示,其中x, y, z分别是点在三个坐标轴上的投影。
两点之间的距离可以通过距离公式计算得到。
直线和平面一条空间直线可以通过一个点和一个方向向量来唯一确定,方向向量可以是直线上任意两点的向量差。
空间平面可以通过一个点和两个不共线的方向向量来唯一确定。
方向余弦方向余弦是描述向量在空间中的方向性质的参数。
一个向量(a, b, c)的方向余弦分别为cosα = a/sqrt(a^2+b^2+c^2),cosβ = b/sqrt(a^2+b^2+c^2),cosγ = c/sqrt(a^2+b^2+c^2)。
应用平面向量和空间解析几何在现实生活中有着广泛的应用。
在工程学中,它们可以用于描述力的合成、速度的方向等;在计算机图形学中,可以用于图形的变换和计算;在物理学中,可以描述空间中的物体运动等。
总的来说,平面向量和空间解析几何不仅是数学中的重要概念,也是现实生活中不可或缺的工具,它们帮助我们更好地理解和描述空间中的种种现象和规律。
高中数学必修知识点空间向量知识点

高中数学必修知识点空间向量知识点在高中数学的学习中,空间向量是一个重要的知识点,它为我们解决空间几何问题提供了全新的思路和方法。
接下来,就让我们一起深入了解一下空间向量的相关知识。
一、空间向量的基本概念空间向量是指具有大小和方向的量。
它与平面向量类似,但存在于三维空间中。
一个空间向量可以用有向线段来表示,有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
空间向量的坐标表示:在空间直角坐标系中,若向量的起点坐标为\((x_1,y_1,z_1)\),终点坐标为\((x_2,y_2,z_2)\),则该向量的坐标为\((x_2 x_1, y_2 y_1, z_2 z_1)\)。
零向量:长度为\(0\)的向量,其方向任意。
单位向量:长度为\(1\)的向量。
二、空间向量的运算1、加法和减法空间向量的加法和减法运算遵循三角形法则和平行四边形法则。
若\(\overrightarrow{a} =(x_1,y_1,z_1)\),\(\overrightarrow{b} =(x_2,y_2,z_2)\),则\(\overrightarrow{a} +\overrightarrow{b} =(x_1 + x_2, y_1 + y_2, z_1 + z_2)\),\(\overrightarrow{a} \overrightarrow{b} =(x_1 x_2, y_1 y_2, z_1z_2)\)2、数乘运算若\(\lambda\)为实数,\(\overrightarrow{a} =(x,y,z)\),则\(\lambda\overrightarrow{a} =(\lambda x, \lambda y, \lambda z)\)数乘运算的规律:\(\lambda (\overrightarrow{a} +\overrightarrow{b})=\lambda\overrightarrow{a} +\lambda\overrightarrow{b}\)3、数量积空间向量的数量积\(\overrightarrow{a} \cdot \overrightarrow{b} =|\overrightarrow{a}||\overrightarrow{b}|\cos <\overrightarrow{a},\overrightarrow{b}>\)若\(\overrightarrow{a} =(x_1,y_1,z_1)\),\(\overrightarrow{b} =(x_2,y_2,z_2)\),则\(\overrightarrow{a} \cdot \overrightarrow{b} = x_1x_2 + y_1y_2 + z_1z_2\)数量积的性质:\(\overrightarrow{a} \perp \overrightarrow{b} \Leftrightarrow \overrightarrow{a} \cdot \overrightarrow{b} = 0\)\(\overrightarrow{a} \cdot \overrightarrow{a} =|\overrightarrow{a}|^2\)4、向量积空间向量的向量积\(\overrightarrow{a} \times \overrightarrow{b}\)是一个向量,其模长为\(|\overrightarrow{a}||\overrightarrow{b}|\sin <\overrightarrow{a},\overrightarrow{b}>\),方向垂直于\(\overrightarrow{a}\)和\(\overrightarrow{b}\)所确定的平面,遵循右手定则。
平面向量空间向量知识点-7页文档资料

平面向量§2.1.1、向量的物理背景与概念1、 了解四种常见向量:力、位移、速度、加速度.2、 既有大小又有方向的量叫做向量. §2.1.2、向量的几何表示1、 带有方向的线段叫做有向线段,有向线段包含三个要素:起点、方向、长度.2、 向量的大小,也就是向量的长度(或称模),记作AB ;长度为零的向量叫做零向量;长度等于1个单位的向量叫做单位向量.3、 方向相同或相反的非零向量叫做平行向量(或共线向量).规定:零向量与任意向量平行. §2.1.3、相等向量与共线向量1、 长度相等且方向相同的向量叫做相等向量. §2.2.1、向量加法运算及其几何意义 1、 三角形加法法则和平行四边形加法法则.2++.§2.2.2、向量减法运算及其几何意义1、 与长度相等方向相反的向量叫做的相反向量.2、 三角形减法法则和平行四边形减法法则. §2.2.3、向量数乘运算及其几何意义1、 规定:实数λ与向量的积是一个向量,这种运算叫做向量的数乘.记作:λ,它的长度和方向规定如下:⑴= ⑵当0>λ时, a λ的方向与a 的方向相同;当0<λ时, a λ的方向与a 的方向相反. 2、 平面向量共线定理:向量()≠与 共线,当且仅当有唯一一个实数λ,使λ=. §2.3.1、平面向量基本定理1、 平面向量基本定理:如果21,e e 是同一平面内的两个不共线向量,那么对于这一平面内任一向量,有且只有一对实数21,λλ,使2211e e λλ+=.§2.3.2、平面向量的正交分解及坐标表示 1、 ()y x y x ,=+=. §2.3.3、平面向量的坐标运算1、 设()()2211,,,y x y x ==,则: ⑴()2121,y y x x ++=+,⑵()2121,y y x x b a --=-, ⑶()11,y x λλλ=, ⑷1221//y x y x =⇔. 2、 设()()2211,,,y x B y x A ,则: ()1212,y y x x --=. §2.3.4、平面向量共线的坐标表示 1、设()()()332211,,,,,y x C y x B y x A ,则 ⑴线段AB 中点坐标为()222121,y y x x ++, ⑵△ABC 的重心坐标为()33321321,y y y x x x ++++.§2.4.1、平面向量数量积的物理背景及其含义1、 θb a =⋅.2、 在θ.3、 2=.4、 =.5、 0=⋅⇔⊥.§2.4.2、平面向量数量积的坐标表示、模、夹角 1、 设()()2211,,,y x y x ==,则:⑴2121y y x x +=⋅2121y x +=⑶121200a b a b x x y y ⊥⇔⋅=⇔+=⑷1221//0a b a b x y x y λ⇔=⇔-= 2、 设()()2211,,,y x B y x A ,则:()()212212y y x x -+-=.3、 两向量的夹角公式2c o s a b a bx θ⋅==+4、点的平移公式平移前的点为(,)P x y (原坐标),平移后的对应点为(,)P x y '''(新坐标),平移向量为(,)PP h k '=, 则.x x h y y k '=+⎧⎨'=+⎩函数()y f x =的图像按向量(,)a h k =平移后的图像的解析式为().y k f x h -=- §2.5.1、平面几何中的向量方法§2.5.2、向量在物理中的应用举例空间向量空间向量的许多知识可由平面向量的知识类比而得.下面对空间向量在立体几何中证明,求值的应用进行总结归纳.1、直线的方向向量和平面的法向量 ⑴.直线的方向向量:若A 、B 是直线l 上的任意两点,则AB 为直线l 的一个方向向量;与AB 平行的任意非零向量也是直线l 的方向向量. ⑵.平面的法向量:若向量n 所在直线垂直于平面α,则称这个向量垂直于平面α,记作n α⊥,如果n α⊥,那么向量n 叫做平面α的法向量. ⑶.平面的法向量的求法(待定系数法): ①建立适当的坐标系.②设平面α的法向量为(,,)n x y z =.③求出平面内两个不共线向量的坐标123123(,,),(,,)a a aa b b b b ==.④根据法向量定义建立方程组0n a n b ⎧⋅=⎪⎨⋅=⎪⎩.⑤解方程组,取其中一组解,即得平面α的法向量.(如图)1、 用向量方法判定空间中的平行关系 ⑴线线平行设直线12,l l 的方向向量分别是a b 、,则要证明1l ∥2l ,只需证明a ∥b ,即()a kb k R =∈. 即:两直线平行或重合两直线的方向向量共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数乘
数量积
模
夹角
平行
垂直
向量的正交分解及坐标表示
坐标面)
,且 ,则A、B、C、三点共线
,且 ,则P、A、B、C、四点共面
数量积
运算律
满足交换律、分配律,不满足三个向量连乘的结合律
向量的运算
线性运算
坐标运算
线性运算
坐标运算
加法
三角形法则:首尾相连首尾连;例如:
平行四边形法则:同起点,对角线
三角形法则:首尾相连首尾连;例如:
减法
三角形法则:同起点,连终点,指向被减向量;例如:
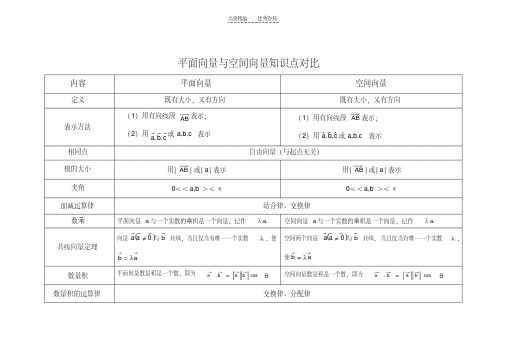
平面向量与空间向量知识点对比
内容
平面向量
空间向量
定义
既有大小,又有方向
既有大小,又有方向
表示方法
(1)用有向线段 表示; (2)用 或a,b,c表示
模
向量的长度,用| |或|a|表示
零向量
长度为0的向量,记为a
单位向量
模为1的向量叫做单位向量
相等向量
长度相等,方向相同的向量叫做相等向量
相反向量
长度相等,方向相反的向量叫做相反向量;例如: 的相反向量是 或者
夹角范围
0≤ ≤π
0≤ ≤π
数乘
平面向量a与一个实数的乘积是一个向量,记作λa.
空间向量a与一个实数的乘积是一个向量,记作λa.
共线向量定理
向量 与 共线,当且仅当有唯一一个实数 ,使
向量 与 共线,当且仅当有唯一一个实数 ,使
向量共线(共面)
向量 与 共线,当且仅当有唯一一个实数 ,使
向量 与 与 共面的充要条件是存在有序实数对(x,y),使
