二次函数常见关系式符号的判定

合集下载

二次函数a.b.c等的符号的确定

y
-1 o 1 x
（5）△=b2-4ac决定抛物线与x轴交点情况：
① △＞0 ② △＝0
抛物线与x轴有两个交点；抛物线与x轴有唯一的公共点；
③ △＜0 抛物线与x轴无交点。
y ox
y ox
y ox
勇攀高峰
1. 二次函数y=ax2+bx+c的图象如图所示，下列结论中：
①abc＞0；② a+b+c＜0 ③ a-b+c＞0 ；
o1 特殊值法
x
y aabb cc 0 0
y=ax2+bx+c 当x 1时 y=a-b+c
y aabbcc0 0 y
y aabbcc00
-1 o
x
y aabbcc00
x=-1
比拼速度
二次函数y ax2 bx c的图象如图，用(< , >或 =)填空: a< 0，b < 0，c > 0，a+b+c< 0，a-b+c> 0， Nhomakorabeay
开口向下
a＜0
数形结合法
x
⑵c决定抛物线与y轴交点（0，c）的位置：
① 图象与y轴交点在y轴正半轴；
c＞0
② 图象过原点
c=0
③ 图象与y轴交点在y轴负半轴
c＜0
y
指出下列二次函数与y轴交点的坐标.
(1) y=x2-8x+7 (2) y=-2x2+9x-17
x
⑶a，b决定抛物线对称轴的位置: 对称轴是直线x =
转化 + 特殊值
根据抛物线y=ax2+bx+c图象位置，你会判断那些字母或代数式的符号？

二次函数中常见关系式符号的判断

为对称轴一ｏ＝２，
二Ｕ
所以一ｂ＝４ａ．
如果二次函数Ｙ＝ａＮ＋＋ｃ（ａ≠０）的对称轴＝
一
则４ａ＋ｂ＝０．
所以④对．
在点（１，０）的左边，则一＜１，当ｏ＞０时，得２ａ＋
当Ｙ＝２时，对应的的值有两个，所以⑤错．
正确是（）．
即①正确．
为一１＜一一＜０，
二“
Ａ． ① ④ Ｃ． ②⑤
，：
Ｂ． ③④ Ｄ． ③⑤
ＪＩ１ Ⅱ一２ａ＜一ｂ．
即２ａ—ｂ＜０．
所以② 正确．一Fra bibliotek，？０ｉ２
：
７、
＼
因为图象经过（一１，２），
当＝一２时，Ｙ＜０，
所以ａ（一２）＋ｂＸ（一２）＋ｃ＜０
贝Ｕ４ Ⅱ一２６＋ｃ＜０．
如图所示，则下列结论①６一４ａｃ＜０， ②ａｂ＞Ｏ， ③ｎ—ｂ＋Ｃ：０，ｇ）４ａ＋ｂ：０， ⑤ 当Ｙ：２时，只能有一个值．其中
Ａ．１个Ｂ．２个
如果二次函数ｙ＝似＋＋ｃ（ａ ≠０）的对称轴＝
一
）．
经过（１，０），２ａ＋ｂ＝０．
举例如下
分析
由象得；
例１已知二次函数Ｙ＝ａｘ＋ｋ＋ｃ（ａ ≠０）的图象
所以选．
ｂ＞０，当ａ＜０时，２０＋ｂ＜０．

二次函数中的符号问题

1
基础回顾：
1、抛物线y=ax2+bx+c的开口方向、形状与什么有关？
a＞0时，开口向上；a＜0时，开口向下。
a 相等
抛物线的形状相同
2、抛物线y=ax2+bx+c与y轴的交点是（0、c）.
3、抛物线y=ax2+bx+c的对称轴是 X=- b .
2a
2
归纳知识点：
抛物线y=ax2+bx+c的符号问题：
y
根据图像可得：
1、a＞0
2、- b ＞0
2a
o
x 3、△=b²-4ac＞0
4、C＞0
6
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
y
根据图像可得：
1、a＞0
b
2、-
＜0
2a
o
x 3、△=b²-4ac＞0
4、C＝0
7
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：
M
B 1
Ax
O
1
17
再想一想：
5.如图，在平面直角坐标系中，二次函数y=ax2+c（a<0）的
图象过正方形ABOC的三个顶点A、B、C，则ac的值是 -2 .
设正方形的对角线长为2n，根据图像可得：
∵A（0、2n）、B（-n、n）、 C（n、n） ∴n=a（±n）²+2n、c=2n，
∴a=- 1 ，∴ac=2n*（-
②如图2a＋b _______0 4a＋2b＋c_______0
12
根据图象填空：
（1）a_____0；（2）b_____0；（3）c______0；（4）b2 4ac _____0；（5）a＋b＋c_____0；（6）a－b＋c_____0；（7）2a＋b_____0；

二次函数图像与性质完整归纳

3 2 -2
3 2 0 5…
2
【例 2】求作函数 y x 2 4 x 3 的图象。
【解】 y x 2 4x 3 ( x2 4x 3)
[( x 2) 2 7] [( x 2) 2 7 先画出图角在对称轴 x 2 的右边部分，列表
x -2 -1 0 1 2 y 76 5 4 3
【点评】画二次函数图象步骤： (1) 配方； (2) 列表； (3) 描点成图；也可利用图象的对称性，先画出函数的左（右）边部分图象，再利用对称性描出右（左）部分就可。
, 3 ] 上是增函数，在区间 [ 3, 10
29 ymaz 20 ) 上是减函数。
【点评】要研究二次函数顶点、对称轴、最值、单调区间等性质时，方法有两个：
(1) 配方法；如例 3
(2) 公式法：适用于不容易配方题目 ( 二次项系数为负数或分数 ) 如例 4，可避免出错。
任何一个函数都可配方成如下形式：
b 时， y 随 x 的增大而增大；当 x b
2a
2a
b ，顶点坐标为 2a
b ，4ac b2 ．当 2a 4a
x b 时， y 随 x 的增大而增大；当 x 2a
2
有最大值 4ac b ． 4a
b 时， y 随 x 的增大而减小；当 x 2a
b 时， y 2a
六、二次函数解析式的表示方法
1. 一般式： y ax 2 bx c （ a ， b ， c 为常数， a 0 ）； 2. 顶点式： y a ( x h)2 k （ a ， h ， k 为常数， a 0 ）；
向下
h ，k
x h 时， y 随 x 的增大而减小； x h 时， y X=h
随 x 的增大而增大； x h 时， y 有最大值 k ．

九年级数学二次函数中a,b,c符号的确定

九年级数学二次函数中a ，b ，c 符号的确定珠海市第四中学（519015）邱金龙二次函数)0(2≠++=a c bx ax y 的图象是抛物线，利用图象来确定a ，b ，c 的符号，是常见的问题，解决的关键是对二次函数的图象和性质的正确理解。

一、a ，b ，c 符号的确定（1）a 符号的确定。

抛物线的开口向上，a ＞0，抛物线的开口向下，a ＜0。

（2）c 符号的确定。

因为x=0时，由c bx ax y ++=2得，y ＝c ，故抛物线与y 轴交点在y 轴的正半轴，c ＞0，抛物线与y 轴交点在y 轴的负半轴，c ＜0，抛物线经过原点，c ＝0。

（3）b 符号的确定。

b 的符号要看对称轴ab x 2-=，再结合a 的符号来确定。

二、应用举例1、二次函数c bx ax y ++=2的图象分别如图所示，试分别判断（A ）（B ）（C ）（D ）图中a ，b ，c 的符号。

分析：（A ）图中，抛物线的开口向上，故a ＞0；抛物线与y 轴的交点P 在y 轴的负半轴，故c ＜0。

对称轴ab x 2-=＞0，而a ＞0，故b ＜0。

（B ）图中，抛物线的开口向下，故a ＜0；抛物线与y 轴的交点P 在y 轴的正半轴，故c ＞0。

对称轴ab x 2-=＜0，而a ＜0，故b ＜0。

（C ）图中（过程略），a ＞0，c ＞0 ，b ＞0。

（D ）图中（过程略），a ＜0， c ＜0 ，b ＞0。

2、（2004重庆中考题）二次函数c bx ax y ++=2的图象如图，则点M （b ，ac ）在（） A 、第一象限 B 、第二象限C 、第三象限D 、第四象限分析：抛物线的开口向下，故a ＜0；抛物线与y 轴的交点在y 轴的正半轴，故c ＞0。

对称轴ab x 2-=＞0，而a ＜0，故b ＞0。

因此，点M （b ，ac ）的横坐标为正，纵坐标为负，在第四象限，选（D ）。

3、（2004陕西中考题）二次函数y =ax 2+bx+c 的图象如图所示，则下列关于a 、b 、c 间的关系判断正确的是（）A 、ab ＜0B 、bc ＜0C 、.a+b+c ＞0D 、a －b+c ＜0分析：抛物线的开口向下，故a ＜0；抛物线与y 轴的交点在y 轴的负半轴，故c ＜0。

二次函数a、b、c及有关代数式判定

课题二次函数图象与系数符号学习目标：1．探索发现二次函数的系数a,b,c,△的符号与图象之间的关系；2．由抛物线确定a,b,c,△及相关代数式的符号；学习过程一、知识回顾：1.抛物线y=ax2+bx+c 的开口方向由决定：⇒开口向上⇒开口向下.2.抛物线y=ax2+bx+c与y轴的交点坐标是（）.c>o⇒与y轴的交点在；c<o⇒与y轴的交点在；c=o⇒抛物线过点3.抛物线y=ax2+bx+c的对称轴是直线 .b=0⇒对称轴是；0⇒对称轴在y轴的侧；a、b同号⇒－b2a0⇒对称轴在y轴的侧.a、b异号⇒－b2a4.若抛物线y=ax2+bx+c与x轴有交点，则交点的横坐标就是一元二次方程ax2+bx+c=0的根，因此抛物线y=ax2+bx+c与x轴的交点个数由决定.抛物线与x轴有两个交点；抛物线与x轴有一个交点；抛物线与x轴没有交点.二、协作归纳，获取新知（一）a、b、c、△=b2-4ac的符号与抛物线位置的关系。

1. 抛物线y=ax2+bx+c开口向上⇒；抛物线y=ax2+bx+c开口向下⇒ .2. 抛物线y=ax2+bx+c与y轴的交点在y轴的负半轴上⇒；抛物线y=ax2+bx+c与y轴的交点在y轴的正半轴上⇒，抛物线经过坐标原点⇒ .3. 抛物线y=ax 2+bx+c 的对称轴是y 轴⇒b 0；抛物线y=ax 2+bx+c 的对称轴在y 轴的左侧⇒－b2a 0⇒a 、b 号；抛物线y=ax 2+bx+c 的对称轴在y 轴的右侧⇒－b 2a 0⇒a 、b 号. 4. 抛物线y=ax 2+bx+c 与x 轴有两个交点⇒△ ；抛物线y=ax 2+bx+c 与x 轴有一个交点⇒△ ；抛物线y=ax 2+bx+c 与x 轴无交点⇒△ . 试一试：根据二次函数c bx ax y ++=2的图象，判断a 、b 、c 、b 2-4ac 的符号，并说明理由.（二）确定代数式a+b+c ； a-b+c ； 4a+2b+c ；4a-2b+c ；2a+b ；2a-b 的符号1.二次函数y=ax 2+bx+c 中，当x=1时，y= ；当x=-1时，y= .2.二次函数y=ax 2+bx+c 中，当x=2时，y= ；当x=-2时，y= . 试一试：抛物线y=ax 2+bx+c 如图所示，判断下列各式的符号（1）a+b+c （2）a-b+c （3）4a+2b+c （4） 4a-2b+c （5）2a+b （6）2a-b三、归纳小结，升华提高四、累化回味，形成技能1.二次函数y=kx2-3x+2k-k2的图象经过原点，则k= .2.若二次函数y=ax2+3x-1与x轴有两个交点，则a的取值范围是 .3.二次函数cbxaxy++=2与一次函数caxy+=在同一坐标系中的图象大致是( )4. 若0,0,0<><c b a ，则抛物线c bx ax y ++=2的大致图象为（）5.若无论x 取何实数，二次函数y=ax 2+bx+c 的值总为负，则下列结论成立的是（） A.a>0且b 2-4ac ≥0 B.a>0且b 2-4ac>0 C.a<0且b 2-4ac<0 D.a <0且b 2-4ac ≤0 五、拓广探索：观察抛物线图象填空：(1)方程ax 2＋bx ＋c ＝0的根为___________; (2)方程ax 2＋bx ＋c ＝－3的根为__________; (3)方程ax 2＋bx ＋c ＝－4的根为__________; (4)不等式ax 2＋bx ＋c ＞0的解集为________; (5)不等式ax 2＋bx ＋c ＜0的解集为________; (6)不等式－4＜ax 2＋bx ＋c ＜0的解集为________.xxxx。

判定二次函数中的a,b,c的符号

10A B C D二次函数：图象位置与a，b，c，（1）a决定抛物线的开口方向：a>0⇔；a<0⇔．（2）C决定抛物线与y轴交点的位置，c>0⇔抛物线交y轴于；c<0⇔抛物线交y轴于；c=0⇔．（3）ab决定抛物线对称轴的位置，当a,b同号时⇔对称轴在y轴；b=0⇔对称轴为；a,b异号⇔对称轴在y轴，简称为．一、通过抛物线的位置判断a，b，△c，的符号．例1．根据二次函数y=ax2+bx+c的图象，判断a、b、c、b2-4ac的符号yx2.看图填空（1）a＋b＋c_______0（2）a－b＋c_______0（3）2a－b_______0（4）4a＋2b＋c_______0二、通过a，b，△c，的符号判断抛物线的位置：例1．若a<0,b>0,c<0，则抛物线y=ax2+bx+c的大致图象为（）y y y yOx O x O x O xA B C D例2．若a＞0，b＞0，c＞△0，＞0，那么抛物线y=ax2+bx+c经过象限．例3.已知二次函数y=ax2+bx+c且a＜0，a-b+c＞0；则一定有b2-4ac0例4．如果函数y=kx+b的图象在第一、二、三象限内，那么函数y=kx2+bx-1的大致图象是（）y yy 1x0x-1x 0-101．若抛物线y=ax2+bx+c开口向上，则直线y=ax+3经过象限．2．二次函数y=ax2+bx+c的图象如图所示,则下列条件不正确的是()yO x3．二次函数 y=ax 2+bx+c 的图象如图，则点, ⎪ 在．（）⎝ b 2 - 4ac b ⎭y yA 、 a < 0, b > 0, c < 0B 、 b 2 - 4ac < 0C 、 a + b + c < 0D 、 a - b + c > 0⎛ a + b ac ⎫yA 、第一象限B 、第二象限C 、第三象限D 、第四象限O4．二次函数 y=ax 2+bx+c 与一次函数 y = ax + c 在同一坐标系中的图象大致是() yyO xO xO x OxABCD5．二次函数 y=ax 2+bx+c (a ≠ 0)的图象，如图，下列结论①c < 0 ② b > 0 ③ 4a + 2b + c > 0 ④ (a + c )2 < b 2 其中正确的有（）A 、1 个B 、2 个C 、3 个D 、4 个6．已知函数 y=ax 2+bx+c 的图象如图所示，关于系数 a, b , cyOxx = 1y有下列不等式① a < 0 ② b < 0 ③ c > 0 ④ 2a + b < 0 ⑤ a + b + c > 0 其中正确个数为．7．已知直线 y=ax 2+bx+c 不经过第一象限，则抛物线y = ax 2 + bx 一定经过（）A ．第一、二、四象限B ．第一、二、三象限C ．第一、二象限D ．第三、四象限8. 如图所示的抛物线是二次函数 y ＝ax 2-3x ＋a 2-1 的图象，那么 a 的值是__．- O 1x．．轴正半轴相交，其顶点坐标为,1⎪ ，下列结论：①ac＜0；② 精品资料欢迎下载9. 若抛物线 y ＝x 2－bx ＋9 的顶点在 x 轴上，则 b 的值为______若抛物线 y ＝x 2－bx ＋9 的顶点在 y 轴上，则 b 的值为______10．已知二次函数 y ＝ax 2＋bx ＋c(a≠0)的图象如图所示，有下列结论：①abc＞0；②a＋b ＋c=2； ③a >结论是( )1 2；④b＜1．其中正确的A ．①②B ．②③C ．②④D ．③④11.二次函数 y ＝ax 2＋bx ＋c(a≠0)的图象开口向上，图象经过点（-1,2）和（1,0），且与 y 轴负半轴交于一点，给出以下结论①abc＜0；②2a＋b ＞0；③a＋c ＝1；④a＞1．其中正确的结论是()A 、1 个B 、2 个C 、3 个D 、4 个12. 二次函数 y ＝ax 2 －2x －1 与 x 轴有交点，则 k 的取值范围________。

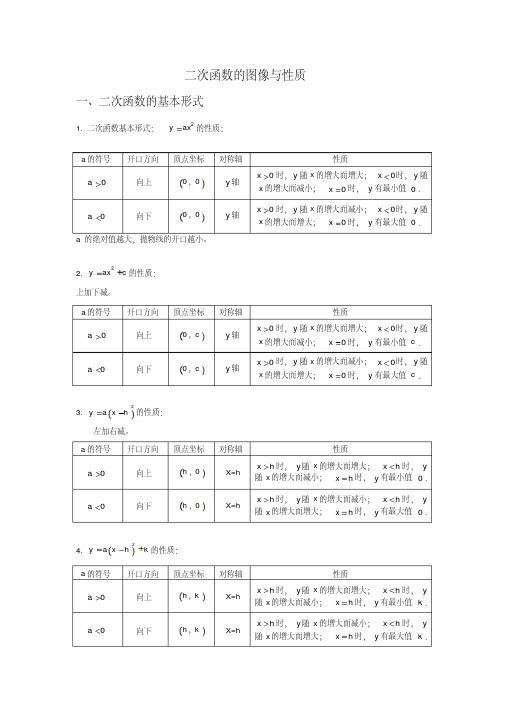
二次函数图像与性质完整归纳

二次函数的图像与性质一、二次函数的基本形式1. 二次函数基本形式：的性质：2y ax =a 的绝对值越大，抛物线的开口越小。

2. 的性质：2y ax c =+上加下减。

3. 的性质：()2y a x h =-左加右减。

4. 的性质：()2y a x h k =-+的符号a 开口方向顶点坐标对称轴性质a >向上()00，轴y 时，随的增大而增大；时，0x >y x 0x <随的增大而减小；时，有最小值y x 0x =y ．00a <向下()00，轴y 时，随的增大而减小；时，0x >y x 0x <随的增大而增大；时，有最大值y x 0x =y ．0的符号a 开口方向顶点坐标对称轴性质a >向上()0c ，轴y 时，随的增大而增大；时，0x >y x 0x <随的增大而减小；时，有最小值y x 0x =y ．c 0a <向下()0c ，轴y 时，随的增大而减小；时，0x >y x 0x <随的增大而增大；时，有最大值y x 0x =y ．c 的符号a 开口方向顶点坐标对称轴性质a >向上()0h ，X=h时，随的增大而增大；时，x h >y x x h <随的增大而减小；时，有最小值y x x h =y ．00a <向下()0h ，X=h时，随的增大而减小；时，x h >y x x h <随的增大而增大；时，有最大值y x x h =y ．0的符号a 开口方向顶点坐标对称轴性质a >向上()h k ，X=h时，随的增大而增大；时，x h >y x x h <随的增大而减小；时，有最小值y x x h =y二、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式，确定其顶点坐标；()2y a x h k =-+()h k ，⑵ 保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：2y ax =()h k，【【【(h <0)【【【【【(h >0)【【【(h 【【|k|【【【2. 平移规律在原有函数的基础上“值正右移，负左移；值正上移，负下移”．h k 概括成八个字“左加右减，上加下减”．方法二：⑴沿轴平移:向上（下）平移个单位，变成c bx ax y ++=2y m c bx ax y ++=2（或）m c bx ax y +++=2m c bx ax y -++=2⑵沿轴平移：向左（右）平移个单位，变成c bx ax y ++=2m c bx ax y ++=2（或）c m x b m x a y ++++=)()(2c m x b m x a y +-+-=)()(2三、二次函数与的比较()2y a x h k =-+2y ax bx c =++从解析式上看，与是两种不同的表达形式，后者通过()2y a x h k =-+2y ax bx c =++配方可以得到前者，即，其中．22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭2424b ac b h k a a -=-=，．k 0a <向下()h k ，X=h时，随的增大而减小；时，x h >y x x h <随的增大而增大；时，有最大值y x x h =y ．k四、二次函数图象的画法2y ax bx c =++五点绘图法：利用配方法将二次函数化为顶点式，确2y ax bx c =++2()y a x h k =-+定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与轴的交点、以及关于对称轴对称的点y ()0c ，()0c ，、与轴的交点，（若与轴没有交点，则取两组关于对称轴()2h c ，x ()10x ，()20x ，x 对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与轴的交点，与轴的交点.x y 五、二次函数的性质2y ax bx c =++ 1. 当时，抛物线开口向上，对称轴为，顶点坐标为．0a >2bx a =-2424b ac b a a ⎛⎫-- ⎪⎝⎭，当时，随的增大而减小；当时，随的增大而增大；当2b x a <-y x 2bx a>-y x 时，有最小值．2b x a =-y 244ac b a- 2. 当时，抛物线开口向下，对称轴为，顶点坐标为．当0a <2bx a =-2424b ac b aa ⎛⎫-- ⎪⎝⎭，时，随的增大而增大；当时，随的增大而减小；当时，2b x a <-y x 2b x a >-y x 2bx a=-有最大值．y 244ac b a-六、二次函数解析式的表示方法1. 一般式：（，，为常数，）；2y ax bx c =++a b c 0a ≠2. 顶点式：（，，为常数，）；2()y a x h k =-+a h k 0a ≠3. 两根式：（，，是抛物线与轴两交点的横坐标）.12()()y a x x x x =--0a ≠1x 2x x 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与轴有交点，即时，抛物线的解析式才可以x 240b ac -≥用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数中，作为二次项系数，显然．2y ax bx c =++a 0a ≠ ⑴ 当时，抛物线开口向上，的值越大，开口越小，反之的值越小，开口越0a >a a 大；⑵ 当时，抛物线开口向下，的值越小，开口越小，反之的值越大，开口越0a <a a 大．总结起来，决定了抛物线开口的大小和方向，的正负决定开口方向，的大小决a a a 定开口的大小．2. 一次项系数b在二次项系数确定的前提下，决定了抛物线的对称轴．a b ⑴ 在的前提下，0a >当时，，即抛物线的对称轴在轴左侧；0b >02ba-<y 当时，，即抛物线的对称轴就是轴；0b =02ba-=y 当时，，即抛物线对称轴在轴的右侧．0b <02ba->y ⑵ 在的前提下，结论刚好与上述相反，即0a <当时，，即抛物线的对称轴在轴右侧；0b >02ba->y 当时，，即抛物线的对称轴就是轴；0b =02ba-=y 当时，，即抛物线对称轴在轴的左侧．0b <02ba-<y 总结起来，在确定的前提下，决定了抛物线对称轴的位置．a b 的符号的判定：对称轴在轴左边则，在轴的右侧则，ab abx 2-=y 0>ab y 0<ab 概括的说就是“左同右异”总结：3. 常数项c⑴ 当时，抛物线与轴的交点在轴上方，即抛物线与轴交点的纵坐标为正；0c >y x y⑵ 当时，抛物线与轴的交点为坐标原点，即抛物线与轴交点的纵坐标为；0c =y y 0 ⑶ 当时，抛物线与轴的交点在轴下方，即抛物线与轴交点的纵坐标为0c <y x y 负．总结起来，决定了抛物线与轴交点的位置．c y 总之，只要都确定，那么这条抛物线就是唯一确定的．a b c ，，二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与轴的两个交点的横坐标，一般选用两根式；x 4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于轴对称x关于轴对称后，得到的解析式是； 2y ax bx c =++x 2y ax bx c =---关于轴对称后，得到的解析式是；()2y a x h k =-+x ()2y a x h k =--- 2. 关于轴对称y关于轴对称后，得到的解析式是； 2y ax bx c =++y 2y ax bx c =-+关于轴对称后，得到的解析式是；()2y a x h k =-+y ()2y a x h k =++ 3. 关于原点对称关于原点对称后，得到的解析式是；2y ax bx c =++2y ax bx c =-+-关于原点对称后，得到的解析式是；()2y a x h k =-+()2y a x h k =-+- 4. 关于顶点对称（即：抛物线绕顶点旋转180°）关于顶点对称后，得到的解析式是；2y ax bx c =++222b y ax bx c a=--+-关于顶点对称后，得到的解析式是．()2y a x h k =-+()2y a x h k =--+ 5. 关于点对称()m n ，关于点对称后，得到的解析式是()2y a x h k =-+()m n ，()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择a 合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图像参考：y=3(x+4)22y=3x 2十一、【例题精讲】一、一元二次函数的图象的画法【例1】求作函数的图象64212++=x x y 【解】)128(21642122++=++=x x x x y 2-4)(214]-4)[(21 2222+=+=x x 以为中间值，取的一些值，列表如下：4-=x x x …-7-6-5-4-3-2-1…y …25023--223-025…【例2】求作函数的图象。

二次函数图像a,b,c各类关系式子的判断

二次函数图像a,b,c各类关系式子的判断一．开口方向：判断a的符号。

若开口向上，则a﹥0；若开口向下，则a﹤0.二．抛物线与y轴的交点：判断c的符号若交点在y轴的正半轴，则c﹥0；若交点在轴的负半轴，则c﹤0；若交点恰为原点，则c=0。

三．顶点的位置1.顶点横坐标－的作用：根据顶点与y轴的左右关系，判明横坐标的符号，再结合a的符号，即可判明b的符号。

（利用对称轴亦有此效，见后四。

1）2.顶点纵坐标(4ac－b2)／4a 的作用：根据顶点与x轴的上下关系，判明纵坐标的符号，再结合a的符号，即可判明b2－4ac的符号。

（利用抛物线与x轴的交点个数，亦有此效）四．对称轴x=－的位置1．判断b的符号：根据对称轴与y轴的左右关系，判明整个－的符号，再结合a的符号，即可判明b的符号。

2．若对称轴已知为x=k,则－ =k,即得出a、b之间的一个等量关系。

3．若对称轴已知为x=k>m，则－ >m,结合a的符号，可得出a、b之间的一个不等关系（如大小关系）。

五．抛物线与x轴的交点：从ax2+bx+c的结构特点入手判断有关命题注意二次函数式ax2+bx+c的结构有如下特点：当x=±3时，ax2+bx+c=9a±3b+c ①当x=±2时，ax2+bx+c=4a±2b+c ②当 x=±1时，ax2+bx+c=a±b+c ③当x=±m时，ax2+bx+c=am2±bm+c ④设抛物线与x轴的交点为A，B，根据x轴上的点（±3,0）,（±2,0）,（±1,0）,(±m,0)等与点A，B的位置关系，即可判断出和上述①②③④四个式子（或其变式）有关的若干命题是否成立。

对于某些较难判断的题目，仅有以上五点总结还不很够，为此，下面再补充一点。

六．以方程组或不等式组的思想为指导，运用相关技巧判断一些较难命题是否成立。

运用口诀判断二次函数的系数关系式

运用口诀判断二次函数的系数关系式学生对二次函数中字母系数a、b、c及其关系式的符号判断常有些不知所措，这里介绍几个口诀来帮助同学们解惑．1．基础四看“基础四看”是指看开口，看对称轴，看与y轴的交点位置，看与x轴的交点个数．“四看”是对二次函数y＝ax2＋bx＋c（a≠0）的图象最初步的认识，而且这些判断都可以通过图象直接得到，同时还可以在此基础上进行一些简单的组合应用．例1 二次函数y＝ax2＋bx＋c(a≠0)的图象如图1所示，则下列说法不正确的是( )(A)b2－4ac>0 (B)a>0(C)c>0 (D)b<0分析根据“基础四看”，由抛物线开口向上，故a>0；由对称轴在y轴的右侧，则a、b异号，故b<0：由抛物线与y轴交于负半轴，故c<0；由抛物线与x轴有两个交点，故b2－4ac>0．所以本题答案是C．例2 函数y＝ax2＋bx＋c和y＝ax＋b在同一坐标系中，如图所示，则正确的是( )分析对于几个函数图象组合的辨别，笔者常用的一种方法是“矛盾排除法”．对A中的图象分析可得：在抛物线中，a>0，b>0，c>0；在直线中，a>0，b>0，无矛盾，可为备选答案．对B中的图象分析可得：在抛物线中，a<0，b<0，c<0；在直线中，a>0，b＝0，有矛盾，故排除．对C中的图象分析可得：在抛物线中，a>0，b<0，c>0；在直线中，a<0，b>0，有矛盾，故排除．对D中的图象分析可得，在抛物线中，a<0，b>0，c<0；在直线中，a<0，b<0，有矛盾，故排除．所以本题答案是A．注从上面介绍中可以看到，对于某个二次函数y＝ax2＋bx＋c(a≠0)的图象我们可以对单独的a、b、c与△进行直接判断，同时也可以对a、b、c的简单乘除组合式进行符号判断．但如果遇到关于a 、b 、c 间的一些加减组合式又如何来处理呢？2．组合二看(1)三全看点在a 、b 、c 间的加减组合式中，最常见的如“a ＋b ＋c"，“a －b ＋c ”，“4a ＋2b ＋c ”，“4a －2b ＋c ”等类型的式子，这类式子a 、b 、c 三个字母都在，并且c 的系数通常为1，这时只要取x 为b 前的系数代入二次函数y ＝ax 2＋bx ＋c 就可以得到所需的形式，从而由其对应的y 的值时进行判断即可．(2)有缺看轴当a 、b 、c 三个字母只出现两个间的组合时，这时对同学们来讲难度是较大的，如何解决呢？其实我们只要想一想为什么会少一个字母，这个问题就可以较好的解决．少一个字母的原因就是因为有对称轴为我们提供了a 、b 之间的转换关系，如果少的是字母c ，则直接用对称轴提供的信息即可解决；如果少的是字母a 或b ，则可利用对称轴提供的a 、b 间转换信息，把a （或b ）用b （或a ）代换即可．例3 已知二次函数（a ≠0）的图象如图3所示，有下列4个结论：①2a ＋b ＝0；②b<a ＋c ；③4a ＋2b ＋c>0；④3a ＋c>0．其中正确的结论有( )(A)1个 (B)2个(C)3个 D ．4个分析本题中的②③三个字母都在，且符合“三全看点”的特征，其中②变形后为a－b ＋c>0，由f(－1)<0，知a －b ＋c<0，不符合；③中由f(2)>0，知4a ＋2b ＋c >0，符合要求．本题中的①④字母不全，且符合“有缺看轴”的特征，其中①少c ，可直接找对称轴，由对称轴方程为直线x ＝－2b a＝1，即2a ＋b ＝0，符合要求；而④少b ，显然是利用对称轴方程中b ＝－2a 这个关系式，将原来式子中的b 代换成了a ，我们可能根据“三全看点”中a 、b 间系数的关系进行推演，不难找到其原有的式子，或为a －b ＋c ，或为9a ＋3b ＋c ，再任取其一判断，可得3a ＋c<0，不符合．所以本题答案是B ．例4 如图4，已知二次函数y ＝ax 2＋bx ＋c 的图象与x 轴相交于（x 1，0），（x 2，0）两点，且0<x 1<1，1<x 2 <2，与y 轴相交于(0，－2)．下列结论：①2a ＋b>1；②3a ＋b>0；③a ＋b<2；④b 2＋8a>0；⑤a －b>2．其中正确结论的个数为( )(A)1个 (B)2个(C)3个 (D)4个分析本题有一个重要数据条件“与y轴相交于（0，－2）”，即c ＝－2．所以本题不少选项中的c 为－2所取代，如在③中要判断a＋b<2是否正确，就是要看a ＋b －2<0是否正确，即判断“a ＋b ＋c ”，所以可以取x ＝1得a ＋b ＋c>0，即a ＋b －2>0，故③错误；同样在⑤和①中，可将原来要判断的式子变为“a －b ＋c ”与“4a ＋2b ＋c ”，分别取x ＝－1与x ＝2，即知①⑤都是错误的．由④所给的“b 2＋8a>0”可联想到“抛物线与x 轴有两个交点”，所以由b 2－4ac>0即得④正确．只有②的辨别可用“有缺看轴”的方法，此抛物线的对称轴为直线x ＝－2b a，由“抛物线与x 轴相交于（x 1，0），（x 2，0）两点，且0<x 1<1，1<x 1<2”可知“12<－2b a <32”，且“抛物线下口向下”知“a<0”，故有“a ＋b>0”或“3a ＋b<0”，可得②错误．所以本题答案是A ．注与“基础四看”相比，“组合二看”的要求显然高的多，尤其是出现字母有缺时，更要求同学们能充分把握函数图象中所给的信息．3．取值计算当解题感到无从下手时，可以尝试取值法，只要根据函数图象的特点及所给出的数据（或范围），取相应点坐标代入函数的解析式中，求出其字母系数，即可进行相关判断．例5 从如图5所示的二次函数y ＝ax 2＋bx ＋c （a ≠0）的图象中，观察得出了下面五条信息：①ab>0；②a ＋b ＋c<0；③b ＋2c>0；④a －2b ＋4c>0；⑤a ＝32b ．你认为其中正确信息的个数有( )(A)2个 (B)3个 (C)4个 (D)5个分析本题可用“取值法”判断．根据对称轴取（－43，0）、(13，0)两点，再任取与y 轴正半轴上的一个交点(0，1)，可求出y ＝－94x 2－32x ＋1，即得a ＝－94，b ＝－32，c ＝1．把它代入到①~⑤中，即可知都是正确的．所以本题答案是D ．注用“取值法”在解决此类问题时，通常只要取一组适合条件的点求出解析式即可，但如果遇到抛物线在某特定范围内变化时，要判断某些字母的取值范围时，我们还要采用“取临界值法”加以研究．例6 如图6所示，抛物线y ＝ax 2＋bx ＋c 与x 轴交于点A （－1，0），顶点坐标为(1，n)，与y 轴的交点在(0，2)、(0，3)之间（包括端点）．有下列结论：①当x>3时，y<0；②3a ＋b>0；③－1≤a ≤－23；④83≤n ≤4．其中正确的有( )(A)1个 (B)2个(C)3个 (D)4个分析本题由对称可知抛物线与x 轴的另一个交点为(3，0)，故①是正确的．由对称轴为直线x ＝－2b a＝1，知b ＝－2a ，则3a ＋b ＝ 3a －2a ＝a<0，故②是错误的．这里③④用逻辑判断就比较难，这时我们可以使用“取值法”．因为“抛物线与y 轴的交点在(0，2)、(0，3)之间（包括端点）”，故可以使用“取临界值法”，分别取(0，2)，(0，3)与(－1，0)，(3，0)进行计算，可求出它们所对应的两个抛物线的解析式为y ＝－23(x －1)2＋83，和y ＝－(x －1)2＋4，所以可知－1≤a ≤－23，83≤n ≤4，即③④都是正确的．所以本题答案是C ．上述方法有时计算量较大，但仍有一定的实用性，笔者希望大家能够了解和掌握．。

2.二次函数有关符号的判断

练一练：
1、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0； ④a+b-c＞0; ⑤a-b+c＞0正确的个数是（ C ） y A、2个 B、3个
C、4个
D、5个
-1 o
1
x
练一练：
2、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中不正确的是（ D ） y A、abc＞0 B、b2-4ac＞0
C、2a+b＞0
D、4a-2b
3、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①b＞0；②c<0；③4a+2b+c ＞ 0； ④（a+c）2＜b2，其中正确的个数是（ B ） A、4个 B、3个
C、2个
D、1个
y
o
x=1
x
谈谈你的收获? 1 a、b、c、△等符号性质 2 a+b+c的符号 3 a-b+c的符号 4 解信息题技巧`
a>0 b<0 c>0 △>0
o
x
做一做
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y
a>0 b>0 c=0 △>0
x
o
练一练
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y
o
a<0 b<0 c>0 △>0
x
你行的!
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y

二次函数解析式的符号确定

3 已知：抛物线y ax2 bx c（a＜0）
经过点(－1，0),且满足4a＋2b＋c＞0．以下结论：
①a＋b＞0；②a＋c＞0； ③－a＋b＋c＞0；④ b2 2ac ＞ 0 ．其中正确的个数有（）个
； https:///
；
我们就成了虚伪的坏蛋。你骗了别人的钱，可以退赔，你骗了别人的爱，就成了无赦的罪人。假如别人不曾识破，那就更惨。除非你已良心丧尽，否则便要承诺爱的假象，那心灵深处的绞杀，永无宁日。爱怕沉默。太多的人，以为爱到深处是无言。其实，爱是很难描述的一种情感，需要详尽的表达和传递。爱需要行动，但爱绝不仅仅是行动，或者说语言和温情的流露，也是行动不可或缺的部分。爱是需要表达的，就像耗费太快的电器，每日都得充电。重复而新鲜地描述爱意吧，它是一种勇敢和智慧的艺术。 ? 爱怕犹豫。爱是羞怯和机灵的，一不留神它就吃了鱼饵闪去。爱的初起往往是柔弱无骨的碰撞和翩若惊鸿的引力。在爱的极早期，就敏锐地识别自己的真爱，是一种能力更是一种果敢。爱一桩事业，就奋不顾身地投入。爱一个人，就斩钉截铁地追求。爱一个民族，就挫骨扬灰地献身。爱一桩事业，就呕心沥血。爱一种信仰，就至死不悔。爱怕模棱两可。要么爱这一个，要么爱那一个，遵循一种“全或无”的铁则。爱，就铺天盖地，不遗下一个角落。不爱就抽刀断水，金盆洗手。迟疑延宕是对他人和自己的不负责任。爱怕沙上建塔。那样的爱，无论多么玲珑剔透，潮起潮落，遗下的只是无珠的蚌壳和断根的水草。爱怕无源之水。沙漠里的河啊，即便不是海市蜃楼，波光粼粼又能坚持几天？当沙暴袭来的时候，最先干涸的正是泪水积聚的咸水湖。爱怕假冒伪劣。真的爱也许不那么外表光滑，色彩艳丽，没有精致的包装，没有夸口的广告，但是它有内在的质量保。真爱并非不会发生短路与损伤，但是它有保修单，那是两颗心的承诺，写在天地间。爱是一个有机整体，怕分割。好似钢化玻璃，据说坦克轧上也不会碎，可惜它的弱点是宁折不弯，脆不可裁。一旦破碎，就裂成了无数蚕豆大的渣滓，流淌一地，闪着凄楚的冷光。再也无法复原。 ?爱的脚力不健，怕远。距离会漂淡彼此相思的颜色，假如有可能，就靠得近一点，再近一点，直到水乳交融亲密无间。万万不要人为地以分离考验它的强度，那你也许后悔莫及。尽量地创造并肩携手天人合一的时光。爱像仙人掌类的花朵，怕转瞬即逝。爱可以不朝朝暮暮，爱可以不卿卿我我，但爱要铁杵磨针，恒远久长。 ?爱怕刻意求工。爱可以披头散发，爱可以荆钗布裙，爱可以粗茶淡饭，爱可以餐风宿露。只要一腔真情，爱就有了依傍。爱的时候，眼珠近视散光，只爱看江山如画。耳是聋的，只爱听莺歌燕舞。爱让人片面，爱让人轻信。爱让人智商下降，爱让人一厢情愿。爱最怕的，是腐败。爱需要天天注入激情的活力，但又如深潭，波澜不惊。 ?说了爱的这许多毛病，爱岂不一无是处？ ?爱是世上最坚固的记忆金属，高温下不融化，冰冻不脆裂。造一艘爱的航天飞机，你就可以驾驶着它，遨游九天。爱是比天空和海洋更博大的宇宙，在那个独特的穹隆中，有着亿万颗爱的星斗，闪烁光芒。一粒小行星划下，就是爱的雨丝，缀起满天清光。 ? 爱是神奇的化学试剂，能让苦难变得香甜，能让一分钟永驻成永远，能让平凡的容颜貌若天仙，能让喃喃细语压过雷鸣电闪。 ? 爱是孕育万物的草原。在这里，能生长出能力、勇气、智慧、才干、友谊、关怀……所有人间的美德和属于大自然的美丽天分，爱都会给赠予你。在生和死之间，是孤独的人生旅程。保有一份真爱，就是照耀人生得以温暖的灯。 ? 2005年12月版《智慧》人生有三件事不可俭省 ?无论世界变得如何奢华，我还是喜欢俭省。这已经变得和金钱没有很密切的关系，只是一个习惯。我这样说，实在是因为俭省的机会其实很廉价，俯拾即是遍地滋生。比如不论牙膏管子多么丰满，但你只能在牙刷毛上挤出1.5到2厘米的膏条,而不是1尺长。因为你用不了那么多，你不能把自己的嘴巴变成螃蟹聚会的洞穴。再比如无论你坐拥多少橱柜的衣服，当暑气蒸人的时候，你只能穿一件纯棉的T恤衫。如果把貂皮大衣捂在身上，轻者长满红肿热痛的痱毒，重了就会中暑倒地一命呜呼。俭省比奢华要容易得多，是偷懒人的好伴侣——用最直截了当的方式和最小的花费直抵目标。然而有三件事你不能俭省。第一件事是学习。学习是需要费用的，就算圣人孔子，答疑解惑也要收干肉为礼。学习费用支出的时候，和买卖其他货物略有不同。你不知道究竟能得到多少知识，这不单决定于老师的水平，也决定于你自己的状态。这在某种情况下就有点隔山买牛的味道，甚至比股票的风险还大。谁也不能保你在付出了学费之后一定能考上大学，你只能先期投入。机遇是牵着婚纱的小童，如果你不学习，新娘就永远不会出现在你人生的殿堂。第二件事是旅游。每个人出生的时候都是蝌蚪，长大了都变作井底之蛙。这不是你的过错，只是你的限制，但你要想法弥补。要了解世界，必须到远方去。旅游是需要花钱的，谁都知道。旅游的好处却不是一眼就能看到的，常常需要日积月累潜移默化地蓄积。有人以为旅游只是照一些相片买一些小小的工艺品，其实不然。旅行让我们的身体感悟到不同的风和水，我们的头脑也在不同风情的滋养下变得机敏和多彩。目光因此老辣，谈吐因此谦逊。第三件事是锻炼身体。古代的人没有专门锻炼身体的习惯，饥一顿饱一顿全无赘肉。生存的需要逼得他们不停奔跑狩猎，闲暇的时候就装神弄鬼，在岩壁上凿画，在篝火边跳舞，都不是轻体力劳动，积攒不下多余的卡路里。社会进步了，物质丰富了，用不完的热量成了我们挥之不去的负担。于是要人为地在机器上跋涉，在充满氯气的池子里浮沉，在人造的雪花和冰面上打滚，在矫揉造作的水泥峭壁上攀爬……这真是愚蠢的奢侈啊，可我们没有办法，只有不间断地投入金钱，操练贫瘠的肌肉和骨骼，以保持最起码的力量和最基本的敏捷。有没有省钱的方法呢？其实也是有的。把人生当作课堂，向一切人学习，就省了上学的钱。徒步到远方去，就省了旅游的钱。不用任何健身器械，就在家里踢毽子高抬腿做广播体操……就省了健身的钱。然而，这也是破费，因为我们付出了时间。让女人丑陋的最根本原因对一个女性最有害的东西，就是怨恨和内疚。前者让我们把恶毒的能量对准他人；后者则是掉转枪口，把这种负面的情绪对准了自身。你可以愤怒，然后采取行动；你也可以懊悔，然后改善自我。但是请你放弃怨恨和内疚，它们除了让女性丑陋以外，就是带来疾病。我有一个面目清秀的女友，多年没见，再相见时，吓了我一跳。一时间张口结舌，不知说什么好。她倒很平静，说，我变老了，是吧？我嗫嚅着说，我也老了。咱们都老了，岁月不饶人嘛！她苦笑了一下说，我不仅是变老了，更重要的是变丑了。对吧？在这样犀利洞见的女子面前，你无法掩饰。我说，好像也不是丑，只是你和原来不一样了，好像换了一个人似的，整个面目都不同了。她说，你不知道我的婚姻很不幸吗？我说，知道一点。她说，我告诉你一件事，一个不幸福的女人是挂相的。我们常常说，某女人一脸苦相。其实，你到小姑娘那里看看，并没有多少女孩子就是这种相貌的。女子年轻的时候，基本上都是天真烂漫的。但是你去看中年妇女，就能看出幸福和不幸福两大阵营。我说，生活是可以雕塑一个人的相貌的，这我知道。但是，好像也没有你说得这样绝对吧？她坚持道，是这样的，不信你以后多留意。到了老年妇女那里，差异就更大了。基本上就分为两类：一种是慈祥的，一种是狞恶的。我就是属于狞恶的那一种。我不知如何接下茬，避重就轻说，不过，我们在照片上看到的老年人，都是慈祥的。她说，对啊。那些不慈祥的，根本活不了太久。比如我，很可能早早就告别人世。话说到这份上，我只好不再躲避。我说，那么你怎样看待自己的相貌变化？她说，我之所以同你讲得这样肯定，就是从我自己身上得出的结论。因为我的婚姻不幸福，我又没有法子离婚，所以一直在怨恨和后悔中生活、煎熬着。对着镜子，我一天天地发现自己变得尖刻和狞厉起来。当然，这不是一天发生的，别人看不出来，但我自己能够看出来。我用从自己身上得到的经验去看别人，竟是百分之百地准确…… 我看着她，说不出话来。在这样透彻冷静的智慧面前，你只能沉默。每当我想起她来，心中都漾过竹签扎进甲床般的痛。她所具有的智慧，是一种波光诡谲入木三分的聪明，犹如冰河中的一缕红绳，鲜艳地冻结在那里，却无法捆绑住任何东西。我愿意把她的心得转述在这里。女人会不会因为心理不健康而变丑，我不敢打包票。因为心理不健康而导致身体上的病患，却是千真万确的。为了不得病，为了不变丑，人们只有更多地让爱意充满心扉。冻顶百合 ?世界上有没有冻顶百合这种花呢？在我写这篇文章之前是没有的，虽然它很容易逗起一种关于晶莹香花的联想，其实是一个拼凑起来的蹩脚词语。记得那一年到台湾访问，去台湾岛内的第一高峰玉山。陪同的女作家不断向我介绍沿路风景，时不时插入“玉山可真美啊”的感叹。玉山诚然美，我却无法附和。对于山，实在是“曾经沧海难为水”啊！十几岁时，当我还未曾见过中国五岳当中的任何一岳，爬过的山峰只限于近郊500米高的香山时，就在猝不及防中，被甩到了世界最宏大山系的祖籍—青藏高原，一住十几年，直到红颜老去。朋友，请原谅我心如止水，我已经在少女时代就把惊骇和称誉献给了藏北。 ? 由于没有恰如其分的回应，女作家也悄了声。山势越来越高了，蜿蜒公路旁突然出现了密集的房屋和人群，原来是众多的游客围着当地的山民在买茶。也许是为了挽救刚才的索然，我夸张地显示好奇：“什么茶？”“冻顶乌龙。“女作家表情淡然。我猜疑她的淡然可能是对我的小小惩罚，很想弥补刚才对玉山的不恭，马上兴致勃勃地说：“冻顶乌龙可是台湾的名产啊，前些年，大陆很有些人以能喝到台湾正宗的冻顶乌龙为时髦呢！”说着，我拿出手袋，预备下车去买冻顶乌龙。女作家看着我，叹了一口气说：“就是爱喝冻顶乌龙的人，才给玉山带来了莫大的危险。”她面色忧郁，目光黯淡。为什么呀？我疑窦丛生。女作家说，台湾的纬度低，通常不下雪也不结霜。玉山峰顶，由于海拔高，有时会落雪挂霜，台湾话就称其“冻顶”。乌龙本是寻常半发酵茶的一种，整个台湾都有出产，但标上了“冻顶”，就说明这茶来自高山。云雾缭绕，人迹罕至，泉水清冽，日照时短，茶品自然上乘。冻顶乌龙可卖高价，很

二次函数知识点总结

二次函数知识点一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：上加下减。

3. ()2y a x h =-的性质：左加右减。

4.()2y a x h k=-+的性质：三、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx axy +++=2（或m c bx axy -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a -=-=，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a<-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2b x a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a>-时，y 随x 的增大而减小；当2b x a=-时，y 有最大值244ac b a-．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化. 八、二次函数的图象与各项系数之间的关系 1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02b a -<，即抛物线的对称轴在y 轴左侧；当0b =时，02b a -=，即抛物线的对称轴就是y 轴；当0b <时，02b a->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即当0b >时，02b a ->，即抛物线的对称轴在y 轴右侧；当0b =时，02b a -=，即抛物线的对称轴就是y 轴；当0b <时，02b a-<，即抛物线对称轴在y 轴的左侧．总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴ab x 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异”总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0；⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k=-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k=-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222by ax bx c a=--+-；()2y a x h k=-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称()2y a x h k=-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离21AB x x =-=② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2'当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <． 2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ； 3. 二次函数常用解题方法总结：⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数；下面以0a >时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：图像参考：y=-2x 2十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函数考查重点与常见题型1．考查二次函数的定义、性质，有关试题常出现在选择题中，如：已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点，则m 的值是2．综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题，如：如图，如果函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（）3．考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如：已知一条抛物线经过(0,3)，(4,6)两点，对称轴为35=x ，求这条抛物线的解析式。

二次函数解析式的符号确定(PPT)3-1

1 二次函数 y ax 2 bx c 的图象
如图所示，则a 0， b 0， c 0
4.抛物线 y ax2 bx c(a 0) 过第
a 二、三、四象限，则
0，b 0，c 0．
Hale Waihona Puke (1)抛物线 y ax2 bx c(a 0) 过第一、
二、四象限，则 a 0,b 0，c 0．
(2)已知抛物线
与x 轴
的交点都在原点的右侧，则点M（）
在第象限．
冰层与变化着的二氧化碳层轮流叠加而成。在北部的夏天，二氧化碳完全升华，留下剩余的冰水层。由于南部的二氧化碳从没有完全消失过，所
以我们无法知道在南部的冰层下是否也存在着冰水层（左图）。这种现象的原因还不知道，但或许是由于火星赤道面与其运行轨道之间的夹角的长期变化引起气候的变化造成的。或许在火星表面下较深处也有水存在。这种因季节变化而产生的两极覆盖层的变化使火星的气压改变了%左右。（由海盗号测量出）。但是通过哈勃望远镜的观察却表明海盗号当时勘测时的环境并非是典型的情况。火星的大气似乎比海盗号勘测出的更冷、
更干。温度火星的轨道是椭圆形。因此，在接受太阳照射的地方，近日点和远日点之间的温差将近摄氏度。这对火星的气候产生巨大的影响。火星上的平均温度大约为8K（开尔文，温度单位，即；赛前分析/zqzxsq/ ；从绝对零度-7.℃开始的摄氏度）（-℃，7℉），但却具有从冬天的K（-℃，-7℉）到夏日白天的将近K（7℃，8℉）的跨度。尽管火星比地球小得多，但它的表面积却相当于地球表面的陆地面积。水远古海洋据美国太空网报道，科学家们已经掌握更多证据证明在数十亿年前火星表面的大部分地区曾经被广阔的海洋覆盖有关这项发现的文章已经刊载于7月日出版的《地球物理学报》上。这些最新的证据来自正围绕火星运行的强大飞船“火星勘测轨道器”(MRO)拍摄的图像。根据这些图像科学家们识别出一个巨大的冲积三角洲这个三角洲所在的河流最终注入一个面积几乎覆盖/火星表面的巨型海洋。论述这项发现的论文作者之一是美国加州理工学院地质学助理教授麦克·兰博(MikeLamb)，他表示：“科学家们长期以来一直认为火星北半球广阔的低地平原是一片干涸的古代海洋，但是苦于缺乏确凿的证据。”此次的研究结果尽管距离给出直接的证据仍然有距离，但它的确进一步支持了这一理论。研究小组仔细审视由火星勘测轨道器搭载的HiRise相机拍摄的火星北半球低地地区一小片区域的高分辨率图像。该设备可以识别火星地表英寸(约合厘米)直径的物体。更加具体而言，科学家们仔细观察了一个名为“AeolisDorsa”的区域中的一部分，面积约㎞，这片地区距离盖尔陨石坑约英里(约合公里)。盖尔陨坑便是美国好奇号火星车登陆的地方，它正在这一地区开展地质考察。这一小块区域中分布有很多隆起的脊线，这主要是长期流水沉积下来的一些较粗砾石堆积形成的这种脊线在其所在的河流干涸很久之后仍然能够继续存在，从而告诉科学家们这里曾经存在过的水系的情况。HiRis

二次函数图像特征与a、b、c、△符号的关系

二次函数系数a 、b 、c 与图像的关系一、首先就y=ax 2+bx+c （a ≠0）中的a ，b ，c 对图像的作用归纳如下： 1、a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下； 2、b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号，说明02<-ab ，则对称轴在y 轴的左边；b 与a 异号，说明，则对称轴在y 轴的右边；特别的，b = 0，对称轴为y 轴．3、c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点（0，c ）c > 0 抛物线与y 轴的交点在y 轴的正半轴； c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的，c = 0，抛物线过原点． 4、a,b,c 共同决定判别式的符号进而决定图象与x 轴的交点与x 轴两个交点与x 轴一个交点与x 轴没有交点5、几种特殊情况：x=1时，y=a + b + c ；x= -1时，y=a - b + c ．当x = 1时，① 若y > 0，则a + b + c >0；② 若y < 时0，则a + b + c < 0 当x = -1时，① 若y > 0，则a - b + c >0；② 若y < 0，则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c 。

反之，给我们相应的二次函数图象，我们可以得到其系数a,b,c 以及它们组合成的一些关系结构（例如对称轴;判别式……等等）的符号二次函数专题训练1——图像特征与a 、b 、c 、△符号的关系1例1、已知二次函数()02≠++=a c b a χχγ的图像如图，则a 、b 、c 满足（A ．a < 0，b < 0，c > 0 ；B ．a < 0，b < 0，c < 0 ；C ． a < 0，b > 0，c > 0 ；D ．a > 0，b < 0，c > 0 ；例2、如图所示为二次函数y=ax 2+bx+c （a ≠0）的图象，在下列选项中错误的是（） A 、ac ＜0 B 、x ＞1时，y 随x 的增大而增大 C 、a+b+c ＞0 D 、方程ax 2+bx+c=0的根是=-1，=31、已知二次函数2y ax bx c =++，如图所示，若0a <，0c >，那么它的图象大致是（）2、已知二次函数2y ax bx c =++的图象如图所示，则点(,)ac bc 在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3、已知二次函数2y ax bx c =++的图象如下，则下列结论正确的是（） A 、0ab < B 、0bc < C 、0a b c ++> D 、0a b c -+<4、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，则下列结论： ①a>0；②c>0；•③b 2-4ac>0，其中正确的个数是（）A ．0个B ．1个C ．2个D ．3个5、二次函数y=ax 2+bx+c 的图像如图1，则点M （b ，ca ）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6、二次函数2y ax bx c =++的图象如图所示，则（）A 、0a >，240b ac -<B 、0a >，240b ac ->C 、0a <，240b ac -<D 、0a <，240b ac ->7、已知函数y=ax+b 的图象经过第一、二、三象限，那么y=ax 2+bx+1的图象大致为( )8、已知函数c bx ax y ++=2的图象如图所示，则下列结论正确的是（）A ．a ＞0，c ＞0B ．a ＜0，c ＜0C ．a ＜0，c ＞0D ．a ＞0，c ＜09、二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列说法不正确的是（）A ．240b ac -> B ．0a > C ．0c > D ．02b a -<10、二次函数y ＝ax 2＋bx ＋c 的图象如图，则下列各式中成立的个数是（）（1）abc ＜0；（2）a ＋b ＋c ＜0；（3）a ＋c ＞b ；（4）a ＜2b -．A ．1B 2C .3 D. 411、已知二次函数的图象如图所示，有下列5 个结论：① ；② ；③ ；④ ；⑤ ，（的实数）其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个12、如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A （－3，0），对称轴为x ＝－1．给出四个结论：①b 2＞4ac ；②2a ＋b =0；③a －b ＋c =0；④5a ＜b ．其中正确结论是（）． A ②④ B ①④ C ②③ D ①③13、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列结论：①c<0，②b>•0，•③4a+2b+c>0，④（a+c ）2<b 2．其中正确的有（）A ．1个B ．2个C ．3个D ．4个14、抛物线)0(2>++=a c bx ax y 的对称轴是直线1=x ，且经过点P （3，0），则c b a +-的值为（） A. 0 B. －1 C. 1 D. 215、已知： ()220y ax bx a b a =+++≠的图像为下列图像之一，则a 的值为（）A .－1B ． 1C . －3D . －416、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( ) A.1个 B.2个 C. 3个 D. 4个17、已知函数2y ax bx c =++(0a ≠)的图象如图所示，有下列结论：①240b ac ->；②0abc >；③80a c +>；④930a b c ++<．其中，正确结论的个数是（） A .1 B .2 C .3 D . 418、已知二次函数y=ax 2+bx+c 的图象，如图所示，下列结论：①a+b+c>0；②a-b+c>0；③abc<0；④2a-b=0，其中正确结论的个数是( )A. 1B. 2C. 3D. 419、已知二次函数y=ax2+bx+c （a ≠0）的图象如图所示，则下列结论：①a 、b 同号；②当x=1和x=3时，函数值相等；③4a+b=0；④当y=-2时，x 的值只能取0.其中正确的个数是（） A ．1个 B ．2个 C ．3个 D ．4个20、已知一次函数y ax c =+与2y ax bx c =++，它们的大致图象是（）21、函数2y kx k =-和(0)ky k x=≠在同一直角坐标系中图象可能是图中的( )22、函数y=ax+b 与y=ax 2+bx+c 的图象如图所示, 则下列选项中正确的是( ) A. ab>0,c>0 B. ab<0,c>0 C. ab>0,c<0 D. ab<0,c<0x O y22、如图，二次函数y=ax 2+bx+c 的图象与x 轴相交于两个点，根据图象回答： (1)b_______0(填“>、<、=)； (2)当x 满足______________时，ax 2+bx+c>0：(3)当x 满足______________时，ax 2+bx+c 的值随x 增大而减小．24、如图为二次函数y=ax 2＋b x ＋c 的图象，在下列说法中： ①ac ＜0；②方程ax 2＋b x ＋c=0的根是x1= －1, x 2= 3 ③a ＋b ＋c ＞0④当x ＞1时，y 随x 的增大而增大。

7.9.1二次函数有关符号的判断

① ② ③ c＞0 c=0 c＜0 图象交y轴正半轴；图象过原点；图象交y轴负半轴。
b 2a
4ac b 2 4a
⑷a,b,c决定顶点坐标: (5)a决定最值:
4ac b 2 b 当x 时, y最值 4a 2a
3
例1.已知： y x 2 3x 2 .
(1)写出抛物线的开口方向,顶点坐标,对称轴,最值;
o x
8
练一练：
2、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①b＞0；②c<0；③4a+2b+c ＞ 0； ④（a+c)2＜b2，其中正确的个数是（ B ） A、4个 B、3个 y
C、2个
D、1个
o x=1
x
9
练一练：
3、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0； ④a+b-c＞0; ⑤a-b+c＞0正确的个数是（ C ） A、2个 B、3个
2.若关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴有两个交点，则a可取的值为 a>-1/4且a≠2 ； 3.(03武汉)已知抛物线y=ax2+bx+c （a＜0)经过点（－1，0），且满足4a＋2b＋c＞0．以下结论：①abc＞0；②b2-4ac＞0； √ × ③2a＋b＞0；④4a-2b+c<0．其中正确的个数有（ B ） √ × （A）1个（B）2个（C）3个（D）4个
y 3x 2 4 x 1
b 4 2 2a 6 3
y 2 x 2 x 3

二次函数中的符号问题

4、（06.浙江省）如图，二次函数、（06.浙江省）如图， 06.浙江省 +bx+c的图象开口向上图象经过点（的图象开口向上， y=ax2+bx+c的图象开口向上，图象经过点（-1，2）），且与轴相交于负半轴．且与y 和（1，0），且与y轴相交于负半轴．
y
练一练
第(1)问：给出四个结论： (1)问给出四个结论： a>0； b>0； c>0； a+b+c=0． ①a>0；② b>0；③c>0；④ a+b+c=0．其中正确结论的序号是 ①④
你还可想到啥？你还可想到啥？
6
快速回答
y
o
x
7
知识应用：知识应用：（1）由a、b、c、∆的符号确定抛物线在坐标系中）、、、的符号确定抛物线在坐标系中致位置；的大致位置；（2）由抛物线的位置确定系数、b、c、∆等符号及）由抛物线的位置确定系数a、、、等符号及有关a、、的代数式的符号的代数式的符号；有关、b、c的代数式的符号；
8
应用一
由a、b、c、∆的符号确定抛、、、的符号确定抛物线在坐标系中的大致位置
例题一 2010年贵州）函数 y = ax + b和y = ax2 + bx + c 年贵州）（2010年贵州
在同一直角坐标系内的图象大致是( 在同一直角坐标系内的图象大致是 C )
9
应用一
由a、b、c、∆的符号确定抛、、、的符号确定抛物线在坐标系中的大致位置
、（2009湖北省荆门市）函数湖北省荆门市）、（湖北省荆门市练一练 1、（ y=ax＋1与y=ax2＋bx＋1（a≠0）的图象＋与＋（）可能是（可能是（ C ）

初三数学_二次函数_知识点总结

初三数学二次函数知识点总结一、二次函数概念：1．二次函数的概念：一般地，形如2=++（a b cy ax bx c，，是常数，0a≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a≠，而b c，能够为零．二次函数的定义域是全体实数．（所以：二次函数应满足两个条件：①二次项的系数不等于0，②x 最高项的指数是2）2. 二次函数2=++的结构特征：y ax bx c⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2．⑵a b c，，是常数，a是二次项系数，b是一次项系数，c是常数项．二、二次函数的基本形式1. 二次函数基本形式：2=的性质：y ax①，a 的绝对值决定开口的大小（a 的绝对值越大，抛物线的开口越小，a 的绝对值越小，抛物线的开口越大）②a 的符号决定开口的方向（a＞0，开口向上，a＜0开口向下）2. 2=+的性质：y ax c上加下减。

（c＞0，将2=的图像向下移=向上移动，c＜0将2y axy ax动＝3. ()2=-的性质：y a x h左加右减。

Array 4. ()2=-+的性质：y a x h k三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k=-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方能够得到前者，即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，其中2424b ac b h k a a-=-=，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选择的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a=-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而减小；当2b x a>-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a -．2. 当0a <时，抛物线开口向下，对称轴为2bx a=-，顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式（又称为对称式）：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式（又称为两点式）：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.注意：任何二次函数的解析式都能够化成一般式或顶点式，但并非所有的二次函数都能够写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才能够用交点式表示．二次函数解析式的这三种形式能够互化.八、二次函数的图象与各项系数之间的关系 1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠． ⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大；⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧；当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba->，即抛物线对称轴在y 轴的右侧． ⑵ 在0a <的前提下，结论刚好与上述相反，即当0b >时，02ba->，即抛物线的对称轴在y 轴右侧；当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧．总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴ab2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结： 3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正；⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0；⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式（三点式）；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式（对称式）；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式（两点）；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况.图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离21AB x x =-=（即. 二次函数与x 轴两个交点的距离）② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1'当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >；2' 当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；十、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少注：在实际应用中凡是需要求最大，最小（或极值）问题一般都要考虑用二次函数的最大值或最小值二次函数考查重点与常见题型1．考查二次函数的定义、性质，相关试题常出现在选择题中，如：已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点，则m 的值是2．综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题，如：如图，假如函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（）xA B C D 3．考查用待定系数法求二次函数的解析式，相关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如：已知一条抛物线经过(0,3)，(4,6)两点，对称轴为35=x ，求这条抛物线的解析式。