二次函数特殊值判断专题
九年级数学上册复习专题08二次函数a、b、c符号判断
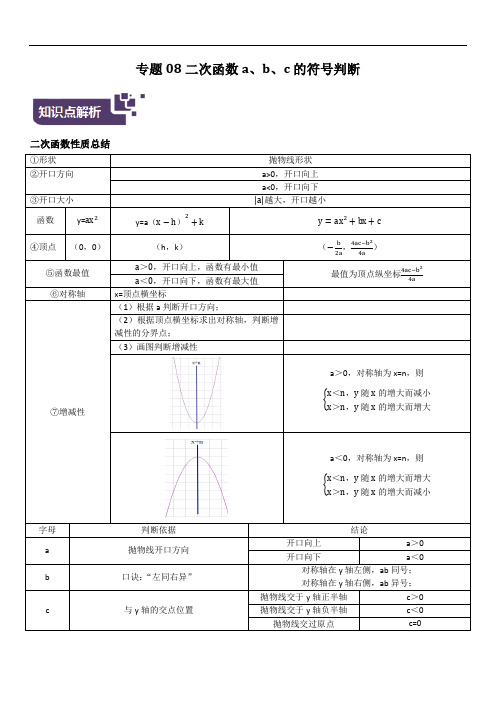
专题08二次函数a、b、c的符号判断二次函数性质总结（3）画图判断增减性判断依据判断下列图像对应的a，b，c的正负：图像字母符号（“正”或“负”）a b c a b c a b c a b c a b1．已知二次函数2y ax bx c =++的图象如图所示，则( )A ．0,0b c >>B ．0,0b c ><C ．0,0b c <<D ．0,0b c <>2．同一平面直角坐标系中，抛物线y ＝(x －a )2与直线y ＝ax +a 的图象可能是（ ）A ．B ．C ．D ．3．在同一平面直角坐标系中，函数y ＝ax 2＋b 与y ＝ax ＋b （ab ≠0）的大致图象可能是（ ）A ．B ．C ．D ．4．如图,在同一直角坐标系中, y ax c =+与2y ax c =+的图象为( )A ．B ．C ．D ．5．在同一坐标系中，一次函数2y mx n =-+与二次函数2y x m =+的图象可能是（ ）．A ．B ．C ．D ．6．如图，在同一坐标系下，一次函数y ax b =+与二次函数24y ax bx =++的图像大致可能是（ ）A ．B ．C ．D ．7．在同一坐标系中，一次函数y =ax +b 与二次函数y =ax 2+b 的大致图象为（ ）A ．B ．C ．D ．8．函数y kx b =+与2y kx b =+的图像大致为（ ）A ．B ．C ．D ．9．二次函数y ＝ax 2与一次函数y ＝ax+a 在同一坐标系中的图象大致为( )A ．B ．C ．D ．10．已知抛物线2y ax bx =+和直线y ax b =+在同一坐标系内的图象如图所示，其中正确的是（ ）11．在同一坐标系中表示2y ax =和()0y ax b ab =+>的图象的是( )A ．B ．C ．D ．12．在同一平面直角坐标系中，一次函数y ）ax +b 和二次函数y ）ax 2+bx +c 的图象可能为（ ）A ．B ．C ．D ．13．已知函数y 1＝mx 2+n ，y 2＝nx +m （mn ≠0），则两个函数在同一坐标系中的图象可能为（ ）A ．B ．C ．D ．14．已知一次函数y=ax+b 与二次函数y=ax 2+bx,它们在同一坐标系内大致图象是（ ）A ．B ．C ．D ．15．函数y=ax 2+ax+a）a≠0）的图象可能是下列图象中的（ ）A ．B ．C ．D ．16．二次函数2y ax ＝与一次函数y ax a ＝在同一坐标系中的大致图象可能是（ ）A ．B ．C ．D ．17．函数y=a 2x ＋c 与y=-ax ＋c(a≠0)在同一坐标系内的图像是图中的（ ）A ．B ．C ．D ．18．在同一坐标系中，函数y=ax 2与y=ax ﹣a （a≠0）的图象的大致位置可能是（ ）A ．B ．C ．D ．19．在同一平面直角坐标系中，若正比例函数(0)y mx m =≠）y 随x 的增大而减小，则它和二次函数2y mx m =+的图象大致是） ）20．在同一坐标系中，一次函数y=ax+1与二次函数y=x 2+a 的图像可能是（ ）A ．B ．C ．D ．21．在同一直角坐标系中y=ax 2+b 与y=ax+b）a≠0）b≠0）图象大致为（ ）A．B．C．D．。
中考复习函数专题19 二次函数的性质与图象判断问题(老师版)
专题19 二次函数的性质与图象判断问题知识对接考点一、二次函数的概念及表达式考点二、二次函数的性质与图象2. 抛物线c bx ax y ++=2与系数a,b,c 的关系一、单选题1．抛物线y＝（x﹣5）2的顶点坐标是（）A．（0，﹣5）B．（﹣5，0）C．（0，5）D．（5，0）【答案】D【分析】根据顶点式解析式写出顶点坐标即可得解．【详解】解：抛物线y=（x-5）2的顶点坐标是（5，0）．故选：D．【点睛】本题考查了二次函数的性质，主要利用顶点式解析式求顶点坐标，是基础题，需熟记．2．对于二次函数y＝2（x＋3）2的图象，下列说法不正确的是（）A．开口向上B．对称轴是直线x＝﹣3C．当x＜﹣3时，y随x的增大而增大D．与x轴仅有一个交点【答案】C【分析】根据抛物线的性质由a＝2得到图象开口向上，根据顶点式得到顶点坐标为（﹣3，0），对称轴为直线x＝﹣3，当x＜﹣3时，y随x的增大而增减小．【详解】解：二次函数y＝2（x＋3）2的图象开口向上，顶点坐标为（﹣3，0），与x轴仅有一个交点，对称轴为直线x ＝﹣3，当x ＜﹣3时，y 随x 的增大而减小，故A 、B 、D 说法正确，C 说法不正确，故选：C ．【点睛】本题主要考查抛物线与x 轴的交点，二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y ＝a （x −h ）2＋k 中，其顶点坐标为（h ，k ），对称轴为x ＝h ．当a ＞0时，抛物线开口向上，当a ＜0时，抛物线开口向下．3．如图1，在平行四边形ABCD 中，60B ∠=︒，2BC AB =；动点P 以每秒1个单位的速度从点A 出发沿线段AB 运动到点B ，同时动点Q 以每秒4个单位的速度从点B 出发，沿折线B C D --运动到点D ．图2是点P 、Q 运动时，BPQ 的面积S 随运动时间t 变化关系的图象，则a 的值是（ ）A ．B ．C ．D ．【答案】A【分析】 根据题意计算得4AB =；再结合题意，得当动点Q 在BC 上时，BPQ 的面积S 随运动时间t 变化呈现二次函数关系；当动点Q 在CD 上时，BPQ 的面积S 随运动时间t 变化呈现一次函数关系，从而得a 对应动点Q 和点C 重合；通过计算BPC S △，即可得到答案．【详解】根据题意，得4t =时到达点B∵动点P 以每秒1个单位的速度从点A 出发沿线段AB 运动到点B∵4AB =∵28BC AB ==结合题意，当动点Q 在BC 上时，BPQ 的面积S 随运动时间t 变化呈现二次函数关系 当动点Q 在CD 上时，BPQ 的面积S 随运动时间t 变化呈现一次函数关系∵a 对应动点Q 和点C 重合，如下图：∵动点Q 以每秒4个单位的速度从点B 出发∵48t =∵2t =∵2AP t ==∵2BP AB AP =-=如图，过点A 作AM CD ⊥，交CD 于点M∵2BC AB =，60B ∠=︒∵2AD BC AB ==,60D B ∠=∠=︒∵sin 8AM AD D =⨯∠==∵11222BPC S BP AM =⨯⨯=⨯⨯=，即a = 故选：A ．【点睛】本题考查了平行四边形、二次函数、一次函数、三角函数的知识；解题的关键是熟练掌握二次函数、一次函数、三角函数的性质，从而完成求解．4．已知二次函数2()y x h =-（h 为常数），当自变量x 的值满足1≤x ≤3时，其对应的函数值y 的最小值为1，则h 的值为（ ）A ．2或4B ．0或4C ．2或3D ．0或3【答案】B【分析】根据函数的对称轴为：x=h 和13x ≤≤的位置关系，分三种情况讨论即可求解．【详解】解：函数的对称轴为：x=h ，∵当3h ≥时，x =3时，函数取得最小值1，即2(3)1h -=，解得h =4或h =2（舍去）；∵当1h ≤时，x =1时，函数取得最小值1，即2(1)1h -=，解得h =0或h =2（舍去）；∵当13h <<时，x=h 时，函数取得最小值1，不成立，综上，h =4或h =0，故选：B ．【点睛】此题考查函数的最值，函数的对称轴，分情况讨论解决问题是解此题的关键． 5．二次函数()213y x =--+图象的顶点坐标是（ ）A ．()1,3-B ．()1,3C ．()1,3--D ．()1,3- 【答案】B【分析】根据二次函数顶点式即可得出顶点坐标．【详解】解：∵二次函数的解析为2(1)3y x =--+，∵二次函数图像顶点坐标为（1，3）.故选B ．【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y =a （x -h ）2+k 中，对称轴为x =h ，顶点坐标为（h ，k ）．6．下列事件中，属于不可能事件的是（ ）A ．抛物线y ＝ax 2的开口向上B ．抛物线y ＝（x ﹣2）2+1中y 有最小值2C ．相似三角形的面积比等于相似比的平方D ．三边对应成比例的两个三角形全等【答案】B【分析】根据事件发生的可能性大小判断相应事件的类型即可．【详解】解：A 、抛物线y ＝ax 2的开口向上是随机事件；B 、抛物线y ＝（x ﹣2）2+1中y 有最小值2是不可能事件；C 、相似三角形的面积比等于相似比的平方是必然事件；。
二次函数的特殊情况讨论与解答
二次函数的特殊情况讨论与解答二次函数是一种重要的数学函数，在数学中有着广泛的应用。
在学习二次函数时，我们常常会遇到一些特殊情况，需要进行具体的讨论和解答。
本文将对二次函数的一些特殊情况进行分析与解答。
1. 零点问题二次函数的零点即函数的根，也就是使得函数取值为零的输入值。
通过求解二次方程 f(x) = ax^2 + bx + c = 0，我们可以确定二次函数的零点。
但是，有时候我们会遇到以下特殊情况：1.1 零点个数为0：当二次函数的判别式 b^2 - 4ac 小于0时，方程无实根，即该二次函数在实数范围内无零点。
1.2 零点个数为1：当二次函数的判别式 b^2 - 4ac 等于0时，方程有一个实根，即该二次函数与 x 轴相切于零点处。
1.3 零点个数为2：当二次函数的判别式 b^2 - 4ac 大于0时，方程有两个不相等的实根，即该二次函数与 x 轴交于两个不同的零点。
2. 凸凹性问题二次函数的凸凹性描述了函数图像开口的方向。
通过判断二次函数的二次项系数 a 的正负性，我们可以确定二次函数的凸凹性。
以下是几种常见情况：2.1 a > 0：当二次函数的二次项系数 a 大于0时，函数图像开口朝上，表示该二次函数是凹函数。
2.2 a < 0：当二次函数的二次项系数 a 小于0时，函数图像开口朝下，表示该二次函数是凸函数。
3. 对称轴问题二次函数的对称轴是函数图像的一个重要性质，它是图像左右对称的一条线。
通过求解二次函数的顶点坐标，我们可以确定二次函数的对称轴。
以下是计算对称轴的方法：3.1 对称轴的 x 坐标为顶点的横坐标：对于二次函数 f(x) = ax^2 + bx + c，其中顶点的横坐标为 x = -b/2a，即对称轴的 x 坐标为 -b/2a。
4. 特殊点问题除了零点和对称轴，二次函数还有其他一些重要的特殊点需要进行讨论。
4.1 顶点：二次函数的顶点是函数图像的最高或最低点，在代数上表示为 (h, k)。
《二次函数a,b,c与特殊方程或不等式》专题
《二次函数c b a 、、与特殊方程或不等式》专题班级 姓名根据c bx ax y ++=2的图象和性质填空：（02=++c bx ax 的实数根记为21x x 、）（1）抛物线c bx ax y ++=2与x 轴有两个交点⇔ac b 42- 0； 与x 轴有两个交点坐标是（ ， ）和（ ， ）（2）抛物线c bx ax y ++=2与x 轴有一个交点⇔ac b 42- 0； 这个交点是 点，表示函数的最 值，这个点坐标是（ ， ）（3）抛物线c bx ax y ++=2与x 轴没有交点⇔ac b 42- 0. 【自主学习】1.抛物线2242y x x =-+和抛物线223y x x =-+-与y 轴的交点坐标分别是 和 。
抛物线c bx ax y ++=2与y 轴的交点坐标是 .2. 抛物线c bx ax y ++=2① 开口向上，所以可以判断a 。
② 对称轴是直线x = ，由图象可知对称轴在y 轴的右侧，则x >0，即 >0，已知a 0，所以可以判定b 0.③ 因为抛物线与y 轴交于正半轴，所以c 0.④ 抛物线c bx ax y ++=2与x 轴有两个交点，所以ac b 42- 0； 【归纳整理】⑴a 的符号由 决定：①开口向 ⇔ a 0；②开口向 ⇔ a 0. ⑵b 的符号由 决定：① 在y 轴的左侧 ⇔b a 、 ；② 在y 轴的右侧 ⇔b a 、 ；③ 是y 轴 ⇔b 0.⑶c 的符号由 决定：①点（0，c ）在y 轴正半轴 ⇔c 0；②点（0，c ）在原点 ⇔c 0；③点（0，c ）在y 轴负半轴 ⇔c 0.⑷ac b 42-的符号由 决定：①抛物线与x 轴有 交点⇔ ac b 42- 0 ⇔方程有 实数根； ②抛物线与x 轴有 交点⇔ac b 42- 0 ⇔方程有 实数根；③抛物线与x 轴有 交点⇔ac b 42- 0 ⇔方程 实数根； ④特别的，当抛物线与x 轴只有一个交点时，这个交点就是抛物线的 点.例题：抛物线c bx ax y ++=2如图所示：看图填空：（1）a _____0；（2）b 0；（3）c 0;（4）ac b 42- 0 ;(5)2a b +______0；（6）0a b c ++⎽⎽⎽⎽；（7）0a b c -+⎽⎽⎽⎽；（8）930a b c ++⎽⎽⎽⎽；（9）420a b c ++⎽⎽⎽⎽【练习】1.利用抛物线图象求解一元二次方程及二次不等式（1）方程02=++c bx ax 的根为___________；（2）方程23ax bx c ++=-的根为__________；（3）方程24ax bx c ++=-的根为__________；（4）不等式20ax bx c ++>的解集为________； （5）不等式20ax bx c ++<的解集为_____ ___；2.根据图象填空：（1）a _____0；（2）b 0；（3）c 0;（4）ac b 42- 0 ;(5)2a b +______0；（6）0a b c ++⎽⎽⎽⎽；（7）0a b c -+⎽⎽⎽⎽；例1、画出函数322--=x x y 的图象，根据图象回答下列问题．（1）图象与x 轴，y 轴的交点坐标分别是什么？（2）当x 取何值时，y =0？这里x 的取值与方程0322=--x x 有什么关系？（3）x 取什么值时，函数值y 大于0？x 取什么值时，函数值y 小于0？。
专题01 二次函数(重点)(解析版)
专题01 二次函数（重点）一、单选题1．下列y 关于x 的函数中，属于二次函数的是（ ）A ．y ＝（x +1）2﹣x 2B ．y ＝ax 2+bx +cC ．y ＝3x 2﹣1D ．y ＝3x ﹣1【答案】C【分析】根据二次函数的定义逐项分析即可，二次函数的定义和概念 一般地，把形如²y ax bx c =++（0a ¹）（a b c 、、是常数）的函数叫做二次函数，其中a 称为二次项系数，b 为一次项系数，c 为常数项．【解析】A. y ＝（x +1）2﹣x 221x =+，不是二次函数，故该选项不正确，不符合题意；B. y ＝ax 2+bx +c （0a ¹），故该选项不正确，不符合题意；C. y ＝3x 2﹣1，是二次函数，故该选项正确，符合题意；D. y ＝3x ﹣1，是一次函数，故该选项不正确，不符合题意；故选C【点睛】本题考查了二次函数的定义，理解二次函数的定义是解题的关键．2．二次函数y ＝2（x ﹣1）2+2图象的顶点坐标（ ）A ．(-1，2)B ．(2，1)C ．(1，2)D ．(1，-2)【答案】C【分析】根据二次函数2()y a x h k =-+ 顶点坐标是()h k ，进行解答即可．【解析】解：∵二次函数2()y a x h k =-+顶点坐标是()h k ，，∴二次函数2212y x +=(﹣)图象的顶点坐标为（1，2）．故选：C ．【点睛】此题考查了二次函数的性质，掌握二次函数顶点式的特点是解题的关键．3．把抛物线y ＝2(x ﹣1)2+3先向右平移3个单位，再向上平移1个单位，得到的抛物线的解析式是（ ）A ．y ＝2(x +2)2+4B ．y ＝2(x ﹣4)2+4C ．y ＝2(x +2)2+2D ．y ＝2(x ﹣4)2+2【答案】B【分析】根据平移的性质先得到平移后得到的抛物线的顶点坐标为()4,4 ，即可求解．【答案】B【分析】利用抛物线与x 轴的交点个数可对A 进行判断；利用抛物线的顶点坐标可对B 进行判断；由顶点坐标得到抛物线的对称轴为直线x =-3，则根据二次函数的性质可对C 进行判断；根据抛物线的对称性得到抛物线y =ax 2+bx +c 上的点（-1，-4）的对称点为（-5，-4），则可对D 进行判断．【解析】解：A 、图象与x 轴有两个交点，方程ax 2+bx +c =0有两个不相等的实数根，b 2﹣4ac ＞0，所以b 2＞4ac ，故A 选项不符合题意；B 、抛物线的开口向上，函数有最小值，因为抛物线的最小值为﹣6，所以ax 2+bx +c ≥﹣6，故B 选项符合题意；C 、抛物线的对称轴为直线x =﹣3，因为﹣4离对称轴的距离等于﹣2离对称轴的距离，所以m =n ，故C 选项不符合题意；D 、根据抛物线的对称性可知，（﹣1，﹣4）关于对称轴的对称点为（﹣5，﹣4），所以关于x 的一元二次方程ax 2+bx +c =﹣4的两根为﹣5和﹣1，故D 选项不符合题意．故选B ．【点睛】本题考查了二次函数图象与系数的关系，二次函数与一元二次方程的关系，熟练运用数形结合是解题的关键．9．如图，ABC V 中，90C Ð=°，15AC =，20BC =．点D 从点A 出发沿折线A C B --运动到点B 停止，过点D 作DE AB ^，垂足为E ．设点D 运动的路径长为x ，BDE △的面积为y ，若y 与x 的对应关系如图所示，则a b -的值为（ ）A ．54B ．52C ．50D ．48【答案】B 【分析】根据点D 运动的路径长为x ，在图中表示出来，设,25AE z BE z ==-，在直角三角形中，找到等量关系，求出未知数的值，得到BDE △的值．【解析】解：当10x =时，由题意可知，10,5AD CD ==，故选：B．【点睛】本题主要考查勾股定理，根据勾股定理列出等式是解题的关键，运用了数形结合的思想解题．10．如图，二次函数2y ax=+上移动，MN∥y轴，NR∥x轴，标的最大值为3，则a -b +c 的最大值是（ ）A ．15B ．18C ．23D ．32【答案】C 【分析】先求出N ，R 的坐标，观察图形可知，当顶点在R 处时，点B 的横坐标为3，由此求出a 值，当=1x -时y a b c =-+，当顶点在M 处时y a b c =-+取最大值，求此可解．【解析】解：(6,2)M --Q ，MN ＝2，NR ＝7，(6,4)N \--，(1,4)R -，由题意可知，当顶点在R 处时，点B 的横坐标为3，则抛物线的解析式为2(1)4y a x =--，将点B 坐标(3,0)代入上式得，20(31)4a =--，解得，1a =，当=1x -时，y a b c =-+，观察图形可知，顶点在M 处时，y a b c =-+取最大值，此时抛物线的解析式为：2(6)2y x =+-，将=1x -代入得，2(16)223y a b c =-+=-+-=，故选：C ．【点睛】本题考查二次函数2y ax bx c =++图像的性质，解题关键时利用数形结合的思想，判断出抛物线顶点在R 处时点B 的横坐标取最大值，由此求出a 值．二、填空题【答案】41x -££【分析】根据图象，写出抛物线在直线上方部分的【解析】解：∵抛物线2y ax c =+∴不等式2ax c kx m +³+的解集是故答案为41x -££．所以当直线y x m =-+与新图象有4个交点时，m 的取值范围为62m -<<-．故答案为：62m -<<-．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数2y ax bx c =++（a ，b ，c 是常数，0a ¹）与x 轴的交点坐标问题转化为解关于x 的一元二次方程．也考查了二次函数图象与几何变换．(1)求A 、B 两点的坐标；(2)根据图象直接写出当21y y <时x 的取值范围．【答案】(1)()1,0A -，()3,0B(1)求点B的坐标和抛物线的表达式．(2)将抛物线顶点向上平移m的值．【答案】(1)B点坐标为(5,0)(2)254 m=(1)求直线AC 的函数表达式；(2)若将直线AC 沿y 轴的正方向向上平移【答案】(1)1y x =+(2)9n 4=(1)求抛物线的表达式；(2)如图1，点E 是抛物线上的第一象限的点，求ACE S V 的最大值，并求(3)如图2，在抛物线对称轴上是否存在一点P ，使ACP △是等腰三角形？若存在，直接写出点若不存在请说明理由．【答案】(1)抛物线解析式为：213222y x x =-++设点213(,2)22E x x x -++，则DE x =，213222DO x x =-++ACE AOC DCEAODE S S S S \=--V V V 梯形211311(4)(2)(22222x x x x =+-++--∵一次函数过定点(3,6)--，∴一次函数36y nx n =+-与n y x=-联立方程组得，36y nx x n y x =+-ìïí=-ïî，整理得，2(3nx n +∵有一个交点，(1)求此抛物线的表达式；(2)若点B是抛物线对称轴上的一点，且点①求B的坐标；②点P足抛物线上的动点，当【答案】(1)抛物线的表达式为(2)①点B的坐标为(2,6-设直线OA 与抛物线对称轴交于点()2BH m \=--．10OAB S =Q △，125102m \´+´=，6m \=-（正值已舍）．即点B 的坐标为()2,6-．设直线AB 的解析式为y nx =把()()5,5,2,6A B --分别代入，得解得1;320.3n d ì=ïïíï=-ïî\直线AB 的解析式为13y =令2120433x x x -+=-，解得。
专题3-1 二次函数中的10类定值、定点问题(原卷版)
专题3-1 二次函数中的10类定值、定点问题二次函数背景下的定值与定点问题，解析法类似于高中，但并不超纲！因为解题方法比较特殊，同学们要专门学习和练习，才能在考场上应对自如，这些方法包括联立、转化等，对同学们的代数功底与几何功底都有较高的要求.知识点梳理一、定值问题二、定点问题题型一 面积定值2022·山东淄博·中考真题2023·福建厦门三模题型二 线段长为定值2024届湖北天门市九年级月考2024届福建龙岩市统考期中2020·西藏·中考真题题型二 线段和定值2023广州市二中月考2022·四川巴中·中考真题2024届湖北黄石市·九年级统考2023·四川乐山·统考二模2023·海口华侨中学考模2023·江苏徐州·4月模拟2022·湖南张家界·中考真题题型三 加权线段和定值2023·四川广元·中考真题2020·四川德阳·中考真题题型四 线段乘积为定值2023·四川南充·中考真题2024届·武汉市东湖高新区统考2024届福建省福州屏东中学月考2024届福州市晋安区统考2023·福建福州·校考三模题型五 比值为定值2023年广西钦州市一模2023福建厦门一中模拟2023年福州市屏东中学中考模拟武汉·中考真题题型六 横（纵）坐标定值2023·湖北潜江、天门、仙桃、江汉油田·中考真题2024届湖北潜江市初12校联考题型七 角度为定值2023·成都武侯区西川中学三模四川乐山·统考中考真题题型八 其它定值问题2023·浙江湖州·统考一模2024届福建省南平市统考2023年湖北省武汉市新观察中考四调题型九 结合韦达定理求定点2023年湖北省武汉市外国语学校中考模拟2024届武汉市青山区九年级统考2024届武汉市新洲区12月统考2024届·福建厦门市第九中学期中2023·武汉光谷实验中学中考模拟2023广东省梅州市九年级下期中2024届福州市九校联盟期中2023年湖北省武汉市新观察中考四调题型十 已知定值求定点2024届武汉市洪山区九年级统考2024届湖北省武汉市新洲区九年级上期中2023年广州市天河外国语学校中考三模知识点梳理一、定值问题一般来说，二次函数求解几何线段代数式定值问题属于定量问题，方法采用:1.参数计算法：即在图形运动中，选取其中的变量(如线段长，点坐标)作为参数,将要求的定值用参数表示出，然后消去参数即得定值。
中考数学解题技巧---取特殊值(二次函数图像信息题)
中考数学解题技巧——取特殊值(二次函数图像信息题)（马铁汉）二次函数图像信息考题，一直是近些年中考热门考题，常规解题方法是通过图像信息，进行推理得出一些新的结论。
常规方法推理需要很扎实的基本功，且需要大量的时间。
这里我们不妨取特殊值，验证结论的正确性，反正是选择题，找出其中的正确答案即可。
下面通过几个中考真题，作简要介绍。
例1、（2021鄂州9．）二次函数()20y ax bx c a =++≠的图象的一部分如图所示．已知图象经过点()1,0-，其对称轴为直线1x =．下列结论： ①0abc <； ②420a b c ++<； ③80a c +<；④若抛物线经过点()3,n -，则关于x 的一元二次方程()200ax bx c n a ++-=≠的两根分别为3-，5．上述结论中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个 一、用常规方法解： ①√o c b a ,0,0∴0abc < ②×当2=x 时，函数值大于0 ∴024>++c b a ③√12=-ab，a b 2-= 当2-=x 时，函数值小于0， ∴024<+-c b a将a b 2-=代入 得80a c +< ④√由抛物线的对称性得知. 故答案选C 二、取特殊值解：已知图象经过点()1,0-，其对称轴为直线1x =，由抛物线的对称性，得到另一个点（3,0）， 又由于抛物线开口向下，这样可令抛物线的解析式为()()-13y x x =+-2=-+2+3x x这样得到特殊值-1,2,3a b c ===. 开始验证：①-123-60abc =⨯⨯=<，∴①0abc <√；②()424122330a b c ++=⨯-+⨯+=>，∴②420a b c ++<×； ③()881350a c +=⨯-+=-<，∴③80a c +<√； ④当3x =-时，()()()()-13=--3+1-3-3=-12y x x =+-∴12n =-得()223120x x -++--=即22150x x --= 解之得123,5x x =-=∴ ④若抛物线经过点()3,n -，则关于x 的一元二次方程()200ax bx c n a ++-=≠的两根分别为3-，5．√. 故答案选C例2（2021恩施12．）如图，已知二次函数y ＝ax 2+bx +c 的图象与x 轴交于（﹣3，0），顶点是（﹣1，m ），则以下结论：①abc ＞0；②4a +2b +c ＞0；③若y ≥c ，则x ≤﹣2或x ≥y(-1,m )O -3y(-1,m )O -30；④b +c ＝m ．其中正确的有（ ）个． A ．1B ．2C ．3D ．4一、常规方法解： ① × abc <0 ②√当x=2时，y>0 ∴4a +2b +c ＞0 ③√如图，知x =0，或-2时，y =c ∴若y ≥c ，则x ≤﹣2或x ≥0 ④×由x =-1，y =m 且x =1时，y =0得a -b +c=m ，a +b +c=0，两式相减得，m b 21-= 由12--=a b 得b a 21=，代入a +b +c=0，得b c 23-= ∴m b c b 4121=-=+故答案选B 二、取特殊值法解图象与x 轴交于（﹣3，0），顶点是（﹣1，m ），由抛物线的对称性知另一交点为（1,0） 又抛物线开口向上，可令抛物线解析式为()()31y x x =+-2=23x x +-这样得到特殊值1,2,3a b c ===-，下面开始验证： ①()12360abc =⨯⨯-=-<，∴①abc ＞0 ×②()424122350a b c ++=⨯+⨯+-=>，∴②4a +2b +c ＞0 √③令223=-3x x +-解之得120,2x x ==-∴3y ≥-时，2x ≤-或0x ≥.∴③若y ≥c ，则x ≤﹣2或x ≥0；√④()24132441m ⨯⨯--==-⨯ ()231b c +=+-=-11-4-222m =⨯=（）∴④b +c ＝m ， × 故答案选B.例3、（2021荆门）10．抛物线2y ax bx c =++（a ，b ，c 为常数）开口向下且过点(1,0)A ，(,0)B m （21m -<<-），下列结论：①20b c +>；②20a c +<；③ (1)0a m b c +-+>；④若方程()(1)10a x m x ---=有两个不相等的实数根，则244ac b a -<.其中正确结论的个数是( ) A ．4B ．3C ．2D ．1一、常规解法解： 结合题意画出草图.由点A 、B 坐标，得0=++c b a ，024<+-c b a 则可得20a c +<……②成立将c b a --=代入②，得20b c +>……①成立当1-=x 时，0>+-c b a ，又0>am 得 (1)a m +-由方程()(1)10a x m x ---=得244ac b a -<…….④成立。
专题08 二次函数中特殊四边形存在性问题的四种考法(解析版)-2024年常考压轴题攻略(9上人教版)
专题08二次函数中特殊四边形存在性问题的四种考法类型一、平行四边形存在性问题(1)求抛物线的表达式；(2)如图1，连接BC ，PB ，PC ，设PBC 的面积为①求S 关于t 的函数表达式；②求P 点到直线BC 的距离的最大值，并求出此时点(3)如图2，设抛物线的对称轴为l ，l 与x 轴的交点为边形CDPM 是平行四边形？若存在，直接写出点【答案】(1)22y x=-(2)①23922S t t =-+；②点P 到直线BC 的距离的最大值为(3)存在，()1,6M 【分析】（1）待定系数法求解析式即可求解；（2）①在图1中，过点P 作PF y ∥轴，交BC 于点P 的坐标为()2,23t t t -++，则点F 的坐标为(t 2139222S PF OB t t =⋅=-+；②根据二次函数的性质得出当32t =时，S 取最大值，最大值为面积法求得点P 到直线BC 的距离，进而得出P （3）如图2，连接PC ，交抛物线对称轴l 于点设直线BC 的解析式为将()3,0B 、()0,3C 代入30,3m n n +=⎧⎨=⎩，解得：∴直线BC 的解析式为∵点P 的坐标为(,t t -∴点F 的坐标为(,t -∴(223PF t t =-++-∴1322S PF OB =⋅=-②12S PF OB =⋅=-∵302-<，∴当32t =时，S 取最大值，最大值为抛物线2y x bx =-++∴抛物线的对称轴为直线 1D C x x -=，∴1P M x x -=，∴2P x =，()2,3P ∴，在223y x x =-++中，当()0,3C ∴，∴3C D y y -=，∴3M P y y -=，∴6M y =，∴点M 的坐标为()1,6；当2P x ¹时，不存在，理由如下，若四边形CDPM 是平行四边形，则 点C 的横坐标为0，点∴点P 的横坐标12t =⨯又 2P x ¹，(1)求点C 的坐标；(2)点P 为直线AC 下方抛物线上一点，过点此时点P 的坐标；(3)抛物线顶点为M ，在平面内是否存在点若存在请求出N 点坐标并在备用图中画出图形；若不存在，请说明理由．【答案】(1)()4,5C (2)315,24P ⎛⎫- ⎪⎝⎭(3)存在，点N 的坐标为：()154N -，，【详解】（1）解：在2=23y x x --中，令解得：11x =-，23x =，()()1,0,3,0A B ∴-，直线y x m =+经过点()1,0A -，∴01m =-+，解得：1m =，∴直线AC 的解析式为1y x =+，联立方程组，得2123y x y x x =+⎧⎨=--⎩，解得：1110x y =-⎧⎨=⎩，2245x y =⎧⎨=⎩()4,5C ∴；（2）如图1，设点2(,23)P n n n --，则点∴2212334()PE n n n n n =+---=-++ 10-<，∴当32n =时，PE 取得最大值254，此时，（3） 2223(1)4y x x x =--=--，∴抛物线顶点为()14M -，，如图2，点,,,A B M N 为顶点的四边形是平行四边形时，设①BM 为对角线时，AN 的中点与BM ∴(1)3122m +-+=，04022n +-+=，解得：∴()154N -，，②AM 为对角线时，BN 的中点与AM ∴31122m +-+=，04022n +-+=，解得：(1)求此拋物线的解析式；(2)在抛物线的对称轴上有一点P ，使得PA PC +值最小，求最小值；(3)点M 为x 轴上一动点，在拋物线上是否存在一点N ，使以边形为平行四边形？若存在，直接写出点N 的坐标；若不存在，请说明理由．【答案】(1)215222y x x =--(2)552(3)54,2⎛⎫- ⎪⎝⎭，5214,2⎛⎫+ ⎪⎝⎭，5214,2⎛⎫- ⎪⎝⎭【分析】（1）把()1,0A -，()5,0B 两点代入求出a 、b 的值即可；（2）因为点A 关于对称轴对称的点B 的坐标为()5,0，连接BC 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论．拋物线的解析式为212y x =-∴其对称轴为直线2b x a =-=-当0x =时，52y =-，50,2C ⎛⎫∴- ⎪⎝⎭，又()5,0B ，∴设BC 的解析式为(y kx b =+5052k b b +=⎧⎪∴⎨=-⎪⎩，解得：12k =，52b =-，∴BC 的解析式为1522y x =-，当2x =时，1532222y =⨯-=-，①当点N 在x 轴下方时，抛物线的对称轴为2x =，0,C ⎛- ⎝154,2N ⎛⎫∴- ⎪⎝⎭，②当点N 在x 轴上方时，如图，过点在2AN D △和2M CO △中，22N AD AN N DA ∠⎧⎪⎨⎪∠⎩252N D OC ∴==，即2N 点的纵坐标为21552222x x ∴--=，解得：2x =+25214,2N ⎛⎫∴+ ⎪⎝⎭，35214,2N ⎛⎫- ⎪⎝⎭综上所述符合条件的N 的坐标有⎛ ⎝【点睛】本题考查的是二次函数综合题，式、平行四边的判定与性质、全等三角形等知识，两点间距离的求解，在解答（意进行分类讨论．(1)求抛物线的解析式：(2)在抛物线的对称轴上是否存在点P ，使PCD 是以CD 为腰的等腰三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；(3)点E 在x 轴上运动，点F 在抛物线上运动，当以点B ，C ，E ，F 为顶点的四边形是平行四边形，直接写出点E 的坐标．【答案】(1)213222y x x =-++(2)存在，3,42⎛⎫ ⎪⎝⎭或35,22⎛⎫ ⎪⎝⎭或35,22⎛⎫- ⎪⎝⎭(3)541,02⎛⎫-+ ⎪ ⎪⎝⎭或541,02⎛⎫-- ⎪ ⎪⎝⎭或(7,0)或(1,0)【分析】（1）用待定系数法即可求解；（2）分两种情况：以C 为顶点，即CP CD =；以D 为顶点，即CD =等腰三角形的定义建立方程即可完成；（3）分三种情况：当BC 是对角线时；当BE 是对角线时；当BF 是对角线时；分别设点与F 的坐标，利用中点坐标公式即可求解．【详解】（1）解：∵点B 的坐标是(40)，，点C 的坐标是(02)，，∴16602a c c ++=⎧⎨=⎩，解得：122a c ⎧=-⎪⎨⎪=⎩，∴所求抛物线解析式为213222y x x =-++；（2）解：存在(1)求抛物线的表达式；(2)若点E 在第一象限内对称右侧的抛物线上，四边形ODEB 的面积为(3)在（2）的条件下，若点F 是对称轴上一点，点H 是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G ，使以E ，F ，G ，H 为顶点的四边形是菱形，且存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)232333y x x =-++(2)()2,33E 2039⎫⎪⎭或532,339⎛⎫⎪⎝⎭）根据待定系数法求解即可；∵232333y x x =-++()23143x =--+，∴()1,43D ．令232333y x x =-++中0y =，则解得=1x -或3x =，抛物线的对称轴与x轴交于点M，过点∵四边形EFGH 是菱形，EFG ∠∴EF FG GH EG ===，∵60EFG ∠=︒，∴EFG 是等边三角形．∴60FEG EF FG ∠=︒=，，∵()2,33E ，()0,33C ，(1,4D ∴2CE CD ==，()24333-+同理可证： EFG 是等边三角形，∵CF FE =，=GE FE ，∴DG ∴CDG CEG ∆∆≌．∴DCG ∠=∴直线CG 的表达式为：33y =与抛物线表达式联立得33y y ⎧=⎪⎨⎪=-(1)求抛物线的表达式；(2)若点D 是直线AC 上方拋物线上一动点，连接BC ，AD ADM △的面积为1S ，BCM 的面积为2S ，当121S S -=时，求点(3)如图2，若点P 是抛物线上一动点，过点P 作PQ x ⊥轴交直线上是否存在点E ，使以P ，Q ，E ，C 为顶点的四边形是菱形，若存在，请直接写出点坐标；若不存在，请说明理由【答案】(1)223y x x =-++(2)271,22⎛⎫+ ⎪ ⎪⎝⎭或271,22⎛⎫- ⎪ ⎪⎝⎭．(3)符合条件的点E 有三个，坐标为：()0,1E ，(10,132E -【分析】（1）把点()30A ，和()10B -，代入解析式求解即可；（2）由121S S -=得121S S =+从而121ABM ABM S S S S +=++ 程求解即可；（3）分类当CQ 为对角线和菱形边时，利用直线AC 与x 轴成标的方程，进而求出点的坐标．【详解】（1）把点()3,0A 和()1,0B -代入得：93330a b a b ++=⎧⎨-+=⎩解得：12a b =-⎧⎨=⎩，∴抛物线的解析式为223y x x =-++；（2）设(),D x y ，对于抛物线223y x x =-++，令0x =，则()0,3C ∴．121S S -= ，121S S ∴=+．∵()30A ，，()0,3C ，∴3OA OB ==，45OCA ∴∠=︒，此时四边形CEQP 是正方形．PQ EQ ∴=．设()2,23P m m m -++，则23PQ m m =-+，23m m m ∴-+=，解得m =此时32OE OC m =-=-=②当CQ 为菱形的边时，如图设()2,23P m m m -++，则∴HQ m =，2PQ m =-+作QH OC ⊥于点H ，45OCA ∠︒= ，∴22CQ HQ m ==．∴23CE PQ m m ==-+=解得：132m =-，23m =()323213OE =+-=+()10,132E ∴-，(20,1E +综上所述，符合条件的点【点睛】本题考查待定系数法求函数的解析式，二次函数的性质，二次函数与几何综合，数形结合是解题的关键．【变式训练2】如图1，在平面直角坐标系中，点（点A 在点B 左侧），与(1)求ABC 的面积；（3）解：∵抛物线212y x x =--∴()211942212y x x x =--+=-2＋＋∵将抛物线2142y x x =--+沿着水平方向向右平移∴新抛物线为：()112y x =--2＋∴原抛物线与新抛物线的交点，∴()()1111992222x x -=--22＋＋＋，∴解得：0x =，【点睛】本题考查了二次函数的图象及性质，二次函数与特殊图形，二次函数的平移规律，掌握二次函数与特殊图形的位置关系是解题的关键．类型三、矩形存在性问题(1)求抛物线的解析式；(2)如图，点P 是抛物线上位于直线直线AC 于点D ，交x 轴于点E ，(3)在抛物线上是否存在点M ，对于平面内任意点一条边的四边形为矩形，若存在，请直接写出【答案】(1)2142y x x =--(2)335,28P ⎛⎫- ⎪⎝⎭；254(3)()4,8M -、()8,4N -【分析】（1）把点()4,0A 和点B a 、b 的值；（2）先用待定系数法求出直线2211,422D t t t t ⎛⎫--- ⎪⎝⎭，然后求出最大值时t 的值，即可求出点P （3）假设抛物线上是存在点M ，一条边的四边形为矩形，过点O 点A 且与OH 平行的直线解析式，经计算验证可得过点立方程可求得M 的坐标，通过平移即可求得点【详解】（1）解：把点()4,0A 和点∵()4,0A ，()0,4C -，∴OAC 为等腰直角三角形，∴点H 为AC 的中点，即(H 则OH 所在的直线方程为y =∵四边形AMNC 为矩形，∴过A 与直线AC 相垂直的直线函数解析式中的∴设AM 所在的直线解析式为∵点A 在直线AM 上，(1)求点A 、B 、C 的坐标；(2)将抛物线L 向右平移1个单位，得到新抛物线对称轴l 上是否存在点D ，使得以点D 的坐标；若不存在，请说明理由．【答案】(1)()1,0A -，()3,0B (2)存在，点D 的坐标为()2,1或【分析】（1）分别令0y =和x （2）先求得平移后的抛物线L 角线时，根据矩形的性质求解即可．【详解】（1）解：令0y =，则解得11x =-，23x =，当AD 为对角线时，连接AC ，过点 ()1,0A -，()0,1C -，∴1OA OC ==，∴45OCA ∠=︒∴45OCG ∠=︒∴1OG OC ==，∴()1,0G ．设CG 所在直线解析式为y kx =+将()0,1C -，()1,0G 代入得，⎧⎨⎩解得11k b =⎧⎨=-⎩，∴CG 所在直线解析式为1y x =-当2x =时，1211y x =-=-=．∴()2,1D ．当AD 为边时，同理过点A 作AC 易得AH 所在直线解析式为y =当AC 为对角线时，DE 也为对角线，∴此种情况不存在．(1)求抛物线的表达式；(2)若点P 为第一象限内抛物线上的一点，设PBC 的面积为S ，求S 坐标；(3)已知M 是抛物线对称轴上一点，在平面内是否存在点N ，使以B 的四边形是矩形？若存在，直接写出N 点坐标；若不存在，请说明理由．【答案】(1)22+3y x x =-+(2)S 最大值为278，315(,)24P (3)存在，点1(2,(317))2N +或1(2,(317))2-或(2,1)-或(4,1)．【分析】（1）运用抛物线交点式解析式求解，设抛物线(1)(y a x x =+解；（2）如图，过点P 作PD AC ⊥，垂足为点D ，交BC 于点E ，设(,P m 的解析式3y x =-+，于是23PE m m =-+，从而13(22S PE OC m ==- 时，S 最大值为278，进而求得315(,)24P ；设2(,23)P m m m -++设直线BC 的解析式为y kx =033k hh =+⎧⎨=⎩，解得13k h =-⎧⎨=⎩∴3y x =-+则点(,3)E m m -+，2PE m =-∴2113(22S PE OC m ==´-+ ∴当32m =时，S 最大值为2782915233344m m -++=-++=∴315(,)24P ；（3）存在．设(1,)M p ，如图，223BC =222(13)(0)CM p p =-+-=如图，当BM 为对角线时，∠222BM CM BC =+，即26p p -+01330n p q +=+⎧⎨+=+⎩解得21n q =-⎧⎨=⎩∴点(2,1)N -如图，当CM 为对角线时，MBC ∠222BM BC CM +=，即26p p -+(1)求抛物线的对称轴方程；(2)若点P 满足PAB PBA ∠=∠，求点P 的坐标；(3)设M 是抛物线的对称轴上一点，N 是坐标平面内一点，正方形的面积．【答案】(1)32x =-(2)()51,51P --+(3)正方形AMPN 的面积为172或372【分析】（1）由4y x =+可知()4,0A -，()0,4B ，进而求得抛物线解析式为即可得抛物线的对称轴方程；（2）由题意可知PAB PBA ∠=∠，可知PA PB =，进而值OP 其与AB 交于点Q ，可得()2,2Q -，可求得OP 的解析式为则90PDM ACM ∠=∠=︒∴DPM PMD PMD ∠+∠=∠∴(AAS PDM MCA △≌△∴PD MC =，MD AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422MD AC ==-=，则90PEM ACM ∠=∠=︒∴EPM PME PME ∠+∠=∠∴(AAS PEM MCA △≌△∴PE MC =，ME AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422ME AC ==-=，则P y CE MC ME ==+=即：32P x m =-，P y m =-(1)求A ，B ，C 三点的坐标，并直接写出直线(2)在点P 的运动过程中，求使四边形(3)点N 为平面内任意一点，在（2N 为顶点的四边形是正方形？若存在，请直接写出点【答案】(1)()1,0A -，()3,0B ，C (2)32m =-(3)()1221,2Q +，2252,2Q ⎛+ ⎝【分析】（1）分别令0y =，0x =，可求出点∵()3,0B ，()0,3C ，∴3OB OC ==，∴BOC 是等腰直角三角形，∴点()221,2Q +，∴()22132322EQ =+--=-∴PE EQ =，此时点()221,2Q +使得以P ，E 如图，过点E 作EQ PM ⊥于点Q ，过点由（2）得：45BED ∠=︒，∵PM BC ∥，∴45BED DPQ ∠=∠=︒，∴PEQ ，PSQ 是等腰直角三角形，∴此时点Q 使得以P ，E ，Q ，N 为顶点的四边形是正方形；∴132222PS SE PE -===，∴点5232,12S ⎛⎫-- ⎪ ⎪⎝⎭，对于321y x =-++，当5212y =-时，222x =+，(1)求抛物线的解析式；(2)点E 在第一象限内，过点E 作EF y ∥轴，交BC 于点F ，作EH 点H 在点E 的左侧，以线段,EF EH 为邻边作矩形EFGH ，当矩形求线段EH 的长；(3)点M 在直线AC 上，点N 在平面内，当四边形OENM 是正方形时，请直接写出点标．【答案】(1)抛物线的解析式为2142y x x =-++；(2)4EH =；(3)点N 的坐标为()44，或7322⎛⎫- ⎪⎝⎭，．【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的解析式为4y x =-+，设2142x E x x ⎛ ⎝-++，对称性质求得21422H x x x ⎛⎫- ⎪+⎝-+⎭，，推出2122GH EF x -=-+矩形周长公式列一元二次方程计算即可求解；（3）先求得直线AC 的解析式为24y x =+，分别过点M 、E 作90OPE MQO ∠=∠=︒，90OEP ∠=︒∴OEP MOQ ≌△△，∴PE OQ =，PO MQ =，设2142m E m m ⎛⎫ ⎪⎝-++⎭，，∴PE OQ m ==-，12P m O M Q ==-∵点M 在直线AC 上，∴244212m m m -⎛⎫=+ ⎪⎝⎭-，解得m =当4m =时，()04M ，，()40E ，，即点M 与点C 重合，点E 与点B 重合时，四边形当1m =-时，512M ⎛⎫-- ⎪⎝⎭，，512E ⎛- ⎝，点O 向左平移52个单位，再向下平移则点E 向左平移52个单位，再向下平移∴551122N ⎛⎫--- ⎪⎝⎭，，即7322N ⎛⎫- ⎪⎝⎭，．课后训练(1)求抛物线的解析式；(2)如图2，点P 、Q 为直线BC 下方抛物线上的两点，点Q 的横坐标比点过点P 作PM y ∥轴交BC 于点M ，过点Q 作QN y ∥轴交BC 于点N ，求值及此时点Q 的坐标；(3)如图3，将抛物线()230y ax bx a =+-≠先向右平移1个单位长度，再向下平移长度得到新的抛物线y '，在y '的对称轴上有一点D ，坐标平面内有一点E D 、E 为顶点的四边形是矩形，请直接写出所有满足条件的点E 的坐标．【答案】(1)抛物线的解析式为2=23y x x --(2)当1a =时，max ()4PM QN +=，()2,3Q -(3)()1,2E --或()5,2-或3171,2⎛⎫-- ⎪ ⎪⎝⎭或3171,2⎛⎫-+ ⎪ ⎪⎝⎭【分析】（1）直接运用待定系数法即可解答；（2）设()2,23P a a a --，则()21,4Q a a +-，进而得到(),3M a a -，(N 出222422(1)4PM QN a a a +=-++=--+，最后根据二次函数的性质即可解答；（3）分以BC 为矩形一边和对角线两种情况，分别根据等腰直角三角形的性质、平移和矩形的判定定理解答即可．【详解】（1）解：把()1,0A -和()3,0B 代入()230y ax bx a =+-≠，得309330a b a b --=⎧⎨+-=⎩，解得1a =，2b =-∴222422(1)4PM QN a a a +=-++=--+∴当1a =时，max ()4PM QN +=∴()2,3Q -．（3）解：由题意可得：()()()222=1213152x y x x x x --'---=---=-，∴y '的对称轴为2x =∵抛物线()230y ax bx a =+-≠与y 轴交于点C ．∴()0,3C -,∵()3,0B ,∴3OC OB ==,45BCO CBO ∠=∠=︒；如图：当BC 为矩形一边时，且点D 在x 轴的下方，过D 作DF y ⊥轴，∵D 在y '的对称轴为2x =，∴2FD =，∴2CF FD ==,325OF =+=,即点()2,5D -，∴点C 向右平移2个单位、向下平移3个单位可得到点D ，则点B 向右平移2个单位、向下平移3个单位可得到()5,3E -；如图：当BC 为矩形一边时，且点D 在x 轴的上方，y '的对称轴为2x =与x 轴交于F ，∵D 在y '的对称轴为2x =，∴2FO =，∴321BF =-=，∵45CBO ∠=︒，即45DBO ∠=︒，∴321BF FD ==-=,即点()2,1D ，∴点B 向左平移1个单位、向上平移1个单位可得到点D ，则点C 向左平移1个单位、向上平移1个单位可得到点()1,2E --；如图：当BC 为矩形对角线时，设∴BC 的中点F 的坐标为32⎛ ⎝∴2322322m d n +⎧=⎪⎪⎨+⎪=⎪⎩，解得：m d =⎧⎨+⎩又∵DE BC =,∴()()22222133d n -+-=+联立173d n d n ⎧-=±⎪⎨+=⎪⎩，解得：∴点E 的坐标为3171,2⎛-- ⎝综上，存在()1,2E --或(5,的四边形是矩形．【点睛】本题主要考查了运用待定系数法求解析式、与几何的综合等知识点，掌握二次函数的性质和矩形的判定定理是解答本题的关键．2．如图，在平面直角坐标系中，抛物线与y 轴交于点C ，点P 为抛物线上的动点．(1)求该抛物线的函数表达式；(2)点D 为直线y x =上的动点，当点P 在第四象限时，求四边形PBDC 面积的最大值及此时点P 的坐标；(3)已知点E 为x 轴上一动点，点Q 为平面内任意一点，是否存在以点P ，C ，E ，Q 为顶点的四边形是以PC 为对角线的正方形，若存在，请直接写出点Q 的坐标，若不存在，请说明理由．【答案】(1)2=23y x x --(2)278，315,24P ⎛⎫- ⎪⎝⎭(3)3333,2⎛⎫+- ⎪ ⎪⎝⎭；3333,2⎛⎫-- ⎪ ⎪⎝⎭；(3,3)-；(3,2)【分析】（1）用待定系数法求函数的解析式即可；（2）作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设()2,23P m m m --，则(,3)H m m -，23PH m m =-+，则2139()228BPC S t ∆=--+，当32t =时，BPC △的面积最大值为从而求出此时四边形PBDC 面积的最大值，P 点坐标；（3）设()2,23P m m m --，(,0)E n ，分四种情况画出图形，利用正方形性质求解即可．【详解】（1）解：将(1,0)A -，(3,0)B 代入23y ax bx =+-中，得309330a b a b --=⎧⎨+--⎩，解得12a b =⎧⎨=-⎩．∴该抛物线的函数表达式为2=23y x x --．（2）解：作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设直线BC 的表达式为：y kx =+得303k n n +=⎧⎨=-⎩，解得13k n =⎧⎨=-⎩，3y x ∴=-．设()2,23P m m m --，则(,H m m ∵BPC CPH BPHS S S =+△△△∴1122BPC S PH OG PH BG =⋅+⋅△∴(21322BPC S PH OB m =⨯=-+△∴28323272BPC S m ⎛⎫=-+ ⎪⎝-⎭△，∴当32m =时，BPC △面积的最大值为BC 与直线y x =平行，1122DBC OBC S S OB OC ∴==⋅=△△∴四边形PBDC 面积的最大值为当32m =时，2332322y ⎛⎫-⨯- ⎪⎝⎭=315,24P ⎛⎫∴- ⎪⎝⎭（3）解：设()2,23P m m m --，I.如图，当点E 在原点时，即点∵四边形PECQ 为正方形，∴点3(3,)Q -，II.如解图3-2，当四边形PECQ 作PI x ⊥轴，垂足为I ，作QH ⊥又∵90CEO OCE ∠+∠=︒，∴OCE PEO ∠=∠，∴(ASA)OCE PEI ≅ △∴3CO IE ==，22EO IP m ==-同理可得：3QH CO IE ===，∴3OE OI IE m =+=+，HO IO=∴2323m m m +=--，解得：m ∴3332HO IO +==，∴点)33(3,32Q +-，同理可得：PI OE CH ==，IE QH =∴3OE IE IO m =-=+，∴2233m m m =---，解得：m =∴3332HO IO -+==，∴点3,(Q -IV.如解图3-4，当四边形PECQ 为正方形时，同理可得：PI OE CH ==，EI HQ =∴2323m m m -=--，解得：m =∴2HO IO ==，∴点(3,2)Q ，综上所述：点Q 坐标为3333,2⎛+- ⎝【点睛】此题重点考查二次函数的图象与性质、数解析式、正方形性质、全等三角形的判定与性质、一元二次方程的解法、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，属于考试压轴题．3．如图，抛物线212y x bx c =++与物线交于A 、D 两点，与y 轴交于点综上所述，341,22N ⎛⎫+ ⎪ ⎪⎝⎭或341,22N ⎛- ⎝【点睛】本题考查了待定系数法求解析式，面积问题，平行四边形的性质，熟练掌握是二次函数的性质解题的关键．4．在平面直角坐标系中，抛物线2y ax =(1)求抛物线的表达式；(2)若直线x m =与x 轴交于点求出抛物线上点M 的坐标；(3)若点P 为抛物线y ax =位长度后，Q 为平移后抛物线上一动点，在（构成平行四边形？若能构成，求出【答案】(1)223y x x =-++(2)315,24⎛⎫ ⎪⎝⎭(3)1(2-，15)4或3(2-，7)4或【分析】（1）利用待定系数法，即可求出抛物线的表达式；（2）由“直线x m =与x 轴交于点的坐标，进而可得出AN 再利用二次函数的性质，即可求出（3）利用平移的性质，可得出平移后抛物线的表达式为点的坐标特征，可求出点点P 的坐标为(1,)m ，点Q 线三种情况考虑，由平行四边形的对角线互相平分，可得出关于得出n 值，再将其代入点【详解】（1）解：将(1,0)-09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得：∴抛物线的表达式为y =-（2） 直线x m =与x 轴交于点∴点M 的坐标为2(,m m -。
二次函数的特殊形式与特殊解析解析
二次函数的特殊形式与特殊解析解析二次函数的特殊形式与特殊解析二次函数是数学中一种重要的函数形式，其一般形式可表示为y=ax^2+bx+c，其中a、b、c是常数，而x是自变量。
在二次函数中，存在一些特殊的形式和解析，它们在数学和实际问题中具有特殊的意义和应用。
本文将重点探讨二次函数的特殊形式和特殊解析。
1. 完全平方形式完全平方形式是二次函数的一种特殊形式，其一般形式可表示为y=a(x-h)^2+k，其中a、h、k是常数，而(x-h)^2表示(x-h)的平方。
在完全平方形式中，常数h表示抛物线的对称轴的横坐标，而k表示抛物线的顶点的纵坐标。
通过完全平方形式，我们可以直接获得抛物线的顶点坐标，进一步研究抛物线的性质和图像。
2. 规范形式规范形式是二次函数的另一种特殊形式，其一般形式可表示为y=a(x-p)(x-q)，其中a、p、q是常数。
在规范形式中，常数p和q表示二次函数的两个根，也即二次函数的零点。
通过规范形式，我们可以直接获得二次函数的根，进一步分析二次函数与x轴的交点情况。
3. 特殊解析在二次函数中，存在由根和顶点坐标导出的特殊解析形式。
特殊解析是将二次函数表达式进行简化，并获得相应的关于根和顶点坐标的解析式。
特殊解析能够直接反映二次函数的性质和特点，使得问题求解更加简洁和直观。
总结：二次函数的特殊形式与特殊解析是分析二次函数性质和求解问题的重要工具。
通过学习和理解完全平方形式和规范形式，我们能够准确地确定二次函数的顶点、根和图像形状；而特殊解析则能够从简化的角度出发，加深我们对二次函数的认识，并在实际问题中更高效地应用二次函数。
本文介绍了二次函数的特殊形式与特殊解析，并阐述了它们的意义和应用。
通过深入理解和掌握二次函数的特殊形式和特殊解析，我们能够更好地应用二次函数解决实际问题，提高数学建模能力。
对于学习者来说，深化对二次函数的认识不仅能够提高数学水平，更能够培养创新思维和解决问题的能力。
二次函数的特殊情况解答解析探究
二次函数的特殊情况解答解析探究二次函数是高中数学中一个重要的内容，也是一种常见的数学模型。
在二次函数中，除了一般情况下的标准形式外，还存在着一些特殊情况。
本文将围绕这些特殊情况展开解答解析，通过对不同情况下的函数图像和性质进行探究，帮助读者更好地理解和掌握二次函数的特殊情况。
一、一次项系数为零的情况在标准形式的二次函数中，一次项系数决定了函数图像的斜率，当一次项系数为零时，二次函数即可简化为一元二次函数。
一元二次函数的标准形式为：f(x) = ax^2 + c其中a和c为常数，且a不等于零。
在这种情况下，二次函数的图像将变为一个抛物线，并且不再有斜率，而是对称于y轴。
二、常数项为零的情况当二次函数的常数项为零时，即c=0时，二次函数的标准形式可以简化为：f(x) = ax^2 + bx此时，函数图像将经过原点(0,0)，并且对称于y轴。
三、系数之间的关系在二次函数中，系数a决定了抛物线的开口方向和形状。
当a大于零时，抛物线开口向上，形状较为平缓；当a小于零时，抛物线开口向下，形状较为陡峭。
系数b对于二次函数图像的位置有一定的影响。
当a不等于零时，如果b大于零，抛物线图像将向右移动；如果b小于零，抛物线图像将向左移动。
当a等于零时，b的值不会对图像的位置造成影响。
四、特殊情况下的函数解析解对于一次项系数为零的情况，一元二次函数的解析解可以通过求解一元一次方程得出，即令f(x)=0，解出x的值。
而对于常数项为零的情况，函数f(x)=ax^2+bx=0可以因式分解得到f(x)=x(ax+b)=0，因此解析解为x=0或x=-b/a。
五、特殊情况下的函数图像通过对二次函数在特殊情况下的解析解和系数关系进行分析，我们可以得到相应的函数图像。
对于一次项系数为零的情况，函数图像为对称于y轴的抛物线，开口的方向由系数a决定。
对于常数项为零的情况，函数图像将经过原点(0,0)，并且对称于y 轴，开口的方向由系数a决定。
二次函数的特殊情况与变化规律
二次函数的特殊情况与变化规律二次函数是高中数学中的一个重要概念，它在各个领域有着广泛的应用。
在二次函数的研究中，我们发现了一些特殊情况和变化规律，它们对于我们理解和应用二次函数都起到了重要的指导作用。
一、特殊情况1. 常数项为0的情况当二次函数的常数项为0时，我们可以将其表示为f(x) = ax²，其中a是一个实数。
这种情况下，二次函数经过原点(0,0)，其图像关于原点对称。
并且，如果a大于0，则二次函数的图像开口向上；如果a小于0，则二次函数的图像开口向下。
这个特殊情况在实际问题中常常出现。
例如，当我们研究抛物线的轨迹时，如果不考虑任何外力因素，那么抛物线的形状就可以用常数项为0的二次函数来描述。
2. 线性函数的情况线性函数是一次函数的特殊情况，它在二次函数中也有一种特殊的表示形式。
当二次函数的系数a为0时，我们可以将其表示为f(x) = bx，其中b是一个实数。
这样的二次函数实际上就是一条直线。
线性函数的特殊情况在解决一些简单的数学问题时非常有用。
例如，在一个简单的物理问题中，若要求物体在匀速直线运动中的位移与时间的关系，我们可以用线性函数来描述。
二、变化规律1. 平移变化在二次函数的研究中，我们经常需要对其进行平移变化。
平移变化可以让二次函数的图像在平面上上下左右移动，而不改变其形状。
对于一般的二次函数f(x) = ax² + bx + c，平移变化可以表示为f(x - h) = a(x - h)² + b(x - h) + c，其中h是一个实数。
当h大于0时，表示二次函数图像向右平移；当h小于0时，表示二次函数图像向左平移。
平移变化能够帮助我们更好地理解二次函数的图像特征。
例如，在研究抛物线的轨迹时，我们可以通过平移变化将抛物线的顶点平移到坐标原点，这样可以更方便地进行计算和分析。
2. 缩放变化二次函数的缩放变化是改变其图像的形状和大小，但不改变其顶点的位置和开口的方向。
2023年中考数学--- a,b,c和二次函数图像的九种考法例题解析
2023年中考数学--- a ，b ，c 和二次函数图像的九种考法例题解析如图，二次函数的图像关于直线对称，与x 轴交于，两点，若考法解决方法本题结果①a,b,ca:二次函数图像开口向上时，a ＞0；开口向下，则a ＜0；b ：和a 共同决定了函数对称轴的位置，“左同右异”，当对称轴在y 轴左侧时，a ，b 同号，当对称轴在y 轴右侧时，a ，b 异号。
c ：c 为图像和y 轴交点的纵坐标。
a ＞0b ＜0c ＜0②b 2−4ac当图像和x 轴有两个交点时，b 2−4ac ＞0； 当图像和x 轴有一个交点时，b 2−4ac =0； 当图像和x 轴没有交点时，b 2−4ac ＜0。
b 2−4ac ＜0 ③a+b+c a-b+c 4a+2b+c 4a-2b+c 9a+3b+c 9a-3b+c 用特殊值进行判断：a+b+c 即为当x=1时的函数值； 4a-2b+c 即为当x=-2时的函数值。
a+b+c ＜0 a-b+c ＜0④3a+2b只有a ，b 时，用对称轴代换，消去一个未知数进行判断∵−b2a = 1，∴b=- 2а，∴3a ＋2b= 3a-4a= -a ，∵a ＞0，∴3a+2b<0⑤c+a 只有a ，c 或只有b ，c 时，先用对称轴代换，消去一个未知数，然后利用④中的结果判断结果∵a －b ＋c<0，∴a ＋c<b ，∵a ＞0， ∴b=-2a<0，∴a ＋c<0， ⑥b+2c若c 的系数不是1，可以先化成1再进行上述计算,或这把③中的某个式子中的c 的系数变成题里的形式。
∵−b 2a=1,∴2a =−b , ∵a+b ＋c<0，∴2a+2b ＋2c<0，-b+2b ＋2c<0，b ＋2c<0 ⑦am 2+bm 和a +b 的小小关系同时加上c ，am 2+bm+c ，a +b+c第一个式子是当x=m 时的函数值，第二个am 2+bm ≥a+b式子是当x=1时的函数值；由图可知，x=1时函数取最小值。
2023年九年级数学中考专题：二次函数综合压轴题(特殊三角形问题)(含简略答案)
（1）求直线 的解析式；
（2）如图1，点 是直线 下方抛物线上的一点，连接 ，当 的面积最大时，连接 ，设 分别是线段 上的点，且 ，求四边形 的面积；
（3）如图2，点 是线段 的中点，将抛物线 沿 轴正方向平移得到新抛物线 ， 经过点 ， 的顶点为 ，在新抛物线 的对称轴上，是否存在点 ，使得 为等腰三角形？若存在，写出点 的坐标；若不存在，请说明理由．
（3）若点Q是上述抛物线上一点，且满足∠ABQ=2∠ABC，求满足条件的点Q的坐标．
11．如图，在平面直角坐标系中，已知抛物线 与直线 相交于 ， 两点，其中 ， ．
（1）求该抛物线的函数表达式；
（2）点 为直线 下方抛物线上的任意一点，连接 ， ，求 面积的最大值；
（3）在抛物线对称轴上找一点 ，使点 ， ， 三点构成的图形是直角三角形，求点 的坐标．
（2）当△PBC的面积最大时，求P点的坐标．
（3）在X轴上是否存在点N，使△NBC是等腰三角形，若存在直接写出所有符合条件的点N的坐标，若不存在说明理由
8．如图，直线 交 轴于点 ，交 轴于点B，抛物线 的顶点为 ，且经过点 ．
（1）求该抛物线所对应的函数表达式；
（2）点 是抛物线上的点， 是以 为直角边的直角三角形，请直接写出点 的坐标．
13．如图，抛物线 经过 ， 两点，且与 轴交于点 ，点 是抛物线的顶点，抛物线的对称轴 交 轴于点 ，连接 ．
（1）求经过 三点的抛物线的函数表达式；
（2）点 在该抛物线的对称轴上，若 是以 为直角边的直角三角形，求点 的坐标；
（3）若 为 的中点，过点 作 轴于点 ， 为抛物线上一动点， 为 轴上一动点， 为直线 上一动点，当以 、 、 、 为顶点的四边形是正方形时，请求出点 的坐标．
二次函数专题知识点 常考(典型)题型 重难点题型(含详细答案)
二次函数和基本性质专题知识点+常考题型+重难点题型（含详细答案）一、目录一、目录 (1)二、基础知识点 (2)1.二次函数的概念 (2)2.二次函数y=ax2的图像和性质 (2)3.二次函数y=a（x-h）2+k（a≠0）的性质 (4)4，用配方法求y=ax2+bx+c（a≠0） (6)5.二次函数图像性质总结 (7)6.二次函数解析式的求法 (7)7.二次函数图像的平移 (9)三、重难点题型 (11)1.由抛物线的位置确定系数的符号 (11)2.用待定系数法求二次函数的解析式 (13)3.运用抛物线的对称性解题 (17)4.用二次函数解决最值问题 (18)5.二次函数的图像 (20)6.二次函数与应用问题 (21)二、基础知识点1.二次函数的概念形如y=ax2+bx+c（a≠0）的函数叫作二次函数。
注：①a、b、c为常数，且a≠0，即二次项必须有，一次项和常数项可以没有②二次函数为函数的一种，满足函数的所有性质。
即在定义域内，自变量x有且仅有唯一应变量y与之对应例1.下列各项中，y是x的二次函数的有：①y=√2x2−x+5；②y=（m−1）x2+x+1（m为常数）；③y=2x2+4x−m（m为常数）；④y=(2x+1)(3x−2)−6x2答案：①是二次函数，二次项系数不为0；②不应定，当m=1时，二次项为0，则不是二次函数；③是二次函数，二次项系数不为0；④化简得：－x－2，因此不是二次函数例2.已知y=（k+3）x k2+k−4是二次函数，求k的值。
答案：因为y=（k+3）x k2+k−4是二次函数所以{k+3≠0 k2+k−4=2解得：k=22.二次函数y=ax2的图像和性质y=ax2（a≠0，b=0，c=0，即一次项和常数项皆为0）的性质：①图形为抛物线形状②a>0，开口向上；a<0，开口向下③过原点（顶点），为最大值或最小值（由a的正负决定）④关于y轴对称，即关于x=0对称⑤|a|越大，开口越小，即上升或下降越快注：关于y轴对称的前提条件是：函数定义域关于y轴对称例1.求等边三角形面积S与边长a的函数关系式。
二次函数专题讲解含答案
二次函数专题专题必要性：高考中的很多题，往往最后都能转化为二次函数、一元二次方程和一元二次不等式问题，因此二次函数贯穿整个高考中，需深度掌握。
一、二次函数的定义：形如(a≠0，a，b，c为常数)的函数为二次函数.二、二次函数的性质：(1)二次函数y=ax2 (a≠0)的图象是一条抛物线，其顶点是原点，对称轴是y轴；当a＞0时，抛物线开口向上，顶点是最低点；当a＜0时，抛物线开口向下，顶点是最高点；函数(2)二次函数的图象是一条抛物线.顶点为(-，)，对称轴；函数抛物线开口向上，并向上无限延伸抛物线开口向下，并向下无限延伸三、二次函数的三种表现形式1）一般式：2）顶点式：；3）两根式： 其中、是二次函数的与轴的两个交点的横坐标，此时二次函数的对称轴为直线. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.四、二次函数根的由来——配方法 第一步：提公因式。
看二次项的系数是否为1，若系数不为1，则要先把系数提公因式，使二次项的系数变成1；若系数是1，就可以直接进行配方。
如：函数2246y x x =++的二次项2(0)y ax bx c a =++≠2()(0),)y a x h k a h k =-+≠此时二次函数的顶点坐标为(12()()y a x x x x =--1x 2x x 122x x x +=系数是2，因此不能直接配方，要先把2提出来，即：22(23)y x x =++。
第二步：配方。
配方的方法是：二次项以及一次项保持不变，在常数项上加上一次项系数一半的平方，同时，为了保持原式不变，加上了一个什么数，就要减去一个相同的数；如：222222[2()()3]22y x x =++-+第三步：整理配方的前三项可以组成一个完全平方式，再把常数项算出最后的结果即 可,如：22[(1)13]y x =+-+ ， 即：22(1)4y x =++ 。
二次函数特殊值
次函数特殊值二次函数特殊值可以根据不同的条件进行计算。
例如，当乘=1时，y=abc；当乘=-1时，y=a-bc；当乘=2时，y=4a2bc；当乘=-2时，y=4a-2bc。
对于二次函数，需要掌握的知识点有：1. 二次函数的定义：一般形式为y=ax^2+bx+c，其中a、b、c为常数，且a ≠0。
2. 二次函数的图像：二次函数的图像是一个抛物线。
根据a的符号，抛物线有不同的开口方向。
当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。
3. 二次函数的对称性：二次函数的图像关于其对称轴对称。
对称轴的方程是x=-b/2a。
4. 二次函数的顶点：二次函数的图像有一个顶点，其坐标为(-b/2a,c-b^2/4a)。
5. 二次函数的单调性：在区间(-∞,-b/2a)和(b/2a,+∞)上，函数是单调递增的；在区间(-b/2a,b/2a)上，函数是单调递减的。
6. 二次函数的最值：当a>0时，函数有最小值，最小值为c-b^2/4a；当a<0时，函数有最大值，最大值为c-b^2/4a。
7. 二次函数的实际应用：二次函数在实际生活中有很多应用，例如物体运动、收益最大化等问题。
除了以上知识点外，还需要注意以下几点：1. 对于二次函数y=ax^2+bx+c，其判别式Δ=b^2-4ac。
当Δ>0时，函数有两个实根；当Δ=0时，函数有一个重根；当Δ<0时，函数没有实根。
2. 二次函数的最值出现在其对称轴上，即x=-b/2a处。
3. 在解决二次函数问题时，需要灵活运用各种知识点和解题技巧。
希望这些信息能帮助你更好地理解二次函数及其特殊值的概念和应用。
如果你还有其他问题或需要更多的帮助，请随时告诉我。
二次函数的特殊情况解答
二次函数的特殊情况解答二次函数是一种常见的数学函数，其表达式可以写为y = ax^2 + bx + c。
在解答二次函数的特殊情况时，我们需要考虑两种情况：当a = 0和当a ≠ 0的情况。
当a = 0时，二次函数的表达式简化为y = bx + c，此时该函数为一次函数。
一次函数的图像是一条直线，它具有特殊的性质：斜率b表示了直线的倾斜程度，截距c表示了直线与y轴的交点位置。
根据这些特点，我们可以很容易地画出直线的图像，进而解答与直线相关的问题。
当a ≠ 0时，二次函数的表达式为y = ax^2 + bx + c。
为了解答这种情况下的问题，我们可以考虑以下几个方面。
首先，我们可以计算二次函数的顶点坐标。
二次函数的顶点坐标可以通过公式x = -b / (2a)和y = -(b^2 - 4ac) / (4a)来求得。
顶点坐标给出了二次函数图像的最高或最低点，它是函数图像的关键特征。
其次，我们可以计算二次函数的判别式。
二次函数的判别式可以通过公式D = b^2 - 4ac来计算。
判别式的值可以告诉我们二次函数的图像与x轴的交点个数和类型：当D > 0时，函数图像与x轴有两个不同的交点，说明函数有两个实数解；当D = 0时，函数图像与x轴有一个重复的交点，说明函数有一个实数解；当D < 0时，函数图像与x轴没有交点，说明函数无实数解。
此外，我们还可以观察二次函数的对称性。
对于任意的实数x，二次函数在顶点x = -b / (2a)处对称。
这意味着，如果我们知道了顶点的坐标和函数的另外一点的坐标，我们就可以描绘出函数的完整图像。
最后，我们还可以根据二次函数的特殊情况来解答具体问题。
例如，当a > 0时，二次函数图像开口向上；当a < 0时，二次函数图像开口向下；当a ≠ 0且b = 0时，二次函数的图像为关于y轴对称的抛物线等。
通过以上的讨论，我们可以看到解答二次函数的特殊情况需要考虑函数的顶点、判别式、对称性和具体问题等方面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c
b 二次函数特殊符号判断练习
1.二次函数y =ax 2+bx+c (a ≠0)的图象如图所示，则a 、b 、c 的符号为（ ）
A . a<0,b>0,c>0, b 2-4ac <0
B . a<0,b >0,c <0, b 2-4ac >0
C . a <0,b <0,c >0, b 2-4ac <0
D . a <0,b <0,c <0, b 2-4ac >0
2.抛物线y =ax 2+bx +c (a ≠0)的图象经过原点和二、三、四象限，
判断a 、b 、c 的符号情况：a 0,b 0,c 0.
3.二次函数y=ax 2+bx+c (a ≠0)，若a >0，b <0，c <0，那么这个二次函数图象的顶点必在第 象限.
4.已知：y=ax 2+bx+c (a ≠0)的图象如图所示，则点M （
，a ）在（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 5.二次函数y=ax 2+bx+c (a ≠0)的图象如图所示，
下列判断不正确的是（ ）.
A. abc >0,
B. b 2-4ac <0,
C. a-b+c <0,
D. 4a+2b+c >0.
6.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示，
则下列结论错误的是( )
A. a >0
B. c <0
C. b 2-4ac <0
D. a+b+c >0
7.二次函数2y ax bx c =++（0a ≠）的图象如图26-18所示，有下列结论：
①0c <；②0b >;③420a b c ++>；④22()a c b +<,
其中正确的有（ ）A ．1个 B ．2个 C ．3个 D ．4个
8.已知二次函数y=ax 2+bx+c (a ≠0)的图象如所示，则下列结论:
①ac >0；② a ＋b ＋c <0 ；③a －b ＋c <0；④2a ＋b ＝0. 错误的有（ ）
A ．1个
B ．2个
C ．3个
D ．4个
9.已知二次函数的图像如图所示，下列结论：
⑴ a+b+c =0; ⑵ a-b+c <0; ⑶ abc <0; ⑷ b =2a.
其中正确的结论的个数是（ ）A. 1个 B. 2个 C. 3个 D. 4个
10.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图3所示，
下列结论：① abc ＞0; ② 4a+2b+c ＞0; ③ 4a －2b+c ＜0;
④ 2a+b ＜0.其中正确结论的个数为（ ）
A.4个
B.3个
C.2个
D.1个
11. 如图所示，二次函数y=ax 2+bx+c(a ≠0)的图象经过点（-1，2），
且与x 轴交点的横坐标分别为x 1,、x 2 ，其中-2＜x 1＜-1，0＜x 2＜1．
下列结论：①4a-2b+c ＜0；②2a-b ＜0；③b ＜-1；④ b 2+8a ＞4ac ．
其中正确结论的序号是 _____________．
12.(2010·天津)已知二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，有下列
结论：①b 2－4ac >0；②abc >0；③8a ＋c >0；④9a ＋3b ＋c <0.
其中，正确结论的个数是( )
A ．1
B ．2
C ．3
D ．4
◆达标检测：
1.已知二次函数的图像如图所示，下列结论：
①a>0； ②c<0； ③abc>0； ④a+b+c=0； ⑤a-b+c>0； ⑥ b=2a ；
⑦4a-2b+c ＜0；⑧b 2-4ac<0；⑨3a+c=0. 其中正确的结论是_______
2.如图，二次函数)0(2
≠++=a c bx ax y 的图象开口向上，
图象经过点（－1，2）和（1，0），与y 轴交于负半轴.四个结论：
①0＞a ；②b 2-4ac <0；③0＞c ；④ 0=++c b a ,其中正确的是（ ）
A ．①②③④
B ．①③④
C ．①④
D ．④
3.二次函数2y ax bx c =++（0a ≠）的图象如图，则下列结论成立的是（ ） A ．0a >，
0bc > B ．0a <，0bc > C ．0a >，0bc < D ．0,0a bc << 4.已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列结论：
①0abc >；②a -b +c >0；③a+b +c <0；④4a +2b+c ＜0.其中正确的结论有。