高等数学复旦大学出版社课后习题答案

合集下载

高等数学复旦大学出版第三版下册课后答案习题全

习题七1. 在空间直角坐标系中，定出下列各点的位置：A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解：点A在第Ⅰ卦限；点B在第Ⅱ卦限；点C在第Ⅷ卦限；点D在xOy面上；点E在yOz面上；点F在x轴上.2. xOy坐标面上的点的坐标有什么特点？yOz面上的呢？zOx面上的呢？答: 在xOy面上的点，z=0;在yOz面上的点，x=0;在zOx面上的点，y=0.3. x轴上的点的坐标有什么特点？y轴上的点呢？z轴上的点呢？答：x轴上的点，y=z=0;y轴上的点，x=z=0;z轴上的点，x=y=0.4. 求下列各对点之间的距离：（1）（0，0，0），（2，3，4）；（2）（0，0，0），（2，-3，-4）；（3）（-2，3，-4），（1，0，3）；（4）（4，-2，3），（-2，1，3）.解：（1）s=(2) s==(3) s==(4) s==5. 求点（4，-3，5）到坐标原点和各坐标轴间的距离.解：点(4，-3，5)到x轴，y轴，z轴的垂足分别为（4，0，0），（0，-3，0），（0，0，5）.故s==xs==ys==5zs==.6. 在z轴上，求与两点A（-4，1，7）和B（3，5，-2）等距离的点.解：设此点为M（0，0，z），则222222(4)1(7)35(2)z z-++-=++--解得149 z=即所求点为M（0，0，149）.7. 试证：以三点A（4，1，9），B（10，-1，6），C（2，4，3）为顶点的三角形是等腰直角三角形.证明：因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证：()()++=++a b c a b c.证明：利用三角形法则得证.见图7-1图7-19. 设2,3.=-+=-+-u a b c v a b c试用a, b, c表示23.-u v解：232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b ca b c a b ca b c10. 把△ABC的BC边分成五等份，设分点依次为D1，D2，D3，D4，再把各分点与A连接，试以AB=c，BC=a表示向量1D A,2D A,3D A和4D A.解：1115D A BA BD=-=--c a2225D A BA BD=-=--c a3335D A BA BD=-=--c a444.5D A BA BD=-=--c a11. 设向量OM的模是4，它与投影轴的夹角是60°，求这向量在该轴上的投影.解：设M的投影为M'，则1Pr j cos604 2.2uOM OM=︒=⨯=12. 一向量的终点为点B（2，-1，7），它在三坐标轴上的投影依次是4，-4和7，求这向量的起点A的坐标.解：设此向量的起点A的坐标A(x, y, z)，则{4,4,7}{2,1,7}AB x y z=-=----解得x=-2, y=3, z=0故A的坐标为A(-2, 3, 0).13. 一向量的起点是P 1（4，0，5），终点是P 2（7，1，3），试求：（1） 12PP 在各坐标轴上的投影；（2） 12PP 的模；（3） 12PP 的方向余弦；（4） 12PP 方向的单位向量.解：（1）12Pr j 3,x x a PP ==12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP ==(3) 12cos 14xa PP α== 12cos 14ya PP β==12cos 14za PP γ==(4) 12012{14PP PP ===+e j. 14.三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解：R =（1-2+3，2+3-4，3-4+5）=（2，1，4）||==Rcoscos cosαβγ=== 15. 求出向量a = i +j +k , b=2i -3j +5k 和c =-2i -j +2k 的模，并分别用单位向量,,a b c e ee 来表达向量a ,b ,c .解：||==a||==b ||3==c, , 3. a b c ==a b c e16. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解：a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k在x 轴上的投影a x =13,在y 轴上分向量为7j .17.解：设{,,}x y z a a a a =则有cos (1,1)3x a ia a i a iπ⋅====⋅ 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =± 又1,a =则2221x y z a a a ++=从而求得11{,,22a =或11{,,22- 18. 已知两点M 1（2，5，-3），M 2（3，-2，5），点M 在线段M 1M 2上，且123M M MM =，求向径OM 的坐标.解：设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为，123M M MM = 所以，11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}.19. 已知点P 到点A （0，0，12）的距离是7，OP 的方向余弦是236,,777，求点P 的坐标. 解：设P 的坐标为（x , y , z ）, 2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+126570cos 6, 749z z γ==⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒== 故点P 的坐标为P （2，3，6）或P （190285570,,494949）. 20. 已知a , b 的夹角2π3ϕ=，且3,4==b a ，计算： (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解：（1）a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b 21. 已知a =(4,-2, 4), b =(6,-3, 2),计算：（1）a ·b ; (2) (2a -3b )·(a + b )；（3）2||-a b解：（1）46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b 222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b 36238499=-⨯+=22. 已知四点A （1，-2，3），B （4，-4，-3），C （2，4，3），D （8，6，6），求向量AB 在向量CD 上的投影.解：AB ={3，-2，-6}，CD ={6，2，3}Pr jCD AB CD AB CD ⋅=4.7==- 23. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角.解: (a +3b )·(7a -5b ) =227||1615||0+⋅-=a a b b ①(a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ② 由①及②可得：222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ，所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==. 24. 设a =(-2,7,6),b =(4, -3, -8),证明：以a 与b 为邻边的平行四边形的两条对角线互相垂直. 证明：以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a －b ,且a +b ={2,4, -2}a -b ={-6,10,14}又(a +b )·(a -b )= 2×(-6)+4×10+(-2)×14=0故(a +b )⊥(a -b ).25. 已知a =3i +2j -k , b =i -j +2k ,求：(1) a ×b ; (2) 2a ×7b ;(3) 7b ×2a ; (4) a ×a . 解：（1） 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .26. 已知向量a 和b 互相垂直，且||3, ||4==a b .计算：(1) |(a ＋b )×(a －b )|；(2) |(3a ＋b )×(a －2b )|.（1）|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin 242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin 842=⨯⨯⨯= 27. 求垂直于向量3i -4j -k 和2i -j +k 的单位向量，并求上述两向量夹角的正弦. 解：411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a =(2,1,－1)和b =(1,－2,1)为邻边，求其对角线夹角的正弦. 解：两对角线向量为13=+=-l a b i j ，232=-=+-l a b i j k因为12|||2610|⨯=++l l i j k12||||==l l 所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.29. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1)，点M ，N ，P 分别是AB ，BC ，CA 的中点，证明：1()4MN MP AC BC ⨯=⨯. 证明：中点M ，N ，P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P -- {2,2,2}MN =--3{1,0,}2MP =- {4,4,4}AC =--{2,0,3}BC =-22222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k故 1()4MN MP AC BC ⨯=⨯. 30.（1）解: x yz x y z ij k a b a a a b b b ⨯==-+-+-y z z y z x x z x y y x a b a b i a b a b j a b a b k （）（）（）则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅（）（）（）（）xy z xy z x y za a ab b b C C C = 若,,C a b 共面，则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=（）反之亦成立. （2）C x y z x y z xy z a a a a b b b b C C C ⨯⋅=（）a x y z x y z xy z b b b b C C C C a a a ⨯⋅=（） b xy z x y z xyz C C C C a a a a b b b ⨯⋅=（）由行列式性质可得: x y z xy z x y z x y z x y z x y z xy z x y z x y z a a a b b b C C C b b b C C C a a a C C C a a a b b b ==故 C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅（）（）（）31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解：设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ，B ，D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+. 32.解：设四面体的底为BCD ∆，从A 点到底面BCD ∆的高为h ，则13BCD V S h =⋅⋅，而11948222BCD S BC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅= 33. 已知三点A (2,4,1), B (3,7,5), C (4,10,9)，证：此三点共线.证明：{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ，B ，C 三点共线.34. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直，求动点的轨迹方程.解：设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y -1)-4(z -1)=0整理得：2x +3y -4z -1=0即为动点M 的轨迹方程.35. 求通过下列两已知点的直线方程：（1）（1，-2，1），（3，1，-1）；（2）（3，-1，0），（1，0，-3）.解：（1）两点所确立的一个向量为s ={3-1，1+2，-1-1}={2，3，-2}故直线的标准方程为：121232x y z -+-==- 或 311232x y z --+==- （2）直线方向向量可取为s ={1-3，0+1，-3-0}={-2，1，-3}故直线的标准方程为：31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程. 解：所给直线的方向向量为 12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点（0，7，17），因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为：771719x t y t z t =⎧⎪=-⎨⎪=-⎩37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程.解：所求平面与平面3x -2y +6z =11平行故n ={3,-2,6}，又过点(4,1,-2)故所求平面方程为：3(x -4)-2(y -1)+6(z +2)=0即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3)，且与连接坐标原点到点M 0的线段OM 0垂直的平面方程.解：所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为：x -1+7(y -7)-3(z +3)=0即x +7y -3z -59=039. 设平面过点(1,2,-1)，而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍，求此平面方程.解：设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上，则有121122b b b-++=得b=2.故所求平面方程为1424x y z++=40. 求过(1,1,-1), (-2,-2,2)和（1，-1，2）三点的平面方程.解：由平面的三点式方程知111212121313131x x y y z zx x y y z zx x y y z z------=---代入三已知点，有1112121210111121x y z--+----+=---+化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置，并画出其图形：(1) y =0; (2) 3x-1=0;(3) 2x-3y-6=0; (4) x–y =0;(5) 2x-3y+4z=0.解：(1) y =0表示xOz坐标面（如图7-2）(2) 3x-1=0表示垂直于x轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z轴且在x轴及y轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x–y=0表示过z轴的平面（如图7-5）(5) 2x-3y+4z=0表示过原点的平面（如图7-6）.图7-4 图7-5 图7-642. 通过两点（1，1，1，）和（2，2，2）作垂直于平面x+y-z=0的平面.解：设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点（1，1，1）在平面上，所以有D=0故平面方程为x-y=0.43. 决定参数k的值，使平面x+ky-2z=9适合下列条件：（1）经过点（5，-4，6）；（2）与平面2x-3y+z=0成π4的角.解：（1）因平面过点（5，-4，6）故有5-4k-2×6=9得k=-4.（2）两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解：（1）n1={2,l,3}, n2={m,-6,-1}12232,18613lm lm⇒==⇒=-=--n n(2) n1={3, -5, l }, n2={1,3,2}12315320 6.l l⊥⇒⨯-⨯+⨯=⇒=n n45. 通过点（1，-1，1）作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面. 解：设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}12203203A CA B CA B C CB⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n nn n又（1，－1，1）在所求平面上，故A－B+C+D=0，得D=0故所求平面方程为233CCx y Cz-++=即2x-y-3z=046. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量. 解：n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点：(1)11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解：（1）直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为（2，-3，6）.（2）直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为（-2，1，3）. 48. 求下列直线的夹角：（1）533903210x y z x y z -+-=⎧⎨-+-=⎩ 和2223038180x y z x y z +-+=⎧⎨++-=⎩；（2）2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解：（1）两直线的方向向量分别为：s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直，夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程：（1）经过点（2，-3，4），且与平面3x -y +2z -4=0垂直；（2）过点（0，2，4），且与两平面x +2z =1和y -3z =2平行；（3）过点（-1，2，1），且与直线31213x y z --==-平行. 解：（1）可取直线的方向向量为 s ={3，-1，2}故过点（2，-3，4）的直线方程为234312x y z -+-==- （2）所求直线平行两已知平面，且两平面的法向量n 1与n 2不平行，故所求直线平行于两平面的交线，于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n故过点（0，2，4）的直线方程为24231x y z --==- （3）所求直线与已知直线平行，故其方向向量可取为 s ={2，-1，3}故过点（-1，2，1）的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系：（1）34273x y z++==--和4x -2y -2z =3; （2）327x y z==-和3x -2y +7z =8;（3）223314x y z -+-==-和x +y +z =3. 解：平行而不包含. 因为直线的方向向量为s ={-2，-7，3}平面的法向量n ={4，-2，-2}，所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0（-3，-4，0）代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量，故直线垂直于平面.(3) 直线在平面上，因为3111(4)10⨯+⨯+-⨯=,而直线上的点（2，-2，3）在平面上. 51. 求过点（1，-2，1），且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程.解：直线的方向向量为12123111-=++-i j ki j k , 取平面法向量为{1，2，3}，故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点（1，-2，3）和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解：设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数，又因为所求平面过点（1，-2，3）故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点（-1，2，0）在平面x +2y -z +1=0上的投影.解：过点（-1，2，0）作垂直于已知平面的直线，则该直线的方向向量即为已知平面的法向量，即s =n ={1，2，-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0得23t =-于是所求点（-1，2，0）到平面的投影就是此平面与垂线的交点522(,,)333-54. 求点（3，-1，2）到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解：过点（3，-1，2）作垂直于已知直线的平面，平面的法向量可取为直线的方向向量即11133211==-=---ij kn s j k 故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-=即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d ==55. 求点（1，2，1）到平面x +2y +2z -10=0距离.解：过点（1，2，1）作垂直于已知平面的直线，直线的方向向量为s =n ={1，2，2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333，且与点（1，2，1）的距离为1d == 即为点到平面的距离.56. 建立以点（1，3，-2）为中心，且通过坐标原点的球面方程.解：球的半径为R ==设(x ,y ,z )为球面上任一点，则(x -1)2+(y -3)2+(z +2)2=14 即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点（2，0，-3）的距离与离点（4，-6，6）的距离之比为3，求此动点的轨迹方程.解：设该动点为M (x ,y ,z )，由题意知222222(2)(0)(3) 3.(4)(6)(6)x y z x y z -+-++=-+++-化简得：8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面，并画出其图形：（1）22()()22a a x y -+=; （2）22149x y -+=; （3）22194x z +=; （4）20y z -=; （5）220x y -=; （6）220x y +=. 解：（1）母线平行于z 轴的抛物柱面，如图7-7. （2）母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 （3）母线平行于y 轴的椭圆柱面，如图7-9. （4）母线平行于x 轴的抛物柱面，如图7-10.图7-9 图7-10（5）母线平行于z 轴的两平面，如图7-11. （6）z 轴，如图7-12.图7-11 图7-1259. 指出下列方程表示怎样的曲面，并作出图形：（1）222149y z x ++=; （2）22369436x y z +-=; （3）222149y z x --=; （4）2221149y z x +-=; （5）22209z x y +-=. 解：（1）半轴分别为1，2，3的椭球面，如图7-13. (2) 顶点在（0，0，-9）的椭圆抛物面，如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面，如图7-15. (4) 单叶双曲面，如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面，其中心轴是z 轴，如图7-17.图7-1760. 作出下列曲面所围成的立体的图形： (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1.解：（1）（2）（3）（4）分别如图7-18，7-19，7-20，7-21所示.图7-18图7-19图7-20 图7-2161. 求下列曲面和直线的交点：(1)222181369x y z++=与342364x y z--+==-;(2)22211694x y z+-=与2434x y z+==-.解：（1）直线的参数方程为334624x ty tz t=+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t=0,t=1.得交点坐标为（3，4，-2），（6，-2，2）.(2) 直线的参数方程为4324x ty tz t=⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t=1,得交点坐标为（4，-3，2）.62. 设有一圆，它的中心在z轴上，半径为3，且位于距离xOy平面5个单位的平面上，试建立这个圆的方程.解：设（x ，y ，z ）为圆上任一点，依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状，并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解：（1）截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.（2）截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线. 解：以曲线为准线，母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解：以曲线为准线，母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=.故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集？并分别指出它们的聚点集和边界： (1) {(x , y )|x ≠0};(2) {(x , y )|1≤x 2+y 2<4}; (3) {(x , y )|y <x 2};(4) {(x , y )|(x -1)2+y 2≤1}∪{(x , y )|(x +1)2+y 2≤1}.解：(1)开集、无界集，聚点集：R 2，边界：{(x , y )|x =0}. (2)既非开集又非闭集，有界集, 聚点集：{(x , y )|1≤x 2+y 2≤4}，边界：{(x , y )|x 2+y 2=1}∪{(x , y )| x 2+y 2=4}. (3)开集、区域、无界集，聚点集：{(x , y )|y ≤x 2}，边界：{(x , y )| y =x 2}.(4)闭集、有界集，聚点集即是其本身，边界：{(x , y )|(x -1)2+y 2=1}∪{(x , y )|(x +1)2+y 2=1}. 2. 已知f (x , y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解：222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u vf u v w u w+=+,试求(,,).f x y x y xy +-解：f ( x + y , x -y , x y ) =( x + y )xy +(x y )x +y +x -y =(x + y )xy +(x y )2x . 4. 求下列各函数的定义域：2(1)ln(21);z y x =-+(2)z =(3)z =(4)u =+(5)z =(6)ln()z y x =-+(7)u =解：2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>> 2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限：10y x y →→ 22001(2)lim;x y x y →→+00x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解：(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O (0，0)处是否连续：33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解：(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=，且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0，0)点，则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0，0)点，则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0，0)处不连续.7. 指出下列函数在向外间断：(1) f (x ,y )=233x y x y -+;(2) f (x ,y )=2222y xy x+-;(3) f (x ,y )=ln(1－x 2－y 2);(4)f (x ,y )=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解：(1)因为当y =-x 时，函数无定义，所以函数在直线y =-x 上的所有点处间断，而在其余点处均连续.(2)因为当y 2=2x 时，函数无定义，所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时，函数无定义，所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0，0)是函数的间断点，而在其余各点处均连续. 8. 求下列函数的偏导数： (1)z = x 2y +2x y ; (2)s =22u v uv+;(3)z = x; (4)z = lntan x y; (5)z = (1+xy )y ; (6)u = z xy ;(7)u = arctan(x -y )z; (8)y zu x =.解：(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+ 2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z z u z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz z u z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .yyzz yy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y =+，求证：3u uxy u x y∂∂+=∂∂. 证明： 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=，求证：222z z xy z x y∂∂+=∂∂. 证明： 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1121ex y z y y⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y ) = x +(y，求f x (x ,1) .解：1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点（2，4，5）处的切线与正向x 轴所成的倾角.解：(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数： (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x; (3)z = y x ;(4)z = 2ex y+.解：(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ，，由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭，2222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x , y , z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解：2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15.设z = x ln ( x y )，求32z x y ∂∂∂及32zx y ∂∂∂.解：ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分： (1)22ex y z +=;(2)z =;(3)zy u x =; (4)yzu x =.解：(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴ 223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分： (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解：(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量，近似计算： (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解：(1)设f (x ,y )=x 3·y 2，则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03，则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d0.05d0.07(4.05,2.93)(4,3)d(4,3)0.053(0.07)]15(0.01)54.998xyf f f==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=x y,则d f(x,y)=yx y-1d x+x y ln x d y，取x=2,y=1,d x=-0.03,d y=0.05,则1.05d0.03d0.05(1.97)(1.97,1.05)(2,1)d(2,1)20.0393 2.0393.xyf f f=-==≈+=+=19.矩型一边长a=10cm，另一边长b=24cm, 当a边增加4mm，而b边缩小1mm时，求对角线长的变化.解：设矩形对角线长为l，则d d).l l x x y y==+当x=10,y=24,d x=0.4,d y=-0.1时，d0.4240.1)0.062l=⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20.解：因为圆锥体的体积为21.3V r hπ=⋅0030,0.1,60,0.5r r h h====-而221.33V VV dV r h yh r r hr hππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h====-时，2213.1430600.130(0.5)33Vπ≈⨯⨯⨯⨯+⨯⨯-230()cm=-21.解：设水池的长宽深分别为,,x y z则有:V xyz=精确值为：50.242 2.850.22 3.6 2.80.2V=⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m=近似值为:V dV zx y xy z ≈=+0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯ 314.8()m =22. 求下列复合函数的偏导数或全导数：(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂； (2)z ＝arc tanx y , x ＝u ＋v ,y ＝u －v , 求z u ∂∂,z v∂∂； (3)ln(e e )xyu =+, y ＝x 3, 求d d ux; (4) u ＝x 2＋y 2＋z 2, x ＝e cos tt , y ＝e sin tt , z ＝e t, 求d d ut. 解：（1）222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y xx x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数，试求下列函数的一阶偏导数： (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解：(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数，证明： .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-，其中f (u )为可导函数，验证： 211z z zx x y y y∂∂+=∂∂. 证明：∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数，求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解：2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知，22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数，求下列函数的二阶偏导数： (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解：(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂。

高等数学下册黄立宏廖基定著复旦大学出版社第十章课后答案

− 2 arcsin y ≤ x ≤ π; arcsin y ≤ x ≤ π − arcsin y.
0 π 1 π − arcsin y
所以 (5) 相应二重积分的积分区域 D 由 D1 与 D2 两部分组成，其中
∫
0
dx ∫
x − sin 2
f ( x, y )dy = ∫ dy ∫
−1
−2arcsin y
∫ （1）
1
2
ww w.
图 10-5 (2) (4)
2 x 的交点(1，2)，与 x=2 的交点为(2，4), （3）区域 D 如图 10-5 所示，直线 y=2x 与曲线 2 2 y= ≤ y ≤ 2 x, 1 ≤ x ≤ 2. x 与 x=2 的交点为（2，1），区域 D 可表示为 x 曲线
y=
1
1− y
f ( x, y )dx
可表示为
y 2 ≤ x ≤ y + 2, − 1 ≤ y ≤ 2 .
图 10-3 所以
图 10-4
2
D
−1
y2
课后
答
案
网
x 所以 . 6. 画出积分区域，改变累次积分的积分次序：
∫∫
D
f ( x, y )dσ = ∫ dx ∫2 f ( x, y )dy
1
2y
2
2x
（1）（2）
课后
I = ∫∫
D
4 + xy dσ , D = {( x, y ) | 0 ≤ x ≤ 2, 0 ≤ y ≤ 2}
2 2
答
∫∫
ln( x + y )dσ < ∫∫ [ln( x + y )]2 dσ

高等数学复旦大学出版社习题答案五

(2)L′(x)=R′(x)－C′(x)=5－2x．
在总利润最大的基础上再多生产100台时，利润的增量为
ΔL(x)= ．
即此时总利润减少1万元.
21．某企业投资800万元，年利率5%，按连续复利计算，求投资后20年中企业均匀收入率为200万元/年的收入总现值及该投资的投资回收期．
解：投资20年中总收入的现值为
在(3，0)处的切线是y=2x+6
两切线交点是( ，3)．故所求面积为
(7)
（8）摆线x=a(tsint)，y=a(1cost)的一拱(0t2)与x轴；
解：当t=0时，x=0,当t=2时，x=2a．
所以
(8)
（9）极坐标曲线ρ=asin3φ；
解：
．
(9)
（10）ρ=2acosφ；
解：
．
(10)
2．求下列各曲线所围成图形的公共部分的面积：
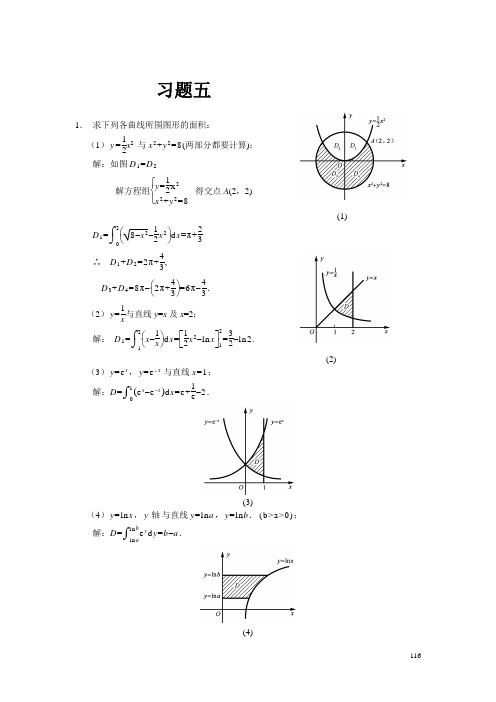
1．求下列各曲线所围图形的面积：
（1）与x2+y2=8(两部分都要计算)；
解：如图D1=D2
解方程组得交点A(2，2)
(1)
∴ ,
．
（2）与直线y=x及x=2；
解： .
(2)
（3）y=ex，y=ex与直线x=1；
解：．
(3)
（4）y=lnx，y轴与直线y=lna，y=lnb．(b>a>0)；
≈0.385386万元=3853.86元．
yt′=3asin2tcost
xt′2+yt′2=9a2sin2tcos2t，利用曲线的对称性，
．
9．求对数螺线相应θ=0到θ=φ的一段弧长．
解：
．
10．求半径为R，高为h的球冠的表面积．

高等数学上_复旦大学出版_习题五答案

(16) 对于任意的 y∈[0，h]，过点(0，y)且垂直于 y 轴的平面截该立体为一椭圆，且该椭圆的半轴为： A a B b x1=A y ，同理可得该椭圆的另一半轴为： x 2 = B y． h h 故该椭圆面积为 A a B b A ( y )= x 1 x 2 = A y B y h h 从而立体的体积为
2 0 2 2
1 y
1+ y ′ 2 d x =2
0
1+
1 dx y2
=2
2 1 y2 1+ y 2 d =2 1+ y 2 d y y 2 0 0 2
= y 1+ y 2 +ln (y + 1+ y 2 ) =2 5 +ln(2+ 5)
0
（2） y =ln x ， 3 ≤x≤ 8 ；解：l = = （3） y =
∴D =
1 a 0
(x x 2 ax )d x
1 1 1 a = (1 a )· x2 x3 3 0 2 = 1 1 a )3 6( 1 9 1 a )3 = 6( 2 得 a=2． (13) 4．求下列旋转体的体积：（1）由 y = x 2 与 y 2 = x 3 围成的平面图形绕 x 轴旋转；
习题五
1．求下列各曲线所围图形的面积： 1 （1） y = x2 与 x 2 + y 2 =8(两部分都要计算)； 2 解：如图 D 1 = D 2
Байду номын сангаас
y = 1 x 2 解方程组 2 得交点 A(2，2) x 2 + y 2 =8
(1) 1 2 D 1 = 8 x 2 x 2 d x =π+ 2 3 0 4 ∴ D 1 + D 2 =2 π + , 3 4 4 D 3 + D 4 =8 π 2 π + =6 π ． 3 3 1 （2） y = 与直线 y=x 及 x=2； x

高等数学复旦大学出版第三版上册课后答案习题全 PDF 版本适合手机

x x x x ] = 时,邮资 y = × 0.80 = ; 20 20 20 25 x x ⎡ x ⎤ ]≠ 时, 由题意知邮资 y = + 1⎥ × 0.80 . ⎢ 20 20 ⎣ 20 ⎦
当 x 不能被 20 整除时,即 [
⎧x ⎡ x⎤ x , 0 < x ≤ 2000且 ⎢ ⎥ = ; ⎪ ⎪ 25 ⎣ 20 ⎦ 20 综上所述有 y = ⎨ ⎪ ⎡ x + 1⎤ × 0.80, 0 < x ≤ 2000且 ⎡ x ⎤ ≠ x . ⎢ ⎪ ⎣ 20 ⎥ ⎦ ⎣ 20 ⎥ ⎦ 20 ⎩⎢
1− x 1− y 解得 x = , 1+ x 1+ y
所以函数 y =
1− x 1− x 的反函数为 y = ( x ≠ −1) . 1+ x 1+ x
y−1
(2) 由 y = ln( x + 2) + 1 得 x = e
−2,
(x ∈R) .
所以, 函数 y = ln( x + 2) + 1 的反函数为 y = e x −1 − 2
习题一
1. 下列函数是否相等,为什么?
(1) f ( x ) = x 2 , g (x ) = x ; x 2 −1 (3) f ( x ) = , g ( x ) = x + 1. x −1
解: (1)相等.
(2)y = sin2 (3x + 1),u = sin2 (3t + 1);
因为两函数的定义域相同 ,都是实数集 R; 由
4
故
f ( x) − f (− x) 为奇函数.
12. 某厂生产某种产品 , 年销售量为 106 件, 每批生产需要准备费 103 元, 而每件的年库存费为 0.05 元, 如果销售是均匀的 , 求准备费与库存费之和的总费用与年销售批数之间的函数 ( 销售均匀是指商品库存数为批量的一半). 解: 设年销售批数为 x, 则准备费为 103x; 又每批有产品

高等数学复旦大学出版第三版上册课后答案习题全

其中
x x x x , 1 分别表示不超过 , 1 的最大整数. 20 20 20 20
14. 已知水渠的横断面为等腰梯形,斜角 =40°,如图所示.当过水断面 ABCD 的面积为定值 S0 时,求湿周 L(L=AB+BC+CD)与水深 h 之间的函数关系式,并指明其定义域.
106 106 106 件,库存数为件,库存费为 0.05 元. x 2x 2x
3
106 0.05 设总费用为,则 y 10 x . 2x
13. 邮局规定国内的平信,每 20g 付邮资 0.80 元,不足 20 g 按 20 g 计算,信件重量不得超过 2kg, 试确定邮资 y 与重量 x 的关系. 解: 当 x 能被 20 整除,即 [
x
7. 证明: f ( x) 2 x 1 和 g ( x)
3
3
x 1 互为反函数. 2
证:由 y 2 x 1 解得 x
3
3
y 1 , 2
2
故函数 f ( x) 2 x 1 的反函数是 y
3
3
x 1 ( x R ) , 这与 g ( x) 2
3
x 1 是同一个函 2
3
又由 1 cos x 1 得 0 1 cos x 2 , 即 0 y 2 , 故可得反函数的定义域为 [0,2], 所以 , 函数 y 1 cos x, x [0, π] 的反函
3
数为 y arccos 3 x 1
(0 x 2) .
9. 判断下列函数在定义域内的有界性及单调性:
(2) f ( x) e
2 x
e 2 x sin( x) e 2 x e 2 x sin x (e 2 x e 2 x sin x) f ( x)

高等数学(经管类)下、林伟初郭安学主编、复旦大学出版社、课后习题答案

fx (x,
y,
z)
x
1 yz
,
fy
(x,
y,
z)
x
z yz
,
fz
(x,
y,
z)
x
y yz
.
故
fx (2, 0,1)
1, 2
fy (2, 0,1)
1, 2
fz (2, 0,1)
0.
3．设 r x 2 y 2 z 2 ，证明：
(1)
r x
2
r y
2
r z
2
1;
(2)
2r x 2
2r y 2
y
x
故所求的定义域为 D={(x,y)| x 1且y x }，表示 xOy 平面上直线 y=x 以下且横坐
标 x 1的部分。
（4）由
1 3 x2 y2 1
x y2 0
可得
2 x2 y2 4
y2 x
故所求的定义域为 D={(x,y)| 2 x2 y2 4且y2 x }。
解：(1) z 3x2 3y, z 3x 3y2.
x
y
(2) z sin y2 , z 1 cos y2 2y.
x
x2 y x
(3) z 1 , z 3 . x x 3y y x 3y
(4) z yxy1 y yxy1 1 , z xy ln x 1 .
x
xy
x y
欢迎下载
-3-
—
习题 7-3
1. 求下列函数偏导数： (1) z=x3+3xy+y3； (3) z ln(x 3y) ；
(2) z sin y 2 ; x
(4) z x y ln x y (x 0，y 0,x 1)

高等数学复旦大学出版第三版课后答案

206习题十1. 根据二重积分性质，比较ln()d D x y σ+⎰⎰与2[ln()]d D x y σ+⎰⎰的大小，其中：（1）D 表示以（0，1），（1，0），（1，1）为顶点的三角形；（2）D 表示矩形区域{(,)|35,02}x y x y ≤≤≤≤.解：（1）区域D 如图10-1所示，由于区域D 夹在直线x +y =1与x +y =2之间，显然有图10-112x y ≤+≤从而 0l n ()x y ≤+<故有2l n ()[l n ()]x y x y+≥+ 所以 2l n ()d [l n ()]dD Dx yx y σσ+≥+⎰⎰⎰⎰（2）区域D 如图10-2所示.显然，当(,)x y D ∈时，有3x y +≥.图10-2从而 ln(x +y )>1 故有2l n ()[l n ()]x y x y+<+207所以 2l n ()d [l n ()]dD Dx yx y σσ+<+⎰⎰⎰⎰2. 根据二重积分性质，估计下列积分的值：（1）,{(,)|02,02}I D x y x y σ==≤≤≤≤⎰⎰;（2）22sin sin d ,{(,)|0π,0π}D I x y D x y x y σ==≤≤≤≤⎰⎰; （3）2222(49)d ,{(,)|4}D I x y D x y x y σ=++=+≤⎰⎰. 解：（1）因为当(,)x y D ∈时，有02x ≤≤, 02y ≤≤因而 04xy ≤≤.从而22≤故2d D D σσσ≤≤⎰⎰⎰⎰⎰⎰即2d d DDσσσ≤≤⎰⎰⎰⎰而 d D σσ=⎰⎰ （σ为区域D 的面积），由σ=4 得8σ≤≤⎰⎰(2) 因为220sin 1,0sin 1x y ≤≤≤≤，从而220sin sin 1x y ≤≤故 220d sin sin d 1d D D D x y σσσ≤≤⎰⎰⎰⎰⎰⎰ 即220sin sin d d D D x y σσσ≤≤=⎰⎰⎰⎰ 而2πσ=所以2220sin sin d πD x y σ≤≤⎰⎰（3）因为当(,)x y D ∈时，2204x y ≤+≤所以22229494()925x y x y ≤++≤++≤故 229d (49)d 25d D D D x y σσσ≤++≤⎰⎰⎰⎰⎰⎰ 即229(49)d 25Dx y σσσ≤++≤⎰⎰208而2π24πσ=⋅=所以2236π(49)d 100πDx y σ≤++≤⎰⎰3. 根据二重积分的几何意义，确定下列积分的值：（1）222(,{(,)|};D a D x y x y a σ=+≤⎰⎰（2）222,{(,)|}.D x y x y a σ=+≤⎰⎰解：（1）(,D a σ⎰⎰在几何上表示以D 为底，以z 轴为轴，以（0，0，a ）为顶点的圆锥的体积，所以31(π3Da a σ=⎰⎰ （2）σ⎰⎰在几何上表示以原点（0，0，0）为圆心，以a为半径的上半球的体积，故32π.3a σ=⎰⎰ 4.设f (x ，y )为连续函数，求2220021lim(,)d ,{(,)|()()}πDr f x y D x y x x y y r r σ→=-+-≤⎰⎰.解：因为f (x ，y )为连续函数，由二重积分的中值定理得，(,),D ξη∃∈使得2(,)d (,)π(,)Df x y f r f σξησξη=⋅=⋅⎰⎰又由于D 是以（x 0，y 0）为圆心，r 为半径的圆盘，所以当0r →时，00(,)(,),x y ξη→ 于是：0022200000(,)(,)11lim(,)d limπ(,)lim (,)ππlim (,)(,)Dr r r x y f x y r f f r r f f x y ξησξηξηξη→→→→=⋅===⎰⎰5. 画出积分区域，把(,)d D f x y σ⎰⎰化为累次积分： (1) {(,)|1,1,0}D x y x y y x y =+≤-≤≥;(2)2{(,)|2,}D x y y x x y =≥-≥209(3)2{(,)|,2,2}D x y y y x x x=≥≤≤解：（1）区域D 如图10-3所示，D 亦可表示为11,01y x y y -≤≤-≤≤.所以1101(,)d d (,)d yD y f x y y f x y x σ--=⎰⎰⎰⎰(2) 区域D 如图10-4所示，直线y =x -2与抛物线x =y 2的交点为（1，-1），（4，2），区域D 可表示为22,12y x y y ≤≤+-≤≤.图10-3 图10-4所以2221(,)d d (,)d y D yf x y y f x y x σ+-=⎰⎰⎰⎰（3）区域D 如图10-5所示，直线y =2x 与曲线2y x=的交点(1，2)，与x =2的交点为(2，4),曲线2y x=与x =2的交点为（2，1），区域D 可表示为22,1 2.y x x x≤≤≤≤图10-5210所以2221(,)d d (,)d xD xf x y x f x y y σ=⎰⎰⎰⎰.6. 画出积分区域，改变累次积分的积分次序： (1) 2220d (,)d yyy f x y x⎰⎰; (2)e ln 1d (,)d xx f x y y ⎰⎰;(3) 1320d (,)d yy f x y x-⎰; (4)πsin 0sin2d (,)d xx x f x y y -⎰⎰;(5) 1233001d (,)d d (,)d yyy f x y y y f x y x -+⎰⎰⎰⎰.解：（1）相应二重保健的积分区域为D ：202,2.y y x y ≤≤≤≤如图10-6所示.图10-6D 亦可表示为：04,.2xx y ≤≤≤所以2224002d (,)d d (,)d .yx yy f x y x x f x y y =⎰⎰⎰⎰(2) 相应二重积分的积分区域D ：1e,0ln .x y x ≤≤≤≤如图10-7所示.图10-7D 亦可表示为：01,e e,y y x ≤≤≤≤211所以e ln 1e10ed (,)d d (,)d y xx f x y y y f x y x =⎰⎰⎰⎰(3) 相应二重积分的积分区域D为：01,32,y x y ≤≤≤≤-如图10-8所示.图10-8D 亦可看成D 1与D 2的和，其中 D 1：201,0,x y x ≤≤≤≤D 2：113,0(3).2x y x ≤≤≤≤-所以2113213(3)2001d (,)d d (,)d d (,)d yx x y f x y x x f x y y x f x y y --=+⎰⎰⎰⎰⎰.(4) 相应二重积分的积分区域D 为：0π,sinsin .2xx y x ≤≤-≤≤如图10-9所示.图10-9D 亦可看成由D 1与D 2两部分之和，其中 D 1：10,2arcsin π;y y x -≤≤-≤≤ D 2：01,arcsin πarcsin .y y x y ≤≤≤≤-所以πsin 0π1πarcsin 0sin 12arcsin 0arcsin 2d (,)d d (,)d d (,)d xyx y yx f x y y y f x y x y f x y x ----=+⎰⎰⎰⎰⎰⎰(5) 相应二重积分的积分区域D 由D 1与D 2两部分组成，其212中 D 1：01,02,y x y ≤≤≤≤D 2：13,03.y x y ≤≤≤≤-如图10-10所示.图10-10D 亦可表示为：02,3;2xx y x ≤≤≤≤- 所以()1233230012d ,d d (,)d d (,)d yyxxy f x y x y f x y x x f x y y --+=⎰⎰⎰⎰⎰⎰7.解：因为(,)Df x y d σ⎰⎰为一常数，不妨设(,)Df x y C =⎰⎰则有(,)x y f xy C =+从而有(,)()x y Df xy f uv C dudv =++⎰⎰而{}2(,)0 1.0D x y x y x =≤≤≤≤21(,)00()u x y f xy uv C dv du ⎡⎤∴=+⎰⎰+⎣⎦2120012u xy uv cv du ⎡⎤=+⎰+⎢⎥⎣⎦ 152012xy u cu du ⎡⎤=+⎰+⎢⎥⎣⎦163011123xy u cu ⎡⎤=++⎢⎥⎣⎦11123xy C =++18C ∴=故(,)18x y f xy ∴=+8. 计算下列二重积分：213(1) 221d d ,:12,;Dx x y D x y x y x≤≤≤≤⎰⎰ (2) e d d ,x yD x y ⎰⎰D由抛物线y 2 = x ,直线x =0与y =1所围；(3) d ,x y ⎰⎰D 是以O (0,0)，A (1，-1)，B (1，1)为顶点的三角形; (4) cos()d d ,{(,)|0π,π}D x y x y D x y x x y +=≤≤≤≤⎰⎰.解：（1）()22222231221111d d d d d d xx D x x x x x x y x y x x x x y yy ==-=-⎰⎰⎰⎰⎰⎰2421119.424x x ⎡⎤=-=⎢⎥⎣⎦(2) 积分区域D 如图10-12所示.图10-12D 可表示为：201,0.y x y ≤≤≤≤所示22110000ed d de d d e d()xx x y y yyyD xx y y x y y y==⎰⎰⎰⎰⎰⎰ 2111100ed (e 1)d e d d y x y y yy y y y y y y y ==-=-⎰⎰⎰⎰1111120000011de d e e d .22yy yy y y y y y =-=--=⎰⎰⎰ (3) 积分区域D 如图10-13所示.214图10-13D 可表示为：01,.x x y x ≤≤-≤≤所以2110d d arcsin d 2xxxx y x y x y x x --⎡==+⎢⎣⎰⎰⎰⎰⎰ 112300ππ1πd .2236x x x ==⋅=⎰ ππππ0πππ0(4)cos()d d d cos()d [sin()]d [sin(π)sin 2]d (sin sin 2)d 11.cos cos 222x Dxx y x y x x y y x y xx x x x x x x x +=+=+=+-=--⎡⎤==+⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰9. 计算下列二次积分：10112111224(1)d d ;(2)d e d d e d .yy y xxyxy x xy x y x +⎰⎰⎰⎰解：（1）因为sin d x x x⎰求不出来，故应改变积分次序。

高等数学习题08答案(复旦大学出版社)

习题八5. 求下列各极限：10(1)y x y →→00(3)x y →→00(4)l ;x y →→222222001cos()(6)lim .()e x y x y x y x y +→→-++ 解：(1)原式0ln 2.=(3)原式=01.4x y →→=-(4)原式=002.x y →→=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 讨论下列函数在原点O (0，0)处的连续性及偏导数：(3) 222222222,0,()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解：(3)若P (x ,y ) 沿直线y =x 趋于(0，0)点，则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0，0)点，则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0，0)处不连续.而…8. 求下列函数的偏导数： (1)z = x 2y +2xy; (6)u = z xy ;解：(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ 12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点（2，4，5）处的切线与正向x 轴所成的倾角.解：(2,4,5)1,1,2z zx x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4.13.求下列函数的二阶偏导数：(3)z = y x ;解：(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ 14.设f (x ,y ,z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解：2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===22. 求下列复合函数的偏导数或全导数：(2)z ＝arc tanxy, x ＝u ＋v ,y ＝u －v , 求z u ∂∂,z v ∂∂；(3)ln(e e )xyu =+, y ＝x 3, 求d d u x;(4) u ＝x 2＋y 2＋z 2, x ＝e cos t t , y ＝e sin t t , z ＝e t, 求d d u t. 解：(2)222222211111x z z x z y y x v y u x u y uy x yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 2222222111(1)11.x z z x z yy v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数，试求下列函数的一阶偏导数： (1)22(,e );xy u f x y =-解：(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ 29. 求下列隐函数的导数或偏导数：(4)333z xyz a -=，求22,z zx y∂∂∂∂.解：(4)设33(,,)3F x y z z xyz a =--, 则23,3,33,x y z F yz F xz F z xy =-=-=-故223,33x z F z yz yz x F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xz y F z xy z xy∂-=-=-=∂--()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z (x ,y ),其中F 可微，求,z z x y ∂∂∂∂.解：12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222110111y z x zy zF F F y F F F F F F F zx x F F x F F F F F y F zy y F F y F ⎛⎫''-=⋅+⋅ ⎪⎝⎭'''=⋅+⋅='-'∂∴=-=-=∂''''-''-∂=-=-=∂''。

高等数学复旦大学出版第三版下册课后答案习题全

习题七1. 在空间直角坐标系中，定出下列各点的位置：A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解：点A在第Ⅰ卦限；点B在第Ⅱ卦限；点C在第Ⅷ卦限；点D在xOy面上；点E在yOz面上；点F在x轴上.2. xOy坐标面上的点的坐标有什么特点yOz面上的呢zOx面上的呢答: 在xOy面上的点，z=0;在yOz面上的点，x=0;在zOx面上的点，y=0.3. x轴上的点的坐标有什么特点y轴上的点呢z轴上的点呢答：x轴上的点，y=z=0;y轴上的点，x=z=0;z轴上的点，x=y=0.4. 求下列各对点之间的距离：（1）（0，0，0），（2，3，4）；（2）（0，0，0），（2，-3，-4）；（3）（-2，3，-4），（1，0，3）；（4）（4，-2，3），（-2，1，3）.解：（1）s=(2) s==(3) s=(4) s==.5. 求点（4，-3，5）到坐标原点和各坐标轴间的距离.解：点(4，-3，5)到x轴，y轴，z轴的垂足分别为（4，0，0），（0，-3，0），（0，0，5）.s==故s==x2224(33)541y s =+-++=2224(3)(55)5z s =+-+-=.6. 在z 轴上，求与两点A （-4，1，7）和B （3，5，-2）等距离的点.解：设此点为M （0，0，z ），则222222(4)1(7)35(2)z z -++-=++--解得 149z = 即所求点为M （0，0，149）. 7. 试证：以三点A （4，1，9），B （10，-1，6），C （2，4，3）为顶点的三角形是等腰直角三角形.证明：因为|AB |=|AC |=7.且有|AC |2+|AB |2=49+49=98=|BC |2.故△ABC 为等腰直角三角形.8. 验证：()()++=++a b c a b c .证明：利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a , b , c 表示23.-u v解：232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c10. 把△ABC 的BC 边分成五等份，设分点依次为D 1，D 2，D 3，D 4，再把各分点与A 连接，试以AB =c ，BC =a 表示向量1D A ,2D A ,3D A 和4D A .解：1115D A BA BD =-=--c a 2225D A BA BD =-=--c a 3335D A BA BD =-=--c a 444.5D A BA BD =-=--c a 11. 设向量OM 的模是4，它与投影轴的夹角是60°，求这向量在该轴上的投影. 解：设M 的投影为M '，则1Pr j cos604 2.2u OM OM =︒=⨯= 12. 一向量的终点为点B （2，-1，7），它在三坐标轴上的投影依次是4，-4和7，求这向量的起点A 的坐标.解：设此向量的起点A 的坐标A (x , y , z )，则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).13. 一向量的起点是P 1（4，0，5），终点是P 2（7，1，3），试求：（1） 12PP 在各坐标轴上的投影；（2） 12PP 的模；（3） 12PP 的方向余弦；（4） 12PP 方向的单位向量.解：（1）12Pr j 3,x x a PP ==12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP == (3) 12cos 14xa PP α== 12cos 14ya PP β==12cos 14za PP γ==(4) 12012{14PP PP===-ej . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解：R =（1-2+3，2+3-4，3-4+5）=（2，1，4）||==Rcoscoscos αβγ=== 15. 求出向量a = i +j +k, b =2i -3j +5k 和c =-2i -j +2k 的模，并分别用单位向量,,a b c e ee 来表达向量a ,b ,c .解：||==a||==b ||3==c, , 3. a b c ==a b c e16. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解：a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k在x 轴上的投影a x =13,在y 轴上分向量为7j . 17.解：设{,,}x y z a a a a =则有cos (1,1)3x a ia a i a iπ⋅====⋅ 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 4a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =± 又1,a =则2221x y z a a a ++=从而求得11{,,22a =或11{,,22- 18. 已知两点M 1（2，5，-3），M 2（3，-2，5），点M 在线段M 1M 2上，且123M M MM =，求向径OM 的坐标.解：设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为，123M M MM = 所以，11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A （0，0，12）的距离是7，OP 的方向余弦是236,,777，求点P 的坐标. 解：设P 的坐标为（x , y , z ）, 2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+ 126570cos 6,749z z γ==⇒== 又122190cos2, 749x x α==⇒== 123285cos 3, 749y y β==⇒==故点P 的坐标为P （2，3，6）或P （190285570,,494949）. 20. 已知a , b 的夹角2π3ϕ=，且3,4==b a ，计算： (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解：（1）a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b 21. 已知a =(4,-2, 4), b =(6,-3, 2),计算：（1）a ·b ; (2) (2a -3b )·(a + b )；（3）2||-a b解：（1）46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b 222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b 36238499=-⨯+=22. 已知四点A （1，-2，3），B （4，-4，-3），C （2，4，3），D （8，6，6），求向量AB 在向量CD 上的投影.解：AB ={3，-2，-6}，CD ={6，2，3}Pr j CD AB CD AB CD ⋅=4.7==- 23. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角. 解: (a +3b )·(7a -5b ) =227||1615||0+⋅-=a a b b ①(a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ②由①及②可得：222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ，所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==. 24. 设a =(-2,7,6),b =(4, -3, -8),证明：以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明：以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a －b ,且a +b ={2,4, -2}a-b ={-6,10,14}又(a +b )·(a-b )= 2×(-6)+4×10+(-2)×14=0故(a +b )⊥(a-b ).25. 已知a =3i +2j -k , b =i -j +2k ,求：(1) a ×b ; (2) 2a ×7b ;(3) 7b ×2a ; (4) a ×a .解：（1） 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .26. 已知向量a 和b 互相垂直，且||3, ||4==a b .计算：(1) |(a ＋b )×(a －b )|；(2) |(3a ＋b )×(a －2b )|.（1）|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin 242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin 842=⨯⨯⨯= 27. 求垂直于向量3i-4j-k 和2i-j +k 的单位向量，并求上述两向量夹角的正弦. 解：411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量()||3⨯==±--+⨯a b e i j k a b||sin ||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a =(2,1,－1)和b =(1,－2,1)为邻边，求其对角线夹角的正弦. 解：两对角线向量为13=+=-l a b i j ，232=-=+-l a b i j k因为12|||2610|⨯=++l l i j k12||||==l l 所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.29. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1)，点M ，N ，P 分别是AB ，BC ，CA 的中点，证明：1()4MN MP AC BC ⨯=⨯. 证明：中点M ，N ，P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P -- {2,2,2}MN =--3{1,0,}2MP =- {4,4,4}AC =--{2,0,3}BC =-22222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k故 1()4MN MP AC BC ⨯=⨯. 30.（1）解: x yz x y z ij k a b a a a b b b ⨯==-+-+-y z z y z x x z x y y x a b a b i a b a b j a b a b k （）（）（）则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅（）（）（）（）x y z xy z x y za a ab b b C C C = 若,,C a b 共面，则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=（）反之亦成立. （2）C x y z x y z xy z a a a a b b b b C C C ⨯⋅=（）a x y z x y z xy z b b b b C C C C a a a ⨯⋅=（） b xy z x y z xy zC C C C a a a a b b b ⨯⋅=（）由行列式性质可得:xy z x y z x y z x y z x y z x y z xy z x y z x y za a ab b b C C C b b b C C C a a a C C C a a a b b b ==故C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅（）（）（）31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积. 解：设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ，B ，D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+. 32.解：设四面体的底为BCD ∆，从A 点到底面BCD ∆的高为h ，则 13BCD V S h =⋅⋅，而11948222BCD S BC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅= 33. 已知三点A (2,4,1), B (3,7,5), C (4,10,9)，证：此三点共线. 证明：{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ，B ，C 三点共线.34. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直，求动点的轨迹方程. 解：设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y-1)-4(z-1)=0整理得：2x +3y-4z-1=0即为动点M 的轨迹方程.35. 求通过下列两已知点的直线方程：（1）（1，-2，1），（3，1，-1）；（2）（3，-1，0），（1，0，-3）. 解：（1）两点所确立的一个向量为s ={3-1，1+2，-1-1}={2，3，-2}故直线的标准方程为：121232x y z -+-==- 或 311232x y z --+==- （2）直线方向向量可取为s ={1-3，0+1，-3-0}={-2，1，-3}故直线的标准方程为：31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程. 解：所给直线的方向向量为12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点（0，7，17），因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为：771719x t y t z t =⎧⎪=-⎨⎪=-⎩37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程.解：所求平面与平面3x -2y +6z =11平行故n ={3,-2,6}，又过点(4,1,-2)故所求平面方程为：3(x -4)-2(y -1)+6(z +2)=0即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3)，且与连接坐标原点到点M 0的线段OM 0垂直的平面方程. 解：所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为：x -1+7(y -7)-3(z +3)=0即x +7y -3z -59=039. 设平面过点(1,2,-1)，而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍，求此平面方程.解：设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上，则有121122b b b-++= 得b =2. 故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和（1，-1，2）三点的平面方程.解：由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点，有1112121*********x y z --+----+=---+ 化简得x -3y -2z =0即为所求平面方程.41. 指出下列各平面的特殊位置，并画出其图形：(1) y =0; (2) 3x -1=0;(3) 2x-3y-6=0; (4) x–y =0;(5) 2x-3y+4z=0.解：(1) y =0表示xOz坐标面（如图7-2）(2) 3x-1=0表示垂直于x轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z轴且在x轴及y轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x–y=0表示过z轴的平面（如图7-5）(5) 2x-3y+4z=0表示过原点的平面（如图7-6）.图7-4 图7-5 图7-642. 通过两点（1，1，1，）和（2，2，2）作垂直于平面x+y-z=0的平面.解：设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点（1，1，1）在平面上，所以有D=0故平面方程为x-y=0.43. 决定参数k的值，使平面x+ky-2z=9适合下列条件：（1）经过点（5，-4，6）；（2）与平面2x-3y+z=0成π4的角.解：（1）因平面过点（5，-4，6）故有 5-4k-2×6=9得k=-4.（2）两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||4θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解：（1）n1={2,l,3}, n2={m,-6,-1}12232,18613lm lm⇒==⇒=-=--n n(2) n1={3, -5, l }, n2={1,3,2}12315320 6.l l⊥⇒⨯-⨯+⨯=⇒=n n45. 通过点（1，-1，1）作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解：设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}12203203A C A B C A B C C B ⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n n n n 又（1，－1，1）在所求平面上，故A －B +C +D =0，得D =0故所求平面方程为2033C Cx y Cz -++= 即2x -y -3z =046. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量.解：n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n 故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点： (1)11126x y z -+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解：（1）直线参数方程为1126x t y t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1故交点为（2，-3，6）.（2）直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0.故交点为（-2，1，3）.48. 求下列直线的夹角：（1）533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩；（2）2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解：（1）两直线的方向向量分别为：s 1={5, -3,3}×{3, -2,1}=533321ij k --={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直，夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程：（1）经过点（2，-3，4），且与平面3x -y +2z -4=0垂直；（2）过点（0，2，4），且与两平面x +2z =1和y -3z =2平行；（3）过点（-1，2，1），且与直线31213x y z --==-平行. 解：（1）可取直线的方向向量为 s ={3，-1，2}故过点（2，-3，4）的直线方程为234312x y z -+-==- （2）所求直线平行两已知平面，且两平面的法向量n 1与n 2不平行，故所求直线平行于两平面的交线，于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n 故过点（0，2，4）的直线方程为24231x y z --==- （3）所求直线与已知直线平行，故其方向向量可取为s ={2，-1，3}故过点（-1，2，1）的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系：（1）34273x y z ++==--和4x -2y -2z =3; （2）327x y z ==-和3x -2y +7z =8; （3）223314x y z -+-==-和x +y +z =3. 解：平行而不包含. 因为直线的方向向量为s ={-2，-7，3}平面的法向量n ={4，-2，-2}，所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0（-3，-4，0）代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量，故直线垂直于平面.(3) 直线在平面上，因为3111(4)10⨯+⨯+-⨯=,而直线上的点（2，-2，3）在平面上.51. 求过点（1，-2，1），且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程. 解：直线的方向向量为12123111-=++-ij k i j k , 取平面法向量为{1，2，3}，故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点（1，-2，3）和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解：设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数，又因为所求平面过点（1，-2，3）故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点（-1，2，0）在平面x +2y -z +1=0上的投影.解：过点（-1，2，0）作垂直于已知平面的直线，则该直线的方向向量即为已知平面的法向量，即s =n ={1，2，-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0 得23t =- 于是所求点（-1，2，0）到平面的投影就是此平面与垂线的交点522(,,)333-54. 求点（3，-1，2）到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解：过点（3，-1，2）作垂直于已知直线的平面，平面的法向量可取为直线的方向向量即11133211==-=---ij k n s j k故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点（1，2，1）到平面x +2y +2z -10=0距离.解：过点（1，2，1）作垂直于已知平面的直线，直线的方向向量为s =n ={1，2，2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333，且与点（1，2，1）的距离为1d == 即为点到平面的距离. 56. 建立以点（1，3，-2）为中心，且通过坐标原点的球面方程.解：球的半径为R ==设(x ,y ,z )为球面上任一点，则(x -1)2+(y -3)2+(z +2)2=14即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点（2，0，-3）的距离与离点（4，-6，6）的距离之比为3，求此动点的轨迹方程.解：设该动点为M (x ,y ,z )，由题意知222222(2)(0)(3) 3.(4)(6)(6)x y z x y z -+-++=-+++- 化简得：8x 2+8y 2+8z 2-68x +108y -114z +779=0即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面，并画出其图形：（1）22()()22a a x y -+=; （2）22149x y -+=; （3）22194x z +=; （4）20y z -=; （5）220x y -=; （6）220x y +=. 解：（1）母线平行于z 轴的抛物柱面，如图7-7.（2）母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8（3）母线平行于y 轴的椭圆柱面，如图7-9.（4）母线平行于x 轴的抛物柱面，如图7-10.图7-9 图7-10（5）母线平行于z 轴的两平面，如图7-11.（6）z 轴，如图7-12.图7-11 图7-12 59. 指出下列方程表示怎样的曲面，并作出图形：（1）222149y zx++=; （2）22369436x y z+-=;（3）222149y zx--=; （4）2221149y zx+-=;（5）22209zx y+-=.解：（1）半轴分别为1，2，3的椭球面，如图7-13.(2) 顶点在（0，0，-9）的椭圆抛物面，如图7-14.图7-13 图7-14(3) 以x轴为中心轴的双叶双曲面，如图7-15.(4) 单叶双曲面，如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面，其中心轴是z 轴，如图7-17.图7-1760. 作出下列曲面所围成的立体的图形： (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1. 解：（1）（2）（3）（4）分别如图7-18，7-19，7-20，7-21所示.图7-18 图7-19图7-20 图7-21 61. 求下列曲面和直线的交点：(1) 222181369x y z ++=与342364x y z --+==-;(2) 22211694x y z +-=与2434x y z +==-. 解：（1）直线的参数方程为334624x t y t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1.得交点坐标为（3，4，-2），（6，-2，2）. (2) 直线的参数方程为4324x ty tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为（4，-3，2）.62. 设有一圆，它的中心在z 轴上，半径为3，且位于距离xOy 平面5个单位的平面上，试建立这个圆的方程.解：设（x ，y ，z ）为圆上任一点，依题意有2295x y z ⎧+=⎨=±⎩即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状，并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解：（1）截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.（2）截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线. 解：以曲线为准线，母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解：以曲线为准线，母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=. 故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集并分别指出它们的聚点集和边界：(1) {(x , y )|x ≠0}; (2) {(x , y )|1≤x 2+y 2<4}; (3) {(x , y )|y <x 2};(4) {(x , y )|(x -1)2+y 2≤1}∪{(x , y )|(x +1)2+y 2≤1}. 解：(1)开集、无界集，聚点集：R 2，边界：{(x , y )|x =0}. (2)既非开集又非闭集，有界集, 聚点集：{(x , y )|1≤x 2+y 2≤4}，边界：{(x , y )|x 2+y 2=1}∪{(x , y )| x 2+y 2=4}. (3)开集、区域、无界集，聚点集：{(x , y )|y ≤x 2}，边界：{(x , y )| y =x 2}.(4)闭集、有界集，聚点集即是其本身，边界：{(x , y )|(x -1)2+y 2=1}∪{(x , y )|(x +1)2+y 2=1}. 2. 已知f (x , y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解：222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u vf u v w u w+=+,试求(,,).f x y x y xy +-解：f ( x + y , x -y , x y ) =( x + y )xy+(x y )x +y +x -y=(x + y )xy +(x y )2x.4. 求下列各函数的定义域：2(1)ln(21);z y x =-+ (2)z=(3)z = (4)u =(5)z =(6)ln()z y x =-+(7)u =解：2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>> 2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限：10y x y →→ 22001(2)lim;x y x y →→+00x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解：(1)原式0ln 2.=(2)原式=+∞. (3)原式=001.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x yx y ++→→→→++==+6. 判断下列函数在原点O (0，0)处是否连续：33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解：(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y ++++≤=≤+⋅++++ 又00lim()0x y y x →→+=，且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0，0)点，则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0，0)点，则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0，0)处不连续.7. 指出下列函数在向外间断：(1) f (x ,y )=233x y x y -+;(2) f (x ,y )=2222y xy x+-;(3) f (x ,y )=ln(1－x 2－y 2);(4)f (x ,y )=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解：(1)因为当y =-x 时，函数无定义，所以函数在直线y =-x 上的所有点处间断，而在其余点处均连续.(2)因为当y 2=2x 时，函数无定义，所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时，函数无定义，所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.120lim (,)lime x x y x xf x y x-→→=→==∞. 故(0，0)是函数的间断点，而在其余各点处均连续. 8. 求下列函数的偏导数：(1)z = x 2y +2xy;(2)s =22u v uv+;(3)z = x(4)z = lntan x y; (5)z = (1+xy )y; (6)u = z xy; (7)u = arctan(x -y )z; (8)y zu x =.解：(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+ 2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+(4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+ []ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z z u z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz z u z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .y yz z yy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y =+，求证：3u uxy u x y∂∂+=∂∂. 证明： 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++.由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=，求证：222z z xy z x y∂∂+=∂∂. 证明： 11112211e e x y x y z x x x ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1121ex y z y y⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y ) = x +(y，求f x (x ,1) .解：1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点（2，4，5）处的切线与正向x 轴所成的倾角.解：(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数： (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x; (3)z = y x ;(4)z = 2ex y+.解：(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ，，由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭， 2222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x yz x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x , y , z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解：2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15.设z = x ln ( x y )，求32z x y ∂∂∂及32zx y ∂∂∂.解：ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分：(1)22exy z +=;(2)z =(3)zy u x =;(4)y zu x =.解：(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )xy xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴ 223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂1ln yz u x x y z∂=⋅⋅∂ ln y z u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz zz y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分： (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解：(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量，近似计算：(1) 3·2;(3).解：(1)设f (x ,y )=x 3·y 2，则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =,d y =，则3·2=f ,≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×+2×12×]=1.(2)设f (x ,y ,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f (x ,y )=x y,则d f (x ,y )=yx y -1d x +x yln x d y ，取x =2,y =1,d x =,d y =,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a =10cm ，另一边长b =24cm, 当a 边增加4mm ，而b 边缩小1mm 时，求对角线长的变化.解：设矩形对角线长为l ，则d d ).l l x x y y ==+当x =10,y =24,d x =,d y =时，d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm. 20.解：因为圆锥体的体积为21.3V r h π=⋅ 0030,0.1,60,0.5r r h h ====- 而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h ====-时， 2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯- 230()cm =-21.解：设水池的长宽深分别为,,x y z 则有:V xyz = 精确值为：50.242 2.850.22 3.6 2.80.2V =⨯⨯+⨯⨯⨯+⨯⨯⨯ 313.632()m = 近似值为:V dV zx y xy z ≈=+0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯ 314.8()m =22. 求下列复合函数的偏导数或全导数：(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,zv∂∂； (2)z ＝arc tanx y , x ＝u ＋v ,y ＝u －v , 求z u ∂∂,z v∂∂； (3)ln(e e )xyu =+, y ＝x 3, 求d d ux; (4) u ＝x 2＋y 2＋z 2, x ＝e cos tt , y ＝e sin tt , z ＝e t, 求d d ut. 解：（1）222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++(2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y xx x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数，试求下列函数的一阶偏导数： (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解：(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数，证明： .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-，其中f (u )为可导函数，验证： 211z z zx x y y y∂∂+=∂∂. 证明：∵ 2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数，求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解：2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,z f x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂由对称性知，22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数，求下列函数的二阶偏导数： (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解：(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂ 2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂。

高等数学复旦大学出版第三版下册课后答案习题全

习题七1. 在空间直角坐标系中，定出下列各点的位置：A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解：点A在第Ⅰ卦限；点B在第Ⅱ卦限；点C在第Ⅷ卦限；点D在xOy面上；点E在yOz面上；点F在x轴上.2. xOy坐标面上的点的坐标有什么特点？yOz面上的呢？zOx面上的呢？答: 在xOy面上的点，z=0;在yOz面上的点，x=0;在zOx面上的点，y=0.3. x轴上的点的坐标有什么特点？y轴上的点呢？z轴上的点呢？答：x轴上的点，y=z=0;y轴上的点，x=z=0;z轴上的点，x=y=0.4. 求下列各对点之间的距离：（1）（0，0，0），（2，3，4）；（2）（0，0，0），（2，-3，-4）；（3）（-2，3，-4），（1，0，3）；（4）（4，-2，3），（-2，1，3）.解：（1）s=(2) s==(3) s==(4) s==5. 求点（4，-3，5）到坐标原点和各坐标轴间的距离.解：点(4，-3，5)到x轴，y轴，z轴的垂足分别为（4，0，0），（0，-3，0），（0，0，5）.故2s=xs==ys==5zs==.6. 在z轴上，求与两点A（-4，1，7）和B（3，5，-2）等距离的点. 解：设此点为M（0，0，z），则222222(4)1(7)35(2)z z-++-=++--解得149 z=即所求点为M（0，0，149）.1731747. 试证：以三点A （4，1，9），B （10，-1，6），C （2，4，3）为顶点的三角形是等腰直角三角形.证明：因为|AB |=|AC |=7.且有 |AC |2+|AB |2=49+49=98=|BC |2. 故△ABC 为等腰直角三角形. 8. 验证：()()++=++a b c a b c . 证明：利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a , b , c 表示23.-u v 解：232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c10. 把△ABC 的BC 边分成五等份，设分点依次为D 1，D 2，D 3，D 4，再把各分点与A 连接，试以AB =c ，BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解：1115D A BA BD =-=--c a 2225D A BA BD =-=--c a3335D A BA BD =-=--c a444.5D A BA BD =-=--c a11. 设向量OM 的模是4，它与投影轴的夹角是60°，求这向量在该轴上的投影. 解：设M 的投影为M '，则1Pr j cos 604 2.2u OM OM =︒=⨯= 12. 一向量的终点为点B （2，-1，7），它在三坐标轴上的投影依次是4，-4和7，求这向量的起点A 的坐标.解：设此向量的起点A 的坐标A (x , y , z )，则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).17513. 一向量的起点是P 1（4，0，5），终点是P 2（7，1，3），试求：（1） 12PP 在各坐标轴上的投影；（2） 12PP 的模；（3） 12PP 的方向余弦；（4） 12PP 方向的单位向量. 解：（1）12Pr j 3,x x a PP == 12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP ==(3) 12cos 14x a PP α==12cos 14y a PP β==12cos 14z a PP γ==.(4) 12012{14PP PP ===+e j . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解：R =（1-2+3，2+3-4，3-4+5）=（2，1，4）||==Rcos cos cos αβγ=== 15. 求出向量a = i +j +k , b =2i -3j +5k 和c=-2i -j +2k 的模，并分别用单位向量,,a b c e e e 来表达向量a, b , c .解：||==a ||==b||3==c, , 3. a b c ===a b c e17616. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解：a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k 在x 轴上的投影a x =13,在y 轴上分向量为7j . 17.解：设{,,}x y z a a a a =则有 c o s (1,1)3x a i a a i a i π⋅====⋅ 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a =求得12y a =± 又1,a =则2221x y z a a a ++= 从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M 1（2，5，-3），M 2（3，-2，5），点M 在线段M 1M 2上，且123M M MM =，求向径OM 的坐标. 解：设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为，123M M MM =所以，11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}.17719. 已知点P 到点A （0，0，12）的距离是7，OP 的方向余弦是236,,777，求点P 的坐标.解：设P 的坐标为（x , y , z ）, 2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+126570cos 6, 749z z γ=⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒==故点P 的坐标为P （2，3，6）或P （190285570,,494949）. 20. 已知a , b 的夹角2π3ϕ=，且3,4==b a ，计算： (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解：（1）a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算：（1）a ·b ; (2) (2a -3b )·(a + b )；（3）2||-a b 解：（1）46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b (3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b36238499=-⨯+=22. 已知四点A （1，-2，3），B （4，-4，-3），C （2，4，3），D （8，6，6），求向量AB 在178向量CD 上的投影.解：AB ={3，-2，-6}，CD ={6，2，3}Pr j CD AB CD AB CD⋅=4.7==-23. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角. 解: (a +3b )·(7a -5b ) =227||1615||0+⋅-=a a b b ① (a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ②由①及②可得：222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ，所以1cos ||||2θ⋅==a b a b , 故1πarccos23θ==. 24. 设a =(-2,7,6),b =(4, -3, -8),证明：以a 与b 为邻边的平行四边形的两条对角线互相垂直. 证明：以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a －b ,且 a +b ={2,4, -2} a -b ={-6,10,14}又(a +b )·(a -b )= 2×(-6)+4×10+(-2)×14=0 故(a +b )⊥(a -b ).25. 已知a =3i +2j -k , b =i -j +2k ,求： (1) a ×b ; (2) 2a ×7b ; (3) 7b ×2a ; (4) a ×a . 解：（1） 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直，且||3, ||4==a b .计算： (1) |(a ＋b )×(a －b )|；(2) |(3a ＋b )×(a －2b )|.（1）|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b179π2||||sin242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin842=⨯⨯⨯= 27. 求垂直于向量3i -4j -k 和2i -j +k 的单位向量，并求上述两向量夹角的正弦. 解：411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a =(2,1,－1)和b =(1,－2,1)为邻边，求其对角线夹角的正弦.解：两对角线向量为13=+=-l a b i j ，232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k12||||l l 所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1)，点M ，N ，P 分别是AB ，BC ，CA 的中点，证明：1()4MN MP AC BC ⨯=⨯. 证明：中点M ，N ，P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P --{2,2,2}MN =--3{1,0,}2MP =-{4,4,4}AC =-- {2,0,3}BC =-18022222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k故 1()4MN MP AC BC ⨯=⨯. 30.（1）解: xy z xyzij k a b a a a b b b ⨯==-+-+-y z z y z x x z x y y x a b a b i a b a b j a b a b k （）（）（）则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅（）（）（）（）xy z xy z xyza a ab b b C C C = 若 ,,C a b 共面，则有a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=（）反之亦成立. （2） C xy z xy z x y za a a ab b b b C C C ⨯⋅=（） a xy z xy z x y z b b b b C C C C a a a ⨯⋅=（） b xy z xy z xy z C C C C a a a a b b b ⨯⋅=（）由行列式性质可得:xy z x y z x y z xy z x y z xy z xyzxyzxyza a ab b b C C C b b b C C C a a a C C C a a a b b b == 故C a a b b C C a ⨯⋅=⨯⋅=⨯⋅（）（）（）18131. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积. 解：设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ，B ，D 三点所确定三角形的面积为111|||542|22S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积12S =+32.解：设四面体的底为BCD ∆，从A 点到底面BCD ∆的高为h ，则 13BCDV S h =⋅⋅，而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h ==故1942323V =⋅⋅= 33. 已知三点A (2,4,1), B (3,7,5), C (4,10,9)，证：此三点共线. 证明：{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ，B ，C 三点共线.34. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直，求动点的轨迹方程. 解：设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y -1)-4(z -1)=0整理得：2x +3y -4z -1=0即为动点M 的轨迹方程. 35. 求通过下列两已知点的直线方程：（1）（1，-2，1），（3，1，-1）；（2）（3，-1，0），（1，0，-3）.182解：（1）两点所确立的一个向量为s ={3-1，1+2，-1-1}={2，3，-2}故直线的标准方程为：121232x y z -+-==- 或 311232x y z --+==- （2）直线方向向量可取为s ={1-3，0+1，-3-0}={-2，1，-3}故直线的标准方程为：31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解：所给直线的方向向量为 12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点（0，7，17），因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为：771719x t y t z t =⎧⎪=-⎨⎪=-⎩37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程. 解：所求平面与平面3x -2y +6z =11平行故n ={3,-2,6}，又过点(4,1,-2)故所求平面方程为：3(x -4)-2(y -1)+6(z +2)=0 即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3)，且与连接坐标原点到点M 0的线段OM 0垂直的平面方程. 解：所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为：x -1+7(y -7)-3(z +3)=0 即x +7y -3z -59=039. 设平面过点(1,2,-1)，而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍，求此平面方程.解：设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上，则有121122b b b-++=183得b =2.故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和（1，-1，2）三点的平面方程. 解：由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点，有1112121210111121x y z --+----+=---+化简得x -3y -2z =0即为所求平面方程.41. 指出下列各平面的特殊位置，并画出其图形： (1) y =0; (2) 3x -1=0; (3) 2x -3y -6=0; (4) x – y =0; (5) 2x -3y +4z =0.解：(1) y =0表示xOz 坐标面（如图7-2） (2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x -3y -6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x =3和y =-2的平面.(如图7-4) (4) x –y =0表示过z 轴的平面（如图7-5）(5) 2x -3y +4z =0表示过原点的平面（如图7-6）.图7-4 图7-5 图7-6 42. 通过两点（1，1，1，）和（2，2，2）作垂直于平面x +y -z =0的平面. 解：设平面方程为Ax +By +Cz +D =0 则其法向量为n ={A ,B ,C }已知平面法向量为n 1={1,1,-1} 过已知两点的向量l ={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点（1，1，1）在平面上，所以有D=0故平面方程为x-y=0.43. 决定参数k的值，使平面x+ky-2z=9适合下列条件：（1）经过点（5，-4，6）；（2）与平面2x-3y+z=0成π4的角.解：（1）因平面过点（5，-4，6）故有5-4k-2×6=9得k=-4.（2）两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解：（1）n1={2,l,3}, n2={m,-6,-1}12232,18613lm lm⇒==⇒=-=--n n(2) n1={3, -5, l }, n2={1,3,2}12315320 6.l l⊥⇒⨯-⨯+⨯=⇒=n n45. 通过点（1，-1，1）作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解：设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}12203203A CA B CA B C CB⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n nn n又（1，－1，1）在所求平面上，故A－B+C+D=0，得D=0故所求平面方程为233CCx y Cz-++=即2x-y-3z=018418546. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量. 解：n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点：(1)11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解：（1）直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为（2，-3，6）.（2）直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为（-2，1，3）. 48. 求下列直线的夹角：（1）533903210x y z x y z -+-=⎧⎨-+-=⎩ 和2223038180x y z x y z +-+=⎧⎨++-=⎩；（2）2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解：（1）两直线的方向向量分别为：s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}186由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直，夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程：（1）经过点（2，-3，4），且与平面3x -y +2z -4=0垂直；（2）过点（0，2，4），且与两平面x +2z =1和y -3z =2平行；（3）过点（-1，2，1），且与直线31213x y z --==-平行. 解：（1）可取直线的方向向量为 s ={3，-1，2}故过点（2，-3，4）的直线方程为234312x y z -+-==- （2）所求直线平行两已知平面，且两平面的法向量n 1与n 2不平行，故所求直线平行于两平面的交线，于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n故过点（0，2，4）的直线方程为24231x y z --==- （3）所求直线与已知直线平行，故其方向向量可取为 s ={2，-1，3}故过点（-1，2，1）的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系：（1）34273x y z++==--和4x -2y -2z =3; （2）327x y z==-和3x -2y +7z =8;187（3）223314x y z -+-==-和x +y +z =3. 解：平行而不包含. 因为直线的方向向量为s ={-2，-7，3}平面的法向量n ={4，-2，-2}，所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0（-3，-4，0）代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量，故直线垂直于平面.(3) 直线在平面上，因为3111(4)10⨯+⨯+-⨯=,而直线上的点（2，-2，3）在平面上. 51. 求过点（1，-2，1），且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程.解：直线的方向向量为12123111-=++-ij ki j k , 取平面法向量为{1，2，3}，故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点（1，-2，3）和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解：设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数，又因为所求平面过点（1，-2，3）故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点（-1，2，0）在平面x +2y -z +1=0上的投影.解：过点（-1，2，0）作垂直于已知平面的直线，则该直线的方向向量即为已知平面的法向量，即s =n ={1，2，-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0188得23t =-于是所求点（-1，2，0）到平面的投影就是此平面与垂线的交点522(,,)333-54. 求点（3，-1，2）到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解：过点（3，-1，2）作垂直于已知直线的平面，平面的法向量可取为直线的方向向量即11133211==-=---ij kn s j k故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为d = 55. 求点（1，2，1）到平面x +2y +2z -10=0距离.解：过点（1，2，1）作垂直于已知平面的直线，直线的方向向量为s =n ={1，2，2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333，且与点（1，2，1）的距离为1d ==即为点到平面的距离.56. 建立以点（1，3，-2）为中心，且通过坐标原点的球面方程.解：球的半径为R =设(x ,y ,z )为球面上任一点，则(x -1)2+(y -3)2+(z +2)2=14 即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点（2，0，-3）的距离与离点（4，-6，6）的距离之比为3，求此动点的轨迹方程.189解：设该动点为M (x ,y ,z )3.=化简得：8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面，并画出其图形：（1）22()()22a a x y -+=; （2）22149x y -+=; （3）22194x z +=; （4）20y z -=; （5）220x y -=; （6）220x y +=. 解：（1）母线平行于z 轴的抛物柱面，如图7-7. （2）母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 （3）母线平行于y 轴的椭圆柱面，如图7-9. （4）母线平行于x 轴的抛物柱面，如图7-10.图7-9 图7-10（5）母线平行于z 轴的两平面，如图7-11. （6）z 轴，如图7-12.图7-11 图7-1219059. 指出下列方程表示怎样的曲面，并作出图形：（1）222149y z x ++=; （2）22369436x y z +-=; （3）222149y z x --=; （4）2221149y z x +-=; （5）22209z x y +-=. 解：（1）半轴分别为1，2，3的椭球面，如图7-13. (2) 顶点在（0，0，-9）的椭圆抛物面，如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面，如图7-15. (4) 单叶双曲面，如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面，其中心轴是z 轴，如图7-17.图7-1760. 作出下列曲面所围成的立体的图形： (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1.191解：（1）（2）（3）（4）分别如图7-18，7-19，7-20，7-21所示.图7-18 图7-19图7-20 图7-21 61. 求下列曲面和直线的交点：(1) 222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-.解：（1）直线的参数方程为334624x ty t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1. 得交点坐标为（3，4，-2），（6，-2，2）. (2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为（4，-3，2）.62. 设有一圆，它的中心在z 轴上，半径为3，且位于距离xOy 平面5个单位的平面上，试建立这个圆的方程.192解：设（x ，y ，z ）为圆上任一点，依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状，并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解：（1）截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.（2）截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线. 解：以曲线为准线，母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解：以曲线为准线，母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=.193故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集？并分别指出它们的聚点集和边界： (1) {(x , y )|x ≠0};(2) {(x , y )|1≤x 2+y 2<4}; (3) {(x , y )|y <x 2};(4) {(x , y )|(x -1)2+y 2≤1}∪{(x , y )|(x +1)2+y 2≤1}.解：(1)开集、无界集，聚点集：R 2，边界：{(x , y )|x =0}. (2)既非开集又非闭集，有界集, 聚点集：{(x , y )|1≤x 2+y 2≤4}，边界：{(x , y )|x 2+y 2=1}∪{(x , y )| x 2+y 2=4}. (3)开集、区域、无界集，聚点集：{(x , y )|y ≤x 2}，边界：{(x , y )| y =x 2}.(4)闭集、有界集，聚点集即是其本身，边界：{(x , y )|(x -1)2+y 2=1}∪{(x , y )|(x +1)2+y 2=1}. 2. 已知f (x , y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解：222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +- 解：f ( x + y , x -y , x y ) =( x + y )xy +(x y )x +y +x -y =(x + y )xy +(x y )2x . 4. 求下列各函数的定义域：2(1)ln(21);z y x =-+(2)z =(3)z =(4)u =(5)z =(6)ln()z y x =-194(7)u =解：2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>>2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限：10(1)y x y →→ 22001(2)lim;x y x y →→+00(3)x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解：(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+1956. 判断下列函数在原点O (0，0)处是否连续：33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解：(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=，且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0，0)点，则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0，0)点，则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0，0)处不连续.7. 指出下列函数在向外间断：(1) f (x ,y )=233x y x y -+; (2) f (x ,y )=2222y xy x +-;(3) f (x ,y )=ln(1－x 2－y 2);(4)f (x ,y )=22e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩196解：(1)因为当y =-x 时，函数无定义，所以函数在直线y =-x 上的所有点处间断，而在其余点处均连续.(2)因为当y 2=2x 时，函数无定义，所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时，函数无定义，所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0，0)是函数的间断点，而在其余各点处均连续. 8. 求下列函数的偏导数：(1)z = x 2y +2xy;(2)s =22u v uv+;(3)z = x;(4)z = lntan x y; (5)z = (1+xy )y ; (6)u = z xy ;(7)u = arctan(x -y )z; (8)y zu x =.解：(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+ 2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+197[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz zu z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .y yz z yy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y=+，求证：3u u x y u x y ∂∂+=∂∂. 证明： 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+.10.设11ex y z ⎛⎫+- ⎪⎝⎭=，求证：222z z xy z x y∂∂+=∂∂. 证明： 11112211e e x y x y z x x x ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1981121e x y z y y ⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y ) = x +(y，求f x (x ,1) .解：1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点（2，4，5）处的切线与正向x 轴所成的倾角.解：(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数： (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x; (3)z = y x ;(4)z = 2ex y+.解：(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ，，由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭，1992222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x , y , z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解：2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15315.设z = x ln ( x y )，求32z x y ∂∂∂及32zx y ∂∂∂.解：ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分： (1)22e xy z +=;(2)z =(3)zyu x =;(4)yzu x =.解：(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )xy x y x y z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴ 223/2d (d d ).()x z y x x y x y =--+ (3)∵11,ln z z z y y z u uy x x x zy x y --∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂154ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分： (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解：(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265e e e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量，近似计算： (1) (1.02)3·(0.97)2;;(3)(1.97)1.05.解：(1)设f (x ,y )=x 3·y 2，则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03，则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则155d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f (x ,y )=x y ,则d f (x ,y )=yx y -1d x +x y ln x d y ，取x =2,y =1,d x =-0.03,d y =0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a =10cm ，另一边长b =24cm, 当a 边增加4mm ，而b 边缩小1mm 时，求对角线长的变化.解：设矩形对角线长为l ，则d d ).l l x x y y ==+当x =10,y =24,d x =0.4,d y =-0.1时，d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20.解：因为圆锥体的体积为21.3V r h π=⋅0030,0.1,60,0.5r r h h ====- 而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h ====-时， 2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯- 230()cm =-21.解：设水池的长宽深分别为,,x y z 则有:V xyz =精确值为：50.242 2.850.22 3.62V =⨯⨯+⨯⨯⨯+⨯⨯⨯ 313.632()m = 近似值为:156V dV zx y xy z ≈=+0.4,0.4,0.2x y z ===430.4530.454V d V ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数：(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,zv∂∂； (2)z ＝arc tanxy, x ＝u ＋v ,y ＝u －v , 求z u ∂∂,z v ∂∂；(3)ln(e e )xyu =+, y ＝x 3, 求d d u x; (4) u ＝x 2＋y 2＋z 2, x ＝e cos tt , y ＝e sin tt , z ＝e t, 求d d ut. 解：（1）222(2)cos (2)sin 3sin cos (cos sin )z z x z yxy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uy x y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 2222222111(1)11.x z z x z yy v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y xx x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.15723. 设f 具有一阶连续偏导数，试求下列函数的一阶偏导数： (1)22(,e );xy u f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解：(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数，证明： .z zxy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+15825. 设22()yz f x y =-，其中f (u )为可导函数，验证： 211z z zx x y y y∂∂+=∂∂. 证明：∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数，求22222,,.z z z x x y y∂∂∂∂∂∂∂解：2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知，22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数，求下列函数的二阶偏导数： (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解：(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂1592212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证：利用变量替换1,3x y x y ξη=-=-,可将方程。

复旦大学出版社,高等数学,第四版,教材习题答案详细解析

高等数学上（复旦大学出版社，第四版）教材习题答案第四章，一元函数积分学。

第三节不定积分与原函数求法，习题4-3，答案5.0 用分部积分，求下列不定积分。

东风冷雪1.0=-=--=--=-+-=-+++⎰⎰⎰⎰⎰222222x sinxdxx dcosx (x cosx 2xcosxdx)(x cosx 2xdsinx)x cosx 2xsinx 2sinxdx x cosx 2xsinx 2cosx c2.0------=-=--=--+⎰⎰⎰x x x x x x xe dx xde (xe e dx)xe e c3.0==-=-+⎰⎰⎰22222111ln xdx (x ln x x *dx)22x11x ln x x c 24x ln xdx4.0==-++-=-+=--+=-+++⎰⎰⎰⎰23332232322322x arctanxdx111x arctanxdx x arctanx 3331x 11x(1x )x x arctanx dx 331x 1111x arctanx (x ln |1x |)3322111x arctanx x ln |1x |c 3665.0=+=-=-+⎰2arccosxdxx *arccosx x *arccosx x *arccosx c6.0=-=-=--=+-=+-+⎰⎰⎰⎰⎰222222x tan xdx1x(sec x 1)dx xdtanx x 21dcos x 1x tanx tanxdx x x tanx x 2cos x 21x tanx ln |cos x |x c 2 7.0------------==-=--=-=-+⎰⎰⎰⎰⎰⎰x x x x x x x x x x x x e cos xdxe dsinx e sinx e dcos xe sinx e cos x cos xe dx2e cos xdx e sinx e cos x1e cos xdx e (sinx cos x)c 28.0==-=--=-++⎰⎰⎰⎰xsinxcosxdx11xsin2xdx xdcos2x 24111(xcos2x cos2xdx)xcos2x sin2x c 4489.0=-=--=-+=--+=---=---+=-++++⎰⎰⎰⎰⎰⎰⎰323233223232232232(lnx)dxx 1ln x 3ln x ln x 1ln xd ()(3ln xd )x x x x xln x 3ln x 6lnx ln x 3ln x 1dx 6lnxd x x x x x xln x 3ln x 6lnx 6dx x x x x 1(ln x 3ln x 6lnx 6)c x10.0===-=--=++-=+++=+=++⎰⎰⎰⎰⎰222222222atant,a sec tdtant a sec t tant a tan tsec tdta (sec t tant (sec t 1)sec tdta (sec t tant ln |sec t tant |sec tdtant)1a (sec t tant ln |sec t tant |)21x x a (*ln ||2a a a 1ln |x 2+|c6.0 求下列不定积分；1.0++-+=+++-+-+-+-+++=+==-=+=-++-+-+=-+++⎰⎰⎰222222222222x 1dx(x 1)(x 1)x 1a b c x 1x 1(x 1)(x 1)(x 1)a(x 1)b(x 1)c(x 2x 1)x 111a ,b 1,c 2211x 1122dx ()dx x 1x 1(x 1)(x 1)(x 1)11ln |x 1|c 2x 12.0++=+++-+-+-++++===-=-==-++-+-+--=+--+=+--++-+=+⎰⎰⎰⎰⎰3222222223dx x 13a bx c x 1(x 1)(x x 1)x x 1a(x x 1)(bx c)(x 1)3a 1,b 1,c 23dx 1x 2dx ()dx x 1(x 1)(x x 1)x x 112x 13ln |x 1|2x x 1131ln |x 1|ln |x x 1|1322(x )24ln |+2c3.0 （这道题，有些坑人，没有意思）+--+-+-++-=----=++++---=+++-+-+-=++-+-+-=-+++-==-=-⎰⎰⎰⎰5423332332233323222x x 8x (x x)x(x x)x x x x 8dx dx x x x x 123x x 33(x x 1)dx x x x x 23x 1113x x x ln |x x |dx 323x(x 1)(x 1)23x a b c 3x(x 1)(x 1)x x 1x 123x a(x 1)b(x x)c(x x)323101a ,b ,c 33-=---+-+=---++++-+---+=---++--=+++--⎰⎰⎰543323323x 12310133dx ()x(x 1)(x 1)3x x 1x 1231013ln |x |ln |x 1|ln |x 1|3331(ln |x |ln |x 1|ln |x 1|23ln |x |10ln |x 1|13ln |x 1|31ln(24ln |x |9ln |x 1|12ln |x 1|)3x x 8dxx x 11x x x 8ln |x |3ln |x 1|32-++4ln |x 1|c 4.0+==++⎰⎰263332x dxx 11dx 1arctanx c 33(x )15.0+-==-=--=-++⎰⎰⎰⎰222sinx dx1sinx sinx(1sinx)dx (tanxsecx tan x)dx cos xsecx (sec x 1)dx secx tanx x c6.0++==+--+==+-++++++-==-=-=-+⎰⎰⎰⎰⎰222222222cot x dxsinx cos x 1x 2t tan ,dx dt 21t 1t 21t 1t 22t *dt **dt 2t 22t 2t 1t 1t 1t 11t 1t 11t 1111()dt (1)dt lnt t 2t 2t 221x 1x ln |tan |tan c 22227.0=====+=++⎰⎰⎰2sect 2sec t tant dt 2sectdt sect tant 2ln |sect tant |2ln ||c8.0==-===-=-+=-+++=-+++⎰⎰⎰(1t,2tdt12(1)2t2ln|1t|2ln|1t11tx4ln|1|c记住口诀，反，对，幂，指，三。

高等数学习题11答案(复旦大学出版社)

261 习题十一3．计算下列对坐标的曲线积分：(1)()22d -⎰L x y x ，其中L 是抛物线y =x 2上从点(0,0)到点(2,4)的一段弧； (2)d Lxy x ⎰ 其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行)；(6)()322d 3d d x x zy y x y z Γ++-⎰，其中Γ是从点(3,2,1)到点(0,0,0)的一段直线；解：(1)L ：y =x 2，x 从0变到2，()()22222435001156d d 3515L x y x x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰(2)如图11-1所示，L =L 1+L 2．其中L 1的参数方程为图11-1cos 0πsin x a a tt y a t =+⎧≤≤⎨=⎩L 2的方程为y =0(0≤x ≤2a )故 ()()()()()12π200π320ππ322003d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2L L L a xy x xy x xy x a a t a a t t xa t t ta t t t t a =+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰ (6)直线Γ的参数方程是32=⎧⎪=⎨⎪=⎩x ty t z tt 从1→0．262故()()32203221031041d 3d d 27334292d 87d 1874874x x zy y x y zt t t tt tt t t Γ++-⎡⎤=⋅+⋅⋅+-⋅⎣⎦==⋅=-⎰⎰⎰ 7．应用格林公式计算下列积分：(1)()()d d 24356+-++-⎰ x y x y x y Γ，其中L 为三顶点分别为(0,0)，(3,0)和(3,2)的三角形正向边界；解：(1)L 所围区域D 如图11-4所示，P =2x -y +4，Q =3x +5y -6，3Q x∂=∂，1P y ∂=-∂，由格林公式得 ()()d d 24356d d 4d d 4d d 1432212LD D Dx y x y x y Q P x y x y x y x y +-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰8．利用曲线积分，求下列曲线所围成的图形的面积：(1)星形线x = a cos 3t ，y = a sin 3t ；解：(1)()()()()()2π3202π2π242222002π202π202π202d sin 3cos d sin 33sin cos d sin 2sin d 43d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416312π+d cos 2cos61623π8L A y x a t a t t t a t t t a t t t a t t t a t t t t t a t t t a =-=-⋅-==⋅=--=--+⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰ 9．证明下列曲线积分与路径无关，并计算积分值：(2)()()()()3,423221,2d d 663x y xy y x y xy +--⎰； (3)()()1,221,1d d x y x x y -⎰沿在右半平面的路径；263 证：(2) P =6xy 2-y 3，Q =6x 2y -3xy 2．显然P ，Q 在xOy 面内有连续偏导数，且2123P xy y y∂=-∂，2123Q xy y x ∂=-∂，有P Q y x ∂∂=∂∂，所以积分与路径无关．取L 为从(1,2)→(1,4)→(3,4)的折线，则()()()()()()[]3,423221,2432214323212d d 663d d 63966434864236x y xy y x y xy y x y y x y y x x +--=+--=+⎡⎤--⎣⎦=⎰⎰⎰ (3)2y P x =，1Q x =-，P ，Q 在右半平面内有连续偏导数，且21P y x ∂=∂，21Q x x∂=∂，在右半平面内恒有P Q y x ∂∂=∂∂，故在右半平面内积分与路径无关．取L 为从(1,1)到(1,2)的直线段，则()()()21,2211,1d d d 11x y x x y y -==--⎰⎰ 10．验证下列P (x , y )d x +Q (x , y )d y 在整个xOy 面内是某一函数u (x , y )的全微分，并求这样的一个函数u (x , y )：(2)2xy d x +x 2d y ；(3)(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y ；(4)(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y ．解：(2)P =2xy ,Q =x 2, 2P Q x y x∂∂==∂∂，故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分．()()(),20,020022d d ,0d d x y x yu xy x x y x y x x y x y=+=+=⎰⎰⎰ (3)P =3x 2y +8xy 2，Q =x 3+8x 2y +12y e y ，2316∂∂=+=∂∂P Q x xy y x，故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y 是某个定义在整个xOy 面内函数u (x ,y )的全微分，()()()()()(),22320,03200322d ,38812e 0d d 812e 412e 12e 12x y y x y y y y u x x y x y x y x x y y x y x x y y x y x y y =++++=+++=++-+⎰⎰⎰。

高等数学复旦大学出版第三版课后答案习题十一

261习题十一1．设L 为xOy 面内直线x =a 上的一段，证明：(),d 0L P x y x =⎰其中P (x , y )在L 上连续．证：设L 是直线x =a 上由(a ,b 1)到(a ,b 2)这一段，则 L ：12x a b t b y t=⎧≤≤⎨=⎩，始点参数为t =b 1，终点参数为t =b 2故()()()221d ,d d 0d 0d b b Lb ba P x y x P a,t t P a,t t t ⎛⎫=⋅=⋅= ⎪⎝⎭⎰⎰⎰2．设L 为xOy 面内x 轴上从点(a ,0)到点(b ,0)的一段直线，证明：()(),d 0d b LaP x y x P x,x =⎰⎰，其中P (x , y )在L 上连续．证：L ：0x x a x b y =⎧≤≤⎨=⎩，起点参数为x =a ，终点参数为x =b ．故()(),d ,0d b LaP x y x P x x =⎰⎰3．计算下列对坐标的曲线积分：(1)()22d -⎰Lx y x ，其中L 是抛物线y =x 2上从点(0,0)到点(2,4)的一段弧；(2)d Lxy x ⎰其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行)；(3)d d Ly x x y +⎰，其中L 为圆周x =R cos t ，y =R sin t 上对应t 从0到π2的一段弧；(4)()()22d d Lx y x x y yx y+--+⎰，其中L 为圆周x 2+y 2=a 2(按逆时针方向绕行)；(5)2d d d x x z y y z Γ+-⎰，其中Γ为曲线x =kθ，y =a cos θ，z =a sin θ上对应θ从0到π的一段弧；(6)()322d 3d d x x zy y x y z Γ++-⎰，其中Γ是从点(3,2,1)到点(0,0,0)的一段直线；(7)d d d Lx y y z -+⎰ ，其中Γ为有向闭拆线ABCA ，这里A ，B ，C 依次为点（1,0,0），(0,1,0)，(0,0,1)；(8)()()222d 2d Lx xy x y xy y -+-⎰，其中L 是抛物线y =x 2上从点(-1,1)到点(1,1)的段弧．解：(1)L ：y =x 2，x 从0变到2，262()()22222435001156d d 3515Lxyx x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰(2)如图11-1所示，L =L 1+L 2．其中L 1的参数方程为图11-1cos 0πsin x a a tt y a t=+⎧≤≤⎨=⎩L 2的方程为y =0(0≤x ≤2a ) 故()()()()()12π200π32ππ3223d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2LL L a xy x xy x xy xa a t a a t t xat t ta t t t ta=+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰(3)()π20π220π220d d sin sin cos cos d cos 2d 1sin 220Ly x x y R t R t R tR t tRt tR t +=-+⎡⎤⎣⎦=⎡⎤=⎢⎥⎣⎦=⎰⎰⎰(4)圆周的参数方程为：x =a cos t ，y =a sin t ，t :0→2π．故()()()()()()222π202π22d d 1cos sin sin cos sin cos d 1d 2πLx y x x y yx ya t a t a t a t a t a t ta a ta+--+=+---⎡⎤⎣⎦=-=-⎰⎰⎰263(5)()()()2π220π322π3320332d d d sin sin cos cos d d 131ππ3x x z y y zkk a a a a kak a k a Γθθθθθθθθθθ+-=⋅+⋅--=-⎡⎤=-⎢⎥⎣⎦=-⎰⎰⎰(6)直线Γ的参数方程是32=⎧⎪=⎨⎪=⎩x ty t z t t 从1→0．故()()3223221031041d 3d d 27334292d 87d 1874874xx zy y x y zt t t t t t t t tΓ++-⎡⎤=⋅+⋅⋅+-⋅⎣⎦==⋅=-⎰⎰⎰(7)AB BC CA Γ=++(如图11-2所示)图11-21:0y xAB z =-⎧⎨=⎩，x 从0→1 ()01d d d 112ABx y y z dx -+=--=-⎡⎤⎣⎦⎰⎰．:1x BC y z =⎧⎨=-⎩，z 从0→1264()()()101120d d d 112d 12232B Cx y y z z dzz zz z -+=--+-⎡⎤⎣⎦=-⎡⎤=-⎢⎥⎣⎦=⎰⎰⎰:1y C A z x =⎧⎨=-⎩，x 从0→1 []1d d d 1001CAx y y z dx -+=-+=⎰⎰．故()()d d d d d d 312122LAB BC C Ax y y z x y y z-+=++-+=-++=⎰⎰⎰⎰(8)()()()()()221224211235412d 2d 222d 224d 1415Lxxy x y xy yx x xxx xx x xx x xx---+-⎡⎤=-⋅+-⋅⋅⎣⎦=-+-=-⎰⎰⎰4．计算()()d d L x y x y x y ++-⎰，其中L 是(1)抛物线y 2=x 上从点(1,1)到点(4,2)的一段弧；(2)从点(1,1)到点(4,2)的直线段；(3)先沿直线从(1,1)到点(1,2)，然后再沿直线到点(4,2)的折线； (4)曲线x = 2t 2+t +1, y = t 2+1上从点(1,1)到点(4,2)的一段弧．解：(1)L ：2x y y y⎧=⎨=⎩，y ：1→2，故()()()()()2221232124321d d 21d 2d 111232343Lx y x y x yy y y y y y yy y yy y y ++-⎡⎤=+⋅+-⋅⎣⎦=++⎡⎤=++⎢⎥⎣⎦=⎰⎰⎰(2)从(1,1)到(4,2)的直线段方程为x =3y -2，y ：1→2265故()()()()()2121221d d 32332d 104d 5411Lx y x y x yy y y y y y yy y ++-=-+⋅+-+⎡⎤⎣⎦=-⎡⎤=-⎣⎦=⎰⎰⎰(3)设从点(1,1) 到点(1,2)的线段为L 1，从点(1,2)到(4,2)的线段为L 2，则L =L 1+L 2．且 L 1：1x y y=⎧⎨=⎩，y ：1→2；L 2：2x x y =⎧⎨=⎩，x ：1→4；故()()()()()12122211d d 101d 1d 212L x y x y x yy y y y y y y ++-=+⋅+-⎡⎤⎣⎦⎡⎤=-=-⎢⎥⎣⎦=⎰⎰⎰()()()()()()24144211d d 220d 12d 22272L x y x y x yx x x x x x ++-=++-⋅⎡⎤⎣⎦⎡⎤=+=+⎢⎥⎣⎦=⎰⎰⎰从而()()()()()12d d d d 1271422LL L x y x y x yx y x y x y++-=+++-=+=⎰⎰⎰(4)易得起点(1,1)对应的参数t 1=0，终点(4,2)对应的参数t 2=1，故()()()()()()12213214320d d 32412d 10592d 10592432323Lx y x y x yt t t t t t ttt t tt t t t ++-⎡⎤=++++--⋅⎣⎦=+++⎡⎤=+++⎢⎥⎣⎦=⎰⎰⎰5．设质点受力作用，力的反方向指向原点，大小与质点离原点的距离成正比，若质点由(a ,0)沿椭圆移动到B (0,b )，求力所做的功．266解：依题意知 F =kxi +kyj ，且L ：cos sin x a t y a t=⎧⎨=⎩，t ：0→π2()()()()π2022π20π22222d d cos sin sin cos d sin 2d 2cos 2222LW kx x ky yka t t kb t b t tk b at tk b at k b a=+=-+⋅⎡⎤⎣⎦-=--⎡⎤=⎢⎥⎣⎦-=⎰⎰⎰(其中k 为比例系数)6．计算对坐标的曲线积分：(1)d Lxyz z ⎰，Γ为x 2+y 2+z 2=1与y =z 相交的圆，方向按曲线依次经过第Ⅰ、Ⅱ、Ⅶ、Ⅷ封限；(2)()()()222222d d d Ly z x z x y x y z -+-+-⎰，Γ为x 2+y 2+z 2=1在第Ⅰ封限部分的边界曲线，方向按曲线依次经过xOy 平面部分，yOz 平面部分和zOx 平面部分．解:(1)Γ：2221x y z y z ⎧++=⎨=⎩即2221x z y z ⎧+=⎨=⎩其参数方程为：cos 22x ty tz t =⎧⎪⎪⎪=⎨⎪⎪=⎪⎩ t ：0→2π 故：2π02π2202π202π0d cos d 222sin cos d 4sin 2d 161cos 4d 16216xyz z t t t t tt t t t t ttΓ===-==⎰⎰(2)如图11-3所示．267图11-3Γ=Γ1+Γ2+Γ3．Γ1：cos sin 0x ty t z =⎧⎪=⎨⎪=⎩t ：0→π2，故()()()()()1222222π2220π3320π320d d d sin sin cos cos d sin cos d 2sin d 24233yzx zxy xyz t t t t t t t tt tΓ-+-+-⎡⎤=--⋅⎣⎦=-+=-=-⋅=-⎰⎰⎰⎰又根据轮换对称性知()()()()()()1222222222222d d d 3d d d 4334yzx zxy xyzyzx zxy xyzΓΓ-+-+-=-+-+-⎛⎫=⨯- ⎪⎝⎭=-⎰⎰7．应用格林公式计算下列积分：(1)()()d d 24356+-++-⎰ x y x y x y Γ，其中L 为三顶点分别为(0,0)，(3,0)和(3,2)的三角形正向边界；(2)()()222d d cos 2sin e sin 2e x x L x y x y x xy x y x x y ++--⎰ ，其中L 为正向星形线()2223330x ya a +=>；(3)()()3222d d 2cos 12sin 3+--+⎰Lx y xy y x y x x y ，其中L 为抛物线2x =πy 2上由点(0,0)到(π2,1)的一段弧；(4)()()22d d sin Lx y x y x y --+⎰，L是圆周y =上由点(0,0)到(1,1)的一段弧；(5)()()d d e sin e cos x x L x y y my y m +--⎰，其中m 为常数，L 为由点(a ,0)到(0,0)经过圆x 2+y 2=ax上半部分的路线（a 为正数）．268图11-4解：(1)L 所围区域D 如图11-4所示，P =2x -y +4， Q =3x +5y -6，3Q x∂=∂，1P y∂=-∂，由格林公式得()()d d 24356d d 4d d 4d d 1432212LD DDx yx y x y Q P x y x y x yx y +-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰(2)P =x 2y cos x +2xy sin x -y 2e x ，Q =x 2sin x -2y e x，则2cos 2sin 2exP x x x x y y∂=+-∂，2cos 2sin 2e xQ x x x x y x∂=+-∂．从而P Q yx∂∂=∂∂，由格林公式得．()()222d d cos 2sin esin 2e d d 0++--∂∂⎛⎫-=⎪∂∂⎝⎭=⎰⎰⎰ xx LD x yxy x xy x y x x y Q Px y xy(3)如图11-5所示，记O A ，AB ， BO 围成的区域为D ．（其中 BO=-L ）图11-5P =2xy 3-y 2cos x ，Q =1-2y sin x +3x 2y 2262cos P xy y xy∂=-∂，262cos Q xy y xx∂=-∂由格林公式有：269d d d d 0L OA ABD Q P P x Q y x y x y -++∂∂⎛⎫-+== ⎪∂∂⎝⎭⎰⎰⎰ 故π21220012202d d d d d d d d ππd d 12sin 3243d 12π4π4++=+=+++⎛⎫=+-+⋅⋅ ⎪⎝⎭⎛⎫=-+ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰LO A ABO A ABP x Q y P x Q yP x Q y P x Q yO x y y y y y y(4)L 、AB 、BO 及D 如图11-6所示．图11-6由格林公式有d d d d ++∂∂⎛⎫-+=- ⎪∂∂⎝⎭⎰⎰⎰L AB BOD Q P P x Q y x y x y而P =x 2-y ，Q =-(x +sin 2y )．1∂=-∂P y，1∂=-∂Q x，即，0∂∂-=∂∂Q P xy于是()d d d d 0+++++=+=⎰⎰⎰⎰LABBOL AB BOP x Q y P x Q y从而()()()()()()()2222221122011300d d d d sin d d d d sin sin d d 1sin 131sin 232471sin 264LL BA O BP x Q y x y xy x y x y x yx y x y xy x y y x xy x y y +=--+=-+--+-+=-++⎡⎤⎡⎤=+-+⎢⎥⎢⎥⎣⎦⎣⎦=-+⎰⎰⎰⎰⎰⎰(5)L ，OA 如图11-7所示．图11-7270P =e xsin y -my ， Q =e xcos y -m ，e cos xP y my∂=-∂，e cos xQ yx∂=∂由格林公式得：22d d d d d d d d 1π22π8L O AD DDQ P P x Q y x y x y m x ym x y a m m a +∂∂⎛⎫-+=⎪∂∂⎝⎭==⎛⎫=⋅⋅ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰ 于是：()()[]220202πd d d d 8πd 0esin 00e cos 08π0d 8π8+=-+=-+⋅⋅-⋅⋅-=-=⎰⎰⎰⎰LO A axxa m a P x Q y P x Q ym a xm m m a xm a8．利用曲线积分，求下列曲线所围成的图形的面积： (1)星形线x = a cos 3t ，y = a sin 3t ； (2)双纽线r 2 = a 2cos2θ； (3)圆x 2+y 2 = 2ax ．解：(1)()()()()()2π322π2π2422222π202π22π202d sin 3cos d sin 33sin cos d sin 2sin d 43d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416312π+d cos 2cos 61623π8LA y x a t a t tt a t t t at t ta tt t a tt t t t at t t a=-=-⋅-==⋅=--=--+⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰(2)利用极坐标与直角坐标的关系x =r cos θ，y =r sin θ得cos x a θ=sin y a θ=从而x d y -y d x =a 2cos2θd θ．于是面积为：271[]π24π4π24π4212d d 2cos 2d sin 22LA x y y x a aaθθθ--=⋅-===⎰⎰(3)圆x 2+y 2=2ax 的参数方程为cos 02πsin x a a y a θθθ=+⎧≤≤⎨=⎩故()()[]()2π22π021d d 21d a+acos sin 2d 1cos 2πcos sin LA x y y xa a aa a θθθθθθθ=-=-=+=⋅-⎰⎰⎰9．证明下列曲线积分与路径无关，并计算积分值： (1)()()()()1,10,0d d x y x y --⎰；(2)()()()()3,423221,2d d 663x y xy yx y xy +--⎰；(3)()()1,221,1d d xy x x y-⎰沿在右半平面的路径；(4)()()6,81,0⎰沿不通过原点的路径；证：(1)P =x -y ，Q =y -x ．显然P ，Q 在xOy 面内有连续偏导数，且1P Q yx∂∂==-∂∂，故积分与路径无关．取L 为从(0,0)到(1,1)的直线段，则L 的方程为：y =x ，x ：0→1．于是()()()()11,100,00d 0d d xx y x y ==--⎰⎰(2) P =6xy 2-y 3，Q =6x 2y -3xy 2．显然P ，Q 在xOy 面内有连续偏导数，且2123P xy yy∂=-∂，2123Q xy yx∂=-∂，有P Q yx∂∂=∂∂，所以积分与路径无关．取L 为从(1,2)→(1,4)→(3,4)的折线，则()()()()()()[]3,423221,2432214323212d d 663d d 63966434864236x y xy yx y xy y xy y x y y x x +--=+--=+⎡⎤--⎣⎦=⎰⎰⎰272(3)2y P x=，1Q x=-，P ，Q 在右半平面内有连续偏导数，且21P yx∂=∂，21Q xx∂=∂，在右半平面内恒有P Q yx∂∂=∂∂，故在右半平面内积分与路径无关．取L 为从(1,1)到(1,2)的直线段，则()()()21,2211,1d d d 11xy x x yy -==--⎰⎰(4) P =，Q =，且P Q yx∂∂==∂∂在除原点外恒成立，故曲线积分在不含原点的区域内与路径无关，取L 为从(1,0)→(6,0)→(6,8)的折线，则()()686,811,081529x y=+⎡=+⎣=⎰⎰⎰10．验证下列P (x , y )d x +Q (x , y )d y 在整个xOy 面内是某一函数u (x , y )的全微分，并求这样的一个函数u (x , y )： (1)(x +2y )d x +(2x +y )d y ； (2)2xy d x +x 2d y ；(3)(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y)d y ； (4)(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y ．解：证：(1)P =x +2y ，Q =2x +y ．2P Q yx∂∂==∂∂，所以(x +2y )d x +(2x +y )d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分．()()()()()(),0,0002222d d ,22d d 2222222x y xyyu x y x y x y x y x x yx y xy xy xyxy =+++=++⎡⎤=++⎢⎥⎣⎦=++⎰⎰⎰(2)P =2xy ,Q =x 2, 2P Q x yx∂∂==∂∂，故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分．()()(),20,020022d d ,0d d x y xy u xy x x y x y x x yx y=+=+=⎰⎰⎰(3)P =3x 2y +8xy 2，Q =x 3+8x 2y +12y e y，2316∂∂=+=∂∂P Q x xy yx，故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y)d y273是某个定义在整个xOy 面内函数u (x ,y )的全微分，()()()()()(),22320,03200322d ,38812e 0d d 812e412e 12e 12x y y xyyyyu x x y x y x y x x y y x yxx y y x y x y y =++++=+++=++-+⎰⎰⎰(4)P =2x cos y +y 2cos x ，Q =2y sin x -x 2sin y ，2sin 2cos P x y y xy∂=-+∂，2cos 2sin Q y x x yx∂=-∂，有P Q yx∂∂=∂∂，故(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y 是某一个定义在整个xOy 面内的函数u (x ,y )的全微分，()()()()()(),220,020022d d ,2cos cos 2sin sin 2d d 2sin sin sin cos x y xy u x y x y x y y x y x x y x x yy x xy y x x y=++-=+-=+⎰⎰⎰11．证明：22d d x x y y x y++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分，并求出这样的一个二元函数．证：22x P x y=+，22y Q x y=+，显然G 是单连通的，P 和Q 在G 内具有一阶连续偏导数，并且．()2222∂∂-==∂∂+P Q xyyxxy，(x ,y )∈G因此22d d x x y y x y++在开区域G 内是某个二元函数u (x ,y )的全微分．由()()22222222d d 11ln 22d x y x x y y dx y x yx y++⎡⎤==+⎢⎥++⎣⎦知()()221ln ,2u x y x y =+．12．设在半平面x >0中有力()3k F xi yj r=-+构成力场，其中k为常数，r =，证明：在此力场中场力所做的功与所取的路径无关．证：场力沿路径L 所作的功为．33d d Lk k W x x y yrr=--⎰其中3kx P r=-，3ky Q r=-，则P 、Q 在单连通区域x >0内具有一阶连续偏导数，并且53(0)P kxy Q x yrx∂∂==>∂∂因此以上积分与路径无关，即力场中场力所做的功与路径无关．13．当Σ为xOy 面内的一个闭区域时，曲面积分()d d ,,R x y x y z ∑⎰⎰与二重积分有什么关系？274解：因为Σ：z =0，在xOy 面上的投影区域就是Σ故()()d d d d ,,,,0R x y R x y x y z x y ∑∑=±⎰⎰⎰⎰当Σ取的是上侧时为正号，Σ取的是下侧时为负号． 14．计算下列对坐标的曲面积分：(1)22d d x y z x y ∑⎰⎰，其中Σ是球面x 2+y 2+z 2=R 2的下半部分的下侧；(2)d d d d d d z x y x y z y z x ∑++⎰⎰，其中Σ是柱面x 2+y 2=1被平面z =0及z =3所截得的在第Ⅰ封限内的部分的前侧；(3)()()()d d 2d d d d ,,,,,,f x y z f y z x f z x y x y z x y z x y z ∑+++++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎰⎰，其中f (x , y , z )为连续函数，Σ是平面x -y +z =1在第Ⅳ封限部分的上侧；(4)d d d d d d xz x y xy y z yz z x ∑++⎰⎰ ，其中Σ是平面x =0, y =0, z =0, x +y +z =1所围成的空间区域的整个边界曲面的外侧；(5)()()()d d d d d d y z z x x y y z x y z x ∑++---⎰⎰ ，其中Σ为曲面z =z = h (h >0)所围成的立体的整个边界曲面，取外侧为正向；(6)()()22d d d d d d +++-⎰⎰ y y z x z x x y y xz x z ∑，其中Σ为x =y =z =0，x =y =z =a 所围成的正方体表面，取外侧为正向；解：(1)Σ：z =Σ在xOy 面上的投影区域D xy 为：x 2+y 2≤R 2．((()()()()()()22222π4222π222222202π2200354*******d d d d d cos sin d 1sin 2d 81d d 1cos421612422π1635xyD RRRxy z x y x yx yr r rR R r r R R RR r R R R r R r ∑θθθθθθθ=-=-=-⎡⎤+--⎣⎦⎡=----⎣=-⋅-+--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰()72220772π105RR r R⎡⎤-⎢⎥⎣⎦=(2)Σ如图11-8所示，Σ在xOy 面的投影为一段弧，图11-8275故d d 0z x y ∑=⎰⎰，Σ在yOz 面上的投影D yz ={(y ,z )|0≤y ≤1，0≤z ≤3}，此时Σ可表示为：x =(y ,z )∈D yz ，故30d d d d 3yzD x y z y z z yy∑===⎰⎰⎰⎰⎰⎰⎰Σ在xOz 面上的投影为D xz ={(x ,z )|0≤x ≤1，0≤z ≤3}，此时Σ可表示为：y =(x ,z )∈D xz ，故30d d d d 3xzD y z x z xz xx∑===⎰⎰⎰⎰⎰⎰⎰因此：d d d d d d 236π643π2z x y x y z y z xx x∑++⎡⎤=⎢⎥⎣⎦==⋅=⎰⎰⎰⎰(3)Σ如图11-9所示，平面x -y +z =1上侧的法向量为n ={1,-1,1}，n 的方向余弦为cos α=cos β=，cos γ=，图11-9由两类曲面积分之间的联系可得：276()()()()()()()()()d d 2d d d d ,,,,,,cos d (2)cos d ()d d cos cos d d (2)d d ()d d cos cos (2)()d d d d 1d d xyD f x y z f y z x fz x yx y z x y z x y z s f y s f z x yf x x y f y x y f z x yf x f y f z x y f x x yx y z x y x y x y ∑∑∑∑∑αβαβγγ+++++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=+++++=+++++=-+++⎡⎤+⎣⎦=-+=+-⎡⎤--⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰d d 111212xyD x y==⨯⨯=⎰⎰⎰⎰(4)如图11-10所示：图11-10Σ=Σ1+Σ2+Σ3+Σ4．其方程分别为Σ1：z =0，Σ2：x =0，Σ3：y =0，Σ4：x +y +z =1，故()()12344110d d 000d d d d 11d d 124xyD x xz x yxz x yx x yx y x x y x y ∑∑∑∑∑∑-=+++=+++=--==--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰由积分变元的轮换对称性可知．1d d dzd 24xy y z yz x ∑∑==⎰⎰⎰⎰因此．d d dyd d d 113248xz x y xy z yz z x∑++=⨯=⎰⎰(5)记Σ所围成的立体为Ω，由高斯公式有：277()()()()()()d d d d d d d d d 0d d d 0y z z x x yy z x y z x y z x y z x x y z x y z x y z ∑ΩΩ++---∂∂⎛⎫--∂-=++ ⎪∂∂∂⎝⎭==⎰⎰⎰⎰⎰⎰⎰⎰(6)记Σ所围的立方体为Ω，P =y (x -z )，Q =x 2，R =y 2+xz ．由高斯公式有()()()()()220000020204d d d d d d d d d d d d d d d d d d 2d 2a aa a a aa a y y z x z x x yy xz x z P Q Rx y z x y z x y z x y x y zx y x a yx y y a x xy a a x ax a∑ΩΩ+++-∂∂∂⎛⎫++=⎪∂∂∂⎝⎭=+=+=+⎡⎤=+⎢⎥⎣⎦⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰15.设某流体的流速V =(k ,y ,0)，求单位时间内从球面x 2+y 2+z 2=4的内部流过球面的流量. 解：设球体为Ω，球面为Σ，则流量3d d d d d d d 432d d d π2π33k y z y z x P Qx y z x y x y z ∑ΩΩΦ=+∂∂⎛⎫+= ⎪∂∂⎝⎭==⋅=⎰⎰⎰⎰⎰⎰⎰⎰ （由高斯公式）16．利用高斯公式，计算下列曲面积分：(1)222d d d d d d x y z y z x z x y ∑++⎰⎰ ，其中Σ为平面x =0，y =0，z =0，x =a ，y =a ，z =a 所围成的立体的表面的外侧；(2)333d d d d d d x y z y z x z x y ∑++⎰⎰ ，其中Σ为球面x 2+y 2+z 2= a 2的外侧；(3)()()2232d d d d d d 2xz y z z x x y x y z xy y z ∑++-+⎰⎰ ，其中Σ为上半球体x 2+y 2≤a 2，0z ≤≤(4)d d d d d d x y z y z x z x y ∑++⎰⎰ ，其中Σ是界于z = 0和z = 3之间的圆柱体x 2+y 2 = 9的整个表面的外侧；278解：(1)由高斯公式()()2224d d d d d d d 2222d 6d 6d d d 3aaaxy z y z x z x yvx y z vx y z x vx x y za∑ΩΩΩ++=++=++==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ 对称性(2)由高斯公式：()3332222ππ45d d d d d d d 3d 3d d sin d 12π5axy z y z x z x yP QR v x y z vx y zr ra∑ΩΩθϕϕ++∂∂∂⎛⎫++=⎪∂∂∂⎝⎭=++==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(3)由高斯公式得()()()2232222π2π2220024π05d d d d d d 2d d d d sin d 2πsin d d 2π5aaxzy z z x x yx y z xy y z P QR v x y z vz x yr r rr ra∑ΩΩθϕϕϕϕ++-+∂∂∂⎛⎫++= ⎪∂∂∂⎝⎭=++=⋅==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(4)由高斯公式得：2d d d d d d d 3d 3π3381πx y z y z x z x yP Q R v x y z v∑ΩΩ++∂∂∂⎛⎫++=⎪∂∂∂⎝⎭==⋅⋅⋅=⎰⎰⎰⎰⎰⎰⎰⎰17.利用斯托克斯公式，计算下列曲线积分： (1)d d d y x z y x z Γ++⎰ ，其中Γ为圆周x 2+y 2+z 2 = a 2，x +y +z = 0，若从x 轴的正向看去，这圆周是取逆时针的方向； (2)()()()222222d d d x y z y z x y z x Γ++---⎰，其中Γ是用平面32x y z ++=截立方体：2790≤x ≤1，0≤y ≤1，0≤z ≤1的表面所得的截痕，若从Ox 轴的正向看去，取逆时针方向；(3)23d d d y x xz y yz z Γ++⎰，其中Γ是圆周x 2+y 2= 2z ，z =2，若从z 轴正向看去，这圆周是取逆时针方向；(4)22d 3d d +-⎰ y x x y z z Γ，其中Γ是圆周x 2+y 2+z 2 = 9，z =0，若从z 轴正向看去，这圆周是取逆时针方向．解：(1)取Σ为平面x +y +z =0被Γ所围成部分的上侧，Σ的面积为πa 2（大圆面积），Σ的单位法向量为{}111cos ,cos ,cos n αβγ==．由斯托克斯公式22d d d cos cos cos d d 3y x z y x zR Q Q P P Rs y z x y z x ss aaΓ∑∑∑αβγ++⎡∂∂∂∂⎤⎛⎫⎛⎫∂∂⎛⎫--=++- ⎪⎢⎥ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦=-=-=-=⎰⎰⎰⎰⎰(2)记为Σ为平面32x y z ++=被Γ所围成部分的上侧，可求得Σ的面积为4长为2的正六边形）；Σ的单位法向量为{}cos ,cos ,cos αβγ==n ．由斯托克斯公式()()()(()()()222222d d d2222d22d3d2432492x y zy z x yz xy z x y sz xsx y zsΓ∑∑∑++---⎡+----=--⎢⎣=-++=-=-⋅=-⎰⎰⎰⎰⎰⎰⎰(3)取Σ：z=2，D xy：x2+y2≤4的上侧，由斯托克斯公式得：()()()2223d d dd d0d d d d3d d35d d5π220π-+=++--+=-+=-=-⨯⨯=-⎰⎰⎰⎰⎰⎰⎰xyDy x xz y yz zy z z x x yzz xx yzx yΓ∑∑(4)圆周x2+y2+z2=9，z=0实际就是xOy面上的圆x2+y2=9，z=0，取Σ：z=0，D xy：x2+y2≤9由斯托克斯公式得：()()()222d3d dd d d d d d000032d dd dπ39π+-=++---===⋅=⎰⎰⎰⎰⎰⎰⎰xyDy x x y z zy z z x x yx yx yΓ∑∑18．把对坐标的曲线积分()()d d,,LP x Q yx y x y+⎰化成对弧长的曲线积分，其中L为：(1)在xOy面内沿直线从点(0,0)到点(1,1)；(2)沿抛物线y = x2从点(0,0)到点(1,1)；(3)沿上半圆周x2+y2 = 2x从点(0,0)到点(1,1)．解：(1)L的方向余弦πcos cos cos42αβ===，280281故()()d d ,,d ,,LLP x Q y x y x y P x Q x y x y s++=⎰⎰(2)曲线y =x 2上点(x ,y )处的切向量T={1,2x }．其方向余弦为cosα=cos β=故()()d d ,,d 2,,LLP x Q y x y x y P x xQ x y x y s++=⎰⎰(3)上半圆周上任一点处的切向量为1x-⎧⎨⎩其方向余弦为cos α=cos 1x β=-故()()()()()d d ,,d ,,1LLP x Q yx y x y s Q x y x y x +⎤=+-⎦⎰⎰19．设Γ为曲线x = t ，y = t 2，z = t 3上相应于t 从0变到1的曲线弧，把对坐标的曲线积分d d d P x Q y R z Γ++⎰化成对弧长的曲线积分．解：由x =t ，y =t 2，z =t 3得d x =d t ，d y =2t d t =2x d t ，d z =3t 2dt =3y d t ，d s t =．故d 1cos d d cos d d cos d x s y s z sαβγ======因而d d d P x Q x R x s ΓΓ++=⎰⎰20．把对坐标的曲面积分()()()d d d d d d ,,,,,,P y z Q z x R x y x y z x y z x y z ∑++⎰⎰化成对面积的曲面积分，其中：282(1) Σ是平面326x y ++=在第Ⅰ封限的部分的上侧； (2) Σ是抛物面z = 8-(x 2+y 2)在xOy 面上方的部分的上侧．解：(1)平面Σ：326x y ++=上侧的法向量为n ={3，2，，单位向量为n 0={35，25，5}，即方向余弦为3cos 5α=，2cos 5β=，cos 5γ=．因此：()()()()d d d d d d ,,,,,,d cos cos cos 32d 555P y z Q z x R x y x y z x y z x y z sP Q R s P Q R ∑∑∑αβγ++=++⎛⎫=++⎪⎝⎭⎰⎰⎰⎰⎰⎰(2)Σ：F (x ,y ,z )=z +x 2+y 2-8=0，Σ上侧的法向量n ={ F x ，F y ，F z }={ 2x ，2y ，1}其方向余弦：cos α=，cos β=，cos γ=故()()()()d d d d d d ,,,,,,d cos cos cos P y z Q z x R x y x y z x y z x y z sP Q R s∑∑∑αβγ++=++=⎰⎰⎰⎰⎰⎰。

高等数学复旦大学出版社课后习题答案

高等数学复旦大学出版第三版下册课后答案习题全

高等数学下册黄立宏廖基定著复旦大学出版社第十章课后答案

高等数学复旦大学出版社习题答案五

高等数学上_复旦大学出版_习题五答案

高等数学复旦大学出版第三版上册课后答案习题全 PDF 版本适合手机

高等数学复旦大学出版第三版上册课后答案习题全

高等数学(经管类)下、林伟初郭安学主编、复旦大学出版社、课后习题答案

高等数学复旦大学出版第三版课后答案

高等数学习题08答案(复旦大学出版社)

高等数学复旦大学出版第三版下册课后答案习题全

高等数学复旦大学出版第三版下册课后答案习题全

复旦大学出版社,高等数学,第四版,教材习题答案详细解析

高等数学习题11答案(复旦大学出版社)

高等数学复旦大学出版第三版课后答案习题十一

最新版高等数学课后习题答案(复旦大学出版社)(李开复编)

最新版高等数学课后习题标准答案(复旦大学出版社)(李开复编)

高等数学 复旦大学出版社 课后习题答案

高等数学复旦大学出版第三版下册课后答案习题全

高等数学下册黄立宏廖基定著复旦大学出版社第十章课后答案

高等数学复旦大学出版社习题答案五

高等数学上_复旦大学出版_习题五答案

高等数学复旦大学出版第三版上册课后答案习题全 PDF 版本适合手机

高等数学复旦大学出版第三版上册课后答案习题全

高等数学(经管类)下、林伟初 郭安学主编、复旦大学出版社、课后习题答案

高等数学复旦大学出版第三版课后答案

高等数学习题08答案(复旦大学出版社)

高等数学复旦大学出版第三版下册课后答案习题全

高等数学复旦大学出版第三版下册课后答案习题全

复旦大学出版社,高等数学,第四版,教材习题答案详细解析

高等数学习题11答案(复旦大学出版社)

高等数学复旦大学出版第三版课后答案习题十一

最新版高等数学课后习题答案(复旦大学出版社)(李开复编)

最新版高等数学课后习题标准答案(复旦大学出版社)(李开复编)

高等数学复旦大学出版社课后习题答案

高等数学(经管类)下、林伟初郭安学主编、复旦大学出版社、课后习题答案