本科生图形学试卷(此卷以算法为主)
本科计算机图形学试卷

XXXXXXX 大学20XX ,20XX 年级(本科)《计算机网络与远程医疗》期末考试试卷(A 卷)姓 名: 学 号: 班 级:考试时间: 补(重)考:(是、否) 题号一 二 三 四 五 六 七 八 总分 核分人 得分 ----------------------------------------说明:本试卷总计100分,全试卷共 页,完成答卷时间80分钟。
----------------------------------------一、名词解释(本大题共10题,每题3分,共 30分)1、ACM SIGGRAPH2、基于图像的绘制3、非真实感绘制4、光线跟踪5、图形处理器6、裁剪7、 反走样 8、 区域采样9、 插值,拟合 10、Bezier 曲线二、简答题(本大题共 5 题,每题 6 分,共 30分)1、请列出八种以上计算机图形学的应用。
医学领域中图形学的应用在哪些方面? 真实的三维物体如何输入,并存储进计算机,?2、三维观察的流水线是什么,每一次转换后的坐标是什么坐标?3、直线的扫描转换中Bresenham 算法的思想? 椭圆的扫面转换算法的思想和重要步骤?4、多边形扫描转化的区域填充算法的思想和重要步骤是怎样的?Cohen-Sutherland 裁剪算法是怎样的思想?5. 消除隐藏面的Z-Buffer 算法的思想,优缺点是什么?三、解答题(本大题共 4 题,每题 10 分,共 40 分)1、已知P1(0,0), P2 (1,3),P3(4,3), P4(6,1),P1,P4是曲线端点,P2,P3 决定曲线走向。
用 Bezier 曲线的递推(de Casteljau)算法,和几何作图法求得3次Bazier 曲线(n=3),分割比率t=3/4的曲线上一点的坐标。
(画出图来)。
2、Phone 光照模型是哪几部分组成的,公式是什么,不足是什么,用什么算法如何解决,写出解决算法的步骤?3.对于任意轴的三维旋转可以由七个变换复合而成,写出公式,并解释每一个步骤。
专升本《计算机图形学》-试卷-答案

专升本《计算机图形学》一、(共57题,共150分)1。
下列设备中属于图形输出设备的是( )①鼠标②LCD ③键盘④LED ⑤打印机⑥扫描仪⑦绘图仪⑧触摸屏(2分)A.①③⑥⑧ B。
②④⑤⑦ C。
②⑤⑥⑦ D.④⑥⑦⑧标准答案:B2。
用正负法画圆,如果圆心在原点(0,0)处,初始点(0,R),顺时针生成圆,若当前点Pi在圆外,则下一点Pi+1向左走一步,递推公式为( )。
(2分)A.B。
C。
D.。
标准答案:D3。
在三维空间中点P(3, 5, 4)绕z轴旋转180o后的坐标为:( ) (2分)A。
(3, 4, 5) B。
(-5,—3, 4) C.(5, 3, 4) D。
(4, 4, 4)。
标准答案:B4. 4.在三维几何实体的表示法中,()表示法的结果难以实现绘图输出. (2分)A。
CSG法 B。
八叉树表示法C。
扫描表示法 D.对称数据结构法标准答案:A5。
在种子填充算法中所提到的四向连通区域算法,( )填充八向连通区。
(2分)A。
可以 B。
不一定。
标准答案:B6. 下列()是用实型量计算,且每一步需对Y进行四舍五入。
(第一象限内,0£k£1的直线) (2分)A。
DDA算法 B.Bresenham算法C。
中点画线算法 D。
DDA算法和Bresenham算法。
标准答案:A7。
在齐次坐标中,最后一维坐标H称为( )因子。
(2分)A.比例B.旋转C.反射D.斜切。
标准答案:A8。
线模型的数据结构简单且易于实现,只要给出所有顶点坐标及线段与其顶点的关系即可。
(2分)A.颜色 B。
角度 C.平面 D.顶点坐标标准答案:D9. 参数曲线的表示有代数形式()和两种。
(2分)A。
几何形式 B.分数 C。
阵列 D.固定形式。
标准答案:A10. 多边形填充时,下述哪个论述是错误的?( ) (2分)A。
多边形被两条扫描线分割成许多梯形,梯形的底边在扫描线上,腰在多边形的边上,并且相间排列;B.多边形与某扫描线相交得到偶数个交点,这些交点间构成的线段分别在多边形内.外,并且相间排列;C.在判断点是否在多边形内时,一般通过在多边形外找一点,然后根据该线段与多边形的交点数目为偶数即可认为在多边形内部,若为奇数则在多边形外部,而且不需考虑任何特殊情况;D.边的连贯性告诉我们,多边形的某条边与当前扫描线相交时,很可能与下一条扫描线相交;。
计算机图形学练习题
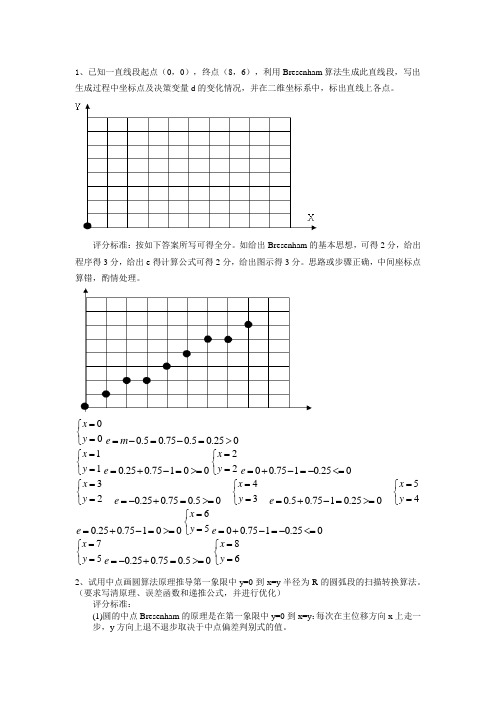
1、已知一直线段起点(0,0),终点(8,6),利用Bresenham 算法生成此直线段,写出生成过程中坐标点及决策变量d 的变化情况,并在二维坐标系中,标出直线上各点。
评分标准:按如下答案所写可得全分。
如给出Bresenham 的基本思想,可得2分,给出程序得3分,给出e 得计算公式可得2分,给出图示得3分。
思路或步骤正确,中间座标点算错,酌情处理。
00x y =⎧⎨=⎩0.50.750.50.250e m =-=-=> 11x y =⎧⎨=⎩0.250.75100e =+-=>=22x y =⎧⎨=⎩00.7510.250e =+-=-<= 32x y =⎧⎨=⎩0.250.750.50e =-+=>=43x y =⎧⎨=⎩0.50.7510.250e =+-=>=54x y =⎧⎨=⎩0.250.75100e =+-=>=65x y =⎧⎨=⎩00.7510.250e =+-=-<= 75x y =⎧⎨=⎩0.250.750.50e =-+=>=86x y =⎧⎨=⎩2、试用中点画圆算法原理推导第一象限中y=0到x=y 半径为R 的圆弧段的扫描转换算法。
(要求写清原理、误差函数和递推公式,并进行优化)评分标准:(1)圆的中点Bresenham 的原理是在第一象限中y=0到x=y :每次在主位移方向x 上走一步,y 方向上退不退步取决于中点偏差判别式的值。
(2)偏差判别式:222)5.0()1()5.0,1(),(R y x y x F y x F d i i i i M M --++=-+==y 方向的变化情况:⎩⎨⎧≥<=+)0(1-)0(1d y d y y i ii (3)递推公式:当d<0时,下一步的中点坐标为:M (x i +2,y i -0.5)。
所以下一步中点偏差判别式为:2221)5.0()2()5.0,2(R y x y x F d i i i i i --++=-+=+3232)5.0()1(222++=++--++=i i i i i x d x R y x当d ≥0时,下一步的中点坐标为:M (x i +2,y i -1.5)。
图形学试题参考答案

图形学试题参考答案一、名词解释(每题3分,共计18分)1.计算机图形学是利用计算机研究图形的表示、生成、显示、处理的学科。
2.改进Bezier 曲线无法表示特征多边形及局部修改性能差的缺陷,具有局部性、对称性、连续性、凸包性和几何不变性等特点。
3.用一种颜色或图案来填充一个二维区域, 确定填充区域象素点的位置以及填充象素亮度植和颜色。
4.任何小于或等于屏幕域的区域都称为视图区。
5.一种输入设备/输出设备 ,是一种对于物体触摸能产生反应的屏幕。
触摸屏由触摸检测部件和控制器组成,提供一种简单、方便、自然的人机交互方式。
6.:帧缓存是屏幕所显示画面的一个直接映象,每一存储单元对应屏幕上的一个像素,整个帧缓存对应一帧图像,用于像素的存取转换。
二、填空题(每空1分,共计20分) 1.请求 事件 2.2223.计算功能 存储功能 交互功能4.像素集合 颜色5.距离 透视6.17.扫描线8.影孔板9. 图形坐标变换(从一个点集从一个坐标系到另一个坐标系) 无穷远 10.浮点数运算 需要取整 11.顶点表示法 12.比划/像素 三、选择题(每题1分,共计10分) 1-5 FTTFT 6-10 TFFTT四、判断题(每题1分,共计10分)1-5 BDCCC 6-10 BCCBC (第6题题目印刷错误,所以全部给分) 五、简答题(每题5分,共计25分)1.种子填充算法使用假设的种子点出发,寻找区域内的所有像素点,可采用栈结构实现。
过程如下: 1) 种子入栈2) 栈若为空,算法结束;若不为空,栈顶像素出栈; 3) 将出栈像素设置为多边形色;4) 将左、上、右、下顺序检查与出栈像素相邻的四个像素,若其中某个像素不在边界且未置为多边形色,则把该像素入栈。
重复2)-4)步骤。
2.取第一象限四分之一圆,从圆弧任意点出发,顺时针方向生成圆,最精逼近该圆的下一个像素只可能为正右方、右下方和正下方像素,记为H 、D 、V 。
将三点到圆心的距离平方与圆的半径差做为H 、D 、V 到圆弧距离的度量,记为SH ,SD ,SV 。
计算机图形学练习测试题及参考答案

计算机图形学练习测试题及参考答案计算机图形学练习测试题及参考答案Prepared on 24 November 2020《计算机图形学》测试题⼀、名词解释:(每个4分)1.计算机图形学2.图象处理3.模式识别4.计算⼏何5.凸多边形6.种⼦填充算法7.窗⼝8.视区9.光顺性10.拟合11.多项式插值12.⼩挠度曲线13.图形变换14.齐次坐标系15.凸包16.轮廓线17.等值线18.图形的翼边表⽰19.ER模型20.图形消隐21.本影22.半影23.⽤户坐标系24.规范化设备坐标系25.构造26.约束技术27.光线跟踪28、⾛样29、CRT(Cathode Ray Tube)30、隔⾏(interlaced)扫描32、取样⽅式(sample mode)33、区域34、边界表⽰法35、复合变换36、⼆维复合平移37.⼆维复合⽐例38.⼆维复合旋转39.视区(Viewport)40、投影变换41、平⾯⼏何投影42. 参数图43. 像素图44.⼈机界⾯45.地理信息系统46.虚拟现实47.⼏何造型技术48.扫描转换49. 插值曲线50.逼近曲线51. ⽤户接⼝52. 交互技术53. 交互式图形系统的基本交互任务54. 定位任务55. 选择任务56. 拾取任务57 .选择技术58. 菜单技术59. ⽂字输⼊任务60. 数值输⼊任务61.动画62.帧63.场64. 消隐65.物体空间的消隐算法66. 漫反射光67. 环境光⼆、选择题(每题2分)1、计算机图形学与计算⼏何之间的关系是( )。
A)学术上的同义词 B)计算机图形学以计算⼏何为理论基础C)计算⼏何是计算机图形学的前⾝D).两门毫不相⼲的学科2、计算机图形学与计算机图象学的关系是( )。
A)计算机图形学是基础,计算机图象学是其发展B)不同的学科,研究对象和数学基础都不同,但它们之间也有可转换部分C)同⼀学科在不同场合的不同称呼⽽已D)完全不同的学科,两者毫不相⼲3、触摸屏是( )设备。
大学计算机绘图试题及答案

大学计算机绘图试题及答案试题一:图形的基本概念与分类1. 请简要解释什么是计算机绘图。
计算机绘图是指利用计算机软件和硬件设备进行图形的创作、编辑和处理的过程。
通过计算机绘图,可以绘制出各种形状、颜色和纹理的图形,实现图像的创作和编辑。
2. 请列举常用的图形文件格式,并简要描述其特点。
常用的图形文件格式包括:JPEG、PNG、GIF和SVG等。
- JPEG:适用于存储照片和其他真实图像的格式,具有较高的压缩比例,但可能会导致图像细节的损失。
- PNG:支持透明背景和多种颜色,无损压缩,适用于网页设计和电子出版等需要保留细节的场景。
- GIF:支持动画和透明背景,适用于简单图形和动画的展示,但色彩表现较为有限。
- SVG:基于XML的矢量图形格式,文件体积较小,允许图像按比例缩放而不失真,适用于Web页面和矢量图形设计。
3. 请解释什么是矢量图形和位图图形,并比较它们的特点。
- 矢量图形:由数学公式描述图像,使用直线、曲线、圆弧等几何元素构建,图像可按比例缩放而不失真。
矢量图形文件通常较小,适合用来表示简单的几何形状和矢量图标。
常见的矢量图形格式有SVG、AI等。
- 位图图形(也称为栅格图形):由像素阵列组成的图像,每个像素可以记录颜色信息。
位图图形在放大时会失真,因为每个像素的大小固定,其详细信息无法再生产。
常见的位图图形格式有JPEG、PNG、GIF等。
4. 请简述光栅化和反光栅化的概念及其应用。
- 光栅化(Rasterization)是将矢量图形转化为位图图形的过程,即将图像转换为由像素阵列组成的图像。
光栅化可以应用于计算机图形学、图像处理和计算机游戏等领域。
- 反光栅化(Anti-aliasing)是在光栅化的基础上进行的处理,通过消除锯齿边缘、减少图像锯齿效应,使图像的视觉效果更加平滑和真实。
试题二:计算机绘图软件的使用1. 请列举常用的计算机绘图软件,并简要介绍其主要功能。
常用的计算机绘图软件包括Photoshop、Illustrator、CorelDRAW和AutoCAD等。
计算机图形学试卷与答案
考试内容
基础知识:计算机图形学的基 本概念、原理和算法
编程技能:使用常见编程语言 实现图形学算法
图像处理:图像处理的基本原 理和技术,如滤波、色彩校正 等
3D图形:3D建模、渲染和动 画技术
难度评估
试卷整体难度:中等 知识点覆盖面:全面 题目设计:有深度和广度 适合人群:有一定计算机图形学基础的学生
深入学习算法:理解图形学 中常用的算法和数据结构,
提高算法设计能力。
关注前沿技术:了解计算机 图形学领域的前沿技术和最 新发展,拓宽视野和思路。
感谢观看
汇报人:XX
• 题目:在计算机图形学中,如何实现透明度? 答案:透明度可以通过混合颜色来实现,通常使用alpha值来描述透 明度。 解析:这道题考查对计算机图形学中透明度实现方式的理解,需要了解颜色混合和alpha值的概念。
• 答案:透明度可以通过混合颜色来实现,通常使用alpha值来描述透明度。 • 解析:这道题考查对计算机图形学中透明度实现方式的理解,需要了解颜色混合和alpha值的概念。
• 答案:纹理映射是将图像贴在三维模型表面的过程。 • 解析:在计算机图形学中,纹理映射是将图像贴在三维模型表面的过程。通过纹理映射,可以增加模型的细节和真实感,使其看起来更加自然和逼真。
• 题目:计算机图形学中,什么是抗锯齿处理? 答案:抗锯齿处理是一种消除图像中锯齿状边缘的技术。 解析:在计算机图形学中, 抗锯齿处理是一种消除图像中锯齿状边缘的技术。通过抗锯齿处理,可以使图像的边缘更加平滑和自然,提高图像的视觉效果。
• 答案:计算机图形学是研究计算机生成和操作图形的科学。 • 解析:简答题考察计算机图形学的定义,答案简洁明了,准确解释了计算机图形学的概念。
• 题目:计算机图形学有哪些应用? 答案:计算机图形学在游戏、电影制作、建筑设计、医学成像等领域有广泛应用。 解析:简答题考察计算机图形学的应用,答案列举了几个常见的应用领域,说明了计算机图形学的实际应用价值。
计算机图形学试题
计算机图形学试题关键信息项1、试题涵盖的计算机图形学知识点范围:____________________________2、试题的题型:____________________________3、试题的分值分布:____________________________4、考试时间限制:____________________________5、答题要求和规范:____________________________6、评分标准:____________________________7、试题的保密级别和使用权限:____________________________11 试题涵盖的计算机图形学知识点范围111 基本图形生成算法,如直线生成算法、圆生成算法等。
112 二维和三维图形变换,包括平移、旋转、缩放等。
113 图形的裁剪和消隐算法。
114 曲线和曲面的表示与生成,如贝塞尔曲线、B 样条曲线等。
115 光照模型和材质处理。
116 纹理映射技术。
117 图形的投影变换,如正投影、透视投影等。
118 图形的动画技术原理和实现方法。
12 试题的题型121 选择题:考查对计算机图形学基本概念、原理和算法的理解和掌握。
122 填空题:要求填写关键的概念、术语或算法步骤。
123 简答题:针对特定的图形学问题,阐述原理、方法和步骤。
124 计算题:通过给定的数据和条件,运用图形学算法进行计算和求解。
125 综合应用题:结合实际场景,运用多种图形学知识和技术解决综合性问题。
13 试题的分值分布131 选择题:占总分的X%,每题X分。
132 填空题:占总分的X%,每题X分。
133 简答题:占总分的X%,每题X分。
134 计算题:占总分的X%,每题X分。
135 综合应用题:占总分的X%,每题X分。
14 考试时间限制141 考试总时长为X小时。
142 考生应合理安排时间,确保在规定时间内完成答题。
15 答题要求和规范151 考生应使用规定的答题纸或答题区域进行作答。
计算机图形学考试题及答案
一、填空题(每空1分)1、分辨率为2048×1024,能显示256种颜色的显示器,至少需要选用帧缓存容量为 2 MB。
2、彩色显示器使用颜色模型,而彩色打印机使用颜色模型。
3、在图形文件中,常用来描述图形元素(点,线,圆,弧等);而在光栅扫描图形显示器中,采用显示所有图形。
4、当三维物体用透视变换方程投影到观察平面上,物体中不与观察平面平行任一簇平行线投影成收敛线,其收敛点为。
物体的平行于某一坐标轴的平行线的灭点为。
5、可见光的波长为纳米。
6、在简单光照模型中,一个点光源照射到物体表面上一点,再反射出来的光,可分为三部分、和。
7、在文件大小上,位图图像要比矢量图形文件。
二、选择题(有的为多选题,每题2分)(1)在下列有关CRT显示器的叙述中,正确的论述为(ABD )A、CRT由五部分组成:电子枪、聚焦系统、加速系统、磁偏转系统和荧光屏;B、电子枪:发射电子流并控制其强弱;C、聚焦系统:将电子束引向荧光屏特定的位置。
D、加速系统:使电子束加速到应有的速度;E、磁偏转系统:将电子流聚焦成很窄的电子。
;(2)下述用数值微分法(DDA)画斜率的绝对值小于1的直线的C语言子程序中哪一行有错(D )V oid drawLineWithDDA(int x1, int y1, int x2, int y2, int color){A、int x, y;B、float k = (float)(y2-y1)(x2-x1);C、for(x=x1,y=y1;x<=x2;x++){putpixel (x, y, color);}D、y+=k;}(3)使用下列二维图形变换矩阵,将产生的变换结果为( D )A、图形放大2倍;B、图形放大2倍,同时沿X、Y坐标轴方向各移动1个绘图单位;C、沿X坐标轴方向各移动2个绘图单位;D、沿X坐标轴方向放大2倍,同时沿X、Y坐标轴方向各平移1个绘图单位。
(4)在下列对投影的描述里,正确的论述为( CD )A、透视投影中灭点最多可以有3个B、透视投影与平行投影相比,视觉效果更有真实感,而且能真实地反映物体的精确的尺寸和形状C、太阳光线产生的投影为平行投影。
计算机图形学试题及答案完整版_
名词解释将图形描述转换成用像素矩阵表示的过程称为扫描转换。
1.图形2.像素图3.参数图4.扫描线5.构造实体几何表示法6.投影7.参数向量方程8.自由曲线9.曲线拟合10.曲线插值11.区域填充12.扫描转换三、填空1.图形软件的建立方法包括提供图形程序包、和采用专用高级语言。
2.直线的属性包括线型、和颜色。
3.颜色通常用红、绿和蓝三原色的含量来表示。
对于不具有彩色功能的显示系统,颜色显示为。
4.平面图形在内存中有两种表示方法,即和矢量表示法。
5.字符作为图形有和矢量字符之分。
6.区域的表示有和边界表示两种形式。
7.区域的内点表示法枚举区域内的所有像素,通过来实现内点表示。
8.区域的边界表示法枚举区域边界上的所有像素,通过给赋予同一属性值来实现边界表示。
9.区域填充有和扫描转换填充。
10.区域填充属性包括填充式样、和填充图案。
11.对于图形,通常是以点变换为基础,把图形的一系列顶点作几何变换后,连接新的顶点序列即可产生新的变换后的图形。
12.裁剪的基本目的是判断图形元素是否部分或全部落在之内。
13.字符裁剪方法包括、单个字符裁剪和字符串裁剪。
14.图形变换是指将图形的几何信息经过产生新的图形。
15.从平面上点的齐次坐标,经齐次坐标变换,最后转换为平面上点的坐标,这一变换过程称为。
16.实体的表面具有、有界性、非自交性和闭合性。
17.集合的内点是集合中的点,在该点的内的所有点都是集合中的元素。
18.空间一点的任意邻域内既有集合中的点,又有集合外的点,则称该点为集合的。
19.内点组成的集合称为集合的。
20.边界点组成的集合称为集合的。
21.任意一个实体可以表示为的并集。
22.集合与它的边界的并集称集合的。
23.取集合的内部,再取内部的闭包,所得的集合称为原集合的。
24.如果曲面上任意一点都存在一个充分小的邻域,该邻域与平面上的(开)圆盘同构,即邻域与圆盘之间存在连续的1-1映射,则称该曲面为。
25.对于一个占据有限空间的正则(点)集,如果其表面是,则该正则集为一个实体(有效物体)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= a*(xi+1+1) +b*( yi+1+0.5)+c- [a*(xi+1) +b*( yi+0.5)+c] = a+b 当 di>=0, yi+1= yi+1 ; =a 当 di<0, yi+1= yi ; 为了保持整数运算,将 d*2,有: 初值:x = x0 ; y = y0 ; d =b+2*a; ⊿d=di+1-di= F(xi+1+1,yi+1-0.5)- F(xi+1,yi-0.5) = 2*a+2*b 当 di>=0, yi+1= yi+1 ; = 2*a 当 di<0, yi+1= yi ; 推毕。
A.二次 B 样条算法简述: 分 n-2 段,每段细分 count 段直线段。 参数:P[i]—控制顶点坐标,n—顶点数,count—直线段数 MoveTo((p[0] +p[1])/2); for(i=0; i<=n-2; i++)//画 n-2 段 { for(j=1; j<=count; j++)//画一段 { t = j/count ; q = ((t*t-2*t+1)*p[i].x+(-2*t*t+2*t+1)*p[i+1]+t*t*p[i+2])/2 ; LineTo(q) ; }} B.算法简述: 经一次分割算法,原 Pi 分割为二段 Bezier 曲线。 参数:Pi—控制顶点坐标,n—顶点数,k—递归次数 #define MAX 50 void SplitBezier(float p[][2], int n, int k) { float q[MAX][2]; int i, j ; for(i=0;i<=n;i++) { q[i][0]=p[0][0]; q[i][1]=p[0][1]; for(j=0;j<n-i; j++) { p[i][0]=(p[i][0]+p[i+1][0])/2 ; p[i][1]=(p[i][1]+p[i+1][1])/2 ;}} if (k>0){ k-- ; SplitBezier(p, n, k) ; SplitBezier(p, n, k) ; } else { DrawBezier(p, n); DrawBezier(p, n); }} void DrawBezier(float p[][2], int n) { moveto(p[0][0], p[0][1]) ; for( int i=0; i<=n; i++) lineto([i][0], p[i][1]) ; }
解答:1、答案见上。 评分标准:共 1 分,有一标错扣 1 分。 2、答案见上述第 2 题填空部分。 评分标准:共 4 分,每空格 1 分 第四空,标 AB 或 KL,或二者均得分,多标 GH 不扣分。 3、答案为算法分二步: 第一步:先编码判断完全可线段和完成不可见线段 求出各线段的二端点的编码 C1、C2; 若 C1=C2=0000 ,线段完全可见; 若 C1&C2≠0000 ,线段完全不可见; 否则, 第二步求不可见部分时,可选以下三种算法之一: P4 a) Cohen-Sutherland 算法: 1) 对二端点编码中为 1 的边,直接计算直线与该边交点,求可见部分; 2) 余下的可见部分重复 1) ,直到所有编码为 1 的求可见部分结束。 3) 最后余下部分为可见部分。 b) Liang-Barsky 算法: 1) 求线段与窗口上、下平行线的交点,记为(t0,t1); 2) 求线段与窗口左、右平行线的交点,记为(tt0,tt1); 3) 可见线段部分为:[t’,t”],其中,t’=max{0,t0,tt0},t”=min{1,t1,tt1} 且 t’<t”。 评分标准:共 6 分 1) 第一步未做,扣 2 分;计算交线部分 4 分。 2) Liang-Barsky 算法中若未注明 t’<t”,扣 1 分; 3) a)和 c)算法中,未提所有编码为 1 的,扣 1 分。 4) 叙述不准确或有误,视情扣分。 4、根据描述的算法给出相应的图示。
四、 线段裁剪算法(14 分) Cohen-Sutherland 窗口裁剪算法,当取编码顺序为(Ct,Cr,Cb,Cl)时: 1、给出线段 GH 二端点的相应编码 0010 、0100;(1 分) 2、(4 分)当满足条件:C1=C2=0000,线段完全可见;下列线段中有:EF 当满足条件:C1&C2≠0000,线段完全不可见;下列线段中有:KL、AB 3、给出判断可能部分可见线段的 Liang-Barsky 或 Cohen-Sutherland 算法的算法 描述;(6 分) 4、根据上述算法图示计算线段 CD 的可见部分计算过程,给出判断结论。(3 分)
评分标准:推导共 3 分
a) 列出中点算法判别式,得 1 分。 b) 推导中点算法递推式,得 2 分。 c) 扣分视完整性定。 2) 、算法描述: 1、置初值: x=x0 ; y=y0 ; d=a+2*b ; 画(x,y) 2、终止条件:while(x<x1) 3、递推: { if (d>=0) { d = d+2*(a-b); y=y+1; } else d = d+2*a ; x=x+1; 4、画点: (x,y); }
评分标准:共 5 分
扣分视完整性定。 第 2 页 共 4 页
3、给出下列控制多边形,请分别画出 Bezier 曲线、二次 B 样条曲线、三次 B 样条 曲线,并标出端点切向量。控制多边形如下:(6 分)
P3 P2 P4
P3
算法描述: (栅栏填空算法) 参数:多边形顶点坐标 P[i],多边形点数 n,color—填空色 1. 取多边形任一顶点,记为(X,Y)作垂直栅栏; 2. 遍历多边形所有边; 3. { 遍历边上所有点; { 从此点至垂直栅栏,判断各点; 若为已画点:则取销该点,否则画该点,即求余; }
扣分视完整性定。 1、算法描述: a)对图形进行平行投影或透视投影变换 用数组 Z-Buffer(,x,y)保存当前填色点的最大 Z 值; Color(x,y)保存当前颜色值; b)数组初始化:Z-Buffer(x,y)=Zmin;Color(x,y)=背景色; c)遍历所有多边形面(次序无关) { 判断面法向量与视线夹角,若为锐角,则不可见;若为钝角,则为可见。 if (面为可见) { 扫描转换该多边形; for (多边形中每个像素(x,y)) { 多边形中和每个像素的深度值 z(x,y); if (z(x,y)>Z-Buffer(x,y)) { Z-Buffer(x,y)= z(x,y); Color(x,y)=(x,y)点的颜色 ;}]} 评分标准:共 8 分 a) 部分未叙述,扣 1 分; b) 部分不准确,扣 2 分; c) 部分循环条件不准确,扣 2 分; d)循环体核心部分错误扣 4 分.
(6)
评分标准:算法部分为 6 分,扣分视完整性定。
算法部分为 4 分,扣分视完整性定。
七、 (每小题 5 分)二维图形变换:(写出相应每步的加边矩阵)
1. 在二维坐标 Oxy 中,求关于对称轴 y=
2 2
x 的对称变换。
P1 P2
2.求对于下面左图变换到右图变换矩阵。 D (0,1) D’(1,2)
评分标准:每选 1 分(第 1 题 2 分) ,未选或选错均扣分。 三、 (10 分)直线点生成的中点算法(条件为 x1-x0>y1-y0>0) 1、推导直线点生成中点算法; 分) (3 2、算法描述直线的点生成的中点算法; 分) (7
评分标准: a) 算法描述共 7 分。初始条件:2 分,递推式 3 分,中止条件 1 分,画 1 分。 b) 画圆改圆填色 2 分。 c) 扣分视完整性定。
九、 (10 分) 算法描述 Z 缓冲区面消隐算法(深度缓冲区算法) ,并逐步图示下面图 形的面消隐过程。
第
4 页
共 4 页
第 3 页
C’(2,2)
共 4 页
P5
P4
A(-1,0)
C(1,0) A’(0,0) B(0,-1) B’(1,0)
评分标准:每一小题各 5 分
扣分视完整性定。
八、 (每小题 5 分)三维图形变换:(写出相应每步的加边矩阵) 1.整体放大 1/2 倍,再透视投影到 Y-Z 平面,视点为(0,10,0),视线为 Y 轴。 2.以点 P(3,-1,2)为中心的 X、Y、Z 向分别缩放 2、-3、1/4 倍,并投影到 Y-Z 平 面。 评分标准:每一小题各 5 分
第 1 页 ቤተ መጻሕፍቲ ባይዱ 4 页
J D
K L
评分标准:共 3 分 结果错扣 2 分,图示不正确或有误,视情扣分。
五、 (16 分) Bezier 曲线与 B 样条曲线: A E C B 0010 G I F 0100 H 1、B 样条的非均匀周期性结点向量(t0,t1,…,tn,…,tn+k)的取法中有二个特例: (4 分) 当结点向量为 0,0,1,2,3,…,n,n 时,特例为 控制多边形 ; 当结点向量为 0,0,0, 0,1,1,1,…1 时,特例为 Bezier 曲线 ; 2、算法描述二次 B 样条曲线的生成算法;或算法描述 Bezier 曲线的递归分裂作图 算法。 (二选一,6 分)
一、 (12 分,每小题 4 分)简述题 1. 简述 CRT 显示器工作原理,并说明帧缓冲区与显示器分辨率间的关系。 2. 选做一题: a)简述汉字库的数据保存形式及用途。 b)图形学算法在 3DAMX 或其它图形软件中的应用。 3. 举例说明三种图形输入输出设备及其用途。 评分标准:每选 4 分,未选或选错均扣分。 二、 (8 分)判断题(请在后面括号中打√或× : ) 1. 2. 3. 4. 5. 6. 7. 8. 若帧缓冲区大小一定,则屏幕分辨率与最大颜色数成正比。 许多图形算法可由硬件实现,而硬件图形算法不可由软件实现。 k 阶 B 样条曲线随着控制顶点的增加,会导致曲线次数的增加。 汉字显示点阵字库与打印点阵字库是一样的。 齐次坐标系不可以表示坐标轴的无穷远点。 二平行直线经线性变换后仍然平行。 Bezier 曲线和均匀结点 B 样条曲线都具有对称性。 单凸多面体的消隐只要判断面的外法向与视线的夹角关系即可。 ( ×) ( ×) (× ) ( ×) ( ×) ( √) (√) (√)
