STK实验卫星轨道参数仿真
STK轨道仿真实验报告

北京科技大学课程设计报告学院:班级:学号:姓名:成绩:2016年12月28日基于STK太阳同步轨道设计与分析摘要:本课程设计训练,要求学生学习基于Satellite Tool Kit(以下简称STK)软件的轨道动力学仿真与设计的基本理论与方法,学会根据设计要求开展设计工作,并能联系实际深入掌握本专业的理论知识,从而使学生具备从事科学技术研究的基本技能。
关键词:STK 卫星轨道仿真卫星地面站引言:随着可视化技术在仿真中的广泛应用,对卫星的轨道和姿态控制仿真不仅要求仿真系统具有精确的模型和实验结果,还要求真实再现航天任务的全过程,因此有必要建立一个视景仿真系统,给设计人员和决策者以更直观更形象的理解。
STK(Satellite Tool Kit)是由美国Analytical Graphics公司开发的卫星仿真工具包,是航天工业领先的商业化分析软件,它可以快速方便地分析复杂的陆、海、空、天任务,并提供易于理解的图表和文本形式的分析结果,用于确定最佳解决方案。
不但具有强大的数据仿真功能,还具有三维模型编辑和三维可视化模块(STK/VO),可以为STK和其它附加模块提供逼真的三维视景显示功能。
在STK中通过建立一定的场景并加入卫星的模型,通过设定该场景的参数,就能实现对卫星运行的二维和三维仿真视景。
虽然它有效的解决了三维视景显示问题,但是在卫星的运行过程中,如果需要对卫星实施变轨或者大角度姿态机动就需要将仿真停止,重新设定相关的参数,不能实现对整个视景系统的连续仿真运行。
软件介绍:STK提供分析引擎用于计算数据、并可显示多种形式的二维地图,显示卫星和其它对象如运载火箭、地面车辆、目标等。
STK的核心能力是产生位置和姿态数据、获取时间、遥感器覆盖分析。
STK专业版扩展了STK的基本分析能力,增加了轨道预报算法、姿态定义、坐标类型和坐标系统、遥感器类型、高级的约束条件定义,以及卫星、城市、地面站和恒星数据库。
STK实验卫星轨道全参数仿真

实验一卫星轨道参数仿真一、实验目的1、了解STK的基本功能;2、掌握六个轨道参数的几何意义;3、掌握极地轨道、太阳同步轨道、地球同步轨道等典型轨道的特点。
二、实验环境卫星仿真工具包STK三、实验原理(1)卫星轨道参数六个轨道参数中,两个轨道参数确定轨道大小和形状,两个轨道参数确定轨道平面在空间中的位置,一个轨道参数确定轨道在轨道平面内的指向,一个参数确定卫星在轨道上的位置。
•轨道大小和形状参数:这两个参数是相互关联的,第一个参数定义之后第二个参数也被确定。
第一个参数第二个参数semimajor axis 半长轴 Eccentricity 偏心率apogee radius 远地点半径 perigee radius 近地点半径apogee altitude 远地点高度 perigee altitude 近地点高度Period 轨道周期 Eccentricity 偏心率mean motion平动 Eccentricity 偏心率图1 决定轨道大小和形状的参数•轨道位置参数:轨道倾角(Inclination)轨道平面与赤道平面夹角升交点赤经(RAAN)赤道平面春分点向右与升交点夹角近地点幅角(argument of perigee)升交点与近地点夹角•卫星位置参数:(2)星下点轨迹在不考虑地球自转时,航天器的星下点轨迹直接用赤经α、赤纬δ表示(如图2)。
直接由轨道根数求得航天器的赤经赤纬。
图2 航天器星下点的球面解法在球面直角三角形SND 中:⎪⎩⎪⎨⎧+==∆∆+Ω=+==)tan(cos tan cos tan )sin(sin sin sin sin f i u i f i u i ωαααωδ (1) 由于地球自转和摄动影响,相邻轨道周期的星下点轨迹不可能重合。
设地球自转角速度为E ω,t 0时刻格林尼治恒星时为0G S ,则任一时刻格林尼治恒星时G S 可表示成:)(00t t S S E G G -+=ω (2)在考虑地球自转时,星下点地心纬度ϕ 与航天器赤纬δ仍然相等,星下点经度(λ)与航天器赤经α的关系为:⎩⎨⎧=---=-=δϕωααλ)(00t t S S E G G (3) 将(1)代入上式,得到计算空间目标星下点地心经纬度()ϕλ,的公式,即空间目标的星下点轨迹方程为:⎩⎨⎧⋅=---⋅+Ω=)sin arcsin(sin )()tan arctan(cos 00u i t t S u i E G ϕωλ (4) 其中ϕ 为星下点的地理纬度,λ 为星下点的地理经度,u 是纬度幅角,ωE 为地球自转角速度。
利用STK进行的在轨段仿真

飞行器在轨段仿真1. 仿真参数圆轨道,轨道倾角42δ= 轨道高度350H km = 地球平均半径6371R km =地球自转角速度57.29210/ie rad s ω-=⨯ 在轨运行的线速度7701.11/v m s = 在轨运行的周期5483.53 1.523T s h ==根据成都方面的说法,飞行器在轨运行时并不进行姿态控制,也就意味着在则2. 坐标系定义(1) o 轴沿机体与地心连线方向,背离地心为正,o Y 轴在轨道平面内与Oz 轴垂直,向前为正,o X 轴通过右手定则确定指向。
图2 轨道坐标系定义图中,ϕ为纬度,k 为飞行器在轨道平面内的回转角度,以升交点为起始点,δ为轨道平面与赤道平面的夹角。
为了方便仿真,暂假设轨道面的升交点经度为零。
(2) 地心惯性坐标系(i 系)原点i O 位于地球球心,i Z 垂直于赤道平面,指向北极,i i X Y 、轴位于赤道面内,i X 轴指向春分点方向,i Y 轴通过右手定则确定指向。
(3) 地球坐标系(e 系)原点e O 位于地球球心,e Z 垂直于赤道平面,指向北极,e e X Y 、轴位于赤道面内,e X 轴指向格林威治零时,e Y 轴通过右手定则确定指向。
(4) 地理坐标系(t 系)原点t O 位于机体所在位置,t Z 垂直于当地水平面指天,t t X Y 、轴位于当地水平面内,t X 轴指东,t Y 轴指北。
(5) 机体坐标系(b 系)原点b O 位于机体质心,b X 轴沿机体横轴指向右,b Y 轴沿机体纵轴指向前,bZ轴沿机体法向轴指向上,通过右手定则确定指向。
当机体系相对轨道系的姿态角均为零时,机体系和轨道系重合。
3. 各个坐标系之间的转换关系 (1)轨道坐标系与地心惯性系i o C设飞行器在轨运行时相对升交点的转角为k ,轨道倾角为δ,则有:sin 0cos ()(90)(90)cos cos sin sin cos cos sin cos sin sin i o x z x kkC R R k R k k k k δδδδδδδ-⎡⎤⎢⎥=----=-⎢⎥⎢⎥⎣⎦ (2)地心惯性系与地球坐标系e i C设飞行器在轨运行时间为t ,则有:cos()sin()0()sin()cos()0001ie ie e i z ie ie ie t t C R t t t ωωωωω⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦(3)地球坐标系与地理坐标系t e C设飞行器的星下点的经纬度为ϕλ、,则有:sin cos 0(90)(90)sin cos sin sin cos cos cos cos sin sin t e x z C R R λλϕλϕλϕλϕϕλϕλϕ-⎡⎤⎢⎥=-+=--⎢⎥⎢⎥⎣⎦ (4)轨道坐标系与机体坐标系bo C设飞行器机体相对轨道坐标系通过俯仰角o θ、横滚角o γ、航向角o ψ来描述,则有:0000cos 0sin 100cos sin 00100cos sin sin cos 0sin 0cos 0sin cos 01oo oo b o o ooo C γγψψθθψψγγθθ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦(5)地理坐标系与机体坐标系t b C设飞行器机体相对地理坐标系通过俯仰角t θ、横滚角t γ、航向角t ψ来描述,则有:cos 0sin 100cos sin 00100cos sin sin cos 0sin 0cos 0sin cos 01tt tt b t t t t tt t t t C γγψψθθψψγγθθ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦4. 导航坐标系选为地理系时的导航仿真当选取地理系为导航坐标系时,在轨导航算法与地面基本相同: (1)姿态更新:()b b b t ttb ib t ie et C ωωωω=-+,而0b ibω=,则可得()b b t t tb t ie et C ωωω=-+,由此通过四元数算法即可更新姿态矩阵b t C ,进而可获得机体系相对地理系的姿态角。
利用STK进行的发射段仿真
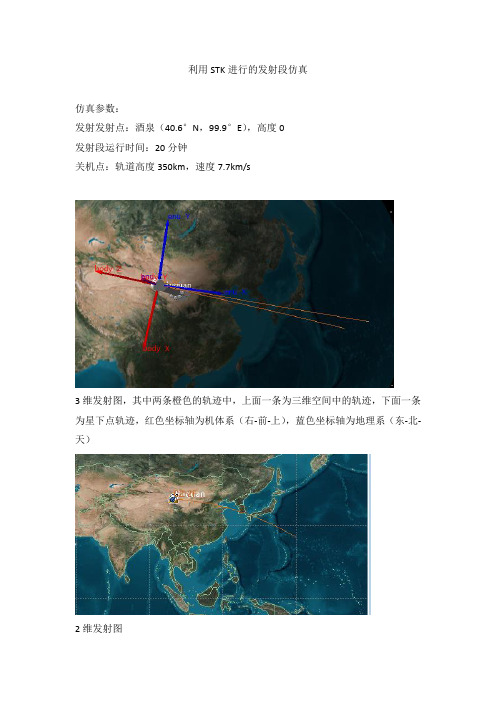
利用STK进行的发射段仿真
仿真参数:
发射发射点:酒泉(40.6°N,99.9°E),高度0
发射段运行时间:20分钟
关机点:轨道高度350km,速度7.7km/s
3维发射图,其中两条橙色的轨迹中,上面一条为三维空间中的轨迹,下面一条为星下点轨迹,红色坐标轴为机体系(右-前-上),蓝色坐标轴为地理系(东-北-天)
2维发射图
星下点轨迹及高度
相对地理坐标系的姿态,需要注意是STK中的pitch俯仰角是相对y轴的,且方向相反,roll横滚角是相对x轴的。
转换为常用的姿态角,则该图中说明了相对地理系的俯仰角初始为90°,经过程序转完后慢慢减小直到接近0°,整个发射过程横滚角不变,航向角由红色曲线给出。
基于STK的卫星轨道预报

《航天器操作与控制试验》综合作业卫星轨道预报姓名:王备学号:38151312院系:宇航学院二〇一〇年十一月一、实验题目:卫星轨道预报二、实验目的1.学会STK(Satellite Tool Kit)软件的使用,掌握STK的基本操作;2.学会使用STK仿真,并实现卫星的轨道预报,重点掌握HPOP高精度轨道预报和LOP长期轨道预报。
三、实验内容(一)、HPOP高精度轨道预报1. 建立两颗卫星HPOP1与HPOP2;2. 设置HPOP1考虑大气阻力,而HPOP2不考虑,其他参数相同;3. 用HPOP高精度轨道预报器生成轨道;4. 动画显示,观察两颗卫星轨道的不同;5. 生成多种类型的卫星轨道数据;6. 计算卫星轨道寿命。
(二)、LOP长期轨道预报1. 建立两颗卫星LOP1与LOP2;2. 设置LOP1考虑大气阻力,而LOP2不考虑,其他参数相同;3. 用HPOP高精度轨道预报器生成轨道;4. 生成多种类型的卫星轨道数据,观察两颗卫星轨道的不同。
四、实验过程描述(一)、HPOP高精度轨道预报1.建立新的场景将其命名为BUAA_HPOP。
2.在浏览窗口选中场景,打开Basic Properties 窗口3.在Time Period栏,输入如下设置:区域值Start Time 1 Jan 2010 00:00:00.00Stop Time 1 Jan 2010 04:00:00.00Epoch 1 Jan 2010 00:00:00.004.选择Animation栏输入如下内容:区域值Start Time 1 Jan 2010 00:00:00.00Stop Time 1 Jan 2010 04:00:00.00Time Step 60 secondsRefresh Delta Change to High Speed5.在Units栏输入如下设置:6.完成后,点击确定,从File菜单中选择Save As…,保存场景为BUAA_HPOP.sc。
STK实验卫星轨道参数仿真要点

STK实验卫星轨道参数仿真要点STK(Systems Tool Kit)是美国AGI(Analytical Graphics Inc.)公司开发的一款用于空间系统分析和仿真的软件工具。
在STK中进行实验卫星轨道参数仿真可以帮助用户更好地了解和分析卫星轨道的运行情况,以便优化设计和规划任务。
以下是进行STK实验卫星轨道参数仿真的要点:1.卫星轨道选择:首先需要选择合适的卫星轨道。
常见的轨道类型包括地球同步轨道(GEO)、太阳同步轨道(SSO)和低地球轨道(LEO)等。
不同的轨道类型适用于不同的应用场景,如通信、气象、资源监测等。
在选择轨道时,需要考虑卫星的任务需求和预算限制。
2.轨道参数输入:在STK中,可以手动输入或导入卫星的轨道参数。
轨道参数包括卫星初始位置、速度、轨道倾角、轨道高度等。
这些参数直接影响卫星的运行轨迹和性能。
用户可以根据实际需求来设定这些参数,以便进行后续的仿真分析。
3.进行轨道传播:在STK中,可以选择合适的方法进行卫星的轨道传播。
常见的轨道传播方法有数值积分法、两体问题解析法和伪谱法等。
不同的传播方法有不同的精度和计算复杂度。
用户需要根据需求和计算能力来选择合适的传播方法。
4.进行轨道优化:在STK中,可以通过调节不同的轨道参数来优化卫星的轨道。
例如,可以调整轨道高度以改变轨道周期;可以调整轨道倾角以达到太阳同步轨道;可以调整轨道偏心率以改变卫星的运行速度等。
优化轨道参数可以提高卫星的性能和效益。
5.分析卫星的运行情况:在STK中,可以通过轨道时刻表、轨迹图、覆盖范围图等工具来分析卫星的运行情况。
这些工具可以帮助用户了解卫星的轨迹、覆盖范围、通信性能等。
用户可以根据分析结果来评估卫星的性能,并做出调整和改进。
6.进行多卫星协调仿真:在STK中,可以模拟多颗卫星之间的协调和合作。
例如,可以设置多颗卫星在同一轨道上运行,以实现无缝覆盖;可以设置多颗卫星之间的相对运动,以实现对地面目标的追踪和监测。
微小卫星轨道工程应用与STK仿真

《微小卫星轨道工程应用与STK仿真》是一本理论和实践相结合的书籍,它不 仅提供了卫星轨道设计的基本知识,还通过具体的实例和操作,让读者更好地 理解和掌握这些知识。这本书对于从事卫星工程的工作人员来说是一本非常有 价值的参考书,对于对卫星工程感兴趣的读者来说也是一本很好的科普读物。
读完这本书后,我深深地感受到了卫星轨道工程的魅力和挑战。在这个高科技 的领域里,科学家们不仅需要深厚的理论知识,还需要丰富的实践经验。而 《微小卫星轨道工程应用与STK仿真》正是这样一本书,它既提供了理论知识, 又提供了实践经验,为我们揭示了卫星轨道工程的真实面貌。
微小卫星轨道工程应用与STK仿真
读书笔记
01 思维导图
03 精彩摘录 05 目录分析
目录
02 内容摘要 04 阅读感受 06 作者简介
思维导图
本书关键字分析思维导图
卫星
介绍
工程
轨道领域仿真工程 Nhomakorabea轨道
卫星
微小 stk
通过
stk
应用
可以
确定
内容
读者
发射
内容摘要
内容摘要
《微小卫星轨道工程应用与STK仿真》是一本全面介绍微小卫星轨道工程应用和STK仿真的书籍。 本书涵盖了微小卫星基础知识、轨道动力学、发射和轨道确定、微小卫星通信系统、空间天气对 微小卫星的影响以及STK仿真等方面的内容。 本书介绍了微小卫星的基本概念、发展历程和应用领域。对于初学者来说,这有助于他们了解微 小卫星的基本情况和背景。同时,本书还详细介绍了轨道动力学的基本原理和方法,包括二体问 题、摄动理论和数值方法等。这些理论知识为后续的轨道确定和仿真提供了基础。 本书重点讲述了微小卫星的发射和轨道确定。这部分内容涉及到了运载火箭、发射场选择、飞行 程序设计和轨道确定等方面的知识。通过这些内容,读者可以了解到微小卫星从发射到进入预定 轨道的全过程。本书还介绍了微小卫星通信系统和空间天气对微小卫星的影响。这些内容对于从 事微小卫星相关工作的读者来说是非常实用的。
基于STK的北斗二代星座仿真及GDOP值分析

Science &Technology Vision 科技视界0引言我国的北斗卫星导航系统的建设是一个由区域到全球,分阶段发展的过程。
2012年12月27日,随着北斗卫星导航系统空间信号接口控制文件(又称ICD 文件)———公开服务信号B1(1.0版)的发布,标志着北斗区域系统正式建成,北斗卫星导航系统的三步走发展战略完成了第二步。
相对于GPS 等全球卫星导航系统,现阶段的北斗卫星导航系统是区域系统,覆盖范围相对有限。
因此,研究BDS 区域星座对中国主要地区的覆盖情况很有必要。
1STK 简介STK (Satellite Tool Kit,卫星仿真工具包)是由美国AGI 公司推出应用于航天领域的卫星系统分析软件。
STK 作为一种通用的卫星设计工具包,具有非常强大的验证及演示功能。
为了实现卫星系统设计的快速化和数字化,同时也为了保证总体设计方案的可靠性,设计人员大多先在STK 仿真的基础上,进行卫星系统数字化设计软件开发;进而利用STK 软件强大的数据分析和报告功能,进行相关的试验及仿真。
STK 可以快速方便地分析复杂的陆、海、空、天任务,获得丰富的报告和图表形式的分析结果。
STK Pro 版可以生成位置和姿态数据、可见性及覆盖分析、通信链路分析、雷达分析、轨道机动等。
STK 是进行的全球定位系统仿真的强大工具[1-3]。
本文采用STK 进行卫星星座仿真及分析。
2北斗二代星座仿真与其他卫星导航系统不同,BDS 的卫星星座由地球同步轨道(GEO)、倾斜同步轨道(IGSO)和中高轨(MEO)三种轨道类型的卫星构成,轨道高度和轨道平面位置不尽相同。
根据北斗ICD 文件对轨道的描述[4]:(1)GEO 卫星的轨道高度为35786km,分别定点于东经58.75°、80°、110.5°、140°和160°。
(2)IGSO 卫星的轨道高度为35786km,轨道倾角为55°,分布在三个轨道面内,升交点赤经分别相差120°,其中三颗卫星的星下点轨迹重合,交叉点经度为东经118°,其余两颗卫星星下点轨迹重合,交叉点经度为东经95°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S T K实验卫星轨道参数
仿真
标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]
实验一卫星轨道参数仿真
一、实验目的
1、了解STK的基本功能;
2、掌握六个轨道参数的几何意义;
3、掌握极地轨道、太阳同步轨道、地球同步轨道等典型轨道的特点。
二、实验环境
卫星仿真工具包STK
三、实验原理
(1)卫星轨道参数
六个轨道参数中,两个轨道参数确定轨道大小和形状,两个轨道参数确定轨道平面在空间中的位置,一个轨道参数确定轨道在轨道平面内的指向,一个参数确定卫星在轨道上的位置。
轨道大小和形状参数:
这两个参数是相互关联的,第一个参数定义之后第二个参数也被确定。
第一个参数第二个参数
semimajor axis 半长轴 Eccentricity 偏心率apogee radius 远地点半径 perigee radius 近地点半径apogee altitude 远地点高度 perigee altitude 近地点高度Period 轨道周期 Eccentricity 偏心率
mean motion平动 Eccentricity 偏心率
图1 决定轨道大小和形状的参数
轨道位置参数:
轨道倾角(Inclination)轨道平面与赤道平面夹角
升交点赤经(RAAN)赤道平面春分点向右与升交点夹角
近地点幅角(argument of perigee)升交点与近地点夹角
卫星位置参数:
表1 卫星位置参数
(2)星下点轨迹
在不考虑地球自转时,航天器的星下点轨迹直接用赤经α、赤纬δ表示(如图2)。
直接由轨道根数求得航天器的赤经赤纬。
图2 航天器星下点的球面解法
在球面直角三角形SND中:
⎪⎩
⎪⎨⎧+==∆∆+Ω=+==)tan(cos tan cos tan )sin(sin sin sin sin f i u i f i u i ωαα
αωδ (1) 由于地球自转和摄动影响,相邻轨道周期的星下点轨迹不可能重合。
设地球自转角速度为E ω,t 0时刻格林尼治恒星时为0G S ,则任一时刻格林尼治恒星时G S 可表示成:
)(00t t S S E G G -+=ω (2)
在考虑地球自转时,星下点地心纬度 与航天器赤纬δ仍然相等,星下点经度()与航天器赤经α的关系为:
⎩⎨⎧=---=-=δ
ϕωααλ)(00t t S S E G G (3) 将(1)代入上式,得到计算空间目标星下点地心经纬度()ϕλ,的公式,即空间目标的星下点轨迹方程为:
⎩
⎨⎧⋅=---⋅+Ω=)sin arcsin(sin )()tan arctan(cos 00u i t t S u i E G ϕωλ (4) 其中 为星下点的地理纬度, 为星下点的地理经度,u 是纬度幅角,E 为地球自转角速度。
由(4)中的第二式可知,i =90时, 取极大值max 。
i =-90时, 取极小值min ,且有
⎩⎨⎧-︒=i i 180max ϕ ︒≥︒≤9090i i ,⎩
⎨⎧︒-=180min i i ϕ ︒≥︒≤9090i i (5) 因此,空间目标的轨道倾角决定了星下点轨迹能达到的南北纬的极值。
四、实验内容
1、结合六个轨道参数的几何意义,每个轨道参数分别取不同值,给出相应的三维图;
2、分析二体条件下圆轨道(根据向导添加)六个轨道参数随时间的变化规律;
卫星参数设置
半长轴
偏心率
轨道倾角
升交点赤经
近地点幅角
真近点角
3、比较分析Polar Orbit、Sun-Synchronous Orbit、HEO、GSO、GEO卫星的特点,并给出相应的图示说明。
(1)Polar Orbit(极地轨道):
(2)Sun-Synchronous Orbit(太阳同步轨道):
(3)HEO(高地球轨道):
(4)GSO(地球静止轨道):
(5)GEO(地球同步轨道):
(加文字描述各种轨道突出特点)。
