平行线性质PPT课件
合集下载
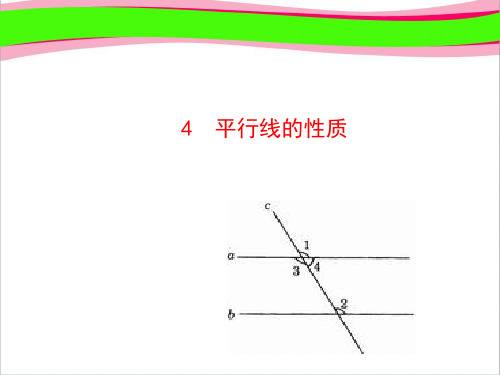
平行线的性质ppt课件
(3) 移： 以关键点为起点作与移动方向平行且与移动距离相
等的线段，得到关键点的对应点；
(4) 连： 按原图顺次连结对应点 .
知4－讲
特别警示
确定一个图形平行移动后的位置需要三个条件：
(1)图形原来的位置；
(2)平行移动的方向；
(3)平行移动的距离.
这三个条件缺一不可.
知4－练
例4 如图 4.2-33，现要把方格纸(每个小正方形的边长均为
知1－讲
特别警示
1. 两条直线平行是前提，只有在这个前提下才
有同位角相等.
2. 按格式进行书写时，顺序不能颠倒，与判定
不能混淆.
知1－讲
3. 平行线的性质与平行线的判定的区别
(1) 平行线的判定是根据两角的数量关系得到两条直线的位
置关系，而平行线的性质是根据两条直线的位置关系得
到两角的数量关系；
又∵ EG 平分∠ BEF，∴∠ BEG=
∠
BEF=70° .
∵ AB ∥ CD， ∴∠ 2= ∠ BEG=70° ．
答案：A
知2－练
2-1. [中 考·烟 台]一杆 古 秤 在 称 物 时 的状 态 如 图
所 示，已 知∠ 1=102°，则 ∠ 2 的度数为
78°
______.
感悟新知
知识点 3 平行线的性质3
若是，可直接求出；若不是，还需要
通过中间角进行转化 .
知1－练
1-1. [中考·台州]用一张等宽的纸条折成如图所示的图
140° .
案，若∠ 1=20 ° ，则 ∠ 2的度数为_______
感悟新知
知识点 2 平行线的性质2
知2－讲
1. 性质 2 两条平行直线被第三条直线所截，内错角相等 .
等的线段，得到关键点的对应点；
(4) 连： 按原图顺次连结对应点 .
知4－讲
特别警示
确定一个图形平行移动后的位置需要三个条件：
(1)图形原来的位置；
(2)平行移动的方向；
(3)平行移动的距离.
这三个条件缺一不可.
知4－练
例4 如图 4.2-33，现要把方格纸(每个小正方形的边长均为
知1－讲
特别警示
1. 两条直线平行是前提，只有在这个前提下才
有同位角相等.
2. 按格式进行书写时，顺序不能颠倒，与判定
不能混淆.
知1－讲
3. 平行线的性质与平行线的判定的区别
(1) 平行线的判定是根据两角的数量关系得到两条直线的位
置关系，而平行线的性质是根据两条直线的位置关系得
到两角的数量关系；
又∵ EG 平分∠ BEF，∴∠ BEG=
∠
BEF=70° .
∵ AB ∥ CD， ∴∠ 2= ∠ BEG=70° ．
答案：A
知2－练
2-1. [中 考·烟 台]一杆 古 秤 在 称 物 时 的状 态 如 图
所 示，已 知∠ 1=102°，则 ∠ 2 的度数为
78°
______.
感悟新知
知识点 3 平行线的性质3
若是，可直接求出；若不是，还需要
通过中间角进行转化 .
知1－练
1-1. [中考·台州]用一张等宽的纸条折成如图所示的图
140° .
案，若∠ 1=20 ° ，则 ∠ 2的度数为_______
感悟新知
知识点 2 平行线的性质2
知2－讲
1. 性质 2 两条平行直线被第三条直线所截，内错角相等 .
平行线的性质课件
利用平行线性质解决几何最值问题
平行线定义：在同一平面内，永不 相交的两条直线
几何最值问题：求线段、角度、面 积等几何量的最大值或最小值
添加标题
添加标题
添加标题
添加标题
平行线性质：平行线之间的线段相 等
利用平行线性质解决几何最值问题 的方法：通过平行线之间的线段相 等，找到几何量的最大值或最小值
平行线的性质在解析几 何中的应用
面的交点
平行线与平面 的夹角：平行 线与平面的夹 角为直线与平
面的夹角
平行线与平面的 平行性：平行线 与平面的平行性 为直线与平面的
平行性
总结与思考
总结平行线的性质及其应用
平行线的定义： 在同一平面内， 永不相交的两
条直线
平行线的性质： 平行线之间的 角度相等，平 行线之间的线
段相等
平行线的应用： 在几何证明、 工程测量、建 筑设计等领域
利用平行线性质解决函数问题
平行线与函数的 关系：平行线是 函数的基本性质 之一，可以应用 于求解函数问题
平行线性质的应 用：利用平行线 性质可以求解函 数的最大值、最 小值、极值等问
题
平行线性质的证 明：利用平行线 性质可以 在更高级的数学 领域中也有广泛 的应用，如微积 分、线性代数等
平行线的性质在代数中 的应用
利用平行线性质解决线性方程组问题
平行线性质：两条直线平行，同位角相等
线性方程组：一组线性方程组成的方程组
利用平行线性质解线性方程组：通过观察方程组中的同位角，找出方程组中的平行线， 从而解出方程组
应用实例：求解线性方程组，如3x+2y=5，4x+3y=6，通过观察方程组中的同位角， 找出方程组中的平行线，从而解出方程组
平行线的性质 课件(共22张PPT)
3
∴∠2=∠3（两直线平行，同位角相等）,
∵∠1=∠3（对顶角相等）,
∴∠1=∠2（等量代换）.
你发现了什么？
两条平行直线被第三条直线所截，内错角相等． 简写成：两直线平行，内错角相等． 表达方式：如图，
∵a∥b(已知)，
∴∠1＝∠2(两直线平行，内错角相等)．
如图，直线a∥b,直线a、b被直线c所截
试一试
翻开你的数学练习横格本，每一页上都有许多如图所示的互 相平行的横线条，随意画一条斜线与这些横线条相交， 找出其中 任意一对同位角.观察或用量角器度量这对同位角，你有什么发现？
∠1＝∠2
那么，一般情况下，如图，如果直线a与直线b平行，直线l与 直线a、b分别交于点O和点P，其中的同位角∠1与∠2也必定相等吗？
A.65°
B.55°
C.45°
D.35°
课堂小结
知识点 平行线的性质
1.两直线平行,同位角 相等 . 2.两直线平行,内错角 相等 . 3.两直线平行,同旁内角 互补 .
已知
同位角相等 内错角相等 同旁内角互补
得到
判定 性质
得到 两直线平行
已知
(2)从∠1=110o可以知道 ∠3是多少度？为什么？
(3)从 ∠1=110 o可以知道∠4 是多少度？为什么？B
D
解：（1）∠2=110o 理由：两直线平行，内错角相等；
（2）∠3=110o 理由：两直线平行,同位角相等；
（3）∠4=70o 理由：两直线平行,同旁内角互补.
C 2E 43
2.如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为 ( B )
例3 将如左图所示的方格图中的图形向右平行移动4格，再向上 平行移动3格，画出平行移动后的图形.
平行线ppt课件
02
平行线判定方法的 误用
提醒学生注意不同判定方法的使 用条件和限制，避免误用或混淆。
03
忽略平行线的存在 性
提醒学生在解题时，不要忽略题 目中可能存在的平行线，否则可 能导致解题错误。
拓展延伸内容推荐
平行线与相似三角形的关系
探讨平行线与相似三角形之间的联系，以及如 何利用平行线的性质解决相似三角形的问题。
交通信号灯
交通信号灯中的红灯、绿灯、黄灯等灯光的排列 也遵循平行线的原则，使得驾驶员和行人能够清 晰地辨认交通信号。
导向标志 道路两侧的导向标志牌上的文字、图案等也采用 平行线排列，方便驾驶员快速获取道路信息。
日常生活用品设计美学体现
家居用品
家居用品中的桌子、椅子、床等家具的设计中经常运用到平行线， 使得家具外观简洁大方，符合现代审美。
图形示例
判定步骤
首先确定两条被截直线和截线，然后 找出同旁内角并测量其角度之和是否 为180度，如果是，则两条直线平行。
在图形中，画出两条被第三条直线所 截的直线，并标出同旁内角。
实际应用场景分析
建筑设计中
在建筑设计中，平行线的概念经常被用来确保建筑物的稳定性和美观性。例如，在设计墙壁、 地板和天花板时，需要确保它们是平行的，以避免出现倾斜或不平整的情况。
在物理学中，平行线的概念被广泛应用于光 学、力学等领域的研究中，如光的反射、折 射等现象都与平行线密切相关。
计算机图形学
工程测量与建设
在计算机图形学中，平行线的绘制和处理是 图形渲染、图像处理等任务中的重要环节之 一。
在工程测量与建设中，平行线的运用可以确 保建筑物的精确度和稳定性，提高工程质量。
05
预备工作
建议学生提前预习相关知识点，回顾平行线的定义、性质及判 定方法，并尝试思考一些与平行线相关的实际问题，为下一讲 的学习做好准备。
5.2.1平行线(新人教版七年级下)PPT课件
❖ （2）平行线指的是“两条直线”，而不是 两条射线或线段；
❖ （3）“不相交”，就是说两条直线没有交 点。
❖ （4）平行线是指在同一平面内的具有特殊 位置关系的两条直线，- 特殊在这两条直线 8
平行线的表示：
我们通常用“//”表示平行。
· · A
B
AB ∥ CD
· · C
D
CD ∥AB
m∥n m
n ∥m -
n
9
做一做
给你一条直线AB，如何画出它的平行线呢？
A
B
可以画多少条平行线呢？
-
10
平行线的画法:
一、放 二、靠 三、推
四、画
-
11
做一做
A
B
可以画多少条平行线呢？ 无数条
-
12
(1)经过点P能画出几条直 线与直线AB平行？
.P
A
BB
① 性质：（平行公理）
经过直线外一点，有且只有一条直 线与这条直线平行。
如果两条直线都和第三条直线平行，那么这两条
直线也互相平行
-
19
1、判断正误：
（1）两条不相交的直线叫做平行线。
（×）
（2）有且只有一个公共点的两直线
是相交直线。
（ √）
（3）在同一平面内的两条直线一定
平行。
（× ）
（4）一个平面内的两条直线，必把
这个平面分为四部分。 （ × ）
-
20
2．下列命题：其中正确的个数是（ C ） （1）长方形的对边所在的直线平行；
E
因为AB//EF，CD//EF 于是过点P就有两条直线AB CD都与EF平行。 根据平行公理，这是不可能的
也就是说，AB与CD不能相交，
❖ （3）“不相交”，就是说两条直线没有交 点。
❖ （4）平行线是指在同一平面内的具有特殊 位置关系的两条直线，- 特殊在这两条直线 8
平行线的表示：
我们通常用“//”表示平行。
· · A
B
AB ∥ CD
· · C
D
CD ∥AB
m∥n m
n ∥m -
n
9
做一做
给你一条直线AB，如何画出它的平行线呢？
A
B
可以画多少条平行线呢？
-
10
平行线的画法:
一、放 二、靠 三、推
四、画
-
11
做一做
A
B
可以画多少条平行线呢？ 无数条
-
12
(1)经过点P能画出几条直 线与直线AB平行？
.P
A
BB
① 性质：（平行公理）
经过直线外一点，有且只有一条直 线与这条直线平行。
如果两条直线都和第三条直线平行，那么这两条
直线也互相平行
-
19
1、判断正误：
（1）两条不相交的直线叫做平行线。
（×）
（2）有且只有一个公共点的两直线
是相交直线。
（ √）
（3）在同一平面内的两条直线一定
平行。
（× ）
（4）一个平面内的两条直线，必把
这个平面分为四部分。 （ × ）
-
20
2．下列命题：其中正确的个数是（ C ） （1）长方形的对边所在的直线平行；
E
因为AB//EF，CD//EF 于是过点P就有两条直线AB CD都与EF平行。 根据平行公理，这是不可能的
也就是说，AB与CD不能相交，
平行线的性质(优质课)获奖课件
3, 1
不是原方程组的解；
(3)把,
②,发现能使方程
x 4,
y
1. 2
①, ②左右两边相等，所以
是原方程组的解.
【跟踪训练】
把下列方程组的解和相应的方程组用线段连起来：
x=1，
y=3-x，
y=2. x=3， y=-2. x=2， y=1.
y3=x2+x2，y=8. x+y=3. y=1-x， 3x+2y=5.
4 5
5.已知2x+3y=4，当x=y 时，x，y的值为_____，当x+y=0时,
-4
4
1
x=_____x，=-y3=______.
2
y=-2
6.已知-1
8
是方3 程2x-4y+2a=3的一个解，则a=______.
8.已知二元一次方程3x-2y=5,若y=0,则x=
.
5
答案： 3
9.下列4组数值中,哪些是二元一次方程2x+y=10的解?
你还累?这么大的 个，才比我多驮 了2个.
哼，我从你背上拿来 1个，我的包裹数就 是你的2倍！
真的?！
我从你背上拿来 1个，我的包裹数 就是你的 2 倍！
你还累?这么大 的个，才比我 多驮了2个.
它们各驮了多少包裹呢?
【解析】设老牛驮了 x 个包裹 , 小马驮了 y个包裹. 老牛的包裹数比小马的多2个,
∵a∥b，∴∠1=∠2，
同理∠2=∠3，∴∠1=∠3，∴a∥c.
【跟踪训练】
根据下列命题，画出图形，并结合图形写出已知、求证
(不写证明过程)：两条平行线的一对内错角的平分线互相
平行.
已知：如图，AB、CD被直线EF所截，且AB∥CD，EG、
《平行线的性质》PPT课件
平行线的性质
- .
如图“三线八角”，把所有的同位角、内错角、同旁内角都找出来（注意分清他们的位置特点）。
a
c
b
4
1
3
2
5
8
7
6
如果图形中的直线a，b是两条平行直线，那么所构成的同位角，内错角，同旁内角之间有什么数量关系哪？
学习目标：1、探索平行线的性质，并能用文字语言、 符号语言表示性质。2、能用性质进行推理和计算。3、理解平行线之间的距离的概念。
你有哪些收获？与同伴交流
小结与回顾
1、如图：AB∥DE，∠B=500，则∠1= ∠2= ∠3= 。
A
B
C
D
E
1
2
3
2、结合右边图形写出推理过程因为AB∥CD（已知）所以 ∠1＝∠ （ ）又因为∠3＝∠2（ ）所以∠1＝∠ （等量代换）因为∠4+∠2＝ （补角定义）所以∠4+∠ ＝180°（等量代换）
解：因为a∥b (已知),所以∠1=∠2(两直线平行,内错 角相等)因为 ∠1= 1060（已知),所以 ∠2= 1060 (等量代换).;因为c∥d(已知),所以∠3=∠2(两直线平行, 同位角相等).又因为 ∠2= 1060（已证)所以∠3=1060 (等量代换)
因为 1+ 2=180°
（补角定义）,
所以 2+ 5=180°
（等量代换）.
两直线平行，同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截， 同旁内角互补.
所以 2+ 5=180°.
因为a∥b,
符号语言:
简写为：
如图,已知直线a∥b,c∥d,∠1 = 1060,求∠2, ∠3的度数.
- .
如图“三线八角”，把所有的同位角、内错角、同旁内角都找出来（注意分清他们的位置特点）。
a
c
b
4
1
3
2
5
8
7
6
如果图形中的直线a，b是两条平行直线，那么所构成的同位角，内错角，同旁内角之间有什么数量关系哪？
学习目标：1、探索平行线的性质，并能用文字语言、 符号语言表示性质。2、能用性质进行推理和计算。3、理解平行线之间的距离的概念。
你有哪些收获？与同伴交流
小结与回顾
1、如图：AB∥DE，∠B=500，则∠1= ∠2= ∠3= 。
A
B
C
D
E
1
2
3
2、结合右边图形写出推理过程因为AB∥CD（已知）所以 ∠1＝∠ （ ）又因为∠3＝∠2（ ）所以∠1＝∠ （等量代换）因为∠4+∠2＝ （补角定义）所以∠4+∠ ＝180°（等量代换）
解：因为a∥b (已知),所以∠1=∠2(两直线平行,内错 角相等)因为 ∠1= 1060（已知),所以 ∠2= 1060 (等量代换).;因为c∥d(已知),所以∠3=∠2(两直线平行, 同位角相等).又因为 ∠2= 1060（已证)所以∠3=1060 (等量代换)
因为 1+ 2=180°
（补角定义）,
所以 2+ 5=180°
（等量代换）.
两直线平行，同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截， 同旁内角互补.
所以 2+ 5=180°.
因为a∥b,
符号语言:
简写为：
如图,已知直线a∥b,c∥d,∠1 = 1060,求∠2, ∠3的度数.
7.4 平行线的性质课件 (30张PPT)北师大版八年级数学上册
所以梯形的另外两个角的度数分别是 80°、65°.
3、如图，由AB//CD，可以得到（C）易错
（A）∠1=∠2
（B）∠2=∠3
（C）∠1=∠4
（D）∠3=∠4
4、如图，已知A、B、C同在一条直线上，D、E、F同在一 条直线上，且∠A=∠F，∠C=∠D，判断AE与BF的位置关 系，并说明理由.
解： ∵∠C=∠D
∴∠1 = ∠D（两直线平行，内错角相等）
∵∠B = ∠D（已知）
∴∠1 = ∠B（等量代换）
∴AD∥BC（同位角相等，两直线平行）
D C
例2 已知：如图，AB∥CD，∠B =∠D.
求证：AD∥BC. 证法三： 如图，连接 BD (构造两组内错角). ∵ AB∥CD (已知)，
A
12
B
D
3 4
C
∴∠1 =∠4 (两直线平行，内错角相等).
条直线与这条直线平行”相矛盾. 这说明∠1 ≠ ∠2 的假设不成立，所以 ∠1 =∠2.
总结归纳
一般地，平行线具有如下性质： 性质1 （定理） 两条平行线被第三条直线所截，同位角
简单说成：两直线平行，同位角相等.
c
应用格式：
1
∵ a∥b（已知），
a
∴∠1 =∠2
2
（两直线平行，同位角相等）. b
议一议
(1) 从∠1 = 110° 可以知道∠2 是多少度？为什么？
(2) 从∠1 = 110° 可以知道∠3 是多少度？为什么？
(3) 从∠1 = 110° 可以知道∠4 是多少度？为什么？
解：(1) ∠2 = 110°，
两直线平行，内错角相等. （2）∠3 = 110°，
两直线平行，同位角相等. （3）∠4 = 70°，
《平行线的性质》课件(共33张PPT)000
如图，是举世闻名的三星堆考古中发掘出 的一个梯形残缺玉片，工作人员从玉片上已经 量得∠A=115°，∠D=110°。已知梯形的两底 AD//BC，请你求出另外两个角的度数。
A
D
115° 110°
B
C
苹果
草莓
梨子
桃子
香蕉
桔子
西瓜
桃子题：
如图，梯子的各条横档互相平行， ∠1=1000，求∠2的度数。
解：∠1=∠3； ∠2 =∠4 理由如下：
∵AB∥DE （已知） A
DC
F
∴∠1=∠3(两直线平行， 同位角相等) ∵ ∠1=∠2 ，∠3=∠4
1
23
4
B
E
∴ ∠2=∠4 （等量代换）
（2 ）反射光线BC与EF也平行吗？
平行：∵ ∠2=∠4 ∴ BC∥EF(同位角相等,两直
线平行)
比一比 、乐一乐：（分组比赛）
4
31
56
8
7
∠1=∠5
a b
探索新知
①已知直线a，画直线b，使b∥a，c
②任画截线c，使它与a、
11718°25°8°b
b都相交，则图中∠1与 ∠2是什么角？它们的 大小有什么关系？
21185728°° a
③旋转截线c，同位角
∠1与∠2的大小关系又
如何？ ∠1＝∠2
通过上面的实验测量，可以得到性质1(公理)：
3 2
目前，它与 地面所成的 较小的角
为∠1=85º
1
苹果
草莓
梨子
桃子
香蕉
桔子
西瓜
杨梅
草莓题：
1 A
D
B
C
1、如果AD//BC，根据___________ 可得∠B= _______
北师大版八年级数学上册《平行线的性质》平行线的证明PPT课件
例1：如图所示，已知四边形ABCD 中， AB∥CD，
AD∥BC,试问∠A与∠C，∠B与∠D 的大小关系如何？
A
D
解：∠A= ∠ C, ∠B=∠D.
理由：∵AB∥CD （已知 ）
B
C
∴∠B+∠C=180°（两直线平行，同旁内角互补 ）
又 ∵ AD∥BC （已知）
∴∠C+∠D=180°（ 两直线平行，同旁内角互补 ）
C
∴∠1=∠4（两直线平行，内错角相等）
∵∠B=∠D（已知）
∴∠B－∠1=∠D－∠4（等式的性质）
∴∠2=∠3
∴AD∥BC（内错角相等，两直线平行）
平行线的判定与性质
讨论：平行线三个性质的条件是什么？结论是
什么？它与判定有什么区别？（分组讨论）
线的关系
判定
角的关系
平行线的判定 两直线平行
平行线的性质
所以∠BDF=∠EDF.
课堂小结
已知
同位角相等 内错角相等 同旁内角互补
得到
判定 性质
得到 两直线平行
已知
已知：直线a∥b，∠1和∠2是直
线a，b被直线c截出的同旁内角. a
求证： ∠1+∠2=180°.
b
证明：∵a∥b (已知)
c
3 1
2
∴∠2＝∠3 (两条直线平行，同位角相等)
∵∠1+∠3 =180°(平角等于180°)
∴∠1+∠2=180 °(等量代换) .
定理：如果两条直线都和第三条直线平行， 那么这两条直线也互相平行.
两直线平行,同旁内角互补.
a
∵ a∥b, ∴ ∠1+∠2=1800 .
b
《平行线的性质》PPT
∵ ∠2=∠3 ( 对顶角相等)
C
1
D
∴∠1=∠2 ( 等量代换 )
F
7-5-2
结论:两直线平行,内错角相等
如图7-5-3， AB∥CD,直线AB，CD被直线EF所截， ∠1和∠2是同旁内角.对∠1+∠2=180°说明理由:
E
理由：
∵ AB∥CD （ 已知）
A
∴ ∠1=∠3 ( 两直线平行，同位角相等)
巩固练习：
A1
D
B
C
1、如果AD//BC，根据__两__直__线__平__行__，__同__位__角__相__等____
可得∠B=∠1 2、如果AB//CD，根据__两__直__线__平__行__，__内__错__角__相__等_____
可得∠D＝∠1 3、如果AD//BC，根据__两__直__线__平__行__，__同__旁__内__角__互__补___
为什么？
（2）由∠1=∠5.能推出两对同旁内角互补吗？为什么？
65
a 78
21 b
34
l 7-5-1
如图7-5-2， AB∥CD,直线AB，CD被直线EF所截，∠1和∠2是 内错角.对∠1=∠2说过程如下:
理由：∵ AB∥CD ( 已知 ) ∴ ∠1=∠3 ( 两直线平行，)同位角相A等
E
3 2
B
考考你：
3、如图是举世闻名的三星堆考古中发掘出的一个梯形 残缺玉片，工作人员从玉片上已经量得∠A=115°， ∠D=100°。已知梯形的两底AD//BC，请你求出另外 两个角的度数。
一起探究：如果两个角的两条边分别平行，那么这两 个角的大小有什么关系？
G
G F
A
E
《平行线的性质》课件
反向平行线的性质
• 反向平行线具有相反的斜率。 • 反向平行线之间的距离保持不变。
三、平行线的特殊角度
同位角及其性质
• 同位角是两条平行线 之间的对应角，它们
• 相同等 位。 角具有相等的补 角、余角。
内错角及其性质
• 内错角是两条平行线 之间的相交角，它们
• 互内补错。角具有相等的对 顶角。
相关角及其性质
《平行线的性质》PPT课 件
这是一份关于平行线的精彩课件，通过介绍平行线的基本定义、性质、应用、 证明，并进行综合练习，帮助大家深入理解和应用平行线的知识。
一、基本定义
平行线的概念
平行线是永远不会相交的两条直线。
平行线的符号表示
用“//”表示两条线段平行。
二、平行线的性质
同向平行线的性质
• 同向平行线具有相等的斜率。 • 同向平行线之间的距离保持不变。
对平行线的思考与感悟
通过学习平行线的性质，反思几何学对我们日常生活的影响和意义。
• 相关角是两条平行线 之间的内角与外角。
• 相关角之和等于180°。
四、平行线的应用
1
平行线的实际应用
2
例如，在城市规划中，平行线可用于 规划马路的设计和建设。
平行线的应用场景
平行线的应用广泛，如建筑设计、地 图制作等。
五、平行线的证明
平行线的证明方法
通过等角、等比和等边等多种证明方法来证明平行线。
平行线证明例题
通过实例演示如何在几何问题中使用平行线的证明。
六、综合练习
பைடு நூலகம்
1
综合运用平行线的知识解题
通过题目练习，提升对平行线性质的理解和应用能力。
2
平行线的综合练习题
平行线的判定及性质课件
05
总结与展望
总结
01
02
03
04
05
直线平行的定义
直线平行的判定 方法
直线平行的性质
平行线在实际生 活中的应用
平行线在数学中 的地位
在同一平面内，不相交的 两条直线叫做平行线。
同位角相等，两直线平行 ；内错角相等，两直线平 行；同旁内角互补，两直 线平行。
两直线平行，同位角相等 ；两直线平行，内错角相 等；两直线平行，同旁内 角互补。
在几何图形中，平行线具 有非常重要的应用价值， 如矩形、菱形、正方形等 都有平行线的性质。
平行线是数学几何学中的 重要概念之一，是研究平 面图形性质的基础之一。 掌握平行线的判定方法和 性质对于学习数学几何学 非常重要。
展望
进一步探索平行线的性质
加强实际应用
除了已经学习的平行线的基本性质外，还 有许多复杂的性质和定理，值得进一步探 索和学习。
详细描述
在制造业中，机器人使用平行线来定位和移动物体，进行高效和精确的生产操作。例如 ，在汽车制造中，机器人通过使用平行线来定位和抓取车辆部件，以提高生产效率和质 量。在医疗领域，手术机器人使用平行线来精确控制手术器械，提高手术的准确性和安
全性。
04
平行线在数学问题中 的应用
代数中与平行线相关的知识点
在道路交通中，平行线是确保车辆安全行驶的重要标志。它们被用来划分车道、标识道路边缘以及引 导驾驶员在正确的车道上行驶。在高速公路上，平行线被用来表示应急车道和车道分隔线，帮助驾驶 员在紧急情况下做出正确的反应。
机器人在工作中的应用
总结词
机器人广泛应用于生产制造、医疗服务和军事等领域，平行线在机器人的工作中发挥着 重要作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例如：
两条直线被第三条直线所截，同位角相等
题设
结论
写成如果…那么…的形式怎么写？
2020年10月2日
6
再如： 对 顶 角 相 等 题设 结论
如果两个角是对顶角，那么这两个角相等
如果一个命题的结论正确，那么这个命题 就是一个真命题，否则就是一个假命题
举出几个命题，说出命题的真假
2020年10月2日
7
复习回顾
2020年10月2日
新课学习
课堂小结 1
1．平行线的判定方法有哪些？ 2．平行线的性质有哪些？
已知
同位角相等 内错角相等 同旁内角互补
判定
得到
两直线平行
性质
得到 2020年10月2日
已知
2
实践与探究
两条平行线间平行线段的长度
用三角尺和直尺画平行线，做成一张
55 个格子的方格纸。观察并思考：
• 练习说出下列命题的题设和结论，并说明其真 假性。
• 1 如果直线a//b,b//c,那么，a//c • 2如果一直线和两条平行线中的一条垂直，那么这
条直线也和另一条垂直
• 3 两个负数之积为正数 • 4 等角的补角相等 • 5若ab＞0，则a＞0，b＞0 • 6如果两个角不是对顶角，那么它们不相等
汇报人：XXX 汇报日期：20XX年10月10日
9
（1）如果两条直线都与第三条直线平行， 那么这两条直线也平行。
（2）对顶角相等
（3）等式两边同加上同一个数，结果仍 是等式
这些句子都是对某一件事情作出
“是”或“不是”的判断
判2020断年10月一2日 件事情的句子， 叫做命题
5
命题由题设和结论两部分组成，
题设是已知项， 结论是由已知项推出的事项 通常写成 “如果…,那么…” 形式
… B1C1,B2C2
B5C 5
都与两条平行线 A1B5,A2C5
垂直吗？
它们的长度相等吗？
2020年10月2日
3
两条平行线的距离：
同时垂直于两条平行线，并且夹在这 两条平行线间的线段长度叫做两条平 行线的距离。
两条平行线的距离处处相等，
而不随垂线段的位置而改变。
2020年10月2日
4
下列语句，分析语句的特点
2020年10月2日
8
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
两条直线被第三条直线所截，同位角相等
题设
结论
写成如果…那么…的形式怎么写？
2020年10月2日
6
再如： 对 顶 角 相 等 题设 结论
如果两个角是对顶角，那么这两个角相等
如果一个命题的结论正确，那么这个命题 就是一个真命题，否则就是一个假命题
举出几个命题，说出命题的真假
2020年10月2日
7
复习回顾
2020年10月2日
新课学习
课堂小结 1
1．平行线的判定方法有哪些？ 2．平行线的性质有哪些？
已知
同位角相等 内错角相等 同旁内角互补
判定
得到
两直线平行
性质
得到 2020年10月2日
已知
2
实践与探究
两条平行线间平行线段的长度
用三角尺和直尺画平行线，做成一张
55 个格子的方格纸。观察并思考：
• 练习说出下列命题的题设和结论，并说明其真 假性。
• 1 如果直线a//b,b//c,那么，a//c • 2如果一直线和两条平行线中的一条垂直，那么这
条直线也和另一条垂直
• 3 两个负数之积为正数 • 4 等角的补角相等 • 5若ab＞0，则a＞0，b＞0 • 6如果两个角不是对顶角，那么它们不相等
汇报人：XXX 汇报日期：20XX年10月10日
9
（1）如果两条直线都与第三条直线平行， 那么这两条直线也平行。
（2）对顶角相等
（3）等式两边同加上同一个数，结果仍 是等式
这些句子都是对某一件事情作出
“是”或“不是”的判断
判2020断年10月一2日 件事情的句子， 叫做命题
5
命题由题设和结论两部分组成，
题设是已知项， 结论是由已知项推出的事项 通常写成 “如果…,那么…” 形式
… B1C1,B2C2
B5C 5
都与两条平行线 A1B5,A2C5
垂直吗？
它们的长度相等吗？
2020年10月2日
3
两条平行线的距离：
同时垂直于两条平行线，并且夹在这 两条平行线间的线段长度叫做两条平 行线的距离。
两条平行线的距离处处相等，
而不随垂线段的位置而改变。
2020年10月2日
4
下列语句，分析语句的特点
2020年10月2日
8
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!