高二下学期期末复习5
高二下学期数学复习讲义(5) 排列组合综合应用

高二下学期数学复习讲义(5)排列组合综合应用一、复习目标:在理解排列、组合的意义的基础上解决一些简单的综合问题。
二、基础训练:1.某天上午要排语文、数学、体育、计算机共4课,其中体育不能排在第一节,那么课表的不同排法有 ( )()A 6 ()B 9 ()C 18 ()D 242.从10种不同的作物种子中选出6种放入6个不同的瓶子展览,如果甲、乙两种种子不许放入第一号瓶内,那么不同的方法有 ( )()A 24108C A ()B 1599C A ()C 1589A A ()D 15992C A3.四个不同的小球全部随意放入三个不同的盒子中,使每个盒子都不空,不同的放法共有 ( ) ()A 72种 ()B 36种 ()C 26种 ()D 40种4.小于50000且含有两个5而其他数字不重复的五位数有 ( )()A 122448A A A 个 ()B 122448C C A 个 ()C 122448C C C 个 ()D 124484C C A 个5.由数字0,1,2,3,4,5组成没有重复数字的6位数,其中个位数字小于十位数字的共有 个.6.从6名运动员中选出4名参加4100 米接力赛,如果甲不跑第一棒,乙不跑第四棒,共有种不同的参赛方法.7.有一块并排10垄的田地中,选择2垄分别种植A 、B 两种作物,每一种作物种植一垄,为了有利于作物生长,要求A 、B 两种作物的间隔不小于6垄,则不同的种植方法有 .三、例题分析:例1.5人站成一排,求在下列条件下的不同排法种数,(1)共有多少种排法? (2)甲必在排头; (3)甲在排头,且乙在排尾;(4)甲乙必在两端; (5)甲不在排头; (6)甲不在排头,且乙不在排尾;(7)甲乙不在两端; (8)甲在乙先; (9)甲在乙先,且乙在丙先;(10)甲乙相邻; (11)甲乙丙相邻; (12)甲乙不相邻; (13)甲乙丙不相邻.例2.有10人组成的篮球队中,有5人只适合打前锋,3人只适合打后卫,2人打前锋打后卫均可,现在选择5人参加比赛(3前锋2后卫),问教练共有多少种不同阵容的安排方法?(仅以前锋、后卫区分)例3.有6本不同的书,分给甲、乙、丙三人,(1)如果每人得2本,有几种分法?(2)如果甲得1本,乙得2本,丙得3本,有几种分法?(3)如果一人得1本,一人得2本,一人得3本,有几种分法?例4.不定方程1250100x x x+++=中,(1)不同的正整数解共多少组?(2)不同的非负整数解共多少组?四、课后作业: 班级 学号 姓名1.由1,4,5,x 四个数字组成没有重复数字的四位数,若所有这些数字各位上的数字之和为288,则数字x 等于 ( ) ()A 1 ()B 2 ()C 3 ()D 62.现有1个碱基A ,2个碱基C ,3个碱基G ,这六个碱基组成的不同的碱基序列( ) ()A 20 ()B 60 ()C 120 ()D 903.若12341001234100s A A A A A =+++++,则s 的个位数字是 ( ) ()A 8 ()B 5 ()C 3 ()D 04.已知*,,m n N m n ∈≤,其中n 为定值,要使m n A 有最大值,则m 的值是 ( )()A m n = ()B 1m n =-()C m n =或1m n =- ()D 不能确定5.从1到100的自然数中,每次取出不同的两个数,使它们的和大于100,则不同的取法有 。
江苏省姜堰市张甸中学2013-2014学年高二下学期数学(文)期末复习(5) 有答案

1、函数)(x f 的图象向右平移1个单位长度,所得图象与曲线x e y =关于y 轴对称,则)(x f =2、已知函数=≥⎩⎨⎧<-≥-=-=))((,31,0,2,0,1)(,13)(2x f g x x x x x x g x x f 则若 3、若命题p :5≠+y x ,命题q :2≠x 或3≠y ,则命题p 是命题q 成立的 条件;4、已知)32(log )(22--=x x x f 的单调增区间为5、曲线y=x 3+3x 2+6x-10的切线中,斜率最小的切线方程是6、已知12121=+==z z z z ,则21z z -等于7、设f (x )为定义在R 上的奇函数,当x ≤0时,f (x )=2x+2x +m (m 为常数),则f (1)= _____8、函数),0(1)1(3)(223>+-+-=k k x k kx x f 的单调减区间是(0,4),则实数=k9、若1x y +=,则22x y +的最小值为 10、已知函数2,1()1,1x ax x f x ax x ⎧-+≤=⎨->⎩ 若1212,,x x R x x ∃∈≠,使得12()()f x f x =成立,则实数a 的取值范围是11、对于大于1的自然数m 的3次幂有如下分解方式:,191715134,11973,532333+++=++=+=根据上述分解规律,若()*∈N m m 3的分解中有一个数为59,则m= ;12、已知)1lg()1lg(---=x ax y 在),10(+∞上是增函数,则a 的取值范围 ;13、设a ,b >0,且ab =1,不等式a a 2+1+b b 2+1≤λ恒成立,则λ的取值范围是_______14、已知,1ln 2)(x x x f -=对于任意的()+∞∈,0,21x x ,有,11)()(2121x x m x f x f -≥-则实数m 的取值范围为15、求二次函数f(x) = x 2-4x - 1在区间[t ,t +2]上的最小值g(t),其中t ∈R .16、已知函数()e e x x f x -=+其中e 是自然对数的底数.(1)证明:()f x 是R 上的偶函数;(2)若关于x 的不等式()e1x mf x m -+-≤在(0)+∞,上恒成立,求实数m 的取值范围;19、已知函数1()()2ln ()f x a x x a x=--∈R . (1)若2a =,求曲线()y f x =在点(1,(1))f 处的切线方程;(2)求函数()f x 的单调区间;(3)设函数()a g x x =-.若至少存在一个0[1,e]x ∈,使得00()()f x g x >成立,求实数a 的取值范围.20、已知函数xx x f ln 1)(+= (1)若函数f (x )在区间(a ,a+1)上有极值,求实数a 的取值范围 (2)当n ∈N*,n ≥2时,求证:nf (n )<2+113121-+++n (提示:证明)0(,)1l n (><+x x x )15、解:函数f(x) = (x -2)2-5的图象的对称轴方程为x =2,开口向上.当2∈[t ,t +2],即t ≤2≤t +2,也就是0≤t ≤2时,g(t)=f(2)=-5;当2[t ,t +2]时,①当t >2时,f(x)在[t ,t +2]上为增函数,故g(t)=f(t)=t 2-4t -1.②当t +2<2,即t <0时,f(x)在[t ,t +2]上为减函数,故g(t)=f(t +2)=(t +2)2-4(t +2)-1=t 2-5.故g(t)的解析式为g(t)=⎩⎪⎨⎪⎧t 2-4t -1,t >2,-5,0≤t ≤2,t 2-5,t <0.17、【答案】(I) a=2, (II) 23a ≤≤.19、【答案】(1)220x y --=;(2)0a ≤时,()f x 在(0,)+∞上单调递减;当01a <<时,单调递增区间为211(0,)a a --和211(,)a a+-+∞,单调递减区间为221111(,)a a a a--+-;1a ≥时,()f x 在(0,)+∞上单调递增;(3)实数a 的取值范围为(0,)+∞.(1)当2a =时,函数1()2()2ln f x x x x=--,(1)0f =,(1)2f '= 所以曲线()y f x =在点(1,(1))f 处的切线方程为02(1)y x -=-即220x y --= 4分(2)函数()f x 的定义域为(0,)+∞1.当0a ≤时,2()20h x ax x a =-+<在()0,+∞上恒成立 则()0f x '<在(0,)+∞上恒成立,此时()f x 在(0,)+∞上单调递减 5分2.当0a >时,244a ∆=-(ⅰ)若01a << 由()0f x '>,即()0h x >,得211a x a --<或211a x a+-> 6分 由()0f x '<,即()0h x <,得221111a a x a a--+-<< 7分 所以函数()f x 的单调递增区间为211(0,)a a --和211(,)a a+-+∞,单调递减区间为221111(,)a a a a--+- 9分 (ⅱ)若1a ≥,()0h x ≥在(0,)+∞上恒成立,则()0f x '≥在(0,)+∞上恒成立,此时()f x 在(0,)+∞上单调递增 10分 综上可知:0a ≤时,()f x 在(0,)+∞上单调递减;当01a <<时,单调递增区间为211(0,)a a --和211(,)a a +-+∞,单调递减区间为221111(,)a a a a--+-;1a ≥时,()f x 在(0,)+∞上单调递增(3)因为存在一个0[1,e]x ∈使得00()()f x g x >则002ln ax x >,等价于002ln x a x >12分 令2ln ()x F x x=,等价于“当[]1,e x ∈ 时,()min a F x >” 对()F x 求导,得22(1ln )()x F x x -'= 13分 因为当[1,e]x ∈时,()0F x '≥,所以()F x 在[1,e]上单调递增 所以min ()(1)0F x F ==,因此0a > 16分。
高中高二数学下学期期末复习试卷(含解析)-人教版高二全册数学试题

2014-2015学年某某省某某市东海县石榴高中高二(下)期末数学复习试卷一、填空题:1.已知集合P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},则P∩Q=.2.若复数z1=3+4i,z2=1+2i(i是虚数单位),则z1﹣z2=.3.命题:∀x∈R,sinx<2的否定是.4.复数z=(1+3i)i(i是虚数单位),则z的实部是.5.已知函数y=f(x),x∈[0,2π]的导函数y=f′(x)的图象,如图所示,则y=f(x)的单调增区间为.6.已知则满足的x值为.7.函数在[2,4]上是增函数的充要条件是m的取值X围为.8.已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值X 围是.9.设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为35,则a+b的最小值为.10.曲线在点(4,e2)处的切线与坐标轴所围三角形的面积为.11.在平面直角坐标系xOy中,若直线y=2a与函数y=|x﹣a|﹣1的图象只有一个交点,则a的值为.12.已知实数a,b,c满足a+b+c=9,ab+bc+ca=24,则b的取值X围是.13.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是.14.观察下面的数阵,第20行第20个数是.12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 25…二、解答题(共6小题,满分0分)15.给定两个命题:p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2﹣x+a=0有实数根,如果p和q中至少有一个为真命题,某某数a的取值X围.16.已知复数z1满足(z1﹣2)(1+i)=1﹣i(i为虚数单位),复数z2的虚部为2,且z1•z2是实数,求z2.17.已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:(Ⅰ)x0的值;(Ⅱ)a,b,c的值.18.因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放a(1≤a≤4,且a∈R)个单位的药剂,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=a•f(x),其中f(x)=.若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?(Ⅱ)若第一次投放2个单位的药剂,6天后再投放a个单位的药剂,要使接下来的4天中能够持续有效治污,试求a的最小值(精确到0.1,参考数据:取1.4).19.试比较n n+1与(n+1)n(n∈N*)的大小,分别取n=1,2,3,4,5加以试验,根据试验结果猜测一个一般性结论.20.对于定义在区间D上的函数f(x)和g(x),如果对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,那么称函数f(x)在区间D上可被函数g(x)替代.(1)若,试判断在区间[[1,e]]上f(x)能否被g(x)替代?(2)记f(x)=x,g(x)=lnx,证明f(x)在上不能被g(x)替代;(3)设,若f(x)在区间[1,e]上能被g(x)替代,某某数a的X围.2014-2015学年某某省某某市东海县石榴高中高二(下)期末数学复习试卷参考答案与试题解析一、填空题:1.已知集合P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},则P∩Q={0,2} .考点:交集及其运算.专题:计算题.分析:通过理解集合的表示法化简集合P和集合Q,两集合的交集是集合P和Q中的共同的数.解答:解:∵P={﹣4,﹣2,0,2,4},Q={x|﹣1<x<3},∴P∩Q={0,2}故答案为:{0,2}点评:本题考查集合的表示法、集合交集的求法.2.若复数z1=3+4i,z2=1+2i(i是虚数单位),则z1﹣z2= 2+2i .考点:复数代数形式的加减运算.专题:计算题.分析:根据复数减法的运算法则,当且仅当实部与虚部分别相减可求.解答:解:Z1﹣Z2=(3+4i)﹣(1+2i)=2+2i故答案为:2+2i点评:本题主要考查了复数减法的基本运算,运算法则:当且仅当实部与虚部分别相减,属于基础试题.3.命题:∀x∈R,sinx<2的否定是“∃x∈R,sinx≥2”.考点:命题的否定.分析:根据命题“∀x∈R,sinx<2”是全称命题,其否定为特称命题,即“∃x∈R,sinx≥2”.从而得到本题答案.解答:解:∵命题“∀x∈R,sinx<2”是全称命题.∴命题的否定是存在x值,使sinx<2不成立,即“∃x∈R,sinx≥2”.故答案为:“∃x∈R,sinx≥2”.点评:本题给出全称命题,求该命题的否定形式.着重考查了含有量词的命题的否定、全称命题和特称命题等知识点,属于基础题.4.复数z=(1+3i)i(i是虚数单位),则z的实部是﹣3 .考点:复数的基本概念.专题:计算题.分析:利用两个复数代数形式的乘法,虚数单位i的幂运算性质,化简=(1+3i)i,依据使不得定义求得z的实部.解答:解:复数z=(1+3i)i=﹣3+i,故实部为﹣3,故答案为﹣3.点评:本题考查两个复数代数形式的乘法,虚数单位i的幂运算性质,以及复数为实数的条件.5.已知函数y=f(x),x∈[0,2π]的导函数y=f′(x)的图象,如图所示,则y=f(x)的单调增区间为[0,π].考点:函数的单调性与导数的关系.专题:数形结合.分析:根据据f′(x)≥0,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减;从图中找到f′(x)≥0的区间即可.解答:解:据f′(x)≥0,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减由图得到x∈[0,π]时,f′(x)≥0故y=f (x)的单调增区间为[0,π]故答案为[0,π]点评:本题考查函数的单调性与导函数符号的关系:f′(x)≥0时,函数f(x)单调递增;f′(x)≤0时,f(x)单调递减6.已知则满足的x值为 3 .考点:分段函数的解析式求法及其图象的作法;函数的值.分析:分x≤1和x>1两段讨论,x≤1时,得,x>1时,得,分别求解.解答:解:x≤1时,f(x)=,x=2,不合题意,舍去;x>1时,,=3综上所示,x=3故答案为:3点评:本题考查分段函数求值问题,属基本题.7.函数在[2,4]上是增函数的充要条件是m的取值X围为.考点:利用导数研究函数的单调性;必要条件、充分条件与充要条件的判断.专题:计算题.分析:先求导函数,要使函数在[2,4]上是增函数,则﹣x2+mx+2≥0在[2,4]上恒成立,故可建立不等式,解之即可求得m的取值X围.解答:解:求导函数要使函数在[2,4]上是增函数,则﹣x2+mx+2≥0在[2,4]上恒成立,构建函数g(x)=﹣x2+mx+2,因为函数图象恒过点(0,2),所以﹣x2+mx+2≥0在[2,4]上恒成立,只需m根据函数的单调递增,解得,即所求m的X围为故答案为:点评:本题考查利用导数研究函数的单调性,解题的关键是求导函数,将问题转化为﹣x2+mx+2≥0在[2,4]上恒成立.8.已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值X 围是﹣1≤a<7 .考点:函数在某点取得极值的条件.专题:计算题.分析:首先利用函数的导数与极值的关系求出a的值,由于函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,所以f′(﹣1)f′(1)<0,进而验证a=﹣1与a=7时是否符合题意,即可求答案.解答:解:由题意,f′(x)=3x2+4x﹣a,当f′(﹣1)f′(1)<0时,函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,解得﹣1<a<7,当a=﹣1时,f′(x)=3x2+4x+1=0,在(﹣1,1)上恰有一根x=﹣,当a=7时,f′(x)=3x2+4x﹣7=0在(﹣1,1)上无实根,则a的取值X围是﹣1≤a<7,故答案为﹣1≤a<7.点评:考查利用导数研究函数的极值问题,体现了数形结合和转化的思想方法.9.设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为35,则a+b的最小值为8 .考点:简单线性规划.专题:计算题;压轴题;数形结合.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再根据目标函数z=abx+y(a>0,b>0)的最大值为35,求出a,b的关系式,再利用基本不等式求出a+b的最小值.解答:解:满足约束条件的区域是一个四边形,如图4个顶点是(0,0),(0,1),(,0),(2,3),由图易得目标函数在(2,3)取最大值35,即35=2ab+3∴ab=16,∴a+b≥2 =8,在a=b=8时是等号成立,∴a+b的最小值为8.故答案为:8点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.10.曲线在点(4,e2)处的切线与坐标轴所围三角形的面积为e2.考点:定积分在求面积中的应用.专题:计算题.分析:先利用复合函数求导法则求已知函数的导函数,再利用导数的几何意义求切线斜率,进而利用直线的点斜式写出切线方程,最后求直线与坐标轴的交点,计算直角三角形的面积即可解答:解:y′=,y′|x=4=e2∴曲线在点(4,e2)处的切线方程为y﹣e2=e2(x﹣4)即y=e2x﹣e2令x=0,得y=﹣e2,令y=0,得x=2∴此切线与坐标轴所围三角形的面积为×2×e2=e2故答案为e2点评:本题主要考查了导数的几何意义,求曲线在某点出的切线方程的方法,利用导数求切线方程是解决本题的关键11.在平面直角坐标系xOy中,若直线y=2a与函数y=|x﹣a|﹣1的图象只有一个交点,则a的值为.考点:函数的零点与方程根的关系.专题:函数的性质及应用.分析:由已知直线y=2a与函数y=|x﹣a|﹣1的图象特点分析一个交点时,两个图象的位置,确定a.解答:解:由已知直线y=2a是平行于x轴的直线,函数y=|x﹣a|﹣1的图象是折线,所以直线y=2a过折线顶点时满足题意,所以2a=﹣1,解得a=﹣;故答案为:.点评:本题考查了函数的图象;考查利用数形结合求参数.12.已知实数a,b,c满足a+b+c=9,ab+bc+ca=24,则b的取值X围是[1,5].考点:函数最值的应用.专题:计算题;综合题.分析:根据a+b+c=9,ab+bc+ca=24,得到a+c=9﹣b,并代入ab+bc+ca=24,得到ac=24﹣(a+c)b,然后利用基本不等式ac,即可求得b的取值X围.解答:解:∵a+b+c=9,∴a+c=9﹣b,∵ab+ac+bc=(a+c)b+ac=24,得ac=24﹣(a+c)b;又∵ac,∴24﹣(a+c)b,即24﹣(9﹣b)b,整理得b2﹣6b+5≤0,∴1≤b≤5;故答案为[1,5].点评:此题考查了利用基本不等式求最值的问题,注意基本不等式成立的条件为一正、二定、三等,以及消元思想的应用,属中档题.13.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是(﹣∞,﹣3)∪(0,3).考点:利用导数研究函数的单调性;函数奇偶性的性质.专题:导数的概念及应用.分析:构造函数h(x)=f(x)g(x),利用已知可判断出其奇偶性和单调性,进而即可得出不等式的解集.解答:解:令h(x)=f(x)g(x),则h(﹣x)=f(﹣x)g(﹣x)=﹣f(x)g(x)=﹣h(x),因此函数h(x)在R上是奇函数.①∵当x<0时,h′(x)=f′(x)g(x)+f(x)g′(x)>0,∴h(x)在x<0时单调递增,故函数h(x)在R上单调递增.∵h(﹣3)=f(﹣3)g(﹣3)=0,∴h(x)=f(x)g(x)<0=h(﹣3),∴x<﹣3.②当x>0时,函数h(x)在R上是奇函数,可知:h(x)在(0,+∞)上单调递增,且h (3)=﹣h(﹣3)=0,∴h(x)<0,的解集为(0,3).∴不等式f(x)g(x)<0的解集是(﹣∞,﹣3)∪(0,3).故答案为(﹣∞,﹣3)∪(0,3).点评:恰当构造函数,熟练掌握函数的奇偶性单调性是解题的关键.14.观察下面的数阵,第20行第20个数是381 .12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 25…考点:归纳推理.专题:综合题;推理和证明.分析:观察这个数列知,第n行的最后一个数是n2,第19行的最后一个数是192=361,由此可求出第20行第20个数.解答:解:观察这个数列知,第n行的最后一个数是n2,第19行的最后一个数是192=361,∴第20行第20个数是361+20=381.故答案为:381.点评:本题给出三角形数阵,求第20行第20个数,着重考查了递归数列和归纳推理等知识点,属于基础题.二、解答题(共6小题,满分0分)15.给定两个命题:p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2﹣x+a=0有实数根,如果p和q中至少有一个为真命题,某某数a的取值X围.考点:复合命题的真假.专题:简易逻辑.分析:根据二次函数恒成立的充要条件,我们可以求出命题p为真时,实数a的取值X围,根据二次函数有实根的充要条件,我们可以求出命题q为真时,实数a的取值X围,则命题p,q中一个为真,分类讨论后,即可得到实数a的取值X围.解答:解:对任意实数x都有ax2+ax+1>0恒成立⇔a=0或⇔0≤a<4;关于x的方程x2﹣x+a=0有实数根⇔△=1﹣4a≥0⇔a≤;p和q中至少有一个为真命题如果p真q假,则有0≤a<4,且a>,∴<a<4;如果p假q真,则有a<0,或a≥4,且a≤∴a<0;如果p真q真,则有0≤a<4,且a≤,∴0≤a≤;所以实数a的取值X围为(﹣∞,4)点评:本题考查的知识点是命题的真假判断与应用,复合命题的真假,函数恒成立问题,其中判断出命题p与命题q为真时,实数a的取值X围,是解答本题的关键.16.已知复数z1满足(z1﹣2)(1+i)=1﹣i(i为虚数单位),复数z2的虚部为2,且z1•z2是实数,求z2.考点:复数代数形式的混合运算.专题:计算题.分析:利用复数的除法运算法则求出z1,设出复数z2;利用复数的乘法运算法则求出z1•z2;利用当虚部为0时复数为实数,求出z2.解答:解:∴z1=2﹣i设z2=a+2i(a∈R)∴z1•z2=(2﹣i)(a+2i)=(2a+2)+(4﹣a)i∵z1•z2是实数∴4﹣a=0解得a=4所以z2=4+2i点评:本题考查复数的除法、乘法运算法则、考查复数为实数的充要条件是虚部为0.17.已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:(Ⅰ)x0的值;(Ⅱ)a,b,c的值.考点:利用导数研究函数的极值.专题:计算题.分析:(1)观察图象满足f′(x)=0的点附近的导数的符号的变化情况,来确定极大值,求出x0的值;(2)根据图象可得f'(1)=0,f'(2)=0,f(1)=5,建立三个方程,联立方程组求解即可.解答:解:(Ⅰ)由图象可知,在(﹣∝,1)上f'(x)>0,在(1,2)上f'(x)<0.在(2,+∝)上f'(x)>0.故f(x)在(﹣∝,1),(2,+∝)上递增,在(1,2)上递减.因此f(x)在x=1处取得极大值,所以x0=1.(Ⅱ)f'(x)=3ax2+2bx+c,由f'(1)=0,f'(2)=0,f(1)=5,得解得a=2,b=﹣9,c=12.点评:本题主要考查了利用导数研究函数的极值,以及观察图形的能力,属于基础题.18.因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放a(1≤a≤4,且a∈R)个单位的药剂,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=a•f(x),其中f(x)=.若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?(Ⅱ)若第一次投放2个单位的药剂,6天后再投放a个单位的药剂,要使接下来的4天中能够持续有效治污,试求a的最小值(精确到0.1,参考数据:取1.4).考点:函数模型的选择与应用.专题:函数的性质及应用.分析:(Ⅰ)通过a=4可知y=,分别令每段对应函数值大于等于4,计算即得结论;(Ⅱ)通过化简、利用基本不等式可知y=2•(5﹣x)+a[﹣1]=(14﹣x)+﹣a﹣4≥﹣a﹣4,再令﹣a﹣4≥4,计算即得结论.解答:解:(Ⅰ)∵a=4,∴y=,当0≤x≤4时,由﹣4≥4,解得x≥0,∴此时0≤x≤4;当4<x≤10时,由20﹣2x≥4,解得x≤8,∴此时4<x≤8;综上所述,0≤x≤8,即若一次投放4个单位的制剂,则有效治污时间可达8天;(Ⅱ)当6≤x≤10时,y=2•(5﹣x)+a[﹣1]=10﹣x+﹣a=(14﹣x)+﹣a﹣4,∵14﹣x∈[4,8],而1≤a≤4,∴∈[4,8],∴y=(14﹣x)+﹣a﹣4≥2﹣a﹣4=﹣a﹣4,当且仅当14﹣x=即x=14﹣4时,y有最小值为﹣a﹣4,令﹣a﹣4≥4,解得24﹣16≤a≤4,∴a的最小值为24﹣16≈1.6.点评:本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.19.试比较n n+1与(n+1)n(n∈N*)的大小,分别取n=1,2,3,4,5加以试验,根据试验结果猜测一个一般性结论.考点:数学归纳法.专题:点列、递归数列与数学归纳法.分析:本题考查的知识点是归纳推理与数学归纳法,我们可以列出n n+1与(n+1)n(n∈N*)的前若干项,然后分别比较其大小,然后由归纳推理猜想出一个一般性的结论,然后利用数学归纳法进行证明.解答:解:当n=1时,n n+1=1,(n+1)n=2,此时,n n+1<(n+1)n,当n=2时,n n+1=8,(n+1)n=9,此时,n n+1<(n+1)n,当n=3时,n n+1=81,(n+1)n=64,此时,n n+1>(n+1)n,当n=4时,n n+1=1024,(n+1)n=625,此时,n n+1>(n+1)n,根据上述结论,我们猜想:当n≥3时,n n+1>(n+1)n(n∈N*)恒成立.证明:①当n=3时,n n+1=34=81>(n+1)n=43=64即n n+1>(n+1)n成立.②假设当n=k时,k k+1>(k+1)k成立,即:>1则当n=k+1时,=(k+1)()k+1>(k+1)()k+1=>1即(k+1)k+2>(k+2)k+1成立,即当n=k+1时也成立,∴当n≥3时,n n+1>(n+1)n(n∈N*)恒成立.点评:本题考查了数学归纳法的应用,证明步骤的应用,归纳推理,考查计算能力,属于中档题.20.对于定义在区间D上的函数f(x)和g(x),如果对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,那么称函数f(x)在区间D上可被函数g(x)替代.(1)若,试判断在区间[[1,e]]上f(x)能否被g(x)替代?(2)记f(x)=x,g(x)=lnx,证明f(x)在上不能被g(x)替代;(3)设,若f(x)在区间[1,e]上能被g(x)替代,某某数a的X围.考点:函数恒成立问题;函数单调性的性质.专题:证明题;综合题;压轴题.分析:(1)构造函数,通过研究h(x)的导数得出其单调性,从而得出其在区间[[1,e]上的值域,可以证出f(x)能被g(x)替代;(2)构造函数k(x)=f(x)﹣g(x)=x﹣lnx,可得在区间上函数k(x)为减函数,在区间(1,m)上为增函数,因此函数k(x)在区间的最小值为k(1)=1,最大值是k(m)大于1,所以不满足对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,故f(x)在上不能被g(x)替代;(3)根据题意得出不等式,去掉绝对值,再根据x﹣lnx的正负转化为或,通过讨论右边函数的最值,得出实数a的X围解答:解:(1)∵,令,∵,∴h(x)在[1,e]上单调增,∴.∴|f(x)﹣g(x)|≤1,即在区间[[1,e]]上f(x)能被g(x)替代.(2)记k(x)=f(x)﹣g(x)=x﹣lnx,可得当时,k′(x)<0,在区间上函数k(x)为减函数,当1<x<m时,k′(x)>0,在区间(1,m)上函数k(x)为增函数∴函数k(x)在区间的最小值为k(1)=1,最大值是k(m)>1,所以不满足对于任意x∈D,都有|f(x)﹣g(x)|≤1成立,故f(x)在上不能被g(x)替代;(3)∵f(x)在区间[1,e]上能被g(x)替代,即|f(x)﹣g(x)|≤1对于x∈[1,e]恒成立.∴.,由(2)知,当x∈[1,e]时,x﹣lnx>0恒成立,∴有,令,∵=,由(1)的结果可知,∴F'(x)恒大于零,∴.②,令,∵=,∵,∴G'(x)恒大于零,∴,即实数a的X围为点评:本题考查了利用导数研究函数的单调性,通过分类讨论解决了不等式恒成立的问题,属于难题.。
【高中语文】名句默写练习+课件+高二下学期语文期末复习

,
”。
(3)《子路、曾皙、冉有、公西华侍坐》中,“
,
”
两句写出孔子哂笑子路的原因。
6.(1)吴楚东南坼 乾坤日夜浮 (2)彩舟云淡 星河鹭起 (3)为国以礼 其言不让
7.补写出下列句子中的空缺部分。
(1)李白在《蜀道难》一诗中,不但直接写蜀山之高峻,还借助
人的行路之难的细节描写进行侧面烘托。其中“
19.补写出下列句子中的空缺部分。 (1)杜甫《客至》中“ ______,______”两句,用平白朴实的家常 话语描写了主人热情待客频频劝酒的欢快情景,让读者体悟到主客 之间的深情厚意。 (2)《种树郭橐驼传》中一些所谓的爱树忧树者与郭橐驼的做法 不同,甚至出现了“ ______,______ ”的极端做法。 (3)贾谊在《过秦论》中交代陈涉的身份,说他不过是个 “ ______,______”,且是被迁戍边的兵卒。 19.(1)盘飧市远无兼味 樽酒家贫只旧醅 (2)爪其肤以验其生枯 摇其本以观其疏密 (3)瓮牖绳枢之子 氓隶之人
绩非凡的句子是“
,
”。
(2)《石钟山记》中“微波入焉”一句是描述噌吰声成因的,其中“焉”
字指代的原文句子是“
,
”。
(3)屈原在《离骚》中用比喻的手法,写出自己才能优秀却遭到嫉妒和造
谣中伤的句子是“
,
”。
11.(1)他植者虽窥伺效慕 莫能如也 (2)则山下皆石穴罅 不知其浅深 (3)众女嫉余之蛾眉兮 谣诼谓余以善淫
(3)古人常在诗词中使用“流水”这一意象来表达对时光易逝、世事无常
、人生虚幻的感慨,《离骚》中“
,
”就是这样的经典名句。
(4)在屈原在《离骚》中表明要趁着年富力强兴利除弊有所作为句子:
,
江苏省南通市李堡中学2013-2014学年高二下学期数学(文)期末复习测试5 Word版含答案

2014年李堡中学高二数学文科期末复习五一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸相应位置上........1.已知全集{}1,2,3,4,5,6U =,集合{}1,3,5A =,{}1,2,4U B ð=,则A B = .2.已知复数z 满足i 2i z ⋅=-,i 为虚数单位,则z 的值为 .3.命题“2x ∀>,24x >”的否定是 .4.用反证法证明某命题时,对结论“自然数,,a b c 至少有1个偶数”的正确假设为“ ”. 5.若函数()f x =,则()f x 的定义域是 . 6.已知复数2(4)3i z a =-+,a ∈R ,则“=2a ”是“z 为纯虚数”的 条件. (填写 “充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中的一个)7.已知ABC △的周长为l ,面积为S ,则ABC △的内切圆半径为2S r l=.将此结论类比到空间,已知四面体ABCD 的表面积为S ,体积为V ,则四面体ABCD 的内切球的半径R = .8.若函数()123, 1,log ,01,x x f x x x -ìïïï>=íïï<ïî≤则()81f f 轾臌的值为 . 9.已知()y f x =是奇函数,当0x ≥时,()3x f x m =+,若()()2g x f x =+,则()1g -的值为 . 10.已知函数321()23f x x mx n =-+(m ,n 为常数),当2x =时,函数()f x 有极值,若函数()y f x =有且只有三个零点,则实数n 的取值范围是 .11.设函数()log (1)a f x x a =>的定义域为[],m n ,值域为[]1,0,若m n -的最小值为13,则实数a 的值为 . 12.设函数11,2,()1(2),2,2x x f x f x x ⎧--<⎪=⎨-⎪⎩≥ 则函数()()1F x xf x =-的零点的个数为 . 13.已知命题p :“若0m ≤,则220x x m -+=有实数解”的逆命题;命题q :“若函数()()2lg 2f x x x a =++的值域为R ,则1a >”.以下四个结论: ①p 是真命题;②p q Ù是假命题;③p q Ú是假命题;④q Ø为假命题.其中所有正确结论的序号为 .14.已知()f x 是定义在R 上的函数,对于任意12,x x R Î,()()()12121f x x f x f x +=+-恒成立,且当0x >时,()1f x >,若()20132014f =,()233f x ax --<对任意()1,1x ?恒成立,则实数a 的取值范围为 .二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.已知复数112i z =-,234i z =+,i 为虚数单位.(1)若复数12z az +对应的点在第四象限,求实数a 的取值范围;(2)若1212z z z z z -=+,求z 的共轭复数z .16. 已知函数()21f x x =+,()51g x x =+的定义域都是集合A ,函数()f x 和()g x 的值域分别是集合S 和T .(1)若[]1,3A =,求S T ;(2)若[]0,A m =,且S T =,求实数m 的值;(3)若对于A 中的每一个x 值,都有()()f x g x =,求集合A .17.一种十字绣作品由相同的小正方形构成,图①,②,③,④分别是制作该作品前四步时对应的图案,按照如此规律,第n 步完成时对应图案中所包含小正方形的个数记为()f n .① ② ③ ④(1)写出()2f ,()3f ,()4f ,()5f 的值;(2)利用归纳推理,归纳出()1f n +与()f n 的关系式;(3)猜想()f n 的表达式,并写出推导过程.18.设函数()x x f x a ka -=+(0a >,且1a ¹)是定义域为R 的奇函数.(1)求实数k 的值;(2)若()312f =. ①用定义证明:()f x 是单调增函数;②设()()222x x g x a a f x -=+-,求()g x 在[)1,+上的最小值.19. 已知函数()32ln f x ax bx x =+,若()f x 在点()()1,1f 处的切线方程为22y x =-.(1)求()f x 的解析式;(2)求()f x 在1[,e]e 上的单调区间和最值;(3)若存在实数[]2,2m ?,函数()()3322ln 239g x x x x m n x =--+在()1,e 上为单调减函数,求实数n 的取值范围.20.设()f x 是定义在(0,)+∞的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥,则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x=-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围; (2)对任给的“n 阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是否为“n阶负函数”?并说明理由.。
专题9-状态动词和动作动词-2020-2021学年高二年级英语下学期期末专项复习(北师大版2019)
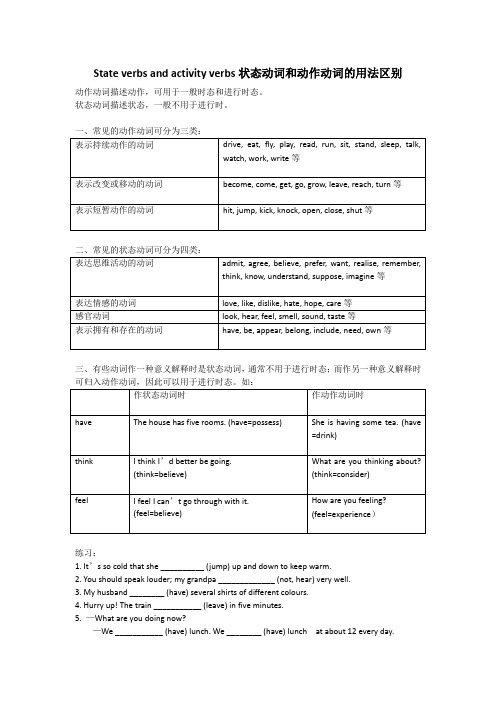
State verbs and activity verbs状态动词和动作动词的用法区别动作动词描述动作,可用于一般时态和进行时态。
状态动词描述状态,一般不用于进行时。
一、常见的动作动词可分为三类:三、有些动词作一种意义解释时是状态动词,通常不用于进行时态;而作另一种意义解释时练习:1. It’s so cold that she __________ (jump) up and down to keep warm.2. You should speak louder; my grandpa _____________ (not, hear) very well.3. My husband ________ (have) several shirts of different colours.4. Hurry up! The train ___________ (leave) in five minutes.5. —What are you doing now?—We ___________ (have) lunch. We ________ (have) lunch at about 12 every day.6. When I saw her in the garden, she __________ (smell) the roses.7.Now I _______ he is an honest man whom I can trust. (believe)8.Would you like to _____ the food I have just cooked? (taste)9.Every year the flowers _______ in early summer. (appear)10. I’m sorry. I didn’t catch you. I ____________ about my plan. (think)答案:is jumping / doesn’t hear/ has/ is leaving/ are having/ have/ was smelling/ believe/ taste/ appear/was thinking。
山东省泰安市泰山国际学校2021学高二历史下学期期末考试复习试题(含解析

C.王权(wánɡ quán)具有神秘色彩
D.崇拜祖先的宗法观念已经形成
【答案】D
【解析】
【详解】依据材料可知,商王求丰年和降雨的“卜辞〞不是向最高神—“帝〞请求,而是“托祖先转达〞,说明祖先在人们心目中的位置重要,反映了崇拜祖先的宗法观念已经形成。因此D选项正确。A选项错误,依据材料可知,“帝〞是商王心中的最高神,祖先地位并未高于神;B、C选项错误,材料强调的是血缘宗法观念,不是占卜决策国家大事,也不是王权的神秘色彩。故正确答案为D选项。
7.据?唐六典?载,在长安城共有114坊,东市和西市(xī shì)各占2坊,每处坊、市皆有围墙。此外,110坊以朱雀大街为界由万年县、长安县分半统辖。东西市共4坊中,亦有城墙与其他居民区坊院隔开,正北面为唐朝中央机构所在地。这种布局表达了
A.中央(zhōngyāng)和地方分片管理首都治安B.政府对商人和市场 严格(yángé)管制
A.中央政府权力遭到严重(yánzhòng)削弱B.地方(dìfāng)与中央的相互制衡
C.中央集权与地方分权相结合D.地方势力威胁中央集权
【答案】C
【解析】
从材料“元朝的行省实际上是封建中央集权分寄于地方,…它负责处理境内政治、军事、经济等各类事务〞可以看出,行省是元朝地方行政机构,行省官员具有处理政治、军事、经济等权力,聚集地方财富上交中央,说明行省制度在加强中央集权的同时也给予地方很大权力,只是地方在行使权力时要受中央节制,故C项符合题意;A、B、D三项不符合史实,故排除。
C.长安是当时全国的政治和经济中心D.中央机构“南面而王〞遵循传统礼制
【答案】B
【解析】
【详解】据材料“?唐六典?载〞“长安城〞“每处坊、市皆有围墙〞等信息可知,材料反映的是唐朝长安城的坊市格局,市有地点限制,说明政府对市场的管理严格,B符合题意;A与材料无关;C不是材料反映的主旨;D与材料无关。
2020-2021学年牛津译林版高二英语下学期期末复习--七选五专练

D.Untreated heat stroke can quickly damage your brain and heart.
E.In most cases, a doctor should be consulted if a person is suspected of having heat stroke.
G.Thememory-boosting effect of reading aloud isespeciallystrong in children.
(二)
When the body temperature reaches 104 degrees Fahrenheit(40℃), a person may be suffering from a serious condition called heatstroke.36Besides, one may suffer from heat stroke when he participates in extreme physical activity in a warm environment.
A. Today, silent reading is the norm.
B.It is worth making a bit more time for reading out loud.
C.Readingsilently hasdistinct advantages
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二下学期期末复习(文)
一、填空题
1.设集合{}
{}2|,|2A x x a B x x =<=<,若A B A ⋂=,则实数a 的取值范围是_______.
2.若复数21(1)z a a i =-++(a R ∈)是纯虚数,则z = .
3.已知函数f(x)的定义域为(-1,0),则函数f(2x +1)的定义域为________.
4.已知幂函数y=f(x)的图象过点(2
),则(16)f = . 5.函数f(x)=12log 121
x x x x ≥⎧⎪⎨⎪<⎩,,,的值域为________.
6.已知函数f(x)=a +
141x +是奇函数,则常数a =________. 7.若函数f(x)=e x -2x -a 在R 上有两个零点,则实数a 的取值范围是________.
8.定义在R 上的函数f(x),对任意x∈R 都有f(x +2)=f(x),当x∈(-2,0)时,f(x)=4x ,则f(2 013)=________.
9.已知函数()()2212f x x a x a =+-+-的一个零点大于1,另一个零点小于1,则实数a 的取值范围为 .
10.函数3()27f x x x =-在区间[33]-,上的最小值是_________________;
11.若曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+,则曲线()()ln f x g x x =+在点(1,(1))f 处切线的方程为 .
12.设321()252
f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的取值范围为 .
13.等差数列{}{}n n a b ,的前n 项和分别为n n S T 、,若n n T S =1
32+n n ,则1111b a =_________ 14.设等比数列{a n }的公比为q ,前n 项和为S n ,若S n+1,S n ,S n+2成等差数列,则q 的值为 .
三、解答题
15.设a 、b 、c 均为大于1的正数,且ab =10,求证:log a c +log b c ≥4lgc.
16.如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,90ACB ∠=o .以AB ,BC 为邻边作平行
四边形ABCD ,连接1DA 和1DC .
(1)求证:1A D //平面11BCC B ;
(2)求证:AC ⊥平面1ADA .
B
D C A C 1A 1
B 1
17.等比数列{}n a 的各项均为正数,且2
12326231,9.a a a a a +== (1)求数列{}n a 的通项公式;
(2)设 31323log log ......log ,n n b a a a =+++求数列1n b ⎧⎫⎨
⎬⎩⎭的前n 项和.
18.已知正项数列{}n a 满足:231=
a , 1323n n n a a a +=+ (1)求通项n a ;
(2)若数列{}n b 满足⎪⎭⎫ ⎝⎛-
=⋅n n n a b 2113,求数列{}n b 的前n 和.
19.设数列{}n a 满足211233333
n n n a a a a -++++=…,n ∈*N . (1)求数列{}n a 的通项;
(2)设n n
n b a =
,求数列{}n b 的前n 项和n S .
20.已知函数()x x x g ln 2+=,()x x
m mx x f ln 2---=,m R ∈. (1)求函数()g x 的极值点;
(2)若()()f x g x -在[)1,+∞上为单调函数,求m 的取值范围;
(3)设2()e h x x
=,若在[]1,e 上至少存在一个0x ,使得000()()()f x g x h x ->成立,求m 的取值范围.
本卷由【在线组卷网 】自动生成,请仔细校对后使用,答案仅供参考。
答案第1页,总1页 参考答案
1.4a ≤
2.2
3.1(1,)2--
4.4
5.(-∞,2)
6.-12
7.(2-2ln2,+∞)
8.14
9.(2,1)-
10.-54
11.3y x =
12.(7,)+∞
13.
2132
14.2- 15.见解析
16.(1)1A D //平面11BCC B ;(2)AC ⊥平面1ADA .
17.(1)a n =13n (2)数列1{}n
b 的前n 项和为21n n -+ 18.(1)32n a n
=;(2)21242n n n S n n -+=+-+ 19.(1)*1()3n n a n N =∈(2)111333244
n n n n S ++=⋅-⋅+ 20.(1)02x =为函数()g x 的极小值点;(2)m 的取值范围是(][),01,-∞+∞U ;
(3)m 的取值范围是24,.1e e ⎛⎫+∞ ⎪-⎝⎭。
