自适应滤波器技术发展剖析共27页
第6章自适应滤波器

硬件的巨大发展,使得工程师更关心系统的稳定性,
而不在乎那么一丁点计算量的减少。因此,自适应滤波器常采用FIR结构。 可分为:横向型(直接型)、对称横向型(线性相位型)、格型
第十四页,编辑于星期三:二十三点 四十分。
第十五页,编辑于星期三:二十三点 四十分。
第十六页,编辑于星期三:二十三点 四十分。
第十七页,编辑于星期三:二十三点 四十分。
第十八页,编辑于星期三:二十三点 四十分。
第十九页,编辑于星期三:二十三点 四十分。
第二十页,编辑于星期三:二十三点 四十分。
1959年,威德诺,Wn+1=Wn+△W(负比例系数的均方误差函数梯度) 。
②递推最小二乘(RLS)算法 :使估计误差的加权平方和最小.
第四十五页,编辑于星期三:二十三点 四十分。
6.4.2 LMS自适应算法
最小均方算法:Least Mean Squares
维纳滤波器的寻优以最小均方误差为准则;
LMS自适应滤波的寻优就在最小均方误差的基础上稍作改动:
RLS收敛快的原因在于采用类似归一化步长。
wˆ (n) wˆ (n 1)
P(n 1)
x(n) (n)
xH (n)P(n 1)x(n)
值得注意的是:自适应滤波器--时变性,非线性。
非线性:系统根据所处理信号特点不断调整自身的滤波器系数。时 变性:系统的自适应响应/学习过程。
所以,自适应滤波器可自动适应信号的传输环境,无须详细知道信 号的特征参数,无须精确设计滤波器本身。
线性自适应滤波器的两个阶段:
自适应滤波器设计分析

自适应滤波器设计分析自适应滤波器是一种根据输入信号的特征自动调整滤波器参数的数字滤波器。
它可以根据输入信号的统计特性,动态地调整滤波器的频率响应,以实现对不同频率成分的有效过滤。
自适应滤波器被广泛应用于信号处理、通信系统、控制系统等领域。
1.自适应滤波器的基本结构:自适应滤波器一般由输入信号、期望输出信号、滤波器系数估计器和滤波器组成。
输入信号经过滤波器和滤波器系数估计器的处理后,输出信号与期望输出信号之间的误差作为反馈输入到滤波器系数估计器中,用于更新滤波器系数。
常用的自适应滤波器结构包括最小均方误差(LMS)滤波器和最小均方误差(RLS)滤波器等。
2.自适应滤波器的性能评价指标:自适应滤波器的性能主要通过均方误差(MSE)和收敛速度来评价。
均方误差反映了滤波器输出与期望输出之间的误差大小,收敛速度表示滤波器算法收敛到稳定状态所需的时间。
较低的均方误差和较快的收敛速度是自适应滤波器设计的目标。
3.自适应滤波器的优化算法:常用的自适应滤波器优化算法包括LMS算法、RLS算法、NLMS算法等。
LMS算法通过最小化均方误差来更新滤波器系数,是一种简单有效的算法,但收敛速度较慢;RLS算法通过最小化加权过去误差序列的均方和来更新滤波器系数,收敛速度较快但计算量大;NLMS算法在LMS算法的基础上进行改进,通过动态调整步长参数来加快收敛速度。
4.自适应滤波器的应用:自适应滤波器广泛应用于信号处理、通信系统、控制系统等领域。
在信号处理领域,自适应滤波器可以应用于降噪、滤波、谱估计等任务;在通信系统中,自适应滤波器可以用于信道均衡、自适应干扰消除等;在控制系统中,自适应滤波器可以用于系统辨识、参数估计、自适应控制等。
综上所述,自适应滤波器设计分析涉及到基本结构、性能评价指标、优化算法和应用等多个方面。
在实际应用中,需要根据具体任务的要求选择适当的自适应滤波器结构和优化算法,并通过性能评价指标来评估滤波器的性能。
自适应滤波器
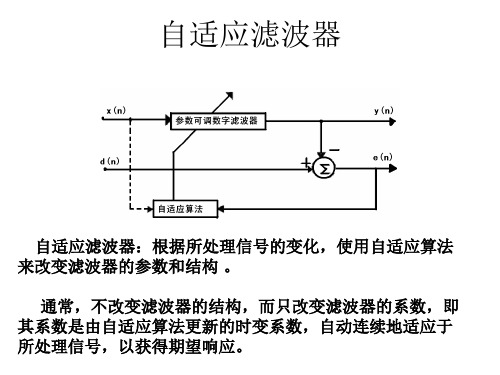
硬件速度的巨大发展,使得工程师更关心系统的稳定性、处理能力的优越性, 而不在乎那么一丁点计算量的减少。因此,自适应滤波器常采用FIR结构。 可分为:横向型、对称横向型、格型
5 自适应滤波器
5.1 引言
①
②
③自适应滤波器的定义
• 按复杂度来分: – 线性自适应滤波器 – 非线性自适应滤波器(包括Volterra滤波器和基于神经网络 的自适应滤波器 。信号处理能力更强,但计算也更复杂。) 值得注意的是: 自适应滤波器常称为:时变性的非线性的系统。 非线性:系统根据所处理信号特点不断调整自身的滤波器 系数,以便使滤波器系数最优。 时变性:系统的自适应响应/学习过程。 实际应用的常见情况: 学习/训练阶段:滤波器根据所处理信号的特点,不断修 正自己的滤波器系数,以使均方误差最小(LMS)。 使用阶段:均方误差达最小值,意味着滤波器系数达最 优并不再变化,此时的滤波器就变成了线性系统,故此类自适 应滤波器被称为线性自适应滤波器,因为这类系统便于设计 且易于数学处理,所以实际应用广泛。本文研究的自适应滤波 器就是线性自适应滤波器。
RLS算法的主要问题:每次迭代中的计算量与阶数M的平 方成正比。虽然比之最小二乘法(M的三次方成正比)好, 但比LMS算法(M成正比)要差。
• 按复杂度来分:
– 线性自适应滤波器 – 非线性自适应滤波器(包括Volterra滤波器和基于神经网络的自适应滤 波器 。信号处理能力更强,但计算也更复杂。)
值得注意的是: 自适应滤波器通常是时变性的非线性的系统,非线性:系 统根据所处理信号特点不断调整自身的滤波器系数。时变性: 系统的自适应响应/学习过程。所以,自适应滤波器可自动适 应信号的传输环境,无须详细知道信号的结构和特征参数,无 须精确设计滤波器本身。 实际应用的常见情况: 当自适应学习过程结束,滤波器系数就不再变化,此时滤 波器就变成了线性系统,故此类自适应滤波器被称为线性自适 应滤波器,因为这类系统便于设计且易于数学处理,所以实际 应用广泛。本文研究的自适应滤波器就是线性自适应滤波器。
自适应滤波器设计分析

青海民族大学毕业论文(设计)论文题目:自适应滤波器设计学生姓名:学号:指导教师:职称:院系:专业班级:年月日独创性声明本人声明所呈交的毕业论文是本人在导师指导下进行的理论学习、实习实践以与研究所取得的成果,除了文中特别加以标注和致谢之处外,论文中不包含其他人已经发表或撰写过的研究成果,也不包含获得或其他教育机构的学位或证书而使用过的材料。
与我一起探讨、工作的同学对本论文所做的任何贡献均已在论文中作了明确的说明并表示了谢意。
毕业论文作者签名:签字日期:年月日毕业论文版权使用授权书本毕业论文作者完全了解青海民族大学有关保留、使用毕业论文的规定。
特授权青海民族大学可以将毕业论文的全部或部分内容编入有关数据库进行检索,并采用影印、缩印或扫描等复制手段保存、汇编以供查阅和借阅。
同意学校向国家有关部门或机构送交论文的复印件和磁盘。
论文作者签名:签字日期:年月日指导教师签名:签字日期:年月日摘要本文介绍了传统滤波器和自适应滤波器基本工作原理和性能,以与滤波技术的现状和发展前景。
然后系统阐述了自适应滤波器的基本结构模型,接着在此基础上引出LMS算法(Least mean square ),中文是最小均方算法。
LMS算法是自适应滤波器中常用的一种算法,与维纳算法不同的是,其系统的系数随输入序列而改变。
在这我运用matlab设计了一个LMS自适应滤波器,接着验证分析了自适应滤波器的性能,最后分析了影响自适应滤波结果的因素,通过适当取值来改善滤波结果。
关键字:自适应滤波器,LMS算法,设计仿真,分析性能AbstractThis article describes the basic working principle and performance of traditional filters and adaptive filters,and filter technology status and development prospects.Systematically expounded the basic structure of the adaptive filter model leads to theLMS algorithm (Least mean square) and then on this basis, the Chinese is the least mean square algorithm. LMS algorithm is commonly used in adaptive filter algorithm,the Wiener algorithm, the coefficients of its system with the input sequence. Use of matlab I designed a LMS adaptive filter, and then verify the performance of the adaptive filter, the last of the factors affecting the results of adaptive filtering to improve the filtering results through the appropriate value.Keywords: Adaptive filter, LMS algorithm, design and simulation, performance analysis目录1绪论 (1)1. 1 引言 (1)1.2滤波器的研究现状 (1)1.3应用领域 (3)2自适应滤波器的理论基础 (3)2. 1 自适应滤波器的原理 (3)2. 2 基本自适应滤波器的模块结构 (4)3LMS滤波原理与算法 (5)3.1最陡下降算法的原理 (5)3.2从最陡下降算法导出L M S算法 (8)3.3L M S算法公式与核心 (9)4M a t l a b实验仿真 (11)4.1.实验原理 (11)4.2.实验程序 (12)4.3.实验结果与分析 (13)(1)收敛因子u对系统仿真结果的影响 (13)(2)级数N对系统仿真结果的影响 (16)(3)适当取值改善滤波结果 (17)5总结 (18)6参考文献 (19)7致谢 (20)1. 绪论1.1 引言滤波器是进行信号处理的一种装置,由于传统滤波技术进行信号处理需要知道有用信号和干扰噪声的统计特性,而在实际应用中,却没有充足的信息来设计固定系数的数字滤波器,或者设计规则会在滤波器正常运行时改变,因此我们需要研究自适应滤波器。
自适应滤波理论及算法研究

自适应滤波理论及算法研究自适应滤波是一种常见的信号处理技术,其应用广泛于图像处理、音频处理、通信系统等领域。
本文将对自适应滤波的理论及算法进行研究与分析。
首先,我们来介绍一下自适应滤波的基本概念。
自适应滤波是指根据输入信号的特性和系统的响应,动态地调整滤波器的参数,以实现对信号的最优处理。
传统的固定滤波器需要提前设置好参数,而自适应滤波器能够根据输入信号的实时变化进行调整,更加适应不同场景的信号处理需求。
接下来,我们将重点研究自适应滤波的理论基础。
自适应滤波的核心思想是根据输入信号和期望输出信号之间的误差,迭代地调整滤波器参数,使误差尽可能地减小。
其中,最常用的自适应滤波算法是最小均方(Mean Square Error, MSE)算法。
MSE算法通过最小化误差的平方和,来寻找最优的滤波器参数。
它利用了输入信号和期望输出信号的统计特性,实现了自适应滤波的效果。
随着深度学习的兴起,神经网络在自适应滤波中得到了广泛应用。
神经网络具有非线性映射的能力,能够更好地适应信号的非线性特性。
深度学习算法通过训练神经网络,将输入信号与期望输出信号进行匹配,从而得到适用于特定信号处理任务的自适应滤波器。
深度学习算法在图像处理、音频降噪等领域取得了显著的成果。
在实际应用中,自适应滤波器的性能往往受到一些因素的影响。
首先是滤波器的步长选择。
步长决定了每次迭代中参数的更新速度,过大的步长可能导致滤波器过早收敛,过小的步长则会延缓收敛速度。
为了获得最佳的参数设置,研究人员通过模拟实验和理论分析,提出了一系列优化方法。
另外一个重要因素是滤波器的收敛性能。
如果滤波器能够在有限步骤内收敛到最优解,我们称其为有限时间收敛。
而有些情况下,滤波器可能无法在有限时间内收敛,这就需要采用一些收敛性保证的技巧。
研究人员提出了一些收敛性分析方法,如平均收敛时间分析、收敛速率分析等。
此外,自适应滤波算法的计算复杂度也是一个需要考虑的问题。
一些复杂的自适应算法会导致大量的计算消耗,限制了其在实际应用中的可行性。
自适应滤波器简介PPT课件

3
第3页/共31页
正交性原理
• 假设线性离散时间滤波器的输入x(n)和脉冲响应w(n)都是复数无穷序列, 则输出y(n)
y n wk*x n k n 1, 2, k 0
• 假设滤波器输入和期望响应都已经是零均值,估计误差和误差均方值为
en d n yn
间
的
状
态
转
移
• v1(n): M×1维向量,描绘状态转移中的加性过程噪声 • y(n):动态系统在时刻n的N×1维观测向量
• C(n): N×N维观测矩阵
• v2(n): N×1维向量,观测噪声向量
18
第18页/共31页
• 卡尔曼滤波问题可以叙述为:利用观测数据向量y(1),y(2),…,y(n) 对n≥1求状态向量x(i)的各个分量的最小二乘估计。根据i和n的不同取 值,卡尔曼滤波可用于: • 滤波(i=n),用n时刻及以前时刻的测量数据来估计n时刻的信息 • 平滑(1≤i≤n),用1~n时刻的全部数据来估计n以前某个时刻的 信息 • 预测(i>n),用n时刻及以前的测量数据来估计n+τ(τ>0)时刻的 信息
J Eene* n Ee2 n
• 为使均方误差最小,其梯度向量的所有元素应为零
J J
k J
ak
bk
0
k 0,1, 2,
wk ak bk
4
第4页/共31页
• 将均方误差表达式代入
k J
e n
E
ak
e*
n
e* n ak
en
en e* bk
n
e* n bk
e n
• 由估计误差的定义可知
《自适应滤波器》课件

自适应滤波器能够用于调制和解调信号,实现信号的调制、解调 、频偏校正等功能。
多径抑制
自适应滤波器能够抑制多径干扰,提高通信系统的传输质量和可 靠性。
自适应滤波器在图像处理中的应用
图像去噪
自适应滤波器能够去除图像中的噪声,提高图像的清晰度和质量。
图像增强
自适应滤波器能够通过增强图像的特定特征,如边缘、纹理等,提 高图像的可读性和识别率。
信噪比增益
比较自适应滤波器在输入信号中增强有用信号 、抑制噪声的能力。
计算复杂度
评估自适应滤波器实现所需的计算资源和时间,包括浮点运算次数、存储需求 等。
04
自适应滤波器的实现方法
递归最小二乘法
01
递归最小二乘法是一种常用的 自适应滤波算法,通过最小化 误差平方和来不断调整滤波器 系数,以达到最优滤波效果。
差分进化NLMS算法
结合差分进化算法,通过种群间的竞争与合 作,实现权值的并行优化,提高算法的收敛 速度。
改进的RLS算法
快速RLS算法
通过改进递推最小二乘法的迭代公式,减少 计算量和存储需求,提高算法实时性。
遗忘因子RLS算法
引入遗忘因子,对历史数据赋予逐渐减小的 权重,以提高算法对非平稳信号的处理能力
工作原理
自适应滤波器通过输入和输出信号的 迭代计算,不断调整其内部参数,以 实现最优滤波效果。
自适应滤波器的应用领域
01
信号处理
自适应滤波器广泛应用于信号处 理领域,如语音、图像和雷达信 号的处理。
02
03
通信
控制系统
在通信领域,自适应滤波器用于 降低噪声和干扰,提高通信质量 。
在控制系统中,自适应滤波器用 于估计系统状态,提高控制精度 和稳定性。
自适应滤波器技术发展分析

吴光弼,祝琳瑜.一种变步长LMS自适应滤波算法.电子学报.1994,22,1.
蒋明峰,郑小林,彭承琳.一种新的变步长LMS自适应算法及其在自适应噪声 对消中的应用.信号处理,2001,27
LOGO LOGO
历史回顾——递归最小二乘算法
1974 Godard应用卡尔曼滤波器理论导出了一种变型算 法,称之为Godard算法
1981
Gentleman和Kung引入了一种基于矩阵代数QR分 解的数值鲁棒的方法来求解RLS问题
1994
Sayed和Kailath的论文揭示了RLS与卡尔曼滤波 器理论之间的一一对应关系,证明了QR分解 的RLS,快速RLS都是卡尔曼滤波器的特例
ˆ e(n) d (n) U T (n)W (n)
P(n 1)u (n) uT (n) P(n 1)u (n) 1 P(n) [ P(n 1) k (n)u T (n) P(n 1)] W (n) W (n 1) k (n)e* (n) k ( n)
历史回顾——随机梯度算法
1959年,Windrow和Hoff 在研究自适应线性元素的 模式识别方案时发明的。 GAL算法,梯度自适应格型 LMS算法鲁棒性能的理论 算法,是与LMS算法紧密相 证明首次被介绍,鲁棒控 关的随机梯度算法之一。 制成为新的研究方向
最早的工作
1959
GAL算法
1977
H 范数
历史回顾——随机梯度算法
历史回顾——随机梯度算法
传统的LMS算法主要缺陷是具有固定的步长μ,因而存在着收敛速度和失调之 间的矛盾。步长越大,收敛速度越快,但失调量也增大;步长越小,失调量越 小,但是收敛速度也相应变慢。
• R.D.Githa曾提出了一种变步长自适应滤波算法,其步长因 子随迭代次数的增加而逐渐减小; • Yasukawa 等提出了使步长因子正比于误差信号的大小; •Githn 提出了一种时间平均估值梯度的自适应滤波算法; •蒋明峰等提出了基于当前误差与上一步误差的自相关估计的 MVSSLMS算法。 ……
