与动点有关的函数图象问题2015.3.27
中考数学狙击重难点系列专题12----与动点问题有关的函数图像的判断(含答案)

与动点问题有关的函数图像的判断1. 如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为()2. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的函数关系用图象描述大致是()3. 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M,N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是()4. 如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为()5. 小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是()6. 如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从顶点A出发,点P 沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D 时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是()7. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC 与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是()8.如图1,已知点E,F,G,H是矩形ABCD各边的中点,AB=2.39,BC=3.57.动点M从点A出发,沿A→B→C→D→A匀速运动,到点A停止.设点M运动的路程为x,点M到四边形EFGH的某一个顶点的距离为y,如果表示y关于x的函数关系的图象如图2所示,那么四边形EFGH的这个顶点是()A. 点EB. 点FC. 点GD. 点H9. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反应当天爷爷离家的距离y(米)与时间t(分钟)之间的大致图象是( )10. 如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是()11. 如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC的AB 边于点D.若设PD为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是()12. 为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图所示,点为矩形边的中点,在矩形的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员从点出发,沿着的路线匀速行进,到达点.设运动员的运动时间为,到监测点的距离为.现有与的函数关系的图象大致如图所示,则这一信息的来源是().A. 监测点B. 监测点C. 监测点D. 监测点13. 如下图所示,已知等腰梯形ABCD,AD∥BC,若动直线l垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )14. 均匀地向如图的容器中注满水,能反应在注水过程中水面高度h随时间t变化的图象是()15. 某蓄水池的横断面示意图如图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度和放水时间之间的关系的是()16. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P 点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是17. 如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是()18. 如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE 和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是()19. 如图,AC,BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是()20. 如图,李老师早晨出门锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是()21. 如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是()答案解析部分一、单选题1.【答案】D【解析】【解答】解:∵AD=5,AN=3,∴DN=2,如图1,过点D作DF⊥AB,∴DF=BC=4,在RT△ADF中,AD=5,DF=4,根据勾股定理得,AF= =3,∴BF=CD=2,当点Q到点D时用了2s,∴点P也运动2s,∴AP=3,即QP⊥AB,∴只分三种情况:①当0<t≤2时,如图1,过Q作QG⊥AB,过点D作DF⊥AB,QG∥DF,∴,由题意得,NQ=t,MP=t,∵AM=1,AN=3,∴AQ=t+3,∴,∴QG= (t+3),∵AP=t+1,∴S=S△APQ= AP×QG= ×(t+1)× (t+3)= (t+2)2﹣,当t=2时,S=6,②当2<t≤4时,如图2,∵AP=AM+t=1+t,∴S=S△APQ= AP×BC= (1+t)×4=2(t+1)=2t+2,当t=4时,S=8,由题意得CQ=t﹣4,PB=t+AM﹣AB=t+1﹣5=t﹣4,∴PQ=BC﹣CQ﹣PB=4﹣(t﹣4)﹣(t﹣4)=12﹣2t,∴S=S△APQ= PQ×AB= ×(12﹣2t)×5=﹣5t+50,当t=5时,S=5,∴S与t的函数关系式分别是①S=S△APQ= (t+2)2﹣,当t=2时,S=6,②S=S△APQ=2t+2,当t=4时,S=8,③∴S=S△APQ=﹣5t+50,当t=5时,S=5,综合以上三种情况,D正确故选D.【分析】先求出DN,判断点Q到D点时,DP⊥AB,然后分三种情况分别用三角形的面积公式计算即可.此题是动点问题的函数图象,考查了三角形的面积公式,矩形的性质,解本题的关键是分段画出图象,判断出点Q在线段CD时,PQ⊥AB是易错的地方.2.【答案】D【解析】【解答】解:如图,过点C作CD⊥AB于点D.∵在△ABC中,AC=BC,∴AD=BD.①点P在边AC上时,s随t的增大而减小.故A、B错误;②当点P在边BC上时,s随t的增大而增大;③当点P在线段BD上时,s随t的增大而减小,点P与点D重合时,s最小,但是不等于零.故C错误;④当点P在线段AD上时,s随t的增大而增大.故D正确.故选:D.【分析】该题属于分段函数:点P在边AC上时,s随t的增大而减小;当点P在边BC上时,s随t的增大而增大;当点P在线段BD上时,s随t的增大而减小;当点P在线段AD上时,s随t的增大而增大.3.【答案】A【解析】【解答】解:(1)当0<x≤1时,如图1,在菱形ABCD中,AC=2,BD=1,AO=1,且AC⊥BD;∵MN⊥AC,∴MN∥BD;∴△AMN∽△ABD,∴,即,∴MN=x,∴y= CP×MN= (0<x≤1),同理证得,△CDB∽△CNM,,即,∴MN=2﹣x,∴y= CP×MN= (2﹣x)×(2﹣x)= ,∵>0,∴函数图象开口向上;综上,答案A的图象大致符合;故答案为:A.【分析】(1)当0<x≤1时,由菱形的性质及平行线分线段成比例得出△AMN∽△ABD,再由相似三角形的性质得出MN=x,再由y= CP×MN得出解析式,找到图像开口方向;(2)当1<x<2,方法同(1)一样得出MN=2﹣x,再由y= CP×MN得出解析式,找到图像开口方向;综上所述得出结论。
动点问题与函数图象

动点问题与函数图象1、如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A 出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y 关于x的函数图象大致为()A B C D【知识点】动点问题的函数图象【分析】注意分析y随x的变化而变化的趋势,而不一定要通过求解析式来解决.【解析】∵等边三角形ABC的边长为3,N为AC的三等分点,∴AN=1.∴当点M位于点A处时,x=0,y=1.①当动点M从A点出发到AM=1的过程中,y随x的增大而减小,故排除D;②当动点M到达C点时,x=6,y=3﹣1=2,即此时y的值与点M在点A处时的值不相等.故排除A、C.故选B.2、如右图所示,已知等腰梯形ABCD,AD∥BC,若动直线l垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是【知识点】动点问题的函数图象【分析】分三段考虑,①当直线l经过BA段时,②直线l经过AD段时,③直线l经过DC 段时,分别观察出面积变化的情况,然后结合选项即可得出答案.【解析】①当直线l经过BA段时,阴影部分的面积越来越大,并且增大的速度越来越快;②直线l经过DC段时,阴影部分的面积越来越大,并且增大的速度保持不变;③直线l经过DC段时,阴影部分的面积越来越大,并且增大的速度越来越小;结合选项可得,A选项的图象符合.故选A.xByPA DClxsA.…xsB.xsxs3、如右图,已知某容器是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图像大致是【解析】注入水的体积增加的速度随着高度x的变化情况是:由慢到快→匀速增长→由快到慢,由慢到快的图象是越来越陡,由快到慢的图象是越来越平缓,所以选A。
4、如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为()A B C D【知识点】动点问题的函数图象【解析】由图中可知:在开始的时候,阴影部分的面积最大,可以排除B,C.随着圆的穿行开始,阴影部分的面积开始减小,当圆完全进入正方形时,阴影部分的面积开始不再变化.应排除D.故选A.5、.如图9,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE = EF = FB = 5,DE = 12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t 秒,y = S△EPF,则y与t的函数图象大致是【解析】:AD=13,sinA=1213,当P在AD上运动时,△PEF的高h=1213t,y = S△EPF=152⨯⨯1213t,是一次函数关系,当点P在CD上运动时,高不变,底不变,三角形的面积不变,当点P在C上运动时,同样也是一次函数关系,故选A。
由动点引起的函数问题

由动点引起的函数图像问题对函数相关的问题,能够从以下两个方面来观察、认识和把握:①能从“总体感知”和“具体对应方式”两个视角来认识与考虑问题; ②能从“整体过程”和某些“特殊值的对应情况”来认识与考虑问题;就要善于从自变量与函数值的对应关系入手,从原背景、关系式、图象三者的统一来认识和解决问题。
例1 如图所示:边长分别为1和2的两个正方形,其一边在同一水平纸上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t ,大正方形内除去小正方形部分的面积为S (阴影部分),那么S 与t 的函数图象大致应为( )ABC 【观察与思考】“总体感知”:大正方形的面积为4,小正方形的面积为1,在小正方形平移的整个过程中阴影部分面积变化的过程是 解:选A 。
(09北京)8.如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D 、E两点,且∠ACD=45°,DF ⊥AB于点F,EG ⊥AB 于点G ,当点C 在AB 上运动时,设AF=x ,DE=y ,下列中图象中,能表示y 与x 的函数关系式的图象大致是(海淀)8. 如图,点E 、F 是以线段BC 为公共弦的两条圆弧的中点,6BC =. 点A 、D 分别为线段EF 、BC 上的动点. 连接AB 、AD ,设BD x =,22AB AD y -=,下列图象中,能表示y 与x 的函数关系的图象是t t t t 减至 4 3 3 定值 4增值BAA .B .C .D .(朝阳)8.如图,四边形ABCD 中,AD ∥BC, ∠B=60o ,AB=AD=BO=4,OC=8,点P 从B 点出发,沿四边形ABCD 的边BA→AD→DC 以每分钟一个单位长度的速度匀速运动,若运动时间为t,△POD 的面积为S ,则S 与t 函数图象大致为(2010年山东省济南市)如图,在ABC △中,2AB AC ==,20BAC ∠= .动点P Q,分别在直线BC 上运动,且始终保持100PAQ ∠= .设B P x =,CQ y =,则y 与x 之间的函数关系用图象大致可以表示为 ( )【答案】A(2010年重庆市潼南县)如图,四边形ABCD是边长为1 的正方形,四边形EFGH 是边长为2的正方形,点D 与点F 重合,点B ,D (F ),H 在同一条直线上,将正方形ABCD 沿F→H 方向平移至点B 与点H重合时停止,设点D 、F 之间的距离为x ,正方形ABCD 与正方形EFGH 重叠部分的面积为y ,则能大致反映y 与 x 之间函数关系的图象是( )【答案】BGHE(F)ABCD题图10A.B.C.D.运动变化中的函数综合问题例1:如图(1)和(2),在等腰梯形ABCD 中,AB//DC ,cm CD cm AB A 4,10,45==︒=∠。
动点问题生成的函数图象专题
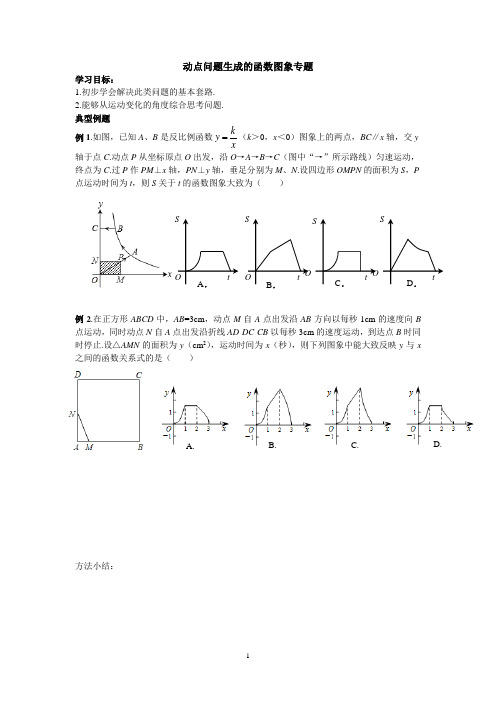
动点问题生成的函数图象专题学习目标:1.初步学会解决此类问题的基本套路.2.能够从运动变化的角度综合思考问题.典型例题例1.如图,已知A、B是反比例函数kyx(k>0,x<0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P 点运动时间为t,则S关于t的函数图象大致为()例2.在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B 点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达点B时同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x 之间的函数关系式的是()方法小结:A. B. C. D.B.OSOC.D.A.O tSttOS St例3.如图,矩形ABCD 中,AB =3,BC =4,动点P 从A 点出发,按A →B →C 的方向在AB 和BC 上移动,记P A =x ,点D 到直线P A 的距离为y ,则y 关于x 的函数图象大致是( )例4.如图,Rt △ABC 中,∠C =90°,AC =3,BC =4,P 是斜边AB 上一动点(不与点A 、B 重合),PQ ⊥AB 交△ABC 的直角边于点Q ,设AP 为x ,△APQ 的面积为y ,则下列图象中,能表示y 关于x 的函数关系的图象大致是( )例5.如图,点P 是⊙O 的弦AB 上任意一点(A ,B 均不重合),点C 在⊙O 上,PC ⊥OP ,已知AB =8,设BP =x ,PC 2=y ,则y 与x 之间的函数图象大致是( )A. B. C.D. A.B. C. D.配套课堂作业(2015.10.12)班级__________ 姓名________________ 1.如图,已知正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为y,AE为x,则y关于x的函数图象大致是()A. B. C. D.2.(2014年江苏徐州)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s 的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发x s时,△P AQ的面积为y cm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为_______________.3.(2014年山东泰安)如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB 上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为()4.(2015•德州)如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=﹣x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是()A. B. C. D.yxO11yxO11111O xyyxO-15.如图,平面直角坐标系中,在边长为1的菱形ABCD的边上有一动点P从点A出发沿A-B-C-D匀速运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是()6.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△P AB的面积y关于x的函数图象大致是()7.如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是()A. B. C.D.A. B. C.D.配套家庭作业(2015.10.12)班级__________ 姓名________________1.如图,在△ABC 中,∠C =90°,M 是AB 的中点,动点P 从点A 出发,沿AC 方向匀速运动到终点C ,动点Q 从点C 出发,沿CB 方向匀速运动到终点B .已知P ,Q 两点同时出发,并同时到达终点.连结MP ,MQ ,PQ .在整个运动过程中,△MPQ 的面积大小变化情况是( )A.一直增大B.一直减小C.先减小后增大D.先增大后减小 2. 如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止.设运动路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则y 关于x 的函数关系式为_____________.3.如图,已知正△ABC 的边长为2,E ,F ,G 分别是AB ,BC ,CA 上的点,且AE =BF =CG ,设 △EFG 的面积为y ,AE 的长为x ,则y 关于x 的函数图象大致是( )4.如图,点P 是▱ABCD 边上一动点,沿A →D →C →B 的路径移动,设P 点经过的路径长为x ,△BAP 的面积是y ,则下列能大致反映y 与x 的函数关系的图象是( )5.如图,E 为矩形ABCD 的边AD 上一点,P ,Q 两点同时从点B 出发,点P 沿折线BE -ED -DC 运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是1cm/s.若P 、Q 同时开始运动,设运动时间为t (s ),△BPQ 的面积为y (cm 2).已知y 与t 的函数图象如图2所示,则下列结论错误的是( ) A.AE =6cm B.sin ∠EBC =45C. 当0<t <10时,225y tD. 当t =12s 时,△PBQ 是等腰三角形A. B. C. D.A. B. C. D.6.如图, A 、B 、C 、D 为O e 的四等分点,动点P 从圆心O 出发,沿O C D O --- 路 线作匀速运动,设运动时间为t (秒),∠APB =y (度),则下列图象中表示y 与t 之间函数关系最恰当的是( )7.(2014•兰州)如图,在平面直角坐标系中,四边形OBCD 是边长为4的正方形,平行于对角线BD 的直线l 从O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,运动到直线l 与正方形没有交点为止.设直线l 扫过正方形OBCD 的面积为S ,直线l 运动的时间为t (秒),下列能反映S 与t 之间函数关系的图象是( )8.如图1,A 、D 分别在x 轴和y 轴上,CD ∥x 轴,BC ∥y 轴.点P 从D 点出发,以1cm/s 的速度,沿五边形OABCD 的边匀速运动一周.记顺次连接P 、O 、D 三点所围成图形的面积为S cm 2,点P 运动的时间为t s .已知S 与t 之间的函数关系如图2中折线段OEFGHI 所示.(1)求A 、B 两点的坐标; (2)若直线PD 将五边形OABCD 分成面积相等的两部分,求直线PD 的函数关系式.A.C.B.D.第6题图AB C DOP B .ty 045 90 D .t y 045 90 A .ty45 90 C .ty 045 90。
动点与函数图像问题剖析

动点问题的函数图象解答此类问题的策略可以归纳为三步:“看” 、“写” 、“选”。
“看”就是认真观察几何图形,彻底弄清楚动点从何点开始出发,运动到何点停止,整个运动过程分为不同的几段,何点(时刻)是特殊点(时刻),这是准确解答的前提和关键;“写”就是计算、写出动点在不同路段的函数解析式,注意一定要注明自变量的取值范围,求出在特殊点的函数数值和自变量的值;“选”就是根据解析式选择准确的函数图像或答案,多用排除法。
首先,排除不符合函数类形的图像选项,其次,对于相同函数类型的函数图像选项,再用自变量的取值范围或函数数值的最大和最小值进行排除,选出准确答案。
一、选择题(共30小题)1.已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有()①图1中的BC长是8cm;②图2中的M点表示第4秒时y的值为24;③图1中的CD长是4cm;④图1中的DE长是3cm;⑤图2中的Q点表示第8秒时y的2y=2.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC→CD 运动至点D 停止.设点P 运动的路程为x ,△APB 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )的面积是×运 动,回到点A 时运动停止.设点P 运动的路程长为长为x ,AP 长为y ,则y 关于x 的函数图象大致是( ). C . 2a+2BD=y=))时,y=)2+22+21+4.(2012•绥化)如图,点A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿OC ﹣﹣DO 的路线做匀速运动,设运动的时间为t 秒,∠APB 的度数为y 度,则下列图象中表示y (度)与t (秒)之间函数关系最恰当的是( ) .BD 上运动时,∠上运动时,∠5.(2010•宜昌)如图,在圆心角为90°的扇形MNK 中,动点P 从点M 出发,沿MN ⇒⇒KM 运动,最后回到点M 的位置.设点P 运动的路程为x ,P 与M 两点之间的距离为y ,其图象可能是( ).6.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数关系的图象是()于是他只好从家出发,乘车沿A⇒B⇒C⇒D的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是()交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是()BE==BE•MN=x x xPQ为一边作正方形PQRS,若BP=x,正方形PQRS与矩形ABCD重叠部份的面积为y,则y与x的函数的大致图象是()动的路程x为自变量,△ABP面积y为函数的图象,如图2,则梯形ABCD的面积是()的面积是(向运动(点P与A不重合).设P的运动路程为x,则下列图象中△ADP的面积y关于x的函数关系()y=回至点O停止,点P在运动过程中速度大小不变,以点O为圆心,线段OP长为半径作圆,则该圆的周长l与点P的运动时间t之间的函数图象大致为().B D13.(2007•泰安)如图,四边形ABCD是边长为2cm的正方形,动点P在ABCD的边上沿A﹣B﹣C﹣D的路径以1cm/s的速度运动(点P不与A,D重合).在这个运动过程中,△APD的面积S(cm)2随时间t(s)的变化关系用图象表示,正确的为()1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是()S=S=此题主要考查了直角梯形的面积求法,以及动点函数的应用,由动点找特殊点,是解决问题的关键.15.(2010•綦江县)如图,在矩形ABCD中,AB=4,BC=3,点P从起点B出发,沿BC、CD逆时针方向向终点D匀速运动.设点P所走过路程为x,则线段AP、AD与矩形的边所围成的图形面积为y,则下列图象中能大致反映y与x函数关系的是()时,所围成的面积为梯形,时,所围成的面积为三角形,驶到景点B,然后从B沿直径BC行驶到⊙D上的景点C.假如旅游船在整个行驶过程中保持匀速,则下面各图中能反映旅游船与景点D的距离随时间变化的图象大致是()17.(2010•十堰)如图,点C,D是以线段AB为公共弦的两条圆弧的中点,AB=4,点E,F分别是线段CD,AB上的动点,设AF=x,AE2﹣FE2=y,则能表示y与x的函数关系的图象是()时间t的关系可能是下列图形中的()19.(2005•兰州)四边形ABCD为直角梯形,CD∥AB,CB⊥AB且CD=BC=AB,若直线L⊥AB,直线L截这个梯形所得的位于此直线左方的图形面积为y,点A到直线L的距离为x,则y与x关系的大致图象为()CD=BC=BCCD=BC=xy=数图象的描述问题.此题主要考查正方形的性质与判定,等腰直角三角形的性质,三角形的面积,梯形的面积以及动点分段函20.如图,BC是⊙D的直径,A为圆上一点.点P从点A出发,沿运动到B点,然后从B点沿BC运动到C点.假如点P在整个运动过程中保持匀速,则下面各图中,能反映点P与点D的距离随时间变化的图象大致是()21.在▭ABCD中,对角线AC=4,BD=6,P是线段BD上一动点,过P作EF∥AC,与▱ABCD的两边分别交于E、F.设BP=x,EF=y,则反映y与x之间关系的图象是()得,化简可得y=时,根据平行线的性质,可得=x+9动到点B,运动时间为t,分别以AP与PB为直径做半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为()=+t24.如图,已知Rt△ABC中,∠BAC=90°,BC=13,AB=12,E是BC边上一点,过点E作DE⊥BC交AC所在直线于点D,若BE=x,△DCE的面积为y,则y与x的函数图象大致是()直到AB与FE重合,直角梯形ABCD与正方形CEFG重叠部分的面积S关于移动时间t的函数图象可能是()运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是()∠向终点B运动,设点P所走过路程CP的长为x,△APB的面积为y,则下列图象能大致反映y与x之间的函数关系的是()y=×自左向右匀速穿过正方形.下图反映了这个运动的全过程,设正三角形的运动时间为t,正三角形与正方形的重叠部分面积为s,则s与t的函数图象大致为().B D29.如图,腰长为1和2的两个等腰直角三角形,其一腰在同一水平线上,小等腰直角三角形沿该水平线自左向右匀速穿过大等腰直角三角形,设穿过的时间为x ,大等腰三角形内减去小等腰直角三角形部分的面积为y (各个图中的阴影部分),则y 与x 的大致图象为( ). BDB 点匀速运动,那么表示△PAB 的面积S (厘米2)与点P 运动时间t (秒)之间的函数关系的图象为图( )。
动点函数图象

动点问题的函数图像1,如图①,在矩形 ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D 路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿 D→C→B→A路线向点A匀速运动,到达点A后停止.若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.(1)请解释图中点H的实际意义?(2)求P、Q两点的运动速度;(3)将图②补充完整;(4)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值.分析:(1)根据P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象得出H点时两点相遇;(2)利用函数图象得出当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留,只有P点运动,再利用纵坐标的值得出P点和Q点运动速度;(3)根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),进而画出图象即可;(4)根据Q,P的位置不同,进行分类讨论得出答案即可.解:(1)图中点H的实际意义:P、Q两点相遇;(2)由函数图象得出,当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒,只有P 点运动,此时纵坐标的值由75下降到45,故P点运动速度为:30cm/s,再根据E点到F点S的值由120变为75,根据P点速度,得出Q点速度为120-75-30=15(cm/s),即P点速度为30cm/s,Q点速度为 15cm/s;(3)如图所示:根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),画出图象即可;(4)如图1所示,当QP=PC,此时12QC=BP,即30-30t=12(30-15t),解得:t=23,故当时间t=23s时,△PCQ为等腰三角形,如图2所示,当D,P重合,QD=QC时,Q为AB中点,则运动时间为:(15+60+30)÷15+1=8(s),故当时间t=8s时,△PCQ为等腰三角形.若PC=CQ故90-30t=30-15t解得:t=4则4+1=5(S)综上所述:t=23或t=5或t=8秒时,△PCQ为等腰三角形.点评:此题主要考查了动点问题的函数图象,主要运用分类讨论的思想,函数的知识和等腰三角形的知识,具有很强的综合性.2.在ABC中,点P从点A开始出发向点C运动,在运动过程中,设线段AP的长为x,线段BP的长为y(如图1),而y关于x的函数图象如图2所示,点Q是函数图象上的最低点,请仔细观察图1和图2,解答下列问题.(1)AC边的长为,BC边的长为;(2)求∠C的度数;(3)若△BPC为钝角三角形,求x的取值范围.分析:(1)观察函数图象得到当x=9时,y=4,说明此时P点运动到了C点,于是得到AC=9,BC=4;(2)作BD⊥AC于D,由函数图象得x=7时,y的值最小,即P点运动到D点时,BP最小,所以AD=7,则DC=2,然后根据含30度的直角三角形三边的关系得到∠CBD=30°,利用互余有∠C=60°;(3)作EB⊥BC交AC于E,则点P在线段AE(不含E点)或线段CD(不含端点)上运动时,△BPC为钝角三角形,利用∠CBD=30°可得到∠EBD=60°,∠BED=30°,在Rt△BCE 中,可计算出EC=8,所以AE=1,于是得到满足条件的x的取值范围为0≤x<1或7<x<9.解:(1)观察图2,当x=9时,y=4,此时P点运动到了C点,所以AC=AP=9,BC=BP=4;故答案为9,4;(2)作BD⊥AC于D,如图,∵点Q是函数图象上的最低点,即x=7时,y的值最小,∴点P运动到D点时,BP最短,即AD=7,∴DC=AC-AD=9-7=2,在Rt△BCD中,CD=2,BC=4,∴∠CBD=30°,∴∠C=60°;(3)作EB⊥BC交AC于E,如图,∵∠CBD=30°,∴∠EBD=60°,∠BED=30°,在Rt△BCE中,EC=2BC=8,∴AE=1,当点P在线段AE(不含E点)或线段CD(不含端点)上运动时,△BPC为钝角三角形,∴x的取值范围为0≤x<1或7<x<9.点评:本题考查了动点问题的函数图象:通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.也考查了含30度的直角三角形三边的关系.3.在△ABC中,点P从B点开始出发向C点运动,在运动过程中,设线段AP的长为y,线段BP的长为x(如图甲),而y关于x的函数图象如图乙所示.Q(1,3)图象上的最低点.请仔细观察甲、乙两图,解答下列问题.(1)请直接写出AB边的长和BC边上的高AH的长;(2)求∠B的度数;(3)若△ABP为钝角三角形,求x的取值范围.分析:(1)当x取0时,y的值即是AB的长度,图乙函数图象的最低点的y值是AH的值.(2)当点P运动到点H时,此时BP(H)=1,AH=3,在RT△ABH中,可得出∠B的度数.(3)分两种情况进行讨论,①∠APB为钝角,②∠BAP为钝角,分别确定x的范围即可.解:(1)当x=0时,y的值即是AB的长度,故AB=2;图乙函数图象的最低点的y值是AH的值,故AH=3;(2)在RT△ABH中,AH=33,故∠B=60°.(3)①当∠APB为钝角时,此时可得0<x<1;②当∠BAP为钝角时,过点A作AP⊥AB,则BP=ABcos∠B=4,即当4<x≤6时,∠BAP为钝角.综上可得0<x<1或4<x≤6时△ABP为钝角三角形.点评:此题考查了动点问题的函数图象,有一定难度,解答本题的关键是结合图象及函数图象得出AB、AH的长度,第三问需要分类讨论,注意不要漏解.4.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPQ 的面积是 .分析:易得当R在PN上运动时,面积不断在增大,当到达点P时,面积开始不变,到达Q后面积不断减小,得到PN和QP的长度,相乘即可得所求的面积.解:∵x=4时,及R从N到达点P时,面积开始不变,∴PN=4,同理可得QP=5,∴矩形的面积为4×5=20.故选C.点评:考查动点问题的函数的有关计算;根据所给图形得到矩形的边长是解决本题的关键.5.如图1,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图2所示.(1)求长方形ABCD的长和宽;(2)求m、a、b的值.分析:(1)由图象可知,CD的长度,当t=6时,S△ABP=16,求出BC的长;(2)当t=a时,S△ABP=8,则点P此时在BC的中点处,从而得出a和m的值,当t=b时,S△ABP=4,从而求得b的值;解:(1)从图象可知,当6≤t≤8时,△ABP面积不变即6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位∴CD=2×(8-6)=4∴AB=CD=4(2分)当t=6时(点P运动到点C),S△ABP=16∴12AB•BC=16∴12×4×BC=16∴BC=8(4分)∴长方形的长为8,宽为4.(2)当t=a时,S△ABP=8=12×16即点P此时在BC的中点处∴PC=12BC=12×8=4∴2(6-a)=4∴a=4(6分)∵BP=PC=4∴m=BP÷a=4÷4=1,当t=b时,S△ABP=12AB•AP=4∴12×4×AP=4,AP=2∴b=13-2=11(9分);点评:本题是一次函数的综合题,重点考查了动点问题的函数图象,考查了学生观察图象的能力,用待定系数法求一次函数的解析式,是一道中考压轴题.6.已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙,若AB=6cm,试回答下列问题:(1)图甲中BC的长度是8cm.(2)图乙中A所表示的数是24.(3)图甲中的图形面积是60cm2.(4)图乙中B所表示的数是17.分析:(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC 的长;(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得图乙中A 所表示的数;(3)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案;(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得图乙中B所表示的数.解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm.故图甲中BC的长度是8cm;(2)由(1)可得,BC=8cm,则:图乙中A所表示的数是:1 2 ×BC×AB=1 2 ×8×6=24(cm2).故图乙中A所表示的数是24;(3)由图可得:CD=2×2=4cm,DE=2×3=6cm,则AF=BC+DE=14cm,又由AB=6cm,则甲中的梯形面积为AB×AF-CD×DE=6×14-4×6=60(cm2).故图甲中的图形面积为60cm2;(4)根据题意,动点P共运动了BC+CD+DE+EF+FA=(BC+DE)+(CD+EF)+FA=14+6+14=34(cm),其速度是2cm/秒,34÷2=17(秒).故图乙中B所表示的数是17.故答案为8cm;24;60cm2;17.解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm.故图甲中BC的长度是8cm;(2)由(1)可得,BC=8cm,则:图乙中A所表示的数是:12×BC×AB=12×8×6=24(cm2).故图乙中A所表示的数是24;(3)由图可得:CD=2×2=4cm,DE=2×3=6cm,则AF=BC+DE=14cm,又由AB=6cm,则甲中的梯形面积为AB×AF-CD×DE=6×14-4×6=60(cm2).故图甲中的图形面积为60cm2;(4)根据题意,动点P共运动了BC+CD+DE+EF+FA=(BC+DE)+(CD+EF)+FA=14+6+14=34(cm),其速度是2cm/秒,34÷2=17(秒).故图乙中B所表示的数是17.故答案为8cm;24;60cm2;17.点评:本题考查动点问题的函数图象,三角形的面积等知识点的理解和掌握,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.7. 如图1,在直角梯形ABCD,∠B=90°,DC∥AB,动点P从B点出发,由B--C--D--A沿边运动,设点P运动的路程为x,△ABP的面积为y,如果关于x的函数y的图象如图2,则△ABC 的面积为()。
动点问题的函数图象

【考点精讲】动点问题是中考的常考点,对于解决动点问题中,点动会牵扯到线动、面动,解决这类题目要“以静制动”,即把动态的问题转化为静态问题来解决,一般方法是抓住变化中的“不变量”,以不变应万变。
而对于动点问题的图象问题的解决,要抓住图形中的关键点,例如与x 轴、y 轴的交点,图象上的转折点、图象中与x 轴、y 轴平行的线等图象。
【典例精析】例题1 (贵州贵阳中考)如图,在直径为AB 的半圆O 上有一动点P 从A 点出发,按顺时针方向绕半圆匀速运动到B 点,然后再以相同的速度沿着直径回到A 点停止,线段OP 的长度d 与运动时间t 之间的函数关系用图象描述大致是( )(A . B. C . D .思路导航:情境分三段,点P 在圆周上、在OB 上,在AO 上,因此图象分三段,根据在每一段上线段OP 的长度d 随运动时间t 的变化来确定。
答案:点P 在圆周上时,d 不随t 的变化而变化,故第一段图象平行x 轴,点P 在OB 上,d 随t 的增加而减小,直到0,故此段图象呈下降趋势,点P 在AO 上,d 随t 的增加而增大,直到增加到半径的长度,即与第一段图象齐平,故选A 。
点评:先根据运动过程理解函数与自变量的变化规律以及分段情况,然后对照所给图象找到满足问题情境变化的规律。
注意弄清函数图象中横轴和纵轴意义,以及每段图象的起始点。
例题2 矩形ABCD 中,AB =20cm ,BC =10cm ,有一点P 沿着矩形从A 向B 再向C 以2cm/s 的速度移动。
(1)求△APC 的面积S 与时间t 的函数解析式,并指出自变量的取值范围。
(2)当面积为20cm2时,求点P的位置。
思路导航:△APC的面积为12AP BC⋅或12AP AB⋅,只要利用含t的代数式表示AP和PC即可。
答案:解:(1)1210(010)21(302)20(1015) 2t tSt t⎧⨯⨯<≤⎪⎪=⎨⎪⨯-⨯<<⎪⎩,化简得:10(010)30020(1015)t tSt t<≤⎧=⎨-<<⎩。
几何画板动点与函数问题

第七节动点与函数问题这类问题主要探究动点在移动过程中,相关线段的长或相关图形的面积随点的移动距离的变化而变化的情况,大多可以通过建立直角坐标系,构造出动态的函数图象,结合图象的动态演示过程,来寻找解题思路,明晰各种情况,使问题得到解决。
一、双直线型双动点与函数问题例1如图,在Rt△OAB中,OA=4,AB=3。
动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动。
当两个动点运动了x秒(0<x<4)时,解答下列问题:(1)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?(2)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由。
分析:由条件易知,两个动点运动4秒时,同时到达终点。
可将点M设置为主动点,利用点M的点值构造出点N。
画图时要注意线段的方向,构造动态函数图象时要注意将测量得到的实际长度和面积转化为特定长度和面积。
作法:⑴构造水平线段AO,双击点A标记中心,将点O按固定比43缩放,得到点C;再将点C按—90°旋转,得到点B。
连接OB,AB,得到Rt△OAB。
将点C隐藏。
在OA上构造任意一点M,选定点M,度量其点值;选定点M的点值及线段OB,点击“绘图”菜单中的“在线段上绘制点”,得到点N。
⑵用“线段直尺工具”连接MN,AM,选定点O,M,N,点击“构造”菜单→“构造三角形的内部”,得到△OMN的内部。
度量点A,O的距离,得到线段AO的长;计算AO长与4的商,得到单位长度。
度量点A,M的距离,得到线段AM的长,计算AM长与单位长度的商,得到线段AM的特定长度,修改其标签为x。
选定△OMN的内部,度量其面积,再用面积除以单位长度的平方,得到△OMN的特定面积,修改其标签为y。
⑶建立直角坐标系并标记坐标系。
选定x及y的值,点击“绘图”菜单→“绘制点(x,y)”,在坐标系中得到对应的点D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、增减性问题——结论
三、图象是否为直线——问题描述
动点 P 从点 A 出发,沿折线 A→B→M 的路径运动, 设点 P 运动的路程长为 x,AP 长为 y. 已知 AB=a,∠ABP= , x a 0 , 0 180 . 讨论 y 关于 x 的函数图象是否为直线.
三、图象是否为直线——分析
AP' AP ,
可知,y 随 x 增大而增大.
二、增减性问题——分析
(4)当 0 90 时,实际运动如下: ①当 P 在 BO 线段上, 根据三角形外角定理, 1 90 2 , 根据大角对大边, AP AP .
'
此时,y 随 x 增大而减小. ②当点 P 运动到射线 OM 上时, 如前面讨论,y 随 x 增大而增大.
P 在 DC 上时, AD a , DP x a 2a , 通过勾股定理可得,
AP2 x2 2ax 2 2ax 4a2 2 2a2
2 2 2 y x 2 ax 2 2 ax 4 a 2 2 a ∴
一、研究问题——是均匀增加的吗?
yx (0 x a )
如图,根据余弦定理, AP AB BP 2 AB BP cos ,
2 2 2
∴y
x 2 2a (1 cos ) x 2a 2 2a 2 cos ( x a 0)
三、图象是否为直线——结论
四、拓展——同一起点出发的两A 速度为 a, 点 B 速度为 b, ∠MON= . 0 180 . 记运动时间为 t,AB 长为 y. 讨论 y 与 t 的函数关系.
y x 2 2ax 2 2ax 4a 2 2 2a 2 ( a 2a x 2a 2a )
一、研究问题——结论
实际运动 1 2 3 4 增减趋势 特殊点 对称性 增加均匀
函数图象 单调性 极值点、拐点、端点 (局部)对称性 线性
二、增减性问题——问题描述
动点 P 从点 A 出发,沿折线 A→B→M 的路径运动, 设点 P 运动的路程长为 x,AP 长为 y. 已知 AB=a,∠ABP= , x a 0 , 0 180 . 讨论 y 关于 x 的函数的增减性.
四、拓展——同一起点出发的两动点问题
用全等三角形证明
M B'' B' B
θ O A A' A'' N
四、拓展——同一起点出发的两动点问题
用余弦定理证明
y 2 a2t 2 b2t 2 2abt 2 cos
2 2 y a b 2ab cos t , ∴
感谢倾听!
与动点有关的函数图象问题
北京一零一中学 陈静
一、研究问题——与动点有关的函数图象
(2013浙江)如图,正方形ABCD的边长为a, 动点P从点A出 发, 沿折线A→B→D→C→A的路径运动,回到点A时运动停止. 设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致 是( D )
A
B
C
D
一、研究问题——是均匀增加的吗?
二、增减性问题——分析
(1)当 0 时,实际运动对应两种情况.如下:
y
y x 2a (a x 2a )
y
y x 2a ( x 2a )
二、增减性问题——分析
(2)当 180 时,实际运动如下:
y
y x ( x a)
二、增减性问题——分析
(3)当 90 180 时,实际运动如下: 根据三角形外角定理, 1 2 , 根据大角对大边,
