动点问题的函数图像
动点问题的函数图象

xxxxyy yyDCBA63636363OOOO图5OCD ABP 动点问题的函数图象1.(2013•牡丹江)如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s 与t 的大致图象应为 ( )2.(2013•北京 )如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB=2,设弦AP 的长为x ,△APO 的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是 ( )3.(2013•葫芦岛)如图5矩形ABCD 的对角线交于点O ,∠BOC=60°,AD=3.动点P 从点A 出发,沿折线AD-DO 以每秒1个单位的速度运动到点O 停止,设运动时间为x 秒,y=S △POC ,则y 与x 的函数关系式为( )4.(2013•兰州)如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回,点P在运动过程中速度不变,则以点B 为圆心,线段BP 长为半径的圆的面积S 与点P 的运动时间t 的函数图象大致为( )A .B . C.D C B A s t o s t o s t o o t sD .5.(2013•铁岭)如图,点G 、E 、A 、B 在一条直线上,Rt △EFG 从如图所示是位置出发,沿直线AB 向右匀速运动,当点G 与B 重合时停止运动.设△EFG 与矩形ABCD 重合部分的面积为S ,运动时间为t ,则S 与t 的图象大致是( ) A .B .C .D .6.(2012•铁岭)如图, ABCD 的边长为8,面积为32,四个全等的小平行四边形对称中心分别在ABCD 的顶点上,它们的各边与 ABCD 的各边分别平行,且与 ABCD 相似.若小平行四边形的一边长为 ,且0< ≤8,阴影部分的面积的和为 ,则与 之间的函数关系的大致图象是 ( )A. B. C. D.7.(2011•安徽)如图,点P 是菱形ABCD 的对角线AC 上的一个动点,过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点.设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象大致形状是 ( )8.(2011•葫芦岛)如图,在矩形中截取两个相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长与宽分别为y 和x ,则y 与x 函数的图象大致是( ).OOOOx x x x y y y y 1 2 1 2 1 2 1 2 A .B .C .D . x x y y x ABCDMN P9.(2012•营口)如图,菱形ABCD 的边长为2,∠B=30°.动点P 从点B 出发,沿B ﹣C ﹣D 的路线向点D 运动.设△ABP 的面积为y (B 、P 两点重合时,△ABP 的面积可以看做0),点P 运动的路程为x ,则y 与x 之间函数关系的图象大致为( )10.(2011•辽阳)如图,等边△ABC 的边长为4,M 为BC 上一动点(M 不与B 、C 重合),若EB =1,∠EMF =60°,点E 在AB 边上,点F 在AC 边上.设BM =x ,CF =y ,则当点M 从点B 运动到点C 时,y 关于x 的函数图象是( ).11.(2011•营口)如图,半径为1的圆和边长为3的正方形在同一水平线上,圆沿水平线从左向右匀速穿过正方形,设穿过时间为t ,正方形除去圆部分的面积为S (阴影部分),则S 与t 的大致图象为( ).12.(2013•营口)如图1,在矩形ABCD 中,动点E 从点B 出发,沿B A DA .B .C .D .A DEyC 方向运动至点C 处停止,设点E 运动的路程为x ,△BCE 的面积为y ,如果y 关于x 的函数图象如图2所示,则当7 x 时,点E 应运动到( )A .点C 处B .点D 处C .点B 处D .点A 处13.(2012•鞍山)如图,在直角梯形ABCD 中,AD ∥BC ,∠A=90°,AB=BC=4,DE ⊥BC 于点E ,且E 是BC 中点;动点P 从点E 出发沿路径ED→DA→AB 以每秒1个单位长度的速度向终点B 运动;设点P 的运动时间为t 秒,△PBC 的面积为S ,则下列能反映S 与t 的函数关系的图象是( ) 14.15.(2013•自贡)如图,已知A 、B 是反比例函数上的两点,BC ∥x轴,交y 轴于C ,动点P 从坐标原点O 出发,沿O→A→B→C 匀速运动,终点为C ,过运动路线上任意一点P 作PM ⊥x 轴于M ,PN ⊥y 轴于N ,设四边形OMPN 的面积为S ,P 点运动的时间为t ,则S 关于t 的函数图象大致是( )A .B .C .D .A .B .C .D .16.(2012•烟台)如图,矩形ABCD 中,P 为CD 中点,点Q 为AB 上的动点(不与A ,B 重合).过Q 作QM ⊥PA 于M ,QN ⊥PB 于N .设AQ 的长度为x ,QM 与QN 的长度和为y .则能表示y 与x 之间的函数关系的图象大致是( ) A . B . C . D .17.(2012•岳阳)如图,两个边长相等的正方形ABCD 和EFGH ,正方形EFGH 的顶点E 固定在正方形ABCD 的对称中心位置,正方形EFGH 绕点E 顺时针方向旋转,设它们重叠部分的面积为S ,旋转的角度为θ,S 与θ的函数关系的大致图象是( ) 18.(2012•攀枝花)如图,直角梯形AOCD 的边OC 在x 轴上,O为坐标原点,CD 垂直于x 轴,D (5,4),AD=2.若动点E 、F 同时从点O 出发,E 点沿折线OA→AD→DC 运动,到达C 点时停止;F 点沿OC 运动,到达C 点是停止,它们运动的速度都是每秒1个单位长度.设E 运动秒x 时,△EOF 的面积为y (平方单位),则y 关于x 的函数图象大致为( )A .B .C .D .19.(2012•桂林)如图,在边长为4的正方形ABCD 中,动点P 从A 点出发,以每秒1个单位A .B .C .D .长度的速度沿AB 向B 点运动,同时动点Q 从B 点出发,以每秒2个单位长度的速度沿BC →CD 方向运动,当P 运动到B 点时,P 、Q 两点同时停止运动.设P 点运动的时间为t ,△APQ 的面积为S ,则S 与t 的函数关系的图象是( )20.(2010•烟台)如图,AB 为半圆的直径,点P 为AB 上一动点,动点P 从点A 出发,沿AB 匀速运动到点B ,运动时间为t ,分别以AP 于PB 为直径做半圆,则图中阴影部分的面积S 与时间t 之间的函数图像大致为A B CD。
初中常见动点问题解题方法PPT课件

p
考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等 边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称 点就在这个图形上。
练习
1、如图,等边△ABC的边长为4,AD是BC边上的中线,
F是AD边上的动点,E是AC边上一点,若AE=2,
当EF+CF取得最小值时,则∠ECF的度数为( )
2单位
/s
30o
5
综上所述,当t= 5 或t=4时△DEF为直角三角形
2
AE
30o
D
BF
C
小结
在变化中找到不变的性质是解决数学 “动点”探究题的基本思路,这也是动态 几何数学问题中最核心的数学本质。
SUCCESS
THANK YOU
•
(1)确定被“搬”的点 (2)确定被“移”的线
二、动点构成特殊图形
问题背景是特殊图形,考查问题也是特殊图 形,所以要把握好一般与特殊的关系;分析过程中,特 别要关注图形的特性(特殊角、特殊图形的性质、图 形的特殊位置).分析图形变化过程中变量和其他量 之间的关系,或是找到变化中的不变量,建立方程 或函数关系解决。
解析:
作点N关于AD的对称点 N ' 此时BM+MN=BM+M N '
要使BM+MN ' 最小 则要满足:① B,M,N ' 三点共线
②B N 垂' 直于 AC
÷ ∴ BM+MN的最小值= BN '=AB
C
N'
M
D
B
A
N
N'
C
MD
A
NB
练习
1. 如图,在△ABC中,∠C=90°,CB=CA=4, ∠A的平分线交BC于点D,若点P、Q分别是AC 和AD上的动点,则CQ+PQ的最小值是____________
专题02 动点问题中的函数图象及规律探索问题(解析版)

专题02 动点问题中的函数图象及规律探索问题一、基础知识点综述动点问题中函数图象的题目的解决方法是:先根据动点运动规律找出所求与动点运动之间的关系,进而获取相应函数的解析式及函数值变化规律,达到求解的目的.考查的重点是分段函数解析式的求解.探索规律问题通常用归纳法,即从简单到复杂,从特殊到一般,这类题目考查的是学生的观察与归纳能力,注意从特殊到一般的归纳方法.二、主要思想方法分类讨论、数学归纳.三、精品例题解析例1. (2019·达州改编)如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在同一条直线上,且A点与F点重合,现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止. 在这个运动过程中,正方形ABCD与△EFG重叠部分的面积S与运动时间t的函数解析式是【答案】()220224t242tSt⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩.【解析】解:(1)(2)当0≤t≤2时,如图(1)所示,由题意知:∠HF A=60°,∠AHF=30°,CCEAF =t ,AH,12S AF AH =⨯⨯=)2122tt =; 当2<t ≤4时,如图(2)所示,由题意知:∠E =60°,∠AHE =30°, AF =t ,AE =4-t , AH)4t -EFG EFA S S S =-△△())2144t 4t 42⎤=⨯---⎦()24t 2=-综上所述,()22024t 242t S t ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩例2. (2019·自贡)均匀的向一个容器内注水,在注满水的过程中,水面的高度h 与时间t 的函数关系如图所示,则该容器是下列四个中的()【答案】D .【解析】解:A 为圆柱体,其函数图象应为一条直线,故不合题意;B 选项下面粗上面细,其函数图象是一条折线,且后半段的变化速率较慢(图象较缓),故不合题意;C 选项函数图象应为一条曲线,故不合题意;D 选项下面细上面粗,其函数图象是一条折线,且后半段的变化速率较快,故符合题意; 故答案为:D .例3. (2019·潍坊改编)如图,在矩形ABCD 中,AB =2,AD =3,动点P 沿着折线BCD 从点B 开始运动到点D ,设运动的路程为x ,△ADP 的面积为y ,则y 与x 之间的函数关系式是【答案】3031533522x y x x ≤≤⎧⎪=⎨-<≤⎪⎩.【解析】解:①当点P 在线段BC 上时,即0≤x ≤3时,132y AD AB =⨯⨯=;②当点P 在线段CD 上时,即3<x ≤5时,()11153352222y AD DP x x =⨯⨯=⨯⨯-=-; 综上所述,3031533522x y x x ≤≤⎧⎪=⎨-<≤⎪⎩.例4. (2019·深圳模拟)如图①,在菱形ABCD 中,动点P 从点B 出发,沿折线B →C →D →B 运动. 设点P 经过的路程为x ,△ABP 的面积为y . 把y 看成x 的函数,函数的图象如图②所示,则图②中的b 等于【答案】【解析】解:由图②可知,当x =4时△ABP 的面积最大,此时P 点运动至点C ,即菱形ABCD 的边长为4,又x =14时停止,即BD =6,DP连接AC交BD于O,AC⊥BD,∴BD=3,在Rt△BOC中,由勾股定理得:OC,∴AC=即b=12AC BC ⨯⨯=故答案为:例5. 如图1,在扇形OAB中,∠O=60°,动点P从点O出发,沿O→A→B以1cm/s的速度匀速运动至点B,图2是点P运动过程中,△OBP的面积y(cm2)随时间x(s)变化的图象,则a,b的值分别为【答案】4,443π+.【解析】解:由题意知:当点P运动至点A时,△OBP的面积为∵∠O=60°,∴△OAB为等边三角形,∴OA=4,即a=4,b=(OA+l AB)÷1=443π+.故答案为:4,443π+.例6. (2019·河南模拟)如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的()A.线段BE B.线段EF C.线段CE D.线段DE【答案】D.【解析】解:A、若线段BE是y,则y随x的增大先减小再增大,在点A的距离是BA,在点C时的距离是BC,因为BA<BC,故A错误;B、若线段EF是y,则y随x的增大越来越小,故B错误;C、若线段CE是y,则y随x的增大越来越小,故C错误;D、若线段DE是y,则y随x的增大先减小再增大,在点A的距离是DA,在点C时的距离是DC,DA>DC,故选项D正确;故答案为:D.例7. (2019·博罗县一模)如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为()A.B.C.D.【答案】A .【解析】解:设∠AOM =β,点P 运动的速度为x , 当点P 从点O 运动到点A 的过程中, S =()()22111cos sin cos sin 222OM PM xt xt x t ββββ⨯⨯=⨯= 由于β及x 均为常量,即21cos sin 2x ββ为定值,可知本段图象应为抛物线,且S 随着t 的增大而增大;故选项B 、C 错误;当点P 从A 运动到B 时,由反比例函数性质可知△OPM 的面积为12k ,保持不变,故本段图象应为与横轴平行的线段;故选项C 错误; 故选:A .例8. (2017·濮阳县一模)如图,等边△ABC 边长为2,四边形DEFG 是平行四边形,DG =2,DE =3,∠GDE =60°,BC 和DE 在同一条直线上,且点C 与点D 重合,现将△ABC 沿D →E 的方向以每秒1个单位的速度匀速运动,当点B 与点E 重合时停止,则在这个运动过程中,△ABC 与四边形DEFG 的重合部分的面积S 与运动时间t 之间的函数关系图象大致是( )A .B .C .D .【答案】B .【解析】解:分三种情况:①0≤t ≤2时,由重叠部分为边长为t 的等边三角形; 如图1,由题意知CD =t ,∠HDC =∠HCD =60°, ∴△CDH 是等边三角形,则S 2;即该段函数图象是开口朝上的抛物线的一部分,S 随t 的增大而增大; ②2<t ≤3时,由重叠部分即为△ABC ; 如图2,S =4×22; 此段函数图象是一条平行于x 轴的线段; ③3<t ≤5时由重叠部分是S △ABC ﹣S △HEC 如图3,根据题意可得CE =CD ﹣DE =t ﹣3,∠C =∠HEC =60°, ∴△CEH 为等边三角形,则S =S △ABC ﹣S △HEC =4×22﹣4(t ﹣3)2=﹣4t 2+2t ﹣4; 此段函数图象为开口朝下的抛物线的一部分,且S 随t 的增大而减小综上所述,0≤t ≤2时函数图象是开口向上的抛物线的一部分,2<t ≤3时函数图象是平行于x 轴的一部分,当3<t ≤5时函数图象是开口向下的抛物线的一部分; 故答案为B .例9. (2019·衡阳)如图,在直角三角形ABC 中,∠C =90°,AC =BC ,E 是AB 的中点,过点E 作AC 和BC 的垂线,垂足分别为点D 和点F ,四边形CDEF 沿着CA 方向匀速运动,点C 与点A 重合时停止运动,设运动时间为t ,运动过程中四边形CDEF 与△ABC 的重叠部分面积为S .则S 关于t 的函数图象大致为()A.B.C.D.【答案】C.【解析】解:∵在直角三角形ABC中,∠C=90°,AC=BC,∴△ABC是等腰直角三角形,∵EF⊥BC,ED⊥AC,∴四边形EFCD是矩形,∵E是AB的中点,∴EF=12AC,DE=12BC,∴EF=ED,∴四边形EFCD是正方形,设正方形的边长为a,如图1,当移动的距离小于a时,S=正方形的面积﹣△EE′H的面积=a2﹣12t2;当移动的距离大于a时,如图2,S=S△AC′H=12(2a﹣t)2=12t2﹣2at+2a2,∴S关于t的函数图象大致为C选项,综上所述,移动距离小于正方形CDEF边长时,函数图象是开口朝下的抛物线一部分,且S随t的增大而减小;移动距离大于正方形CDEF边长时,函数图象是开口朝上的抛物线一部分,且S随t的增大而减小;故答案为:C.例10.a是不为1的有理数,我们把11a-成为a的差倒数,如2的差倒数是-1,-1的差倒数是0.5. 已知a1=5,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……,以此类推,则a2019的值是.【答案】4 5 .【解析】解:由题意知:a1=5,a2=14-,a3=45,a4=5,……2019÷3=673,即a2019=4 5 .例11. (2019·潍坊)如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点O,它们的半径分别为1,2,3,……,按照“加1”依次递增,一组平行线,l0,l1,l2,l3,……都与x轴垂直,相邻两直线的间距为1,其中l0与y轴重合. 若半径为2的圆与l1在第一象限交于点P1,半径为3的圆与l2在第一象限交于点P2,……,半径为n+1的圆与ln在第一象限交于点P n,则点P n的坐标为【答案】4.【解析】解:连接OP 1,设l 1与x 轴交于点A 1,由题意知:OP 1=2,OA 1=1, 在RtOP 1A 1中,由勾股定理得:P 1A 1即P 1(;同理得:P 2(,P 3(,P 4(…… 即P n(n .例12. (2019·连云港) 如图,将一等边三角形三条边各八等分按顺时针方向标注各等分点的序号0、1、2、3、4、5、6、7、8,如图所示,将和为8的点连接起来,得到了“三角形坐标系”.在建立的坐标系中,每一点的坐标用过这一点且平行(重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点A 的坐标为(1,2,5),点B 的坐标为(4,1,3),则点C 的坐标为【答案】(2,4,2).【解析】由题意知,通过点C 的数字依次是2,4,2(顺时针),故答案为(2,4,2).例13. (2019·衡阳)在平面直角坐标系中,抛物线y =x 2的图象如图所示.已知A 点坐标为(1,1),过点A 作AA 1∥x 轴交抛物线于点A 1,过点A 1作A 1A 2∥OA 交抛物线于点A 2,过点A 2作A 2A 3∥x 轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为.【答案】(﹣1010,10102).【解析】解:∵A点坐标为(1,1),∴直线OA为y=x,A1(﹣1,1),∵A1A2∥OA,∴直线A1A2为y=x+2,联立y=x+2,y=x2得,A2(2,4),A3(﹣2,4),∵A3A4∥OA,∴直线A3A4为y=x+6,同理得:A4(3,9),A5(﹣3,9)…,∴A2019(﹣1010,10102),故答案为(﹣1010,10102).例14. (2019·怀化)探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是.【答案】n-1. 【解析】解:由题意“分数墙”的总面积=2×12+3×13+…+n×1n=n﹣1,故答案为n﹣1.。
2020年浙江省中考数学题型专练一 动点问题的函数图像含答案
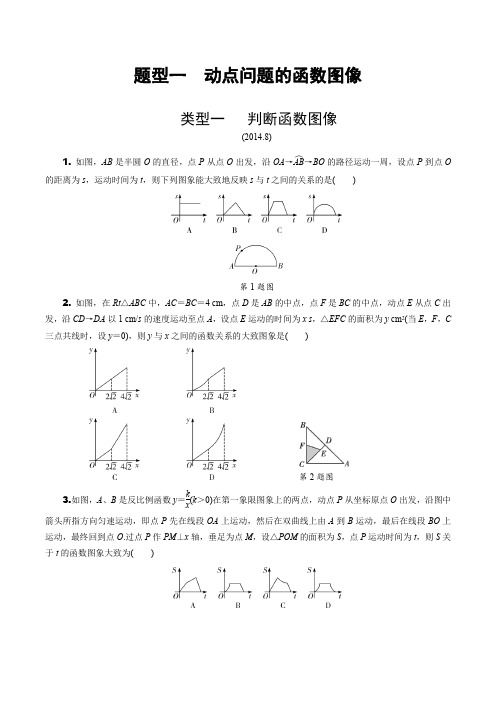
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图,AB 是半圆O 的直径,点P 从点O 出发,沿OA →AB ︵→BO 的路径运动一周,设点P 到点O的距离为s ,运动时间为t ,则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图,在Rt △ABC 中,AC =BC =4 cm ,点D 是AB 的中点,点F 是BC 的中点,动点E 从点C 出发,沿CD →DA 以1 cm/s 的速度运动至点A ,设点E 运动的时间为x s ,△EFC 的面积为y cm 2(当E ,F ,C 三点共线时,设y =0),则y 与x 之间的函数关系的大致图象是( )第2题图3.如图,A 、B 是反比例函数y =k x(k >0)在第一象限图象上的两点,动点P 从坐标原点O 出发,沿图中 箭头所指方向匀速运动,即点P 先在线段OA 上运动,然后在双曲线上由A 到B 运动,最后在线段BO 上运动,最终回到点O .过点P 作PM ⊥x 轴,垂足为点M ,设△POM 的面积为S ,点P 运动时间为t ,则S 关于t 的函数图象大致为( )第3题图4.如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图,在矩形ABCD中,对角线AC与BD交于点O,点M为线段AC上一个动点,过点M作EF∥BD 交AD(或DC)于点E,交AB(或BC)于点F,已知AC=5,设AM=x,EF=y,则y关于x的函数图象大致为()第5题图6. (2019衢州)如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C 移动至终点C,设点P经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①,点P从矩形ABCD的顶点B出发,沿射线BC的方向以每秒1个单位长度的速度运动,过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象,其中点Q是第一段曲线(抛物线的一部分)的最高点,则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①,四边形ABCD中,AB∥CD,∠B=90°,AC=A D.动点P从点B出发,沿折线B-A-D-C方向以 1 cm/s的速度匀速运动,在整个运动过程中,△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示,则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①,菱形ABCD中,∠B=60°,动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位的速度自点B出发沿折线B-C-D运动到点D.图②是点P、Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①,在正方形ABCD中,动点E从点A出发,沿A-B-C运动,当点E到达点C时停止运动,过点E作EF⊥AE,交CD于点F,设点E运动的路程为x,FC=y(当点A,E重合时,点D,F重合;当点C,E重合时,不妨设y=0),y与x的函数关系的大致图象如图②,当点E在BC上运动时,FC的最大长度是1,则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①,在矩形ABCD中,动点P从点A出发,沿A→B→C运动,设P A=x,点D到直线P A的距离为y,且y关于x的函数图象如图②所示,则当△PCD和△P AB的面积相等时,y的值为.第5题图6.如图①,已知点E,F,G,H是矩形ABCD各边的中点,动点M从点E出发,沿E→F→G匀速运动,设点M运动的路程为x,点M到矩形顶点B的距离为y,如果表示y关于x函数关系的图象如图②所示,那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中,s 随着t 的增大而增大,点P 在AB ︵上运动时,s =OP =12AB (定值),点P 在OB 上从点B 向点O 运动的过程中,s 随着t 的增大而减小. 2. A 【解析】∵在Rt △ABC 中,AC =BC =4,∴AB =42,AD =CD =22,CF =2,当点E 在CD 上时,CE =x ,点E 到BC 的距离h 1=22x ,∴y =12×2×22x =22x (0≤x ≤22);当点E 在AD 上时,BE =BD +DE =CD +DE =x ,∴点E 到FC 的距离h 2=22BE =22x ,∴y =12×2×22x =22x (22≤x ≤42). 3. D 【解析】设∠AOM =α,点P 运动的速度为a ,当点P 从点O 运动到点A 的过程中,S =12OM ·PM =12at ·cos α·at ·sin α=12a 2·cos α·sin α·t 2,由于α及a 均为常量,从而可知图象本段应为抛物线,且S 随着t 的增大而增大;当点P 从A 运动到B 时,由反比例函数性质可知△OPM 的面积为12k ,保持不变,本段图象应为与x 轴平行的线段;同理可得,当点P 从B 运动到O 过程中,S 也是t 的二次函数,且S 随着t 的增大而减小.4. B 【解析】∵四边形ABCD 为菱形,且∠B =60°,AB =2,∴当0<t <2时,△APQ 的面积y =12t ·(2-t )·sin60°=-34t 2+32t ,函数图象为开口向下的一段抛物线,且当t =1时,y 最大值为34;当2<t <4时,△APQ 的面积y =12(t -2)·(t -2)·sin60°=34(t -2)2,函数图象为开口向上的一段抛物线,且当t =4时,y 最大值为3,故选B .5. B 【解析】当0≤x ≤2.5时,如解图①,∵四边形ABCD 是矩形,∴OA =OB =OC =OD ,∴∠OAD =∠ODA ,∵EF ∥BD ,∴∠ODA =∠MEA ,∴∠OAD =∠MEA ,∴ME =MA ,同理可得AM =MF ,∴EM =AM =MF ,∴EF =2AM ,即y =2x ;当2.5<x ≤5时,如解图②,由题意知CM =AC -AM =5-x ,∵ME=MC =MF ,∴EF =2MC ,即y =2(5-x )=10-2x .综上所述,y =⎩⎪⎨⎪⎧2x (0≤x ≤2.5)10-2x (2.5<x ≤5).图① 图②第5题解图6. C 【解析】∵AB =4,点E 是AB 的中点,∴AE =BE =2,当0≤x ≤2时,如解图①,y =S △CPE =12PE·BC=2x,∴此段函数图象是正比例函数的一部分;当2<x≤6时,如解图②,y=S△CPE=S正方形ABCD-S△BCE -S△APE-S△PCD=42-12×4×2-12×2×(x-2)-12×4×[4-(x-2)]=x+2,∴此段函数图象是一次函数的一部分;当6<x≤10时,如解图③,y=S△CPE=12PC·BC=12(10-x)×4=-2x+20,∴此段函数图象是一次函数的一部分,综上所述,根据各段图象及x的取值范围,可得函数图象如选项C所示.图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得:当点P 运动到点C 的位置时,CG =0,∴BC =4.当点P运动到线段BC 的中点时,CG =43.∵∠B =90°,∴∠BAP +∠APB =90°,∵PG ⊥AP ,∴∠APG =90°,∴∠APB +∠CPG =90°,∴∠BAP =∠CPG ,又∵∠ABP =∠PCG =90°,∴△ABP ∽△PCG ,∴AB PC =BP CG,当点P 为BC 的中点时,BP =PC =2,∴AB 2=243,解得AB =3. 2. B 【解析】结合图形分析函数图象可得,当t =3时,点P 到达A 处,即AB =3;如解图,过点A作AE ⊥CD 于点E ,则四边形ABCE 为矩形,∵AC =AD ,∴DE =CE =12CD .当S =15时,点P 到达点D 处,则S =12CD ·BC =12·2AB ·BC =3×BC =15,则BC =5,在Rt △ABC 中,由勾股定理得,AD =AC =AB 2+BC 2=34.第2题解图3. D 【解析】由题图②得,t =4时两点停止运动,∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒,∴AB =4,∵点Q 运动到点C 之前和之后,△BPQ 面积算法不同,即t =2时,S 的解析式发生变化,∴题图②中点M 对应的横坐标为2,此时P 为AB 中点,点C 与点Q 重合,如解图,连接AC ,∵菱形ABCD 中,AB =BC =4,∠B =60°,∴△ABC 是等边三角形,∴CP ⊥AB ,BP =12AB =2,∴CP =BC 2-BP 2=42-22=23,∴a =12BP ·CP =12×2×23=2 3.第3题解图4. C 【解析】如解图,设AB =a ,当点E 在BC 上运动时(不与点B 、C 重合),∵AE ⊥EF ,∴△EFC∽△AEB ,∴EC AB =FC EB ,即2a -x a =y x -a ,∴y =-1a x 2+3x -2a ,-1a <0,当x =-32×(-1a )=32a 时,y 取得最大值,此时点E 为BC 的中点,y =1,把(32a ,1)代入y =-1ax 2+3x -2a ,解得a =4,即AB =4,故正方形ABCD 的面积为4×4=16.第4题解图5. 121313【解析】当P 点在AB 上运动时,D 点到AP 的距离不变,始终是AD 长,从图象可以看出AD =4,当P 点到达B 点时,从图象看出x =3,即AB =3.当△PCD 和△P AB 的面积相等时,P 点在BC 中点处,此时△ADP 面积为12×4×3=6,在Rt △ABP 中,AP =AB 2+BP 2=13,则12AP ·y =6,解得y =121313. 6. 24 【解析】如解图,连接BD ,EG ,FH ,∵点E ,F ,G ,H 是矩形ABCD 各边的中点,∴EF ∥BD ∥GH ,EF =GH =12BD ,∴四边形EFGH 是平行四边形,又∵EF =EH ,∴平行四边形EFGH 是菱形,由题图②得BE =3,点M 运动到点G 时,运动路程为10,又∵EF =FG ,则可知菱形的边长为5,即EF =FG =GH =HE =5,∴AF =4,AD =8,∴S 菱形EFGH =12EG ·FH =24.第6题解图。
2020年浙江省中考数学题型专练一 动点问题的函数图像含答案

题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图,AB 是半圆O 的直径,点P 从点O 出发,沿OA →AB ︵→BO 的路径运动一周,设点P 到点O的距离为s ,运动时间为t ,则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图,在Rt △ABC 中,AC =BC =4 cm ,点D 是AB 的中点,点F 是BC 的中点,动点E 从点C 出发,沿CD →DA 以1 cm/s 的速度运动至点A ,设点E 运动的时间为x s ,△EFC 的面积为y cm 2(当E ,F ,C 三点共线时,设y =0),则y 与x 之间的函数关系的大致图象是( )第2题图3.如图,A 、B 是反比例函数y =k x(k >0)在第一象限图象上的两点,动点P 从坐标原点O 出发,沿图中 箭头所指方向匀速运动,即点P 先在线段OA 上运动,然后在双曲线上由A 到B 运动,最后在线段BO 上运动,最终回到点O .过点P 作PM ⊥x 轴,垂足为点M ,设△POM 的面积为S ,点P 运动时间为t ,则S 关于t 的函数图象大致为( )第3题图4.如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图,在矩形ABCD中,对角线AC与BD交于点O,点M为线段AC上一个动点,过点M作EF∥BD 交AD(或DC)于点E,交AB(或BC)于点F,已知AC=5,设AM=x,EF=y,则y关于x的函数图象大致为()第5题图6. (2019衢州)如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C 移动至终点C,设点P经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①,点P从矩形ABCD的顶点B出发,沿射线BC的方向以每秒1个单位长度的速度运动,过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象,其中点Q是第一段曲线(抛物线的一部分)的最高点,则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①,四边形ABCD中,AB∥CD,∠B=90°,AC=A D.动点P从点B出发,沿折线B-A-D-C方向以 1 cm/s的速度匀速运动,在整个运动过程中,△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示,则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①,菱形ABCD中,∠B=60°,动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B,同时动点Q以每秒2个单位的速度自点B出发沿折线B-C-D运动到点D.图②是点P、Q运动时,△BPQ的面积S随时间t变化关系图象,则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①,在正方形ABCD中,动点E从点A出发,沿A-B-C运动,当点E到达点C时停止运动,过点E作EF⊥AE,交CD于点F,设点E运动的路程为x,FC=y(当点A,E重合时,点D,F重合;当点C,E重合时,不妨设y=0),y与x的函数关系的大致图象如图②,当点E在BC上运动时,FC的最大长度是1,则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①,在矩形ABCD中,动点P从点A出发,沿A→B→C运动,设P A=x,点D到直线P A的距离为y,且y关于x的函数图象如图②所示,则当△PCD和△P AB的面积相等时,y的值为.第5题图6.如图①,已知点E,F,G,H是矩形ABCD各边的中点,动点M从点E出发,沿E→F→G匀速运动,设点M运动的路程为x,点M到矩形顶点B的距离为y,如果表示y关于x函数关系的图象如图②所示,那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中,s 随着t 的增大而增大,点P 在AB ︵上运动时,s =OP =12AB (定值),点P 在OB 上从点B 向点O 运动的过程中,s 随着t 的增大而减小. 2. A 【解析】∵在Rt △ABC 中,AC =BC =4,∴AB =42,AD =CD =22,CF =2,当点E 在CD 上时,CE =x ,点E 到BC 的距离h 1=22x ,∴y =12×2×22x =22x (0≤x ≤22);当点E 在AD 上时,BE =BD +DE =CD +DE =x ,∴点E 到FC 的距离h 2=22BE =22x ,∴y =12×2×22x =22x (22≤x ≤42). 3. D 【解析】设∠AOM =α,点P 运动的速度为a ,当点P 从点O 运动到点A 的过程中,S =12OM ·PM =12at ·cos α·at ·sin α=12a 2·cos α·sin α·t 2,由于α及a 均为常量,从而可知图象本段应为抛物线,且S 随着t 的增大而增大;当点P 从A 运动到B 时,由反比例函数性质可知△OPM 的面积为12k ,保持不变,本段图象应为与x 轴平行的线段;同理可得,当点P 从B 运动到O 过程中,S 也是t 的二次函数,且S 随着t 的增大而减小.4. B 【解析】∵四边形ABCD 为菱形,且∠B =60°,AB =2,∴当0<t <2时,△APQ 的面积y =12t ·(2-t )·sin60°=-34t 2+32t ,函数图象为开口向下的一段抛物线,且当t =1时,y 最大值为34;当2<t <4时,△APQ 的面积y =12(t -2)·(t -2)·sin60°=34(t -2)2,函数图象为开口向上的一段抛物线,且当t =4时,y 最大值为3,故选B .5. B 【解析】当0≤x ≤2.5时,如解图①,∵四边形ABCD 是矩形,∴OA =OB =OC =OD ,∴∠OAD =∠ODA ,∵EF ∥BD ,∴∠ODA =∠MEA ,∴∠OAD =∠MEA ,∴ME =MA ,同理可得AM =MF ,∴EM =AM =MF ,∴EF =2AM ,即y =2x ;当2.5<x ≤5时,如解图②,由题意知CM =AC -AM =5-x ,∵ME=MC =MF ,∴EF =2MC ,即y =2(5-x )=10-2x .综上所述,y =⎩⎪⎨⎪⎧2x (0≤x ≤2.5)10-2x (2.5<x ≤5).图① 图②第5题解图6. C 【解析】∵AB =4,点E 是AB 的中点,∴AE =BE =2,当0≤x ≤2时,如解图①,y =S △CPE =12PE·BC=2x,∴此段函数图象是正比例函数的一部分;当2<x≤6时,如解图②,y=S△CPE=S正方形ABCD-S△BCE -S△APE-S△PCD=42-12×4×2-12×2×(x-2)-12×4×[4-(x-2)]=x+2,∴此段函数图象是一次函数的一部分;当6<x≤10时,如解图③,y=S△CPE=12PC·BC=12(10-x)×4=-2x+20,∴此段函数图象是一次函数的一部分,综上所述,根据各段图象及x的取值范围,可得函数图象如选项C所示.图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得:当点P 运动到点C 的位置时,CG =0,∴BC =4.当点P运动到线段BC 的中点时,CG =43.∵∠B =90°,∴∠BAP +∠APB =90°,∵PG ⊥AP ,∴∠APG =90°,∴∠APB +∠CPG =90°,∴∠BAP =∠CPG ,又∵∠ABP =∠PCG =90°,∴△ABP ∽△PCG ,∴AB PC =BP CG,当点P 为BC 的中点时,BP =PC =2,∴AB 2=243,解得AB =3. 2. B 【解析】结合图形分析函数图象可得,当t =3时,点P 到达A 处,即AB =3;如解图,过点A作AE ⊥CD 于点E ,则四边形ABCE 为矩形,∵AC =AD ,∴DE =CE =12CD .当S =15时,点P 到达点D 处,则S =12CD ·BC =12·2AB ·BC =3×BC =15,则BC =5,在Rt △ABC 中,由勾股定理得,AD =AC =AB 2+BC 2=34.第2题解图3. D 【解析】由题图②得,t =4时两点停止运动,∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒,∴AB =4,∵点Q 运动到点C 之前和之后,△BPQ 面积算法不同,即t =2时,S 的解析式发生变化,∴题图②中点M 对应的横坐标为2,此时P 为AB 中点,点C 与点Q 重合,如解图,连接AC ,∵菱形ABCD 中,AB =BC =4,∠B =60°,∴△ABC 是等边三角形,∴CP ⊥AB ,BP =12AB =2,∴CP =BC 2-BP 2=42-22=23,∴a =12BP ·CP =12×2×23=2 3.第3题解图4. C 【解析】如解图,设AB =a ,当点E 在BC 上运动时(不与点B 、C 重合),∵AE ⊥EF ,∴△EFC∽△AEB ,∴EC AB =FC EB ,即2a -x a =y x -a ,∴y =-1a x 2+3x -2a ,-1a <0,当x =-32×(-1a )=32a 时,y 取得最大值,此时点E 为BC 的中点,y =1,把(32a ,1)代入y =-1ax 2+3x -2a ,解得a =4,即AB =4,故正方形ABCD 的面积为4×4=16.第4题解图5. 121313【解析】当P 点在AB 上运动时,D 点到AP 的距离不变,始终是AD 长,从图象可以看出AD =4,当P 点到达B 点时,从图象看出x =3,即AB =3.当△PCD 和△P AB 的面积相等时,P 点在BC 中点处,此时△ADP 面积为12×4×3=6,在Rt △ABP 中,AP =AB 2+BP 2=13,则12AP ·y =6,解得y =121313. 6. 24 【解析】如解图,连接BD ,EG ,FH ,∵点E ,F ,G ,H 是矩形ABCD 各边的中点,∴EF ∥BD ∥GH ,EF =GH =12BD ,∴四边形EFGH 是平行四边形,又∵EF =EH ,∴平行四边形EFGH 是菱形,由题图②得BE =3,点M 运动到点G 时,运动路程为10,又∵EF =FG ,则可知菱形的边长为5,即EF =FG =GH =HE =5,∴AF =4,AD =8,∴S 菱形EFGH =12EG ·FH =24.第6题解图。
中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)

中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)1.(2021•益阳)如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是()A.B.C.D.【答案】B【解答】解:∵▱ABCD的面积为4,x+y是平行四边形面积的一半,∴x+y=2,∴y=2﹣x,∴y是x的一次函数,且当x=0时,y=2;x=2时,y=0;故只有选项B符合题意.2.(2021•河南)如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,PA﹣PE=y,图2是点P运动时y随x变化的关系图象,则BC的长为()A.4B.5C.6D.7【答案】C【解答】解:由函数图象知:当x=0,即P在B点时,BA﹣BE=1.利用三角形两边之差小于第三边,得到PA﹣PE≤AE.∴y的最大值为AE,∴AE=5.在Rt△ABE中,由勾股定理得:BA2+BE2=AE2=25,设BE的长度为t,则BA=t+1,∴(t+1)2+t2=25,即:t2+t﹣12=0,∴(t+4)(t﹣3)=0,由于t>0,∴t+4>0,∴t﹣3=0,∴BC=2BE=2t=2×3=6.故选:C.3.(2022•鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.【答案】B【解答】解:∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,AC=BC=6,∵CD⊥AB,∴CD=AC=3,AD=CD=3,BD=BC=,∴当M在AD上时,0≤t≤3,MD=AD﹣AM=3﹣t,DN=DC+CN=3+t,∴S=MD•DN=(3﹣t)(3+t)=﹣t2+,当M在BD上时,3<t≤4,MD=AM﹣AD=t﹣3,∴S=MD•DN=(t﹣3)(3+t)=t2﹣,故选:B.4.(2022•菏泽)如图,等腰Rt△ABC与矩形DEFG在同一水平线上,AB=DE =2,DG=3,现将等腰Rt△ABC沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰Rt△ABC与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为()A.B.C.D.【答案】B【解答】解:如图,作CH⊥AB于点H,∵AB=2,△ABC是等腰直角三角形,∴CH=1,当0≤x≤1时,y=×2x•x=x2,当1<x≤3时,y==1,当3<x≤4时,y=1﹣=﹣(x﹣3)2+1,故选:B.5.(2022•鄂尔多斯)如图①,在正方形ABCD中,点M是AB的中点,点N 是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为()A.B.2C.D.【答案】 A【解答】解:如图,连接AC交BD于点O,连接NC,连接MC交BD于点N′.∵四边形ABCD是正方形,∴O是BD的中点,∵点M是AB的中点,∴N′是△ABC的重心,∴N′O=BO,∴N′D=BD,∵A、C关于BD对称,∴NA=NC,∴AN+MN=NC+MN,∵当M、N、C共线时,y的值最小,∴y的值最小就是MC的长,∴MC=2,设正方形的边长为m,则BM=m,在Rt△BCM中,由勾股定理得:MC2=BC2+MB2,∴20=m2+(m)2,∴m=4,∴BD=4,∴a=N′D=BD=×4=,故选:A.6.(2021•鞍山)如图,△ABC是等边三角形,AB=6cm,点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B,同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作MP∥CA交AB于点P,连接MN,NP,作△MNP关于直线MP对称的△MN′P,设运动时间为ts,△MN′P与△BMP重叠部分的面积为Scm2,则能表示S与t之间函数关系的大致图象为()A.B.C.D.【答案】A【解答】解:如图1中,当点N′落在AB上时,取CN的中点T,连接MT.∵CM=t(cm),CN=2t(cm),CT=TN,∴CT=TN=t(cm),∵△ABC是等边三角形,∴∠C=∠A=60°,∴△MCT是等边三角形,∴TM=TC=TN,∴∠CMN=90°,∵MP∥AC,∴∠BPM=∠A=∠MPN=60°,∠BMP=∠C=60°,∠C+∠CMP=180°,∴∠CMP=120°,△BMP是等边三角形,∴BM=MP,∵∠CMP+∠MPN=180°,∴CM∥PN,∵MP∥CN,∴四边形CMPN是平行四边形,∴PM=CN=BM=2t,∴3t=6,∴t=2,如图2中,当0<t≤2时,过点M作MK⊥AC于K,则MK=CM•sin60°=t,∴S=•(6﹣t)•t=﹣t2+t.如图3中,当2<t≤6时,S=•MQ•PQ=×(6﹣t)×(6﹣t)=×(6﹣t)2,观察图象可知,选项A符合题意,故选:A.7.(2021•威海)如图,在菱形ABCD中,AB=2cm,∠D=60°,点P,Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是()A.B.C.D.【答案】A【解答】解:∵四边形ABCD为菱形,∴AB=BC=CD=DA=2cm,∠B=∠D=60°.∴△ABC、△ACD都是等边三角形,∴∠CAB=∠ACB=∠ACD=60°.如图1所示,当0≤x≤1时,AQ=2xcm,AP=xcm,作PE⊥AB于E,∴PE=sin∠PAE×AP=(cm),∴y=AQ•PE=×2x×=,故D选项不正确;如图2,当1<x≤2时,AP=xcm,CQ=(4﹣2x)cm,作QF⊥AC于点F,∴QF=sin∠ACB•CQ=(cm),∴y===,故B选项不正确;如图3,当2<x≤3时,CQ=(2x﹣4)cm,CP=(x﹣2)cm,∴PQ=CQ﹣CP=2x﹣4﹣x+2=(x﹣2)cm,作AG⊥DC于点G,∴AG=sin∠ACD•AC=×2=(cm),∴y===.故C选项不正确,故选:A.8.(2021•日照)如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是()A.B.C.D.【答案】D【解答】解:当Q在AD上时,即点P在AO上时,有0<x≤1,此时阴影部分为等腰直角三角形,∴y=,该函数是二次函数,且开口向上,排除B,C选项;当点Q在弧BD上时,补全图形如图所示,阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积,再减去平面图形PBQ的面积即减去弓形QBF的面积,设∠QOB=θ,则∠QOF=2θ,∴,S弓形QBF=﹣S△QOF,当θ=45°时,AP=x=1+≈1.7,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.14,当θ=30°时,AP=x≈1.87,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.24,当θ=60°时,AP=x≈1.5,y≈0.98,在A,D选项中分别找到这两个特殊值,对比发现,选项D符合题意.故选:D.法二、当1<x<2时,即P在OB之间时,设∠QOD=θ,则θ∈(0,),则PQ=cosθ,OP=sinθ,则弧QD的长为θπ,此时S阴影=+θπ+sinθcosθ=+θ+sin2θ,∴y随x的增大而增大,而且增加的速度越来越慢,分析四个选项中的图象,只有选项D符合.故选:D.9.(2021•辽宁)如图,在矩形ABCD中,AB=6,AD=4,E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN 的面积为S,则能大致反映S与x之间函数关系的图象是()A.B.C.D.【答案】B【解答】解:如图,∵E是CD的中点,∴CE=DE,∵四边形ABCD是矩形,∴∠D=∠DCF=90°,AD=BC=4,在△ADE与△FCE中,,∴△ADE≌△FCE(SAS),∴CF=AD=4,∴BF=CF+BC=8,∴AF=,当点M在AB上时,在Rt△AMN和Rt△AFB中,tan∠NAM=,∴NM=x=x,∴△AMN的面积S=×x×x=x2,∴当点M在AB上时,函数图象是开口向上、经过原点的抛物线的一部分;当点M在BF上时,如图,AN=x,NF=10﹣x,在Rt△FMN和Rt△FBA中,tan∠F=,∴=﹣,∴△AMN的面积S==﹣,∴当点M在BF上时,函数图象是开口向下的抛物线的一部分;故选:B.10.(2021•苏州)如图,线段AB=10,点C、D在AB上,AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动.在点P移动过程中作如下操作:先以点P为圆心,PA、PB的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面,设点P的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵AB=10,AC=BD=1,∴CD=10﹣1﹣1=8,∵PC=t,∴AP=t+1,PB=8﹣t+1=9﹣t,设围成的两个圆锥底面圆半径分别为r和R则:2πr=;.解得:r=,R=,∴两个圆锥的底面面积之和为S===,根据函数关系式可以发现该函数图象是一个开口向上的二次函数.故选:D.11.(2021•甘肃)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为()A.3B.6C.8D.9【答案】B【解答】解:由图2知,AB+BC=2,∵AB=BC,∴AB=,∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD²+BD²=AB²=13①,设点M到AC的距离为h,∴S△ADM=AD•h,∵动点M从A点出发,沿折线AB→BC方向运动,∴当点M运动到点B时,△ADM的面积最大,即h=BD,由图2知,△ADM的面积最大为3,∴AD•BD=3,∴AD•BD=6②,①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,∴(AD+BD)²=25,∴AD+BD=5(负值舍去),∴BD=5﹣AD③,将③代入②得,AD(5﹣AD)=6,∴AD=3或AD=2,∵AD>BD,∴AD=3,∴AC=2AD=6,故选:B.12.(2021•百色)如图,矩形ABCD各边中点分别是E、F、G、H,AB=2,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是()A.B.C.D.【答案】D【解答】解:①当M点运动在AE段,此时S=S△HAE+S△GHD﹣S△EOM﹣S△GPS,∵四边形ABCD是矩形,直线l⊥AB,H、E、F、G为AD、AB、BC、CD的中点,∴AH=AD==1,AE=AB=,S△HAE=S△GHD,S△EOM=S△GPS,∴S=2S△HAE﹣2S△EOM,∴S△HAE=AE•AH=;∵直线l⊥AB,∴∠OME=∠A=90°,∠HEA=∠OEM,∴△HAE∽△OME,∴,∴OM=,又∵ME=AE﹣AM=﹣x,∴OM=ME=,∴S△EOM=,∴S=2S△HAE﹣2S△EOM=,此时,对应抛物线开口向下;②当M点运动到在BE段,此时,S=S△HAE+S△GHD+S△EO1M1+S△GP1S1,即S=2S△HAE+2S△EO1M1,与①同理,O1M1=,又∵M1E=AM1﹣AE=x﹣,∴O1M1=M1E=,∴S△EO1M1=,∴S=2S△HAE+2S△EO1M1=,此时,对应抛物线开口向上,故选:D.13.(2021•鄂尔多斯)如图①,在矩形ABCD中,H为CD边上的一点,点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止,点N从点A出发沿AB 运动到点B停止,它们的运动速度都是1cm/s,若点M、N同时开始运动,设运动时间为t(s),△AMN的面积为S(cm2),已知S与t之间函数图象如图②所示,则下列结论正确的是()①当0<t≤6时,△AMN是等边三角形.②在运动过程中,使得△ADM为等腰三角形的点M一共有3个.③当0<t≤6时,S=.④当t=9+时,△ADH∽△ABM.⑤当9<t<9+3时,S=﹣3t+9+3.A.①③④B.①③⑤C.①②④D.③④⑤【答案】A【解答】解:由图②可知:点M、N两点经过6秒时,S最大,此时点M在点H处,点N在点B处并停止不动,如图,①∵点M、N两点的运动速度为1cm/s,∴AH=AB=6cm,∵四边形ABCD是矩形,∴CD=AB=6 cm.∵当t=6s时,S=9cm2,∴×AB×BC=9.∴BC=3cm.∵当6≤t≤9时,S=且保持不变,∴点N在B处不动,点M在线段HC上运动,运动时间为(9﹣6)秒,∴HC=3 cm,即点H为CD的中点.∴BH=cm.∴AB=AH=BH=6cm,∴△ABM为等边三角形.∴∠HAB=60°.∵点M、N同时开始运动,速度均为1cm/s,∴AM=AN,∴当0<t≤6时,△AMN为等边三角形.故①正确;②如图,当点M在AD的垂直平分线上时,△ADM为等腰三角形:此时有两个符合条件的点;当AD=AM时,△ADM为等腰三角形,如图:当DA=DM时,△ADM为等腰三角形,如图:综上所述,在运动过程中,使得△ADM为等腰三角形的点M一共有4个.∴②不正确;③过点M作ME⊥AB于点E,如图,由题意:AM=AN=t,由①知:∠HAB=60°.在Rt△AME中,∵sin∠MAE=,∴ME=AM•sin60°=tcm,∴S=AN×ME=cm2.∴③正确;④当t=9+时,CM=cm,如图,由①知:BC=3cm,∴MB=BC﹣CM=2cm.∵AB=6cm,∴tan∠MAB=,∴∠MAB=30°.∵∠HAB=60°,∴∠DAH=90°﹣60°=30°.∴∠DAH=∠BAM.∵∠D=∠B=90°,∴△ADH∽△ABM.∴④正确;⑤当9<t<9+3时,此时点M在边BC上,如图,此时MB=9+3﹣t,∴S=×AB×MB=×6×(9+3﹣t)=27+9﹣3t.∴⑤不正确;综上,结论正确的有:①③④.故选:A.14.(2021•通辽)如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图象大致是()A.B.C.D.【答案】C【解答】解:当0≤x≤3时,在Rt△APQ中,∠QAP=90°,AP=AQ=x,∴PQ2=2x2.∴y=PQ2=2x2;当3≤x≤4时,DQ=x﹣3,AP=x,∴y=PQ2=32+32=18;当4≤x≤7时,CP=7﹣x,CQ=7﹣x,∴y=PQ2=CP2+CQ2=2x2﹣28x+98.故选:C.15.(2021•湖北)如图,AC为矩形ABCD的对角线,已知AD=3,CD=4,点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动(运动到D点停止),过点P作PE⊥BC于点E,则△CPE的面积y与点P运动的路程x间的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵BC∥AD,∴∠ACB=∠DAC,∵∠PEC=∠D=90°,∴△PCE∽△CAD,∴==,∵AD=3,CD=4,∴AC==5,∴当P在CA上时,即当0<x≤5时,PE==x,CE==x,∴y=PE•CE==x2,当P在AD上运动时,即当5<x≤8时,PE=CD=4,CE=8﹣x,∴y=PE•CE=×4×(8﹣x)=16﹣2x,综上,当0<x≤5时,函数图象为二次函数图象,且y随x增大而增大,当5<x≤8时,函数图象为一次函数图象,且y随x增大而减小,故选:D.16.(2021•衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q 两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P 的运动路线为O﹣A﹣D﹣O,点Q的运动路线为O﹣C﹣B﹣O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.【答案】(2+3)【解答】解:由图分析易知:当点P从O→A运动时,点Q从O→C运动时,y不断增大,当点P运动到A点,点Q运动到C点时,由图象知此时y=PQ=2cm,∴AC=2cm,∵四边形ABCD为菱形,∴AC⊥BD,OA=OC==cm,当点P运动到D点,Q运动到B点,结合图象,易知此时,y=BD=2cm,∴OD=OB=BD=1cm,在Rt△ADO中,AD===2(cm),∴AD=AB=BC=DC=2cm,如图,当点P在A﹣D段上运动,点P运动到点E处,点Q在C﹣B段上运动,点Q运动到点F处时,P、Q两点的距离最短,此时,OE=OF==,AE=CF===,∴当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为:(cm),故答案为:(2+3).17.(2021•武汉)如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y 关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是.【答案】﹣1【解答】解:∵图象过点(0,2),即当x=AD=BE=0时,点D与A重合,点E与B重合,此时y=AE+CD=AB+AC=2,∵△ABC为等腰直角三角形,∴AB=AC=1,过点A作AF⊥BC于点F,过点B作NB⊥BC,并使得BN=AC,如图所示:∵AD=BE,∠NBE=∠CAD,∴△NBE≌△CAD(SAS),∴NE=CD,又∵y=AE+CD,∴y=AE+CD=AE+NE,当A、E、N三点共线时,y取得最小值,如图所示,此时:AD=BE=x,AC=BN=1,∴AF=AC•sin45°=,\又∵∠BEN=∠FEA,∠=∠AFE∴△NBE∽△AFE∴,即,解得:x=,∴图象最低点的横坐标为:﹣1.故答案为:.18.(2022•营口)如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则y=cm2.【答案】【解答】解:过点D作DE⊥AB,垂足为E,在Rt△ADE中,∵∠AED=90°,∠EAD=45°,∴,∵点P的速度为cm/s,点Q的速度为2cm/s,∴AP=x,AQ=2x,∴,在△APQ和△AED中,=,∠A=45°,∴△AED∽△APQ,∴点Q在AD上运动时,△APQ为等腰直角三角形,∴AP=PQ=x,∴当点Q在AD上运动时,y=AP•AQ=×x×x=x2,由图像可知,当y=9此时面积最大,x=3或﹣3(负值舍去),∴AD=2x=6cm,当3<x≤4时,过点P作PF⊥AD于点F,如图:此时S△APQ=S△APF+S四边形PQDF﹣S△ADQ,在Rt△APF中,AP=x,∠PAF=45°,∴AF=PF=x,FD=6﹣x,QD=2x﹣6,∴S△APQ=x2+(x+2x﹣6)•(6﹣x)﹣×6×(2x﹣6),即y=﹣x2+6x,当x=时,y=﹣()2+6×=,故答案为:.。
新泸教版数学八年级上册小专题(二) 动点下的函数图象
小专题( 二)动点下的函数图象解决动态函数图象问题,要能化动为静,再由静生动,动静结合思考问题.其中关键是确定图形变化联系瞬间的静态图形位置,从而得到分界点,然后再作动态思考,确定各种情况下的取值范围.最后求出各部分对应的函数表达式,运用函数的图象、性质分析作答.有时,直接根据各运动状态( 如前后图形的对称状态带来函数图象的对称,前后图形面积的增减变化带来函数图象的递增或递减等)就能求解.类型1分析判断函数的图象判断函数图象从以下方面:①看图象的升降趋势,当函数随着自变量的增加而增加时,图象呈上升趋势,反之,呈下降趋势;②看图象的曲直,函数随着自变量的变化而均匀变化的,图象是直线,函数随着自变量的变化而不均匀变化的,图象是曲线;③表示函数不随自变量的变化而变化,即函数是一个定值,图象与横轴平行.1.用固定的速度往如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( A)2.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止( 不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( D)3.小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( D)4.( 2019·阜阳颍上期末)如图,正方形ABCD的边长为4,P为正方形边上一个动点,沿A→D→C→B→A的路径匀速移动.设P点经过的路径长为x,△APD的面积是y,则下列图象能反映y与x之间的函数关系的是( B)类型2观察图象,求解综合问题用函数图象刻画实际问题中变量之间的关系,需要注意:( 1 )结合实际,理清有哪些变量;( 2 )用图象表示时,明确坐标轴表示的意义.一般方法规律是解决动点的分段函数图象问题,一是要注意分段的“段数”,二是要注意从何时起分段,该段到何时结束,三是要注意在每个分段上函数的具体变化情况.特别要抓住图象中的转折点及拐点,这些拐点处往往是运动状态发生改变或者数量关系发生改变的地方.5.如图1,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPQ 的面积( C)A.10B.16C.20D.366.( 2019·合肥45中期中)小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y( 单位:m )与跑步时间t( 单位:s )的对应关系如下图所示.下列叙述正确的是②④.( 填上你认为正确的序号)①两人从起跑线同时出发,同时到达终点;②小苏跑全程的平均速度小于小林跑全程的平均速度;③小苏前15 s跑过的路程大于小林前15 s跑过的路程;④小林在跑最后100 m的过程中,与小苏相遇2次.7.如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设点P,Q之间的距离为s( 厘米),动点P的运动时间为t( 秒),图2表示s与t之间的函数关系.( 1 )求动点P,Q运动的速度;( 2 )图2中,a=3,b=6,c=6.解:( 1 )设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒.根据题意,得2( x+2x)=12,解得x=2.答:动点P,Q运动的速度分别是2厘米/秒、4厘米/秒.8.一个游泳池长90米,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,请根据图形回答:( 1 )甲、乙两人分别游了几个来回?( 2 )甲、乙两人在整个游泳过程中,谁曾休息过?休息过几次?( 3 )甲游了多长时间?游泳的速度是多少?( 4 )在整个游泳过程中,甲、乙两人相遇了几次?解:( 1 )甲游了3个来回,乙游了2个来回.( 2 )乙曾休息了两次.( 3 )甲游了180秒,游泳的速度是90×6÷180=3米/秒.( 4 )甲、乙相遇了5次.9.已知动点P以每秒2 cm的速度沿如图甲所示的边框按照B→C→D→E→F→A的路径移动,相应的△ABP的面积S( cm2)关于时间t( s )的函数图象如图乙所示.若AB=6 cm,试回答下列问题:( 1 )动点P在线段CD和EF上运动的过程中△ABP的面积S保持不变.( 2 )BC=8cm;CD=4cm;DE=6cm;EF=2cm.( 3 )求出图乙中的a与b的值.( 4 )在上述运动过程中,求△ABP面积的最大值.解:( 3 )由图得,a是点P运行4秒时△ABP的面积,所以a=×6×8=24,因为b为点P走完全程的时间,所以b=9+1+7=17.( 4 )因为点P移动到点E时,△ABP的面积达到最大值,所以最大面积S=×6×( 8+6 )=42( cm2).。
数学动点问题
初三生必须复习的重点,动点问题讲解分析1:如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是()考点分析:动点问题的函数图象.题干分析:△ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象.初三生必须复习的重点,动点问题讲解分析2:如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.(1)当t为何值时,点Q与点D重合?(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.(3)若⊙P与线段QC只有一个公共点,求t的取值范围.考点分析:圆的综合题.题干分析:(1)由题意知CD⊥OA,所以△ACD∽△ABO,利用对应边的比求出AD的长度,若Q与D重合时,则,AD+OQ=OA,列出方程即可求出t的值;(2)由于0<t≤5,当Q经过A点时,OQ=4,此时用时为4s,过点P作PE ⊥OB于点E,利用垂径定理即可求出⊙P被OB截得的弦长;(3)若⊙P与线段QC只有一个公共点,分以下两种情况,①当QC与⊙P相切时,计算出此时的时间;②当Q与D重合时,计算出此时的时间;由以上两种情况即可得出t的取值范围.解题反思:本题考查圆的综合问题,涉及圆的切线判定,圆周角定理,相似三角形的判定与性质,学生需要根据题意画出相应的图形来分析,并且能综合运用所学知识进行解答.很多动点类综合问题一般都是以几何基础知识或具体的几何图形作为背景,在几何图形中渗透运动变化的观点,通过点、线、形的运动,图形的平移、翻折、旋转等等把图形的有关性质和图形之间的数量关系和位置关系看作是在变化的、相互依存的状态之中。
2023年中考数学高频考点训练——动点问题的函数图象
2023年中考数学高频考点训练——动点问题的函数图象一、综合题1.小亮在学习中遇到了这样一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,即90,6cm C AC BC ∠=︒==,点D 在AB 上,DE BC ⊥于点E ,射线DF 与射线AC 交于点F ,60EDF ∠=︒,顶点D 在斜边AB 上移动,设BE 两点间的距离为cm x ,EF 两点间的距离为cm EF y ,DE 两点间的距离为cm DE y .(1)当点F 与点C 重合时,求x 的长度(保留一位小数);(2)通过测量,得到了x 与EF y 的几组值,如下表:将线段BE 的长度作为自变量x ,EF DE 直角坐标系xOy 中画出函数EF y 和DE y 的图象;(3)结合图象直接写出:当DEF 为等边三角形时,BE 长度的近似值(结果保留一位小数)2.在以点O 为原点的平面直角坐标系中,边长为1的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,现将正方形OABC 绕点О顺时针旋转,当点A 第一次落在直线y x =上时,停止转动,旋转过程中,AB 边交直线y x =于点M ,BC 边交轴于点N.(1)旋转停止时正方形旋转的度数是.(2)在旋转过程中,当MN 和AC 平行时,①OAM 与OCN 是否全等?此时正方形OABC 旋转的度数是多少?②直接写出MBN 的周长的值,并判断这个值在正方形OABC 的旋转过程中是否发生变化.3.如图,点C 是以点O 为圆心,AB 为直径的半圆上的动点(不与点A ,B 重合),AB =6cm ,过点C 作CD ⊥AB 于点D ,E 是CD 的中点,连接AE 并延长交 AB 于点F ,连接FD .小腾根据学习函数的经验,对线段AC ,CD ,FD 的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:(1)对于点C 在 AB 上的不同位置,画图、测量,得到了线段AC ,CD ,FD 的长度的几组值,如表:位置1位置2位置3位置4位置5位置6位置7位置8AC /cm 0.10.5 1.0 1.9 2.6 3.2 4.2 4.9CD /cm 0.10.5 1.0 1.8 2.2 2.5 2.3 1.0FD /cm 0.2 1.0 1.8 2.8 3.0 2.7 1.80.5在AC ,CD ,FD 的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是.4.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,点D是AB的中点,以D 为顶点作∠MDN=∠A,∠MDN的两边分别与线段AC交于点M.N(点M在点N左边).设A,M两点间的距离为xcm,C、N两点间的距离为ycm.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:x/cm00.6 1.2 1.8 2.3 2.9 3.4 3.5 4.0 4.3 4.5 4.7 4.8 y/cm a 4.6 4.3 3.9 3.6 3.1 2.6 2.4b 1.20.90.40.2请你补全表格:a=;b=.(2)描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象:(3)探究性质:随着自变量x的不断增大,函数y的变化趋势:.(4)解决问题:当AM=CN时,A、M两点间的距离大约是cm.(保留一位小数)中,D为AB的中点,P是BC边上一动点,连接5.如图1,在Rt ABC,,设PC x=(当点P与点C重合时,x的值为0),==BC AC,.若43PD PA+=.PA PD y小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.(1)通过取点、画图、计算,得到了x与y的几组值,如下表:(参考数据: 1.414 3.162 3.606≈≈).(2)如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.(3)观察图象,下列结论正确的有_.①函数有最小值,没有最大值②函数有最小值,也有最大值③当43x >时,y 随着x 的增大而增大④当 1.5x <时,y 随着x 的增大而减小6.如图如图1,在矩形ABCD 中,3cm AB =,4cm BC =,圆弧 AE 过点A 和AD 延长线上的点E ,圆心R 在CD 上, AE 上有一个动点P ,PQ AC ⊥,交直线AC 于点Q .线段AP 的长cm x 与PQ 的长cm PQ y 以及RQ 的长cm RQ y 之间的几组对应值如下表所示.(1)将线段AP 的长度作为自变量,在平面直角坐标系中画出了函数PQ y 的图象,如图2所示.请在同一坐标系中画出函数RQ y 的图象.(2)结合函数图象填空:(结果精确到0.1)线段PQ 的长度的最大值约为;线段RQ 的长度的最小值约为;圆弧 AE 所在圆的半径约等于;连结PC ,PAC 面积的最大值约为.(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当以点P 、Q 、R 为顶点构成的三角形为等腰三角形时,线段AP 的长度的近似值.(结果精确到0.1)7.动点P 在□ABCD 边上沿着A→B→C→D 的方向匀速移动,到达点D 时停止移动.已知P 的速度为1个单位长度/s ,其所在位置用点P 表示,P 到对角线BD 的距离(即垂线段PQ 的长)为d 个单位长度,其中d 与t 的函数图象如图2所示.(1)若a =3,求当t =8时△BPQ 的面积;(2)如图3,点M ,N 分别在函数第一和第三段图象上,线段MN 平行于横轴,M 、N 的横坐标分别为t 1、t 2,设t 1、t 2时点P 走过的路程分别为12l l 、,若12l l +=16,求t 1、t 2的值.8.如图1,已知四边形OABC 的顶点O 在坐标原点,点A 在y 轴上,点C 在x 轴上,AB x 轴,动点P 从点O 出发,以每秒1单位的速度,沿O A B C O →→→→运动一周,顺次连结P ,O ,C 三点所围成图形的面积为S ,点P 的运动时间为t 秒,S 与t 之间的函数关系如图2中折线ODEFG 所示已知4AB =,点D ,点F 横坐标分别为8和22.(1)求a 和b 的值.(2)求直线EF 的函数解析式.(3)当P 在BC 上时,用t 表示P 点的纵坐标.9.“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车沿同一路线去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程(y 米)与时间(x 分钟)的关系如图.请结合图象,解答下列问题:(1)a=;b=.(2)求出m 的取值是多少?(3)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时的时间.10.如图1,在菱形ABCD 中,1cm AB =,连结AC BD ,.设DAB x ∠=()0180x y AC BD <<=- ,,小宁根据学习函数的经验,对变量y 与x 之间的关系进行了如下探究.(1)【探究】列表:通过观察补全下表(精确到0.01)./x153045607590105120135150165/cm y 1.72 1.080.3700.73 1.08 1.41 1.72描点、连线:在图2中描出表中各组数值所对应的点() x y ,,并画出y 关于x的函数图象.(2)【发现】结合画出的函数图象,写出该函数的两条性质:①;②.(3)【应用】有一种“千斤顶”,它是由4根长为30cm 的连杆组成的菱形ABCD ,当手柄顺时针旋转时,B D 、两点的距离变小(如图3).在这个过程中,当33cm AC BD -=时,BAD ∠的度数约为.(精确到1°).11.快、慢两车分别从相距360km 的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h 后出发,到达佳市后停止行驶;快车到达哈市后,立即按原路原速返回佳市(快车掉头的时间忽略不计).快、慢两车距哈市的路程1y (单位:km ),2y (单位:km )与快车出发时间x (单位:h )之间的函数图象如图所示,请结合图象信息解答下列问题:(1)直接写出慢车的行驶速度和a 的值;(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?(3)快车出发多少小时两车相距100km ?请直接写出答案.12.如图,在Rt △ABC 中,∠B =90°,点P 从点A 出发,以12cm/s 的速度沿AB 向终点B 运动;2s 后,又有一动点Q 从点B 出发,沿B→C→A 方向以3cm/s 的速度向终点A 运动.第二幅图是△PQC 的面积S (cm 2)关于点P 的运动时间t (s )的函数图象,请结合图中提供的信息解决下面的问题;(1)线段AB =cm ,a=,m=;(2)求当t 为何值时,PQ ∥AC ;(3)求图中EF 段函数解析式.13.如图,在ABC 中,60C ∠=︒,3BC =厘米,4AC =厘米,点P 从点B 出发,沿B C A →→以每秒1厘米的速度匀速运动到点A .设点P 的运动时间为x 秒,B 、P 两点间的距离为y 厘米.小新根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:x(s)01234567y(cm)0 1.0 2.0 3.0 2.7 2.7m 3.6m的值是.(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;中画出(3ABC点P所在的位置,此时P运动的时间为▲秒14.已知图形ABCDEF的相邻两边垂直,AB=8cm.当动点M以2cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动时,△ABM的面积S随时间t的变化如图②所示.回答下列问题:(1)求a的值和EF的长度;(2)当点M运动到DE上时,求S与t的关系式.15.已知动点P以每秒2㎝的速度沿图甲的边框按从的路径移动,相应的△ABP 的面积S 与时间t 之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题:(1)图甲中的BC 长是多少?(2)图乙中的a 是多少?(3)图甲中的图形的面积是多少?(4)图乙中的b 是多少?16.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a +=(x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x =+>,请利用特征点求出该函数的最小值.17.如图,在正方形ABCD 中,1AB =,延长BC 至M ,使5BM =.以BD BM ,为邻边作DBMN .动点P 从点D 出发,以每秒1个单位的速度沿DN 向终点N 运动,过点P 作PQ ⊥BM 交BM 或BM 的延长线于点Q ,以PQ 为边向右作正方形PQRS .设正方形PQRS .设正方形PQRS 与DBMN 的重叠部分的面积为y ,点P 运动的时间为x (0x >.单位:秒).(1)用含x 的代数式表示线段PN 为;(2)当点S 与点N 重合时,求x 的值;(3)当正方形PQRS 与DBMN 的重叠部分不是正方形时,求y 与x 之间的函数关系式;(4)当DQS 或PRN 是直角三角形时,直接写出x 的值.18.如图,已知在平面直角坐标系中,矩形ABCD 的边AB//x 轴,AD//y 轴,点A 的坐标为(2,1),AB=4,AD=3.(1)求直线BD 的解析式.(2)已知双曲线(0)ky k x =>与折线ABC 的交点为E ,与折线ADC 的交点为F .①连接CE ,当S △BCE =3时,求该双曲线的解析式,并求出此时点F 的坐标;②若双曲线(0)ky k x =>与矩形ABCD 各边和对角线BD 的交点个数为3,请直接写出k 的取值范围.19.如图①,在矩形ABCD 中,AB <AD ,对角线AC ,BD 相交于点O,动点P 由点A 出发,沿AB→BC→CD 向点D 运动,设点P 的运动路程为x ,△AOP 的面积为y ,y与x的函数关系图象如图②所示:(1)AD边的长为.(2)如图③,动点P到达点D后从D点出发,沿着DB方向以1个单位长度/秒的速度匀速运动,以点P为圆心,PD长为半径的⊙P与DB、DC的另一个交点分别为M、N,与此同时,点Q从点C出发,沿着CD方向也以1个单位长度/秒的速度匀速运动,以点Q为圆心、2为半径作⊙Q.设运动时间为t秒(0<t≤5).①当t为何值时,点Q与点N重合?②当⊙P与BC相切时,求点Q到BD的距离.20.已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMNP和点同时停止运动.设运动时间为t秒,解答问题:(1)在整个运动过程中,当点G在线段AE上时,求t的值;(2)在整个运动过程中,是否存在点P ,使△APQ 是等腰三角形,若存在,求出t 的值;若不存在,说明理由;(3)在整个运动过程中,设△GMN 与△AEF 重叠部分的面积为S ,请直接写出S 与t 的函数关系式以及自变量t 的取值范围.21.如图,直角三角形ABC ∆中,90 4 60ACB AC A ∠︒=∠︒=,,=,O 为BC 中点,将ABC ∆绕O 点旋转180︒得到DCB ∆.一动点P 从A 出发,以每秒1的速度沿A B D →→的路线匀速运动,过点P 作直线PM ,使PM AC ⊥.(1)当点P 运动2秒时,另-动点Q 也从A 出发沿A-→B→D 的路线运动,且在AB 上以每秒1的速度匀速运动,在BD.上以每秒2的速度匀速运动,过Q 作直线QN 使//QN PM ,设点Q 的运动时间为t 秒,(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值(2)当点P 开始运动的同时,另一动点R 从B 处出发沿B C D →→的路线运动,且在BC 上以每秒32的速度匀速运动,在CD 上以每秒2的速度匀度运动,是否存在这样的P,R ,使BPR ∆为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由.22.如图,直线l :243y x =-+分别与x 轴,y 轴交于A ,B 两点,在OB 上取一点()01C ,,以线段BC 为边向右作正方形BCDE ,正方形BCDE 沿CD 的方向以每秒1个单位长度的速度向右作匀速运动,设运动时间为t 秒()0t >.(1)求A,B两点的坐标;(2)在正方形BCDE向右运动的过程中,若正方形BCDE的顶点落在直线l 上,求t的值;(3)设正方形BCDE两条对角线交于点P,在正方形向右运动的过程中,是否存在实数t,使得OP PA+有最小值?若存在,求出t的值:若不存在,请说明理由.23.如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.(1)写出数轴上点A、C表示的数;(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=23CQ.设运动的时间为t(t>0)秒.①求数轴上点M、N表示的数(用含t的式子表示);②t为何值时,M、N两点到原点的距离相等?24.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:(注:圆周率π的值取3)(1)请直接写出:花坛的半径是米,a=.(2)当2t<时,求s与t之间的关系式;(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:①蚂蚁停下来吃食物的地方,离出发点的距离.②蚂蚁返回O所用时间.答案解析部分1.【答案】(1)解:在Rt DEB 中,DE BE x ==,在Rt DEF 中,6EF BF BE x =-=-,60EDF ∠=︒tan EFEDF DE∠=∴6xx -=,解得 2.2x ≈将 2.2x ≈代入分式方程左边中得6 2.23.8=1.732.2 2.2-=≈故x 的长约为 2.2cm(2)解:由题意可知DE BE x ==,∴DE y x=又根据EF y 经过表中的那些点,所以取点,画图即可得到其图象.(3)解:如图所示,当△DEF 为等边三角形时,EF=DE∵∠B=45°,射线DE ⊥BC 于点E∴BE=EF∴EF=DE∴在(2)中EF y 与DE y 的交点横坐标即为BE 的长经测量可知 3.2x ≈∴BE 的长约为3.2.【解析】【分析】(1)由题意得出△ABC 为等腰直角三角形,结合DE ⊥BC ,得出BE=DE=x ,当点F 与点C 重合时,在Rt △DEF 中,EF=6-x ,∠EDF=60°,利用正切函数列构建方程求解即可;(2)根据△ABC 为等腰直角三角形,推出△BDE 为等腰直角三角形,则可求出y DE 与x 的函数关系并画出图象,根据表格提供的数据,并通过描点法画出在同一个平面直角坐标系中函数yEF 的图象;(3)根据等边三角形的性质得出EF=DE ,结合∠B=45°,DE ⊥BC ,得出BE=EF ,即y=x ,再根据y EF 与y DE 相交时,交点的横坐标即为BE 的长度,得出BE 的近似值.2.【答案】(1)45°(2)解:①∵//MN AC ,∴45BMN BAC ∠=∠=︒,45BNM BCA ∠=∠=︒,∴BMN BNM ∠=∠,∴BM BN =,又∵BA BC =,∴AM CN =,∵在OAM 和OCN 中,AM CNOAM OCN AO CO=⎧⎪∠=∠⎨⎪=⎩,∴()SAS OAM OCN ∆ ≌,∴1()2AOM CON AOC MON ∠=∠=∠-∠1(9045)22.52︒=⨯-︒=︒,∴旋转过程中,当MN 和AC 平行时,正方形OABC 旋转的度数为4522.522.5︒-︒=︒.②MBN 的周长的值为2,且在正方形OABC 的旋转过程中不发生变化.理由如下:如图所示,延长BA 交y 轴于点E,则45AOE EOM AOM AOM ∠=∠-∠=︒-∠,∵904545CON AOC MON AOM AOM AOM ∠=∠-∠-∠=︒-︒-∠=︒-∠,∴AOE CON ∠=∠,又∵OA OC =,1809090OAE OCN ∠=︒-︒=︒=∠,在OAE 和OCN 中,AOE CONOA OC OAE OCN∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA OAE OCN ≌,∴OE ON =,AE CN =.在OME 和OMN 中,OE ONEOM NOM OM OM=⎧⎪∠=∠⎨⎪=⎩,∴()SAS OME OMN ≌,∴MN ME AM AE ==+.∴MN AM CN =+,∴MBN 的周长为2MN BN BM AM CN BN BM AB BC ++=+++=+=.∴在正方形OABC 的旋转过程中,MBN 的周长不发生变化.【解析】【解答】解:(1)∵A 点第一次落在直线y x =上时停止旋转,直线y x =与y轴的夹角是45 ,∴OA旋转了45°;【分析】(1)根据直线y=x图象上点的特点,得出线y=x与y轴的夹角是45°,即可得出求得边OA旋转的角度;(2)①利用SAS得出全等,根据正方形一个内角的度数求出∠AOM的度数,即可得出答案;②利用全等把△MBN的各边整理到成与正方形的边长有关的式子即可.3.【答案】(1)AC;CD;FD(2)解:函数图象如图所示:(3)3.5cm<x<5cm【解析】【解答】解:(1)由题意可知:AC是自变量,CD,DF是自变量AC的函数.故答案为:AC,CD,FD.(3)观察图象可知CD>DF时,3.5cm<x<5cm.故答案为:3.5cm<x<5cm.【分析】(1)根据函数的定义可得结论;(2)利用描点法画出函数图象即可;(3)利用图象法,观察图象写出函数CD的图象在函数DF的图象上方时,自变量的取值范围即可。
《数轴动点问题》课件
目 录
• 数轴动点的定义与特性 • 数轴动点的运动规律 • 数轴动点的应用实例 • 数轴动点的解题策略与技巧 • 数轴动点的综合练习题 • 数轴动点问题的反思与总结
01
数轴动点的定义与特性
数轴动点的定义
01
数轴动点是指在数轴上可以移动 的点,这些点通常与某些数学问 题相关联,如追及问题、相遇问 题等。
相遇问题
总结词
相遇问题是数轴动点问题的另一种常见类型,主要研究两个动点在数轴上从两端相向而行直至相遇的 问题。
详细描述
相遇问题需要利用数轴上的距离和速度关系,计算出两个物体相遇所需的时间或距离。这类问题通常 涉及到相对速度的概念,即两个物体相对运动的速度等于各自速度之和或之差。
最大距离与最小距离问题
02
数轴动点问题通常涉及到速度、 时间、距离等概念,是数学中常 见的题型之一。
数轴动点的特性
数轴动点具有连续性
由于动点在数轴上可以连续移动,因 此其位置和状态会随着时间的变化而 变化。
数轴动点具有不确定性
由于动点的位置和状态是随机的,因 此其运动轨迹和结果也是不确定的, 需要根据具体问题进行分析和计算。
匀速运动规律
总结词
描述动点在数轴上以恒定速度进行的直线运动。
详细描述
在数轴上,如果一个动点以恒定的速度沿直线移动,那么它所经过的每一个单位 长度所用的时间都是相等的。匀速运动可以用公式表示为:距离 = 速度 × 时间 。
变速运动规律
总结词
描述动点在数轴上以非恒定速度进行的直线或曲线运动。
详细描述
04
数轴动点的解题策略与技巧
建立数轴模型
总结词
明确问题背景
详细描述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动点问题得函数图像复习指要
【典例分析】
例1(2014•贵阳,第9题,3分)如图,三棱柱得体积为10,其侧棱AB上有一个点P从点A开始运动到点B停止,过P点作与底面平行得平面将这个三棱柱截成两个部分,它们得体积分别为x、y,则下列能表示y与x之间函数关系得大致图象就是()
A.B.C.D.
考点:动点问题得函数图象.
分析:根据截成得两个部分得体积之与等于三棱柱得体积列式表示出y与x得函数关系式,再根据一次函数得图象解答.
解答:解:∵过P点作与底面平行得平面将这个三棱柱截成两个部分得体积分别为x、y,∴x+y=10,
∴y=﹣x+10(0≤x≤10),
纵观各选项,只有A选项图象符合.
故选A.
点评:本题考查了动点问题得函数图象,比较简单,理解分成两个部分得体积得与等于三棱柱得体积就是解题得关键.
例2 (2014年•河南省,第8题,3分)如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s得速度沿折线AC→CB→BA运动,最终回到点A,设点P得运动时间为x(s),线段AP得长度为y(cm),则能够反映y与x之间函数关系得图象大致就是()
A.B.
C.D.
考点:动点问题得函数图象.
分析:这就是分段函数:①点P在AC边上时,y=x,它得图象就是一次函数图象得一部分;
②点P在边BC上时,利用勾股定理求得y与x得函数关系式,根据关系式选择图象;
③点P在边AB上时,利用线段间得与差关系求得y与x得函数关系式,由关系式选择图象.
解答:解:①当点P在AC边上,即0≤x≤1时,y=x,它得图象就是一次函数图象得一部分.故C错误;
②点P在边BC上,即1<x≤3时,根据勾股定理得AP=,即y=,
则其函数图象就是y随x得增大而增大,且不就是线段.故B、D错误;
③点P在边AB上,即3<x≤3+时,y=+3﹣x=﹣x+3+,其函数图象就是直线得一部分.
综上所述,A选项符合题意.
故选:A.
点评:本题考查了动点问题得函数图象.此题涉及到了函数y=得图象问题,在初中阶段没有学到该函数图象,所以只要采取排除法进行解题.
例3(2014•广西桂林,第12题,3分)如图1,
在等腰梯形ABCD中,∠B=60°,PQ同时从B
出发,以每秒1单位长度分别沿BADC与BCD
方向运动至相遇时停止,设运动时间为t(秒),
△BPQ得面积为S(平房单位),S与t得函数图
象如图2所示,则下列结论错误得就是()
A.当t=4秒时,S=43
B.AD=4
C.当4≤t≤8时,S=23t
D.当t=9秒时,BP平分梯形ABCD得面积
考点:动点问题得函数图象.
分析:根据等腰梯形得性质及动点函数图象得性质,综合判断可得答案.
解答:解:由答图2所示,动点运动过程分为三个阶段:
(1)OE段,函数图象为抛物线,运动图形如答图1﹣1所示.
此时点P在线段AB上、点Q在线段BC上运动.
△BPQ为等边三角形,其边长BP=BQ=t,高h=t,
∴S=BQ•h=t•t=t2.
由函数图象可知,当t=4秒时,S=4,故选项A正确.
(2)EF段,函数图象为直线,运动图形如答图1﹣2所示.
此时点P在线段AD上、点Q在线段BC上运动.
由函数图象可知,此阶段运动时间为4s,
∴AD=1×4=4,故选项B正确.
设直线EF得解析式为:S=kt+b,将E(4,4)、F(8,8)代入得:,
解得,
∴S=t,故选项C错误.
(3)FG段,函数图象为直线,运动图形如答图1﹣3所示.
此时点P、Q均在线段CD上运动.
设梯形高为h,则S梯形ABCD=(AD+BC)•h=(4+8)•h=6h;
当t=9s时,DP=1,则CP=3,
∴S△BCP=S△BCD=××8×h=3h,
∴S△BCP=S梯形ABCD,即BP平分梯形ABCD得面积,故选项D正确.
综上所述,错误得结论就是C.
故选:C.
点评:本题考查了动点问题得函数图象分析,有一定得难度,解题关键就是结合函数图象与
几何图形得性质求解.
例4(2014•黄冈,第8题,3分)已知:在△ABC中,BC=10,BC边上得高h=5,点E在
边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点
E到BC得距离为x,则△DEF得面积S关于x得函数图象大致为()
A.B.C.D.
考点:动点问题得函数图象.
分析:判断出△AEF与△ABC相似,根据相似三角形对应边成比例列式求出EF,再根据三角形得面积列式表示出S与x得关系式,然后得到大致图象选择即可.
解答:解:∵EF∥BC,
∴△AEF∽△ABC,
∴=,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x ﹣)2+,
∴S与x得关系式为S=﹣(x ﹣)2+(0<x<10),
纵观各选项,只有D选项图象符合.
故选D.
点评:本题考查了动点问题函数图象,主要利用了相似三角形得性质,求出S与x得函数关系式就是解题得关键,也就是本题得难点.
例5(2014•山东菏泽,第8题,3分)如图,Rt△ABC中,AC=BC=2,正方形CDEF得顶点D、F分别在AC、BC边上,设CD得长度为x,△ABC与正方形CDEF重叠部分得面积为y,
则下列图象中能表示y与x之间得函数关系得就是
考点:动点问题得函数图象.
分析:分类讨论:当0<x≤1时,根据正方形得面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠得面积等于正方形得面积减去
等腰直角三角形MNE得面积得到y=x2-2(x-1)2,配方得到y=-(x-2)2+2,然后根据二次函数得性质对各选项进行判断.
解答:当0<x≤1时,y=x2,当1<x≤2时,ED交AB于M,EF交AB于N,CD=x,则AD=2-x,∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,∴DM=2-x,∴EM=x-(2-x)=2x-2,
∴S△EN M=0、5,(2x-2)2=2(x-1)2,
∴y=x2-2(x-1)2=-x2+4x-2=-(x-2)2+2,
故选A.
点评:本题考查了动点问题得函数图象:通过瞧图获取信息,不仅可以解决生活中得实际问题,还可以提高分析问题、解决问题得能力.用图象解决问题时,要理清图象得含义即会识图.也考查了等腰直角三角形得性质.
例6(2014年•福建漳州,第10题,4分)世界文化遗产“华安二宜楼”就是一座圆形得土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB
也匀速走到点B,紧接着沿回到南门,下面可以近似地刻画小王与土楼中心O得距离s 随时间t变化得图象就是()
A.B.
C.D.
考点:动点问题得函数图象.
分析:从A→O得过程中,s随t得增大而减小;直至s=0;从O→B得过程中,s随t得增大而增大;从B沿回到A,s不变.
解答:解:如图所示,当小王从A到古井点O得过程中,s就是t得一次函数,s随t得增大而减小;
当停留拍照时,t增大但s=0;
当小王从古井点O到点B得过程中,s就是t得一次函数,s随t得增大而增大.
当小王回到南门A得过程中,s等于半径,保持不变.
综上所述,只有C符合题意.
故选:C.
点评:主要考查了动点问题得函数图象.此题首先正确理解题意,然后根据题意把握好函数图象得特点,并且善于分析各图象得变化趋势.。
