1.3空间几何体的表面积与体积
2020版人教A数学必修2:1.3.1 柱体、锥体、台体的表面积与体积

的底面积 S= 1 ×4×2=4,棱锥的高 h=4,所以棱锥的体积 V= 1 ×4×4= 16 .
2
3
3
故选 B.
[备用例2] 1.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和 最长母线长分别为2和3,求该几何体的体积.
解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱 的体积为π×22×5=20π,故所求几何体的体积为10π.
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图, 则此几何体的体积为( B )
(A)6 (B)9 (C)12 (D)18 解析:由三视图可知该几何体为底面是斜边为 6 的等腰直角三角形,高为 3 的 三棱锥,其体积为 1 × 1 ×6×3×3=9.
32
3.(2018·天津河西区高一期中)一个几何体的三视图如图所示,则该几何
体的体积为
.
解析:几何体上部是圆锥,下部是圆柱,所以几何体的体积为π·12×4+ 1 × 3
22π×2= 20π . 3
答案: 20π 3
4.(2018·杭州高一期中)某几何体的三视图如图所示,则该几何体的体积
是
;表面积是
.
解析:由题意几何体是棱长为 2 的正方体,挖去一底面半径为 1,高为 1 的圆锥,
π rl+π
r2
. .
圆台
上底面面积:S上底= 下底面面积:S下底=
π r′2 . π r2 .
侧面积:S侧= π l(r+r′) .
表面积:S= π (r′2+r2+r′l+rl) .
2.柱体、锥体、台体的体积公式 柱体的体积公式 V=Sh(S 为底面面积,h 为高);
必修二_1.3_空间几何体的表面积和体积同步练习和详细答案

1.3空间几何体的表面积和体积【知识总结】1. 多面体的面积和体积公式名称 侧面积(S 侧) 全面积(S 全)体积(V )棱 棱柱 直截面周长x IS 侧+2S 底S底• h=S 直截面• h柱直棱柱 chS 底• h「棱锥棱锥 各侧面积之和1S 底• h3 正棱锥 1『 —ch 2S 侧+S 底棱台各侧面面积之和1—h(S 上底+S 下底+3棱 台正棱台1一 (c+c ' )h '2S 侧+S 上底+S 下底S 下底’S 下底)表中表示面积,'、分别表示上、下底面周长,表斜咼,'表示斜咼,表示侧棱长。
2 .旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧 2 n rl n rl n (r 1+「2)lS 全 2 n r(l+r) n r(l+r) 2 2n (r 1+r 2)l+ n (r 1+r24 n RVn r 2h(即 n r 2l)1r 2h —n r h312 2—n h(r 1+r 1「2+r 2)3 43—n R3 表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径,r i 、「2分别表示圆台上、下底面半径,R 表示半径。
【知能训练】A:多面体的表面积和体积 一•选择题1.如图,在直三棱柱 ABC-ABC i 中,AA=AB=2 BC=1, / ABC=90,若规 定主(正)视方向垂直平面 ACCA ,则此三棱柱的左视图的面积为 ( )A.—— B . 2 - C . 4 D . 22•某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底 边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、 高为4的等腰三角形,则该几何体的表面积为()3.—个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1: 2,则截面把棱锥的一条侧棱分成的两段之比是()A . 1 : 4B . 1 : 2C . 1 : ( "- 1 )D . 1: ( 一+1 ) 4.正六棱台的两底边长分别为1cm, 2cm,高是1cm,它的侧面积为()A . 80B . 24 一+88C. 24 一+40 D . 118A .9 ~ 2cm2B . 9 cmC. - cm 22D. 3 cm5. 要制作一个容积为 4卅,高为1m 的无盖长方体容器,已知该容器的底面造价是每平方米 20元,侧面造价是每平方米 10元,则该容器的最低总造价是( )A . 80 元B . 120 元C . 160 元D. 240 元6. (文) 四棱锥S-ABCD 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱 锥及其三视图如图(AB 平行于主视图投影平面)则四棱锥 A . 24 B . 18 C . - - D . 87. 某空间组合体的三视图如图所示,则该组合体的体积为( A . 48B . 56C . 64D. 72&各棱长均为a 的三棱锥的表面积为( )A. 4 _a 2B . 3 "a 2C .2 _a 2D9.已知一个四棱锥的高为 3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为()10. 如图,在三棱柱 ABC-ABC 中,D, E , F 分别是AB, AC, AA 的中点,设三棱锥 F-ADE的体积为V 1,三棱柱 ABG-ABC 的体积为V 2,则V 1: V ___________________________________ .11. _______ 将边长为2的正方形沿对角线 AC 折起,以A, B, C, D 为顶点的三棱锥的体积最大值等 于 ____ .12.如图,一个三棱柱形容器中盛有水,且侧棱AA=8.若AAB 1B 水平放置时,液面恰好过AC BC, AC , BC 的中点,则当底面 ABC 水平放置时,液面的高为 _________________ . 13. 四棱锥P-ABCD 的底面ABCE 为正方形,且PD 垂直于底面 ABCD N 为PB 中点,则三棱锥 P-ANC 与四棱锥P-ABCD 的体积比为 ________________ .14.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为S-ABCD 的体积=( )A .B . 6C. -D . 2直角三角形,则它的体积为_________________15.如图所示,在三棱柱ABC-ABQ 中,AB=AC=AA=2, BC=2 ;且/ AAB=/ A i AC=60,则该三棱柱的体积是_________________________ .B:旋转体的表面积和体积1•如果圆锥的底面半径为,高为2,那么它的侧面积是()A. 4 n B . 2 n C . 2 n D . 4 n2.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A. 5 nB. 4 nC. 3 nD. 2 n3•如果圆锥的轴截面是正三角形(此圆锥也称等边圆锥),则此圆锥的侧面积与全面积的比是()A. 1 : 2 B. 2: 3 C. 1 : 一 D. 2: _4•圆锥侧面积为全面积的,则圆锥的侧面展开图圆心角等于()A. - nB. nC. 2 nD.以上都不对5.圆台的上、下底面半径和高的比为 1 : 4: 4,母线长为10,则圆台的侧面积为()A. 81 nB. 100 nC. 14 nD. 169 n6.已知球的直径SC=8 A, B是该球球面上的两点,AB=2 ,/ SCAN SCB=60,则三棱锥S-ABC 的体积为()A. 2 ~B. 4 ~C. 6 ~D. 8 ~7.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S、S,则S:Sa=()A. 1 : 1B. 2: 1C. 3: 2D. 4: 1&若两个球的表面积之比为1: 4,则这两个球的体积之比为()A. 1 : 2B. 1 : 4C. 1 : 8D. 1 : 169.体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S , S, S3,那么它们的大小关系为()A. S1 v S2 v S3B. S1 v S3V S2C. S2V S3 v S1D. S2 v S1 v S3二.填空题(共5小题)10.圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为________________n和n的矩形, 11 .已知一个圆柱的侧面展开图是一个长和宽分别为则该圆柱的体积是____________________12.在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S= cm 2.13.球的体积与其表面积的数值相等,则球的半径等于14•已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O的表面积为15.已知A, B, C是球面上三点,且AB=AC=4cm/ BAC=90,若球心O到平面ABC的距离为2 ,则该球的表面积为cm3.11.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD7卜接球表面积为三.解答题(共3小题)16•如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成•已知球的直径是6cm,圆柱筒长2cm.(1)这种“浮球”的体积是多少cm (结果精确到0.1 ) ?(2 )要在这样2500个“浮球”表面涂一层胶质,如果每平方米需要涂胶100克,共需胶多少?17.(文)如图,球O的半径长为10(1)求球O的表面积;(2)求球O的体积;(3)若球O的小圆直径AB=3Q求A、B两点的球面距离.18.设底面直径和高都是4厘米的圆柱的内切球为O.(1)求球O的体积和表面积;(2)与底面距离为1的平面和球的截面圆为M AB是圆M内的一条弦,其长为2 ,求AB 两点间的球面距离.参考答案: A:I、A 2、B 3、C 4、A 5、C 6、D 7、C 8、D 9、D10、解:因芮D,E,分S]是Ab肌的中自所以血虫DE;S AA BC=1:仆又F是宜納的中点,所以A T aS面的范离H为F到虧面距离h的2倍• 即三複栓盘卩1门-2匚的壽是三棱穩F-ME高的7倍-斷以如;畑空兰空=4T=1:西.故答案为1; 24.II、铅:妇也肪示,评正方也就口叭対術钱M * 3DSt + iO>甲n折更启的位豈为F・连揺即‘ *苛一TAZJLBC,AC l-BD* - BaflD- QrO--ACX 耶®IT g匡b> =楼帕的作祗対V D -kBC"v^EOC' -^Vc-BCC~ ;BCD' k AO*j52kBOD' x J S^ISOD_卞航:王方世的迪丢为2・可J?■■- BOD ft AH - To LABC谜劉昴尢值■*:S/\ 二 0D* =? x j^x忑小血乂目□力'二w in上aoii *’,丄i ?rv「.q-TTY-M' l「=丄工」•王5V.怡巧「此t」导.乂RJ农虻-土故告案为;半12、解:不妨令此三棱柱为直三棱柱,如图当侧面AA1B1B水平放置时,水的形状为四棱柱形,底面是梯形.设△ ABC的面积为S,贝U S梯形ABFE= S,V水=S? AA1=6S .当底面ABC水平放置时,水的形状为三棱柱形,设水面高为h,则有V水=Sh,••• 6S=Sh,.•• h=6 .故当底面ABC水平放置时,液面高为6 .故答案为:613、1:4 14、15、2解:團柱的側面展开囹星长利员务别为和TT的矩用,当毋线为戈氏时,區1桂的庙面半襌是扌此时囿桂体粮是(l)1 2Ttx3it=^;当母线为H时,圆柱酌展面半轻是学此时圆柱的体釈是(芥II"二竺匕£-t 4综上所求圈柱的体稅杲:—16、解:(1 )T该“浮球”的圆柱筒直径d=6cm ,•••半球的直径也是6cm,可得半径R=3cm,•两个半球的体积之和为V球=-冗R = - n ? 27 = 6 n cm3 * S 6…(2分)斗412、解:将相同的两个几何体,对接为圆柱,则圆柱的侧面展开,侧面展开图的面积 S=[ ( 50+80) X 20 n x 2]/2=2600 n cm2. 故答案为:2600 n13、 3 14、8 n 15、64 n学习参考而V 圆柱=n R ? h= n X 9X = n cm3…(2 分)•该“浮球”的体积是:V=V球+V圆柱=36 n +18 n =54 n" 169.6cm 3…(4分)(2)根据题意,上下两个半球的表面积是S 球表= n R = Xn X 9= 6 n cm?…(6 分)而“浮球”的圆柱筒侧面积为:S圆柱侧=2 n Rh=2 Xn X 3 X 2=12 n cm2…(8分)6 n n n• 1个“浮球”的表面积为S = —0一= —m因此,2500个“浮球”的表面积的和为2500 S = 00 X —= n m2…(10分)•/每平方米需要涂胶100克,•总共需要胶的质量为:100 X 12 n =1200 n (克)…(12分)答:这种浮球的体积约为169.6cm 3;供需胶1200 n克.…(13分)17、解:(1)球的表面积为4 n r 2=1200 n ; …(4分)(2)球的体积V=-n r3= 4000 _n ; …(8 分)(3)设球心为O,在△ AOB中,球O的小圆直径AB=30,球O的半径长为10解得Z AOB=",所以A、B两点的球面距离为0 n n . …(15分)18、解:(1)•••底面直径和高都是4厘米的圆柱的内切球为O,•球O的半径为2cm,.•.球O的体积为-n ? 2=,表面积4 n ? 22=16 n ;(2)•/ AB是圆M内的一条弦,其长为2 ,• Z AOB= n , • AB两点间的球面距离为".。
苏教版必修2数学课件-第1章立体几何初步第3节空间几何体的表面积和体积教学课件

栏目导航
合作探究 提素养
栏目导航
棱柱、棱锥和棱台的侧面积和表面积 【例 1】 正四棱锥的侧面积是底面积的 2 倍,高是 3,求它的 表面积. 思路探究:由 S 侧与 S 底的关系,求得斜高与底面边长之间的关系, 进而求出斜高和底面边长,最后求表面积.
所以 S 侧=3×12×(20+30)×DD′=75DD′. 又 A′B′=20 cm,AB=30 cm,则上、下底面面积之和为 S 上+S 下 = 43×(202+302)=325 3(cm2).
栏目导航
由 S 侧=S 上+S 下,得 75DD′=325 3, 所以 DD′=133 3(cm), 又因为 O′D′= 63×20=103 3(cm), OD= 63×30=5 3(cm),
错点)
运算核心素养.
3.会求简单组合体的体积及表面积.(难点)
栏目导航
自主预习 探新知
栏目导航
1.柱体、锥体、台体的体积
几何体
体积
柱体 锥体
V 柱体= Sh (S 为底面面积,h 为高), V 圆柱= πr2h (r 为底面半径) 1
V 锥体= 3Sh (S 为底面面积,h 为高), V 圆锥= π3r2h (r 为底面半径)
栏目导航
台体
V 台体= 13h(S+ SS′+S′) (S′,S 分别为上、下底面面 积,h 为高),V 圆台= 13πh(r′2+rr′+r2) (r′,r 分别为上、 下底面半径)
思考:柱体、锥体、台体的体积公式之间的关系. 提示:V=Sh―S′―=→S V=13(S′+ S′S+S)h―S′―=→0 V=13Sh.
栏目导航
[解] 如图所示,设 SE 是侧面三角形 ABS 的高,则 SE 就是正 四棱锥的斜高.
高中数学1.3.1 柱体、锥体、台体的表面积与体积

(3)柱体、锥体、台体的体积公式之间的关系
(4)求台体的体积转化为求锥体的体积.根据台体的定义进行“补形”, 还原为锥体,采用“大锥体”减去“小锥体”的方法求台体的体积.
【题型探究】 类型一 柱体、锥体、台体的表面积 【典例】1.(2015·陕西高考)一个几何体的三视图如图所示,则该几 何体的表面积为 ( )
2
四个侧面的面积和为(2+8+5×2)×10=200.
所以四棱柱的表面积为S=40+200=240.
【方法技巧】空间几何体的表面积的求法技巧 (1)多面体的表面积是各个面的面积之和. (2)组合体的表面积应注意重合部分的处理. (3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展 为平面图形计算,而表面积是侧面积与底面圆的面积之和.
2.旋转体的侧面积与表面积的求解 (1)求圆柱、圆锥、圆台的侧面积或表面积时,可直接使用公式.但像 圆台的表面积公式比较复杂,不要求记忆,因此,表面积的求解方法是 最重要的. (2)在计算圆柱、圆锥、圆台的侧面积时,应根据条件计算旋转体的母 线长和底面圆的半径长. (3)这些公式的推导方法向我们提示了立体几何问题的解题思路,主要 通过空间观念等有关知识,将立体几何问题转化为平面几何问题.
Байду номын сангаас
积S1=πr2=π,侧面积S2=2×2+12 ·2πr·2=2π+4,所以此几何体的
表面积S=S1+S2=π+2π+4=3π+4.
2.选D.由已知得l=2r,
S侧 S底
=
rl r 2
=
l r
=2.
3.选D.几何体为直四棱柱,其高为10,底面是上底为2,下底为8,高为4的
21-22版:1.3.1 柱体、锥体、台体的表面积与体积(创新设计)

中心,则该圆柱的体积为________. 解析 由题意知圆柱的高恰为四棱锥的高的一半,圆柱的底面直径恰为四棱
锥的底面正方形对角线的一半.因为四棱锥的底面正方形的边长为 2,所以底
面正方形对角线长为 2,所以圆柱的底面半径为12.又因为四棱锥的侧棱长均为 5,所以四棱锥的高为 ( 5)2-12=2,所以圆柱的高为 1.所以圆柱的体
∵S△A1D1E=21EA1·A1D1=41a2, 又三棱锥 F-A1D1E 的高为 CD=a,
∴V 三棱锥 F-A1D1E=13×a×14a2=112a3,∴V 三棱锥 A1-D1EF=112a3.
20
课前预习
课堂互动
课堂反馈
方向2 割补法求体积
【例3—2】 如图所示,已知ABCDA1B1C1D1是棱长为a的正方体,
7
课前预习
课堂互动
课堂反馈
@《创新设计》
【预习评价】
1.若长方体的长、宽、高分别为3 cm,4 cm,5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3 C.64 cm3
D.125 cm3
解析 V长方体=3×4×5=60(cm3). 答案 B
8
课前预习
课堂互动
课堂反馈
@《创新设计》
25
课前预习
课堂互动
课堂反馈
@《创新设计》
A.90π
B.63π
C.42π D.36π
解 析 (1) 如 图 所 示 的 正 方 体 ABCDA1B1C1D1 的 棱 长 为 4 , 去 掉 四 棱 柱 MQD1A1NPC1B1(其底面是一个上底为 2,下底为 4,高为 2 的直角梯形)所得的几 何体为题中三视图对应的几何体,故所求几何体的体积为 43-12×(2+4)×2×4
高一数学人教A版必修2:1-3-1-2 柱体、锥体、台体的体积

第十一页,编辑于读教材P25-26,回答下列问题: 1.柱体的体积 (1)棱柱(圆柱)的高是指 两底面 之间的距离,即从一底面 上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的 交点)之间的距离. (2)柱体的底面积为S,高为h,其体积V= Sh .特别地,圆 柱的底面半径为r,高为h,其体积V= πr2h .
第一章 1.3 1.3.1 第2课时
第二十六页,编辑于星期日:二十二点 二分。
[分析]明确几何体的形状及相应的体积公式是解决这类问 题的关键.因为玻璃杯是圆柱形的,所以铅锤取出后,水面 下降部分实际是一个小圆柱,这个小圆柱的底面与玻璃杯的 底面一样,是一直径为20cm的圆,它的体积正好等于圆锥形 铅锤的体积,这个小圆柱的高就是水面下降的高度.
第一章
空间几何体
第一章 空间几何体
第一页,编辑于星期日:二十二点 二分。
第一章
1.3 空间几何体的表面积与体积
第一章 空间几何体
第二页,编辑于星期日:二十二点 二分。
第一章
1.3.1 柱体、锥体、台体的表面积与体积
第一章 空间几何体
第三页,编辑于星期日:二十二点 二分。
第一章
第2课时 柱体、锥体、台体的体积
[答案] (6+π)
第一章 1.3 1.3.1 第2课时
第三十三页,编辑于星期日:二十二点 二分。
[解析] 此几何体是由一个长为3,宽为2,高为1的长方 体与底面直径为2,高为3的圆锥组合而成的,故V=V长方体+V圆 锥=3×2×1+π3×12×3=(6+π)m3.
第一章 1.3 1.3.1 第2课时
第一章 1.3 1.3.1 第2课时
第二十八页,编辑于星期日:二十二点 二分。
:1.3.1.1柱体、椎体、台体的表面积

(2)面积:台体的表面积 S 表=S 侧+S 上底+S 下底.特别地,圆台的上、下 底面半径分别为 r',r,母线长为 l,则侧面积 S 侧=π(r+r')l,表面积 S 表 =π(r2+r'2+rl+r'l).
【检测 3】 圆台的上、下底面半径分别是 3 和 4,母线长为 6,
则其表面积等于( )
底面积:S 底=πr2 侧面积:S 侧=2πrl 表面积:S=2πr(r+l)
底面积:S 底=πr2 侧面积:S 侧=πrl 表面积:S=πr(r+l)
上底面面积:������上底=πr'2 下底面面积:������下底=πr2
侧面积:S 侧=πr'l+πrl 表面积:S=π(r'2+r2+r'l+rl)
求组合体的表面积时,通常先将所给组合体分成基本的柱、锥、
台体,再通过这些基本的柱、锥、台体的表面积,进行求和或作差,从 而获得组合体的表面积.本题中将组合体的表面积表达为正方体的 表面积与圆柱侧面积的和是非常有创意的想法,如果忽略正方体没 有被打透这一点,思考就会变得复杂,当然结果也会是错误的.
题型二
A.72
B.42π
C.67π
D.72π
小结:本节课你学到什么?
多面体的展开 图及其表面积
公式
圆锥的侧 面展开图 及其侧面、 表面积公
式
圆柱的侧 面展开图 及侧面、 表面积公
式
圆台的侧 面展开图 及其侧面、 表面积公
式
图形 多面体
表面积公式
多面体的表面积就是各个面 的面积的和,也就是多面体展开图 的面积
空间几何体的表面积和体积公式大全
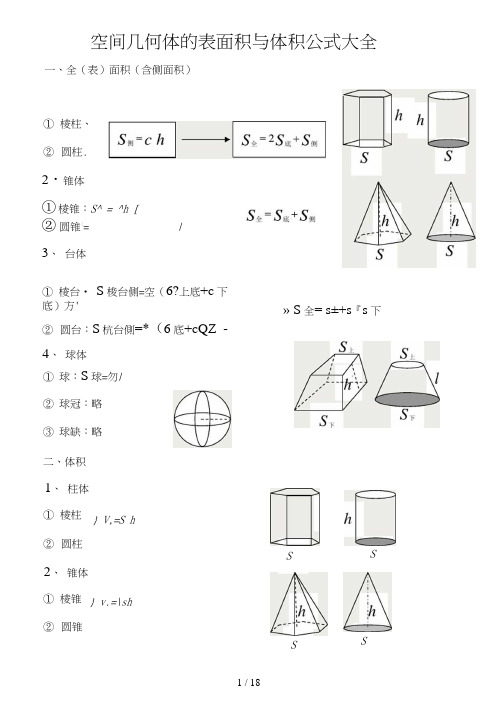
空间几何体的表面积与体积公式大全一、全(表)面积(含侧面积)①棱柱、②圆柱.2・锥体①棱锥:S^ = ^h [②圆锥:= /3、台体①棱台• S梭台侧=空(6?上底+c下底)方'» S全= s±+s『s下②圆台:S杭台側=*(6底+cQZ -4、球体①球:S球=勿/②球冠:略③球缺:略二、体积1、柱体①棱柱} V,=S h②圆柱S S 2、锥体①棱锥} v.=\sh②圆锥S S3、 台体V 台肓//(S 匕+ JS 上S F + S 下)台=齐方(厂上+Jr 上厂下+厂下) 4、 球体①球:V 球② 球冠:略VyT/③ 球缺:略说明:棱锥、棱台计算侧面积时使用侧面的斜高力计算;而圆锥、圆台的 侧面积计算时使用母线/计算。
三、拓展提高1、 祖眶原理:(祖璀:祖冲之的儿子)夹在两个平行平面间的两个几何体,如果它们在任意高度上的平行截面面积都相等,那么这两个几何体的体积相等。
最早推导出球体体积的祖冲之父子便是运用这个原理实现的。
2、 阿基米德原理:(圆柱容球)圆柱容球原理:在一个高和底面直径都是2厂的圆柱形容器内装一个最大 的球体,则该球体的全面积等于圆柱的侧面积,体积等于圆柱体积的?。
①棱台 ②圆台丿分析:圆柱体积:V H1 = s h =(^r)x2r = 2^/圆柱侧面积:S叭削= c/z = (2岔)X2广=4兀/2 彳4 彳因lit :球体体积:|/厅=—x2/r^ =_龙厂球体表面积:S球=4兀厂通过上述分析,我们可以得到一个很重要的关系(如图)即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式:几冷〃(S上+、恳瓦+ S』证明:如图过台体的上下两底面中心连线的纵切面为梯形ABCD。
延长两侧棱相交于一点P 0设台体上底面积为Si,下底面积为S下高为// °易知:\PDCs 型AB,设卩£ =人,则Pf+h由相似三角形的性质得:孚=袋AB PF即:(相似比等于面积比的算术平方根)、用hi整理得:人=尺刃又因为台体的体积二大锥体体积一小锥体体积u台=§s下(九+力r s上人人(S下-S上)+§s下方即:(、瓦+丫瓦)+扣下力=|/z $ + 应7+S卜)4、球体体积公式推导分析:将半球平行分成相同高度的若干层(兀层),〃越大,每一层越近似于圆柱'"T -HZ)时»每一层都可以看作是一个圆柱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
B
2 3 2 3 OA AB r 3 2 3
例6、已知过球面上三点A、B、C的截面到球 心O的距离等于球半径的一半,且 AB=BC=CA=2cm,求球的体积、表面积。
2 2 2 在Rt OO A中, OA O O O A ,
R
2
4 R . 3 4 4 4 3 256 3 V R ( ) ; 3 3 3 81 16 64 2 S 4 R 4 . 9 9
r O
l
O
2 r
圆柱的侧面展开图是矩形
S 2 r 2 rl 2 r ( r l )
2
S r 2 rl r (r l )
2r
l
r
圆锥的侧面展开图是扇形
O
(1)联系圆柱和圆锥的展开图,你能想 象圆台展开图的形状并且画出它吗?
(2)如果圆台的上,下底面半径分别 为 r , r ,母线长为l,你能计算出它 的表面积吗?
S 球 S圆柱侧
(2)
Q S 圆柱全
4 R
2
2 R
2
2
6 R
2
S 球 4R 2 S 球 S圆柱全 3
练习 p28 1、2、3
例5.如图,正方体的棱长为a,它的各个顶点都 在球的球面上,求球的表面积和体积。
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体体对角线与球的直径相等。
圆台的侧面展开图 是扇环
r 'O’
l
2r '
2r
r
O
S ( r r 2 r ' l rl )
'2
r 'O’
l
x
2r '
2r
r
O
圆柱、圆锥、圆台三者的表面积公式之间 有什么关系?
S ( r r 2 r ' l rl )
'2
l
r
O
r 'O’
l
l
r
O
3 S 4 R2 16 且V 4 R 3 32 3
例6、已知过球面上三点A、B、C的截面到球心O 的距离等于球半径的一半,且AB=BC=CA=2cm, 求球的体积、表面积.
解:如图,设球O半径为R, 截面⊙O′的半径为r,
O A
O
R OO , ABC是正三角形, 2
S [( 15 2 15 20 1.5 ) 15 15] ( )2 2 2 2 2
1000(cm 2 ) 0.1( m 2 ) 涂100个花盆需油漆:
0.1 100 100 1000 (毫升)
15 cm
15 cm
答:涂100个这样的花盆约需要1000毫升 油漆.
解:Q 正方体内接于球 球的直径等于正方体的体对角线长 ( 2 R ) 3a R
2 2
3 2
D A O D1 A1 B1 B
C
a
3 3 3 S 4 R2 3a2 且V 4 3 R 2 a
C1
两个几何体相接:一个几何体的所有顶点都 在另一个几何体的表面上。
例1.已知棱长为 a ,各面均为 等边三角形的四面体S-ABC,求 它的表面积 .
S
A
B
C
例1.已知棱长为 a ,各面均为等边三角形的四 面体S-ABC,求它的表面积 .
分析:四面体的展开图是由四个全等的正三角形组成. 解:过点S作 SD BC , 交BC于点D.
S A B D ∵ BC a , SD SB 2 BD 2 a 2 ( a )2 3 a 2 2
在初中已经学过了正方体和长方体的表面积, 你知道正方体和长方体的展开图与其表面积的关 系吗?
几何体表面积
展开图
平面图形面积 平面问题
空间问题
棱柱、棱锥、棱台都是由多 个平面图形围成的几何体,它们 的展开图是什么?如何计算它们 的表面积?
棱柱,棱锥,棱台的表面积
棱柱
棱锥
棱台
一般地,多面体的表面积就是各个面的面积之和
R 2 2 3 2 ( ) ( ) , 2 3
O A
O
C
B
柱体体积公式
S
S
S
等底等高的柱体等体积
柱体的体积公式 :
V柱体 Sh
S是柱体的底面积,h是柱体的高
锥体体积公式
等底等高的棱锥与圆锥体积相同
圆锥的体积
1 V= 3 Sh
S是圆锥的底面积, h是高
棱锥的体积
1 V= 3
Sh
S是棱锥的底面积, h是高
台体体积公式
由于圆台(棱台)是由圆锥 (棱锥)截成的,因此可以利 用两个锥体的体积差.得到 圆台(棱台)的体积公式.
V VP ABCD VP ABCD
1 ( S S S S )h 3
A
P
A
S
B
D
C
h
S
D
C
B
台体的体积公式
1 V ( S S S S )h 3 其中 S , S 分别为上、下底面面积,h为台体的高.
例3
3 有一堆规格相同的铁制(铁的密是 7.8g/cm ) 六角螺帽共重5.8kg,已知底面是正六边形, 边长为12mm,内孔直径为10mm,高为10mm, 问这堆螺帽大约有多少个(π取3.14)?
1.球的体积
4 V R 3 3
2.球的表面积
S 4R 2
例4、如图,圆柱的底面直径与高都等于球的直径, 求证:(1)球的表面积等于圆柱的侧面积. (2)球的表面积等于圆柱全面积的三分之二. 证明: (1)设球的半径为R, 则圆柱的底面半径为R,高为2R. 2 得: S 球 4R 2 R S圆柱侧 2R 2 R 4R O
解:六角螺帽的体积是六棱柱的体积与圆 柱体积之差,即:
3 10 2 2 V 12 6 10 3.14 ( ) 10 4 2 3 3 2956(mm ) 2.956(cm )
所以螺帽的个数为
(个)
答:这堆螺帽大约有252个.
1.3.2球体体积和表面积
球体的体积公式
15 cm
15 cm
例2.如图,一个圆台形花盆盆口直径20cm,盆底直 径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为 了美化花盆的外观,需要涂油漆.已知每平方米用100毫 升油漆,涂100个这样的花盆需要多少油漆(取 3.14, 结果精确到1毫升,可用计算器)? 解:花盆外壁的表面积: 20 cm
r
O
S r 2 rl r (r l )
O
S 2 r 2 2 rl 2 r (r l )
例、圆台的上、下底面半径分别是10cm和20cm, 它的侧面展开图的扇环的圆心角是1800,那么 圆台的侧面积是
例2.如图,一个圆台形花盆盆口直径20cm, 盆底直径为15cm,底部渗水圆孔直径为1.5cm, 盆壁长15cm.为了美化花盆的外观,需要涂油 漆.已知每平方米用100毫升油漆,涂100个这样 的花盆需要多少油漆(取 3.14,结果精确到 1毫升,可用计算器)? 21 3 3 2 BC SD a a a 2 2 2 4
3 2 S 4 a 3a 2 4
因此,四面体S-ABC的表面积为
练习:已知正四棱锥底面正方形的边长为4cm, 高与斜高的夹角为300,求正四棱锥的侧面积 和表面积。
如何根据圆柱,圆锥的几何结 构特征,求它们的表面积?
(变式) 球的内接长方体的长、宽、高分别为 3、 2、 3 ,求此球体的表面积和体积。
分析:长方体内接于球,则由球和长方 体都是中心对称图形可知,它们中心重 合,则长方体体对角线与球的直径相等。
解: Q 长方体内接于球 球的直径等于长方体的体对角线长 ( 2 R )2 32 22 ( 3 )2 16 R 2
利用三视图求几何体面积
1、若某空间几何体的三视图如图所示,则该几 何体的表面积是
2
1
2
2、一个几何体的三视图如图,该几何体的表面 积是 (A)372 (B)360 (C)292 (D)280
3、若一个底面是正三角形的三棱柱的正视图如图 所示,则其侧面积等于 ( ) A. B.2 C. D.6
柱体、锥体、台体、球体的体积
