大学物理2-1上册复习资料剖析
大学物理习题答案解析第二章

第二章牛顿定律2 -1如图(a)所示,质量为m的物体用平行于斜面的细线联络置于圆滑的斜面上,若斜面向左方作加速运动 ,当物体刚离开斜面时,它的加快度的大小为()(A) gsin θ(B) gcos θ(C) gtan θ(D) gcot θ剖析与解当物体走开斜面瞬时 ,斜面对物体的支持力消逝为零,物体在绳索拉力 F T (其方向仍可认为平行于斜面 )和重力作用下产平生行水平面向左的加快度a,如图 (b) 所示 ,由其可解得合外力为 mgcot θ,应选 (D).求解的重点是正确剖析物体刚走开斜面瞬时的物体受力状况和状态特点.2 -2 用水平力 F N把一个物体压着靠在粗拙的竖直墙面上保持静止.当 F N渐渐增大时 ,物体所受的静摩擦力 F f的大小 ()(A)不为零 ,但保持不变(B)随 F N成正比地增大(C)开始随 F N增大 ,达到某一最大值后 ,就保持不变(D)没法确立剖析与解与滑动摩擦力不一样的是 ,静摩擦力可在零与最大值μF N范围内取值.当F N增加时,静摩擦力可取的最大值成正比增加 ,但详细大小则取决于被作用物体的运动状态.由题意知 ,物体向来保持静止状态 ,故静摩擦力与重力大小相等 ,方向相反 ,并保持不变 ,应选 (A) .2 -3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()(A)不得小于(C)不得大于μgR (B) 一定等于μgRμgR (D) 还应由汽车的质量m 决定剖析与解由题意知 ,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只好由路面与轮胎间的静摩擦力供给,能够供给的最大向心力应为μF N.由此可算得汽车转弯的最大速率应为 v=μRg.所以只需汽车转弯时的实质速率不大于此值,均能保证不侧向打滑.应选 (C) .2 -4 一物体沿固定圆弧形圆滑轨道由静止下滑,在下滑过程中 ,则 ( )(A)它的加快度方向永久指向圆心,其速率保持不变(B)它遇到的轨道的作使劲的大小不停增加(C)它遇到的合外力大小变化 ,方向永久指向圆心(D)它遇到的合外力大小不变 ,其速率不停增加剖析与解 由图可知 ,物体在下滑过程中遇到大小和方向不变的重力以实时辰指向圆轨道中心的轨 道支持力 F N 作用 ,其合外力方向并不是指向圆心 ,其大小和方向均与物体所在地点有关.重力的切向分 量 (m g cos θ) 使物体的速率将会不停增加 ( 由机械能守恒亦可判断 ),则物体作圆周运动的向心力 (又称法向力 )将不停增大 ,由轨道法向方向上的动力学方程F Nmgsin θ mv 2可判断 ,随 θ 角的不停增R大过程 ,轨道支持力 F N 也将不停增大 ,因而可知应选 (B) .2 -5 图 (a)示系统置于以 a = 1/4 g 的加快度上涨的起落机内 ,A 、B 两物体质量相同均为 m,A 所在的桌面是水平的 ,绳索和定滑轮质量均不计 ,若忽视滑轮轴上和桌面上的摩擦,其实不计空气阻力 ,则绳中张力为 ( )(A) 58 mg (B) 12 mg (C) mg (D) 2 mg剖析与解此题可考虑对 A 、B 两物体加上惯性力后 ,以电梯这个非惯性参照系进行求解. 此时 A 、B两物体受力状况如图 (b)所示 ,图中 a ′为 A 、B 两物体相对电梯的加快度 ,ma ′为惯性力. 对 A 、B 两物体 应用牛顿第二定律 ,可解得 F = 5/8 mg .应选 (A) .T议论 关于习题 2 -5 这种种类的物理问题 ,常常从非惯性参照系 (此题为电梯 )察看到的运动图像较为 明确 ,但因为牛顿定律只合用于惯性参照系,故从非惯性参照系求解力学识题时,一定对物体加上一个虚构的惯性力.如以地面为惯性参照系求解,则两物体的加快度 a A 和a B 均应付地而言 ,此题中 a A 和 a 的大小与方向均不相同.此中 aA 应斜向上.对 a A 、a 、a 和a ′之间还要用到相对运动规律 ,求解BB过程较繁.有兴趣的读者不如自己试试试看.2 -6 图示一斜面 ,倾角为 α,底边 AB 长为 l = 2.1 m,质量为 m 的物体从题 2 -6 图斜面顶端由静止开始向下滑动 ,斜面的摩擦因数为 μ= 0.14 .试问 ,当 α为何值时 ,物体在斜面上下滑的时间最短? 其数值为多少?剖析动力学识题一般分为两类:(1) 已知物体受力争其运动状况;(2) 已知物体的运动状况来剖析其所受的力.自然,在一个详细题目中,这两类问题并没有截然的界线,且都是以加快度作为中介,把动力学方程和运动学规律联系起来.此题重点在列出动力学和运动学方程后,解出倾角与时间的函数关系α= f(t),而后运用对 t 求极值的方法即可得出数值来.解取沿斜面为坐标轴Ox,原点 O 位于斜面极点,则由牛顿第二定律有mgsin α mgμcosαma(1) 又物体在斜面上作匀变速直线运动,故有l 1 at2 1g sin α μcosαt 2cosα 2 2则t2l(2) gcosαsin α μcosα为使下滑的时间最短,可令dt0 ,由式(2)有dα则可得此时sin αsin α μcosαcosαcosα μsin α0 tan 2α 1 , 49oμt 2l 0.99 sgcosαsin α μcosα2 -7 工地上有一吊车 ,将甲、乙两块混凝土预制板吊起送至高空.甲块质量为 m 2 k g,乙块= 2.00 10×1质量为 m2= 1.00 ×102 kg.设吊车、框架和钢丝绳的质量不计.试求下述两种状况下,钢丝绳所受的张力以及乙块对甲块的作使劲:(1) 两物块以 10.0 m ·s-2的加快度上涨; (2) 两物块以 1.0 m s·-2的加快度上涨.从此题的结果,你能领会到起吊重物时一定迟缓加快的道理吗?剖析预制板、吊车框架、钢丝等可视为一组物体.办理动力学识题往常采纳“隔绝体”的方法物体所受的各样作使劲 ,在所选定的惯性系中列出它们各自的动力学方程.依据连结体中物体的多少可列出相应数量的方程式.联合各物体之间的互相作用和联系 ,可解决物体的运动或互相作使劲.,剖析解按题意 ,可分别取吊车(含甲、乙 )和乙作为隔绝体,画示力争 ,并取竖直向上为Oy 轴正方向 (如图所示 ).当框架以加快度 a 上涨时 ,有FT-(m1 + m )g =(m + m )a (1)2 1 2FN2- m g = m a (2)2 2解上述方程 ,得F = 1 2 (3)TFN2 =m (g + a) (4) 2(1)当整个装置以加快度 a = 10 m ·s-2上涨时 ,由式 (3) 可得绳所受张力的值为FT=10×3 N乙对甲的作使劲为N2 N2 2(g + a) =3F′=-F = -m 10× N(2)当整个装置以加快度 a = 1 m·s-2上涨时 ,得绳张力的值为FT=10×3 N此时 ,乙对甲的作使劲则为F′ N2=103× N由上述计算可见,在起吊相同重量的物体时,因为起吊加快度不一样 ,绳中所受张力也不一样,加快度大 ,绳中张力也大.所以,起吊重物时一定迟缓加快,以保证起吊过程的安全.2 -8 如图 (a)所示 ,已知两物体 A、 B 的质量均为 m = 3.0kg 物体 A 以加快度 a = 1.0 m ·s-2 运动 ,求物体 B 与桌面间的摩擦力. (滑轮与连结绳的质量不计)剖析该题为连结体问题 ,相同可用隔绝体法求解.剖析时应注意到绳中张力大小到处相等是有条件的 ,即一定在绳的质量和伸长可忽视、滑轮与绳之间的摩擦不计的前提下成立.同时也要注意到张力方向是不一样的.解分别对物体和滑轮作受力剖析[图(b)].由牛顿定律分别对物体 A 、B 及滑轮列动力学方程,有m A g -F T=m A a (1)F′1 -Ff= m B a′(2)TF′ -2FT1= 0 (3)T考虑到 mTTT1 T,a ′= 2a,可联立解得物体与桌面的摩擦力A =mB =m, F =F′ ,F = F′1F f mg m 4m a7.2 N2议论动力学识题的一般解题步骤可分为:(1) 剖析题意 ,确立研究对象,剖析受力 ,选定坐标; (2) 根据物理的定理和定律列出原始方程组; (3) 解方程组 ,得出文字结果; (4) 查对量纲 ,再代入数据 ,计算出结果来.2 -9 质量为m′的长平板 A 以速度v′在圆滑平面上作直线运动,现将质量为m 的木块 B 轻轻安稳地放在长平板上 ,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板获得共同速度?剖析当木块 B 安稳地轻轻放至运动着的平板 A 上时 ,木块的初速度可视为零,因为它与平板之间速度的差别而存在滑动摩擦力,该力将改变它们的运动状态.依据牛顿定律可获得它们各自相对地面的加快度.换以平板为参照系来剖析,此时 ,木块以初速度-v ′(与平板运动速率大小相等、方向相反)作匀减速运动 ,其加快度为相对加快度,按运动学公式即可解得.该题也可应用第三章所叙述的系统的动能定理来解.将平板与木块作为系统,该系统的动能由平板原有的动能变成木块和平板一同运动的动能,而它们的共同速度可依据动量定理求得.又因为系统内只有摩擦力作功,依据系统的动能定理,摩擦力的功应等于系统动能的增量.木块相对平板挪动的距离即可求出.解 1 以地面为参照系 ,在摩擦力 Ff=μmg的作用下 ,依据牛顿定律分别对木块、平板列出动力学方程F f=μ mg=ma1F ′f=-F f= m′a2a1和 a2分别是木块和木板相对地面参照系的加快度.若以木板为参照系,木块相对平板的加快度 a = a1+ a2 ,木块相对平板以初速度- v ′作匀减速运动直至最后停止.由运动学规律有2- v′= 2as由上述各式可得木块有关于平板所挪动的距离为sm v 22 μg m m解 2 以木块和平板为系统 ,它们之间一对摩擦力作的总功为W =F f(s +l ) -F fl=μ mgs式中 l 为平板相对地面挪动的距离.因为系统在水平方向上不受外力,当木块放至平板上时,依据动量守恒定律,有m′v′= (m′+ m) v″由系统的动能定理 ,有μmgs 1 m v 2 1 m m v 22 2由上述各式可得sm v 22 μg m m2 -10 如图 (a)所示 ,在一只半径为 R 的半球形碗内 ,有一粒质量为 m 的小钢球 ,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时 ,它距碗底有多高?剖析保持钢球在水平面内作匀角速度转动时,一定使钢球遇到一与向心加快度相对应的力(向心力 ), 而该力是由碗内壁对球的支持力 F N的分力来供给的 ,因为支持力 F N一直垂直于碗内壁,所以支持力的大小和方向是随ω而变的.取图示 Oxy 坐标 ,列出动力学方程 ,即可求解钢球距碗底的高度.解取钢球为隔绝体 ,其受力剖析如图 (b) 所示.在图示坐标中列动力学方程F N sin θ ma n mRω2sin θ(1)F N cosθ mg (2)且有由上述各式可解得钢球距碗底的高度为R h cos θ(3)Rgh Rω2可见 ,h 随 ω的变化而变化.2 -11 火车转弯时需要较大的向心力,假如两条铁轨都在同一水平面内 (内轨、外轨等高 ),这个向心力只好由外轨供给 ,也就是说外轨会遇到车轮对它很大的向外侧压力 ,这是很危险的.所以 ,对应于火车的速率及转弯处的曲率半径,一定使外轨适合地超出内轨,称为外轨超高.现有一质量为m 的火车 ,以速率 v 沿半径为 R 的圆弧轨道转弯 ,已知路面倾角为 θ,试求: (1) 在此条件下 ,火车速率 v 0 为多大时 ,才能使车轮对铁轨内外轨的侧压力均为零?(2) 假如火车的速率 v ≠v 0 ,则车轮对铁轨的侧压力为多少?剖析如题所述 ,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平重量F N sin θ 提供 (式中 θ角为路面倾角 ).从而不会对内外轨产生挤压. 与其对应的是火车转弯时一定以规定的速率v 0行驶.当火车行驶速率 v ≠v 0 时,则会产生两种状况: 如下图 ,如 v > v 0 时 ,外轨将会对车轮产生斜向 内的侧压力 F 1 ,以赔偿原向心力的不足,如 v < v 0时 ,则内轨对车轮产生斜向外的侧压力F 2 ,以抵消剩余的向心力 ,不论哪一种状况火车都将对外轨或内轨产生挤压. 由此可知 ,铁路部门为何会在每个铁轨的转弯处规准时速 ,从而保证行车安全.解 (1) 以火车为研究对象 ,成立如下图坐标系.据剖析 ,由牛顿定律有F N sin θ mv 2(1)RF N cos θ mg 0(2)解 (1)(2) 两式可得火车转弯时规定速率为v 0gRtan θ(2) 当 v > v 0 时 ,依据剖析有F N sin θ F 1cos θ m v2(3)RF N cos θ F 1sin θ mg 0(4)解 (3)(4) 两式 ,可得外轨侧压力为F 1 m v 2cos θ gsin θR当 v < v 0 时,依据剖析有2F N sin θ F 2cos θ mv(5)RF N cos θ F 2sin θ mg(6)解 (5)(6) 两式 ,可得内轨侧压力为F 2 m gsin θ v 2cos θR2 -12 一杂技演员在圆筒形建筑物内表演飞车走壁.设演员和摩托车的总质量为 m,圆筒半径为 R,演员骑摩托车在直壁上以速率 v 作匀速圆周螺旋运动 ,每绕一周上涨距离为 h,如下图.求壁对演员和摩托车的作使劲.剖析 杂技演员 (连同摩托车 )的运动能够当作一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加.其旋转一周所形成的旋线轨迹睁开后,相当于如图 (b)所示的斜面. 把演员的运动速度分解为图示的 v 1 和 v 2 两个重量 ,明显 v 1是竖直向上作匀速直线运动的分速度 ,而 v 2则是绕圆筒壁作水平圆周运动的分速度,此中向心力由筒壁对演员的支持力F N 的水平重量 F N2 供给 ,而竖直重量 F N1则与重力相均衡.如图 (c) 所示 ,此中 φ角为摩托车与筒壁所夹角.运用牛顿定律即可求得筒壁支持力 的大小和方向解 设杂技演员连同摩托车整体为研究对象 ,据 (b)(c)两图应有FN1mg 0(1) F N 2m v 2(2)Rv 2vcos θ v2πR(3)R 2 h 22πF NF N 21 F N 2 2(4)以式 (3) 代入式 (2),得22 22 2m4π R v4π RmF N 222222v2(5)RhR 4πRh 4π将式 (1) 和式 (5)代入式 (4),可求出圆筒壁对杂技演员的作使劲( 即支承力 )大小为2222224πRF NFN1F N 2 m g2 2 v2h4πR与壁的夹角 φ为FN 222arctan4πRv2arctan2 2FN 14πRh g议论 表演飞车走壁时 , 演员一定控制好运动速度,行车路线以及摩托车的方向 ,以保证三者之间知足解题用到的各个力学规律.2 -13 一质点沿 x 轴运动 ,其受力如下图 ,设 t = 0 时 ,v 0= 5m ·s-1,x 0= 2 m, 质点质量 m = 1kg, 试求该 质点 7s末的速度和地点坐标.剖析 第一应由题图求得两个时间段的 F(t)函数 ,从而求得相应的加快度函数,运用积分方法求解题目所问 ,积分时应注意积分上下限的取值应与两时间段相应的时辰相对应. 解 由题图得F t2t, 0 t 5s 35 5t,5s t 7s由牛顿定律可得两时间段质点的加快度分别为a 2t , 0 t 5sa 35 5t , 5s t 7s对 0 < t < 5s 时间段 ,由 adv 得dtvd tv 0 adtv积分后得 v 5 t 2再由 vdx 得dtxt dxvdtx 0积分后得 x 2 5t1 t 33将 t = 5s 代入 ,得 v 5= 30 m ·s-1 和 x 5 = 68.7 m 对 5s< t <7s 时间段 ,用相同方法有vtdva 2dtv 0 5 s得v 35t2xt再由dx vdtx5 5 s得x =23 -82.5t +将 t =7s代入分别得 v 7= 40 m ·s -1 和 x 7 = 142 m2 -14 一质量为 10 kg 的质点在力 F 的作用下沿 x 轴作直线运动 ,已知 F =120t + 40,式中 F 的单位为 N, t 的单位的s.在 t = 0 时 ,质点位于 x =5.0 m 处 ,其速度 v 0 =6.0 m ·s-1 .求质点在随意时辰的速度和地点.剖析 这是在变力作用下的动力学识题. 因为力是时间的函数 ,而加快度 a = dv/dt,这时 ,动力学方程就成为速度对时间的一阶微分方程 ,解此微分方程可得质点的速度v (t);由速度的定义 v =dx /d t,用积分的方法可求出质点的地点.解 因加快度 a = dv/dt,在直线运动中 ,依据牛顿运动定律有120t40m dvdt依照质点运动的初始条件 ,即t 0 = 0 时 v 0 = 6.0 m s·-1 ,运用分别变量法对上式积分,得vt4.0 dtdv 0 vv =2又因 v = dx /dt,并由质点运动的初始条件: t 0 = 0 时 x 0 = 5.0 m,对上式分别变量后积分 ,有xt6.0t 2dtdxx 0x =2 +2.0 t 32 -15 轻型飞机连同驾驶员总质量为10×3 kg .飞机以 55.0 m s·-1 的速率在水平跑道上着陆后,驾驶员开始制动 ,若阻力与时间成正比 ,比率系数 α= 5.0 ×102 N ·s -1,空气对飞机升力不计 ,求: (1) 10 s后飞机的速率; (2) 飞机着陆后 10s内滑行的距离.剖析 飞机连同驾驶员在水平跑道上运动可视为质点作直线运动. 其水平方向所受制动力 F 为变力 ,且是时间的函数.在求速率和距离时,可依据动力学方程和运动学规律,采纳分别变量法求解.解 以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有 Fma mdvαtαt dtdtvdt vmv 0得v v 0α t 22m所以 ,飞机着陆 10s后的速率为v = 30 m s· -1xt α t 2 dt又dxv 0x02m故飞机着陆后 10s内所滑行的距离s x x 0 v 0tα t 3 467 m6m2 -16 质量为 m 的跳水运动员 ,从 10.0 m 高台上由静止跳下落入水中.高台距水面距离为 h .把跳水运动员视为质点 ,并略去空气阻力.运动员入水后垂直下沉,水对其阻力为 bv 2 ,此中 b 为一常量.若以水面上一点为坐标原点O,竖直向下为Oy轴,求: (1)运动员在水中的速率v 与 y的函数关系;(2) 如 b/m=-1 , 跳水运动员在水中下沉多少距离才能使其速率v 减少到落水速率v 0的1 /10?(假设跳水运动员在水中的浮力与所受的重力大小恰巧相等)剖析该题能够分为两个过程,入水前是自由落体运动,入水后 ,物体受重力 P、浮力 F 和水的阻力 F f的作用 ,其协力是一变力 ,所以 ,物体作变加快运动.固然物体的受力剖析比较简单 ,可是 ,因为变力是速度的函数(在有些问题中变力是时间、地点的函数 ),对这种问题列出动力学方程其实不复杂 ,但要从它计算出物体运动的地点和速度就比较困难了.往常需要采纳积分的方法去解所列出的微分方程.这也成认识题过程中的难点.在解方程的过程中 ,特别需要注意到积分变量的一致和初始条件确实定.解 (1) 运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P -F f-F =ma由题意 P = F、 F f= bv2 ,而a = dv /dt = v (d v /dy),代入上式后得-bv2= mv (d v /dy)考虑到初始条件 y0=0 时 , v0 2gh ,对上式积分,有mv dvtdy0b v0 vv v0e by / m 2ghe by / m(2) 将已知条件 b/m = 0.4 m -1 ,v =0 代入上式 ,则得y m ln v 5.76 mb v0*2 -17 直升飞机的螺旋桨由两个对称的叶片构成.每一叶片的质量m= 136 kg,长 l = 3.66 m.求当它的转速 n= 320 r/min 时 ,两个叶片根部的张力.(设叶片是宽度必定、厚度平均的薄片)剖析 螺旋桨旋转时 ,叶片上各点的加快度不一样,在其各部分双侧的张力也不一样;因为叶片的质量是连续散布的 ,在求叶片根部的张力时 ,可选用叶片上一小段 ,剖析其受力 ,列出动力学方程 ,而后采纳积分的方法求解.解 设叶片根部为原点 O,沿叶片背叛原点 O 的方向为正向 ,距原点 O 为 r 处的长为 dr 一小段叶片 ,其 双侧对它的拉力分别为 F T(r) 与 F T (r + dr ).叶片转动时 ,该小段叶片作圆周运动 ,由牛顿定律有dF T F T rF T r drmω2 rdrl因为 r =l 时外侧 F T = 0,所以有t dF Tlm ω2F T rl r drrF T m ω2 2r 22πmn 22r 2rll2ll上式中取 r =0,即得叶片根部的张力F T 0 =10×5 N负号表示张力方向与坐标方向相反.2 -18 一质量为 m 的小球最先位于如图 (a)所示的 A 点 ,而后沿半径为 r 的圆滑圆轨道 ADCB 下滑.试求小球抵达点 C 时的角速度和对圆轨道的作使劲.剖析 该题可由牛顿第二定律求解. 在取自然坐标的状况下 ,沿圆弧方向的加快度就是切向加快度a ,t与其相对应的外力 F 是重力的切向重量 mgsin α,而与法向加快度 a n 相对应的外力是支持力 F N 和重力t的法向重量 mgcos α.由此 ,可分别列出切向和法向的动力学方程F = mdv/dt 和F n =ma n .因为小球在t滑动过程中加快度不是恒定的 ,所以 ,需应用积分求解 ,为使运算简易 ,可变换积分变量. 倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度 ,方法比较简易.但它不可以直接给出小球与圆弧表面之间的作使劲.解 小球在运动过程中遇到重力 P 和圆轨道对它的支持力 F N .取图 (b) 所示的自然坐标系,由牛顿定律得F tmgsin α mdv(1)dtF n F Nmgcos α mmv 2(2)R由 vdsr α r α运动到点 C 的始末条件 ,进行积分 ,有d ,得 dtd ,代入式 (1),并依据小球从点 Adtdtvvαv 0d90org sin αd αv v得v2rgcos α则小球在点 C 的角速度为ωv2 cos α/rr g由式 (2)得F Nm mv 2 mgcos α 3mgcos αr由此可得小球对圆轨道的作使劲为F NF N 3mgcos α负号表示 F ′N 与 e n 反向.2 -19 圆滑的水平桌面上搁置一半径为 R 的固定圆环 ,物体紧贴环的内侧作圆周运动 ,其摩擦因数为μ,开始时物体的速率为 v 0 ,求: (1) t 时辰物体的速率; (2) 当物体速率从 v 0减少到 12 v 0时 ,物体所经历的时间及经过的行程.剖析运动学与动力学之间的联系是以加快度为桥梁的,因此 ,可先剖析动力学识题.物体在作圆周运动的过程中,促进其运动状态发生变化的是圆环内侧对物体的支持力 F N和环与物体之间的摩擦力 F f,而摩擦力大小与正压力 F N′成正比 ,且F N与F N′又是作使劲与反作使劲 ,这样 ,便可经过它们把切向和法向两个加快度联系起来了 ,从而可用运动学的积分关系式求解速率和行程.解 (1) 设物体质量为 m,取图中所示的自然坐标 ,按牛顿定律 ,有mv2F N ma nRdvF f ma tdt由剖析中可知,摩擦力的大小 Ff=μF ,由上述各式可得N2μv dvR dt取初始条件 t =0 时 v =v 0 ,并对上式进行积分,有t R v dvdt20 μ v0 vv Rv0R v0μt(2)当物体的速率从 v 0减少到 1/2v 0时 ,由上式可得所需的时间为tRμv0物体在这段时间内所经过的行程t stRv0dt vdtv0μt0 RsRln 2μ2 -20 质量为 45.0 kg 的物体 ,由地面以初速 60.0 m·s-1 竖直向上发射 ,物体遇到空气的阻力为 F r=kv, 且 k = 0.03 N/( m-1最大高度为多少?s· ). (1) 求物体发射到最大高度所需的时间.(2)剖析物体在发射过程中 ,同时遇到重力和空气阻力的作用,其协力是速率v 的一次函数 ,动力学方程是速率的一阶微分方程,求解时 ,只需采纳分别变量的数学方法即可.可是,在求解高度时 ,则一定将时间变量经过速度定义式变换为地点变量后求解 ,并注意到物体上涨至最大高度时 ,速率应为零.解 (1) 物体在空中受重力 mg 和空气阻力 F r = kv 作用而减速.由牛顿定律得mg k mdv(1)vdt依据始末条件对上式积分,有t vddtmvvv 0mg kvtmln 1 kv 06.11 skmgdv dv(2) 利用v 的关系代入式 (1),可得dtdydvmg kv mv分别变量后积分y 0dyv 0mvdvmgkv故m mg ln 1kv 0 v 0183 mykmgkv 0 和 y 2议论 如不考虑空气阻力 ,则物体向上作匀减速运动.由公式tv 0 分别算得 t ≈s和g2gy ≈184 m,均比实质值略大一些.2 -21 一物体自地球表面以速率 v 0 竖直上抛.假设空气对物体阻力的值为F r = kmv 2 ,此中 m 为物体的质量 ,k 为常量.试求: (1) 该物体能上涨的高度; (2)物体返回地面时速度的值. (设重力加快度为常量. )剖析因为空气对物体的阻力一直与物体运动的方向相反 ,所以 ,物体在上抛过程中所受重力 P 和阻力 F r 的方向相同;而下落过程中 ,所受重力 P 和阻力 Fr 的方向则相反.又因阻力是变力 ,在解动力学方程时 ,需用积分的方法.解 分别对物体上抛、 下落时作受力剖析 ,以地面为原点 ,竖直向上为 y 轴 (如下图 ) .(1) 物体在上抛过程中 ,依据牛顿定律有mg km 2 m dv m vdvv dt dy 依照初始条件对上式积分,有y 0 v ddy v2v0 g kvy 1ln g kv 2 2k g kv02物体抵达最高处时, v = 0,故有hymax 1 ln g kv 022k g (2)物体下落过程中 ,有2vdvmg kmv m对上式积分 ,有ydy 0vdv0 v0 g k2vkv 2 1/ 2v则v0 1g2 -22 质量为 m 的摩托车 ,在恒定的牵引力 F 的作用下工作 ,它所受的阻力与其速率的平方成正比,它能达到的最大速率是 v m.试计算从静止加快到mv /2所需的时间以及所走过的行程.剖析该题依旧是运用动力学方程求解变力作用下的速度和地点的问题,求解方法与前两题相像,只是在解题过程中一定想法求出阻力系数k.因为阻力 Fr = kv2 ,且 F r又与恒力 F 的方向相反;故当阻力随速度增加至与恒力大小相等时,加快度为零 ,此时速度达到最大.所以,依据速度最大值可求出阻力系数来.但在求摩托车所走行程时,需对变量作变换.解设摩托车沿 x 轴正方向运动 ,在牵引力 F 和阻力 F r同时作用下 ,由牛顿定律有F k 2 m dv(1)v dt当加快度 a = dv/dt = 0 时,摩托车的速率最大,所以可得k=F/v m2 (2) 由式 (1) 和式 (2)可得依据始末条件对式(3)积分 ,有t mdtFF 1 v 2 m dv (3)v m2 dt1v m v2 12 dv1 2v m则tmv m ln3 dvmvdv 2F(3)积分 ,有又因式 (3) 中 m,再利用始末条件对式dtdxxmdxF 1v m v212 dv0 12v m则xmv m2ln40.144 mv m 22F3F*2 -23 飞机下降时 ,以 v 0 的水平速度下落伍自由滑行,滑行时期飞机遇到的空气阻力 F 1= -k 1 v 2, 升力F 2= k 2 v 2, 此中 v 为飞机的滑行速度 ,两个系数之比 k 1/ k 2 称为飞机的升阻比.实验表示,物体在流体中运动时 ,所受阻力与速度的关系与多种要素有关 ,如速度大小、流体性质、物体形状等.在速度较小或流体密度较小时有 F ∝ v,而在速度较大或流体密度较大的有 F ∝ v 2 ,需要精准计算时则应由实验测定.此题中因为飞机速率较大,故取 F ∝v 2 作为计算依照.设飞机与跑道间的滑动摩擦因数为μ,试求飞机从触地到静止所滑行的距离.以上计算实质上已成为飞机跑道长度设计的依照之一.剖析 如下图 ,飞机触地后滑行时期遇到 5 个力作用 ,此中 F 1 为空气阻力 , F 2 为空气升力 , F 3 为跑道作用于飞机的摩擦力 , 很明显飞机是在合外力为变力的状况下作减速运动 ,列出牛顿第二定律方程 后 ,用运动学第二类问题的有关规律解题.因为作用于飞机的合外力为速度 v 的函数 ,所求的又是飞机 滑行距离 x,所以比较简易方法是直接对牛顿第二定律方程中的积分变量dt 进行代换 ,将 dt 用dx取代 ,获得一个有关 v 和 x 的微分方程 ,分别变量后再作积分.v解 取飞机滑行方向为 x 的正方向 ,着陆点为坐标原点,如下图 ,依据牛顿第二定律有F N k 1v 2m dv(1)k 2v 2dtF Nmg 0(2)将式 (2)代入式 (1),并整理得μmg k μkv 2m dvm dv12dt v dx分别变量并积分 ,有vm dvv2dxμmgk 1 μk 2v 0v得飞机滑行距离xm ln μmg k 1 μk 2 v 2(3)2 k 1 μk 2 μmg考虑飞机着陆瞬时有 F N = 0 和v = v 0 ,应有 k 2v 02= mg,将其代入 (3)式 ,可得飞机滑行距离 x 的另一表达。
物理选修2-1第一章第一节知识点归纳
第一章静电场1.电荷及其守恒定律:一.电荷:电荷是一种物质属性。
(1)自然界只有正,负两种电荷:正电荷:与丝绸摩擦过的玻璃棒所带的电荷同种的电荷。
带负电带正电负电荷:与毛皮摩擦过的橡胶棒所带的电荷同种的电荷。
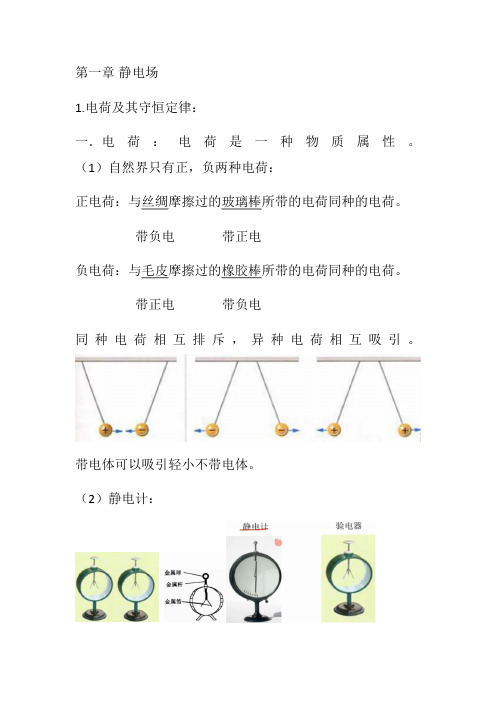
带正电带负电同种电荷相互排斥,异种电荷相互吸引。
带电体可以吸引轻小不带电体。
(2)静电计:工作原理:二.起电的方法:(1)原子:原子的构成:稳定原因:质子和中子之间有强相互作用。
(核力)核外电子在原子核的吸引力作用下维系在原子核附近。
金属导体内部特征:每个正离子都在自己的平衡位置附近振动而不移动。
金属内有自由移动的电子。
(自由电子)绝缘体(电介质):电子不能自由移动,被牢牢地束缚在原子核周围。
(玻璃,橡胶)(2)摩擦起电:实质:摩擦时电子从一个物体转移到另一个物体上。
得到电子的物体:带负电。
失去电子的物体:带正电。
(3)感应起电:利用静电感应使物体带电。
静电感应:把电荷移近不带电的导体,可以使导体带电的现象,叫静电感应。
归律:近端感应异种电荷,远端感应同种荷。
(4)接触带电:两个完全相同的带电导体,接触后再分开,二者将原来所带电量的代数和平均分配。
(5)起电的本质:无论是哪种起电方式,其本质都是将正负电荷分开,使电荷发生转移,并不是创造电荷。
三.电荷守恒定律:表述一:电荷既不能创造,也不能消灭,它只能从一个物体转移到另一个物体,或从物体的一部分转移到另一部分,在转移的过程中,系统的电荷总数保持不变。
在一定条件下,带电粒子可以产生和湮灭。
带电粒子总是成对产生和湮灭,两个粒子带电数量相等但正负相反,电荷的代数和不变。
表述二:一个与外界没有电荷交换的系统,电荷的代数和总是保持不变的。
(1)表示电荷多少的物理量:电荷量(电量)单位:库伦(c )比较电荷带电的多少,要比较的使其电荷量的绝对值。
电荷量的正负不表示电荷量的大小,只代表电荷的性质。
(2)元电荷:最小的电荷量是电子(或质子,正电子)所带的电荷量。
《大学物理1-2》知识点小结

《大学物理1-2》知识点小结
电磁学
一、静电场
1、高斯定理求场强和电通量
1)具有球对称的均匀带电球壳、球体,高斯面:球面
2)具有柱对称的无限长带电细棒,高斯面:柱面
2、电势
1)点电荷的电势(多个电荷存在时要考虑电势的叠加)
2)电场力做功和电势的关系
二、静磁场
1、安培环路定理求磁感应强度B
无限长载流导线或载流导体的磁感应强度;同轴电缆的磁感应强度(见书上相应的作业)
2、磁通的计算
3、安培定理:会判断安培力的方向,安培力简单的计算
三、电磁感应
1、法拉第电磁感应定律的应用(感应电动势大小、方向的确定)(基本公式)
或:
2、动生电动势的计算
光学
1、干涉
1)杨氏双缝干涉的计算,重点记住相邻明纹中心或暗纹中心的间距公式
2)光程或光程差的计算
3)劈尖干涉(空气膜、垂直入射):
4)单缝衍射:基本公式(暗纹条件)的应用:如求缝宽、半波带的划分、光程差和相位差的关系、中央明纹的线宽等
5)光栅衍射:缺级的计算
6)马吕斯定律的应用
7)布儒斯特定律(光线以布儒斯特入射时反射光、折射光的特点,入射角和折射角之间的关系)
相对论与量子物理
1、相对论:狭义相对论的两条基本原理、同时性的相对性的简单计算、爱因斯坦质能方程的简单计算。
(见课后选择、填空的相应习题,掌握方法)
2、量子物理:爱因斯坦的光电效应方程(见课后选择、填空的相应习题,掌握方法)。
大学物理2复习总结

大学物理2复习总结一、知识点回顾大学物理2是物理学的一个重要分支,它涵盖了力学、电磁学、光学、热学等多个方面的知识。
在复习过程中,我首先对各个知识点进行了回顾,包括:牛顿运动定律、动量守恒定律、能量守恒定律、电场强度、电势、磁场、光的干涉和衍射、波动等。
通过对这些知识点的复习,我巩固了基础,为后续的解题打下了坚实的基础。
二、重点难点解析在复习过程中,我发现有一些知识点是特别重要的,也是我在学习中遇到的难点。
比如,牛顿运动定律的综合应用、电磁场的理解、光的干涉和衍射的原理和计算等。
对于这些重点难点,我进行了深入的分析和理解,通过大量的例题和练习题来加深对这些知识点的理解和掌握。
三、解题方法总结大学物理2的解题方法非常重要,掌握了解题方法,才能更好地解决各种问题。
在复习过程中,我总结了一些常用的解题方法,如:牛顿运动定律的矢量表示、动量守恒定律的代数表示、能量守恒定律的综合应用、电场强度的计算、电势的计算、磁场的计算、光的干涉和衍射的计算等。
通过这些方法的掌握,我能够更好地解决各种问题。
四、错题总结与反思在复习过程中,我发现自己在一些问题上容易出错,比如:对牛顿运动定律的理解不够深入、对电磁场的理解不够准确、对光的干涉和衍射的计算不够熟练等。
对于这些问题,我进行了总结和反思,分析了出错的原因,并通过大量的练习来避免类似的错误再次发生。
五、知识框架构建在复习结束后,我构建了大学物理2的知识框架,将各个知识点有机地在一起。
通过这个知识框架,我能够更好地理解和掌握大学物理2的知识点,也能够更好地应用这些知识点解决实际问题。
六、备考策略优化在备考过程中,我还优化了自己的备考策略。
我制定了详细的复习计划,将每个知识点都安排在合理的复习时间内。
我注重了课堂听讲和笔记整理的结合,确保自己对每个知识点都有深入的理解。
我注重了练习和反思的结合,通过大量的练习来提高自己的解题能力,同时不断反思自己的解题方法和思路。
通过这次复习总结,我对大学物理2有了更深入的理解和掌握,同时也提高了自己的解题能力和思维能力。
大学物理2复习资料

大学物理2复习资料大学物理2是物理系及相关专业中的重要课程,它主要涉及电磁学、光学和热学三大方面。
这门课程不仅重要,难度也不小,需要大量的复习资料作为支撑。
本文就来给大家分享一些适合复习大学物理2的资料。
1. 课本大学物理2的课本是我们学习的主要教材,原理深入浅出,内容全面。
建议大家通过阅读课本,对知识点进行理解和记忆,加深对物理概念的理解。
同时,也可以参考课本上的案例和例题,巩固自己的应用能力。
2. 讲义讲义是教授在课上授课时所使用的笔记,一般会对重点知识点进行讲解和解释。
由于讲义是教授精心制作的,因此一些细节和重点都会被深入阐述。
复习时,我们可以通过阅读讲义,巩固自己对知识点的理解,并做好笔记。
同时,也可以针对不懂的问题向教授请教,加深理解。
3. 习题集习题集是我们巩固知识点的重要方式之一。
通过做习题,我们可以深入理解并掌握课本和讲义中的知识点。
在背诵公式的同时,练习能够让我们了解公式的运用,帮助我们更好地解决问题。
建议大家选择习题难度适中的题目,做到掌握基础知识和能力的同时,也可以探索一些难点。
4. 复习资料除了课本、讲义和习题集外,我们还可以通过一些复习资料来巩固知识点。
例如一些复习笔记、学生整理的课堂笔记、老师提供的有关资料等等。
这些资料可能会对我们难以理解的知识点有很大的帮助。
一些基础知识比较薄弱的同学可以先通过相关的资料进行复习,在知识点掌握的基础上再去加深理解。
5. 思维导图对于复杂的知识点,我们可以试着制作一些思维导图,将知识点分门别类地进行整理。
思维导图可以帮助我们对知识点有一个整体的观念,并方便我们找到相关的知识点和公式。
同时,在制作思维导图的过程中,也可以帮助我们加深对知识点的理解,达到熟练掌握的效果。
总的来说,要想复习好大学物理2,就需要充分利用各种复习资料。
在复习中,我们需要注重理解和记忆,同时也需要强化应用能力。
希望本文能够帮助大家更好地复习大学物理2,取得更好的成绩。
(完整版)大学物理知识点、重点、难点

《大学物理》(上) 知识点、重点及难点 质 点 运 动 学知识点:1. 参考系为了确定物体的位置而选作参考的物体称为参考系。
要作定量描述,还应在参考系上建立坐标系。
2. 位置矢量与运动方程 位置矢量(位矢):是从坐标原点引向质点所在的有向线段,用矢量r 表示。
位矢用于确定质点在空间的位置。
位矢与时间t 的函数关系:k ˆ)t (z j ˆ)t (y iˆ)t (x )t (r r ++==ϖϖ称为运动方程。
位移矢量:是质点在时间△t内的位置改变,即位移:)t (r )t t (r r ϖϖϖ-+=∆∆轨道方程:质点运动轨迹的曲线方程。
3. 速度与加速度平均速度定义为单位时间内的位移,即:t r v ∆∆ϖϖ=速度,是质点位矢对时间的变化率:dtrd v ϖϖ=平均速率定义为单位时间内的路程:ts v ∆∆=速率,是质点路程对时间的变化率:dsdtυ=加速度,是质点速度对时间的变化率:dtvd a ϖϖ=4. 法向加速度与切向加速度加速度 τˆa n ˆa dt vd a t n +==ϖϖ 法向加速度ρ=2n v a ,方向沿半径指向曲率中心(圆心),反映速度方向的变化。
切向加速度dtdva t =,方向沿轨道切线,反映速度大小的变化。
在圆周运动中,角量定义如下:角速度 dt d θ=ω 角加速度 dtd ω=β 而R v ω=,22n R R v a ω==,β==R dtdv a t 5. 相对运动对于两个相互作平动的参考系,有'kk 'pk pk r r r ϖϖϖ+=,'kk 'pk pk v v v ϖϖϖ+=,'kk 'pk pk a a a ϖϖϖ+=重点:1. 掌握位置矢量、位移、速度、加速度、角速度、角加速度等描述质点运动和运动变化的物理量,明确它们的相对性、瞬时性和矢量性。
2. 确切理解法向加速度和切向加速度的物理意义;掌握圆周运动的角量和线量的关系,并能灵活运用计算问题。
大学物理上复习资料

大学物理上复习资料在大学物理学习中,复习资料是不可或缺的重要元素。
不同于初中、高中时期的课程,大学物理更注重深度和实践性,需要我们充分掌握基础知识,并能够熟练运用于实际问题的解决。
以下是针对大学物理复习的一些建议和资料推荐。
1. 基础知识总结在大学物理学习中,不可避免地会遇到大量的公式和概念。
为了更好地理解和掌握这些知识,我们可以制作一份基础知识总结的笔记。
这份笔记需要涵盖大学物理的基本概念、定律和公式,帮助我们快速回忆课程内容,为后续学习提供便利。
2. 经典题目选解大学物理的复习过程中,练习题是必不可少的。
然而,由于时间和精力的限制,我们可能无法做完所有的题目。
因此,需要针对性地挑选一些经典的题目来进行练习。
这些题目可以覆盖大学物理学习的重点知识点,对于深入理解课程内容和提高解题能力都非常有帮助。
3. 近年考试真题为了更好地了解大学物理考试的出题方向和考察内容,我们可以查找近年来的考试真题进行复习。
这些真题可以帮助我们熟悉考试的难度和形式,从而更好地调整备考策略和心理状态,提高应试能力。
4. 视频教程和课件除了传统的纸质资料外,现代科技的发展也为我们提供了更加丰富的学习资源。
在大学物理学习中,我们可以利用网络上的视频教程和课件来辅助学习。
这些资料通常生动形象,讲解清晰,可以更好地帮助我们理解和掌握课程内容。
5. 交流和讨论在学习的过程中,与同学和老师的交流和讨论也是非常重要的。
通过交流和讨论,我们可以更好地理解和消化课程内容,发现存在的问题并加以解决。
同时,听取他人的想法和见解,也可以帮助我们更好地拓展思路和提高解题能力。
大学物理复习资料的选择和使用需要因人而异,因为每个人的学习风格和需求都不同。
然而,细心地、有序地、有计划地利用各类复习资料,对于高效、系统地进行大学物理复习,是非常有益的。
希望以上建议和资料推荐能够帮助到大家,祝大家在复习和考试中取得好成绩!。
大学物理2-1上册复习课件

x x 'yy 'z z 'O O'S S 'u∙P ),,(),,(z y x z y x '''第一章 质点运动学 1.描述运动的主要物理量位置矢量: 位移矢量: 速度矢量:加速度矢量: 速度的大小: 加速度的大小: 2.平面曲线运动的描述切向加速度: 法相加速度: (圆周运动半径为R ,则a n = ) 3.圆周运动的角量描述角位置: 角速度: 角加速度: 圆周运动的运动方程: 4.匀角加速运动角量间的关系ω= θ=5.角量与线量间的关系ΔS= V= a t = a n = 6.运动的相对性速度相加原理: 加速度相加关系:7. 以初速度v 0由地面竖直向上抛出一个质量为m 的小球,若上抛小球受到与其瞬时速率成正比的空气阻力,求小球能升达的最大高度是多大?8.一飞轮以n =1500r/min 的转速转动,受到制动而均匀地减速,经t =50s 后静止。
(1)求角加速度β和从制动开始到静止时飞轮的转数N 为多少? (2)求制动开始t =25s 时飞轮的角速度ω(3)设飞轮的半径R =1m 时,求t =25s 时,飞轮边缘上一点的速度、切向加速度和法向加速度9.一带蓬卡车高h =2m ,它停在马路上时雨点可落在车内到达蓬后沿前方d =1m 处,当它以15 km/h 速率沿平直马路行驶时,雨滴恰好不能落入车内,求雨滴相对地面的速度及雨滴相对车的速度。
第二章 牛顿运动定律 1.经典力学的时空观(1) (2) (3) 2.伽利略变换 (Galilean transformation ) (1)伽利略坐标变换X ’= Y ’= Z ’= t ’=(2)伽利略速度变换V ’= (3)加速度变换关系 a ’=3.光滑桌面上放置一固定圆环,半径为R ,一物体贴着环带内侧运动,如图所示。
物体与环带间的滑动摩擦系数为μ。
设在某一时刻质点经A 点时的速度为v 0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x x 'yy 'z z 'O O'S S 'u•P ),,(),,(z y x z y x '''第一章 质点运动学 1.描述运动的主要物理量位置矢量: 位移矢量: 速度矢量:加速度矢量: 速度的大小: 加速度的大小: 2.平面曲线运动的描述切向加速度: 法相加速度: (圆周运动半径为R ,则a n = ) 3.圆周运动的角量描述角位置: 角速度: 角加速度: 圆周运动的运动方程: 4.匀角加速运动角量间的关系ω= θ=5.角量与线量间的关系ΔS= V= a t = a n = 6.运动的相对性速度相加原理: 加速度相加关系:7. 以初速度v 0由地面竖直向上抛出一个质量为m 的小球,若上抛小球受到与其瞬时速率成正比的空气阻力,求小球能升达的最大高度是多大?8.一飞轮以n =1500r/min 的转速转动,受到制动而均匀地减速,经t =50s 后静止。
(1)求角加速度β和从制动开始到静止时飞轮的转数N 为多少? (2)求制动开始t =25s 时飞轮的角速度ω(3)设飞轮的半径R =1m 时,求t =25s 时,飞轮边缘上一点的速度、切向加速度和法向加速度9.一带蓬卡车高h =2m ,它停在马路上时雨点可落在车内到达蓬后沿前方d =1m 处,当它以15 km/h 速率沿平直马路行驶时,雨滴恰好不能落入车内,求雨滴相对地面的速度及雨滴相对车的速度。
第二章 牛顿运动定律 1.经典力学的时空观(1) (2) (3) 2.伽利略变换 (Galilean transformation ) (1)伽利略坐标变换X ’= Y ’= Z ’= t ’=(2)伽利略速度变换V ’= (3)加速度变换关系 a ’=3.光滑桌面上放置一固定圆环,半径为R ,一物体贴着环带内侧运动,如图所示。
物体与环带间的滑动摩擦系数为μ。
设在某一时刻质点经A 点时的速度为v 0 。
求此后t 时刻物体的速率和从A 点开始所经过的路程。
4.一个小球在粘滞性液体中下沉,已知小球的质量为 m ,液体对小球的有浮力为 ,阻力为 。
若t = 0时 ,小球的速率为v 0,试求小球在粘滞性液体中下沉的速率随时间的变化规律。
Fv k f -=vB v A α5.一条长为l 质量均匀分布的细链条AB ,挂在半径可忽略的光滑钉子上,开始处于静止状态。
已知BC 段长为 ,释放后链条作加速运动,如图所示。
试求 时,链条的加速度和速度。
第三章 功和能 1.元功: 总功:弹簧弹力的元功: 重力的元功: 万有引力的元功: 摩擦力的元功:2.保守力: 做功只与始末位置 ,而与路径 的力。
非保守力:做功不仅与始末位置 ,而且与路径 的力 。
3.势能: 势能差:4.质点系的动能定理 :5.质点系的功能原理 :6.机械能守恒定律 :7.质量为m 、线长为l 的单摆,可绕o 点在竖直平面内摆动。
初始时刻摆线被拉至水平,然后自由放下,求摆线与水平线成θ角时,摆球的速率和线中的张力。
8.在光滑的水平桌面上平放有半圆形屏障。
质量为m 的滑块以速度v 0 沿切线方向进入屏障内,滑块与屏障间的摩擦系数为μ,试证明:当滑块从屏障的另一端滑出时,摩擦力所作的功为: 9.物体mA 和mB 通过一不能伸缩的细绳相连,mA 由静止下滑,mB 上升,mA 滑过S 的距离时, mA 和mB 的速率v = ? (摩擦力及滑轮的质量不计)。
第四章 动量和角动量 1.质点的动量定理动量定理的微分式: 动量定理的积分式: 2.质点系的动力学方程: 3.质点系的动量定理: 4.质心运动定理: 5.质点及质点系的角动量:6.质点及质点系的角动量定理:7.质点及质点系的角动量守恒定律:32/l BC =)/l L /l (L 322<<)1(21220--πμe mv8.质量为M,仰角为α的炮车发射了一枚质量为m的炮弹,炮弹发射时相对炮身的速率为u,不计摩擦,求∶(1)炮弹出口时炮车的速率;(2)发射炮弹过程中,炮车移动的距离(炮身长为L)。
9.光滑水平面与半径为R的竖直光滑半圆环轨道相接,两滑块A,B的质量均为m,弹簧的倔强系数为k,其一端固定在O点,另一端与滑块A接触,开始时滑块B静止于半圆环轨道的底端,今用外力推滑块A,使弹簧压缩一段距离x后再释放,滑块A脱离弹簧后与B作完全弹性碰撞,碰后B将沿半圆环轨道上升,升到C点与轨道脱离,O’C与竖直方向成α=60°,求弹簧被压缩的距离x.10.一长为L,密度分布不均匀的细棒,其质量线密度λ=λ0x/L.λ0为常量,x从轻端算起,求其质心。
11.质量为m、线长为l 的单摆,可绕点O 在竖直平面内摆动,初始时刻摆线被拉成水平,然后自由放下。
求: ①摆线与水平线成θ角时,摆球所受到的力矩及摆球对点O 的角动量;②摆球到达点B 时,角速度的大小。
12.我国在1971年发射的科学实验卫星在以地心为焦点的椭圆轨道上运行.已知卫星近地点的高度h1=226km,远地点的高度h2=1823km,卫星经过近地点时的速率v1=8.13km/s,试求卫星通过远地点时的速率和卫星运行周期(地球半径R=6.37×103km).13.两人质量相等,位于同一高度,各由绳子一端开始爬绳,绳子与轮的质量不计,轴无摩擦。
他们哪个先达顶?14.质量为m的小球A,以速度v0沿质量为M半径为R的地球表面切向水平向右飞出,地轴OO’与v0平行,小球A的运动轨道与轴OO’相交于点C,OC=3R,若不考虑地球的自转和空气阻力,求小球A在点C的速度与OO’轴之间的夹角θ。
15.质量分别为m和m′的两个小球,系于等长线上,构成连于同一悬挂点的单摆,如图所示。
将m拉至h高处,由静止释放。
在下列情况下,求两球上升的高度。
(1)碰撞是完全弹性的;(2)碰撞是完全非弹性的。
第五章刚体力学基础1.刚体定轴转动的角量描述角位置:角位移: 平均角速度:角速度:(矢量)角加速度:(矢量)2.角量与线量的关系:ΔS= V= a t= a n= a=3.转动惯量的计算:J= 平行轴定理:J=4.刚体的定轴转动定律:M=5.一般刚体动能:E k=6.力矩功的表达式:根据质点力学中功率的定义,力矩的功率可表示为:7.刚体的角动量原理:8.一细棒绕O 点自由转动,并知L 为棒长。
求: 1) 棒自水平静止开始运动,θ = π /3 时, 角速度ω ?2) 此时端点A 和中点B 的线速度为多大?9.一轻绳跨过一质量为m的定滑轮(视为半径为r 的薄圆盘)绳两端挂质量为m1和m2两物体,且m2>m1,滑轮轴间摩擦阻力矩为M f,绳与滑轮无相对滑动,求物体的加速度和绳中的张力。
10.质量为m 1、半径为R 的定滑轮可绕轴自由转动,一质量为m 2 的物体悬挂于绕过滑轮的细绳上。
求:物体m 2 的下落加速度a 和滑轮转动的角加速度β.11.一刚体由长为 l ,质量为m 的均匀细棒和质量为m的小球组成,且可绕O 轴在竖直平面内转动,且轴处无摩擦。
求: 1)刚体绕轴O 的转动惯量。
2)若棒自水平静止开始运动到棒与竖直方向成θ角时, 小球的角速度和法向加速度。
12.一恒力矩M作用于斜面顶点的滑轮上,滑轮的半径为r,质量为m1,质量为m2的重物通过一不可伸长的轻绳固定在轮的边缘,重物沿倾角为α的斜面上升.重物与斜面间的摩擦系数为μ。
求:轮子由静止开始转过角Δφ后获得多大的角速度?13.一长为l质量为m的匀质细棒,如图所示,可绕图中水平轴o在竖直面内旋转,若轴间光滑,今使棒从水平位置自由下摆。
求:(1)在水平位置和竖直位置棒的角加速度β(2)在竖直位置时棒的角速度ω、质心的速度和加速度各为多少?14.一质量为M半径为R的水平转台(可看作匀质圆盘)可绕通过中心的竖直光滑轴自由转动,一个质量为m的人站在转台边缘。
人和转台最初相对地面静止。
求当人在转台上边缘走一周时,人和转台相对地面各转过的角度是多少?第六章狭义相对论1.狭义相对论的两个基本假设:(1)(2)2.洛仑兹变换:3.相对论的速度变换式:4.狭义相对论的时空观一、同时的相对性(1).不同地事件的同时性是 (2).同地事件的同时性是(3).两个独立事件的时间次序是 (4).关联事件的时间次序是二、时间膨胀效应:三、长度收缩效应:5.相对论质量公式:相对论动能公式:爱因斯坦质能关系式:动量和能量的关系:6.甲、乙两人所乘飞行器沿x轴作相对运动,甲测得两事件的时空坐标为x1=6×104,y1=z1=0,t1=2×10-4s,x1=12×104, y2=z2=0,t2=1×10-4 s,。
如果乙测得这两个事件同时发生于t1时刻,问:(1)乙对于甲的运动速度是多少?(2)乙测得的两个事件的空间间隔是多少?7.在地面上测得有两个飞船分别以+0.9c和-0.9c的速度向相反方向飞行。
求一个飞船相对另一个飞船的速度是多大?8.北京和上海直线相距1000km,在某一时刻从两地同时各开出一列火车,现有一艘飞船沿北京到上海的方向在高空飞过,速率为u,若①u=9km/s,②u=0.999c,问在这两种情况下宇航员测得两列火车开出时刻的间隔是多少?那一列先开出?9.带电π介子静止时的平均寿命为2.6×10-8s,某加速器射出的带电π介子的速率为2.4×10 8 m/s,试求①在实验室中测得这种粒子的平均寿命;②这种π介子衰变前飞行的平均距离。
10.在S′系中有一根米尺与o'x'轴成30°角,且位于x'o'y′平面内,若要使这一米尺与S系中的ox 轴成45°角,①试问S′系应以多大的速率u 沿x 轴方向相对S系运动?②在S系中测得米尺的长度是多少?11.有一加速器将质子加速到76GeV的动能。
试求①加速后的质量;②加速后质子的速率。
12.两个静止质量都是m0的小球,其中一个静止,另一个以v=0.8c 运动。
在它们做对心碰撞后粘在一起,求碰撞后合成小球的静止质量。
第七章气体动理论1.理想气体的状态方程:2.理想气体的压强:3.理想气体的温度和平均平动动能:4.能量均分原理每一个自由度的平均动能为:一个分子的总平均动能为:摩尔理想气体内能:5.麦克斯韦速率分布函数:三种速率(1)最概然速率:(2)算术平均速率:(3)方均根速率:6.玻耳兹曼分布律重力场中粒子按高度的分布:大气压强随高度的变化:7.气体分子的平均碰撞频率和平均自由程平均碰撞频率:平均自由程:8.若气体分子的平均平动动能等于1eV(电子伏特),问气体的温度为多少?当温度为27ºC 时,气体分子的平均平动动能为多少?9.若某种气体在温度T1=300K时的方均根速率等于温度为T2时的平均速率,求T2=?10.有N个粒子,其速率分布函数为:(1)画出速率分布曲线;(2)由N和v0求常数c ;(3)求粒子的平均速率;(4)求粒子的方均根速率。
