初一上数学总复习
七年级上册数学总复习资料

七年级上册数学总复习资料1第一章有理数--------------1.1正数与负数①大于0的数叫正数。
②在正数前面加上“-”号的数,叫做负数。
③0既不是正数也不是负数。
0是正数和负数的分界,是的中性数。
④搞清相反意义的量:南北;东西;上下;左右;上升下降;高低;增长减少等。
⑤正整数、0、负整数统称整数(结合数轴和一元一次方程出题),正分数和负分数统称分数。
整数和分数统称有理数。
⑥非负数就是正数和零;非负整数就是正整数和0。
⑦“基准”题:有固定的基准数,和的求法:基准数×个数+与基准数相比较的数的代数和;平均数的求法:基准数+与基准数相比较的数的代数和÷个数(写出原数,也可用小学知识解答);“非基准”题:无固定的基准数,如明天和今天比,后天和明天比。
-------------1.2数轴①通常用一条直线上的点表示数,这条直线叫数轴。
②数轴三要素:原点、正方向、单位长度。
③数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴上的点,不都是表示有理数。
④只有符号不同的两个数叫做互为相反数(和为零)。
(例:2的相反数是-2,如:2+(-2)=0;0的相反数是0)⑤数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
从几何意义上讲,数的绝对值是两点间的距离(无方向性,有两个点)。
⑥数轴上两点间的距离=|M—N|⑥正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。
⑦两个负数,绝对值大的反而小。
⑧|a|≥0(即非负性);绝对值等于一个正数的值有两个(两个互为相反数)如:|a|=5,a=5或a=-5-------------1.3有理数的大小①数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大。
②负数小于零,零小于正数,负数小于正数。
③两个负数的比较大小,绝对值大的反而小。
-------------1.4有理数的加减法①有理数加法法则:1.同号两数相加,取相同的符号,并把绝对值相加。
七年级(上)数学期末总复习

等于20分钟的人数占总人数的40% 大于20分钟的人数占总人数的20% (3)老师随机地问一个同学,最可能得到 的答案是20分钟.
课后练习 一、填空题 1.数一数,在图中,共有_2_2_条线段.
2.如图 ( 1 ) 如 果 AD//BC , 那 么 根 据两__直__线__平__行__同__位__角__相__等__ ,
例6.下面是某班30学生每天上学单程所到时间(分钟)
(1)在这个统计表中,单程花_______分钟这一数 据的频数最大.
(2)若把这些数据分成小于20分钟,等于20分钟, 和大于20分钟这三档,则各档人数各占总人数的多少.
(3)Байду номын сангаас如老师随机地问一个同学,你认为老师最可 能得到的答案是几分钟
答:
(2)线段、射线、直线等简单平面图形的有关概念,特 征和表示法,三者的区别和联系,及线段中点概念,和进 行有关的简单计算.
(3)角的有关概念.表示法,度、分、秒、间的 换算及简单的计算.会比较角的大小及分类.
(4)平行线,相交线,了解了有关平行线垂线 的特征及识别.
4.数据的收集 通过解决简单的实际问题,体会大千世界的 不确定性,熟悉收集,整理数据,学会根据 不同问题选择适当统计图描述数据得到较明 显的结论,理解频数、频率,不可能发生, 可能发生和必然发生的概念.
二、典型例题分析 例1.把下面各数填入表示它所在数集里.
-3,11, 2 ,0,2003,0.414,-0.618,-7% 5
解:
例2.有理数a、b、c在数轴上的位置如图所示: 化简|a+b|-|c-b|
解:由a、b、c在数轴上所处的 位置可知:a<0、b>0、c<0, 且|a|<|b|<|c|.a+b>0,c-b<0 所以|a+b|=a+b,|c-b|=b-c. |a+b|-|c-b|=a+b-(b-c)=a+c.
初一上学期数学知识点总复习

初一上学期数学知识点总复习
1. 整数
- 正整数、零、负整数的概念
- 整数的加减法、乘除法
- 判断一个数的正负性
2. 分数
- 分数的概念和表示方法
- 分数的四则运算
- 分数与整数的相互转换
3. 小数
- 小数的概念和表示方法
- 小数的四则运算
- 小数与分数的相互转换
4. 百分数
- 百分数的概念和表示方法
- 百分数的换算
- 百分数与小数、分数的相互转换
5. 数据统计
- 数据的收集、整理和展示
- 平均数、中位数、众数的计算- 折线图、柱形图的绘制和分析
6. 几何图形
- 几何图形的概念和基本要素
- 直线、线段、射线的认识和绘制- 不同类型几何图形的性质和特点
7. 方程与不等式
- 方程的概念和解的意义
- 一元一次方程的解法
- 不等式的概念和解的意义
- 一元一次不等式的解法
8. 几何运动
- 直线运动与曲线运动的概念
- 单位速度、位移与时间的关系
- 运动图像的绘制和分析
9. 数据的处理
- 数据的分类和整理
- 求出简单统计指标
- 制作直方图和折线图
10. 三角形
- 三角形的概念和分类
- 三角形的性质和判定
- 三角形内角和外角的性质
以上是初一上学期数学的主要知识点总结,希望能对你的复有所帮助。
初一数学重难点总结复习

初一数学重难点总结复习初一数学重难点总结复习【4篇】复习总结还可以跨学科地进行,将不同学科的知识点联系起来,形成知识网络。
复习总结应该注重对自己的要求,不断提高自己的学术标准和道德水平。
下面就让小编给大家带来初一数学重难点总结复习,希望大家喜欢!初一数学重难点总结复习1(1)凡能写成形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a也不一定是正数;p不是有理数;(2)有理数的分类: ① 整数②分数(3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数 0和正整数;a0 a是正数;a0 a是负数;a≥0 a是正数或0 a是非负数;a≤ 0 a是负数或0 a是非正数.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 0,小数-大数 0.初一数学重难点总结复习2一、知识梳理知识点1:正、负数的概念:我们把像3、2、+0.5、0.03%这样的数叫做正数,它们都是比0大的数;像-3、-2、-0.5、-0.03%这样数叫做负数。
它们都是比0小的数。
0既不是正数也不是负数。
我们可以用正数与负数表示具有相反意义的量。
知识点2:有理数的概念和分类:整数和分数统称有理数。
有理数的分类主要有两种:注:有限小数和无限循环小数都可看作分数。
知识点3:数轴的概念:像下面这样规定了原点、正方向和单位长度的直线叫做数轴。
知识点4:绝对值的概念:(1)几何意义:数轴上表示a的点与原点的距离叫做数a的绝对值,记作|a|;(2)代数意义:一个正数的绝对值是它的本身;一个负数的绝对值是它的相反数;零的绝对值是零。
七年级上期数学期末总复习题
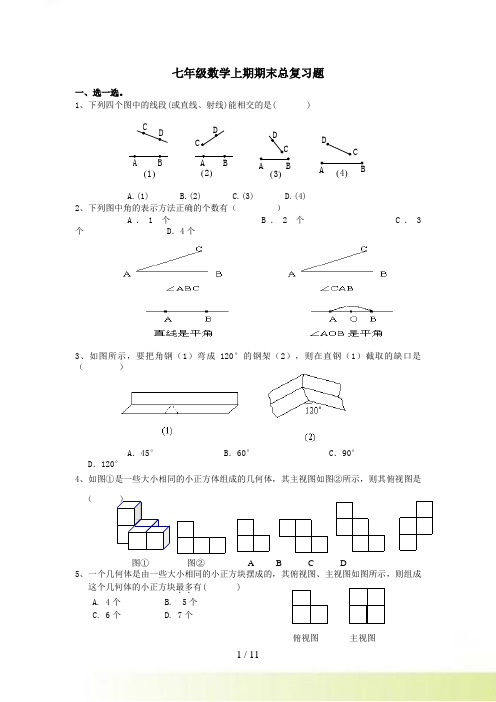
七年级数学上期期末总复习题一、选一选。
1、下列四个图中的线段(或直线、射线)能相交的是( )1()CDBA2()CD BA3()C D BA4()CDBAA.(1)B.(2)C.(3)D.(4) 2、下列图中角的表示方法正确的个数有( )A .1个B .2个C .3个 D .4个3、如图所示,要把角钢(1)弯成120°的钢架(2),则在直钢(1)截取的缺口是( )A .45°B .60°C .90°D .120°4、如图①是一些大小相同的小正方体组成的几何体,其主视图如图②所示,则其俯视图是( )5、一个几何体是由一些大小相同的小正方块摆成的,其俯视图、主视图如图所示,则组成这个几何体的小正方块最多..有( ) A. 4个 B. 5个 C. 6个 D. 7个图① 图② A B C D俯视图主视图6、已知线段AB=6厘米,在直线AB 上画线段AC=2厘米,则BC 的长是( ) A .8厘米 B .4厘米 C .8厘米或4厘米 D .不能确定7、如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是( )8、下列说法中正确的是( )A.若AP=21AB ,则P 是AB 的中点 B.若AB =2PB ,则P 是AB 的中点 C .若AP =PB ,则P 为AB 的中点 D.若AP =PB=21AB ,则P 是AB 的中点9、甲看乙的方向为北偏东30°,那么乙看甲的方向是( )A .南偏东60°B .南偏西60°C .南偏东30°D .南偏西30° 10、如右图,AB 、CD 交于点O ,∠AOE=90°,若∠AOC :∠COE=5:4,则∠AOD 等于 ( ) A .120° B .130°C .140°D .150°11、下列各组数中,不相等...的一组是 ( ) A .()23-与23- B .-23-与23- C . -33-与 33- D .()33- 与33-12、《广东省重点建设项目计划(草案)》显示,港珠澳大桥工程估算总726亿元,用科学记数法表示正确的是( ) A .107.2610⨯ 元 B .972.610⨯ 元 C .110.72610⨯ 元 D .117.2610⨯元 13、国家体育场“鸟巢”建筑面积达25.8万平方米,将25.8万平方米用科学记数法(四舍五入保留2个有效数字)表示约为( )A .42610⨯平方米B .42.610⨯平方米 C .52.610⨯平方米D .62.610⨯平方米14、如果ab <0,那么下列判断正确的是( ).A .a <0,b <0B . a >0,b >0C . a ≥0,b ≤0D . a <0,b >0或a >0,b <0 15、实数a ,b 在数轴上的对应点如图所示,则下列不等式中错误的是( ) A .0ab > B .0a b +< C .ba<0 D .0a b -< 16、下列运算正确的是( )A .b a b a --=--2)(2B .b a b a +-=--2)(2C .b a b a 22)(2--=--D .b a b a 22)(2+-=--17、已知一个多项式与239x x +的和等于2341x x +-,则这个多项式是( )ab 0A B C DA .51x --B .51x +C .131x --D .131x +18、下列变形中,正确的是( )A 、若ac=bc ,那么a=b 。
七年级上册数学总复习资料

七年级上册数学总复习资料七年级上册数学总复习资料1第三章七年级上册数学总复习资料2第四章直线与角-------------4.1几何图形形状:方的、圆的等(1)①几何图形大小:长度、面积、体积等位置:相交、垂直、平行等②几何体也简称体。
包围着体的是面。
③常见的立体图形:圆柱(一曲面二平面)、圆椎(一曲面一平面)、圆台、球(一曲面)、长方体(六面八点十二棱)、四面体(三棱锥)、三棱柱(各部分不都在一个平面内,在一个平面内就是平面图形。
)新课标第一网④点线面体:是组成几何图形的基本元素(是几何图形);点动成线,线动成面,面动成体。
(2)展开与折叠:圆柱的侧面展开图是矩形;圆锥的侧面展开图是扇形;正方体展开六个面可用“1字型”、“Z字型”模型认识。
(3)三视图:主视图(从正面看)、左视图(从左面看)、俯视图(从上面看)。
----------4.2直线、射线、线段1.特点与表示方法:①直线没有端点,向两方无限延伸(不能用延长描述),可用两个大写字母或小字字母表示;②射线只有一个端点,向一方无限延伸,用端点和延伸方向中的任意一点表示;端点相同,延伸方向相同的两条射线是同一条射线(两个相同)。
③线段有两个端点,可用两个大写字母或小字字母表示(不能延长)。
2.连接两点间的线段的长度,叫做这两点之间的距离。
线段是图形,距离有大小。
3.经过两点有一条直线,并且只有一条直线。
(两点确定一条直线)。
4.经过两点的所有连线中----------线段最短(两点之间,线段最短)------------4.3线段的长短比较①线段的比较:叠合法(线段上、线段的延长线上)或度量法。
②中点:将一条线段分成两条相等的线段的点称这条线段的中点。
③线段的和、差、倍、分(整体求部分,部分求整体)可以设未知数④点在线段上、点在线段的延长线上、甚至在线段外。
-----------4.4角1、定义:有公共端点的两条射线组成的图形叫角。
角的端点为顶点,两条射线为角的两边(一条射线绕端点旋转后形成的图形)。
初一年级上册数学复习题

初一年级上册数学复习题一、数的认识与运算1. 整数的分类- 正整数- 负整数- 零2. 整数的四则运算- 加法:如 23 + 45 = 68- 减法:如 78 - 23 = 55- 乘法:如3 × 15 = 45- 除法:如48 ÷ 6 = 83. 有理数的分类- 正有理数- 负有理数- 零4. 有理数的四则运算- 加法:如 -3 + 5 = 2- 减法:如 -6 - 2 = -8- 乘法:如 -2 × 3 = -6- 除法:如 -18 ÷ 3 = -65. 绝对值- 正数的绝对值是其本身- 负数的绝对值是其相反数- 零的绝对值是零6. 有理数的大小比较- 正数大于零,零大于负数- 两个负数比较大小,绝对值大的反而小二、代数基础1. 代数式- 单项式:如 3x- 多项式:如 2x^2 + 5x - 32. 同类项- 所含字母相同,并且相同字母的指数也相同的项3. 合并同类项- 如 3x + 2x = 5x4. 代数式的值- 如当 x = 2 时,3x + 1 = 3 × 2 + 1 = 75. 代数式的简化- 如 5x^2 - 3x + 2x - 4 可以简化为 5x^2 - x - 4三、方程与不等式1. 一元一次方程- 如 2x + 5 = 112. 解一元一次方程- 如解方程 2x + 5 = 11,得 x = 33. 一元一次不等式- 如 x + 3 > 54. 解一元一次不等式- 如解不等式 x + 3 > 5,得 x > 25. 一元一次方程组- 如:\[ \begin{cases} x + y = 7 \\ x - y = 1 \end{cases} \]6. 解一元一次方程组- 如解方程组:\[ \begin{cases} x + y = 7 \\ x - y = 1 \end{cases} \] 得 x = 4, y = 3四、几何初步1. 线段、射线、直线- 线段有起点和终点,长度有限- 射线有一个起点,无限延伸- 直线无起点无终点,无限延伸2. 角的分类- 锐角:小于90°- 直角:等于90°- 钝角:大于90°小于180°- 平角:等于180°- 周角:等于360°3. 角的度量- 度(°)是角的基本度量单位4. 垂直与平行线- 垂直线:两条直线相交成90°角- 平行线:在同一平面内,且无论延伸多远都不相交的两条直线5. 三角形的分类- 按边分:等边三角形、等腰三角形、不等边三角形- 按角分:锐角三角形、直角三角形、钝角三角形6. 三角形的内角和- 三角形的内角和等于180°7. 四边形的分类- 正方形、长方形、平行四边形、梯形等8. 圆的基本概念- 圆心、半径、直径、圆周角等五、数据的收集与处理1. 数据的收集- 调查、观察、实验等方法收集数据2. 数据的整理- 制作表格、绘制图表等方法整理数据3. 数据的描述- 用平均数、。
人教版七年级数学上册第一章 《有理数》总复习教案

人教版七年级数学上册第一章《有理数》总复习教案第一章《有理数》总复习一、内容分析小结与复习分作两个部分。
第一部分概述了正数与负数、有理数、相反数、绝对值等概念,以及有理数的加、减、乘、除、乘方的运算方法与运算律,从而给出全章内容的大致轮廓,第二部分针对这一章新出现的内容、方法等提出了5个问题;通过这5个问题引发学生的思考,主动进行新的知识的建构。
二、课时安排:小节与复习的要求是要把这一章内容系统化,从而进一步巩固和加深理解学习内容。
本章的主要内容可以概括为有理数的概念与有理数的运算两部分。
因此,本章总复习的二课时这样安排(测验课除外):第一课时复习有理数的意义及其有关概念;第二课时复习有理数的运算。
三、教学方法的确定:设计典型例题,检测学生知识,科学地进行小结与归纳。
四、教学安排:第一课时:本节课将复习有理数的意义及其有关概念。
其内容包括正负数、有理数、数轴、有理数大小的比较、相反数与绝对值等。
在教学过程中,应利用数轴来认识、理解有理数的有关概念,借助数轴,把这些概念串在一起形成一个用以描述有理数特征的系统。
另外,在运用有理数概念的同时,还应注意纠正可能出现的错误认识。
一、教学目标;1.理解五个重要概念:有理数、数轴、倒数、绝对值、倒数。
2.使学生提高区分概念的能力,正确运用概念解决问题。
3、能正确比较两个有理数的大小。
二、教学重点:有理数五个概念的理解与应用:有理数、数轴、倒数、绝对值、倒数。
三、教学难点:对绝对值概念的理解与应用。
四、教学过程:(一)知识梳理:1.正数和负数:(给出四个问题,帮助学生理解负数的必要性及其在生产生活中的应用。
)回答下列问题(1)温度为-4℃是什么意思?(2)如果向正北规定为正,那么走-70米是什么意思?(3)21世纪的第一年,日本的服务出口额比上一年增长了-7.3%,这里的“服务出口额比上一年增长了-7.3%”是什么意思?(4)请同学们谈一谈,为什么要引入负数?你还能举出生活中有关负数的例子吗?2.有理数的分类:(通过两个问题让学生掌握有理数的两种分类方法,理解有理数的含义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
清大学习吧
七年级(上)数学 总复习
主讲人:徐老师
②有理数减法法则:减去一个数,等于加这个数的相反数。用字母表示为:a-b=a+(-b)。 2.有理数加法的运算律 ⑴加法交换律:a+b=b+a ⑵加法结合律:(a+b)+c=a+(b+c) 3.有理数加减法 观察式子,保证第一个数的符号是正的,做计算时要注意先处理符号再去做加减。 (-8)+(-7)+(-6)+(+5)=-8-7-6+5 1.7 有理数的乘除法 ①有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘﹙计算时首先处理符号﹚; 任何数同 0 相乘,都得 0;乘积是 1 的两个数互为倒数。几个不是 0 的数相乘, 负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数(奇负 偶正) ②有理数除法法则:除以一个不等于 0 的数,等于乘这个数的倒数; (把除号变成乘号)0 除以任 何一个不等于 0 的数,都得 0。 2.有理数的乘除混合运算(先处理符号) (1)乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果。 (2)有理数的加减乘除混合运算,先乘方,再乘除,最后加减;同级运算,从左到右进行;如有括 号,先做括号内的运算,按小括号、中括号、大括号依次进行。 1.8 倒数 乘积是 1 的两个数互为倒数,其中一个数叫做另一个数的倒数,用式子表示为 a· 是说 a 和
第四章
一元一次方程
3.1 一元一次方程 1、一元一次方程的概念:只含有一个未知数(元)且未知数的指数是 1(次)的方程叫做一元一次 方程。一般形式:ax+b=0(a≠0)
奇迹是努力的另一个名字!加油!做题的时候多想想,这个数学题一定能解,并且一定有人能解对, 为什么我就不能做出来呢? 4
清大学习吧
1 =1(a≠0) ,就 a
1 1 1 互为倒数,即 a 是 的倒数, 是 a 的倒数。 a a a
注意:① 0 没有倒数; 2 求假分数或真分数的倒数,只要把这个分数的分子、分母点颠倒位置即可; 3 求带分数的倒数时,先把带分数化为假分数,再把分子、分母颠倒位置; 4 正数的倒数是正数,负数的倒数是负数。 (求数的倒数,不改变这个数的性质) ; 5 倒数等于它本身的数是 1 或-1,不包括 0。 1.9 有理数的乘方 1、求 n 个相同因数的积的运算,叫乘方,记作 a 。负数的奇次幂是负数,负数的偶次幂是正数。 正数的任何次幂都是正数,0 的任何次幂都是 0。 1.10 科学记数法 把一个大于 10 的数表示成 a 10 的形式(其中 1 a 10 , n 是正整数) ,这种记数法是科学记
n n
数法,注意 a 的范围为 1≤a <10。 从一个数的左边第一个非 0 数字起,到末位数字止,所有数字都是这个数的有效数字。四舍五入遵 从精确到哪一位就从这一位的下一位开始,而不是从数字的末尾往前四舍五入。比如:3.5449 精确 到 0.01 就是 3.54 而不是 3.55。3.10 万精确到百位。 第二章 代数式
1 以省略不写或用“· ”表示,并把数字放到字母前; 出现除式时,用分数表示; 带分数与字母相乘时,带分数要化成假分数; 若运算结果为加减的式子,当后面有单位时,要用括号把整个式子括起来。
注意单项式和多项式的每一项都包括它前面的符号。 合并同类项 同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项。与字母前面的系数(≠0)无 关。 (1)所含字母相同; (2)相同字母的次数相同,同类项与系数大小、字母的排列顺序无关 合并同类项的法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。 去括号的法则(注意加括号) :去括号,看符号:是正号,不变号;是负号,全变号。 (1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变; (2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。 (括号 一般是从里到外,先去小括号再中括号、大括号,但也可以由外到里,先去大括号) 第三章 整式的加减
奇迹是努力的另一个名字!加油!做题的时候多想想,这个数学题一定能解,并且一定有人能解对, 为什么我就不能做出来呢? 1
清大学习吧
七年级(上)数学 总复习
主讲人:徐老师
4.数轴的应用。 1.4 相反数:只有符号不同的两个数叫做互为相反数。 (例:2 的相反数是-2;0 的相反数是 0)其中 一个是另一个的相反数。 (1)任何数都有相反数,且只有一个; (2)0 的相反数是 0; (3)互为相反数的两数和为 0,和为 0 的两数互为相反数,即 a,b 互为相反数,则 a+b=0 (4)相反数的几何意义 在数轴上与原点距离相等的两点表示的两个数,是互为相反数;互为相反数的两个数,在数轴上的 对应点(0 除外)在原点两旁,并且与原点的距离相等。0 的相反数对应原点;原点表示 0 的相反数。 说明:在数轴上,表示互为相反数的两个点关于原点对称。 (5)相反数的表示方法 一般地,数 a 的相反数是-a ,其中 a 是任意有理数,可以是正数、负数或 0。 当 a>0 时,-a<0(正数的相反数是负数) 当 a<0 时,-a>0(负数的相反数是正数) 当 a=0 时,-a=0, (0 的相反数是 0) 1.5 绝对值: (1)数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值,记作|a|。从几何意义上讲, 数的绝对值是两点间的距离。 (2)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0 的绝对值是 0。 两个负数,绝对值大的反而小。 2.绝对值的几何定义:表示两点间的距离 一般地,数轴上表示数 a 的点与原点的距离叫做 a 的绝对值,记作|a|。 3.绝对值的代数定义 ⑴一个正数的绝对值是它本身; ⑵一个负数的绝对值是它的相反数; ⑶0 的绝对值是 0. 可用字母表示为: ①如果 a>0,那么|a|=a; ②如果 a<0,那么|a|=-a; ③如果 a=0,那么|a|=0。 4.绝对值的性质 任何一个有理数的绝对值都是非负数,也就是说绝对值具有非负性。所以,a 取任何有理数,都有 |a|≥0。即⑴0 的绝对值是 0;绝对值是 0 的数是 0.即:a=0 <═> |a|=0; ⑵一个数的绝对值是非负数,绝对值最小的数是 0.即:|a|≥0; ⑶任何数的绝对值都不小于原数。即:|a|≥a; ⑷绝对值相同的数有两个,它们互为相反数。即:若|x|=a(a>0) ,则 x=±a; ⑸互为相反数的两数的绝对值相等。即:|-a|=|a|或若 a+b=0,则|a|=|b|; ⑹绝对值相等的两数相等或互为相反数。即:|a|=|b|,则 a=b 或 a=-b; ⑺若几个数的绝对值的和等于 0,则这几个数就同时为 0。即|a|+|b|=0,则 a=0 且 b=0。 (非 负数的常用性质:若几个非负数的和为 0,则有且只有这几个非负数同时为 0) 5.绝对值的化简 ①当 a≥0 时, |a|=a ; ②当 a≤0 时, |a|=-a 6.已知一个数的绝对值,求这个数(两个值) 一个数 a 的绝对值就是数轴上表示数 a 的点到原点的距离,一般地,绝对值为同一个正数的有理数 有两个,它们互为相反数,绝对值为 0 的数是 0,没有绝对值为负数的数。 1.6 有理数的加减法 ①有理数加法法则: 同号两数相加,取相同的符号,并把绝对值相加。
3.1 整式:单项式和多项式统称为整式。注意:分母上含有字母的不是整式。 (分式) 3.2 整式的加减 整式的加减:进行整式的加减运算时,如果有括号先去括号,再合并同类项。 整式加减的步骤: (1)列出代数式; (2)去括号; (3)合并同类项。 整式加减的一般步骤: 一去、二找、三合 (1)如果遇到括号按去括号法则先去括号. (2)结合同类项. (3)合并同类项 考点:计算题,化简求值 本册重点,无处不在
3
奇迹是努力的另一个名字!加油!做题的时候多想想,这个数学题一定能解,并且一定有人能解对, 为什么我就不能做出来呢?
清大学习吧
七年级(上)数学 总复习
主讲人:徐老师
代数式:用基本运算符号把数和字母连接而成的式子叫做代数式,如 n,-1,2n+500,abc。单独的一 个数或一个字母也是代数式。 单项式:由数字和字母乘积组成的式子,单项式指的是数或字母的积的代数式。单独的一个数或一 个字母也是代数式。判断代数式是否是单项式,关键要看代数式中数与字母是否是乘积关系,即分 母中不含有字母,若式子中含有加、减运算关系,其也不是单项式。 单项式的系数:单项式中的数字因数 单项式的次数:一个单项式中,所有字母的指数和 多项式:几个单项式的和叫做多项式。每个单项式叫做多项式的项,不含字母的项叫做常数项。多 项式里次数最高项的次数,叫做这个多项式的次数, a b 是次数最高项,其次数是 6。常数项的次 数为 0。特别注意多项式的项包括它前面的性质符号。 代数式书写规范:
清大学习吧
七年级(上)数学 总复习
主讲人:徐老师
七年级数学上册知识点 第一章 有理数 1.1 正数与负数 ①正数:大于 0 的数叫正数。 (根据需要,有时在正数前面也加上“+” ) ②负数:在以前学过的 0 以外的数前面加上负号“—”的数叫负数。表示比 0 小的数,与正数具有 相反意义。 ③0 既不是正数也不是负数。0 是正数和负数的分界,表示没有,是唯一的中性数。 考点:注意:①字母 a 可以表示任意数,当 a 表示正数时,-a 是负数;当 a 表示负数时,-a 是正数; 当 a 表示 0 时,-a 仍是 0。判断:+a 表示大于 0 的数 ( ) 注意诸如 0 的其他应用,0 不能做除数等等。 1.2 有理数 1、有理数:整数和分数统称有理数。 ⑴正整数、0、负整数统称为整数(0 和正整数统称为自然数) ⑵正分数和负分数统称为分数 ⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。 理解:只有能化成分数的数才是有理数。 (π是有理数吗) 1 π是无限不循环小数,不能写成分数形式,不是有理数。 ②有限小数和无限循环小数都可化成分数,都是有理数。 2、有理数的分类 ⑴按有理数的意义分类 ⑵按正、负来分 正整数 正整数 整数 0 正有理数 负整数 正分数 有理数 有理数 0 (0 不能忽视) 正分数 负整数 分数 负有理数 负分数 负分数 总结:①正整数、0 统称为非负整数(也叫自然数) ②负整数、0 统称为非正整数 ③正有理数、0 统称为非负有理数 ④负有理数、0 统称为非正有理数 1.3 数轴(1)定义 :通常用一条直线上的点表示数,这条直线规定了原点,正方向,单位长度 (2)数轴三要素:原点、正方向、单位长度; (3)原点:在直线上任取一个点表示数 0,这个点叫做原点; (4)数轴上的点和有理数的关系:所有的有理数都可以用数轴上的点表示出来,但数轴 上的点,不都是表示有理数。 2.数轴上的点与有理数的关系 所有的有理数都可以用数轴上的点表示出来,但数轴上的点不都表示有理数,也就是说,有理数与 数轴上的点不是一一对应关系。 (如,数轴上的点π不是有理数) 3.利用数轴表示两数大小 ⑴在数轴上数的大小比较,右边的数总比左边的数大; ⑵正数都大于 0,负数都小于 0,正数大于负数; ⑶两个负数比较,距离原点远的数比距离原点近的数小。
