【高中资源】广东省广州市第二中学2015-2016学年高二上学期第一次月考数学理试卷 Word版含答案
广东省广州市2015-2016学年高二学业水平测试数学试题 含解析

2015-2016学年度广州市高中二年级学生学业水平测试2015年12月24日一、选择题:本大题共10小题,每小题5分.1。
已知集合M =-1,0,1{},{}xxx N ==2|,则M ÇN =()A.1{} B 。
0,1{} C 。
-1,0{} D 。
-1,0,1{}2.已知等比数列a n{}的公比为2,则a 4a 2值为()A. 14B 。
12C 。
2 D.43。
直线l 过点1,-2(),且与直线2x +3y -1=0垂直,则l 的方程是()A.2x +3y +4=0B.2x +3y -8=0 C 。
3x -2y -7=0 D.3x -2y -1=04.函数f x ()=12æèçöø÷x-x +2的零点所在的一个区间是()A.-1,0() B 。
0,1() C.1,2() D 。
2,3()5.已知非零向量与的方向相同,下列等式成立的是()BD6.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查消费购买力的某项指标;(2)从某中学高二年级的10名体育特长生中抽取3人调查学习负担情况,应采取的抽样方法是()A 。
(1)用系统抽样法,(2)用简单随机抽样法C 。
(1)用分层抽样法,(2)用简单随机抽样法 D.(1)(2)都用分层抽样法7.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+,03,02,01y x x y x ,则z =x -y 的最大值为()A. 3 B 。
1 C 。
1- D 。
5- 8。
某几何体的三视图及其尺寸图,则该几何体的体积为()A. 6 B 。
9 C 。
12 D. 18 9。
函数f x ()=12-cos2p 4-x æèçöø÷的单调增区间是() A 。
2k p -p 2,2k p +p 2éëêùûú,k ÎZ B. 2k p +p 2,2k p +3p 2éëêùûú,k ÎZC.k p +p 4,k p +3p 4éëêùûú,k ÎZ D.k p -p 4,k p +p 4éëêùûú,k ÎZ 10.设a >1,b >2且ab =2a +b 则a +b 的最小值为()A 。
广东省广州市执信中学2015-2016学年高二上学期期中考试理科数学试卷

2015-2016学年度第一学期 高二级(理科)数学期中考试试卷 本试卷分选择题和非选择题两部分,共10页,满分为150分。
考试用时120分钟。
注意事项:1、答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和学号填写在答题卡和答卷密封线内相应的位置上,用2B铅笔将自己的学号填涂在答题卡上。
2、选择题每小题选出答案后,有2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3、非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答,答案必须写在答卷纸各题目指定区域内的相应位置上,超出指定区域的答案无效;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4、考生必须保持答题卡的整洁和平整。
参考公式:柱体的体积,其中是体的底面积,是体的高体的体积,其中是体的底面积,是体的高本卷共小题,每小题5分,共分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
,则 ( ). A. B. C.D. :,则命题为() A. B.C. D. 函数是() A.最小正周期为的奇函数 B.最小正周期为的偶函数 C.最小正周期为的奇函数 D.最小正周期为的偶函数 ”是“直线与直线垂直”的 A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件 ),则它的体积是(). A. B. C. D. 6. 已知执行如左图所示的程序框图,输出的, 则判断框内的条件是() A. B. C. D. A. B. C. D. 8. 偶函数满足,且在时,,若直线与函数的图像有且仅有三个交点,则的取值范围是() A. B. C. D. ,,,则与的夹角是 . 10. 把函数图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),接着向右平移个单位,得到的函数解析式为 . 11. 若变量满足约束条件则的最值是________ 12. 已知在定义域上是减函数,且,则的取值范围是. 13. 与椭圆共焦点且过点的双曲线方程是 . 14. 已知椭圆与双曲线有相同的焦点,点是两曲线的一个公共点,又分别是两曲线的离心率,若,则的最小值为 . 三、解答题:本大题共6小题,共80分。
广东省广州市执信、广雅、二中、六中四校联考2015-2016学年高二数学上学期期末试卷理(含解析)

2021 -2021学年广东省广州市执信、广雅、二中、六中四校联考高二〔上〕期末数学试卷〔理科〕一、选择题〔本大题共14小题,每题5分,共60分,在每题给出四个选项中,只有一项为哪一项正确〕1.集合A={y|y=2x},B={y|y=},那么A∩B等于〔〕A.{y|y≥0} B.{y|y>0} C.{y|y≥1} D.{y|y>1}2.“α≠β〞是“cosα≠cosβ〞〔〕条件.A.充分不必要B.必要不充分C.充要D.既不充分又不必要3.=〔〕A.B.C.D.4.运行如下图程序语句后,输出结果是〔〕A.17 B.19 C.21 D.235.从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,那么b>a概率是〔〕A.B.C.D.6.等比数列{a n}中,各项都是正数,且a1,,2a2成等差数列,那么=〔〕A.1+B.1﹣C.3+2D.3﹣27.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间〔0,1〕上单调递减函数序号是〔〕A.①②B.②③C.③④D.①④8.〔题类A〕双曲线﹣=1〔a>0,b>0〕,过焦点F1弦AB长为m〔A,B在同一支上〕,另一个焦点为F2,那么△ABF2周长为〔〕A.4a﹣2m B.4a C.4a+m D.4a+2m9.〔题类B〕设f〔x〕=sinx2,那么f′〔x〕等于〔〕A.sin2x B.cosx2 C.2xsinx2D.2xcosx210.假设变量x,y满足约束条件,那么z=2x+y最大值为〔〕A.1 B.2 C.3 D.411.某几何体三视图如下图〔均为直角边长为2等腰直角三角形〕,那么该几何体外表积为〔〕A.4+4B.4+4C.6+2D.812.假设,是非零向量,且⊥,||≠||,那么函数f〔x〕=〔x+〕〔x﹣〕是〔〕A.一次函数且是奇函数B.一次函数但不是奇函数C.二次函数且是偶函数D.二次函数但不是偶函数13.假设直线y=x+b与曲线有公共点,那么b取值范围是〔〕A.[,] B.[,3] C.[﹣1,] D.[,3]14.正实数a,b满足a b=b a,且0<a<1,那么a,b大小关系是〔〕A.a>b B.a=b C.a<b D.不能确定二、填空题(本大题共5小题,每题5分,共20分)15.cosx﹣sinx=,那么= .16.〔题类A〕抛物线y=ax2焦点坐标为〔0,〕,那么a= .17.计算定积分〔x2+sinx〕dx= .18.假设正实数x,y满足2x+y+6=xy,那么xy最小值是.19.如图,正三棱锥A﹣BCD侧棱长为2,底面BCD边长为2,E,分别为BC,BD中点,那么三棱锥A﹣BEF外接球半径R= ,内切球半径r= .三、解答题〔本大题共6个小题,共70分,解容许写出文字说明、证明过程或演算步骤〕.20.甲乙两机床同时加工直径为100mm零件,为检验质量,随机从中各抽取5件,测量结果如图,请说明哪个机床加工零件较好?甲9910098100103乙9910010299100 21.△ABC中,D为边BC上一点,BD=33,sinB=,cos∠ADC=,求AD.22.在三棱锥S﹣ABC中,△ABC是边长为4正三角形,平面SAC ⊥平面ABC,SA=SC=2,M为AB中点.〔1〕求证:AC⊥SB;〔2〕求二面角S﹣CM﹣A平面角余弦值.23.如图,A,B,C坐标分别为〔﹣,0〕,〔,0〕,〔m,n〕,G,O′,H分别为△ABC重心,外心,垂心.〔1〕写出重心G坐标;〔2〕求外心O′,垂心H坐标;〔3〕求证:G,H,O′三点共线,且满足|GH|=2|OG′|.24.数列{a n}是公差d不为0等差数列,a1=2,S n为其前n项与.〔1〕当a3=6时,假设a1,a3,a,a…,a成等比数列〔其中3<n1<n2<…<n k〕,求n k表达式;〔2〕是否存在适宜公差d,使得{a n}任意前3n项中,前n项与与后n项与比值等于定常数?求出d,假设不存在,说明理由.25.〔题类A〕以椭圆+y2=1〔a>1〕短轴端点A〔0,1〕为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件三角形.26.函数f〔x〕=ln〔1+x〕﹣x,g〔x〕=xlnx.〔Ⅰ〕求函数f〔x〕最大值;〔Ⅱ〕设0<a<b,证明0<g〔a〕+g〔b〕﹣2g〔〕<〔b﹣a〕ln2.2021 -2021学年广东省广州市执信、广雅、二中、六中四校联考高二〔上〕期末数学试卷〔理科〕参考答案与试题解析一、选择题〔本大题共14小题,每题5分,共60分,在每题给出四个选项中,只有一项为哪一项正确〕1.集合A={y|y=2x},B={y|y=},那么A∩B等于〔〕A.{y|y≥0} B.{y|y>0} C.{y|y≥1} D.{y|y>1}【考点】交集及其运算.【分析】分别求出A与B中y范围确定出两集合,求出A与B交集即可.【解答】解:由A中y=2x>0,得到A={y|y>0},由B中y=≥0,得到B={y|y≥0},那么A∩B={y|y>0},应选:B.2.“α≠β〞是“cosα≠cosβ〞〔〕条件.A.充分不必要B.必要不充分C.充要D.既不充分又不必要【考点】必要条件、充分条件与充要条件判断.【分析】根据充分必要条件定义结合三角函数性质判断即可.【解答】解:假设“α≠β〞那么“cosα≠cosβ〞逆否命题是:假设“cosα=cosβ〞那么“α=β〞,∵α=β⇒cosα=cosβ,又当cosα=cosβ时,α=±β+2kπ,k∈Z,∴cosα=cosβ推不出α=β,∴“cosα=cosβ〞是“α=β〞必要非充分条件,即“α≠β〞是“cosα≠cosβ〞必要不充分条件.应选:B.3.=〔〕A.B.C.D.【考点】复数代数形式混合运算.【分析】化简复数分母,然后复数分子、分母同乘分母共轭复数,即可求得结果.【解答】解:=应选B.4.运行如下图程序语句后,输出结果是〔〕A.17 B.19 C.21 D.23【考点】伪代码.【分析】根据代码流程依次计算程序运行结果,直到满足条件i≥8,计算输出S值.【解答】解:模拟执行程序,可得i=1i=3,S=9,i=2不满足条件i≥8,i=4,S=11,i=3不满足条件i≥8,i=5,S=13,i=4不满足条件i≥8,i=6,S=15,i=5不满足条件i≥8,i=7,S=17,i=6不满足条件i≥8,i=8,S=19,i=7不满足条件i≥8,i=9,S=21,i=8满足条件i≥8,退出循环,输出S值为21.应选:C.5.从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,那么b>a概率是〔〕A.B.C.D.【考点】等可能事件概率.【分析】由题意知此题是一个古典概型,试验包含所有事件根据分步计数原理知共有5×3种结果,而满足条件事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果.【解答】解:由题意知此题是一个古典概型,∵试验包含所有事件根据分步计数原理知共有5×3种结果,而满足条件事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果,∴由古典概型公式得到P==,应选D.6.等比数列{a n}中,各项都是正数,且a1,,2a2成等差数列,那么=〔〕A.1+B.1﹣C.3+2D.3﹣2【考点】等差数列性质;等比数列性质.【分析】先根据等差中项性质可知得2×〔〕=a1+2a2,进而利用通项公式表示出q2=1+2q,求得q,代入中即可求得答案.【解答】解:依题意可得2×〔〕=a1+2a2,即,a3=a1+2a2,整理得q2=1+2q,求得q=1±,∵各项都是正数∴q>0,q=1+∴==3+2应选C7.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间〔0,1〕上单调递减函数序号是〔〕A.①②B.②③C.③④D.①④【考点】函数单调性判断与证明.【分析】此题所给四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型图象与性质;①为增函数,②为定义域上减函数,③y=|x﹣1|有两个单调区间,一增区间一个减区间,④y=2x+1为增函数.【解答】解:①是幂函数,其在〔0,+∞〕上即第一象限内为增函数,故此项不符合要求;②中函数是由函数向左平移1个单位长度得到,因为原函数在〔0,+∞〕内为减函数,故此项符合要求;③中函数图象是由函数y=x﹣1图象保存x轴上方,下方图象翻折到x轴上方而得到,故由其图象可知该项符合要求;④中函数图象为指数函数,因其底数大于1,故其在R上单调递增,不合题意.8.〔题类A〕双曲线﹣=1〔a>0,b>0〕,过焦点F1弦AB长为m〔A,B在同一支上〕,另一个焦点为F2,那么△ABF2周长为〔〕A.4a﹣2m B.4a C.4a+m D.4a+2m【考点】双曲线简单性质.【分析】先根据双曲线定义可知,|AF2|﹣|AF1|=2a,|BF2|﹣|BF1|=2a,两式相加求得|AF2|+|BF2|=4a+m,进而根据代入|AF2|+|BF2|+|AF1|+|BF1|求得答案.【解答】解:由双曲线定义可知,|AF2|﹣|AF1|=2a,|BF2|﹣|BF1|=2a,∴△ABF2周长为|AF2|+|BF2|+|AF1|+|BF1|=4a+|AF1|+|BF1|+|AF1|+|BF1| =4a+2m,应选:D.9.〔题类B〕设f〔x〕=sinx2,那么f′〔x〕等于〔〕A.sin2x B.cosx2 C.2xsinx2D.2xcosx2【考点】导数运算.【分析】根据复合函数求导法那么进展计算.【解答】解:令u〔x〕=x2,h〔u〕=sinu,那么h〔u〔x〕〕=f〔x〕=sinx2,∴f′〔x〕=h′〔u〕•u′〔x〕=cosx2•2x.10.假设变量x,y满足约束条件,那么z=2x+y最大值为〔〕A.1 B.2 C.3 D.4【考点】简单线性规划应用.【分析】先根据约束条件画出可行域,设z=2x+y,再利用z几何意义求最值,只需求出直线z=2x+y过可行域内点B时,从而得到m 值即可.【解答】解:作出可行域,作出目标函数线,可得直线与y=x与3x+2y=5交点为最优解点,∴即为B〔1,1〕,当x=1,y=1时z max=3.应选C.11.某几何体三视图如下图〔均为直角边长为2等腰直角三角形〕,那么该几何体外表积为〔〕A.4+4B.4+4C.6+2D.8【考点】由三视图求面积、体积;简单空间图形三视图.【分析】作出几何体直观图,计算出各面面积.【解答】解:该几何体为三棱锥,作出直观图如下图,那么SC⊥平面ABC,AB⊥AC,AB=AC=SC=2.∴BC=2,SA=2.AB⊥平面SAC.∴S=+++==4+4.应选A.12.假设,是非零向量,且⊥,||≠||,那么函数f〔x〕=〔x+〕〔x﹣〕是〔〕A.一次函数且是奇函数B.一次函数但不是奇函数C.二次函数且是偶函数D.二次函数但不是偶函数【考点】平面向量数量积运算.【分析】f〔x〕=x﹣x,因为||≠||,所以f〔x〕=〔〕x,所以函数f〔x〕是一次函数且是奇函数.【解答】解:∵⊥,∴•=0∴f〔x〕=〔x+〕〔xb﹣〕=x﹣x,∴所以f〔x〕=〔〕x所以函数f〔x〕是一次函数且是奇函数应选A.13.假设直线y=x+b与曲线有公共点,那么b取值范围是〔〕A.[,] B.[,3] C.[﹣1,] D.[,3]【考点】函数与方程综合运用.【分析】此题要借助图形来求参数b取值范围,曲线方程可化简为〔x ﹣2〕2+〔y﹣3〕2=4〔1≤y≤3〕,即表示圆心为〔2,3〕半径为2半圆,画出图形即可得出参数b范围.【解答】解:曲线方程可化简为〔x﹣2〕2+〔y﹣3〕2=4〔1≤y≤3〕,即表示圆心为〔2,3〕半径为2半圆,如图依据数形结合,当直线y=x+b与此半圆相切时须满足圆心〔2,3〕到直线y=x+b距离等于2,即解得或,因为是下半圆故可知〔舍〕,故当直线过〔0,3〕时,解得b=3,故,应选D.14.正实数a,b满足a b=b a,且0<a<1,那么a,b大小关系是〔〕A.a>b B.a=b C.a<b D.不能确定【考点】不等式比拟大小.【分析】法一、由a b=b a,得,构造函数y=,求导后利用其单调性分析;法二由0<a<1,a b=b a,得blog a a=alog a b,即=log a b,然后利用反证法说明a=b.【解答】解:法一、由a b=b a,得blna=alnb,从而,考虑函数y=〔x>0〕,y′=.∵在〔0,1〕内f′〔x〕>0,∴f〔x〕在〔0,1〕内是增函数,由于0<a<1,b>0,∴a b<1,从而b a=a b<1.由b a<1及a>0,可推出b<1.由0<a<1,0<b<1,假设a≠b,那么根据f〔x〕在〔0,1〕内是增函数,得f〔a〕≠f〔b〕,即,从而a b≠b a,这与a b=b a矛盾.∴a=b;法二、∵0<a<1,a b=b a,∴blog a a=alog a b,即=log a b,假设a<b,那么>1,∵a<1,根据对数函数性质,得log a b<log a a=1,从而,这与矛盾,∴a不能小于b假设a>b,那么<1,而log a b>1,这也与矛盾.∴a不能大于b,因此a=b.应选:B.二、填空题(本大题共5小题,每题5分,共20分)15.cosx﹣sinx=,那么= .【考点】二倍角余弦.【分析】利用二倍角公式以及两角与正弦函数化简所求表达式,然后求解即可.【解答】解:cosx﹣sinx=,那么==〔cosx﹣sinx〕==.故答案为:.16.〔题类A〕抛物线y=ax2焦点坐标为〔0,〕,那么a= .【考点】抛物线简单性质.【分析】化简抛物线方程为标准方程,然后利用焦点坐标求解即可.【解答】解:抛物线y=ax2标准方程为:x2=y,它焦点坐标为〔0,〕,可得,解得a=.故答案为:.17.计算定积分〔x2+sinx〕dx= .【考点】定积分.【分析】求出被积函数原函数,再计算定积分值.【解答】解:由题意,定积分===.故答案为:.18.假设正实数x,y满足2x+y+6=xy,那么xy最小值是18 .【考点】根本不等式.【分析】首先左边是xy形式右边是2x+y与常数与形式,考虑把右边也转化成xy形式,使形式统一.可以猜测到应用根本不等式.转化后变成关于xy方程,可把xy看成整体换元后求最小值.【解答】解:由条件利用根本不等式可得,令xy=t2,即t=>0,可得.即得到可解得.又注意到t>0,故解为,所以xy≥18.故答案应为18.19.如图,正三棱锥A﹣BCD侧棱长为2,底面BCD边长为2,E,分别为BC,BD中点,那么三棱锥A﹣BEF外接球半径R= 1 ,内切球半径r= 2﹣.【考点】球体积与外表积;球内接多面体.【分析】利用勾股定理求出三棱锥A﹣BEF外接球半径,利用等体积求出内切球半径.【解答】解:设三棱锥A﹣BEF外接球球心为O,那么O在平面BEF 上射影O′为△BEF中心,∴BO′=×=∵A到平面BCD距离为=,∴三棱锥A﹣BEF外接球半径R==1,三棱锥A﹣BEF体积V==,又S=+2×+=2+,∴=〔2+〕r,∴r=2﹣.故答案为:1,2﹣.三、解答题〔本大题共6个小题,共70分,解容许写出文字说明、证明过程或演算步骤〕.20.甲乙两机床同时加工直径为100mm零件,为检验质量,随机从中各抽取5件,测量结果如图,请说明哪个机床加工零件较好?甲9910098100103乙9910010299100【考点】众数、中位数、平均数;极差、方差与标准差.【分析】分别求出两个车床加工零件平均数与方差,由此能判断哪个机床加工零件较好.【解答】解:==100,∴它们有整体水平相当,又==2 .8,==1 .2,∴乙车床相对稳定,故乙车床加工零件相对较好.21.△ABC中,D为边BC上一点,BD=33,sinB=,cos∠ADC=,求AD.【考点】同角三角函数根本关系运用;正弦定理.【分析】先由cos∠ADC=确定角ADC范围,因为∠BAD=∠ADC ﹣B所以可求其正弦值,最后由正弦定理可得答案.【解答】解:由cos∠ADC=>0,那么∠ADC<,又由知B<∠ADC可得B<,由sinB=,可得cosB=,又由cos∠ADC=,可得sin∠ADC=.从而sin∠BAD=sin〔∠ADC﹣B〕=sin∠ADCcosB﹣cos∠ADCsinB==.由正弦定理得,所以AD==.22.在三棱锥S﹣ABC中,△ABC是边长为4正三角形,平面SAC ⊥平面ABC,SA=SC=2,M为AB中点.〔1〕求证:AC⊥SB;〔2〕求二面角S﹣CM﹣A平面角余弦值.【考点】二面角平面角及求法;直线与平面垂直性质.【分析】〔1〕取AC中点O,连结OS、OB,由推导出AC⊥OS,AC⊥OB,由此能证明AC⊥SB.〔2〕平面SAC⊥平面ABC,SO⊥AC,从而SO⊥面ABC,过O 作OD⊥CM于D,连结SD,那么∠SDO是二面角N﹣CM﹣B平面角,由此能求出二面角S﹣CM﹣A平面角余弦值.【解答】证明:〔1〕取AC中点O,连结OS、OB,∵SA=SC,∴AC⊥OS,∵BA=BC,∴AC⊥OB,又OS,OB⊂平面OSB,OS∩OB=O,∴AC⊥平面OSB,∴AC⊥SB.解:〔2〕∵平面SAC⊥平面ABC,SO⊥AC,∴由面面垂直性质定理,得SO⊥面ABC,过O作OD⊥CM于D,连结SD,由三垂线定理,得SD⊥CM,∴∠SDO是二面角N﹣CM﹣B平面角,又SO=2,OD=1,∴SD==3,∴cos∠SDO=,∴二面角S﹣CM﹣A平面角余弦值为.23.如图,A,B,C坐标分别为〔﹣,0〕,〔,0〕,〔m,n〕,G,O′,H分别为△ABC重心,外心,垂心.〔1〕写出重心G坐标;〔2〕求外心O′,垂心H坐标;〔3〕求证:G,H,O′三点共线,且满足|GH|=2|OG′|.【考点】向量在几何中应用.【分析】〔1〕根据重心坐标公式即可求出,〔2〕设外心O′,垂心H坐标为〔0,a〕,〔m,b〕,根据向量坐标运算得到=〔m﹣,n〕,D坐标为〔+,〕,=〔+,﹣a〕,=〔m+,b〕,由题意得到由,化简计算得到即,即可求出外心O′,垂心H坐标;〔3〕根据向量坐标运算得到=2,根据向量共线条件即可证明.【解答】解:〔1〕重心G坐标为〔,〕,〔2〕设外心O′,垂心H坐标为〔0,a〕,〔m,b〕,BC中点为D,∵A,B,C坐标分别为〔﹣,0〕,〔,0〕,〔m,n〕,∴=〔m﹣,n〕,D坐标为〔+,〕,∴=〔+,﹣a〕,=〔m+,b〕,由,那么,即,∴外心O′坐标为〔0,〕,垂心H坐标为〔m,〕,〔3〕由〔1〕〔2〕可知=〔,〕,得=2,∴G,H,O′三点共线,且满足|GH|=2|OG′|.24.数列{a n}是公差d不为0等差数列,a1=2,S n为其前n项与.〔1〕当a3=6时,假设a1,a3,a,a…,a成等比数列〔其中3<n1<n2<…<n k〕,求n k表达式;〔2〕是否存在适宜公差d,使得{a n}任意前3n项中,前n项与与后n项与比值等于定常数?求出d,假设不存在,说明理由.【考点】数列求与.【分析】〔1〕数列{a n}公差d=,可得:a n=2n.另一方面,a1,a3,a,a…,a成等比数列〔其中3<n1<n2<…<n k〕,可得q=.利用等比数列通项公式即可得出.〔2〕等差数列{a n}中,S n=n2+•n,可得S3n﹣S2n,令S3n ﹣S2n=λS n,解出即可得出.【解答】解:〔1〕数列{a n}公差d===2.∴a n=2+2〔n﹣1〕=2n,另一方面,a1,a3,a,a…,a成等比数列〔其中3<n1<n2<…<n k〕,∴q==3.∴═a1•3k+2﹣1=2•n k,∴n k=3k+1.〔2〕等差数列{a n}中,S n=na1+=n2+•n,S3n﹣S2n=﹣=•n2+,令S3n﹣S2n=λS n,那么•n2+=λ[n2+•n],∴,解得或〔舍去〕.∴d=4,满足题意,且定常数为5.25.〔题类A〕以椭圆+y2=1〔a>1〕短轴端点A〔0,1〕为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件三角形.【考点】椭圆简单性质.【分析】由题意设出等腰直角三角形两边所在直线方程:l AB:y=kx+1〔k>0〕,l AC:y=﹣x+1,分别联立直线方程与椭圆方程,求出|AB|,|AC|长度,利用|AB|=|AC|得,k3﹣a2k2+a2k﹣1=0,然后分析方程根情况得答案.【解答】解:设三角形另外两顶点为B,C,不妨设l AB:y=kx+1〔k >0〕,l AC:y=﹣x+1.由,得〔1+a2k2〕x2+2ka2x=0,∴|AB|==.同理可得:|AC|=.由|AB|=|AC|得,k3﹣a2k2+a2k﹣1=0,即〔k﹣1〕[k2+〔1﹣a2〕k+1]=0,解得k=1或k2+〔1﹣a2〕k+1=0.对于k2+〔1﹣a2〕k+1=0,由〔1﹣a2〕2﹣4=0,得a=,此时方程根k=1;当1<a<时,方程k2+〔1﹣a2〕k+1=0无实根;当a>时,方程k2+〔1﹣a2〕k+1=0有两个不等实数根.∴当a>时,这样三角形有3个;当1<a≤时这样三角形有1个.26.函数f〔x〕=ln〔1+x〕﹣x,g〔x〕=xlnx.〔Ⅰ〕求函数f〔x〕最大值;〔Ⅱ〕设0<a<b,证明0<g〔a〕+g〔b〕﹣2g〔〕<〔b﹣a〕ln2.【考点】利用导数求闭区间上函数最值;平均值不等式在函数极值中应用.【分析】〔1〕先求出函数定义域,然后对函数进展求导运算,令导函数等于0求出x值,再判断函数单调性,进而可求出最大值.〔2〕先将a,b代入函数g〔x〕得到g〔a〕+g〔b〕﹣2g〔〕表达式后进展整理,根据〔1〕可得到lnx<x,将、放缩变形为、代入即可得到左边不等式成立,再用根据y=lnx单调性进展放缩<.然后整理即可证明不等式右边成立.【解答】〔Ⅰ〕解:函数f〔x〕定义域为〔﹣1,+∞〕..令f′〔x〕=0,解得x=0.当﹣1<x<0时,f′〔x〕>0,当x>0时,f′〔x〕<0.又f〔0〕=0,故当且仅当x=0时,f〔x〕取得最大值,最大值为0.〔Ⅱ〕证明:由〔Ⅰ〕结论知ln〔1+x〕﹣x<0〔x>﹣1,且x≠0〕,由题设,因此ln=﹣ln〔1+〕>﹣,所以.又,<.=〔b﹣a〕ln<〔b﹣a〕ln2综上.。
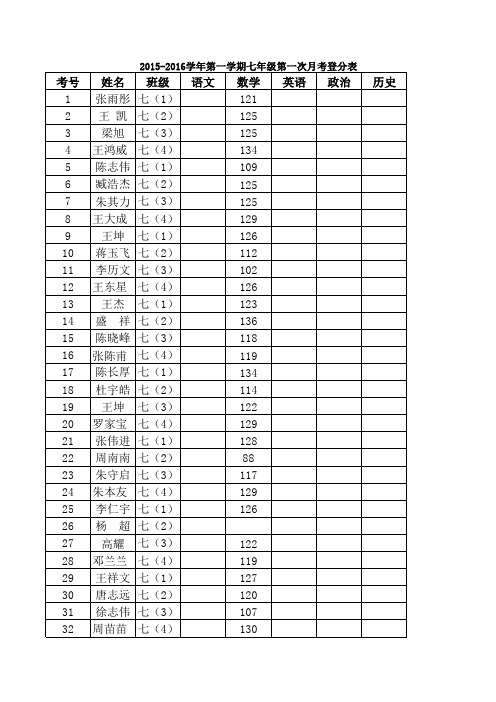
2015-2016学年第一学期七年级第一次月考登分表
语文
数学 121 125 125 134 109 125 125 129 126 112 102 126 123 136 118 119 134 114 122 129 128 88 117 129 126 122 119 127 120 107 130
英语
政治
历史
33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65
宋新政 夏瑞 姚如 周荣霞 杜彬杰 陈天宇 雍万鹏 宋傲祥 杜英杰 王倩倩 赵志杨 李莹莹 杭建楠 张小喜 朱立豪 黄恩琪 周鹏 胡浩东 陈勇 缪 丽 王祥亮 柏婷婷 何韩玲 张欣欣 王平 牛海霞 秦鹏 刘陈龙 卢瑞杰 许赵 张长富 方健翔 吴超
七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3) 七(4) 七(1) 七(2) 七(3)
2015-2016学年第一学期七年级第一次月考登分表
考号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
姓名 张雨彤 王 凯 梁旭 王鸿威 陈志伟 臧浩杰 朱其力 王大成 王坤 蒋玉飞 李历文 王东星 王杰 盛 祥 陈晓峰 张陈甫 陈长厚 杜宇皓 王坤 罗家宝 张伟进 周南南 朱守启 朱本友 李仁宇 杨 超 高耀 邓兰兰 王祥文 唐志远 徐志伟 周苗苗
2015-2016学年第一学期月考考成绩表 (空白) - 副本
四(2)
学号 姓名
1 陈涵
2 钟铭淦
3 肖文杰
4
刘卓熙
5 赖允祺
6 曾少羿
7 吴雨舒
8 黄雪涵
9 叶柳妃
10 赖诗涵
11 欧阳金
12 刘槿雯
13 林煌东
14 蔡丰泽
15 叶晶晴
16 肖烨
17 曾馨缘
18 刘莹钦
19 钟其宏
20 黄文涛
21 叶静茹
22 刘薇
23 林瑶
24 刘议联
达标率 优秀人数(80分
优秀率 特优人数(90以
特优率 后20%平均分
五(2) 学号 姓名
1 叶芸萱 2 叶灵 3 叶智鹏 4 刘龙建 5 黄朦瑶 6 蔡惠 7 黄明强 8 曾文杰 9 廖宁锋 10 李晋成 11 钟榕 12 李位杰 13 刘帅 14 杨子韬 15 吴一雄 16 肖舒彤 17 徐智超 18 钟菊 19 钟培 20 刘钰烁 21 钟治语 22 邱庆松 23 赖鸿涛 24 邱泽豪 25 刘俊伟 26 李美靓 27 钟宇林 28 廖胤宇 29 廖鑫源 30 刘宏曜 31 唐文昱 32 刘楠 33 叶怡成 34 李芳萍 35 李家建 36 钟日城 37 刘煌晖 38 谢冰 39 黄建翀
龙南实验中学2015——2016学年第一学期月考考试 成绩统计表
语文
数学
总分
名次
0.70
平均分
及格人数 及格率
达标人数(70 达标率
优秀人数(80分 优秀率
特优人数(90以 特优率
后20%平均分
两科均 及格人
数 语数及格率
两科均达标人
两科均达标率
两科均优秀人
两科均优秀率 龙南实验中学2015——2016学年第一学期月考考试
广东省广州市第二中学20152016学年高二上学期第一次月考数学理试卷Word版含答案[高考].doc
![广东省广州市第二中学20152016学年高二上学期第一次月考数学理试卷Word版含答案[高考].doc](https://img.taocdn.com/s3/m/f644f8e4ddccda38376bafe9.png)
广州市第二中学2015-2016学年高二上学期第一次月考试题数 学(理 科) 2015.10一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
请把答案填在答卷的相应位置。
1. 已知集合},01|{R x x xx A ∈≥-=,},12|{R x y y B x ∈+==,则=)(B A C R I ( ) A.]1,(-∞ B. )1,(-∞ C. ]1,0( D. ]1,0[ 2.函数)22sin(2x y -=π是( )A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为2π的偶函数 D .最小正周期为2π的奇函数 3. 已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为 ( ) (A )若,,αγβγ⊥⊥则αβ∥ (B )若,,m n αα⊥⊥则m n ∥ (C )若,m n αα∥∥,则m n ∥ (D )若,,m m αβ∥∥则αβ∥ 4. 已知各项均为正数的等比数列}{n a 中,13213a ,a ,2a 2成等差数列,则=++1081311a a a a ( ) A. 1-B. 3C. 1-或3D. 275. 如图所示的程序框图的运行结果为35S =,那么判断框中应填入的关于k 的条件是( )A .5k >B .6k ≥C .7≥kD .7>k6. 已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为( ) A .43 B .34 C .34- D .43-7. 函数()2sin 1xf x x =+的图象大致为( )8. 将一个长方体截掉一个小长方体,所得几何体的俯视图与侧视图如右图所示,则该几何体的正视图为 ( )A.B.C.D.9. 某工厂对一批新产品的长度(单位:mm )进行检测,如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )(A )20 (B )25 (C )22.5 (D )22.7510. 函数)sin()(ϕω+=x x f (其中2||πϕ<)的图象如图所示,为了得到sin y x ω=的图象,只需把()y f x =的图象上所有点( )(A )向左平移6π个单位长度 (B )向右平移12π个单位长度(C )向左平移12π个单位长度(D )向右平移6π个单位长度11. 若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2,则这样的直线有A .1条B .2条C .3条D .4条12. 已知函数2|lg |0()10x x f x xx >⎧=⎨-≤⎩,则方程2(2)(0)f x x a a +=>的根的个数不可能为A .3B .4C .5D .6二、填空题:本大题共4小题,每小题5分,满分20分。
广州市高二上学期化学第一次月考试卷

广州市高二上学期化学第一次月考试卷姓名:________ 班级:________ 成绩:________一、选择题(本大题共25小题,每小题2分,共50分。
) (共25题;共50分)1. (2分) (2018高三下·绥化开学考) 下列物质属于纯净物的是()A . 液氯B . 氯水C . 漂白粉D . 碘酒2. (2分) (2018高三上·曹县期中) 下列根据化学事实所得出的结论正确的是()选项化学事实结论A BeO与Al2O3均为两性氧化物Be与Al处于周期表中同一主族B HCl与SO2的水溶液均能导电HCl与SO2均是电解质C酸性:H3PO4>HNO3>H2SiO3非金属性:P>N>SiD熔融的AlF3和MgCl2均能导电AlF3和MgCl2均为离子化合物A . AB . BC . CD . D3. (2分) (2016高二上·广州期中) ClO2是一种消毒杀菌效率高、二次污染小的水处理剂.实验室可通过以下反应制得ClO2:2KClO3+H2C2O4+H2SO4 2ClO2↑+K2SO4+2CO2↑+2H2O.下列说法中错误的是()A . KClO3在反应中得到电子B . ClO2中氯的化合价为+4价C . 在反应中H2C2O4是还原剂D . 1 mol KClO3参加反应有2mol电子转移4. (2分) (2016高一上·安庆期中) 今有三个氧化还原反应:①2FeCl3+2KI=2FeCl2+2KCl+I2②2FeCl2+Cl2=2FeCl3③2KMnO4+16HCl=2KCl+2MnCl2+5Cl2↑+8H2O若某溶液中有Fe2+和Cl﹣、I﹣共存,要氧化除去I﹣而又不影响Fe2+和Cl﹣.可加入的试剂是()A . Cl2B . KMnO4C . FeCl3D . HCl5. (2分)中华民族很早就把化学技术应用到生产、生活中.下列有关说法错误的是()A . 英文的“中国”(China)又指“瓷器”,中国很早就应用化学技术制作陶瓷B . “四大发明”之一黑火药是由硫黄、硝石、木炭三种物质按一定比例配制的混合物C . 《淮南万毕术》中有“曾青得铁则化为铜”的记载,其含义是铁可从铜盐溶液中置换出铜D . 杜康用高粱酿酒的原理是通过蒸馏法将高粱中的乙醇分离出来6. (2分)下列物质性质与应用对应关系正确的是()A . 氨气具有碱性,可用作制冷剂B . 二氧化硅能与氢氟酸反应,可用于生产光导纤维C . 铝具有良好导电性和耐腐蚀性,可用于制作高压输电线D . 二氧化铅具有强氧化性,可用于铅蓄电池的负极材料7. (2分)有关化学用语正确的是()A . 乙烯的实验式C2H4B . 乙醇的分子式C2H5OHC . 乙酸乙酯的结构简式 CH3CH2OOCCH3D . 羟基8. (2分) (2019高一上·云南期末) 下图所示的实验装置图正确且能达到相应实验目的的是()图1 图2 图3 图4A . 用图1所示装置除去Cl2中的HClB . 用图2所示装置实验室制NH3C . 用图3所示装置分离MnO2和KClD . 用图4所示装置蒸干NH4Cl饱和溶液制备NH4Cl晶体9. (2分) (2019高二上·齐齐哈尔期中) 下列说法错误的是()A . 人类在远古时代就通过燃烧植物的方式开始利用生物质能B . 氢能是理想的绿色能源,但人们只能将氢气的化学能转化为热能C . 煤中含有硫元素,大量的直接燃烧煤会引起酸雨等环境问题D . 太阳能以光和热的形式传送到地面,人们可以直接利用这些光和热10. (2分)下列实验操作正确的是()A . 给烧杯里的液体直接加热B . 将配制的NaOH溶液保存在配有玻璃塞的细口瓶中C . 用蒸发方法使KCl 从溶液中析出时,应将蒸发皿中KCl 溶液全部加热蒸干D . 分液时,分液漏斗下层液体从下口放出,上层液体从上口倒出11. (2分) (2018高一上·定海期中) 下列说法正确的是()A . 实验室制氯气时,为了防止环境污染,多余的氯气可以用澄清石灰水吸收B . 新制氯水的氧化性强于久置氯水C . 检验HCl气体中是否混有Cl2的方法是将气体通入硝酸银溶液D . 除去HCl气体中的Cl2 ,可将气体通入饱和食盐水12. (2分) (2018高一下·泰州期末) 给定条件下,下列选项中所示的物质间转化,均能一步实现的是()①SO2 (NH4)2SO3 (NH4)2SO4②煤焦炭 (CO+H2) CH3OH③C4H10 C2H4④(C6H10O5)n(淀粉) C6H12O6(葡萄糖) C2H5OHA . ①②③④B . ①③④C . ③④D . ①②13. (2分)下列叙述中能肯定说明金属A比金属B的活泼性强的是()A . A原子最外层电子数比B原子的最外层电子数少B . 将A、B组成原电池时,A为正极C . 1molA从酸中置换生成的H2比1mol B从酸中置换生成的H2多D . 将A和B用导线相连接,一同放入CuSO4溶液中,B的表面有红色的铜析出14. (2分) (2017高一下·射洪期中) 下列有关能源和能量转换的叙述正确的是()A . 推广使用太阳能、风能、海洋能、氢能,有利于缓解温室效应B . 乙醇和汽油都是可再生能源,应大力推广“乙醇汽油”C . 普通锌锰干电池不含环境污染物,用完后可以随意扔掉,使用方便D . 燃料电池是利用燃料燃烧,将化学能转化为热能,然后再转化为电能的化学电源15. (2分) (2015高二下·红河期中) 下列反应的离子方程式表示正确的是()A . 碳酸钙与醋酸溶液反应:CaCO3+2H+=Ca2++CO2+H2OB . 苯酚钠溶液和少量CO2反应:2C6H5O﹣+CO2+H2O=2C6H5OH+CO32﹣C . 溴乙烷与氢氧化钠溶液共热:C2H5Br+OH﹣ C2H5OH+Br﹣D . 用银氨溶液检验乙醛的醛基:CH3CHO+2Ag(NH4)2++2OH﹣ CH3COO﹣+NH4++3NH3+2Ag↓+H2O16. (2分) (2018高二下·林州月考) 2014年我国科学家首次拍摄到水分子团簇的空间取向图像,模型如图。
2015-2016学年高一上学期第一次月考数学试题_Word版含答案

2015--2016学年度高一第一学期第一次月考数学试题(时间:90分钟,总分100分)一、选择题(共10小题,每小题4分)1、已知集合P={x ∈N | 1≤x ≤10},Q={x ∈R| x 2+x -6=0},则P ∩Q=( )A. { 1, 2, 3 }B. { 2, 3}C. { 1, 2 }D. { 2 }2、已知集合U={ 1, 2, 3, 4, 5, 6, 7 },A={ 2, 4, 5, 7 },B={ 3, 4, 5 }则(C ∪A )∪(C ∪B )=( )A. { 1, 6 }B. { 4, 5}C. { 2, 3, 4, 5, 7 }D. { 1, 2, 3, 6, 7 }3、设集合A={ 1, 2 },则满足A ∪B = { 1, 2, 3 }的集合B 的个数是( )A. 1B. 3C. 4D. 84、函数f(x)=x 2+mx+1的图象关于直线x=1对称,则( )A. m=-2B. m=2C. m=-1D. m=15、设f(x)是定义在R 上的奇函数,当x ≤0时,f(x)=2x 2-x, 则f(1)等于( )A. -3B. -1C. 1D. 36、在区间(-∞,0)上为增函数的是( )A. y=1B. y=2x1x +- C. 1x 2x y 2---= D. y=1+x 27、若函数y=f(x)的定义域[-2,4],则函数g(x) = f(x) + f(-x)的定义域是( )A. [-4,4]B. [-2,2]C. [-4,-2]D. [2,4]8、设abc>0,二次函数f(x) = ax 2 + bx + c 的图象可能是( )A. B. C. D.9、函数x2y =的单调减区间为( ) A. R B. (-∞, 0)∪(0, +∞)C. (-∞, 0), (0, +∞)D. (0,+∞)10、已知定义在R 上的奇函数f(x)在(-∞, -1)上是单调减函数,则f(0), f(-3)+f(2)的大小关系是( )A. f(0)<f(-3)+f(2)B. f(0)=f(-3)+f(2)C. f(0)> f(-3) +f(2)D. 不确定二、填空题(本大题共5小题,每小题4分)11、已知集合A={-1, 1, 2, 4}, B={-1, 0, 2},则A ∩B= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市第二中学2015-2016学年高二上学期第一次月考试题数 学(理 科) 2015.10一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
请把答案填在答卷的相应位置。
1. 已知集合},01|{R x x xx A ∈≥-=,},12|{R x y y B x ∈+==,则=)(B A C R ( ) A.]1,(-∞ B. )1,(-∞ C. ]1,0( D. ]1,0[ 2.函数)22sin(2x y -=π是( )A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为2π的偶函数 D .最小正周期为2π的奇函数 3. 已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为 ( ) (A )若,,αγβγ⊥⊥则αβ∥ (B )若,,m n αα⊥⊥则m n ∥ (C )若,m n αα∥∥,则m n ∥ (D )若,,m m αβ∥∥则αβ∥ 4. 已知各项均为正数的等比数列}{n a 中,13213a ,a ,2a 2成等差数列,则=++1081311a a a a ( ) A. 1-B. 3C. 1-或3D. 275. 如图所示的程序框图的运行结果为35S =,那么判断框中应填入的关于k 的条件是( )A .5k >B .6k ≥C .7≥kD .7>k6. 已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为( ) A .43 B .34 C .34- D .43-7. 函数()2sin 1xf x x =+的图象大致为( )8. 将一个长方体截掉一个小长方体,所得几何体的俯视图与侧视图如右图所示,则该几何体的正视图为 ( )A.B.C.D.9. 某工厂对一批新产品的长度(单位:m m )进行检测,如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )(A )20 (B )25 (C )22.5 (D )22.7510. 函数)sin()(ϕω+=x x f (其中2||πϕ<)的图象如图所示,为了得到sin y x ω=的图象,只需把()y f x =的图象上所有点( )(A )向左平移6π个单位长度 (B )向右平移12π个单位长度(C )向左平移12π个单位长度(D )向右平移6π个单位长度11. 若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2,则这样的直线有A .1条B .2条C .3条D .4条12. 已知函数2|lg |0()10x x f x xx >⎧=⎨-≤⎩,则方程2(2)(0)f x x a a +=>的根的个数不可能为A .3B .4C .5D .6二、填空题:本大题共4小题,每小题5分,满分20分。
请把答案填在答题卷的相应位置。
13. 已知平面向量,a b 的夹角为2,2,13a b π==,则a b += 14. 为了调查城市PM2.5的值,按地域把36个城市分成甲、乙、丙三组,对应的城市数 分别为6、12、18。
若用分层抽样的方法抽取12个城市,则乙组中应抽取的城市数 为15. 若x ,y 满足约束条件0,0,1,3412,x y y x x y ≥⎧⎪≥⎪⎨-≥-⎪⎪+≤⎩则x y +的最大值为_______.16. 在三棱锥BCD A -中,底面BCD 为边长为2的正三角形,顶点A 在底面BCD 上的射 影为BCD ∆的中心, 若E 为BC 的中点,且直线AE 与底面BCD 所成角的正切值为,则三棱锥BCD A -外接球的表面积为 ________.三、解答题:本大题共6小题,共70分。
解答应写出文字说明、证明过程或演算步骤 17.(本题满分10分)某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知甲、乙两组技工在单位时间内加工的合格零件的平均数都为10.(1)分别求出m ,n 的值;(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差2s 甲和2s 乙,并由此分析两组技工的加工水平;注:方差2222121=[()()()]n s x x x x x x n-+-+-+ (其中x 为数据12,,,n x x x 的平均数.)18.(本小题满分12分)设函数π()4cos sin()3f x x x =-+,x ∈R . (Ⅰ)当π[0,]2x ∈时,求函数()f x 的值域;(Ⅱ)已知函数()y f x =的图象与直线1y =有交点,求相邻两个交点间的最短距离.19.(本题满分12分)在四棱锥E ABCD -中,底面ABCD 是正方形,AC 与BD 交于点,O EC ⊥底面ABCD ,F 为BE 的中点.(1)求证://DE 平面ACF ;(2)若AB =,在线段EO 上是否存在点G ,使CG ⊥平面BDE ?若存在,求出EGEO的值;若不存在,请说明理由.20.(本小题满分12分)已知点P (0,5)及圆C :x 2+y 2+4x -12y +24=0.(1)若直线l 过点P 且被圆C 截得的线段长为43,求l 的方程; (2)求过P 点的圆C 的弦的中点的轨迹方程.21.(本题满分12分)已知数列{}n a 的前n 项和为n S ,10a =,1n n S n a ++=,*n ∈N . (Ⅰ) 求证:数列{1}n a +是等比数列;(Ⅱ) 设数列{}n b 的前n 项和为n T ,11b =,点1(,)n n T T +在直线112x y n n -=+上,若不等式1212911122n n nb b b m a a a a +++≥-++++ 对于*n ∈N 恒成立,求实数m 的最大值.22. (本题满分12分)已知()f x 是定义在R 上的不恒为零的函数,且对于任意的,x y R ∈都满足:()()()f x y x f y y f x=+. (Ⅰ)判断函数()f x 的奇偶性,并写出证明过程;(Ⅱ) 已知(2)2f =,设n a =(2)nf (n ∈N*),求数列{n a }的通项公式.;(Ⅲ) 若211n nn b n a +=⋅+,数列{}n b 的前n 项和为n S .求证:1n S <.2015-2016学年高二上学期第一次月考(理科数学)参考答案7.A 函数()f x 定义域为R ,又()()()()22sin sin 11x xf x f x x x --==-=-+-+ ,∴函数()f x 为奇函数.其图像关于原点对称.故排除C 、D ,又当0πx <<时,sin 0x >,所以()0f x >可排除B ,故A 正确. 10.D 由图可知74123T T πππ=-⇒= 则22πωπ== ,又sin(2)03πϕ⨯+=,结合2||πϕ<可知3πϕ=,即()s i n3(2)f x x π=+,为了得到sin 2y x =的图象,只需把()s i n (2)s i 3n 26y f x x x ππ⎡⎤⎛⎫==+=+ ⎪⎢⎥⎝⎭⎣⎦的图象上所有点向右平移6π个单位长度.二、填空题.三、解答题. 17.(本小题满分10分)详细分析:(1)根据题意可得:10)10121087(51=+++++=m x甲,∴3=m , 10)1211109(51=++++=n x乙,∴8=n;(2)根据题意可得:2222221[(710)(810)(1010)(1210)(1310)] 5.25s =-+-+-+-+-=甲,2222221[(810)(910)(1010)(1110)(1210)]25s =-+-+-+-+-=乙,∵乙甲x x =,22乙甲s s <,∴甲乙两组的整体水平相当,乙组更稳定一些; 18. (本小题满分12分)详细分析:(Ⅰ)解:因为1()4cos (sin )2f x x x x =-+2π2sin cos cos sin 2cos 22sin(2)3x x x x x x =-+=-=-因为π02x ≤≤, 所以ππ2π2333x --≤≤. 所以sin(π2)123x --≤, 即()2f x ≤,其中当5π12x =时,()f x 取到最大值2;当0x =时,()f x 取到最小值所以函数()f x 的值域为[. (Ⅱ)依题意,得π2sin(2)13x -=,π1sin(2)32x -=, 所以ππ22π36x k -=+ 或 π5π22π36x k -=+, 所以ππ4x k =+ 或 7ππ12x k =+()k ∈Z ,所以函数()y f x =的图象与直线1y =的两个相邻交点间的最短距离为π3.19.(本小题满分12分) 详细分析:(1)证明:连接OF由四边形ABCD 是正方形可知,点O 为BD 的中点 又F 为BE 的中点,所以//OF DE又OF ⊂平面ACF ,DE ⊄平面ACF .所以//DE 平面ACF (2)解法一:若CG ⊥平面BDE ,则必有CG OE ⊥ 于是作CG OE ⊥于点G由EC ⊥底面ABCD ,所以BD EC ⊥,又底面ABCD 是正方形 所以BD AC ⊥,又EC AC C ⋂=,所以BD ⊥平面ACE而CG ⊂平面ACE ,所以CG BD ⊥,又OE BD O ⊥=,所以CG ⊥平面BDE又AB =,所以CO AB CE ==.所以G 为EO 的中点,所以12EG EO = 解法二:取EO 的中点G ,连接CG ,在四棱锥E ABCD -中AB =,CO AB CE ==,所以CG EO ⊥ 又由EC ⊥底面ABCD ,BD ⊂底面ABCD ,所以EC BD ⊥ 由四边形ABCD 是正方形可知,AC BD ⊥又AC EC C ⋂=.所以BD ⊥平面ACE , 而BD ⊂平面BDE 所以,平面ACE ⊥平面BDE ,且平面ACE ⋂平面BDE EO =因为CG EO ⊥,CG ⊂平面ACE ,所以CG ⊥平面BDE 故在线段EO 上存在点G ,使CG ⊥平面BDE .由G 为EO 的中点,得12EG EO =20.(本小题满分12分)解 (1)如图所示,|AB |=43,将圆C 方程化为标准方程为 (x +2)2+(y -6)2=16,∴圆C 的圆心坐标为(-2,6),半径r =4,设D 是线段AB 的中点,则CD ⊥AB , ∴|AD |=23,|AC |=4.C 点坐标为(-2,6). 在Rt △ACD 中,可得|CD |=2.设所求直线l 的斜率为k ,则直线l 的方程为:y -5=kx ,即kx -y +5=0. 由点C 到直线AB 的距离公式:|-2k -6+5|k 2+(-1)2=2,得k =34.故直线l 的方程为3x -4y +20=0.又直线l 的斜率不存在时,也满足题意,此时方程为x =0. ∴所求直线l 的方程为x =0或3x -4y +20=0. (2)设过P 点的圆C 的弦的中点为D (x ,y ), 则CD ⊥PD ,即·=0,∴(x +2,y -6)·(x ,y -5)=0,化简得轨迹方程为x 2+y 2+2x -11y +30=0.21. (本小题满分12分) 详细分析:(Ⅰ)由1n n S n a ++=, 得11(2)n n S n a n -+-=≥ ,两式相减得121n n a a +=+, 所以112(1)n n a a ++=+ (2n ≥), 因为10a =,所以111a +=,2111a a =+=,2112(1)a a +=+ 所以{1}n a +是以1为首项,公比为2的等比数列 (Ⅱ)由(Ⅰ)得121n n a -=-,因为点1(,)n n T T +在直线112x y n n -=+上,所以1112n n T T n n +-=+, 故{}n T n是以111T =为首项,12为公差的等差数列,则11(1)2n T n n =+-,所以(1)2n n n T +=, 当2n ≥时,1(1)(1)22n n n n n n n b T T n -+-=-=-=, 因为11b =满足该式,所以n b n =所以不等式1212911122n n nb b b m a a a a +++≥-++++ , 即为2123912222n n n m -+++≥- , 令21231222n n n R -=+++ ,则23112322222n n nR =+++ ,两式相减得231111112(1)122222222n n n n n n R -+-=++++-=- ,所以1242n n n R -+=-由92n n R m ≥-恒成立,即2542nn m --≥恒成立, 又11232527(4)(4)222n n n n n n ++------=,故当3n ≤时,25{4}2n n --单调递减;当3n =时,323531428⨯--=; 当4n ≥时,25{4}2n n --单调递增;当4n =时,4245614216⨯--=; 则2542nn --的最小值为6116,所以实数m的最大值是6116 22. (本小题满分12分)解:(Ⅰ)f (x )是奇函数,证明如下: f (1)=f (1·1)=1·f (1)+1·f (1),得f (1)=0.因为f (1)=f [(-1)2]=-f (-1)-f (-1)=0 所以f (-1)=0∴f (-x )=f (-1·x )=-f (x )+xf (-1)=-f (x ).因此,f (x )为奇函数 ……4分 (Ⅱ) 1(2)2,a f == 且()()()f xy xf y yf x =+ 令12,2n x y -==1111(2)(22)2(2)2(2)2(2)2n n n n n n f f f f f ----∴=⋅=+=+即122(2),n n n a a n -=+≥111222n n n n n n a a a --⎧⎫∴=+∴⎨⎬⎩⎭是以1为首项,1为公差的等差数列, 1(1)2nn a n n ∴=+-=,即2n n a n =⋅ ……8分 (Ⅲ)因为n n 1212112[]1n(n 1)22(n 1)2n n n n n b n a n +++=⋅==-+++, ……10分 所以 122311111112[()()...()]122222322(1)2n n n S n n +=-+-++-⋅⋅⋅⋅⋅+⋅ 1112[]12(1)2n n +=-<+⋅ …………12分。
