概率统计课件7-1
合集下载
《统计与概率》课件

概率基础
1 概率定义
概率是事件发生的可能性,介于0和1之间。 通过概率可以评估随机事件的发生概率。
2 概率规则
概率规则包括加法规则、乘法规则和条件概 率等,用于计算复杂事件的概率。
数据收集和分析
1 数据收集方法
数据收集可以通过实验、调查、观察等方式 进行,确保数据的准确性和可靠性。
2 数据分析技术
《统计与概率》PPT课件
欢迎来到《统计与概率》的PPT课件!在这个课件中,我们将一起探索统计学 和概率论的基本概念、方法以及它们在实际应用中的重要性。
什么是统计与概率
统计与概率是数据分析和决策支持的基石。统计学关注数据的收集、整理和 解释,而概率论关注不确定性和随机事件的概率分布。
基本概念:统计学和概率论
总结和提高建议
通过本课件的学习,你将了解统计与概率的基本概念和方法,以及它们在实 际应用中的重要性。掌握这些知识将有助于你在数据分析和决策过设检验、回 归分析等,帮助我们从数据中提取有用信息 和洞察。
统计与概率的应用
1 实际应用案例
统计与概率在医学研究、市场调查、金融风 险评估等领域有广泛的应用。
2 统计与概率的重要性
统计与概率的应用可以为决策制定提供科学 依据,并预测事件的可能结果,帮助我们做 出更明智的选择。
统计学
通过收集和分析数据来描述和理解现象,帮助 我们揭示数据背后的规律和趋势。
概率论
研究随机现象的可能性和概率,为我们预测和 评估事件的发生提供基础。
统计方法
1 描述统计
2 推断统计
通过图表、概括统计量等方法,对数据进行 整理、总结和描述,揭示数据的特征和趋势。
基于样本数据,利用统计方法进行推断,对 总体的特征和参数进行估计和判断。
概率统计各章节知识点总结.ppt

概率统计各章节总结
第一章
概率的计算
1)统计定义: fn ( A) n 稳定值 P( A)
2)概率的性质:1~5
3)等可能概型:P(
A)
m n
4)条件概率:P(B
A)
k m
P( AB) P( A)
独立
5)乘法定理: P( AB) P( A)P(B A) P(A)P(B)
1 P(A B)
A AB1 U AB2
1 n
n k 1
Xk
P
p
X1, X 2 , , X n , 相互独立
E( Xk ) 同分布
1
n
n k 1
Xk
P
n
X1 , X 2 , , X n , 相互独立
X k n 近似
同分布E( X k ) D( X k ) 2 k1 n
~ N (0,1)
Xn ~ B(n, p)
Xn np
X ~ N (, 2 ) Th1 X ~ N (, 2 n),
Th2
X1, X 2 , , X n (n 1)S 2 2 ~ 2(n 1) 独立
X , S 2
1n X n i1 X i
S 2
1 n1
n i 1
(Xi
X )2
X ~ t(n 1)
Sn
第六章
常用统计量及抽样分布
2统计量
6)全概率公式:P( A) P(B1 )P( A B1 ) P(B2 )P( A B2 )
7)贝叶斯公式:P(B1
A)
P(B1 )P( A B1 ) P( A)
A
B1
互斥
B2
第二章
随机变量概率分布
离散型随机变量
连续型随机变量
第一章
概率的计算
1)统计定义: fn ( A) n 稳定值 P( A)
2)概率的性质:1~5
3)等可能概型:P(
A)
m n
4)条件概率:P(B
A)
k m
P( AB) P( A)
独立
5)乘法定理: P( AB) P( A)P(B A) P(A)P(B)
1 P(A B)
A AB1 U AB2
1 n
n k 1
Xk
P
p
X1, X 2 , , X n , 相互独立
E( Xk ) 同分布
1
n
n k 1
Xk
P
n
X1 , X 2 , , X n , 相互独立
X k n 近似
同分布E( X k ) D( X k ) 2 k1 n
~ N (0,1)
Xn ~ B(n, p)
Xn np
X ~ N (, 2 ) Th1 X ~ N (, 2 n),
Th2
X1, X 2 , , X n (n 1)S 2 2 ~ 2(n 1) 独立
X , S 2
1n X n i1 X i
S 2
1 n1
n i 1
(Xi
X )2
X ~ t(n 1)
Sn
第六章
常用统计量及抽样分布
2统计量
6)全概率公式:P( A) P(B1 )P( A B1 ) P(B2 )P( A B2 )
7)贝叶斯公式:P(B1
A)
P(B1 )P( A B1 ) P( A)
A
B1
互斥
B2
第二章
随机变量概率分布
离散型随机变量
连续型随机变量
概率论与数理统计课件7.1

P( X xi , Y y j ) pij , i 1,2, ; j 1,2,
则随机变量 X、Y的数学期望分别为
E ( X ) xi pi
i 1
x p
i 1 j 1
i
ij
E (Y ) y j p j y j pij
n i n i n i i 1 i 1 ( n 1) ( i 1) np Cn q 1 p n
n
i i 1
np C
i0
i 1 n 1
i n 1
p q
i
( n 1) i
np( p q)
n 1
np
例3 设X ~ P( ), 求E ( X ).
i 1 j 1
注意:数学上要求 | g ( xi , y j ) | pij .
i 1 j 1
6、 设二维连续随机变量 ( X , Y )的联合密度函数
为f ( x, y),
则随机变量函数 Z g ( X , Y )的数学期望为
E (Z ) E[ g ( X , Y )]
5.设X , Y是两个随机变量 , a, b为常数,则 E (aX bY ) aE( X ) bE(Y )
6.设X , Y是相互独立的随机变量 ,则 E ( XY ) E ( X ) E (Y )
注: 1. 性质(5)和(6)可以推广到有限个随机 变量X1, X2, …, Xn 的情况; 2. 对于“和”,不要求X1,X2,…,Xn相互 独立; 对于“积”要求X1,X2,…,Xn相互独立。
: 例12 已知X和Y相互独立,分布列如下
0
x
dx xde x
《概率统计》PPT课件

后抽比先抽的确实吃亏吗?
“大家不必争先恐后,你们一个一个 按次序来,谁抽到‘入场券’的机会都 一样大.”
到底谁说的对呢?让我们用概率 论的知识来计算一下,每个人抽到“ 入场券”的概率到底有多大?
“先抽的人当然要比后抽的人抽到的机会大。”
我们用Ai表示“第i个人抽到入场券” i=1,2,3,4,5. 则 A 表示“第 i个人未抽到入场券” i 显然,P(A1)=1/5,P( A1)=4/5
P(A2)=0.4×0.5×(1-0.7)+0.5×0.7×(1-0.4)+ 0.4×0.7×(1-0.5)=0.41, P(A3)=0.4×0.5×0.7=0.14 P(B|A0)=0, P(B|A1)=0.2, P(B|A2)=0.6, P(B|A3)=1, 根据全概率公式有
P( B) P( B | Ai )P( Ai ) 0.458
P(Ai|B),表示症状B由Ai引起的概率 若P(Ai|B), i=1,2,…,n中,最大的一个是P(A1|B),
我们便认为A1是生病的主要原因,下面的关键是:
计算 P(Ai|B), i=1,2,…,n
P( Ai B) P( B | Ai ) P( Ai ) P( Ai | B) n Bayes公式 P( B) P( B | Ai ) P( Ai )
也就是说,
第1个人抽到入场券的概率是1/5.
由于 由乘法公式
A2 A1 A2
因为若第2个人抽到 了入场券,第1个人 肯定没抽到.
P ( A2 ) P ( A1 ) P ( A2 | A1 )
也就是要想第2个人抽到入场券,必须第1个人未 抽到, 计算得:
P(A2)= (4/5)(1/4)= 1/5
概率论与数理统计(王明慈第二版)第2章随机变量及其分布7-1节
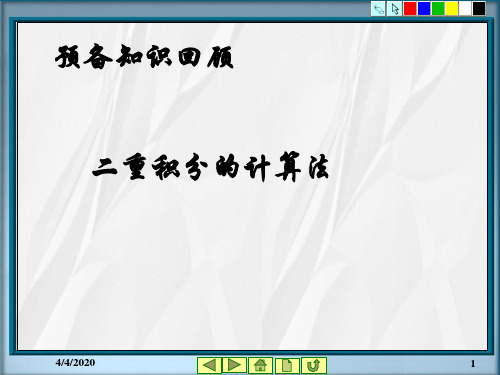
D
1
dx
1 x e( x y)dy.
00
y
1
x y1
1e xdx 1 x e ydy
0
0
D
0
1x
1e x (e y )1 x dx
0
0
1e x (1 ex1) dx 1(e x e1) dx
0
0
1 2e1 0.2642
4/4/2020
26
例 4 设二维随机变量X, Y 的密度函数为
x 0
y 0
f (u, v) du dv,
x 0, y 0,
0,
其他.
x 0
y e(uv) dudv,
0
x 0, y 0,
0,
其他.
(1
e
x
)(1
e
y
),
0,
x 0, y 0, 其他.
4/4/2020
25
(2) P{(X ,Y ) D} p( x, y)dx dy.
4/4/2020
18
X Y
x1 x2 xi
y1
p11 p21 … pi1 …
y2 p12 p22 … pi2 …
……
…… ……
y j p1 j p2 j … pij …
其中 pij满足: (1) pij 0, (i, j 1,2, );
(2) pij 1.
i1 j1
4/4/2020
预备知识回顾 二重积分的计算法
4/4/2020
1
利用直角坐标计算二重积分
被积函数 f (x, y) 且在积分区域D上连续时,
若D为 X - 型区域
y y 2(x)
则
高三数学(理科)二轮(专题7)《概率与统计1-7-1》ppt课件
热点二 排列组合
[命题方向] 1.排列组合的简单应用.2.排列组合的综合应用.
山 东 金 太 阳 书 业 有 限 公 司
菜 单 隐藏
高考专题复习 ·数学(理)
析热点 高考 聚集
研思想 方法 提升
课时 跟踪
1.(2014年重庆高考)某次联欢会要安排3个歌舞类节目、2个小品
训练
类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是
提升
课 时 讨论.其一:|x1|+|x2|+|x3|+|x4|+|x5|=1,此时,从 x1,x2,x3,x4,x5
跟踪
训 练 中任取一个让其等于 1 或-1,其余等于 0,于是有 C15C12=10 种情况;
其二:|x1|+|x2|+|x3|+|x4|+|x5|=2,此时,从 x1,x2,x3,x4,x5 中任取两
()
A.72
B.120
C.144
D.168
山
东
解析:依题意,先仅考虑 3 个歌舞类节目互不相邻的排法种数为 A33 金
太 A34=144,其中 3 个歌舞类节目互不相邻但 2 个小品类节目相邻的排法种 阳
书 数为 A22A22A33=24,因此满足题意的排法种数为 144-24=120,选 B. 业
C.145 D.146
解析:分四种情况进行讨论:
(1)a3 是 0,a1 和 a2 有 C25种排法,a4 和 a5 有 C25种排法,则五位自然
山 东
数中“凹数”有 C25C25=100 个;(2)a3 是 1,有 C24C24=36 个;(3)a3 是 2,
金 太
有 C23C23=9 个;(4)a3 是 3,有 C22C22=1 个.由分类加法计数原理知五位
[命题方向] 1.排列组合的简单应用.2.排列组合的综合应用.
山 东 金 太 阳 书 业 有 限 公 司
菜 单 隐藏
高考专题复习 ·数学(理)
析热点 高考 聚集
研思想 方法 提升
课时 跟踪
1.(2014年重庆高考)某次联欢会要安排3个歌舞类节目、2个小品
训练
类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是
提升
课 时 讨论.其一:|x1|+|x2|+|x3|+|x4|+|x5|=1,此时,从 x1,x2,x3,x4,x5
跟踪
训 练 中任取一个让其等于 1 或-1,其余等于 0,于是有 C15C12=10 种情况;
其二:|x1|+|x2|+|x3|+|x4|+|x5|=2,此时,从 x1,x2,x3,x4,x5 中任取两
()
A.72
B.120
C.144
D.168
山
东
解析:依题意,先仅考虑 3 个歌舞类节目互不相邻的排法种数为 A33 金
太 A34=144,其中 3 个歌舞类节目互不相邻但 2 个小品类节目相邻的排法种 阳
书 数为 A22A22A33=24,因此满足题意的排法种数为 144-24=120,选 B. 业
C.145 D.146
解析:分四种情况进行讨论:
(1)a3 是 0,a1 和 a2 有 C25种排法,a4 和 a5 有 C25种排法,则五位自然
山 东
数中“凹数”有 C25C25=100 个;(2)a3 是 1,有 C24C24=36 个;(3)a3 是 2,
金 太
有 C23C23=9 个;(4)a3 是 3,有 C22C22=1 个.由分类加法计数原理知五位
概率与统计第7章——概率论课件PPT
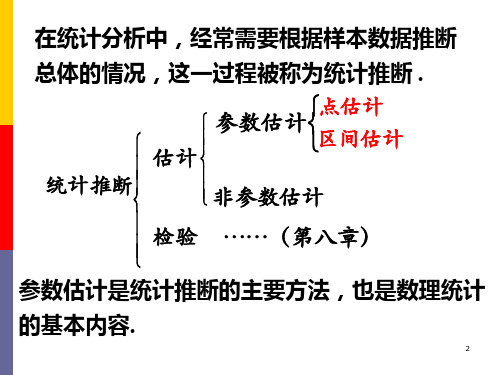
ˆ 是θ的无偏估计,并不保证在任何情况下 (即对于任何一次样本观测值),估计值 ˆ (x1,x2,…,xn)必等于θ 。
无偏性只保证没有系统偏差,即用 ˆ估计θ时, 偏差 ˆ 是随机的,有时大于零,有时小于 零,而平均为零。显然,平均为零这一点只有 在大量重复使用时才能体现出来。 但是选取的样本容量是有限的
在统计分析中,经常需要根据样本数据推断
总体的情况,这一过程被称为统计推断 .
统计推断
估计
参数估计区点间估估计计
非参数估计
检验
……(第八章)
参数估计是统计推断的主要方法,也是数理统计
的基本内容.
2
在参数估计问题中,假定
形式已
知,未知的仅仅是一个或几个参数.
参数估计问题的一般提法
已知统计总体的分布函数为 F(x, ),
6
7.1 点估计及其优良性
7.1.1 点估计的概念
例7.1 已知某连续生产线上生产的灯泡的使用寿
命X ~N(, 2),其中, 2是未知参数,从中随机
抽出5只灯泡,测得使用寿命(单位:h)为: 1529 1513 1600 1527 1411试估 Nhomakorabea, 2的值.
7
由于参数 和2 分别是总体X的均值和方差,即
S 2
1 n1
n
(Xi
i 1
X )2
14
那么要问:
样本均值是否是 的一个好的估计量? 样本方差是否是 2的一个好的估计量?
这就需要讨论以下几个问题:
(1) 我们希望一个“好的”估计量具有什么 特性?
(2) 怎样决定一个估计量是否比另一个估计 量“好”?
(3) 如何求得合理的估计量?
15
7.1.2 估计量的优良性 我们知道,对同一未知参数可以构造出许多的 估计量。 评价这些估计量的好坏, 有以下几个标准:
无偏性只保证没有系统偏差,即用 ˆ估计θ时, 偏差 ˆ 是随机的,有时大于零,有时小于 零,而平均为零。显然,平均为零这一点只有 在大量重复使用时才能体现出来。 但是选取的样本容量是有限的
在统计分析中,经常需要根据样本数据推断
总体的情况,这一过程被称为统计推断 .
统计推断
估计
参数估计区点间估估计计
非参数估计
检验
……(第八章)
参数估计是统计推断的主要方法,也是数理统计
的基本内容.
2
在参数估计问题中,假定
形式已
知,未知的仅仅是一个或几个参数.
参数估计问题的一般提法
已知统计总体的分布函数为 F(x, ),
6
7.1 点估计及其优良性
7.1.1 点估计的概念
例7.1 已知某连续生产线上生产的灯泡的使用寿
命X ~N(, 2),其中, 2是未知参数,从中随机
抽出5只灯泡,测得使用寿命(单位:h)为: 1529 1513 1600 1527 1411试估 Nhomakorabea, 2的值.
7
由于参数 和2 分别是总体X的均值和方差,即
S 2
1 n1
n
(Xi
i 1
X )2
14
那么要问:
样本均值是否是 的一个好的估计量? 样本方差是否是 2的一个好的估计量?
这就需要讨论以下几个问题:
(1) 我们希望一个“好的”估计量具有什么 特性?
(2) 怎样决定一个估计量是否比另一个估计 量“好”?
(3) 如何求得合理的估计量?
15
7.1.2 估计量的优良性 我们知道,对同一未知参数可以构造出许多的 估计量。 评价这些估计量的好坏, 有以下几个标准:
《概率统计》课件

常用概率分布
正态分布
探索正态分布的特点和应用,在数据分析中发挥重要作用。
泊松分布
介绍泊松分布的概念和用途,用于计数型随机事件的建模。
二项分布
了解二项分布的性质和应用,用于描述二元随机实验的结果。
常用统计推断方法
假设检验
学习如何根据样本数据对总体参 数进行推断并做出决策。
置信区间
了解如何构建置信区间,对总体 参数进行估计。
探索数据可视化的重要性,并学 习如何使用图表和图形来传达统 计信息。
统计推断
了解统计推断的基本原理和方法, 从样本中得出总体的结论。
概率与统计的关系
1
概率理论的基础
说明概率理论是统计学建率现象中的重要性。
3
共同目标
强调概率与统计的共同目标是推断和预测未来事件。
回归分析
探索回归分析的基本概念和方法, 研究变量之间的关系。
结论及总结
通过本课程,我们希望您能够充分理解概率与统计的基本概念和应用。祝您在概率与统计的世界中取得巨大成 功!
了解事件的定义和样本空 间的概念,以及它们在概 率计算中的重要性。
2 概率的性质
探索概率的基本性质,如 加法规则、乘法规则和条 件概率。
3 随机变量
介绍随机变量的概念,了 解离散和连续随机变量以 及它们的应用。
统计的基本概念
数据收集与整理
数据可视化
学习如何有效地收集和整理数据, 并了解常见的数据类型。
《概率统计》PPT课件
PPT课件的目的 课程概述 概率的基本概念 统计的基本概念 概率与统计的关系 常用概率分布 常用统计推断方法 结论及总结
引言
欢迎来到《概率统计》的世界!在这个课程中,我们将探讨概率与统计的基 础知识,了解它们的关系以及如何应用它们来解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故
θˆ = max{x1 , x2 ,⋯ , xn }
武汉科技大学理学院 15
当未知参数不止一个时,似然函数L是一个多元函 数,这个多元函数的最大值点就是未知参数的最 大似然估计。
2 2 例 设 X ~ N ( µ , σ ), µ , σ 是未知参数,x1 , x2 ,⋯ , xn
2 是来自总体X的样本值,求 µ , σ 的最大似然估计.
= 8θ 4 (1 − 3θ )
ln L(θ ) = ln 8 + 4 ln θ + ln(1 − 3θ )
d ln L(θ ) 4 3 ˆ= 4 = − = 0 ⇒θ dθ 15 θ 1 − 3θ
两种估计方法所得结果不一样.
武汉科技大学理学院
14
例 设总体X在(0,θ)上服从均匀分布, X 1 ,⋯ , X n 是来自总体的样本,求θ的最大似然估计。 解
µ1 = A1 µ = A 2 2 ⋮ µk = Ak
1 n l 其中µl = E ( X l ), Al = ∑ X i l = 1, 2,⋯ k n i =1 上述方程组包含k个未知参数 θ1 , θ 2 ,⋯θ k ,其解
武汉科技大学理学院 3
θi = θi ( A1 , A2 ,⋯ , Ak ), i = 1, 2,⋯ , k ˆ 称为 θi 的矩估计,记为θ , i = 1, 2,⋯ k .
武汉科技大学理学院
5
求矩估计的一般步骤: 求矩估计的一般步骤: ⑴观察未知参数的个数k,算出 µ1 , µ2 ,⋯ , µk . ⑵构造方程(组)µi = Ai , i = 1, 2,⋯ , k ⑶解上述方程(组),其解即为未知参数的矩估 计。 常见情况: k=1,解下列方程:
EX = X
K=2时,解下列方程组
第七章 参数估计 第一次课
•点估计
武汉科技大学理学院
1
§1点估计
问题的提法:设总体 X ~ F ( x, θ ), F 形式已知, 问题的提法: θ是待估参数。利用样本构造适当的统计量
ˆ θ ( X 1 ,⋯ , X n ),以 其观察值作为未知参数θ的近似
ˆ 值,则称 θˆ( X 1 ,⋯ , X n )为θ的估计 的估计,简记为 θ .
1 = (2π ) (σ ) exp − 2 2σ
∑ ( xi − µ ) i =1
n 2
n n 1 ln L = − ln(2π ) − ln σ 2 − 2 2 2 2σ
( xi − µ ) 2 ∑
i =1
n
令
∂ 1 n ln L = 2 ∑ xi − nµ = 0 σ i =1 ∂µ n ∂ ln L = − n + 1 ( xi − µ ) 2 = 0 ∑ ∂σ 2 2σ 2 2σ 4 i =1
L(θ ) A f ( x1 , θ ) f ( x2 , θ )⋯ f ( xn , θ )
武汉科技大学理学院 8
定义
n ∏ P{ X = xi }, 当X 为离散型 i =1 L(θ ) = n ∏ f ( xi ,θ ), 当X 为连续型 i =1
称为总体X 的似然函数。
解得
ˆ µ = X,
1 n ˆ σ = ∑ ( X i − X )2 n i =1
2
武汉科技大学理学院 17
与相应的矩估计相同。
最大似然估计的传递性
ˆ 若θ 是θ的最大似然估计,u = u (θ )具有单值反函数, ˆ ˆ 则u = u (θ )是u (θ )的最大似然估计。
1 n ˆ σ 2的最大似然估计σ 2= ∑ ( X i − X ) 2 , 则σ 的最大 例如, n i =1
主要问题: 主要问题:如何构造合适的统计量? 下面介绍两种常见的方法:矩估计法 最大 矩估计法和最大 矩估计法 似然估计法. 似然估计法
武汉科技大学理学院 2
一、矩估计法 根据 设θ1 , θ 2 ,⋯θ k 是总体X 分布中的待估参数, 辛钦大数定律,样本的各阶原点矩依概率收敛于 总体的对应阶的原点矩,故令
EX = A1 2 EX = A2
EX = X 1 n 2 2 DX + ( EX ) = n ∑ X i i =1
6
即
武汉科技大学理学院
二、最大似然估计 1.最大似然原理:在一次试验中,有很多个事 最大似然原理: 最大似然原理 件可能发生,结果事件A发生了,则有理由认 为A发生的概率最大。 例 一袋中装有红白两种球,共100个。其中一 种颜色的球99个,另一种颜色的1个,从中任取 一个是红球,试判断,哪种颜色的球为99个? 分析 应判断为红色的球是99个,否则不符合最 大似然原理。
µ1 = EX = µ µ2 = EX 2 = DX + ( EX ) 2 = σ 2 + µ 2
µ = A1 µ1 = A1 由 ⇒ 2 µ2 = A2 µ + σ 2 = A2 ˆ µ = A1 = X ⇒ 2 1 n 2 1 n n −1 2 2 2 2 ˆ σ = A2 − A1 = n ∑ X i − X = n ∑ ( X i − X ) = n S i =1 i =1
θ ∈Θ
ˆ 则称θ 为θ的最大似然估计。
如果 L(θ ) 可微,可用求导的办法找到它的最大值点, 为了求导方便,通常求 的最大值点。 ln L(θ )
武汉科技大学理学院 11
例 设 X ~ b(1, p ), x1 , x2 ,⋯ , xn 为样本,求p的最大似 然估计。 解
X 的分布率为P{ X = x} = p (1 − p ) , x = 0,1
θ
EX = θ + 4θ + 3(1 − 3θ ) = 3 − 4θ
由
1 X = (1 + 2 + 2 + 2 + 3) = 2 5 ˆ EX = X ⇒ 3 − 4θ = 2 ⇒ θ = 0.25
武汉科技大学理学院 13
⑵最大似然估计 似然函数 L(θ ) = P{ X = 1}P{ X = 2}P{ X = 2}P{ X = 2}P{ X = 3}
L 注 当样本观察值 x1 , x2 ,⋯ , xn 看成变量时, (θ )
就是样本 X 1 ,⋯ , X n 的概率分布; x1 , x2 ,⋯ , xn 看成已知数时, L(θ ) 是未知参数θ的函数, 便是似然函数。
武汉科技大学理学院 9
例 设总体
X 的密度为
λ
λ e − λ x , x > 0 f ( x, λ ) = x≤0 0,
x
1− x
似然函数为
L( p) = ∏ p (1 − p )
xi i =1 n 1− xi
= p i=1 (1 − p )
∑ xi
n
n−
∑ xi
i =1
n
n n ln L( p ) = ∑ xi ln p + n − ∑ xi ln(1 − p ) i =1 i =1
= P{ X 1 = x1}⋯ P{ X n = xn } = p ( x1 , θ )⋯ p ( xn , θ ) A L(θ )
L(θ ) 是参数θ的函数,表示事件A发生的概率.
若X 是连续型,密度函数为f ( x,θ ) 根据离散型
随机变量与连续型的对应关系: p( xi ,θ ) ~ f ( xi ,θ )
令
d ln L( p ) = dp
∑x
i =1
n
i
p
−
n − ∑ xi 1− p
i =1
n
1 n ˆ = 0 ⇒ p = ∑ xi = X n i =1
12
武汉科技大学理学院
例 设总体X的分布率为
X
1
2
3
θ
2θ
1 − 3θ
1,2,2,2,3,为一组样本观察值,求 的矩估计和最大似然估计. 解 ⑴矩估计
武汉科技大学理学院
7
2.似然函数 似然函数
设总体X 的分布率为P{ X = xi } = p( xi , θ ), i = 1, 2,⋯
x1 , x2 ,⋯ xn 是样本观察值,记
则 P( A) = P{ X 1 = x1 ,⋯ , X n = xn }
A = { X 1 = x1 ,⋯ , X n = xn }
解
X 的密度为
f ( x;µ , σ 2 ) = 1 1 exp − 2 ( x − µ ) 2 2πσ 2σ
似然函数为
武汉科技大学理学院
16
L( µ , σ ) = ∏
2 i =1
n
1 1 exp − 2 ( xi − µ ) 2 2πσ 2σ
− n 2 2 − n 2
1 , 0≤x≤θ X 的密度f ( x) = θ 0, 其它
似然函数
1 n , 0≤x1 , x2 ,⋯ , xn ≤θ L(θ ) = θ 0, 其它
由于要满足 θ≥x1 , x2 ,⋯ , xn 因此,当
θ = max{x1 , x2 ,⋯ , xn }时,L(θ )最大
L(θ ) = P{ X = 1}P{ X = 2}P{ X = 2}P{ X = 3} = 4θ 3 (1 − 3θ )
武汉科技大学理学院 10
3.最大似然估计 最大似然估计 似然函数的值越大,对应的样本出现(或落在样 本的邻域)的概率也越大,因此,应选使似然函 数值最大的参数值作为未知参数的估计。 定义 设总体X 的似然函数为L(θ ), θ的取值范围为Θ, ˆ 若θ ∈ Θ满足 ˆ L(θ ) = max L(θ ),
1 n ˆ ˆ 似然估计σ= σ 2= ∑ ( X i − X )2 n i =1
θˆ = max{x1 , x2 ,⋯ , xn }
武汉科技大学理学院 15
当未知参数不止一个时,似然函数L是一个多元函 数,这个多元函数的最大值点就是未知参数的最 大似然估计。
2 2 例 设 X ~ N ( µ , σ ), µ , σ 是未知参数,x1 , x2 ,⋯ , xn
2 是来自总体X的样本值,求 µ , σ 的最大似然估计.
= 8θ 4 (1 − 3θ )
ln L(θ ) = ln 8 + 4 ln θ + ln(1 − 3θ )
d ln L(θ ) 4 3 ˆ= 4 = − = 0 ⇒θ dθ 15 θ 1 − 3θ
两种估计方法所得结果不一样.
武汉科技大学理学院
14
例 设总体X在(0,θ)上服从均匀分布, X 1 ,⋯ , X n 是来自总体的样本,求θ的最大似然估计。 解
µ1 = A1 µ = A 2 2 ⋮ µk = Ak
1 n l 其中µl = E ( X l ), Al = ∑ X i l = 1, 2,⋯ k n i =1 上述方程组包含k个未知参数 θ1 , θ 2 ,⋯θ k ,其解
武汉科技大学理学院 3
θi = θi ( A1 , A2 ,⋯ , Ak ), i = 1, 2,⋯ , k ˆ 称为 θi 的矩估计,记为θ , i = 1, 2,⋯ k .
武汉科技大学理学院
5
求矩估计的一般步骤: 求矩估计的一般步骤: ⑴观察未知参数的个数k,算出 µ1 , µ2 ,⋯ , µk . ⑵构造方程(组)µi = Ai , i = 1, 2,⋯ , k ⑶解上述方程(组),其解即为未知参数的矩估 计。 常见情况: k=1,解下列方程:
EX = X
K=2时,解下列方程组
第七章 参数估计 第一次课
•点估计
武汉科技大学理学院
1
§1点估计
问题的提法:设总体 X ~ F ( x, θ ), F 形式已知, 问题的提法: θ是待估参数。利用样本构造适当的统计量
ˆ θ ( X 1 ,⋯ , X n ),以 其观察值作为未知参数θ的近似
ˆ 值,则称 θˆ( X 1 ,⋯ , X n )为θ的估计 的估计,简记为 θ .
1 = (2π ) (σ ) exp − 2 2σ
∑ ( xi − µ ) i =1
n 2
n n 1 ln L = − ln(2π ) − ln σ 2 − 2 2 2 2σ
( xi − µ ) 2 ∑
i =1
n
令
∂ 1 n ln L = 2 ∑ xi − nµ = 0 σ i =1 ∂µ n ∂ ln L = − n + 1 ( xi − µ ) 2 = 0 ∑ ∂σ 2 2σ 2 2σ 4 i =1
L(θ ) A f ( x1 , θ ) f ( x2 , θ )⋯ f ( xn , θ )
武汉科技大学理学院 8
定义
n ∏ P{ X = xi }, 当X 为离散型 i =1 L(θ ) = n ∏ f ( xi ,θ ), 当X 为连续型 i =1
称为总体X 的似然函数。
解得
ˆ µ = X,
1 n ˆ σ = ∑ ( X i − X )2 n i =1
2
武汉科技大学理学院 17
与相应的矩估计相同。
最大似然估计的传递性
ˆ 若θ 是θ的最大似然估计,u = u (θ )具有单值反函数, ˆ ˆ 则u = u (θ )是u (θ )的最大似然估计。
1 n ˆ σ 2的最大似然估计σ 2= ∑ ( X i − X ) 2 , 则σ 的最大 例如, n i =1
主要问题: 主要问题:如何构造合适的统计量? 下面介绍两种常见的方法:矩估计法 最大 矩估计法和最大 矩估计法 似然估计法. 似然估计法
武汉科技大学理学院 2
一、矩估计法 根据 设θ1 , θ 2 ,⋯θ k 是总体X 分布中的待估参数, 辛钦大数定律,样本的各阶原点矩依概率收敛于 总体的对应阶的原点矩,故令
EX = A1 2 EX = A2
EX = X 1 n 2 2 DX + ( EX ) = n ∑ X i i =1
6
即
武汉科技大学理学院
二、最大似然估计 1.最大似然原理:在一次试验中,有很多个事 最大似然原理: 最大似然原理 件可能发生,结果事件A发生了,则有理由认 为A发生的概率最大。 例 一袋中装有红白两种球,共100个。其中一 种颜色的球99个,另一种颜色的1个,从中任取 一个是红球,试判断,哪种颜色的球为99个? 分析 应判断为红色的球是99个,否则不符合最 大似然原理。
µ1 = EX = µ µ2 = EX 2 = DX + ( EX ) 2 = σ 2 + µ 2
µ = A1 µ1 = A1 由 ⇒ 2 µ2 = A2 µ + σ 2 = A2 ˆ µ = A1 = X ⇒ 2 1 n 2 1 n n −1 2 2 2 2 ˆ σ = A2 − A1 = n ∑ X i − X = n ∑ ( X i − X ) = n S i =1 i =1
θ ∈Θ
ˆ 则称θ 为θ的最大似然估计。
如果 L(θ ) 可微,可用求导的办法找到它的最大值点, 为了求导方便,通常求 的最大值点。 ln L(θ )
武汉科技大学理学院 11
例 设 X ~ b(1, p ), x1 , x2 ,⋯ , xn 为样本,求p的最大似 然估计。 解
X 的分布率为P{ X = x} = p (1 − p ) , x = 0,1
θ
EX = θ + 4θ + 3(1 − 3θ ) = 3 − 4θ
由
1 X = (1 + 2 + 2 + 2 + 3) = 2 5 ˆ EX = X ⇒ 3 − 4θ = 2 ⇒ θ = 0.25
武汉科技大学理学院 13
⑵最大似然估计 似然函数 L(θ ) = P{ X = 1}P{ X = 2}P{ X = 2}P{ X = 2}P{ X = 3}
L 注 当样本观察值 x1 , x2 ,⋯ , xn 看成变量时, (θ )
就是样本 X 1 ,⋯ , X n 的概率分布; x1 , x2 ,⋯ , xn 看成已知数时, L(θ ) 是未知参数θ的函数, 便是似然函数。
武汉科技大学理学院 9
例 设总体
X 的密度为
λ
λ e − λ x , x > 0 f ( x, λ ) = x≤0 0,
x
1− x
似然函数为
L( p) = ∏ p (1 − p )
xi i =1 n 1− xi
= p i=1 (1 − p )
∑ xi
n
n−
∑ xi
i =1
n
n n ln L( p ) = ∑ xi ln p + n − ∑ xi ln(1 − p ) i =1 i =1
= P{ X 1 = x1}⋯ P{ X n = xn } = p ( x1 , θ )⋯ p ( xn , θ ) A L(θ )
L(θ ) 是参数θ的函数,表示事件A发生的概率.
若X 是连续型,密度函数为f ( x,θ ) 根据离散型
随机变量与连续型的对应关系: p( xi ,θ ) ~ f ( xi ,θ )
令
d ln L( p ) = dp
∑x
i =1
n
i
p
−
n − ∑ xi 1− p
i =1
n
1 n ˆ = 0 ⇒ p = ∑ xi = X n i =1
12
武汉科技大学理学院
例 设总体X的分布率为
X
1
2
3
θ
2θ
1 − 3θ
1,2,2,2,3,为一组样本观察值,求 的矩估计和最大似然估计. 解 ⑴矩估计
武汉科技大学理学院
7
2.似然函数 似然函数
设总体X 的分布率为P{ X = xi } = p( xi , θ ), i = 1, 2,⋯
x1 , x2 ,⋯ xn 是样本观察值,记
则 P( A) = P{ X 1 = x1 ,⋯ , X n = xn }
A = { X 1 = x1 ,⋯ , X n = xn }
解
X 的密度为
f ( x;µ , σ 2 ) = 1 1 exp − 2 ( x − µ ) 2 2πσ 2σ
似然函数为
武汉科技大学理学院
16
L( µ , σ ) = ∏
2 i =1
n
1 1 exp − 2 ( xi − µ ) 2 2πσ 2σ
− n 2 2 − n 2
1 , 0≤x≤θ X 的密度f ( x) = θ 0, 其它
似然函数
1 n , 0≤x1 , x2 ,⋯ , xn ≤θ L(θ ) = θ 0, 其它
由于要满足 θ≥x1 , x2 ,⋯ , xn 因此,当
θ = max{x1 , x2 ,⋯ , xn }时,L(θ )最大
L(θ ) = P{ X = 1}P{ X = 2}P{ X = 2}P{ X = 3} = 4θ 3 (1 − 3θ )
武汉科技大学理学院 10
3.最大似然估计 最大似然估计 似然函数的值越大,对应的样本出现(或落在样 本的邻域)的概率也越大,因此,应选使似然函 数值最大的参数值作为未知参数的估计。 定义 设总体X 的似然函数为L(θ ), θ的取值范围为Θ, ˆ 若θ ∈ Θ满足 ˆ L(θ ) = max L(θ ),
1 n ˆ ˆ 似然估计σ= σ 2= ∑ ( X i − X )2 n i =1
