第四章图形认识初步巩固拓展卷1(复习课)
七年级数学上册《图形认识初步》复习【最新】

略
h
7
8.两个完全相同的正方体,将一面完全重合,构成 的几何体面数有( D ). A.12 个 B.11 个 C.10 个 D.6 个
9.从上面看一个物体所得到的平面图形是圆,则该 物体的形状是( D ). A.球体 B.圆柱 C.圆锥 D.以上都有可能
h
8
10.如图 6 所示为正方体的平面展开图,现已填上 三个字,请你填上所空的三个字,请之与相对的面 内的字具有相反意义.
h
16
18.陈光同学为班级的“学生专栏”设计了报头图 案,并用文字对图案的含义进行了说明,如图 13, 请你用最基本的几何图形(如直线、射线、线段、 角、三角形、四边形、多边形、圆弧等)中的若干 个,为“环保专栏”(在图 13(2)的方框中)设 计一个报头图案,并简要说明图案的含义.
略
h
17
3.从上向下看图 2,应是下图中所示的( D ).
h
3
典型题型
【问题 1】如图 3,某同学在制作正方体模型的时 候,在方格纸上画出几个小正方(图上阴影部分), 但是一不小心,少画了一个,请你给他补上一个, 可以组合成正方体,你有几种画法,在图上用阴 影注明.
略
h
4
【问题 2】用五个小正方体搭成如图 4 的几何体, 请分别画出从正面、从正面、从上面看这个几何 体所得到的平面图形.
略
h
5
题组训练
4.长方形绕其一边旋转一周形成的几何体 叫 圆柱 ,直角三角形绕其中一条直角边旋转 一周形成的几何体叫 圆锥 .
5.圆柱和圆锥的不同之处在于( B ).
A.底面的形状
B.底面的个数
C.侧面的个数
D.无法确定
h
6
6.点滚动后形成( B ). A.点 B.线 C.面
第四章图形认识初步复习与提高(含答案)

第四章积累与提高【要点归纳】1.几何图形的有关概念棱柱的特点有:(1)_上下底面相同___;(2)侧面都是长方形___.从不同方向观察物体时,要学会用语言合理清晰地表达出__物体形状__,体会到从不同方向观察物体可能看到__不一样的结果.2.直线、射线、线段的关系射线是直线上一点和它一旁的部分,线段是直线上两点之间的部分,直线、射线不能度量,线段有长度,能计算和度量. 线段的中点把线段分成两条相等的线段3.角的有关概念角是由两条有公共端点的射线组成的图形:角分为锐角、钝角、直角、平角、周角.1°=60′,1′=60″4.角平分线是一条射线,它把已知角分成两个相等的角.4.余角、补角的定义.两角之和为90°的角是互为余角,两角之和为180°的角是互为补角.5.几个重要性质(1)两点确定一条直线.(2)两点之间线段最短.(3)同角(或等角)的余角相等;同角(或等角)的补角相等.本章需要注意的几个问题:1.关于点和线的理解,要明确线段、射线、直线的区别与联系,以及它们的表示方法,掌握线段、直线的性质,能够正确进行线段、线段的中点的相关计算.2.对于角的计算问题,要明确角的有关概念及分类,会进行角的和、差、倍、分的计算,了解角平分线和互余、互补两角的定义及性质.3.对于解答、推理或计算问题要明确用到的定义及性质,找到它们之间的联系,才能得出正确的结果或结论.本章主要的数学思想与方法:转化思想、数形结合思想、分类讨论思想、方程思想.【题型归类】类型一、几何体和它的平面展开图例1.如图2是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“迎”相对的面上的汉字是(A)A. 文B.明C.奥D.运「分析」解决此题的关键在于,要准确把握住正方体的展开图的每行或每列中若出现相连的3个面,不相邻的两个面就是相对面.因此与“迎” 相对面上的汉字应该是“文”.类型二、线段的有关计算例2.如图4-2-32,点B、C在线段AD上,M是AB的中点,N是CD的中点,若MN=a,BC=b,求AD的长.「分析」本题首先将线段AD转化成五条线段的和,然后通过线段中点的等量关系进行合并,再将未知线段转化为已知线段,此过程中巧妙转化是解题的关键.解:AD = AM+MB+BC+CN+ND= 2(BM+CN)+BC= 2(MN-BC)+BC= 2(a b-)+b= 2a b-.类型三、角的有关计算例3.如图4-3-14,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC,(1)求∠MON 的度数;(2)如果(1)中∠AOB=α,其它条件不变,求∠MON 的度数;(3)如果(1)中∠AOC=β(β为锐角),其它条件不变,求∠MON 的度数; (4)从(1)、(2)、(3)的结果中,你能看出什么规律?「分析」线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法。
华东师大版数学-七年级上册-第四章-图形的初步认识-巩固练习(包含答案)
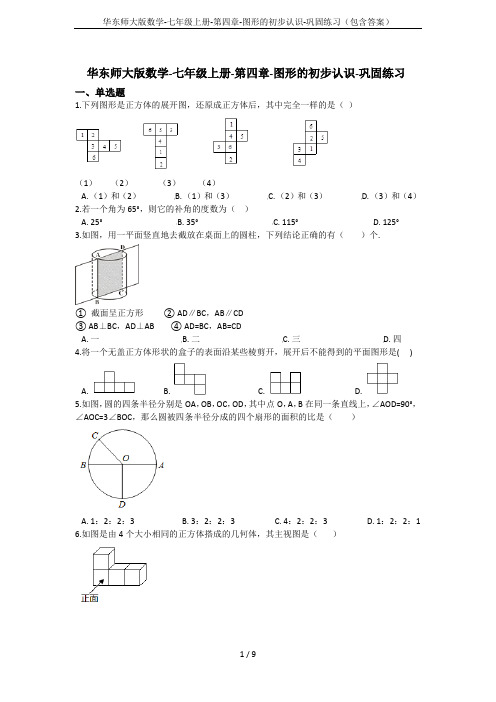
华东师大版数学-七年级上册-第四章-图形的初步认识-巩固练习一、单选题1.下列图形是正方体的展开图,还原成正方体后,其中完全一样的是()(1)(2)(3)(4)A. (1)和(2)B. (1)和(3)C. (2)和(3)D. (3)和(4)2.若一个角为65°,则它的补角的度数为()A. 25°B. 35°C. 115°D. 125°3.如图,用一平面竖直地去截放在桌面上的圆柱,下列结论正确的有()个.① 截面呈正方形② AD∥BC,AB∥CD③ AB⊥BC,AD⊥AB ④ AD=BC,AB=CDA. 一B. 二C. 三D. 四4.将一个无盖正方体形状的盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A. B. C. D.5.如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B在同一条直线上,∠AOD=90°,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是()A. 1:2:2:3B. 3:2:2:3C. 4:2:2:3D. 1:2:2:16.如图是由4个大小相同的正方体搭成的几何体,其主视图是()A. B. C. D.7.如图,左边的平面图形绕轴旋转一周,可以得到的立体图形是()A. B. C. D.8.如图是由几块小立方块所搭成的几何体的俯视图,小正方体中的数字表示该位置小立方块的个数,则该几何体的左视图是()A. B. C. D.9.如图,正方体的棱长为cm,用经过A、B、C三点的平面截这个正方体,所得截面的周长是()A. 2cmB. 3 cmC. 6cmD. 8cm二、填空题10.已知线段AB,点C、点D在直线AB上,并且CD=8,AC:CB=1:2,BD:AB=2:3,则AB=________.11.如果∠A=30°,则∠A的余角是________度;如果∠1+∠2=90°,∠1+∠3=90°,那么∠2与∠3的大小关系是________.12.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有________种.13.已知点A、B、C在同一条直线上,且线段AB=5,BC=4,则A、C两点间的距离是________.14.钟面上3点40分时,时针与分针的夹角的度数是________度.15.钟表上4时15分钟,时针与分针的夹角的度数是________.16.如图,一副三角尺按不同的位置摆放,摆放位置中=的图形是________.(只填写图形编号)①②③④17.如图所示,是一个简单几何体的三视图,则这个几何体的侧面积等于________.三、计算题18. 计算:(1)28°32′46″+15°36′48″;(2)(30°-23′40″).19.计算:(1)40°26'+30°30'30″÷6(2)13°53'×3-32°5'31″四、解答题20.正方体是由六个平面图形围成的立体图形.设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形.但同一个正方体,按不同的方式展开所得的平面展开图悬不一样的,下面的图形是由6个大小一样的正方彤,拼接而成的,请问这些图形中哪些可以折成正方体?21.一个角的余角比这个角的多21°,求这个角的度数.五、综合题22.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)23.如图,C是线段AB上一点,M是AC的中点,N是BC的中点(1)若AM=1,BC=4,求MN的长度.(2)若AB=6,求MN 的长度.24.如图所示的是某个几何体从三种不同方向所看到的图形.(1)说出这个立体图形的名称;(2)根据图中的有关数据,求这个几何体的表面积和体积.答案一、单选题1.【答案】D【解析】【分析】利用正方体及其表面展开图的特点解题。
图形的初步认识全章复习与巩固

符号
1 颗星 1 面旗
旁白
1 颗星 1 面旗
同学摆擂台!(写在黑板上)
要求:(1)出自网校资源(靠旁白)、非难偏怪题 (2)标明出处、奖励规则。 (3)擂主会解题。
一、师生问好
同学们好!
课前就位
• 发测评截图的同学:…..加3颗星星 截屏快捷键:Ctrl + PrntScr ; 截图Ctrl + Alt+A) 有高清课堂观看笔记 的 加3颗星星 • 上周积分情况汇报
老师摆擂
10. 如图所示, AB AC (1)AC=BC+______; (2)CD=AD-______; BD (3)CD=______-BC; (4)AB+BC=______-CD. AD
课堂小结及点评
1、合上学案,回想一下这节课我们都复习了 哪些知识点和类型题? 2、各小组积分情况点评。
布置学案
D
5、点评:理解概念,掌握概念与概念的本质区别
例2.(天门、潜江、仙桃)如图所示,是每个面上都有一个 汉字的正方体的一种展开图,那么在原正方体的表面上, 与“看”相对的面上的汉字是 ( ) A.南 B.世 C.界 D.杯
解题思路:由图形可以判定“南”与“世”相对, “看”与“界”相对,“非”与“杯”相对 点评:判断两个面是对面的根据是:展开图的对面没有公共边 或公共顶点
要点梳理——检测
知识点一:多姿多彩的图形 2.立体图形与平面图形的相互转化
抢答
(1)立体图形的平面展开图: 把立体图形按一定的方式展开就 平面图形 会得到-------- ----,把平面图形按一定的途径进行折叠就 会得
到相应的立体图形
正 左、右 上
抢答 知识点二:直线、射线、线段的区别与联系
人教版七年级数学上册第四章几何图形初步复习课

例 3: 点A,B,C 在同一条直线上,AB=
3 cm,BC=1 cm.求AC的长.
解:(1)如图①,因为AB=3 cm,BC= 1 cm, 所以AC=AB+BC=3+1=4 (cm).
A
B CA
CB
图①
图②
(2)如图②,因为AB=3 cm,BC=1 cm, 所以AC=AB-BC=3-1=2(cm).
所以有∠MEB′=1 ∠BEB′,∠NEA′1= ∠AEA′.
2
2
因为∠BEB′+∠AEA′=180°,
所以∠NEM =∠NEA′+∠MEB′
= 1 ∠AEA′+ 1∠BEB′
2
2
=
1 (∠AEA′+∠BEB′) 2
=90°.
【问题5】通过对本章内容的复习, 你有哪些新的收获?
14
课后作业
教科书第147页复习题4 中的第3、4、6、7题.
例4:已知∠α和∠β互为补角,并且∠β的一半 比∠α小30°,求∠α,∠β.
解:设∠α=x°,则∠β=180°-x°. 根据题意 ,得∠β=2(∠α - 30°), 即 180- x° =2(x°-30°), 解得 x°= 80°. 所以∠α= 80°,∠β= 100°.
【问题4】对于几何中的一些概念、性质及 关系,应把几何意义与数量表示结合起来 加以认识,到达形与数的统一.如此,你 能从数和形两个方面认识线段中点和角平 分线的概念吗?
15
对待生活中的每一天若都像生命中的最后 一天去对待,人生定会更精彩.
5
在下列图形中(每个小四边形皆为全等的正方
形),可以是一个正方体表面展开图的是(C )
A
B
C
D
6
《图形认识初步》全章复习与巩固(提高)巩固练习.docx

《图形认识初步》全章复习与巩固(提高)巩固练习撰稿:孙景艳 审稿:赵炜【巩固练习】一、选择题1. 分析下列说法,正确的有( )①长方体、正方体都是棱柱;②三棱柱的侧而是三角形;③圆锥的三视图屮:主视图、左视 图是三角形,俯视图是圆;④球体的三种视图均为同样人小的图形;⑤直六棱柱有六个侧面、 侧面为长方形.A. 2种B. 3种C. 4种D. 5种2. 在4个图形中,只有一个是由如图所示的纸板折叠而成,请你选出正确的一个( ).)A. M 是线段AB 的中点,则AB=2AMB. 直线上的两点和它们之间的部分叫做线段C. 一条射线把一个角分成两个角,这条射线叫做这个角的平分线D. 同角的补角相等 4. 从点0出发有五条射线,可以组成的角的个数是()A. 4个B. 5个 5. 用一副三角板画角, A. 15°的角6. 女口图所示,已知射线0C 平分ZAOB,射线OD, 0E 三等分ZAOB,又OF 平分ZAOD, 则图中等于ZBOE 的角共有().&平而内两两相交的6条总线,其交点个数最少为ni 个,最多为n 个,则m+n 等于(A. 12B. 16C. 20D.以上都不对C.D.3.下面说法错误的是( C. 7 个 D. 10 个 卜•面的角不能画•出的是( ) B. 135°的角 C. 145°的角 D. 150°的角C. 3个D. 4个7.已知:线段AC 和BC 在同一条直线上,如果AC 二5cm, BC=.3cm,线段AC 和BC 中点间的距离是()A. 6B. 4C. 1D. 4 或 1 B.二、填空题9.把一个周角7等分,每一份是. 的角(精确到秒).10. _________________ 若Zci是它的余角的2倍,是的2倍,那么把Z C1和ZB拼在一起(有一条边重合)组成的角是叟.11・如图是用一样的小立方体摆放的一组儿何体,观察该组儿何体并探索:照这样摆下去,第五个几何体屮共有_________ 个小立方体,第n个几何体屮共有_________ 个小立方体.12. _______________________________ 如图所示的是山儿个相同的小正方体搭成的儿何体从不同的方向看所得到的图形,则搭成这个儿何体的小正方体的个数是.®ZEOD=90°;②ZCOE=ZAOD;③ZCOE二ZBOD;④ZCOE+ZBOD=90・其中正确的是______14.如图,ZAOB是钝角,0C、0D、0E是三条射线,若0C丄OA, 0D平分ZAOB, 0E平分ZB0C,那么ZD0E的度数是___________三、解答题15.钟表在12点钟时三针重合,经过多少分钟秒针第一次将分针和时针所夹的锐角平分?16.已知:如图h ZAOBf.(1)如图2.射线OC 在ZAOB 的内部.OD 平分ZAOC >若ZBOD=40\求ZBOC 的度数)⑵ 若ZBOD=3ZBOC (ZBOCV45。
湘教版数学-七年级上册-第四章-图形的认识-巩固练习(包含答案)

湘教版数学-七年级上册-第四章-图形的认识-巩固练习一、单选题1.如图是一个长方体包装盒,则它的平面展开图是()A. B. C. D.2.若∠1=5005'∠2=50.50则∠1与∠2的大小关系是()A.∠1=∠2B.∠1>∠2C.∠1<∠2D.无法确定3.如图是一个正方体纸盒的展开图,其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”,将其围成一个正方体后,则与“5”相对的是()A.0B.2C.数D.学4.如图中的线段,直线或射线,能相交的是()A. B. C. D.5.下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是()A. B.C. D.6.如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则()A.乙比甲先到B.甲和乙同时到C.甲比乙先到D.无法确定7.在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点1000m的A地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了500m到达目的地C,此时小霞在营地A的A.北偏东20°方向上B.北偏东30°方向上C.北偏东40°方向上D.北偏西30°方向上二、填空题8.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是________.9.如图,点A、O、B在一条直线上,∠AOC=130°,OD是∠BOC的平分线,则∠COD=________度.10.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC= ∠AOD,则∠AOD=________.11.有如下线段,比一比,量一量,比较其中a、b的长度.则结论是a________ b(用>,=,<填).12.如图,C、D是线段AB上两点,D是AC的中点,若CB=3,DB=7,则AC的长为________.13.已知线段AB=acm,在直线AB上截取BC=bcm,且b<a,D是AC的中点,则线段BD=________cm.14.已知在平面内,∠AOB=60°,OD是∠AOB的角平分线,∠BOC=20°,则∠COD的度数是________.15.如图,已知AB=5,点C在直线AB上,且BC=4,M为BC的中点,则线段AM的长度为________.三、解答题16.一个角的余角比它的补角的还少40°,求这个角。
七年级数学上册第四章《图形认识初步》全章复习与巩固(提高)知识讲解新人教版
《图形认识初步》全章复习与巩固(提高)知识讲解【学习目标】1.认识一些简单的几何体的平面展开图及三视图,初步培养空间观念和几何直观;2.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;3.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;4.逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形,会用语句描述简单的图形.【高清课堂:图形认识初步章节复习 399079 本章知识结构】【知识网络】【要点梳理】要点一、多姿多彩的图形1.几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果. 2.立体图形与平面图形的相互转化立体图形:棱柱、棱锥、圆柱、圆锥、球等.⎧⎨⎩平面图形:三角形、四边形、圆等.几何图形⎧⎨⎩(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来. 要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践. (2)从不同方向看:主(正)视图---------从正面看 几何体的三视图 (左、右)视图-----从左(右)边看 俯视图---------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图. ②能根据三视图描述基本几何体或实物原型. (3)几何体的构成元素及关系几何体是由点、线 、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成. 要点二、直线、射线、线段1. 直线,射线与线段的区别与联系2. 基本性质(1)直线的性质:两点确定一条直线. (2)线段的性质:两点之间,线段最短. 要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巩固拓展卷 总分:50分
错题更正处
班级_____姓名__________分数_________
一、 填空题 (每题5分,共20分)
1.如图,线段AB______AC+BC(填“<”“>”或“=”);
理由是_________________________ 2.已知线段AC 和BC 在同一条直线上,如果AC=5.6,BC=2.4,那么线段AB=_________。
3.乘火车从A 站出发,沿途经过3个车站可到达B 站,那么在A,B 两站之间最多共有________ 种不同的票价。
4.小明每天下午5:30回家,这时分针与时针所成的角的度数为____度。
二、 选做题 (每题10分,共30分)
⑴如图所示,点O 是直线AB 上一点,OE ,OF 分别平分∠AOC 和∠BOC ,若∠AOC =68°, 则∠BOF 和∠EOF 是多少度?
⑵ 一个角的补角比它的余角的3倍少20°,求这个角的大小。
(3) 如下图,在已知角内画射线,画1条射线,图中共有
个角;画2条射线,图中共有
个角;画3条射线,图中共有 个角,求画n 条射线所得的角的个数 。
C B A。
