河北中考数学复习 第2讲 整式
中考数学(河北专版)总复习考点整合 能力突破课件:第2节 代数式与整式 (共33张PPT)

相同的项.
系数 相加,所得结果作为 3.合并同类项:只把同类项的 ________ 不变 . 系数,字母和字母的指数________
4.去括号、添括号法则:关键看括号前面的符号,括号 前面是“+”,去、添括号,括号里各项符号都 不变 ,括号前面是“-”,去、添括号,括号里 ________
改变 各项符号都________.
注意
代数式的书写规则.
3.代数式求值:用具体数值代替代数式中的字母,按运算
顺序计算得出结果.
考点二 整式及整式的运算
多项式 ; 单项式 和________ 1.整式分为________
注意
单项式是由系数、字母和字母的指数构成的,系数不
可以是带分数. 字母 相同,并且相同字母的 ________ 指数 也 2 .同类项:所含 ________
第一单元 数与式
第 2 节 代数式与整式
目录
01
特色分析
考点整合梳理
02
03
中考命题剖析
本节在中考试题中以基本技能、基本计算为主要 考查内容,以容易题为主,多为选择题、填空题;
整式的变形在其他题目中渗透广泛.所占分值日渐
增多,2015,2017年以解答题形式出题,预计2018 年在河北省中考题中仍会以解答题出现.
5.整式的运算: 合并同类项 ; (1)整式的加减:本质是去括号与_____________ (2)整式的乘法:包括单项式乘以单项式、单项式乘以多
项式、多项式乘以多项式.
注意
(1)单项式乘以单项式结果仍然是单项式; (2)单项式乘以多项式结果为多项式,其项数与原多项
式的项数一致;
(3)计算时要注意符号问题,多项式的每一项要包括它 前面的符号,也要注意单项式前面的符号; (4)多项式乘以多项式展开时,有同类项的要合并; (5)公式中的字母可以表示数,也可以表示单项式或多
河北省中考数学系统复习 第一单元 数与式 第2讲 整式及因式分解(8年真题训练)练习

第2讲 整式及因式分解命题点1 代数式及其求值1.(2018·河北T12·2分)用一根长为a(单位:cm)的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩1(单位:cm)得到新的正方形,则这根铁丝需增加(B)A .4 cmB .8 cmC .(a +4)cmD .(a +8)cm2.(2013·河北T9·3分)如图,淇淇和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x ,淇淇猜中的结果应为y ,则y =(B) A .2 B .3 C .6 D .x +33.(2018·河北T18·3分)若a ,b 互为相反数,则a 2-b 2=0.4.(2012·河北T15·3分)已知y =x -1,则(x -y)2+(y -x)+1的值为1. 5.(2016·河北T18·3分)若mn =m +3,则2mn +3m -5mn +10=1. 命题点2 幂的运算6.(2018·河北T13·2分)若2n +2n +2n +2n=2,则n =(A)A .-1B .-2C .0D.14命题点3 整式的运算及求值7.(2012·河北T2·2分)计算(ab)3的结果是(C)A .ab 3B .a 3bC .a 3b 3D .3ab 8.(2016·河北T2·3分)下列运算正确的是(D)A .(-5)0=0B .x 2+x 3=x 5C .(ab 2)3=a 2b 5D .2a 2·a -1=2a 9.(2011·河北T4·2分)下列运算正确的是(D)A .2x -x =1B .x +x 4=x 5C .(-2x)3=-6x 3D .x 2y ÷y =x 210.(2015·河北T4·3分)下列运算正确的是(D)A .(12)-1=-12B .6×107=6 000 000C .(2a)2=2a 2D .a 3·a 2=a 511.(2015·河北T21·10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:(1)求所捂的二次三项式;(2)若x=6+1,求所捂二次三项式的值.解:(1)设所捂的二次三项式为A,根据题意,得A=x2-5x+1+3x=x2-2x+1.(2)当x=6+1时,A=(x-1)2=(6)2=6.12.(2018·河北T20·8分)嘉淇准备完成题目:化简:(x2+6x+8)-(6x+5x2+2).发现系数“”印刷不清楚.(1)他把“”猜成3,请你化简:(3x2+6x+8)-(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“”是几?解:(1)(3x2+6x+8)-(6x+5x2+2)=3x2+6x+8-6x-5x2-2=-2x2+6.(2)设“”是a,则原式=(ax2+6x+8)-(6x+5x2+2)=ax2+6x+8-6x-5x2-2=(a-5)x2+6.∵标准答案的结果是常数,∴a-5=0.解得a=5.13.(2017·河北T22·9分)发现:任意五个连续整数的平方和是5的倍数.验证:(1)(-1)2+02+12+22+32的结果是5的几倍?(2)设五个连续整数的中间一个为n ,写出它们的平方和,并说明是5的倍数.延伸:任意三个连续整数的平方和被3除的余数是几呢?请写出理由.解:验证:(1)∵(-1)2+02+12+22+32=1+0+1+4+9=15=5×3,∴(-1)2+02+12+22+32的结果是5的3倍.(2)由题意,得(n-2)2+(n-1)2+(n+1)2+(n+2)2+n2=5n2+10=5(n2+2).∵n为整数,∴五个连续整数的平方和是5的倍数.延伸:余数是2.理由:设中间的整数为n,则(n-1)2+n2+(n+1)2=3n2+2.∴任意三个连续整数的平方和被3除的余数是2.命题点4 乘法公式的应用14.(2018·河北T4·3分)将9.52变形正确的是(C)A.9.52=92+0.52B.9.52=(10+0.5)(10-0.5)C.9.52=102-2×10×0.5+0.52D.9.52=92+9×0.5+0.52命题点5 因式分解15.(2013·河北T4·2分)下列等式从左到右的变形,属于因式分解的是(D)A .a(x -y)=ax -ayB .x 2+2x +1=x(x +2)+1C .(x +1)(x +3)=x 2+4x +3D .x 3-x =x(x +1)(x -1)16.(2014·河北T3·2分)计算:852-152=(D)A .70B .700C .4 900D .7 000 17.(2011·河北T3·2分)下列分解因式正确的是(D)A .-a +a 3=-a(1+a 2) B .2a -4b +2=2(a -2b)C .a 2-4=(a -2)2D .a 2-2a +1=(a -1)2重难点1 幂的运算根据幂的运算法则,把a 6写成幂的运算形式,并说明依据哪种运算法则.(要求至少写出2种,且每种依据的运算不相同)例如:依据同底数幂的乘法可得,a 6=a 2·a 4.【自主解答】 解:答案不唯一,例如:依据同底数幂的乘法可得,a 6=a 3·a 3=a ·a 5……;依据同底数幂的除法可得,a 6=a 8÷a 2=a 7÷a ……;依据幂的乘方可得,a 6=(a 3)2=(a 2)3;依据单项式乘法可得,a 6=2a ·0.5a 5…….【变式训练1】(2018·保定二模)下列计算正确的是(D)A .a 4÷a 3=1B .a 4+a 3=a 7C .(2a 3)4=8a 12D .a 4·a 3=a 7【变式训练2】(2018·威海)已知5x =3,5y =2,则52x -3y=(D)A.34B .1C.23D.98方法指导我们把加减称为一级运算,乘除称为二级运算,乘方开方称为三级运算.幂的运算法则实质是把幂的运算转化为指数运算,因为指数本身处在高级位置,所以幂的运算转化为指数运算要降一级.如:同底数幂相乘(除)变为指数相加(减),幂的乘方变为指数相乘,积的乘方就是乘方对乘法的分配律,相当于乘法分配律升级. 重难点2 整式的运算(2018·邵阳)先化简,再求值:(a -2b)(a +2b)-(a -2b)2+8b 2,其中a =-2,b =12.【自主解答】解:原式=a 2-4b 2-a 2+4ab -4b 2+8b 2=4ab.当a =-2,b =12时,原式=-4.【变式训练3】【整体思想】若a 2-2a -3=0,代数式a 2·2-a 3的值是(D)A .0B .-a23C .2D .-12【变式训练4】(2018·河北考试说明)若m +n =2,mn =1,则m 2+n 2=2.【变式训练5】 【整体思想】(2018·临沂)已知m +n =mn ,则(m -1)(n -1)=1.方法指导先观察式子的结构特征,确定解题思路,结合数学思想:整体代入、降次、数形结合、逆向思维等,使解题更加方便快捷. 重难点3 因式分解把4a 2添上1项或2项,使它能够进行因式分解.(1)写出3个且要用三种不同的分解方法;(2)若要求能进行2步或2步以上分解,如何添加?请写出一个即可.【自主解答】 解:(1)答案不唯一,例如:4a 2+2a =2a(2a +1);4a 2+4a +1=(2a +1)2;4a 2-1=(2a -1)(2a +1). (2)答案不唯一,例如:①4a 2-4b 2=4(a 2-b 2)=4(a +b)(a -b);②4a 2-a 4=a 2(4-a 2)=a 2(2-a)(2+a);③4a 2-8ab +4b 2=4(a 2-2ab +b 2)=4(a -b)2.【变式训练6】 (2018·唐山乐亭县一模)下列各式由左到右的变形,属于因式分解的是(C)A .a(m +n)=am +anB .a 2-b 2-c 2=(a -b)(a +b)-c 2C .10x 2-5x =5x(2x -1)D .x 2-16+6x =(x +4)(x -4)+6x 【变式训练7】 (2018·河北中考预测)计算(919)2+2×919×89+(89)2的结果正确的是(A)A .100B .10 000C .1 000D .9 900【变式训练8】 (2018·唐山乐亭县七年级期末)2x 3y 2与12x 4y 的公因式是2x 3y .【变式训练9】 (2018·石家庄二模)分解因式:xy 2-2xy +x =x(y -1)2.【变式训练10】 【整体思想】(2018·苏州)若a +b =4,a -b =1,则(a +1)2-(b -1)2的值为12. 易错提示必须分解到每一个多项式都不能再分解为止.1.(2018·荆州)下列代数式中,整式为(A)A .x +1B.1x +1C.x 2+1D.x +1x2.(2018·河北中考预测)若(x +3)(x +n)=x 2+mx -15,则m 等于(A)A .-2B .2C .-5D .53.(2018·河北中考预测)下列各式中,计算结果为a 8的是(C)A .a 4+a 4B .a 4·a -2C .a 10÷a 2D .(-2a 4)24.(2018·包头)如果2xa +1y 与x 2yb -1是同类项,那么ab的值是(A)A.12B.32C .1D .35.(2018·淄博)若单项式am -1b 2与12a 2b n 的和仍是单项式,则n m的值是(C)A .3B .6C .8D .96.(2018·石家庄新华区二模)已知x 2+4mx +16是完全平方式,则m 的值为(C)A .2B .4C .±2D .±47.(2018·齐齐哈尔)我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予3a 实际意义的例子中,不正确的是(D)A .若葡萄的价格是3元/千克,则3a 表示买a 千克葡萄的金额B .若a 表示一个等边三角形的边长,则3a 表示这个等边三角形的周长C .将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a 表示桌面受到的压强,则3a 表示小木块对桌面的压力D .若3和a 分别表示一个两位数中的十位数字和个位数字,则3a 表示这个两位数8.(2018·青岛)计算(a 2)3-5a 3·a 3的结果是(C)A .a 5-5a 6B .a 6-5a 9C .-4a 6D .4a 69.【整体思想】(2018·邢台一模)若m -x =2,n +y =3,则(m -n)-(x +y)=(A)A .-1B .1C .5D .-510.(2018·河北考试说明)计算:552-152=(D)A .40B .1 600C .2 400D .2 80011.(2018·重庆)按如图所示的运算程序,能使输出的结果为12的是(C)A .x =3,y =3B .x =-4,y =-2C .x =2,y =4D .x =4,y =212.(2018·枣庄)如图,将边长为3a 的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长为2b 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为(A)A .3a +2bB .3a +4bC .6a +2bD .6a +4b13.(2018·株洲)单项式5mn 2的次数为3.14.分解因式:m 3-9mn 2=m(m -3n)(m +3n).15.(2018·张家口一模)已知多项式A =(x +1)2-(x 2-4y).(1)化简多项式A ;(2)若x +2y =1,求A 的值.解:(1)A =(x +1)2-(x 2-4y)=x 2+2x +1-x 2+4y =2x +4y +1. (2)∵x +2y =1,由(1),得A =2x +4y +1=2(x +2y)+1, ∴A =2×1+1=3.16.(2018·唐山乐亭县七年级期末)下列说法:①(-2)101+(-2)100=-2100;②2 0182+2 018一定可以被2 019整除;③16.9×18+15.1×18能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的有(A)A .4个B .3个C .2个D .1个17.(2018·河北中考预测)若a 2-3ab =-5,b 2+ab =14,则a -b 的值为3或-3.18.(2018·河北中考预测)如图,已知大正方形的边长为a +b +c ,利用图形的面积关系可得:(a +b +c)2=a 2+b 2+c 2+2ab +2bc +2ac.当大正方形的边长为a +b +c +d 时,利用图形的面积关系可得:(a +b +c +d)2=a 2+b 2+c 2+d 2+2ab +2ac +2ad +2bc +2bd +2cd.一般地,n 个数的和的平方等于这n 个数的平方和加上它们两两乘积的2倍.根据以上结论解决下列问题:(1)若a +b +c =6,a 2+b 2+c 2=14,则ab +bc +ac =11;(2)从-4,-2,-1,3,5这五个数中任取两个数相乘,再把所有的积相加,若和为m ,求m 的值.解:∵-4-2-1+3+5=1,∴两边平方后得(-4-2-1+3+5)2=(-4)2+(-2)2+(-1)2+32+52+2m=55+2m=1.∴m=(1-55)÷2=-54÷2=-27.19.(2018·保定一模)若3×9m×27m=321,则m的值为(B)A.3 B.4 C.5 D.620.(2018·张家口一模)若x+3y=0,则2x·8y=1.21.(2018·河北模拟)在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.”(1)若小明同学心里想的是数5,请帮他计算出最后结果;(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.解:(1)第一步:(5+1)2-(5-1)2=20;第二步:20×25=500;第三步:500÷5=100.∴小明计算出最后结果为100.(2)∵[(a+1)2-(a-1)2]×25÷a=(a+1+a-1)(a+1-a+1)×25÷a=4a×25÷a=100,∴结论成立.。
冀教版中考数学《第2讲整式与因式分解》知识梳理
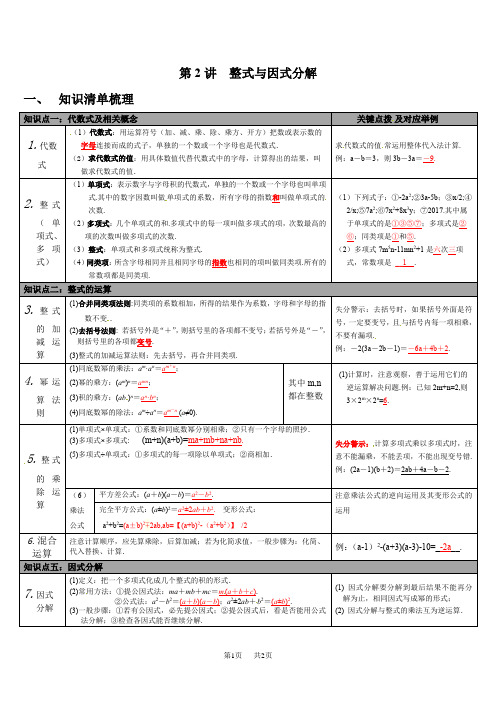
第2讲整式与因式分解一、知识清单梳理知识点一:代数式及相关概念关键点拨及对应举例(1)代数式:用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式.(2)求代数式的值:用具体数值代替代数式中的字母,计算得出的结果,叫做求代数式的值.求代数式的值常运用整体代入法计算.例:a-b=3,则3b-3a=-9.(1)单项式:表示数字与字母积的代数式,单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数,所有字母的指数和叫做单项式的次数.(2)多项式:几个单项式的和.多项式中的每一项叫做多项式的项,次数最高的项的次数叫做多项式的次数.(3)整式:单项式和多项式统称为整式.(4)同类项:所含字母相同并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.知识点二:整式的运算(1)合并同类项法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.(2)去括号法则: 若括号外是“+”,则括号里的各项都不变号;若括号外是“-”,则括号里的各项都变号.(3)整式的加减运算法则:先去括号,再合并同类项.失分警示:去括号时,如果括号外面是符号,一定要变号,且与括号内每一项相乘,不要有漏项.例:-2(3a-2b-1)=-6a+4b+2.(1)同底数幂的乘法:a m·a n=a m+n;(2)幂的乘方:(a m)n=a mn;(3)积的乘方:(ab)n=a n·b n;(4)同底数幂的除法:a m÷a n=a m-n(a≠0).5.整式的乘除运算(1)单项式×单项式:①系数和同底数幂分别相乘;②只有一个字母的照抄.失分警示:计算多项式乘以多项式时,注意不能漏乘,不能丢项,不能出现变号错.例:(2a-1)(b+2)=2ab+4a-b-2.6.混合知识点五:因式分解(1)定义:把一个多项式化成几个整式的积的形式.(2)常用方法:①提公因式法:ma+mb+mc=m(a+b+c).②公式法:a2-b2=(a+b)(a-b);a2±2ab+b2=(a±b)2.(3)一般步骤:①若有公因式,必先提公因式;②提公因式后,看是否能用公式法分解;③检查各因式能否继续分解.。
精品 中考数学一轮综合复习 第02课 整式(整式的加减乘除及因式分解)

8.若 m+n=3,则 2m 2 4mn 2n 2 6 的值为( A.12 B.6
C.3
D.0
9.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式 ,如 a b c 就是完 ..... 全对称式.下列三个代数式:① ( a b) ;② ab bc ca ;③ a 2b b 2 c c 2 a .其中是完全对称式的是
例 3.当 x=1 时,代数式 ax 3 bx 2014 等于 2013,则当 x=-1 时,代数式 ax 3 bx 2014 值为多少?
例 4.若多项式 4 x 2 6 xy 2 x 3 y 与 ax 2 bxy 3ax 2by 的和不含二次项,求 a、b 的值。
5
7.若 2 x 3,4 y 5 ,则 2 x 2 y 的值为( A.
3 5
9 3
B.-2
2
3 5 5
D.
6 5
8.已知 a=1.610 ,b=410 ,则 a 2b=(
7 A.210
)
5 C.3.210 14 D.3.210
B.410
14
9.把多项式 ax 2 ax 2a 分解因式,下列结果正确的是( A. a ( x 2)( x 1) B. a ( x 2)( x 1) C. a( x 1) 2
第 4 页 共 8 页
2 (5) 27 x 18 x 3
2 2 (6) 3a 6ab 3b
3 (7) 2 x 8 x
2 (8) x 5 x 6
(9) x 2 12 x 35
(10) ax 2 3ax 28a
(11) x 2 6 x 16
中考数学专题复习:第2课 整式及其运算优质课件PPT

【答案】 2
【类题演练 4】 (2018·扬州)计算:(2x+3)2-(2x+3)(2x -3).
【解析】 原式=4x2+12x+9-(4x2-9)=12x+18.
1.整式的加减实质就是合并同类项,整式的乘除实质就 是幂的运算.
2.本课主要用到以下三种数学思想方法: (1)数形结合思想: 在列代数式时,常常会遇到一种题型:题中提供一 定的图形,要求通过对图形的观察、探索,提取图 形中反馈的信息,并根据相关的知识列出相应的代 数式,也能用图形来验证整式的乘法和乘法公式.
A.34
B.1
C.23
D.98
【答案】 D
()
题型一 幂的运算
熟记法则,依照法则进行计算.
【典例 1】 有下列运算:①a2·a3=a6;②(a3)2=a6;③a5
÷a5=a;④(ab)3=a3b3.其中结果正确的个数为 ( )
A.1
B.2
C.3
D.4
【解析】 ①a2·a3=a5,故本项错误;②(a3)2=a6,故本 项正确;③a5÷a5=1,故本项错误;④(ab)3=a3b3,故本 项正确.故选 B.
注意公式的变形及整体思想的应用.
【典例 3】 (2018·河北)将 9.52 变形正确的是 ( ) A.9.52=92+0.52 B.9.52=(10+0.5)(10-0.5) C.9.52=102-2×10×0.5+0.52 D.9.52=92+9×0.5+0.52
【解析】 9.52=(10-0.5)2=102-2×10×0.5+0.52.
【答案】 C
【类题演练 3】 (2018·乐山)已知实数 a,b 满足 a+b=2,
ab=34,则 a-b=
()
A.1
中考数学专题训练第2讲整式(知识点梳理)

整式知识点梳理考点01 代数式1.代数式的概念:用运算符号把数和字母连接而成的式子叫作代数式。
单独一个数或一个字母也是代数式.运算符号是指加、减、乘、除、乘方等。
2.代数式的书写规则:(1)含有乘法运算的代数式的书写规则:字母与字母相乘,乘号一般可以省略不写,字母的排列顺序不变.数字与字母相乘,乘号一般也可以省略,但数字一定要写在字母的前面,且当数字是带分数时,必须写成假分数的形式.数字与数字相乘,乘号不能省略.带括号的式子与字母的地位相同。
(2)含有除法运算的代数式的书写规则:当代数式中含有除法运算时,一般不用“÷”,而改用分数线.因为分数线具有括号的作用,所以分数线又称括线。
(3)含有单位名称的代数式的书写规则:若代数式是和或差的形式,如需注明单位,则必须用括号把整个式子括起来后再写单位.若代数式是积或商的形式,则无需加括号,直接在代数式后面写出单位即可。
3.代数式的值(1)代数式的值:一般地,用具体数值代替代数式中的字母,按照代数式中指明的运算计算出的结果,叫作代数式的值。
(2)求代数式的值的步骤:第1步:代入,用具体数值代替代数式里的字母.第2步:计算,按照代数式里指明的运算,计算出结果。
(3)求代数式的值时要注意:一个代数式中的同一个字母,只能用同一个数值去代替.如果代数式里省略了乘号,那么字母用数值代替时要添上乘号,代入负数和分数时要加括号.代入数值时,不能改变原式中的运算符号及数字。
(4)运算时,要注意运算顺序。
(先算乘方,再算乘除,最后算加减,有括号的要求先算括号里面的)考点02 单项式和多项式一、单项式1.单项式的概念:如3、a 、xy 、ab 31-等这些代数式都是数字、字母、数字与字母的积、字母与字母的积,像这样的式子叫单项式,单独的一个数或一个字母也是单项式。
2.单项式中不能含有加减法运算,但可以含有除法运算。
3.单项式的系数:单项式中的数字因数叫作这个单项式的系数,确定单项式的系数的注意事项:(1)确定单项式的系数时,最好现将单项式写成数与字母的乘积的形式,在确定系数.(2)圆周率π是常数,单项式中出现π时,应看作系数.(3)当一个单项式的系数是1或-1时,1通常省略不写,负数做系数应包括前面的符号.(4)单项式的系数是带分数时,通常写成假分数。
中考数学专题复习2整式的运算(解析版)

整式的运算复习考点攻略考点01 整式的有关概念1.整式:单项式和多项式统称为整式.2.单项式:单项式是指由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数. 【注意】单项式的系数包括它前面的符号3.多项式:几个单项式的和叫做多项式;多项式中.每一个单项式叫做多项式的项.其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数.4.同类项:多项式中所含字母相同并且相同字母的指数也相同的项叫做同类项. 【例1】单项式3212a b 的次数是_____. 【答案】5 【解析】单项式3212a b 的次数是325+=.故答案为5. 【例2】下列说法中正确的是( )A .25xy -的系数是–5 B .单项式x 的系数为1.次数为0C .222xyz -的次数是6D .xy +x –1是二次三项式 【答案】D【解析】A.25xy -的系数是–15.则A 错误;B.单项式x 的系数为1.次数为1.则B 错误;C.222xyz -的次数是1+1+2=4.则C 错误;D.xy +x –1是二次三项式.正确.故选D.【例3】若单项式32m x y 与3m nxy +是同类项.2m n +_______________.【答案】2【解析】由同类项的定义得:13m m n =⎧⎨+=⎩解得12m n =⎧⎨=⎩221242m n +=⨯+==故答案为:2.【例4】按一定规律排列的单项式:a .2a -.4a .8a -.16a .32a -.….第n 个单项式是( )A .()12n a --B .()2na -C .12n a -D .2n a【答案】A 【解析】解:a .2a -.4a .8a -.16a .32a -.….可记为:()()()()()()0123452,2,2,2,2,2,,a a a a a a ------•••∴ 第n 项为:()12.n a -- 故选A .【例5】如图.图案均是用长度相等的小木棒.按一定规律拼搭而成.第一个图案需4根小木棒.则第6个图案需小木棒的根数是( )A .54B .63C .74D .84【答案】A【解析】拼搭第1个图案需4=1×(1+3)根小木棒. 拼搭第2个图案需10=2×(2+3)根小木棒. 拼搭第3个图案需18=3×(3+3)根小木棒. 拼搭第4个图案需28=4×(4+3)根小木棒. …拼搭第n 个图案需小木棒n (n +3)=n 2+3n 根. 当n =6时.n 2+3n =62+3×6=54. 故选A.考点02 整式的运算1.幂的运算:a m ·a n =a m +n ;(a m )n =a mn ;(ab )n =a n b n ;a m ÷a n =m n a -. 2. 整式的加减:几个整式相加减.如有括号就先去括号.然后再合并同类项。
河北省地区中考数学总复习 第2讲 整式及其运算课件

幂的运算
【例3】 (1)(2014·济南)下列运算中,结果是a5的是( A ) A.a3·a2 B.a10÷a2 C.(a2)3 D.(-a)5 (2)(2012·南京)计算(a2)3÷(a2)2的结果是( B ) A.a B.a2 C.a3 D.a4
解析:(a2)3÷(a2)2=a6÷a4=a2 【点评】 (1)幂的运算法则是进行整式乘除法的基 础,要熟练掌握,解题时要明确运算的类型,正确 运用法则;(2)在运算的过程中,一定要注意指数、 系数和符号的处理.
• 12.(2010·河北)已知x=1是一元二次方程x2+mx+n=0 的一个根,则m2+2mn+n2的值为__1__.
整式的加减运算
【例1】 (1)(2014·邵阳)下列计算正确的是( A )
A.2x-x=x
B.a3·a2=a6
C.(a-b)2=a2-b2 D.(a+b)(a-b)=a2+b2
(2)(2014·威海)已知x2-2=y,则x(x-3y)+y(3x-1)-
同类项的概念及合并同类项
【例2】 若-4xay+x2yb=-3x2y,则a+b =__3__.
解析:-4xay+x2yb=-3x2y,可知-4xay ,x2yb,-3x2y是同类项,则a=2,b=1,所 以a+b=3
【点评】 (1)判断同类项时,看字母和相应字母的指 数,与系数无关,也与字母的相关位置无关,两个只 含数字的单项式也是同类项;(2)只有同类项才可以合 并.
第二讲 整式及其运算
1.单项式:由__数与字母__或__字母与字母__相乘组成 的代数式叫做单项式,所有字母指数的和叫做__单项式的次 数__,数字因数叫做__单项式的系数__.单独的数、字母也
是单项式. 2.多项式:由几个__单项式相加__组成的代数式叫做多
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲整式1. (2019,河北)用一根长为a cm的铁丝,首尾相接围成一个正方形.要将它按如图所示的方式向外等距扩1 cm,得到新的正方形,则这根铁丝需增加(B)第1题图A. 4 cmB. 8 cmC. (a+4)cmD. (a+8)cm【解析】由图形观察出正方形的边长增加2 cm,则周长增加8 cm.2. (2019,河北)有三种不同质量的物体“”“”“”,其中,同一种物体的质量都相等.现左右手中同样的盘子中都放着不同个数的物体,只有一组左右质量不相等,则该组是(A)A BC D【解析】设“”的质量为a,“”的质量为b,“”的质量为c.若各个选项中左右两边相等,则选项A可表示为2a=3b.选项B可表示为a+2c=2b+2c,即a=2b. 选项C可表示为a+c=2b+c,即a=2b.选项D可表示为2a =4b,即a=2b.只有选项A与其他等式不同.3. (2019,河北)若2n+2n+2n+2n=2,则n的值是(A)A. -1B. -2C. 0D. 1 4【解析】∵2n+2n+2n+2n=2n×4=2n×22=2n+2,∴2n+2=2.∴n +2=1,即n=-1.4. (2019,河北)将9.52变形正确的是(C)A. 9.52=92+0.52B. 9.52=(10+0.5)(10-0.5)C. 9.52=102-2×10×0.5+0.52D. 9.52=92+9×0.5+0.52【解析】利用乘法公式简便计算,正确运用完全平方公式.9.52=(10-0.5)2=102-2×10×0.5+0.52.5. (2019,河北)若a,b互为相反数,则a2-b2=0 .【解析】∵a,b互为相反数,∴a+b=0.∵a2-b2=(a+b)(a-b),∴a2-b2=0.6. (2019,河北)嘉淇准备完成题目:化简(■x2+6x+8)-(6x+5x2+2).发现系数“■”印刷不清楚.(1)他把“■”猜成3,请你化简(3x2+6x+8)-(6x+5x2+2);(2)他的妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“■”是几?【思路分析】(1)去括号,合并同类项即可.(2)整式加减的结果是常数,即二次项的系数等于0.解:(1)原式=3x2+6x+8-6x-5x2-2=-2x2+6.(2)设“■”内的数字为a.原式=(ax2+6x+8)-(6x+5x2+2)=ax2+6x+8-6x-5x2-2=(a-5)x2+6.因为妈妈看到该题的结果是常数,所以a-5=0,即a=5.所以原题中“■”为5.列代数式例1 (2019,桂林)用代数式表示:a的2倍与3 的和.下列表示正确的是(B)A. 2a-3B. 2a+3C. 2(a-3)D. 2(a+3)【解析】a的2倍,即2a;2a与3的和,即2a+3.针对训练1 (2019,衢州)有一张边长为a cm的正方形桌面,因为实际需要,需将正方形的边长增加b cm ,木工师傅设计了如图所示的三种方案:方案一 方案二方案三训练1题图小明发现这三种方案都能验证公式:a 2+2ab +b 2=(a +b )2.对于方案一,小明是这样验证的:a 2+ab +ab +b 2=a 2+2ab +b 2=(a +b )2.请你根据方案二、方案三,写出公式的验证过程.【思路分析】 方案二是将图形分割成一个正方形和两个矩形来计算;方案三是将图形分割成一个正方形和两个梯形来计算.解:方案二:a 2+ab +(a +b )b=a 2+ab +ab +b 2=a 2+2ab +b 2=(a +b )2.方案三:a 2+[a +(a +b )]b 2+[a +(a +b )]b 2 =a 2+ab +12b 2+ab +12b 2 =a 2+2ab +b 2=(a +b )2.求代数式的值例2 (2019,河北)若mn=m+3,则2mn+3m-5nm+10= 1 . 【解析】2mn+3m-5nm+10=2(m+3)+3m-5(m+3)+10=2m+6+3m-5m-15+10=1.针对训练2 (2019,邢台一模)若m-x=2,n+y=3,则(m-n)-(x +y)的值为(A)A. -1B. 1C. 5D. -5【解析】(m-n)-(x+y)=(m-x)-(n+y)=-1.整式的运算例3 (2019,张家口宣化区二模)两个多项式A,B,其中B=-x2+3x-5.在求A-B时,小明看错题目,误看成了A+B,结果得到x2-6.(1)求多项式A和A-B;(2)若|x-1|=2 0180,求A-B的值.【思路分析】(1)根据B与A+B可求得A,进而求得A-B.(2)由|x-1|=2 0180可得|x-1|=1,进而求得结果.解:(1)由题意,得A+B=x2-6.∵B=-x2+3x-5,∴A=2x2-3x-1.∴A-B=(2x2-3x-1)-(-x2+3x-5)=3x2-6x+4.(2)∵|x-1|=2 0180=1,∴(x-1)2=1.∴A-B=3x2-6x+4=3(x-1)2+1=3×1+1=4.针对训练3 (2019,张家口桥西区模拟)已知多项式A=(x+2)2+x(1-x)-9.(1)如图,化简多项式A时,小明的结果与其他同学的不同.请你检查小明同学的解题过程,在标出①②③④的几项中出现错误的是①;写出正确的解题过程;训练3题图(2)小亮说:“只要给出x2-2x+1的合理的值,即可求出多项式A 的值.”小明给出x2-2x+1的值为4,请你求出此时A的值.【思路分析】正确使用完全平方公式.解:(1)①A=(x+2)2+x(1-x)-9=x2+4x+4+x-x2-9=5x-5.(2)∵x2-2x+1=4,即(x-1)2=4,∴x-1=±2.∴A=5x-5=5(x-1)=±10.因式分解例4 (2019,恩施州)因式分解:8a3-2ab2=2a(2a+b)(2a-b) .【解析】8a3-2ab2=2a(4a2-b2)=2a(2a+b)(2a-b).针对训练4 (2019,安徽)下列分解因式正确的是(C)A. -x2+4x=-x(x+4)B. x2+xy+x=x(x+y)C. x(x-y)+y(y-x)=(x-y)2D. x2-4x+4=(x+2)(x-2)【解析】A. -x2+4x=-x(x-4).B. x2+xy+x=x(x+y+1).C. x(x-y)+y(y-x)=x(x-y)-y(x-y)=(x-y)2.D. x2-4x+4=(x-2)2.一、选择题1. (2019,石家庄新华区质检)计算-a2+2a2的结果是(A)A. a2B. -a2C. 2a2D. 0【解析】根据合并同类项法则进行计算.2. (2019,南京)计算a3·(a3)2的结果是(B)A. a8B. a9C. a11D. a18【解析】根据幂的运算法则,得a3·(a3)2=a3·a6=a9.3. (2019,唐山路南区二模)下列算式中,结果等于x 6的是(A)A. x 2·x 2·x 2B. x 2+x 2+x 2C. x 2·x 3D. x 4+x 2【解析】 选项A 结果为x 6.选项B 结果为3x 2.选项C 结果为x 5.选项D 已是最简结果.4. (2019,邯郸一模)下列运算中,正确的是(A)A. (a 3)3=a 9B. a 2·a 2=2a 2C. a -a 2=-aD. (ab )2=ab 2【解析】 选项A 结果正确.选项B 结果为a 4.选项C 已是最简结果.选项D 结果为a 2b 2.5. 下列计算正确的是(D)A. (3xy 2)3=9x 3y 6B. (x +y )2=x 2+y 2C. x 6÷x 2=x 3D. 2x 2y -12yx 2=32x 2y【解析】 选项A 结果为27x 3y 6.选项B 结果为x 2+2xy +y 2.选项C 结果为x 4.选项D 结果正确.6. (2019,张家口桥西区模拟)已知m -n =100,x +y =-1,则代数式(n +x )-(m -y )的值是(D)A. 99B. 101C. -99D. -101【解析】 (n +x )-(m -y )=n +x -m +y =-(m -n )+(x +y )=-101.7. (2019,唐山丰南区一模)如果a ,b 互为相反数,x ,y 互为倒数,那么14(a +b )+72xy 的值是(C)A. 2B. 3C. 72D. 4【解析】 将a +b =0,xy =1代入,原式=72.8. (2019,唐山路北区一模)下列各式从左到右的变形中,属于因式分解的是(C)A. a (m +n )=am +anB. a 2-b 2-c 2=(a -b )(a +b )-c 2C. 10x 2-5x =5x (2x -1)D. x 2-16+6x =(x +4)(x -4)+6x【解析】 选项A 是整式乘法,选项B ,D 的结果是和的形式,只有选项C 结果是乘积的形式.9. (2019,河北)计算852-152的结果是(D)A. 70B. 700C. 4 900D. 7 000 【解析】 原式=(85+15)×(85-15)=100×70=7 000.10. (2019,石家庄长安区质检)下列各式中,不是多项式2x 2-4x +2的因式的是(D)A. 2B. 2(x -1)C. (x -1)2D. 2(x -2)【解析】 2x 2-4x +2=2(x 2-2x +1)=2(x -1)2.二、 填空题11. (2019,株洲)单项式5mn 2的次数是 3 .【解析】 m ,n 的指数的和.12. (2019,石家庄质检)若x a y 与3x 2y b 是同类项,则ab 的值为 2 .【解析】 根据同类项的定义可知a =2,b =1,所以ab =2.13. (2019,岳阳)已知a 2+2a =1,则3(a 2+2a )+2的值为 5 .【解析】 将a 2+2a =1代入,原式= 3×1+2=5.14. (2019,菏泽)若a +b =2,ab =-3,则代数式a 3b +2a 2b 2+ab 3的值为 -12 .【解析】 a 3b +2a 2b 2+ab 3=ab (a 2+2ab +b 2)=ab (a +b )2=-3×22=-12.15. (2019,株洲)因式分解:a 2(a -b )-4(a -b )= (a -b )(a +2)(a -2) .【解析】 a 2(a -b )-4(a -b )=(a -b )(a 2-4)=(a -b )(a +2)(a -2).三、 解答题16. (2019,扬州)化简:(2x +3)2-(2x +3)(2x -3).【思路分析】 计算中正确运用乘法公式.解:原式=4x 2+12x +9-4x 2+9=12x +18.17. (2019,邵阳)先化简,再求值:(a -2b )(a +2b )-(a -2b )2+8b 2,其中a =-2,b =12.【思路分析】 计算中正确运用乘法公式,化简后,再代入求值. 解:原式=a 2-(2b )2-(a 2-4ab +4b 2)+8b 2=a 2-4b 2-a 2+4ab -4b 2+8b 2=4ab .将a =-2,b =12代入,得原式=4×(-2)×12=-4.18. (2019,石家庄桥西区质检)(1)计算:972-32;(2)已知a =-13.6,b =3.6,求代数式a 2+2ab +b 2的值.【思路分析】 (1)运用平方差公式因式分解.(2)先运用完全平方和公式因式分解再求值.解:(1)原式=(97+3)×(97-3)=100×94=9 400.(2)原式= (a +b )2.当 a =-13.6,b =3.6时,原式=(-13.6+3.6)2=(-10)2=100.1. (2019,石家庄新华区质检,导学号5892921)已知(x -1)3=ax 3+bx 2+cx +d ,则a +b +c +d 的值为(B)A. -1B. 0C. 1D. 无法确定【解析】 当x =1时,已知等式可化为0=a +b +c +d .2. (2019,张家口桥东区模拟)若M =(x -3)(x -5),N =(x -2)(x -6),则M 与N 的关系为(B)A. M =NB. M >NC. M <ND. M 与N 的大小由x 的取值而定【解析】∵M=x2-8x+15,N=x2-8x+12,∴M-N>0.∴M>N.3. (2019,张家口桥东区模拟,导学号5892921)若a≠0,b≠0,则代数式a|a|+b|b|+ab|ab|的取值共有(A)A. 2个B. 3个C. 4个D. 5个【解析】分情况讨论.若a>0,b>0,原式=3;若a>0,b<0或a<0,b>0或a<0,b<0,原式=-1.4. (导学号5892921)已知x+y=0.2,x+3y=1,则代数式x2+4xy +4y2的值为0.36 .【解析】将已知的两个等式相加,得2x+4y=1.2,∴x+2y=0.6.∴x2+4xy+4y2=(x+2y)2=0.36.5. (2019,达州)已知a m=3,a n=2,则a2m-n的值为 4.5 .【解析】a2m-n=(a m)2÷a n=32÷2=4.5.6. (导学号5892921)若a2n=9,b2n=25,则(ab)n=±15 .【解析】根据幂的运算,得a2n b2n=[](ab)n2=9×25,∴(ab)n =±15.。
