一种求解2条任意类型缓和曲线交点的通用算法
缓和曲线知识与计算公式

缓和曲线知识与计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , lh =s 则 lh=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,as= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3° ——29° 之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线任意点坐标的公式

随着交通运输事业的发展,高等级公路、城市立交桥建设的需要,曲线桥梁在中国发展起来。
曲线桥梁的理论分析计算方面,中国不少院校、科研单位进行了一些理论研究与探索。
但目前很少看到有关曲线桥梁的几何设计计算资料,这给桥梁设计者及施工技术人员在设计、施工中带来许多困难。
曲线桥梁常用的曲线形状,有圆曲线和缓和曲线。
对于圆曲线,桥梁中线以及桥梁内外边缘线均为一同心圆曲线,几何设计计算较为简单,而对于缓和曲线段,桥梁中线为缓和曲线,但对边缘线、栏杆轴线及主梁边腹板曲线等是随中线曲率变化的1条渐变曲率曲线,而不再是缓和曲线。
在过去的设计中,对缓和段上述特征曲线的计算,是近似按缓和曲线来计算,这对于曲率大、曲线段较长的情况,误差会很大,特别是对有加宽、超高的缓和段,误差更不可忽视。
以往设计主梁钢筋骨架时,按缓和曲线计算,则骨架出现过长或过短的情况。
本文以缓和曲线长度作为参数,提出了弯桥缓和段特征曲线的几何计算式及超高计算式。
1 缓和段特征曲线几何设计计算1.1 缓和曲线的坐标、切线角对缓和曲线(桥中线)上任一点M(x,y),如图1所示,相应的坐标、切线角β为(1)式中:l为任意点M至原点0(即ZH点)的曲线长;R为缓和曲线终点的曲率半径;ls为缓和曲线全长。
图1 缓和曲线1.2 平行于内(外)边缘线曲线的参数方程对于一般加宽,可在缓和曲线范围内完成。
设自ZH点开始,桥梁内、外侧沿缓和曲线长按线性加宽。
平行于内侧边缘线的曲线A1B1上任一点M1(x1,y1)在缓和曲线上点M(x ,y)处的曲率半径上,且设M1N1=d1,如图2所示。
由几何关系可得(2)式中:b1(l)为M、N1之间的距离,即点M处桥内侧宽度,可按下式计算式中:b1(0)、b1(ls)分别为缓和段起点和终点桥中线至内侧边缘宽度;其它符号意义同前。
图2 平行于内、外边缘线曲线参数方程计算图式将式(2)中sinβ、cosβ分别以级数表示,即将上式及式(1)代入式(2)并略去高阶项后得曲线A1B1的参数方程(3)同理,可得平行于外侧边缘线曲线A2B2参数方程(4)式中:d2为曲线A2B2与外边缘线间的距离;b2(l)为缓和曲线长l处外侧桥宽,计算式为(5)式中:b2(0)、b2(ls)分别为缓和段起点和终点中线至外侧边缘宽度;其它符号意义同前。
缓和曲线交点桩号计算公式

缓和曲线计算方法(ZH~HY)中线首先计算直线段坐标方位角(即ZH~JD坐标方位角),及ZH点坐标。
备用偏角公式:{30*L/(π*RLS)缓和曲线}计算待求点偏角=((L/10)2 *(57296/(RLS ))/60。
其中L=待求点至ZH距离、R=圆曲线半径、LS =缓和曲线长。
待求点方位角=直线方位角±待求点偏角。
(曲线左转-偏角,曲线右转+偏角)待求点至ZH点弦长=L—L5 /(90*R2 *LS 2),其中L=待求点至ZH距离(里程)、R=圆曲线半径。
待求点坐标:X=ZH点X坐标+COS(待求点方位角)*弦长Y= ZH点Y坐标+SIN(待求点方位角)*弦长缓和曲线计算左右边线坐标(ZH~HY)左侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)—边线与中线夹角。
右侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)+边线与中线夹角。
左侧边线坐标:X=该点中线X坐标+COS(左侧方位角)*边线至中线距离Y=该点中线Y坐标+SIN(左侧方位角)*边线至中线距离右侧边线坐标:X=该点中线X坐标+COS(右侧方位角)*边线至中线距离Y=该点中线Y坐标+SIN(右侧方位角)*边线至中线距离圆曲线计算方法(HY~YH)中线注:(ZY-YZ)同理,方位角=用直线方位角-待求点偏角首先计算直线段坐标方位角(即ZH~JD坐标方位角),及HY点坐标。
求出缓圆点(HY)偏角=(LS*90)/(π* R)。
求待求点偏角=(L*90)/(π* R)。
其中:L=待求点至HY距离(里程)、R=圆曲线半径、LS =缓和曲线长。
待求点至HY点弦长=2* R*SIN(待求点偏角)。
待求点方位角=直线方位角±HY点偏角±待求点偏角,(曲线左转-偏角,曲线右转+偏角)。
待求点坐标:X=HY点X坐标+COS(待求点方位角)*弦长Y=HY点Y坐标+SIN(待求点方位角)*弦长圆曲线计算左右边线坐标左侧方位角=(待求点方位角±偏角—边线与中线夹角)。
缓和曲线计算

缓和曲线计算方法如下:
1.确定两个直线或两条曲线的交点。
2.确定圆曲线的半径。
圆曲线的半径应该足够大,使车辆或列车
可以在转弯时平稳地行驶,同时也不能太大,以免影响道路或
铁路的设计。
3.确定过渡曲线的长度。
过渡曲线是圆曲线和直线之间的曲线,
用于将两者之间的变化平滑地连接起来。
过渡曲线的长度应该
足够长,以确保车辆或列车可以逐渐进入或离开圆曲线,从而
减少冲击和颠簸。
4.根据圆曲线和过渡曲线的参数,计算出缓和曲线的形状和尺寸。
需要注意的是,计算缓和曲线需要考虑多种因素,包括车辆或列车的速度、载重、惯性等因素,以及道路或铁路的设计标准和要求。
因此,在进行缓和曲线计算时,需要综合考虑各种因素,以确保计算结果的准确性和可行性。
缓和曲线常用计算公式

缓和曲线常用计算公式-CAL-FENGHAI.-(YICAI)-Company One1一、缓和曲线常数1、 内移距P :3420268824Rl R l P n -= 2、 切垂距m :2302402R l l m -= 3、缓和曲线基本角:Rl R l πβ000902== 3、 缓和曲线偏角: Rl R l πδ000306== 5、缓和曲线反偏角: Rl R l b π000603== 缓和曲线常数既有线元素,又有角元 素,且均 为圆曲线半径R 和缓和曲线长0l 的函数。
线元素要计算到mm ,角元素要计算到秒。
二、缓和曲线综合要素切线长:()m P R T +⎪⎭⎫ ⎝⎛+=2tan α曲线长:()0022l R L +-=βα外视距:R P R E -⎪⎭⎫ ⎝⎛+=2cos 0α切曲差:L T q -=2曲线综合要素均为线元素,且均为转向角 α、圆曲线半径R 和缓和曲线长0l 的函数。
曲线综合要素计算到cm 。
三、缓和曲线任意点偏角计算2020202902306Rl l Rl l Rl l Rl l t t t t t t πβπδ====0202603Rl l Rl l b t t t π==实际应用中,缓和曲线长0l 均选用10m 的倍数。
1 四、偏角法测设缓和曲线遇障碍 ()()T B B T l l l l Rl 2610+-=βδ()()()()T F T F T F T F F l l l l Rl l l l l Rl 23026100+-=+-=πδ—B l 为靠近ZH(HZ)点的缓和曲线长; —T l 为置镜点的缓和曲线长; —F l 为远离ZH(HZ)点的缓和曲线长。
五、直角坐标法1、缓和曲线参数方程: 5202401a a a l l R l x -= 30373033661l R l l Rl y a a a -= 2、圆曲线m R x b b +=αsin()P R y b b +-=αcos 1 式中,b α为圆心O 到切线的垂线方向和到B 的半径方向所形成的圆心角,按下式计算:00βα+-=Rl l b b ()()T B B T l l l l Rl 2610+-=βδ ()()T B B T l l l l Rl 2300+-=π。
缓和曲线交点桩号计算公式

缓和曲线交点桩号计算公式缓和曲线交点桩号计算公式是用来确定两条缓和曲线的交点位置的数学公式。
缓和曲线是设计道路时用来平滑过渡曲线的一种工程技术。
在道路设计中,缓和曲线通常用于连接两条直线段或两个曲线段,以减少车辆行驶时的冲击和转向的难度。
缓和曲线交点桩号计算公式的推导基于以下几个假设:1.假设两条缓和曲线是相等的,即两条曲线的半径相等。
2.假设两条缓和曲线的长度相等,即两条曲线的切线长相等。
3.假设两条缓和曲线的起点和终点相对位置相同,即两条曲线的起点和终点的切线夹角相等。
基于上述假设,缓和曲线交点桩号计算公式可以推导如下:1.首先,计算两条缓和曲线的长度。
缓和曲线的长度可以通过以下公式计算: L = (V^2) / (127 * R)其中,L是缓和曲线的长度,V是车辆的速度,R是缓和曲线的半径。
2.然后,计算两条缓和曲线的起点和终点的坐标。
缓和曲线的起点和终点的坐标可以通过以下公式计算:X = L * cos(θ) Y = L * sin(θ)其中,X和Y分别是缓和曲线的起点和终点的横坐标和纵坐标,L是缓和曲线的长度,θ是缓和曲线的切线夹角。
3.最后,计算两条缓和曲线的交点桩号。
缓和曲线的交点桩号可以通过以下公式计算: P = P1 + X1 + X2其中,P是缓和曲线的交点桩号,P1是第一条缓和曲线的起点桩号,X1是第一条缓和曲线的起点到交点的距离,X2是第二条缓和曲线的交点到起点的距离。
需要注意的是,以上公式仅适用于两条缓和曲线的半径相等、长度相等和起点终点位置相同的情况。
在实际的道路设计中,可能会存在不同的情况,需要根据具体情况进行调整和计算。
以上就是缓和曲线交点桩号计算公式的基本推导和应用。
在道路设计中,合理使用缓和曲线交点桩号计算公式,可以帮助工程师更好地设计平滑的道路曲线,提高行车的安全性和舒适性。
缓和曲线)计算公式
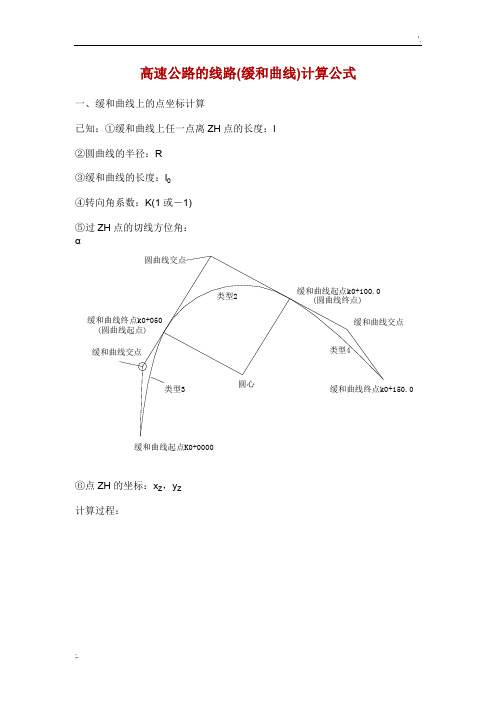
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
缓和曲线)计算公式
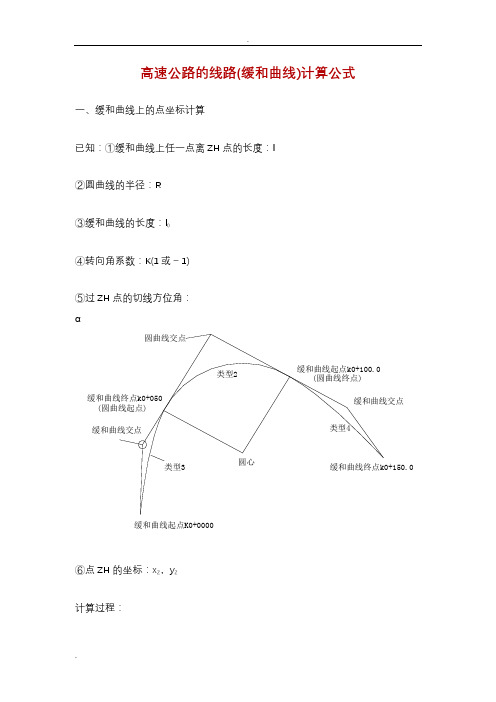
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
李" 伟, 蒲" 浩 ( 中南大学 土木建筑学院, 湖南 长沙 #$%%&’ )
!
摘" 要: 针对 ! 条缓和曲线交点坐标的计算在线路设计中的难点, 而且目前的计算方法都只针对普通的三次抛物线型缓和 曲线, 不能适用于高次缓和曲线的情况, 建立各种类型缓和曲线坐标计算的通用计算模型, 导出了 ! 条缓和曲线相对纵距 , 并深入研究了该函数在各种缓和曲线相交情况下的特性。在此基础上, 提出一种适用于各 ! ! 与缓长 " 的关系函数 !( ! ") 类型缓和曲线交点坐标计算的通用算法, 并用 () * * +, % 编制了计算程序。该算法与同类方法相比在速度、 精度、 稳健性 等方面具有明显优势。 关键词: 缓和曲线; 线路设计; 公路线形; 铁路选线 中图分类号: -.//&" " " 文献标识码: 0" " " 文章编号: $+&! 1 &%!/ ( !%%& ) %$ 1 %%&& 1 %’
?@
铁 道 科 学 与 工 程 学 报 + + + + + + + + + + + + + + + %##? 年 % 月
干线采用半波正弦型缓和曲线, 英国和法国采用三 次抛物线改进型缓和曲线。我国铁科院铁建所经 过大量实验研究, 建议最高速度为 !"# $ %&# ’( ) * 的客运 专 线 宜 采 用 半 波 正 弦 型 缓 和 曲 线
$ ! ! $ 01/ (%! ) [ ( ] ; (") $# %! ’ # $# % $% ( 前半部) ; ’ # $% # (?)
=型 ( < > < 型) : % & % &
!+ 各种类型缓和曲线任意点坐标计 算的通用方法
一般是先给出任意点的外轨超高 ! 关于距离 然后按照车辆匀 " # 或 # " 点的长度 $ 的计算公式。 速通过缓和曲线的假设计算出任意点处曲率 % 关 于 $ 的计算公式。
!"#$ ! $%& ’()*+,’,&* -.(/0+1 (02)’,/0 /0(’,-)2 3,+’)*-0 ,* ’40 +)50 (060(0*-0 6()50
!7 !# !( ! $ )函数的特性 在同一坐标系下, 建立以 % 为自变量, ! ! 为因 变量, 定义域为 % , [ &% , ’% ] 的函数。 从下面列出的 两缓和曲线的位置关系图 ( 实线为第一条缓和曲 线, 虚线为第二条缓和曲线)和 !( ! % )函数的图像 可以得出以下结论: " )! 条缓和曲线交点处 ! ! " 8 (见 ! )! 条缓和曲线不相交时, ! ! 始终大于 8 图 9 )或者始终小于 8 ( 见图 : ) 。
$ % ! [! ( % (! ( ) ) ] ( 后半部) 。 (@) $# ’#
以下计算以半波正弦缓和曲线为例。 根据曲率的定义, 缓和曲线的偏角 ! 和曲率 % 存在如下关系: 9$ & *9$。 (A) " * 对 $ 积分, 得到偏角 ! 关于 $ 的表达式: 9! & ! & !$ 9$ & ( ! ( 430 ) ’ 9! & ’ *9$ & ’ %!’ $
# # # # $ $ $
$# $ ! !$ [ ( 01/ ) ] 。 ( !# ) $# % ’ $# ! +, , 坐标和偏角 ! 存在如下几何关系: 9+ & 430!・9$; 9, & 01/!・9$。 由此得出 + 和 , 坐标的表达式如下: + &
$
( !! ) ( !% )
’ 9+ & ’ 430!・9$ &
[ %]
!# ( 半波正弦: % & 全波正弦: % &
$ < $ & )(< ( ) ] ; (<) $# $# (&)
。因
! !$ ( ! ( 430 ) ; % ’# $#
此, 必须研究一种针对各种缓和曲线交点计算的稳 健而简单的通用方法。在此, 本文作者提出一种求 解 % 条任意类型缓和曲线交点的通用算法。
。关于 !
条缓和曲线交点计算坐标计算的论题, 许多学者进 行了研究, 提出了许多方法, 如: 将两缓和曲线相交
!
收稿日期: !%%+ 1 %/ 1 $% 基金项目: 湖南省科技攻关项目 ( %#;ST%R$ ) 作者简介: 李" 伟 ( $/R# 1 ) , 男, 江西进贤人, 博士研究生, 从事道路与铁道工程信息技术研究
[ !] 各类型缓和曲线曲率 % 计算公式 如下: ! $ 三次抛物线: % & ( ) ; (!) ’ # $# $ % $ ; ! ( ) (% ( ) ] ; (%) % & [; 五次抛物线: $# $# ’# $ & $ < ! ( ) ( !& ( ) ) 七次抛物线: % & [" $# $# ’# $ ; ] ; (;) !# ( ) $# $ % $ ; ! ( ) ( !# ( ) ) 七次四项式: % & [& $# $# ’#
第" 期# # # # # # # # # #
李#
伟, 等: 一种求解 ! 条任意类型缓和曲线交点的通用算法
AB
标差值称为 “ 两缓和曲线的相对纵距” , 即 ! ! " !! # !" 。
# # 9 )! 条缓和曲线有 个交点 ( 相切)时, !! 由 一正值单调递减至 8 再由 8 单调递增到另一正值, 或者 ! ! 由一负值单调递增到 8 再由 8 单调递减到 另一负值, 如图 > 所示。
! "#$%&’()* )*+,’$-./ 0,’ 1)*1"*)-$#+ $#-&’(&1-$,# 2,$#1,,’3$#)-&( ,0 -4, ’)#3,/ -’)#($-$,# 1"’%&(
23 456, 7. 89:
( ;<=::> :? )6@6> 9AB 0C<=6D5<DEC9> FAG6A55C6AG, )5ADC9> ;:ED= .A6@5CH6DI, )=9AGH=9 #$%%&’ , )=6A9)
> )! 条缓和曲线有 ! 个交点时, ! ! 由一正值单 调递减至一负值再由该负值单调递增到另一正值, 或者 ! ! 由一负值单调递增至一正值再由该正值单 调递减到另一负值, 如图 A 所示。
图 !#
两缓和曲线在同一坐标系下的相对纵距 ! ! 图 ># ! 条缓和曲线只有 " 个交点 (相切)时的 !( ! %)图像 !"#$ > ;5)<0 &6 !( ! % ) %40* ’%& ’()*+,’,&* -.(/0+ 4)/0 &*0 ,*’0(+0-’,&* =&,*’ ( ’)*<0*-?)
# #
$
$
! $ !$ ] ・9 $; [ ( 01/ ) ’ 430! %’ $ $ ! , & ’ 9, & ’ 01/!・9$ & $ ! $ !$ ( 01/ ) ] ・9 $。 [ ’ 01/! %’ $ $ !
# # # $ $ # # $ # # # #
$#
( !; )
( !< )
图 !+ 05:7-7876.213/
缓和曲线局部坐标及超高
!"#$ ! ,-./01213/ 45-67 834.8 433-91/.270 ./9
+ 和 , 坐标的表达式是关于 $ 的积分, 选择合适 的数值积分方法编制程序可以快速精确地计算出 缓和曲线上任意点 + 和 , 坐标。 根据式 ( ! ) -( @ ) , 采用类似的方法可以计算 = 全波正弦、 五次抛物线、 七次抛物线、 七次四项式、 型等缓和曲线。
" " 在公路和铁路线路平面几何设计中, 缓和曲线 作为一种主要的线形, 其相交问题在平面交叉和多
[ $ 1 $% ] 层枢纽连接中经常出现 。尤其是在互通式立
的方程式 直 接 进 行 数 学 变 换 得 到 迭 代 式 后 再 求
[ ’, R] 解 ; 对两缓和曲线相交的方程组进行适当简化 [ +] 得到近似方程式后再迭代求解 ; 采用最优化方 [ &] 等。但这些算法都只局限于普通三 法迭代求解
!"#$%&’$: 8:J D: B5D5CK6A5 D=5 6AD5CH5<D6:A L:6AD <::CB6A9D5H :? DJ: DC9AH6D6:A <EC@5H J9H 9 B6??6<E>D LC:M>5K 6A 9>6GAK5AD B5H6GA, N5H6B5H,?:CK5C 9>G:C6D=KH <:E>B A:D 9LL>I D: =6G= L:J5C L9C9M:>9 DC9AH6D6:A <EC@5 ,M5<9EH5 D=5I J5C5 B5H6GA5B ?:C <:KK:A D=C55 L:J5C L9C9M:>9 DC9AH6D6:A <EC@5, 0 EA6@5CH9> K:B5> D=9D <9A <9><E>9D5 D=5 6AD5CH5<D6:A L:6AD <::CB6A9D5H :? 9>> O6ABH :? DC9AH6D6:A <EC@5H J9H H5D , 9AB D=5 ?EA<D6:A !( I > )D=9D B5H<C6M5H D=5 C5>9D6:AH=6L :? DJ: DC9AH6D6:A <EC@5HP C5>9D6@5 @5CD6<9> B6HD9A<5 9AB D=5 B6HD9A<5 ?C:K 9 C9AB:K L:6AD D: Q 8 :C 8 Q J9H HDEB65B, -=5 ?EA<D6:A <=9C9<D5C6HD6<H J=5A DJ: DC9AH6D6:A <EC@5H =9B B6??5C5AD 6AD5CH5<D6:A L:6AD <:EADH J5C5 C5H59C<=5B, 0 EA6@5CH9> 9>G:C6D=K ?:C <9><E>9D6AG 6AD5CH5<D6:A L:6AD <::CB6A9D5H :? DJ: C9AB:K DC9AH6D6:A <EC@5H J9H LC:L:H5B 9AB 9 LC:GC9K J9H B5H6GA5B EH6AG () * * +, %, ):KL9C5B J6D= D=5 H6K6>9C 9>G:C6D=KH ,6D =9H :M@6:EH HEL5C6:C6DI 6A HL55B , LC5<6H6:A 9AB C:MEHDA5HH, 5D<, ()* +,%-#: DC9AH6D6:A <EC@5; 9>6GAK5AD B5H6GAH; C:9B 9>6GAK5AD; C96>J9I >:<9D6:A
