数值分析第4章答案
数值分析第四章习题
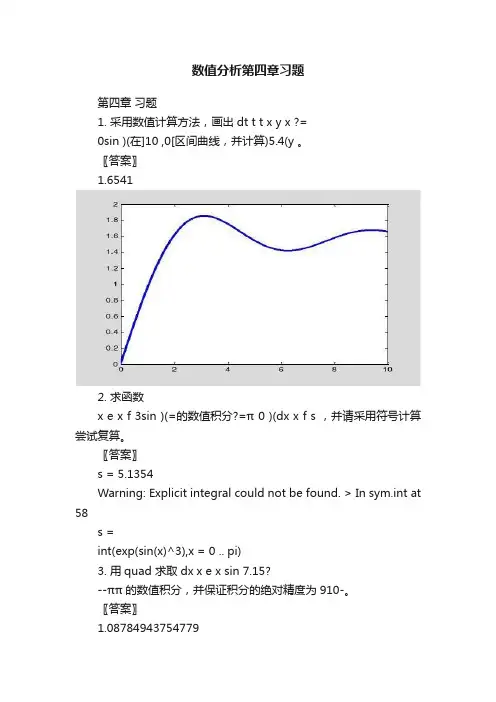
数值分析第四章习题第四章习题1. 采用数值计算方法，画出dt t t x y x ?=0sin )(在]10 ,0[区间曲线，并计算)5.4(y 。
〖答案〗1.65412. 求函数x e x f 3sin )(=的数值积分?=π 0 )(dx x f s ，并请采用符号计算尝试复算。
〖答案〗s = 5.1354Warning: Explicit integral could not be found. > In sym.int at 58s =int(exp(sin(x)^3),x = 0 .. pi)3. 用quad 求取dx x e x sin 7.15?--ππ的数值积分，并保证积分的绝对精度为910-。
〖答案〗1.087849437547794. 求函数5.08.12cos 5.1)5(sin )(206.02++-=t t t et t f t 在区间]5,5[-中的最小值点。
〖答案〗最小值点是-1.28498111480531 相应目标值是-0.186048010065455. 设0)0(,1)0(,1)(2)(3)(22===+-dt dy y t y dt t dy dt t y d ，用数值法和符号法求5.0)(=t t y 。
〖答案〗数值解y_05 = 0.78958020790127符号解ys =1/2-1/2*exp(2*t)+exp(t)ys_05 =.789580356470605529168507052137806. 求矩阵b Ax =的解，A 为3阶魔方阵，b 是)13(?的全1列向量。
〖答案〗x =0.06670.06670.06677. 求矩阵b Ax =的解，A 为4阶魔方阵，b 是)14(?的全1列向量。
〖答案〗解不唯一x =-0.0074 -0.0809 0.1397 0.0662 0.0588 0.1176 -0.0588。
数值方法课后习题答案第4章
解线性方程组迭代法
第四章 解线性方程组迭代法
习题4-1
第四章
解线性方程组迭代法
Байду номын сангаас
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
解线性方程组迭代法
第四章
习题4
习题4
习题4
习题4
8.
设A为严格对角优势阵，证明：
习题4
9. A是n阶非奇异阵，B是n阶奇异阵，试求证：
习题4
习题4
P91
P91.
x0
p0 r0
Ap0
x1
r1
p1
Ap1
x2
r2
0
3
7
30/29=
17/29=
1360/841=
1530/841=
14/9=
0.3
P91
1.034482758 0 1 8 10/29= 0.344827586
0.570796875 0.493315839 0.500166165 0.499999398 1.001438281 0.998173633 1.000074653 1.000013383 -0.49943416 -
0.500558834 0.499923587 0.500003961
w=1.03
10 29 a0 =10/29=0.344827586
2890/841=3.436385254 260100/24389=10.66464388 a1 =8381/26010=0.322222222 -289/29= -9.965517218 b0 =289/841=0.343638524
《数值分析》第四章答案
习题41. 给定x x f =)(在144,121,100=x 3点处的值，试以这3点建立)(x f 的2次(抛物)插值公式，利用插值公式115求的近似值并估计误差。
再给13169=建立3次插值公式，给出相应的结果。
解：x x f =)( 2121)(-='x x f ，2341)(--=''x x f ,2583)(-='''x x f ,27)4(1615)(--=x x f，72380529.10)115(=f1000=x ， 1211=x ， 1442=x ， 1693=x 100=y ， 111=y ， 122=y ， 133=y))(())(())(())(())(())(()(1202102210120*********x x x x x x x x y x x x x x x x x y x x x x x x x x y x L ----+----+----= )121144)(100144()121115)(100115(12)144121)(100121()144115)(100115(11)144100)(121100()144115)(121115(10)115(2----⨯+----⨯+----⨯=L=2344)6(1512)23(21)29(1511)44)(21()29)(6(10⨯-⨯⨯+-⨯-⨯⨯+----⨯72276.1006719.190683.988312.1=-+=))()((!3)()()(2102x x x x x x f x L x f ---'''=-ξ ，144100<<ξ )44115()121115()100115()(max 61)115()115(1441002-⨯-⨯-⋅'''≤-≤≤x f L f x 296151083615⨯⨯⨯⨯⨯≤-001631.0101631.02=⨯=- 实际误差 22101045.0)115()115(-⨯=-L f))()(())()(())()(())()(()(312101320130201032103x x x x x x x x x x x x y x x x x x x x x x x x x y x L ------+------= ))()(())()(())()(())()((23130321033212023102x x x x x x x x x x x x y x x x x x x x x x x x x y ------+------+ )169100()144100()121100()169115()144115()121115(10)115(3-⨯-⨯--⨯-⨯-⨯=L )169121()144121()100121()169115()144115()100115(11-⨯-⨯--⨯-⨯-⨯+)169144()121144()100144()169115()121115()100115(12-⨯-⨯--⨯-⨯-⨯+)144169()121169()100169()144115()121115()100115(13-⨯-⨯--⨯-⨯-⨯+)48()23(21)54()29(1511)69()44()21()54()29()6(10-⨯-⨯-⨯-⨯⨯+-⨯-⨯--⨯-⨯-⨯= 254869)29()6(1513)25(2344)54()6(1512⨯⨯-⨯-⨯⨯+-⨯⨯-⨯-⨯⨯+ 723571.10409783.0305138.2145186.11473744.1=+-+= ))()()((!4)()()(3210)4(3x x x x x x x x f x L x f ----=-ξ，169100<<ξ)169115)(144115)(121115)(10115(101615241)115()115(73----⨯⨯⨯≤--L f )54()29()6(151016152417-⨯-⨯-⨯⨯⨯⨯=- 0005505.0105505.03=⨯=-实际误差 321023429.0)115()115(-⨯=-L f 2. 设j x 为互异节点),,1,0(n j =求证： (1)k nj j k j x x l x =∑=)(0),,1,0(n k =;(2)0)()(0=-∑=x l x x j knj j ),,1(n k =。
数值分析课后习题及答案
第一章 绪论（12） 第二章 插值法（40-42）2、当2,1,1-=x 时，4,3,0)(-=x f ，求)(x f 的二次插值多项式。
[解]372365)1(34)23(21)12)(12()1)(1(4)21)(11()2)(1()3()21)(11()2)(1(0))(())(())(())(())(())(()(2221202102210120120102102-+=-++--=+-+-⨯+------⨯-+-+-+⨯=----+----+----=x x x x x x x x x x x x x x x x x x x y x x x x x x x x y x x x x x x x x y x L 。
3、给出x x f ln )(=的数值表用线性插值及二次插值计算54.0ln 的近似值。
X 0.4 0.5 0.6 0.7 0.8 x ln -0.916291 -0.693147 -0.510826 -0.357765 -0.223144[解]若取5.00=x ，6.01=x ，则693147.0)5.0()(00-===f x f y ，510826.0)6.0()(11-===f x f y ，则604752.182321.1)5.0(10826.5)6.0(93147.65.06.05.0510826.06.05.06.0693147.0)(010110101-=---=--⨯---⨯-=--+--=x x x x x x x x x y x x x x y x L ，从而6202186.0604752.19845334.0604752.154.082321.1)54.0(1-=-=-⨯=L 。
若取4.00=x ，5.01=x ，6.02=x ，则916291.0)4.0()(00-===f x f y ，693147.0)5.0()(11-===f x f y ，510826.0)6.0()(22-===f x f y ，则 217097.2068475.404115.2)2.09.0(5413.25)24.0(3147.69)3.01.1(81455.45)5.06.0)(4.06.0()5.0)(4.0()510826.0()6.05.0)(4.05.0()6.0)(4.0()693147.0()6.04.0)(5.04.0()6.0)(5.0(916291.0))(())(())(())(())(())(()(22221202102210120120102102-+-=+--+-⨯++-⨯-=----⨯-+----⨯-+----⨯-=----+----+----=x x x x x x x x x x x x x x x x x x x x x x y x x x x x x x x y x x x x x x x x y x L ，从而61531984.0217097.21969765.259519934.0217097.254.0068475.454.004115.2)54.0(22-=-+-=-⨯+⨯-=L补充题：1、令00=x ，11=x ，写出x e x y -=)(的一次插值多项式)(1x L ，并估计插值余项。
数值分析智慧树知到答案章节测试2023年湖南师范大学
第一章测试1.在数值计算中因四舍五入产生的误差称为（）A:观测误差B:舍入误差C:模型误差D:方法误差答案:B2.当今科学活动的三大方法为（）。
A:实验B:数学建模C:科学计算D:理论答案:ACD3.计算过程中如果不注意误差分析，可能引起计算严重失真。
A:对B:错答案:A4.算法设计时应注意算法的稳定性分析。
A:错B:对答案:B5.在进行数值计算时，每一步计算所产生的误差都是可以准确追踪的。
A:错B:对答案:A第二章测试1.A:B:C:D:答案:C2.某函数过(0,1)，(1,2)两点，则其关于这两点的一阶差商为A:0B:1C:2D:3答案:B3.A:B:C:D:答案:B4.下列说法不正确的是A:分段线性插值的导数一般不连续B:高次多项式插值不具有病态性质C:分段线性插值逼近效果依赖于小区间的长度D:分段线性插值的几何图形就是将插值点用折线段依次连接起来答案:D5.下列关于分段线性插值函数的说法，正确的是A:二次函数的分段线性插值函数是该二次函数本身B:一次函数的分段线性插值函数是该一次函数本身C:对于光滑性不好的函数优先用分段线性插值D:对于光滑性较好的函数优先用分段线性插值答案:BC6.A:B:C:D:答案:BCD7.同一个函数基于同一组插值节点的牛顿插值函数和拉格朗日插值函数等价。
A:对B:错答案:A第三章测试1.A:B:C:D:答案:B2.以下哪项是最佳平方逼近函数的平方误差A:B:C:D:答案:C3.当区间为[-1,1],Legendre多项式族带权 ( ) 正交。
A:B:C:D:答案:A4.n次Chebyshev多项式在 (-1,1) 内互异实根的个数为A:n-1B:nC:n+1D:n+2答案:B5.用正交函数族做最小二乘法有什么优点A:每当逼近次数增加1时，系数需要重新计算B:得到的法方程非病态C:每当逼近次数增加1时，之前得到的系数不需要重新计算D:不用解线性方程组，系数可简单算出答案:BCD6.用正交多项式作基求最佳平方逼近多项式，当n较大时，系数矩阵高度病态，舍入误差很大。
数值分析 第四章第一,二,三节
令n 2k (k 1, 2, )
n 0
t (t 1)
k k
(t n)dt t (t 1)
0
2k
(t k )(t k 1)
(t 2k 1)(t 2k )dt
(u k )(u k 1) 令H (u ) H (u ) (u k )(u k 1)
4 b 1 5 ba 4 ab 4 5 4 a 4 b a x dx 5 (b a ) 6 2 ba ab f (a) 4 f f (b ) 6 2 即抛物线求积公式的代数精度为3.
(n) b a x a th ( 1) n i (b a) n t (t 1) (x) (t n ) dx dt (x x i ) '(x i ) n i ! ( n i)! 0 t i
n t (t 1) (1) n i (t n) dt 0 n i ! (n i )! t i
b a
f ( x)dx
b a
3 ba 2 b a 2 (b a 2) x dx 3 2 3
19
定理4.2 : Newton Cotes求积公式至少具有n 次代数精确度. 当n为偶数时, 代数精确度至少为n 1次.
f ( n 1) ( ) f ( x) pn ( x) ( x) (a b), ( x) (n 1)! 若f ( x)是不超过n次的多项式, 则f ( n 1) ( x) 0
u t k
u (u 1) u (u 1)
(u k 1)(u k )du (u k 1)(u k ) (u k 1)(u k )
《数值分析》杨大地 答案(第四章)
⑴ 2 3 1 ，求按模最大特征值和对应的特征向量，精确到小数三位。
解：由幂法公式有:
1i n
//P67 页
(1) | a r | max | a i | ,其中 ai 是uk −1 = (a1 , a2 , . . . , an )T 的各分量； (2) y k 1
∴ i t 为������ − ������������ 的特征值。 令 为 A 的特征向量，则有： A i 又∵ A tI A tI i t i t ∴ 也为������ − ������������ 的特征向量； ∴ i t 是 A tI 的特征值，且 A 和������ − ������������特征向量相同。
T
1
当计算到第 9 次时，λ 1 的小数点前三位精度开始稳定，满足题目要求，所以此时 A 矩阵的按模最大特 征值 1 =7.288，对应的特征向量为（1.000,0.523,0.242）T 5．若 A 的特征值为 1, 2 ,, n , t 是一实数，证明： i t 是 A tI 的特征值，且特征向量不变． 证明： ∵ A 的特征值为 ∴｜ i I A ｜=0 假设������是 A tI 的特征值，则有：
k 0 1 2 3 4 5 6 7 8 9 ukT 1.000,1.000,1.000 9.000,6.000,3.000 7.6667,4.3333,2.000 7.3913,3.9565,1.8261 7.3177,3.8530,1.7824 7.2966,3.8231,1.7701 7.2906,3.8146,1.7666 7.2887,3.8119,1.7655 7.2882,3.9112,1.7652 7.2880,3.8109,1.7651 ykT 1.000,1.000,1.000 1.000,0.6667,0.3333 1.000,0.5653,0.2609 1.000,0.5353,0.2471 1.000,0.5265,0.2436 1.000,0.5240,0.2426 1.000,0.5232,0.2423 1.000,0.5230,0.2422 1.000,0.5229,0.2422 9.0000 7.6667 7.5913 7.3177 7.2966 7.2916 7.2887 7.2882 7.2880
华中科技大学出版社—数值分析第四版—课后习题及答案
14. 由于 x1 , x 2 , , x n 是 f ( x ) 的 n 个互异的零点，所以 f ( x) a 0 ( x x1 )( x x 2 ) ( x x n )
a 0 ( x xi ) a 0 ( x x j ) ( x xi ),
i 1 i 1 i j n n
4 7 h 3 时，取得最大值 max | l 2 ( x ) |
10 7 7 x 0 x x3 27 . k x , x , , x n 处进行 n 次拉格朗日插值，则有 6. i) 对 f ( x) x , (k 0,1, , n) 在 0 1 x k Pn ( x ) Rn ( x ) l j ( x) x k j
。
14．
1000000000 999999998 x1 1.000000, x2 1.000000 999999999 999999999 方程组的真解为 ，
x 1.00, x2 1.00 ， 而无论用方程一还是方程二代入消元均解得 1 结果十分可 靠。 s b sin ca a sin cb ab cos cc a b c tan c c s ab sin c a b c 15．
可 得
计
算
( f1 ) ln(1
( f 2 ) ln(1
x x 1
2
) )
1 ( x x 2 1) 60 104 3 103 2 x x 1 ，
2
x x 1
2
x x 1
2
1 1 104 8.33 107 60 2
。
(Y100 ) 100
数值分析答案第四章
令
f (x) = x ，则
0 = −1 + 2 x1 + 3 x2
令 f ( x ) = x 2 ，则
2 2 = 1 + 2 x12 + 3 x2
从而解得
⎧ x1 = −0.2899 ⎧ x1 = 0.6899 或⎨ ⎨ ⎩ x2 = 0.5266 ⎩ x2 = 0.1266
令 f ( x ) = x 3 ，则
∫
1
−1
f ( x)dx = ∫ x3 dx = 0
−1
1
[ f ( −1) + 2 f ( x1 ) + 3 f ( x2 )] / 3 ≠ 0
故
∫
1
−1
f ( x)dx = [ f (− 1) + 2 f ( x1 ) + 3 f ( x2 )] / 3不成立。
h
因此，原求积公式具有 2 次代数精度。 （4）若
7 h T8 = [ f ( a) + 2∑ f ( xk ) + f ( b)] = 0.11140 2 k =1
复化辛普森公式为
7 7 h S8 = [ f ( a) + 4∑ f ( x 1 ) + 2∑ f ( xk ) + f ( b)] = 0.11157 k+ 6 k=0 k =1 2 1
令 f ( x ) = x 2 ，则
b 1 3 3 2 f ( x ) dx = ∫a ∫a x dx = 3 (b − a ) b −a 1 3 3 [7 f ( x0 ) + 32 f ( x1 ) + 12 f ( x2 )+ 32 f ( x (b − a ) 3 )+ 7 f ( x 4 )]= 90 3 b
数值分析课后习题答案
7、计算的近似值，取。
利用以下四种计算格式，试问哪一种算法误差最小。
〔1〕〔2〕〔3〕〔4〕解：计算各项的条件数由计算知，第一种算法误差最小。
解：在计算机上计算该级数的是一个收敛的级数。
因为随着的增大，会出现大数吃小数的现象。
9、通过分析浮点数集合F=〔10，3，-2，2〕在数轴上的分布讨论一般浮点数集的分布情况。
10、试导出计算积分的递推计算公式，用此递推公式计算积分的近似值并分析计算误差，计算取三位有效数字。
解：此算法是数值稳定的。
第二章习题解答1.〔1〕 R n×n中的子集“上三角阵〞和“正交矩阵〞对矩阵乘法是封闭的。
〔2〕R n×n中的子集“正交矩阵〞，“非奇异的对称阵〞和“单位上〔下〕三角阵〞对矩阵求逆是封闭的。
设A是ｎ×ｎ的正交矩阵。
证明A-1也是ｎ×ｎ的正交矩阵。
证明：〔2〕A是ｎ×ｎ的正交矩阵∴A A-1 =A-1A=E 故〔A-1〕-1=A∴A-1〔A-1〕-1=〔A-1〕-1A-1 =E 故A-1也是ｎ×ｎ的正交矩阵。
设A是非奇异的对称阵，证A-1也是非奇异的对称阵。
A非奇异∴A可逆且A-1非奇异又A T=A ∴〔A-1〕T=〔A T〕-1=A-1故A-1也是非奇异的对称阵设A是单位上〔下〕三角阵。
证A-1也是单位上〔下〕三角阵。
证明：A是单位上三角阵，故|A|=1，∴A可逆，即A-1存在，记为〔b ij〕n×n由A A-1 =E，那么〔其中 j＞i时，〕故b nn=1, b ni=0 (n≠j)类似可得，b ii=1 (j=1…n) b jk=0 (k＞j)即A-1是单位上三角阵综上所述可得。
R n×n中的子集“正交矩阵〞，“非奇异的对称阵〞和“单位上〔下〕三角阵〞对矩阵求逆是封闭的。
2、试求齐次线行方程组Ax=0的根底解系。
A=解：A=～～～故齐次线行方程组Ax=0的根底解系为，3.求以下矩阵的特征值和特征向量。
数值分析-第四版-课后习题答案-李庆扬
第一章1、设0>x ，x 的相对误差为δ，求x ln 的误差。
[解]设0*>x 为x 的近似值，则有相对误差为δε=)(*x r ，绝对误差为**)(x x δε=，从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x ， 相对误差为****ln ln )(ln )(ln x x x x r δεε==。
2、设x 的相对误差为2%，求n x 的相对误差。
[解]设*x 为x 的近似值，则有相对误差为%2)(*=x r ε，绝对误差为**%2)(x x =ε，从而n x 的误差为n n x x n x n x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε， 相对误差为%2)()(ln )(ln ***n x x x n r ==εε。
3、下列各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出它们是几位有效数字：1021.1*1=x ，031.0*2=x ，6.385*3=x ，430.56*4=x ，0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字；0031.0*2=x 有2位有效数字；6.385*3=x 有4位有效数字；430.56*4=x 有5位有效数字；0.17*5⨯=x 有2位有效数字。
4、利用公式（3.3）求下列各近似值的误差限，其中*4*3*2*1,,,x x x x 均为第3题所给的数。
（1）*4*2*1x x x ++；[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε；（2）*3*2*1x x x ；[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k k εεεε；（3）*4*2/x x 。
数值分析课后答案（4）
数值分析课后答案（4）习题四1.已知ln(2.0)=0.6931;ln(2.2)=0.7885,ln(2.3)=0.8329, 试用线性插值和抛物插值计算.ln2.1的值并估计误差解：线形插值：取02.0x = 00.6931y = 12.2x = 10.7885y = 22.3x = 20.8329y = 110 2.1 2.3 2.1 2.0(0)(1)0.69310.832901102.0 2.32.3 2.0x x x x L f x f x x x x x ----=+=+----=0.7410抛物线插值：12200102()()()()x x x x l x x x x --=-- 02211012()()()()x x x x l x x x x --=-- 01222021()()()()x x x x l x x x x --=--2200211222L l y l y l y =++=0.7422.已知x=0,2,3,5对应的函数值分别为y=1,3,2,5.试求三次多项式的插值解：解：取00x = 12x = 23x = 35x = 12330010203()()()()()()x x x x x x l x x x x x x ---=--- 023********()()()()()()x x x x x x l x x x x x x ---=---01332202123()()()()()()x x x x x x l x x x x x x ---=--- 01233303132()()()()()()x x x x x x l x x x x x x ---=---3300311322333L l y l y l y l y =+++=1156261310323++-x x x3.设函数f(x)在[a,b]上具有直到二阶的连续导数,且f(a)=f(b)=0, 求证:2"1m ax |()|()m ax |()|8a x ba x bf x b a f x ≤≤≤≤≤-解：取01;x a x b ==，1()()0x a x b L f a f b a bb a--=+=--''''211()()()|()()||()()|||||224f f b a R f x L x x a x b εε-=-≤--≤∴''21()()|()||()|||||24f b a f x L x ε-≤+''1()|()||||()|8f L x b a ε=+-|||8)("|a b f -=ε4.证明n 次Lagrange 插值多项式基函数满足∑==ni ki n ki x x l x 0,)(, n k ≤≤0解：取()kf x x = 则n 0()nki i Ln lx x ==∑(1)()()()!n nii fx f x Ln Rn x x n +=-==-∑(1)0()()!k n nii x x x n +==-∑=0所以()()f x Ln x = 即证 5.证明 )(')()()(,xi x x x x l n i n i n ωω-=证明：、01110111()()()()()ln ()()()()()i i n i i i i i i i n x x x x x x x x x x i x x x x x x x x x x -+-+-----= -----01110111()()()()()()()()()()i i ni i ii i i i i nix x x x x x x x x x x x x x x x x x x x x x x x -+-+------=------取 0111()()()()()()n i ii n x x xx xxxx x x x x ω-+=------则 '1020111011()()()())()()()()()()()()()n nn i in n x x x x x x x x x x x x x xx xx x x x x x x x x xxω-+-=--+---+-----++--- （'0111()()()()()()n i i i i i i i i n x x x x x x x x x x x ω-+=-----所以，'()ln ()()n i n i x i x x x ωω=-6.设nn x a x a a x f ++=10)(有n 个不同的实根.,,21n x x x证明:=-=∑11,0)('n ni i kia x f x证明：取()kx x ?= 1()()n n x x xx ω=-- 而，0()nn f x a a x =++ 有n 个不同的实根。
《数值分析》第四章答案
习题41. 给定x x f =)(在144,121,100=x 3点处的值，试以这3点建立)(x f 的2次(抛物)插值公式，利用插值公式115求的近似值并估计误差。
再给13169=建立3次插值公式，给出相应的结果。
解：x x f =)( 2121)(-='x x f ，2341)(--=''x x f ,2583)(-='''x x f ,27)4(1615)(--=x x f，72380529.10)115(=f1000=x ， 1211=x ， 1442=x ， 1693=x 100=y ， 111=y ， 122=y ， 133=y))(())(())(())(())(())(()(1202102210120*********x x x x x x x x y x x x x x x x x y x x x x x x x x y x L ----+----+----= )121144)(100144()121115)(100115(12)144121)(100121()144115)(100115(11)144100)(121100()144115)(121115(10)115(2----⨯+----⨯+----⨯=L=2344)6(1512)23(21)29(1511)44)(21()29)(6(10⨯-⨯⨯+-⨯-⨯⨯+----⨯72276.1006719.190683.988312.1=-+=))()((!3)()()(2102x x x x x x f x L x f ---'''=-ξ ，144100<<ξ )44115()121115()100115()(max 61)115()115(1441002-⨯-⨯-⋅'''≤-≤≤x f L f x 296151083615⨯⨯⨯⨯⨯≤-001631.0101631.02=⨯=- 实际误差 22101045.0)115()115(-⨯=-L f))()(())()(())()(())()(()(312101320130201032103x x x x x x x x x x x x y x x x x x x x x x x x x y x L ------+------= ))()(())()(())()(())()((23130321033212023102x x x x x x x x x x x x y x x x x x x x x x x x x y ------+------+ )169100()144100()121100()169115()144115()121115(10)115(3-⨯-⨯--⨯-⨯-⨯=L )169121()144121()100121()169115()144115()100115(11-⨯-⨯--⨯-⨯-⨯+)169144()121144()100144()169115()121115()100115(12-⨯-⨯--⨯-⨯-⨯+)144169()121169()100169()144115()121115()100115(13-⨯-⨯--⨯-⨯-⨯+)48()23(21)54()29(1511)69()44()21()54()29()6(10-⨯-⨯-⨯-⨯⨯+-⨯-⨯--⨯-⨯-⨯= 254869)29()6(1513)25(2344)54()6(1512⨯⨯-⨯-⨯⨯+-⨯⨯-⨯-⨯⨯+ 723571.10409783.0305138.2145186.11473744.1=+-+= ))()()((!4)()()(3210)4(3x x x x x x x x f x L x f ----=-ξ，169100<<ξ)169115)(144115)(121115)(10115(101615241)115()115(73----⨯⨯⨯≤--L f )54()29()6(151016152417-⨯-⨯-⨯⨯⨯⨯=- 0005505.0105505.03=⨯=-实际误差 321023429.0)115()115(-⨯=-L f 2. 设j x 为互异节点),,1,0(n j =求证： (1)k nj j k j x x l x =∑=)(0),,1,0(n k =;(2)0)()(0=-∑=x l x x j knj j ),,1(n k =。
数值分析习题第四章
第四章 习题1．确定下列求积公式中的待定参数，使其代数精度尽量高，并指明所构造出的求积公式所具有的代数精度： （1）()()()()⎰--++-≈hhh f A f A h f A dx x f 110；（2）()()()()⎰--++-≈hh h f A f A h f A dx x f 221010；（3）()()()()[]3/3211121⎰-++-≈x f x f f dx x f ；（4）()()()[]()()[]h f f ah h f f h dx x f h'0'2/020+++≈⎰解：（1）求积公式中含有三个待定参数，即101A A A ，，-，将()21x x x f ，，=分别代入求积公式，并令其左右相等，得()()⎪⎪⎩⎪⎪⎨⎧=+=+-=++---3112111013202h A A h A A h h A A A 解得h A h A A 3431011===-，。
所求公式至少具有2次代数精度。
又由于()()()()4443333333h h h h dx x h h h h dx x h hhh⎰⎰--+-≠+-≈故()()()()⎰--++-≈hhh f A f A h f A dx x f 110具有三次代数精度。
（2）求积公式中含有三个待定系数：101A A A ，，-，故令公式对()21x x x f ，，=准确成立，得()()⎪⎪⎩⎪⎪⎨⎧=+=+-=++---31121110131604h A A h A A h h A A A ，解得h h h A h A h A A 34316424381011-=-=-===-，故()()()[]()0343822hf h f h f h dx x f hh -+-≈⎰- 因()⎰-=hhdx x f 220而()()[]03833=+-h h h 又[]445562243831652h h h h h dx x hh +=≠=⎰-所以求积公式只具有三次代数精度。
数值分析课程第五版课后习题答案(李庆扬等)(OCR)
根是ｘ，，２…，ｘ－，且Ｖ。ｘ，ｘ…·，ｘ）＝Ｖ，Ｃｘ６，ｘ…·）（ｘ－ｘ）…（ｘ－ｘ）。
Ｖ，（ｘｏ，ｘ，…ｘ－ｘ）＝１１】 －ｘ，）用ａ－ｘ，）
［证明］由
可得求证。
＝Ｖ，（Ｃｘ８，ｘ，…，ｘＸ））１１（ｘ－ｘ）
２、当ｘ＝１－１，２时，ｆ（ｘ）＝０，－３．４，求ｆ（ｘ）的二次插值多项式。
Ｌ，（ｘ）＝ｙ％（（ｘｘ６－－ｘｘ，）（（ｘｘ－２ｘ－ｘ２２））
ｙ＝ｆ（ｘ）＝ｆ０．５）＝－０．６９３１４７，ｙ２＝ｆ（ｘ）＝ｆ（０．６）＝－０．５１０８２６，则
Ｌ２（ｘ）＝ｙ。 （ｘ－ｘ）（ｘ－ｘ２）
（ｘ６－ｘ）ｘ－ｘ）
（ｘ－ｘ）（ｘ－ｘ）
（ｘ－ｘ）（ｘ－ｘ２）
（ｘ－ｘｏ）（ｘ－ｘ） （ｘ２－ｘｏ）（ｘ２－ｘ）
＝－０．９１６２９１×．（０（．ｘ４－０－．０５．）５（）ｘ（－００．．６４）－０．６－．
３０—＋２—９．ｘ９５８３ｘ３１￣０２＇＝０．８３３６×１０４
１４、试用消元法解方程ｘ组１＋１０＂ｘ＝１００
ｘ＋ｘ２＝２
，假定只有三位数计算，问结果是否
可靠？
［解］精确解为ｘ１＝０１００－＊１ １０＂－２ ，当使用三位数运 算时，得到
ｘ ＝１，ｘ２＝１，结果可靠。
１５、已知三角形面积ｓ＝ｓ去＝ ａｂｓｉｎｃ，其中ｃ为弧度，０＜ｃ＜ 且测量ａ，ｂ，ｃ
位有效数字；ｘ＝５６．４３０有５位有效数字；ｘ＝７×１０有２位有效数字。 ４、利用公式（３．３）求下列各近似值的误差限，其中ｘ，ｘ；，ｘ，ｘ；均为第３题所给
的数。
（１）ｘ＋ｘ２＋ｘ：
ｅ（ｘ＋ｘ写＋ｘ）＝＞
［解］
Ｅ（ｘ）＝Ｅ（ｘ）＋Ｅ（ｘ）＋Ｅ（ｘ；）
３＋ｔｘ１０＝１．０５×１０３
（２）ｘｘｘ；
数值分析第四版习题与答案
第四版数值分析习题第一章 绪 论1. 设x >0,x 的相对误差为δ,求ln x 的误差.2. 设x 的相对误差为2％,求nx 的相对误差.3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:*****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====⨯4. 利用公式(3.3)求下列各近似值的误差限:********12412324(),(),()/,i x x x ii x x x iii x x ++其中****1234,,,x x x x 均为第3题所给的数.5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少?6. 设028,Y =按递推公式1n n Y Y -=( n=1,2,…)计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差?7. 求方程25610x x -+=的两个根,使它至少具有四位有效数字27.982).8. 当N 充分大时,怎样求211Ndx x +∞+⎰?9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2? 10. 设212S gt =假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小.11. 序列{}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字),计算到10y 时误差有多大?这个计算过程稳定吗?12. 计算61)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好?3--13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式ln(ln(x x =-计算,求对数时误差有多大?14. 试用消元法解方程组{101012121010;2.x x x x +=+=假定只用三位数计算,问结果是否可靠?15. 已知三角形面积1sin ,2s ab c =其中c 为弧度,02c π<<,且测量a ,b ,c 的误差分别为,,.a b c ∆∆∆证明面积的误差s ∆满足.s a b cs a b c ∆∆∆∆≤++第二章 插值法1. 根据(2.2)定义的范德蒙行列式,令2000011211121()(,,,,)11n n n n n n n n n x x x V x V x x x x x x x xxx ----==证明()n V x 是n 次多项式,它的根是01,,n x x -,且 101101()(,,,)()()n n n n V x V x x x x x x x ---=--.2. 当x = 1 , -1 , 2 时, f (x)= 0 , -3 , 4 ,求f (x )的二次插值多项式.3. 给出f (x )=ln x 的数值表用线性插值及二次插值计算ln 0.54 的近似值.4. 给出cos x ,0°≤x ≤90°的函数表,步长h =1′=(1/60)°,若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界.5. 设0k x x kh =+,k =0,1,2,3,求032max ()x x x l x ≤≤.6. 设j x 为互异节点(j =0,1,…,n ),求证:i)()(0,1,,);nkkj j j x l x xk n =≡=∑ii)()()1,2,,).nk jj j xx l x k n =-≡0(=∑7. 设[]2(),f x Ca b ∈且()()0f a f b ==,求证21()()().8max max a x ba xb f x b a f x ≤≤≤≤≤-"8. 在44x -≤≤上给出()x f x e =的等距节点函数表,若用二次插值求x e 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少?9. 若2n n y =,求4n y ∆及4n y δ.10. 如果()f x 是m 次多项式,记()()()f x f x h f x ∆=+-,证明()f x 的k 阶差分()(0)k f x k m ∆≤≤是m k -次多项式,并且()0(m l f x l +∆=为正整数).11. 证明1()k k k k k k f g f g g f +∆=∆+∆. 12. 证明110010.n n kkn n k k k k f gf g f g g f --+==∆=--∆∑∑13. 证明1200.n j n j y y y -=∆=∆-∆∑14. 若1011()n n n n f x a a x a x a x --=++++有n 个不同实根12,,,n x x x ,证明{10,02;, 1.1()n k njk n a k n j jx f x -≤≤-=-=='∑15. 证明n 阶均差有下列性质: i)若()()F x cf x =,则[][]0101,,,,,,n n F x x x cf x x x =;ii) 若()()()F x f x g x =+,则[][][]010101,,,,,,,,,n n n F x x x f x x x g x x x =+.16. 74()31f x x x x =+++,求0172,2,,2f ⎡⎤⎣⎦及0182,2,,2f ⎡⎤⎣⎦.17. 证明两点三次埃尔米特插值余项是 (4)22311()()()()/4!,(,)k k k k R x f x x x x x x ++=ξ--ξ∈并由此求出分段三次埃尔米特插值的误差限.18. 求一个次数不高于4次的多项式()P x ,使它满足(0)(1)P P k =-+并由此求出分段三次埃尔米特插值的误差限.19. 试求出一个最高次数不高于4次的函数多项式()P x ,以便使它能够满足以下边界条件(0)(0)0P P ='=,(1)(1)1P P ='=,(2)1P =.20. 设[](),f x C a b ∈,把[],a b 分为n 等分,试构造一个台阶形的零次分段插值函数()n x ϕ并证明当n →∞时,()n x ϕ在[],a b 上一致收敛到()f x .21. 设2()1/(1)f x x =+,在55x -≤≤上取10n =,按等距节点求分段线性插值函数()h I x ,计算各节点间中点处的()h I x 与()f x 的值,并估计误差.22. 求2()f x x =在[],a b 上的分段线性插值函数()h I x ,并估计误差.23. 求4()f x x =在[],a b 上的分段埃尔米特插值,并估计误差.试求三次样条插值并满足条件 i) (0.25) 1.0000,(0.53)0.6868;S S '='= ii)(0.25)(0.53)0.S S "="=25. 若[]2(),f x C a b ∈,()S x 是三次样条函数,证明 i)[][][][]222()()()()2()()()bbbbaaaaf x dx S x dx f x S x dx S x f x S x dx"-"="-"+""-"⎰⎰⎰⎰;ii) 若()()(0,1,,)i i f x S x i n ==,式中i x 为插值节点,且01n a x x x b =<<<=,则[][][]()()()()()()()()()baS x f x S x dx S b f b S b S a f a S a ""-"="'-'-"'-'⎰.26. 编出计算三次样条函数()S x 系数及其在插值节点中点的值的程序框图(()S x 可用(8.7)式的表达式).第三章 函数逼近与计算1. (a)利用区间变换推出区间为[],a b 的伯恩斯坦多项式.(b)对()sin f x x =在[]0,/2π上求1次和三次伯恩斯坦多项式并画出图形,并与相应的马克劳林级数部分和误差做比较. 2. 求证:(a)当()m f x M ≤≤时,(,)n m B f x M ≤≤. (b)当()f x x =时,(,)n B f x x =.3. 在次数不超过6的多项式中,求()sin 4f x x =在[]0,2π的最佳一致逼近多项式.4. 假设()f x 在[],a b 上连续,求()f x 的零次最佳一致逼近多项式.5. 选取常数a ,使301max x x ax≤≤-达到极小,又问这个解是否唯一?6. 求()sin f x x =在[]0,/2π上的最佳一次逼近多项式,并估计误差.7. 求()xf x e =在[]0,1上的最佳一次逼近多项式.8. 如何选取r ,使2()p x x r =+在[]1,1-上与零偏差最小?r 是否唯一? 9. 设43()31f x x x =+-,在[]0,1上求三次最佳逼近多项式.10. 令[]()(21),0,1n n T x T x x =-∈,求***0123(),(),(),()T x T x T x T x . 11. 试证{}*()nT x 是在[]0,1上带权ρ=的正交多项式.12. 在[]1,1-上利用插值极小化求11()f x tg x -=的三次近似最佳逼近多项式. 13. 设()xf x e =在[]1,1-上的插值极小化近似最佳逼近多项式为()n L x ,若n f L ∞-有界,证明对任何1n ≥,存在常数n α、n β,使11()()()()(11).n n n n n T x f x L x T x x ++α≤-≤β-≤≤14. 设在[]1,1-上234511315165()128243843840x x x x x xϕ=-----,试将()x ϕ降低到3次多项式并估计误差.15. 在[]1,1-上利用幂级数项数求()sin f x x =的3次逼近多项式,使误差不超过0.005. 16. ()f x 是[],a a -上的连续奇(偶)函数,证明不管n 是奇数或偶数,()f x 的最佳逼近多项式*()n n F x H ∈也是奇(偶)函数.17. 求a 、b 使[]22sin ax b x dx π+-⎰为最小.并与1题及6题的一次逼近多项式误差作比较.18. ()f x 、[]1(),g x C a b ∈,定义 ()(,)()();()(,)()()()();b baaa f g f x g x dxb f g f x g x dx f a g a =''=''+⎰⎰问它们是否构成内积?19. 用许瓦兹不等式(4.5)估计6101x dx x +⎰的上界,并用积分中值定理估计同一积分的上下界,并比较其结果.20. 选择a ,使下列积分取得最小值:1122211(),x ax dx x ax dx----⎰⎰.21. 设空间{}{}10010121,,,span x span x x 1ϕ=ϕ=,分别在1ϕ、2ϕ上求出一个元素,使得其为[]20,1x C ∈的最佳平方逼近,并比较其结果. 22. ()f x x =在[]1,1-上,求在{}2411,,span x x ϕ=上的最佳平方逼近.23.sin (1)arccos ()n n x u x +=是第二类切比雪夫多项式,证明它有递推关系()()()112n n n u x xu x u x +-=-.24. 将1()sin 2f x x=在[]1,1-上按勒让德多项式及切比雪夫多项式展开,求三次最佳平方逼近多项式并画出误差图形,再计算均方误差.25. 把()arccos f x x =在[]1,1-上展成切比雪夫级数.26. 用最小二乘法求一个形如2y a bx =+的经验公式,使它与下列数据拟合,并求均方误差.27.求运动方程.28. 在某化学反应里,根据实验所得分解物的浓度与时间关系如下:用最小二乘拟合求.29. 编出用正交多项式做最小二乘拟合的程序框图. 30. 编出改进FFT 算法的程序框图.31. 现给出一张记录{}{}4,3,2,1,0,1,2,3k x =,试用改进FFT 算法求出序列{}k x 的离散频谱{}k C (0,1,,7).k =第四章 数值积分与数值微分1. 确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度: (1)101()()(0)()hh f x dx A f h A f A f h --≈-++⎰; (2)21012()()(0)()hh f x dx A f h A f A f h --≈-++⎰;(3)[]1121()(1)2()3()/3f x dx f f x f x -≈-++⎰;(4)[][]20()(0)()/1(0)()hf x dx h f f h ah f f h ≈++'-'⎰.2. 分别用梯形公式和辛普森公式计算下列积分:(1)120,84xdx n x =+⎰; (2)1210(1),10x e dx n x --=⎰;(3)1,4n =⎰; (4),6n =.3. 直接验证柯特斯公式(2.4)具有5次代数精度.4. 用辛普森公式求积分1x e dx-⎰并计算误差.5. 推导下列三种矩形求积公式:(1)2()()()()()2ba f f x dxb a f a b a 'η=-+-⎰; (2)2()()()()()2ba f f x dxb a f b b a 'η=---⎰;(3)3()()()()()224baa b f f x dx b a f b a +"η=-+-⎰.6. 证明梯形公式(2.9)和辛普森公式(2.11)当n →∞时收敛到积分()baf x dx⎰.7. 用复化梯形公式求积分()baf x dx⎰,问要将积分区间[],a b 分成多少等分,才能保证误差不超过ε(设不计舍入误差)?8. 1x e dx-,要求误差不超过510-.9. 卫星轨道是一个椭圆,椭圆周长的计算公式是S a =θ,这里a 是椭圆的半长轴,c 是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,H 为远地点距离,6371R =公里为地球半径,则(2)/2,()/2a R H h c H h =++=-.我国第一颗人造卫星近地点距离439h =公里,远地点距离2384H =公里,试求卫星轨道的周长. 10. 证明等式3524sin3!5!n nn n ππππ=-+-试依据sin(/)(3,6,12)n n n π=的值,用外推算法求π的近似值. 11. 用下列方法计算积分31dyy ⎰并比较结果.(1) 龙贝格方法; (2) 三点及五点高斯公式;(3) 将积分区间分为四等分,用复化两点高斯公式. 12. 用三点公式和五点公式分别求21()(1)f x x =+在x =1.0,1.1和1.2处的导数值,并估计误差.()f x 的值由下表给出:第五章 常微分方程数值解法1. 就初值问题0)0(,=+='y b ax y 分别导出尤拉方法和改进的尤拉方法的近似解的表达式，并与准确解bx ax y +=221相比较。
李庆扬-数值分析第五版第4章习题答案(20130714)
4） h f (x)dx h[ f (0) f (h)]/ 2 ah2[ f (0) f (h)] 。 0
h
1） h f (x)dx A1 f (h) A0 f (0) A1 f (h)
由于需要确定 3 个 未知量，因此，需要给定 3 个方程。
设 f (x) 1, x, x2 ，有
2h
A1
A0
A1
0 hA1 hA1
2
3
h3
h2 A1
h2 A1
2h A1 A0 A1
解出
A1
1 3 4
h
A0
3
h
A1
1 3
h
令 f (x) x3 ，
有 h (h)3 4h 03 h h3 1 h4 1 h4 0 h x3dx 0
3
3
3
33
h
令 f (x) x4 ，
需要确定 2 个待定参数，因此，令
设 f (x) 1, x, x2 ，有
h h 0
h
2
2
h2 2
0
h3 3
h3
/
2 2ah3
解出 a 1 ，h 为任意常数 12
令 f (x) x3 ，有
h4 h x3dx h f (x)dx h4 / 2 1 h4 1 h4
40
0
44
k 1
f
(xk )
f
(b)]
Rn ( f )
I
Sn
ba 180
h 2
4
f
(4) (), [a, b]
8、什么是龙贝格求积？它有什么优点？ 龙贝格求积公式也称为逐次分半加速法。它是在梯形公式、辛普森公式和柯特斯公式之间的 关系的基础上，构造出一种加速计算积分的方法。使用理查森外推算法, 它在不增加计算量 的前提下提高了误差的精度. 在等距基点的情况下，用计算机计算积分值通常都采用把区间逐次分半的方法进行。这样， 前一次分割得到的函数值在分半以后仍可被利用,且易于编程。 龙贝格算法公式
(完整版)数值分析课后习题答案
第一章绪论习题一1.设x>0,x*的相对误差为δ，求f(x)=ln x的误差限。
解：求lnx的误差极限就是求f(x)=lnx的误差限，由公式(1.2.4)有已知x*的相对误差满足，而，故即2.下列各数都是经过四舍五入得到的近似值，试指出它们有几位有效数字，并给出其误差限与相对误差限。
解：直接根据定义和式(1.2.2)(1.2.3)则得有5位有效数字，其误差限，相对误差限有2位有效数字，有5位有效数字，3.下列公式如何才比较准确？（1）（2）解：要使计算较准确，主要是避免两相近数相减，故应变换所给公式。
（1）（2）4.近似数x*=0.0310,是 3 位有数数字。
5.计算取，利用：式计算误差最小。
四个选项：第二、三章插值与函数逼近习题二、三1. 给定的数值表用线性插值与二次插值计算ln0.54的近似值并估计误差限. 解：仍可使用n=1及n=2的Lagrange插值或Newton插值,并应用误差估计（5.8）。
线性插值时，用0.5及0.6两点，用Newton插值误差限，因，故二次插值时，用0.5，0.6，0.7三点，作二次Newton插值误差限，故2. 在-4≤x≤4上给出的等距节点函数表，若用二次插值法求的近似值，要使误差不超过，函数表的步长h 应取多少?解：用误差估计式（5.8），令因得3. 若，求和.解：由均差与导数关系于是4. 若互异，求的值，这里p≤n+1.解：，由均差对称性可知当有而当P＝n＋1时于是得5. 求证.解：解：只要按差分定义直接展开得6. 已知的函数表求出三次Newton均差插值多项式，计算f(0.23)的近似值并用均差的余项表达式估计误差.解：根据给定函数表构造均差表由式(5.14)当n=3时得Newton均差插值多项式N3(x)=1.0067x+0.08367x(x-0.2)+0.17400x(x-0.2)(x-0.3) 由此可得f(0.23) N3(0.23)=0.23203由余项表达式(5.15)可得由于7. 给定f(x)=cosx的函数表用Newton等距插值公式计算cos 0.048及cos 0.566的近似值并估计误差解：先构造差分表计算，用n=4得Newton前插公式误差估计由公式（5.17）得其中计算时用Newton后插公式（5.18)误差估计由公式（5.19）得这里仍为0.5658．求一个次数不高于四次的多项式p(x),使它满足解：这种题目可以有很多方法去做，但应以简单为宜。
数值分析第四版习题及答案
第一章 绪 论1. 设x >0,x 的相对误差为δ,求ln x 的误差.2. 设x 的相对误差为2％,求nx 的相对误差.3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====⨯4. 利用公式(3.3)求下列各近似值的误差限:********12412324(),(),()/,i x x x ii x x x iii x x ++其中****1234,,,x x x x 均为第3题所给的数.5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少?6. 设028,Y =按递推公式1n n Y Y -=( n=1,2,…)计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差?7. 求方程25610x x -+=的两个根,使它至少具有四位有效数字27.982).8. 当N 充分大时,怎样求211Ndx x +∞+⎰?9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2? 10. 设212S gt =假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小. 11. 序列{}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字),计算到10y 时误差有多大?这个计算过程稳定吗?12.计算61)f =,1.4≈,利用下列等式计算,哪一个得到的结果最好?3--13.()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式ln(ln(x x =-计算,求对数时误差有多大?14. 试用消元法解方程组{101012121010;2.x x x x +=+=假定只用三位数计算,问结果是否可靠?15. 已知三角形面积1sin ,2s ab c =其中c 为弧度,02c π<<,且测量a ,b ,c 的误差分别为,,.a b c ∆∆∆证明面积的误差s ∆满足.s a b cs a b c ∆∆∆∆≤++第二章 插值法1. 根据(2.2)定义的范德蒙行列式,令2000011211121()(,,,,)11n n n n n n n n n x x x V x V x x x x x x x xx x ----==证明()n V x 是n 次多项式,它的根是01,,n x x -,且 101101()(,,,)()()n n n n V x V x x x x x x x ---=--.2. 当x = 1 , -1 , 2 时, f (x)= 0 , -3 , 4 ,求f (x )的二次插值多项式.3.4. 给出cos x ,0°≤x ≤90°的函数表,步长h =1′=(1/60)°,若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界.5. 设0k x x kh =+,k =0,1,2,3,求032max ()x x x l x ≤≤.6. 设jx 为互异节点(j =0,1,…,n ),求证:i) 0()(0,1,,);nk kj j j x l x xk n =≡=∑ii)()()1,2,,).nk jj j xx l x k n =-≡0(=∑7. 设[]2(),f x C a b ∈且()()0f a f b ==,求证21()()().8max max a x b a x b f x b a f x ≤≤≤≤≤-"8. 在44x -≤≤上给出()x f x e =的等距节点函数表,若用二次插值求x e 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少?9. 若2n n y =,求4n y ∆及4n y δ.10. 如果()f x 是m 次多项式,记()()()f x f x h f x ∆=+-,证明()f x 的k 阶差分()(0)k f x k m ∆≤≤是m k -次多项式,并且()0(m l f x l +∆=为正整数).11. 证明1()k k k k k k f g f g g f +∆=∆+∆. 12. 证明110010.n n kkn n k k k k f gf g f g g f --+==∆=--∆∑∑13. 证明1200.n j n j y y y -=∆=∆-∆∑14. 若1011()n n n n f x a a x a x a x --=++++有n 个不同实根12,,,n x x x ,证明{10,02;, 1.1()n k njk n a k n j jx f x -≤≤-=-=='∑15. 证明n 阶均差有下列性质: i)若()()F x cf x =,则[][]0101,,,,,,n n F x x x cf x x x =;ii) 若()()()F x f x g x =+,则[][][]010101,,,,,,,,,n n n F x x x f x x x g x x x =+.16. 74()31f x x x x =+++,求0172,2,,2f ⎡⎤⎣⎦及0182,2,,2f ⎡⎤⎣⎦.17. 证明两点三次埃尔米特插值余项是(4)22311()()()()/4!,(,)k k k k R x f x x x x x x ++=ξ--ξ∈并由此求出分段三次埃尔米特插值的误差限.18. 求一个次数不高于4次的多项式()P x ,使它满足(0)(1)P P k =-+并由此求出分段三次埃尔米特插值的误差限. 19. 试求出一个最高次数不高于4次的函数多项式()P x ,以便使它能够满足以下边界条件(0)(0)0P P ='=,(1)(1)1P P ='=,(2)1P =.20. 设[](),f x C a b ∈,把[],a b 分为n 等分,试构造一个台阶形的零次分段插值函数()n x ϕ并证明当n →∞时,()n x ϕ在[],a b 上一致收敛到()f x .21. 设2()1/(1)f x x =+,在55x -≤≤上取10n =,按等距节点求分段线性插值函数()h I x ,计算各节点间中点处的()h I x 与()f x 的值,并估计误差.22. 求2()f x x =在[],a b 上的分段线性插值函数()h I x ,并估计误差.23. 求4()f x x =在[],a b 上的分段埃尔米特插值,并估计误差.试求三次样条插值并满足条件 i) (0.25) 1.0000,(0.53)0.6868;S S '='= ii)(0.25)(0.53)0.S S "="=25. 若[]2(),f x C a b ∈,()S x 是三次样条函数,证明 i)[][][][]222()()()()2()()()bbbba a a a f x dx S x dx f x S x dx S x f x S x dx "-"="-"+""-"⎰⎰⎰⎰;ii) 若()()(0,1,,)i i f x S x i n ==,式中i x 为插值节点,且01n a x x x b =<<<=,则[][][]()()()()()()()()()baS x f x S x dx S b f b S b S a f a S a ""-"="'-'-"'-'⎰.26. 编出计算三次样条函数()S x 系数及其在插值节点中点的值的程序框图(()S x 可用(8.7)式的表达式).第三章 函数逼近与计算1. (a)利用区间变换推出区间为[],a b 的伯恩斯坦多项式.(b)对()sin f x x =在[]0,/2π上求1次和三次伯恩斯坦多项式并画出图形,并与相应的马克劳林级数部分和误差做比较. 2. 求证:(a)当()m f x M ≤≤时,(,)n m B f x M ≤≤. (b)当()f x x =时,(,)n B f x x =. 3. 在次数不超过6的多项式中,求()sin 4f x x =在[]0,2π的最佳一致逼近多项式. 4. 假设()f x 在[],a b 上连续,求()f x 的零次最佳一致逼近多项式. 5. 选取常数a ,使301max x x ax≤≤-达到极小,又问这个解是否唯一?6. 求()sin f x x =在[]0,/2π上的最佳一次逼近多项式,并估计误差.7. 求()xf x e =在[]0,1上的最佳一次逼近多项式.8. 如何选取r ,使2()p x x r =+在[]1,1-上与零偏差最小?r 是否唯一?9. 设43()31f x x x =+-,在[]0,1上求三次最佳逼近多项式.10. 令[]()(21),0,1n n T x T x x =-∈,求***0123(),(),(),()T x T x T x T x . 11. 试证{}*()nT x 是在[]0,1上带权ρ=的正交多项式.12. 在[]1,1-上利用插值极小化求11()f x tg x -=的三次近似最佳逼近多项式.13. 设()xf x e =在[]1,1-上的插值极小化近似最佳逼近多项式为()n L x ,若nf L ∞-有界,证明对任何1n ≥,存在常数n α、n β,使11()()()()(11).n n n n n T x f x L x T x x ++α≤-≤β-≤≤14. 设在[]1,1-上234511315165()128243843840x x x x x x ϕ=-----,试将()x ϕ降低到3次多项式并估计误差. 15. 在[]1,1-上利用幂级数项数求()sin f x x =的3次逼近多项式,使误差不超过0.005.16. ()f x 是[],a a -上的连续奇(偶)函数,证明不管n 是奇数或偶数,()f x 的最佳逼近多项式*()n n F x H ∈也是奇(偶)函数.17. 求a 、b 使[]22sin ax b x dx π+-⎰为最小.并与1题及6题的一次逼近多项式误差作比较.18. ()f x 、[]1(),g x C a b ∈,定义 ()(,)()();()(,)()()()();b baaa f g f x g x dxb f g f x g x dx f a g a =''=''+⎰⎰问它们是否构成内积?19. 用许瓦兹不等式(4.5)估计6101x dx x +⎰的上界,并用积分中值定理估计同一积分的上下界,并比较其结果.20. 选择a ,使下列积分取得最小值:1122211(),x ax dx x ax dx----⎰⎰.21. 设空间{}{}10010121,,,span x span x x 1ϕ=ϕ=,分别在1ϕ、2ϕ上求出一个元素,使得其为[]20,1x C ∈的最佳平方逼近,并比较其结果.22. ()f x x =在[]1,1-上,求在{}2411,,span x x ϕ=上的最佳平方逼近.23.sin (1)arccos ()n n x u x +=是第二类切比雪夫多项式,证明它有递推关系()()()112n n n u x xu x u x +-=-.24. 将1()sin 2f x x=在[]1,1-上按勒让德多项式及切比雪夫多项式展开,求三次最佳平方逼近多项式并画出误差图形,再计算均方误差. 25. 把()arccos f x x =在[]1,1-上展成切比雪夫级数.26.2y a bx =+. 27.用最小二乘拟合求.29. 编出用正交多项式做最小二乘拟合的程序框图. 30. 编出改进FFT 算法的程序框图. 31. 现给出一张记录{}{}4,3,2,1,0,1,2,3k x =,试用改进FFT 算法求出序列{}k x 的离散频谱{}k C (0,1,,7).k =第四章 数值积分与数值微分1. 确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度:(1)101()()(0)()hh f x dx A f h A f A f h --≈-++⎰; (2)21012()()(0)()hh f x dx A f h A f A f h --≈-++⎰;(3)[]1121()(1)2()3()/3f x dx f f x f x -≈-++⎰;(4)[][]20()(0)()/1(0)()hf x dx h f f h ah f f h ≈++'-'⎰.2. 分别用梯形公式和辛普森公式计算下列积分:(1)120,84xdx n x =+⎰; (2)1210(1),10x e dx n x --=⎰;(3)1,4n =⎰;(4),6n =.3. 直接验证柯特斯公式(2.4)具有5次代数精度.4. 用辛普森公式求积分10x e dx-⎰并计算误差. 5. 推导下列三种矩形求积公式:(1)2()()()()()2ba f f x dxb a f a b a 'η=-+-⎰; (2)2()()()()()2ba f f x dxb a f b b a 'η=---⎰;(3)3()()()()()224baa b f f x dx b a f b a +"η=-+-⎰. 6. 证明梯形公式(2.9)和辛普森公式(2.11)当n →∞时收敛到积分()baf x dx⎰.7. 用复化梯形公式求积分()baf x dx⎰,问要将积分区间[],a b 分成多少等分,才能保证误差不超过ε(设不计舍入误差)?8.1x e dx-,要求误差不超过510-.9. 卫星轨道是一个椭圆,椭圆周长的计算公式是S a =θ,这里a 是椭圆的半长轴,c 是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,H 为远地点距离,6371R =公里为地球半径,则(2)/2,()/2a R H h c H h =++=-.我国第一颗人造卫星近地点距离439h =公里,远地点距离2384H =公里,试求卫星轨道的周长. 10. 证明等式3524sin3!5!n nn n ππππ=-+-试依据sin(/)(3,6,12)n n n π=的值,用外推算法求π的近似值.11. 用下列方法计算积分31dyy ⎰并比较结果.(1) 龙贝格方法;(2) 三点及五点高斯公式;(3) 将积分区间分为四等分,用复化两点高斯公式.12. 用三点公式和五点公式分别求21()(1)f x x =+在x =1.0,1.1和1.2处的导数值,并估计误()f x 第五章 常微分方程数值解法1. 就初值问题0)0(,=+='y b ax y 分别导出尤拉方法和改进的尤拉方法的近似解的表达式，并与准确解bx ax y +=221相比较。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 数值积分与数值微分1.确定下列求积公式中的特定参数，使其代数精度尽量高，并指明所构造出的求积公式所具有的代数精度：10121012112120(1)()()(0)();(2)()()(0)();(3)()[(1)2()3()]/3;(4)()[(0)()]/2[(0)()];hhhh hf x dx A f h A f A f h f x dx A f h A f A f h f x dx f f x f x f x dx h f f h ah f f h -----≈-++≈-++≈-++''≈++-⎰⎰⎰⎰解：求解求积公式的代数精度时，应根据代数精度的定义，即求积公式对于次数不超过m 的多项式均能准确地成立，但对于m+1次多项式就不准确成立，进行验证性求解。
（1）若101(1)()()(0)()hhf x dx A f h A f A f h --≈-++⎰令()1f x =，则1012h A A A -=++令()f x x =，则110A h A h -=-+令2()f x x =，则3221123h h A h A -=+ 从而解得011431313A h A h A h -⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩令3()f x x =，则3()0hhhhf x dx x dx --==⎰⎰101()(0)()0A f h A f A f h --++=故101()()(0)()hhf x dx A f h A f A f h --=-++⎰成立。
令4()f x x =，则4551012()52()(0)()3hhhhf x dx x dx h A f h A f A f h h ---==-++=⎰⎰故此时，101()()(0)()hhf x dx A f h A f A f h --≠-++⎰故101()()(0)()h hf x dx A f h A f A f h --≈-++⎰具有3次代数精度。
（2）若21012()()(0)()hhf x dx A f h A f A f h --≈-++⎰令()1f x =，则1014h A A A -=++令()f x x =，则110A h A h -=-+令2()f x x =，则32211163h h A h A -=+ 从而解得11438383A h A h A h -⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩令3()f x x =，则22322()0hhhhf x dx x dx --==⎰⎰101()(0)()0A f h A f A f h --++=故21012()()(0)()hhf x dx A f h A f A f h --=-++⎰成立。
令4()f x x =，则22452264()5hhhhf x dx x dx h --==⎰⎰510116()(0)()3A f h A f A f h h --++=故此时，21012()()(0)()hhf x dx A f h A f A f h --≠-++⎰因此，21012()()(0)()h hf x dx A f h A f A f h --≈-++⎰具有3次代数精度。
（3）若1121()[(1)2()3()]/3f x dx f f x f x -≈-++⎰令()1f x =，则1121()2[(1)2()3()]/3f x dx f f x f x -==-++⎰令()f x x =，则120123x x =-++令2()f x x =，则22122123x x =++从而解得120.28990.5266x x =-⎧⎨=⎩或120.68990.1266x x =⎧⎨=⎩ 令3()f x x =，则11311()0f x dx x dx --==⎰⎰12[(1)2()3()]/30f f x f x -++≠故1121()[(1)2()3()]/3f x dx f f x f x -=-++⎰不成立。
因此，原求积公式具有2次代数精度。
（4）若20()[(0)()]/2[(0)()]hf x dx h f f h ah f f h ''≈++-⎰令()1f x =，则(),hf x dx h =⎰2[(0)()]/2[(0)()]h f f h ah f f h h ''++-=令()f x x =，则20221()21[(0)()]/2[(0)()]2hh f x dx xdx h h f f h ah f f h h ==''++-=⎰⎰令2()f x x =，则2302321()31[(0)()]/2[(0)()]22hhf x dx x dx h h f f h ah f f h h ah ==''++-=-⎰⎰故有33211232112h h ah a =-=令3()f x x =，则340024441()41111[(0)()]/2[(0)()]12244hh f x dx x dx h h f f h h f f h h h h==''++-=-=⎰⎰令4()f x x =，则450025551()51111[(0)()]/2[(0)()]12236hhf x dx x dx h h f f h h f f h h h h==''++-=-=⎰⎰故此时，21()[(0)()]/2[(0)()],12hf x dx h f f h h f f h ''≠++-⎰因此，201()[(0)()]/2[(0)()]12hf x dx h f f h h f f h ''≈++-⎰具有3次代数精度。
2.分别用梯形公式和辛普森公式计算下列积分：12012101(1),8;4(1)(2),10;(3),4;(4),6;x xdx n x e dx n xn n ϕ-=+-===⎰⎰⎰解：21(1)8,0,1,,()84xn a b h f x x=====+ 复化梯形公式为781[()2()()]0.111402k k hT f a f x f b ==++=∑复化辛普森公式为7781012[()4()2()()]0.111576k k k k hS f a f x f x f b +===+++=∑∑121(1)(2)10,0,1,,()10x e n a b h f x x--===== 复化梯形公式为9101[()2()()] 1.391482k k hT f a f x f b ==++=∑复化辛普森公式为99101012[()4()2()()] 1.454716k k k k hS f a f x f x f b +===+++=∑∑(3)4,1,9,2,()n a b h f x =====复化梯形公式为341[()2()()]17.227742k k hT f a f x f b ==++=∑复化辛普森公式为3341012[()4()2()()]17.322226(4)6,0,,,()636k k k k hS f a f x f x f b n a b h f x ππ+===+++======∑∑复化梯形公式为561[()2()()] 1.035622k k hT f a f x f b ==++=∑复化辛普森公式为5561012[()4()2()()] 1.035776k k k k hS f a f x f x f b +===+++=∑∑3。
直接验证柯特斯教材公式（2。
4）具有5交代数精度。
证明：柯特斯公式为01234()[7()32()12()32()7()]90bab af x dx f x f x f x f x f x -=++++⎰令()1f x =，则01234()90[7()32()12()32()7()]90bab a f x dx b af x f x f x f x f x b a -=-++++=-⎰令()f x x =，则2222012341()()21[7()32()12()32()7()]()902bb a af x dx xdx b a b a f x f x f x f x f x b a ==--++++=-⎰⎰令2()f x x =，则23333012341()()31[7()32()12()32()7()]()903bb a af x dx x dx b a b a f x f x f x f x f x b a ==--++++=-⎰⎰令3()f x x =，则34444012341()()41[7()32()12()32()7()]()904bb a af x dx x dx b a b a f x f x f x f x f x b a ==--++++=-⎰⎰令4()f x x =，则45555012341()()51[7()32()12()32()7()]()905bb a af x dx x dx b a b a f x f x f x f x f x b a ==--++++=-⎰⎰令5()f x x =，则56666012341()()61[7()32()12()32()7()]()906bb a af x dx x dx b a b a f x f x f x f x f x b a ==--++++=-⎰⎰令6()f x x =，则012340()[7()32()12()32()7()]90hb af x dx f x f x f x f x f x -≠++++⎰因此，该柯特斯公式具有5次代数精度。
4。
用辛普森公式求积分1x e dx -⎰并估计误差。
解：辛普森公式为[()4()()]62b a a bS f a f f b -+=++ 此时，0,1,(),x a b f x e -===从而有1121(14)0.632336S e e --=++=误差为4(4)04()()()1802110.00035,(0,1)1802b a b a R f f e ηη--=-≤⨯⨯=∈5。
推导下列三种矩形求积公式：223()()()()();2()()()()();2()()()()();224ba ba baf f x dx b a f a b a f f x dx b a f b b a a b f f x dx b a f b a ηηη'=-+-'=---''+=-+-⎰⎰⎰证明：(1)()()()(),(,)f x f a f x a a b ηη'=+-∈两边同时在[,]a b 上积分，得()()()()()bbaaf x dx b a f a f x a dx η'=-+-⎰⎰即2()()()()()2(2)()()()(),(,)baf f x dx b a f a b a f x f b f b x a b ηηη'=-+-'=--∈⎰两边同时在[,]a b 上积分，得()()()()()bbaaf x dx b a f a f b x dx η'=---⎰⎰即22()()()()()2()(3)()()()()(),(,)22222baf f x dx b a f b b a a b a b a b f a b f x f f x x a b ηηη'=---''++++'=+-+-∈⎰两连边同时在[,]a b 上积分，得2()()()()()()()22222bb b aa a ab a b a b f a b f x dx b a f f x dx x dx η''++++'=-+-+-⎰⎰⎰ 即3()()()()();224b aa b f f x dx b a f b a η''+=-+-⎰6。