趣题：不用三角函数求出∠BAC的度数

合集下载

【微专题】2023学年八年级数学上册常考点(人教版) 共定点等边三角形的六大结论及应用(解析版)

共定点等边三角形的六大结论及应用六大结论基本模型：如图 △ABC 和△CDE 是共顶点（C ）三角形则有以下六大结论.结论1：△ACD ≌△BCE （SAS ） ∴AD =BE 结论2：∠AOB=60°结论3：△ACP ≌△BCQ （ASA ） ∴AP =BQ PC =QC 结论4：△PCQ 是等边三角形结论5：∴PQ AE ∥ 结论6：点C 在∠AOE 的平分线上1．如图 C 为线段AE 上一动点（不与点A 、E 重合）在AE 同侧分别作正三角形ABC 和正三角形CDE AD 与BE 交于点O AD 与BC 交于点P BE 与CD 交于点Q 连接PQ 以下七个结论：①AD BE =；②//PQ AE ；③AP BQ =；④DE DP =；⑤60AOB ∠=︒；⑥PCQ ∆是等边三角形；⑦点C 在AOE ∠的平分线上其中正确的有（）A ．3个B ．4个C ．5个D ．6个【答案】D【解析】【分析】由△ABC 和△CDE 是正三角形其性质得三边相等三个角为60° 平角的定义和角的和差得∠ACD =∠BCE 边角边证明△ACD ≌△BCE 其性质得结论①正确；由△ACD ≌△BCE 可得∠CAP =∠CBQ 可得60,AOB ACB 故⑤正确角边角证明△ACP ≌△BCQ 得AP =BQ 其结论③正确；等边三角形的判定得△PCQ 是等边三角形结论⑥正确；∠CPQ =∠ACB =60°判定两线PQ AE ∥ 结论②正确；反证法证明命题DE ≠DP 结论④错误；利用全等三角形的对应高相等可证明点C 在∠AOE 的平分线上结论⑦正确；即正确结论共6个．【详解】解：如图1所示：∵△ABC和△CDE是正三角形∴AC=BC DC=EC∠ACB=∠ECD=60°又∵∠ACD=∠ACB+∠BCD∠BCE=∠DCE+∠BCD ∴∠ACD=∠BCE在△ACD和△BCE中AC BCACD BCE CD CE=⎧⎪=⎨⎪=⎩∠∠∴△ACD≌△BCE（SAS）∴AD=BE∴结论①正确；∵△ACD≌△BCE∴∠CAP=∠CBQ,BPO APC60,AOB ACB故⑤正确又∵∠ACB+∠BCD+∠DCE=180° ∴∠BCD=60°在△ACP和△BCQ中CAP CBQ AC BC ACP BCQ∴△ACP≌△BCQ（ASA）∴AP=BQ PC=QC故③正确∴△PCQ是等边三角形故⑥正确∴∠CPQ=∠CQP=60°∴∠CPQ=∠ACB=60°∴PQ AE∥故②正确若DE=DP∵DC=DE∴DP=DC∴∠PCD=∠DPC又∵∠PCD=60°∴∠DPC=60°与△PCQ是等边三角形相矛盾假设不成立∴结论④错误；过点C分别作CM⊥AD CN⊥BE于点M、N两点如图2所示：∵CM ⊥AD CN ⊥BE,ACD BCE ≌∴CM =CN 又∵OC 在∠AOE 的内部∴点C 在∠AOE 的平分线上∴结论⑦正确；综合所述共有6个结论正确．故选：D ．【点睛】本题综合考查了全等三角的判定与性质等边三角形的判定与性质三角形的内角和定理平行线的判定角平分线性质定理的逆定理和假设法证明命题等相关知识重点掌握全等三角形的判定与性质等边三角形的判定与性质难点是用角平分线性质定理的逆定理作辅助线证明一点已知角的角平分线上．2．已知如图ABC 是锐角三角形分别以边AB 、AC 为边向外作ABD △和ACE ABD △和ACE 均为等边三角形且BE 和CD 交于点F 连接AF ．（1）求证：ACD AEB ≅；（2）求出CFE ∠的度数；（3）求证：AFB BFC AFC ∠=∠=∠．【答案】（1）见解析；（2）60︒；（3）见解析．【解析】【分析】（1）由ABD ∆和ACE ∆均为等边三角形可得边角关系由SAS 即可证明ACD AEB ≌；（2）由ACD AEB ≌可得点A 、F 、C 、E 四点共圆再由圆的性质即可求解；（3）由点A 、F 、C 、E 四点共圆可得∠=∠FAC FEC 再由AFE ∆内角和为180︒可得60AFE ∠=︒ 由点A 、F 、B 、D 四点共圆同理可得60AFD ∠=︒ 从而可得120,120,120∠=︒∠=︒∠=︒AFB AFC BFC 故可得AFB BFC AFC ∠=∠=∠．【详解】解：（1）∵ABD ∆和ACE ∆均为等边三角形∴60DAB EAC ∠=∠=︒ AE AC = AB AD =∴∠+∠=∠+∠BAC DAB BAC EAC 即DAC EAB ∠=∠∴在三角形ABD △和ACE 中AE AC DAC EAB AB AD =⎧⎪∠=∠⎨⎪=⎩∴()ACD AEB SAS ≌△△；（2）∵ACD AEB ≌∴DAC EAB ∠=∠∴点A 、F 、C 、E 四点共圆∴CFE CAE ∠=∠∵ACE ∆均为等边三角形∴60CAE ∠=︒∴60CFE ∠=︒；（3）由（2）点A 、F 、C 、E 四点共圆点A 、F 、B 、D 四点共圆∴∠=∠FAC FEC在AFE ∆中180∠+∠+∠+∠=︒AEF CAE FAC AFE∴180∠+∠+∠+∠=︒AEF CAE FEC AFE即180∠+∠+∠=︒AEC CAE AFE∵60∠=∠=︒AEC CAE∴180606060∠=︒-︒-︒=︒AFE同理可得60AFD ∠=︒∵EFC BFD ∠=∠ 60EFC ∠=︒∴60BFD ∠=︒∴6060120∠+∠=︒+︒=︒AFD BFD6060120∠+∠=︒+︒=︒AFE EFC∴360120120120∠=︒-︒-︒=︒BFC∴AFB BFC AFC ∠=∠=∠．【点睛】本题考查了三角形全等的判定与性质四点共圆的性质三角形内角和定理等边三角形的性质解题的关键是熟练掌握各知识点利用好数形结合的思想．3．已知：如图 △ABC 、△CDE 都是等边三角形 AD 、BE 相交于点O 点M 、N 分别是线段AD 、BE 的中点．(1)求∠DOE 的度数；(2)试判断△MNC 的形状并说明理由；(3)连接OC 求证：OC 是∠AOE 的平分线．【答案】(1)∠DOE 的度数是60°(2)△MNC 是等边三角形理由见解析(3)见解析【解析】【分析】（1）根据等边三角形的性质及角的和差关系可得∠ACD ＝∠BCE 利用SAS 可证明△ACD ≌△BCE 可得AD ＝BE ∠ADC ＝∠BEC 利用角的和差关系及外角性质可得∠AOE =120° 根据平角定义即可得答案；（2）根据全等三角形的性质可得∠CAD ＝∠CBE AD ＝BE AC ＝BC 根据中点的定义可得AM ＝BN 利用SAS 可证明△ACM ≌△BCN 可得CM ＝CN ∠ACM ＝∠BCN 利用角的和差关系可得∠MCN ＝60° 即可证明△MNC 是等边三角形；（3）连接OC过C作CG⊥AD垂足为G；过C作CH⊥BE 垂足为H根据全等三角形的性质可得AD＝BE S△ACD=S△BCE即可得出CG＝CH根据角平分线的判定定理即可得出结论．(1)∵△ABC、△CDE都是等边三角形∴AC＝BC CD＝CE∠ACB＝∠DCE＝60°∴∠ACB＋∠BCD＝∠DCE＋∠BCD∴∠ACD＝∠BCE在△ACD和△BCE中AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE∴AD＝BE∠ADC＝∠BEC∵等边三角形DCE∴∠CED＝∠CDE＝60°∴∠ADE＋∠BED＝∠ADC＋∠CDE＋∠BED ＝∠BEC＋60°＋∠BED＝∠CED＋60°＝60°＋60°＝120°∴∠AOE=120°∴∠DOE＝180°-∠AOE=60°．(2)△MNC是等边三角形理由如下：∵△ACD≌△BCE∴∠CAD＝∠CBE AD＝BE AC＝BC∵点M、N分别是线段AD、BE的中点∴AM＝12AD BN＝12BE∴AM＝BN在△ACM和△BCN中AC BCCAM CBNAM BN=⎧⎪∠=∠⎨⎪=⎩∴△ACM≌△BCN∴CM＝CN∠ACM＝∠BCN∵∠ACB＝60°∴∠ACM＋∠MCB＝∠BCN+∠MCB=∠ACB=60°∴∠MCN＝60°∴△MNC是等边三角形．(3)连接OC过C作CG⊥AD垂足为G；过C作CH⊥BE 垂足为H．∵△ACD≌△BCE∴AD＝BE S△ACD=S△BCE∴1122AD CG BE CH⋅=⋅∴CG＝CH∵CG⊥AD CH⊥BE∴OC是∠AOE的平分线．【点睛】本题主要考查了全等三角形的性质与判定、等边三角形的性质与判定、三角形外角性质及角平分线的判定定理能够熟练掌握等边三角形的性质与判定条件是解题关键．4．如图已知△CAD与△CEB都是等边三角形BD、EA的延长线相交于点F．（1）求证：△ACE≌△DCB．（2）求∠F的度数．（3）若AD⊥BD请直接写出线段EF与线段BD、DF之间的数量关系．【答案】（1）见解析；（2）60°；（3）EF＝BD+2DF.【解析】【分析】（1）根据等边三角形的性质得到CB=CE CD=CA ∠BCE=∠DCA=60° 由全等三角形的判定定理即可得到结论；（2）设BC与EF相交于G 根据全等三角形的性质得到∠1=∠2 根据三角形的内角和即可得到结论；（3）根据垂直的定义得到∠ADF=90° 求得∠DAF=30° 根据直角三角形的性质得到AF=2DF 根据全等三角形的性质得到AE=BD 于是得到结论．【详解】（1）∵△CAD与△CEB都是等边三角形∴CB＝CE CD＝CA ∠BCE＝∠DCA＝60°∴∠BCD＝∠ECA∴△ACE≌△DCB（SAS）；（2）设BC与EF相交于G由（1）可知△ACE≌△DCB∴∠1＝∠2∵∠1+∠BGF+∠F＝∠2+∠AGC+∠BCE＝180°而∠BGF＝∠AGC∴∠F＝∠BCE＝60°；（3）EF＝BD+2DF 理由如下：∵AD⊥BD∴∠ADF ＝90°∵∠F ＝60°∴∠DAF ＝30°∴AF ＝2DF∵△ACE ≌△DCB∴AE ＝BD∴EF ＝AE+AF ＝BD+2DF ．【点睛】本题考查了全等三角形的判定和性质等边三角形的性质直角三角形的性质正确的识别图形是解题的关键．5．已知点C 为线段AB 上一点分别以AC 、BC 为边在线段AB 同侧作△ACD 和△BCE 且CA=CD CB=CE ACD BCE ∠∠= 直线AE 与BD 交于点F ．（1）如图1 证明：△ACE ≌△DCB ；（2）①如图1 若ACD 60∠=︒ 则AFB ∠=________；②如图2 若ACD α∠= 则AFB ∠=______；（用含α的式子表示）（3）将图2中的△ACD 绕点C 顺时针旋转任意角度（交点F 至少在BD 、AE 中的一条线段上）如图3 试探究A FB ∠与α的数量关系并予以证明．【答案】（1）证明见解析；（2）120° 180°-β；（3）∠AFB=180°-α 证明见解析．【解析】【分析】（1）求出∠ACE=∠DCB 根据SAS证出两三角形全等即可；（2）根据全等三角形性质得出∠AEC=∠DBC ∠CDB=∠CAE 求出∠EAB+∠DBA=∠ACD ∠AFB=180°-（∠EAB+∠DBC）代入求出即可得出①②的结论；（3）由“SAS”可证△ACE≌△DCB 可得∠AEC=∠DBC 由三角形内角和定理可求解．【详解】解：（1）证明：∵∠ACD=∠BCE∴∠ACD+∠DCE=∠BCE+∠DCE∴∠ACE=∠DCB在△ACE和△DCB中∵AC CDACE DCBCE CB=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△DCB；（2）①∵∠ACD=60°∴∠CDB+∠DBC=∠ACD=60°∵△ACE≌△DCB∴∠AEC=∠DBC ∠CDB=∠CAE∴∠CAE+∠DBC=60°∴∠AFB=180°-60°=120°故答案为：120；②当∠ACD=β时∠AFB=180°-β 理由是：∵∠ACD=β∴∠CDB+∠DBC=∠ACD=β∵△ACE≌△DCB∴∠AEC=∠DBC ∠CDB=∠CAE∴∠CAE+∠DBC=β∴∠AFB=180°-（∠CAE+∠DBC）=180°-β；故答案为：180°-β．（3）∠AFB=180°-α；证明：∵∠ACD=∠BCE=α 则∠ACD+∠DCE=∠BCE+∠DCE 即∠ACE=∠DCB．在△ACE和△DCB中∵AC DCACE DCBCE CB=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△DCB（SAS）．则∠CBD=∠CEA如下图∵∠FGE=∠CGB∴∠EFB=∠ECB=α．∠AFB=180°-∠EFB=180°-α．【点睛】本题是三角形综合题考查了全等三角形的判定及其性质、三角形内角和定理等知识本题还综合了旋转的知识点是一道综合性比较强的题．要熟练掌握全等三角形的判定和性质定理．6．如图①在等边△ABC中线段AM为BC边上的中线．动点D在直线AM上时以CD为一边在CD的下方作等边△CDE 连结BE．（1）当点D在线段AM上时（如图①）则AD BE（填“＞”“＜”或“=”）∠CAM= 度；（2）当点D在线段AM的延长线上时（如图②）直线BE与直线AM的交点为O 求∠AOB的度数；（3）当动点D在线段AM的反向延长线上时直线BE与直线AM的交点为O 试判断∠AOB的度数是否发生变化？若变化请求出∠AOB的度数若不变请说明理由．【答案】（1）=；30；（2）60°；（3）不变见解析【解析】【分析】（1）根据SAS就可以得出△ADC≌△BEC 则AD=BE；根据等边三角形的性质可以直接得出∠CAM的度数；（2）根据等边三角形的性质就可以得出AC=BC DC=EC ∠ACB=∠DCE=60° 由等式的性质就可以∠BCE=∠ACD 根据SAS就可以得出△ADC≌△BEC 进而得到∠AOB的度数；（3）当点D在线段MA的延长线上时如图3 通过得出△ACD≌△BCE就可以得出结论．【详解】（1）∵△ABC与△DEC都是等边三角形∴AC=BC CD=CE ∠ACB=∠DCE=60°∴∠ACD+∠DCB=∠DCB+∠BCE∴∠ACD=∠BCE．在△ADC和△BEC中AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE（SAS）∴AD=BE；∵△ABC是等边三角形∴∠BAC=60°．∵线段AM为BC边上的中线∴∠CAM=12∠BAC∴∠CAM=30°故答案为：= 30；（2）∵△ABC和△CDE都是等边三角形∴AC=BC DC=EC ∠ACB=∠DCE=60°∵∠ACD=∠ACB+∠DCB ∠BCE=∠DCE+∠DCB ∴∠ACD=∠BCE∴△ACD≌△BCE（SAS）∴∠CAD=∠CBE∵∠AMC=∠BMO∴∠AOB=∠ACB=60°；（3）不变理由如下：∵点D在线段MA的延长线上且△ABC与△DEC都是等边三角形∴AC=BC CD=CE ∠ACB=∠DCE=60°∴∠ACD+∠ACE=∠BCE+∠ACE=60°∴∠ACD=∠BCE在△ACD和△BCE中AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE（SAS）∴∠CBE=∠CAD同理可得：∠CAM=30°∴∠CBE=∠CAD=150°∴∠CBO=30° ∠BAM=30°∴∠BOA=90°-30°=60°．【点睛】本题是三角形综合题考查了等边三角形的性质的运用等腰三角形的性质的运用全等三角形的判定及性质的运用解答时证明三角形全等是关键．7．已知点C 为线段AB 上一点分别以AC 、BC 为边在线段AB 同侧作ACD △和BCE 且AC DC = CB CE = ACD BCE ∠=∠ 直线AE 与BD 交于点F ．（1）如图① 试说明：ACE DCB ≌；（2）如图① 若60ACD ∠=︒ 则AFB ∠=________°；如图② 若90ACD ∠=︒ 则AFB ∠=________°；如图③ 若120ACD ∠=︒ 则AFB ∠=________°；（3）如图④ 若ACD α∠= 求AFB ∠的值（用含α的代数式表示）；（4）若A 、B 、C 三点不在同一直线上线段AC 与线段BC 交于点C （交点F 至少在BD 、AE 中的一条线）如图⑤ 若ACD α∠= 试判断AFB ∠与α的数量关系并说明理由．【答案】（1）见解析；（2）120 90 60；（3）180α︒-；（4）180AFB α∠=︒- 见解析【解析】【分析】（1）求出∠ACE =∠DCB 根据SAS 证出两三角形全等即可；（2）根据全等三角形性质得出∠AEC =∠DBC ∠CDB =∠CAE 求出∠EAB+∠DBA=∠ACD ∠AFB =180°-（∠EAB +∠DBC ）代入求出即可；（3）根据全等三角形的性质、三角形的内角和与三角形的外角性质求出即可．（4）知道ACD BCE ∠=∠ 得到ACE DCB ∠=∠ 证明()ACE DCB SAS ∆≅∆即可求解．【详解】解：（1）ACD BCE ∠=∠ACD DCE BCE DCE ∴∠+∠=∠+∠ACE DCB ∴∠=∠在ACE ∆和DCB ∆中CE CB ⎪=⎩()ACE DCB SAS ∴∆≅∆（2）解：∵∠ACD =60°∴∠CDB +∠DBC =∠ACD =60°∵△ACE ≌△DCB∴∠AEC =∠DBC ∠CDB =∠CAE∴∠CAE +∠DBC =60°∴∠AFB =180°-60°=120°；当∠ACD =90°时∵∠ACD =90°∴∠CDB +∠DBC =∠ACD =90°∵△ACE ≌△DCB∴∠AEC =∠DBC ∠CDB =∠CAE∴∠CAE +∠DBC =90°∴∠AFB =180°-90°=90°；同理：∠ACD =120°时∠AFB =60°故答案为：120 90 60（3）由（1）可知ACE DCB ∆≅∆CAE CDB ∴∠=∠180180AFB CDB CDA DAE CDA DAE BAE CDA DAC ACD α∴∠=∠+∠+∠=∠+∠+∠=∠+∠=︒-∠=︒-故答案为：180α︒-（4）180AFB α∠=︒-理由如下：ACD BCE ∠=∠ACD DCE BCE DCE ∴∠+∠=∠+∠ACE DCB ∴∠=∠在ACE ∆和DCB ∆中CE CB ⎪=⎩()ACE DCB SAS ∴∆≅∆AEC DBC ∴∠=∠180180AFB AEC CEB EBD DBC DBE EBC CEB EBC ECB α∴∠=∠+∠+∠=∠+∠+∠=∠+∠=︒-∠=︒-即180α︒-．【点睛】本题考查了全等三角形的性质和判定三角形的外角性质三角形的内角和定理解此题的关键是找出已知量和未知量之间的关系．8．（1）发现：如图1 点A 为线段BC 外一动点且BC =a AB =b ．当点A 位于______时线段AC 的长取得最大值最大值为______．（用含a b 的式子表示）（2）应用：点A 为线段BC 外一动点且BC =3 AB =1．如图2所示分别以AB AC 为边作等边△ABD 和等边△ACE 连接CD BE ．①请找出图中与BE 相等的线段并说明理由；②直接写出BE 长的最大值．【答案】（1）CB 的延长线 a +b ；（2）①DC =BE 理由见解析；②4；（1）根据点A 位于CB 的延长线上时线段AC 的长取得最大值即可得到结论；（2）①根据等边三角形的性质得到AD =AB AC =AE ∠BAD =∠CAE =60° 推出△CAD ≌△EAB 根据全等三角形的性质得到CD =BE ；②由于线段BE 长的最大值=线段CD 的最大值根据（1）中的结论即可得到结果；【详解】解：（1）由题意可知当点A 位于CB 的延长线上时线段AC 的长取得最大值且最大值为AB +BC 即a +b故答案为：CB 的延长线 a +b ；（2）①DC =BE 理由如下：∵△ABD 与△ACE 都是等边三角形∴AD =AB AC =AE ∠BAD =∠CAE =60°∴∠BAD +∠BAC =∠CAE +∠BAC即∠CAD =∠EAB在△CAD 与△EAB 中AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△EAB （SAS ）∴DC =BE ；②线段BE 长的最大值是4由（1）得点D 在CB 的延长线上时 CD 最大最大值为DB +BC =AB +BC =4∵△CAD ≌△EAB∴DC =BE∴线段BE 长的最大值为4．9．如图所示已知B （﹣2 0） C （2 0） A 为y 轴正半轴上的一点点D 为第二象限一动点点E 在BD 的延长线上 CD 交AB 于点F 且∠BDC ＝∠BAC ．(1)求证：∠ABD ＝∠ACD ；(2)求证：AD 平分∠CDE ；(3)若在D 点运动的过程中始终有DC ＝DA +DB 在此过程中 ∠BAC 的度数是否发生变化？如果变化请说明理由；如果不变请求出∠BAC 的度数．【答案】(1)证明过程见解析(2)证明过程见解析(3)∠BAC =60° 理由见解析【解析】【分析】(1)根据∠BDC=∠BAC∠DFB=∠AFC再结合∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AF C=180° 即可得出结论．(2)过点A作AM⊥CD于点M作AN⊥BE于点N．运用“AAS”证明△ACM≌△ABN得AM=AN．根据“到角的两边距离相等的点在角的平分线上”得证；(3)运用截长法在CD上截取CP=BD连接AP．证明△ACP≌ABD得△ADP为等边三角形从而求∠BAC的度数．(1)证明：∵∠BDC=∠BAC∠DFB=∠AFC又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°∴∠ABD=∠ACD；(2)证明：过点A作AM⊥CD于点M作AN⊥BE于点N如下图所示：则∠AMC=∠ANB=90°．∵OB=OC OA⊥BC∴AB=AC由(1)可知：∠ABD=∠ACD∴△ACM≌△ABN (AAS)∴AM=AN．∴DA平分∠CDE．(角的两边距离相等的点在角的平分线上)；(3)解：∠BAC的度数为60° 理由如下：在CD上截取CP=BD连接AP如下图所示：∵CD=AD+BD∴AD=PD ．∵AB=AC ∠ABD =∠ACD BD=CP∴△ABD ≌△ACP (SAS )∴AD=AP ∠BAD =∠CAP∴AD=AP=PD 即△ADP 是等边三角形∴∠DAP =60°．∴∠BAC =∠BAP +∠CAP =∠BAP +∠BAD =60°．【点睛】此题考查全等三角形的判定与性质运用了角平分线的判定定理和“截长补短”的数学思想方法综合性较强．10．如图1 点M 为锐角三角形ABC 内任意一点连接,,AM BM CM ．以AB 为一边向外作等边三角形ABE △ 将BM 绕点B 逆时针旋转60︒得到BN 连接EN ．（1）求证：AMB ENB △≌△；（2）若AM BM CM ++的值最小则称点M 为ABC 的费马点．若点M 为ABC 的费马点求此时,,AMB BMC CMA ∠∠∠的度数；（3）受以上启发你能想出作锐角三角形的费马点的一个方法吗？请利用图2画出草图并说明作法以及理由．【答案】（1）见解析；（2）120BMC ∠=︒：120AMB ∠=︒；120AMC ∠=︒；（3）见解析【解析】【分析】（1）结合等边三角形的性质根据SAS 可证△AMB ≌△ENB（2）连接MN 由（1）的结论证明ΔBMN 为等边三角形所以BM =MN 即AM+BM+CM =EN+MN+CM 所以当E 、N 、M 、C 四点共线时 AM+BM+CM 的值最小从而可求此时∠AMB 、∠BMC 、ΔCMA 的度数；（3）根据（2）中费马点的定义又△ABC 的费马点在线段EC 上同理也在线段BF 上因此线段EC 和BF 的交点即为△ABC 的费马点．【详解】解：（1）证明：∵ABE △为等边三角形∴,60AB BE ABE =∠=︒．而60MBN ∠=︒∴ABM EBN ∠=∠．在AMB 与ENB △中AB BEABM EBNBM BN=⎧⎪∠=∠⎨⎪=⎩∴(SAS)AMB ENB ≌．（2）连接MN ．由（1）知 AM EN =．∵60,MBN BM BN ∠=︒=∴BMN △为等边三角形．∴BM MN =．∴AM BM CM EN MN CM ++=++．∴当E 、N 、M 、C 四点共线时 AM BM CM ++的值最小．此时 180120BMC NMB ∠=︒-∠=︒：180120AMB ENB BNM ∠=∠=︒-∠=︒；360120AMC BMC AMB ∠=-∠-∠=︒︒．（3）如图2 分别以ABC 的AB AC 为一边向外作等边ABE △和等边ACF 连接,CE BF 相交于M 则点M 即为ABC 的费马点由（2）知 ABC 的费马点在线段EC 上同理也在线段BF 上．因此线段EC 与BF 的交点即为ABC 的费马点．（方法不唯一正确即可）【点睛】本题考查了等边三角形的性质三角形全等的判定与性质,掌握三角形全等的判定和性质是解题的关键．11．已知：△ABC 与△BDE 都是等腰三角形．BA ＝BC BD ＝BE （AB ＞BD ）且有∠ABC ＝∠DBE ．（1）如图1 如果A 、B 、D 在一直线上且∠ABC ＝60° 求证：△BMN 是等边三角形；（2）在第（1）问的情况下直线AE 和CD 的夹角是 °；（3）如图2 若A 、B 、D 不在一直线上但∠ABC ＝60°的条件不变则直线AE 和CD 的夹角是 °；（4）如图3 若∠ACB ＝60° 直线AE 和CD 的夹角是 °．【答案】（1）证明见解析；（2）60；（3）60；（4）60；【解析】【分析】（1）根据题意得∠ABC ＝∠DBE ＝60° 从而得ABE DBC ∠=∠；通过证明ABE CBD ≌ 得BAE BCD ∠=∠；通过证明BAM BCN ≌ 得BM BN = 根据等边三角形的性质分析即可完成证明；（2）结合题意通过证明ABC 为等边三角形得60BAC BCA ∠=∠=︒；结合（1）的结论根据三角形外角性质推导得120AOD ∠=︒ 从而完成求解；（3）同理通过证明ABC 为等边三角形得60BAC BCA ∠=∠=︒；通过证明ABE CBD ≌ 得BAE BCD ∠=∠；根据三角形外角性质推导得120AOD ∠=︒ 从而完成求解；（4）根据题意通过证明ABC 为等边三角形推导得ABE CBD ∠=∠ 通过证明ABE CBD ≌ 得BAE BCD ∠=∠ 结合三角形外角的性质计算即可得到答案．【详解】（1）∵∠ABC ＝∠DBE ＝60°∴18060MBN ABC DBE ∠=︒-∠-∠=︒ ABE ABC MBN ∠=∠+∠ DBC DBE MBN ∠=∠+∠ ∴ABE DBC ∠=∠∵BA ＝BC BD ＝BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠ BAM 和BCN △中60BAE BCD AB BC ABC MBN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴BAM BCN ≌∴BM BN =∴BMN △为等边三角形；（2）∵∠ABC ＝∠DBE ＝60°, BA ＝BC∴ABC 为等边三角形；∴60BAC BCA ∠=∠=︒根据题意 AE 和CD 相交于点O∵BAE BCD ∠=∠∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒ 即直线AE 和CD 的夹角是60︒故答案为：60；（3）∵∠ABC ＝∠DBE ＝60°, BA ＝BC∴ABC 为等边三角形；∴60BAC BCA ∠=∠=︒∵ABE ABC MBN ∠=∠+∠ DBC DBE MBN ∠=∠+∠ ∠ABC ＝∠DBE ＝60°∴ABE DBC ∠=∠∵BA ＝BC BD ＝BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠如图延长AE 交CD 于点O∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒ 即直线AE 和CD 的夹角是60︒故答案为：60；（4）∵BA ＝BC∴ACB CAB ∠=∠∵∠ACB ＝60°∴60ACB CAB ∠=∠=︒∴ABC 为等边三角形∵BD ＝BE ∠ABC ＝∠DBE∴60DBE ∠=︒∵ABE ABC CBE ∠=∠-∠ CBD DBE CBE ∠=∠-∠∴ABE CBD ∠=∠ABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠分别延长CD 、AE 相较于点O 如下图：∴AOF OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOF BAC BCA ∠=∠+∠=︒∴18060AOC AOF ∠=︒-∠=︒ 即直线AE 和CD 的夹角是60︒故答案为：60．【点睛】本题考查了等腰三角形、等边三角形、全等三角形、补角、三角形外角的知识；解题的关键是熟练掌握等边三角形、全等三角形、三角形外角的性质从而完成求解．12．如图已知点B （-2 0） C （2 0） A 为y 轴正半轴上一点点D 为第二象限内的一个动点 M 在BD 的延长线上 CD 交AB 于点F 且∠ABD =∠ACD ．（1）求证：∠BDC =∠BAC ；（2）求证：DA平分∠CDM；（3）若在D点运动的过程中始终有DC=DA+DB在此过程中∠BAC的度数是否变化？如果变化请说明理由；如果不变请求出∠BAC的度数？【答案】（1）见详解；（2）见详解；（3）∠BAC的度数不变化；理由见详解．【解析】【分析】（1）由三角形的内角和定理以及对顶角相等即可得到结论成立；（2）过点A作AH⊥CD于点H作AG⊥BM于点G．运用“AAS”证明△ACH≌△ABG得AH=AG．根据“到角的两边距离相等的点在角的平分线上”得证；（3）运用截长法在CD上截取CP=BD连接AP．证明△ACP≌ABD得△ADP为等边三角形从而求∠BAC的度数．【详解】解：（1）由题意在△ACF和△BDF中ACD AFC CAB ABD BFD BDC∠+∠+∠=∠+∠+∠=︒180∵∠ABD=∠ACD∠AFC=∠BFD∴∠BDC=∠BAC；（2）过点A作AH⊥CD于点H作AG⊥BM于点G如图：则∠AHC=∠AGB=90°∵OB=OC OA⊥BC∴AB=AC∵∠ABD=∠ACD∴△ACH≌△ABG（AAS）∴AH=AG．∴AD平分∠CDM．（3）∠BAC的度数不变化．在CD上截取CP=BD连接AP．∵CD=AD+BD∴AD=PD．∵AB=AC∠ABD=∠ACD BD=CP∴△ABD≌△ACP．∴AD=AP；∠BAD=∠CAP．∴AD=AP=PD即△ADP是等边三角形∴∠DAP=60°．∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°．【点睛】此题考查全等三角形的判定与性质运用了角平分线的判定定理和“截长补短”的数学思想方法综合性较强．。

七年级数学上册2.1整式(2)多项式课时练

2.1 整式（2）多项式1．在代数式x+yz，中，下列结论正确的是（）A．有4个单项式，2个多项式B．有5个单项式，3个多项式C．有7个整式D．有3个单项式，2个多项式2．多项式1+xy﹣xy2的次数及最高次项的系数分别是（）A．2，1 B．2，﹣1 C．3，﹣1 D．5，﹣13．若多项式是关于x的二次三项式，则m的值是（）A．2 B．-2 C．2或-2 D．34．一个五次多项式，它的任何一项的次数（）A．都小于5 B．都等于5 C．都不大于5 D．都不小于55．通信市场竞争日益激烈，某通信公司的手机本地话费标准按原标准每分钟降低a元后，再次下调了20%.现在收费标准是每分钟b元，则原收费标准每分钟是（）A．（a+b）元B．（a﹣b）元C．（a+5b）元D．（a﹣5b）元6．把下列代数式的代号填入相应的集合括号里．（A）a2b+ab2；（B）x﹣x2+1；（C）；（D）﹣；（E）0；（I）3x2+．（F）﹣x+；（G）a2+ab2+b3；（H）；（1）单项式集合：；（2）多项式集合：；（3）整式集合：；（4）二项式集合：；（5）三次多项式集合：；（6）非整式集合：．7．把多项式2x2﹣3x+x3按x的降幂排列是．8．已知单项式2x m+1是一次单项式，多项式3x n﹣1﹣x3﹣7是四次式，则代数式1﹣n2﹣m2004的值为．9．学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为册（用含a，b的代数式表示）．10．已知3x2y|m|﹣（m﹣1）y+5是关于x，y的三次三项式，求2m2﹣3m+1的值．参考答案1．答案：A 解析：单项式有：，abc，0，π，共4个；多项式有x+yz，3x2﹣2x﹣3，共2个．故选A．2．答案：C 解析：多项式1+xy﹣xy2的次数及最高次项的系数分别是3，﹣1．故选C．3．答案：B 解析：由题意得，|m|=2，m=2或﹣2；﹣（m﹣2）≠0，m≠2，那么m=﹣2．故选B．4．答案：C 解析：由于多项式的次数是“多项式中次数最高的项的次数”，因此五次多项式中，次数最高的项是五次的，其余项的次数可以是五次的，也可以是小于五次的，却不能是大于五次的．因此五次多项式中的任何一项都是不大于五次的．故选C．5．答案：A 解析：b÷（1﹣20%）+a=a+b．故选A．6．（1）单项式集合：（D），（E）；（2）多项式集合：（A），（B），（C），（F），（G）；（3）整式集合：（A），（B），（C），（D），（E），（F），（G）；（4）二项式集合：（A），（C），（F）；（5）三次多项式集合：（A），（G）；（6）非整式集合：（H），（I）7．按x的降幂排列是x3+2x2﹣3x．8．解：∵单项式2x m+1是一次单项式，多项式3x n﹣1﹣x3﹣7是四次式，∴m+1=1，n﹣1=4，∴m=0，n=5，∴1﹣n2﹣m2004=1﹣25﹣0=﹣24，故答案为﹣24．9．解：由题意得，这批图书共有ab册，则图书的一半是册．故答案为．10．解：由题意可知m﹣1≠0，即m≠1，由3x2y|m|可知|m|=1，即m=±1，∴m=﹣1．当m=﹣1时，原式=2×（﹣1）2﹣3×（﹣1）+1=2+3+1=6．2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．下列说法错误的是（） A.倒数等于本身的数只有±1 B.两点之间的所有连线中，线段最短 C.-23x yz π的系数是3π-，次数是4D.角的两边越长，角就越大2．如图，AD 是∠EAC 的平分线，AD ∥BC ，∠B=30°，则∠C 的度数为（）A ．50° B．40° C．30° D．20° 3．在解方程+=5时，去分母的过程正确的是（）A.3（x ﹣5）+2（3x+7）=30B.3（x ﹣5）+2（3x+7）=5C.x ﹣5+3x+7=5D.x ﹣5+3x+7=304．一列长为150米的火车，以每秒15米的速度通过600米的隧道，从火车进入隧道口算起，这列火车完全通过隧道所需要的时间是（） A.30秒B.40秒C.50秒D.60秒5．如图，将一张正三角形纸片剪成四个全等的正三角形，得到4个小正三角形，称为第一次操作；然后，将其中的一个正三角形再剪成四个小正三角形，共得到7个小正三角形，称为第二次操作；再将其中的一个正三角形再剪成四个小正三角形，共得到10个小正三角形，称为第三次操作；……，以上操作n 次后，共得到49个小正三角形，则n 的值为（）A ．13n =B ．14n =C ．15n =D ．16n =6．下列各式运用等式的性质变形，错误的是（） A ．若a b -=-，则a b = B ．若a bc c=，则a b = C ．若ac bc =，则a b =D ．若22(1)(1)m a m b +=+，则a b =7．把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m ，宽为n ）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分的周长和是（）A.4nB.4mC.()2m n +D.()4m n -8．下列运算中，正确的是（） A ．2a+3b ＝5ab B ．2a 3+3a 2＝5a 5 C ．4a 2b ﹣4ba 2＝0D ．6a 2﹣4a 2＝09．在﹣22、（﹣2）2、﹣（﹣2）、﹣|﹣2|中，负数的个数是（） A ．4个 B ．3个 C ．2个 D ．1个10．有理数 a ，b 在数轴上的点的位置如图所示，则正确的结论是（）A.a ＜﹣4B.a+ b ＞0C.|a|＞|b|D.ab ＞011．12的相反数是（） A.﹣2B.﹣12C.12D.212．甲从点A 出发沿北偏东35°方向走到点B ，乙从点A 出发沿南偏西20°方向走到点C ，则∠BAC 等于（） A.15° B.55°C.125°D.165°二、填空题13．已知线段AB=6cm ，C 是线段AB 的中点，E 是直线AB 上的一点，且CE=13AB ，则线段AE=______cm ． 14．在同一平面内，两条直线相交时最多有1个交点，三条直线相交时最多有3个交点，四条直线相交时最多有6个交点，…，那么十条直线相交时最多有____个交点．15．一个两位数，设它的个位上的数字为x ，十位上的数字比个位上的数字大1，这个两位数的2倍加2等于66，根据题意所列方程是_____．16．轮船从A 港顺流行驶到B 港，比从B 港返回A 港少用3小时，若船速为26千米/小时，水速为2千米/时，则A 港和B 港相距_______千米． 17．若代数式3a x ﹣2b 2y+1与13a 3b 2是同类项，则x=_____，y=_____． 18．已知多项式﹣πx 2y m+1+xy 2﹣4x 3﹣8是五次多项式，单项式3x 2n y 6-m 与该多项式的次数相同，则m ＝_____，n ＝_____．19．小明在做解方程的作业时，不小心将方程中的一个常数污染得看不清楚，方程是：122y y +=--¤ ．小明翻看了书后的答案，此方程的解是y= 12- ，则这个常数是_______．20．若|x|＝2，则x的值是_____．三、解答题21．如图，∠AOB=120°，射线OC从OA开始，绕点O逆时针旋转，旋转的速度为每分钟20°；射线OD从OB开始，绕点O逆时针旋转，旋转的速度为每分钟5°，OC和OD同时旋转，设旋转的时间为t（0≤t≤15）．（1）当t为何值时，射线OC与OD重合；（2）当t为何值时，∠COD=90°；（3）试探索：在射线OC与OD旋转的过程中，是否存在某个时刻，使得射线OC，OB与OD中的某一条射线是另两条射线所夹角的角平分线？若存在，请求出所有满足题意的t的取值，若不存在，请说明理由．22．在做解方程练习时，学习卷中有一个方程“2y–12=12y+■”中的■没印清晰，小聪问老师，老师只是说：“■是一个有理数，该方程的解与当x=2时代数式5（x–1）–2（x–2）–4的值相同．”小聪很快补上了这个常数．同学们，你们能补上这个常数吗？23．如图，AB=12cm，点C是线段AB上的一点，BC=2AC．动点P从点A出发，以3cm/s的速度向右运动，到达点B后立即返回，以3cm/s的速度向左运动；动点Q从点C出发，以1cm/s的速度向右运动．设它们同时出发，运动时间为ts．当点P与点Q第二次重合时，P、Q两点停止运动．（1）AC=__cm，BC=__cm；（2）当t为何值时，AP=PQ；（3）当t为何值时，PQ=1cm．24．（1）观察思考：如图，线段AB上有两个点C、D，请分别写出以点A、B、C、D为端点的线段，并计算图中共有多少条线段；（2）模型构建：如果线段上有m个点（包括线段的两个端点），则该线段上共有多少条线段？请说明你结论的正确性；（3）拓展应用：某班45名同学在毕业后的一次聚会中，若每两人握1次手问好，那么共握多少次手？请将这个问题转化为上述模型，并直接应用上述模型的结论解决问题．25．某影院共有24排座位，第1排有12个座位数，从第2排开始，每一排都比前一排增加m个座位（1）请你在下表的空格里填写一个适当的代数式：（2）已知第17排座位数是第3排座位数的2倍，那么影院共有多少个座位?26．先化简，再求值：[（2x﹣y）2﹣（2x+y）（2x﹣y）]÷y，其中x＝1，y＝2．27．在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：14，﹣9，+8，﹣7，13，﹣6，+12，﹣5．（1）请你帮忙确定B地位于A地的什么方向，距离A地多少千米？（2）若冲锋舟每千米耗油0.5升，油箱容量为28升，求冲锋舟当天救灾过程中至少还需补充多少升油？（3）救灾过程中，冲锋舟离出发点A最远处有多远？28．计算：（1）12+（﹣7）﹣（﹣15）（2）4+（﹣2）3×5﹣（﹣0.28）÷4．【参考答案】***一、选择题1．D2．C3．A4．C5．D6．C7．A8．C9．C10．C11．B12．D二、填空题13．1或514．15．2〔10(x＋1) ＋x〕＋2＝6616．50417．SKIPIF 1 < 0解析：1218．SKIPIF 1 < 0 解析：1219．1 20．±2．三、解答题21．（1）t=8min 时，射线OC 与OD 重合；（2）当t=2min 或t=14min 时，射线OC ⊥OD ；（3）存在，详见解析. 22．见解析 23．824．（1）6条线段；（2）()112m m -；（3）990次. 25．（1）12+(1)m n -；（2）564个. 26．﹣4x+2y ，当x ＝1，y ＝2时，原式＝0．27．(1) B 地在A 地的东边20千米；(2) 9升油；(3) 25千米. 28．（1）20；（2）﹣35.3．2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．下列说法正确的是( )A．一个平角就是一条直线B．连结两点间的线段，叫做这两点的距离C．两条射线组成的图形叫做角D．经过两点有一条直线，并且只有一条直线2．如图所示，已知∠AOC=∠BOD=80°，∠BOC=30°，则∠AOD的度数为( )A.160°B.110°C.130°D.140°3．如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的相对面上的字是( )A．的B．中C．国D．梦4．规定a cad bcb d⎛⎫=-⎪⎝⎭，若2331xx⎛⎫=⎪--⎝⎭，则x=（）A.0B.3C.1D.25．把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为m厘米，宽为n厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）A.4m厘米B.4n厘米C.2（m+n）厘米D.4（m-n）厘米6．下列选项中，不是同类项的是( )A．－1和0 B．－x2y和3yx2 C．－2xy2和2x2yz D．－m2和6m27．某车间28名工人生产螺栓和螺母，螺栓与螺母个数比为1：2刚好配套，每人每天平均生产螺栓12个或螺母18个，求多少人生产螺栓？设：有x名工人生产螺栓，其余人生产螺母．依题意列方程应为( ) A．12x＝18(28﹣x) B．2×12x＝18(28﹣x)C ．12×18x＝18(28﹣x)D ．12x ＝2×18(28﹣x)8．鸡兔同笼问题是我国古代著名趣题之一. 大约在1500年前，《孙子算经》中就记载了这个有趣的问题. 书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头;从下面数，有94只脚.求笼中各有几只鸡和兔？经计算可得（）A.鸡23只，兔12只B.鸡12只，兔23只C.鸡15只，兔20只D.鸡20只，兔15只 9．现有五种说法：①-a 表示负数；②绝对值最小的有理数是0；③3×102x 2y 是5次单项式；④5x y是多项式．其中正确的是（） A.①③B.②④C.②③D.①④10．若（）﹣（﹣5）=﹣3，则括号内的数是（） A ．﹣2 B ．﹣8 C ．2 D ．8 11．﹣2018的相反数是（） A.﹣2018B.2018C.±2018D.﹣1201812．四个有理数﹣1，2，0，﹣3，其中最小的是（） A ．﹣1 B ．2 C ．0 D ．﹣3 二、填空题13．已知一个角的补角等于这个角的2倍，则这个角等于__________度． 14．如图，点C ，D 为线段AB 上两点，AC+BD ＝a ，若AD+BC ＝75AB ，用含a 代数式表示CD 的长为_____．15．将一堆糖果分给幼儿园的小朋友，如果每人2颗，那么就多8颗；如果每人3颗，那么就少12颗．设幼儿园里有x 个小朋友，可得方程___________.16．已知a ，b ，c 在数轴上的位置如图所示，化简：|a ﹣b|+|b+c|+|c ﹣a|＝_____．17．如图1是一个的圆（∠AOB=90°），芳芳第一次在图1中画了一条线，将图1等分成2份，第二次又加了两条线，将图1等分成4份，第三次由加了四条线，将图1等分成8份，第四次又加了八条线，将图1等分成16份，如图2所示，则第n （n ＞1）次可将图1等分成_____份，当n=5时，图1中的每份的角度是_____（用度，分，秒表示）18．计算：﹣4+（﹣5）=________19．某种零件，标明要求是φ：20±0.02mm（φ表示直径，单位：毫米），经检查，一个零件的直径是19.9mm，该零件______（填“合格”或“不合格”）．20．一个两位数，个位上的数字是十位上数字的3倍，它们的和是12，那么这个两位数是____．三、解答题21．如图5，O为直线AB上一点，∠AOC=48°,OE平分∠AOC, ∠DOE=90°(1)求∠BOE的度数。

如图1.在△ABC中.∠BAC=...

1．如图1，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E在AC边上，连结BE交AD于点O，AF⊥BE于点F，交BC于点G．（1）求证：△ABO≌△CAG；（2）如图2，若点E是AC边的中点，连结EG，求证：AG+EG=BE；（3）如图3，若点E是AC边上的动点，连结DF．当点E在AC边上（不含端点）运动时，∠DFG的⼤⼩是否改变？如果不变，请求出∠DFG的度数；如果要变，请说明理由．分析（1）根据等腰直⾓三⾓形的性质得到∠BAD=∠C=45°，根据余⾓的性质得到∠AOB=∠AGC，即可得到结论；（2）过点C作CM⊥AC交AG延长线于点M，易证△ABE≌△CAM，可得AE=CM，∠AEB=∠M，AM=BE，即可证明△EGC≌△MCG，可得EG=GM，于是问题得证；（3）由AD⊥BC于点D，AF是△ABE的⾼，得到A，B，D，F四点共圆，根据圆内接四边形的性质得到∠ABD+∠AFD=180°．由邻补⾓的定义得到∠AFD+∠DFG=180°，于是得到∠DFG=∠ABD，即可得到结论．解答（1）证明：∠BAC=90°，AB=AC，AD⊥BC于点D，∴∠BAD=∠C=45°，∵AG⊥BE，∴∠AFO=∠ADG=90°，∴∠AOB=∠OAF+90°，∠AGC=∠OAF+90°，∴∠AOB=∠AGC，在△ABO与△AGC中，$\left\{\begin{array}{l}{∠BAO=∠C}\\{∠AOB=∠AGC}\\{AB=AC}\end{array}\right.$，∴△ABO≌△CAG；（2）证明：如图，过点C作CM⊥AC交AG延长线于点M，在△ABE和△CAM中，$\left\{\begin{array}{l}{∠ABE=∠CAM}\\{AB=AC}\\{∠BAC=∠ACM}\end{array}\right.$，∴△ABE≌△CAM（ASA），∴AE=CM，∠AEB=∠M，BE=AM，∵AE=EC，∴EC=CM，∵AB=AC，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠ACM=90°，∴∠GCM=90-45°=45°=∠ACG，在△EGC和△MGC中，$\left\{\begin{array}{l}{EC=MC}\\{∠GCM=∠ECG}\\{CG=CG}\end{array}\right.$，∴△EGC≌△MCG（SAS），∴GE=EM，∵AM=AG+GM=AG+GE，∴AG+GE=BE；（3）∠DFG的⼤⼩不会改变，∵AD⊥BC于点D，AF是△ABE的⾼，∴∠AFB=∠ADB=90°，∴A，B，D，F四点共圆，∴∠ABD+∠AFD=180°．∵∠AFD+∠DFG=180°，∴∠DFG=∠ABD，∵∠BAC=90°，AB=AC，∴∠ABC=45°，∴∠DFG=∠ABD=45°．点评本题考查了全等三⾓形的判定，等腰直⾓三⾓形的性质，四点共圆，三⾓形的中位线的性质，考查了全等三⾓形对应边、对应⾓相等的性质，本题中求证△ABE≌△CAM、△EFC≌△MCF是解题的关键．。

数学趣题：不用三角函数求出∠BAC的度数

数学趣题：不用三角函数求出∠BAC的度数
这道题看上去似乎非常简单，但稍作尝试你就会发现，仅仅是在这几个角度之间来回倒腾，是没法求出∠BAC 的度数的。

听说过Langley 问题（就是那个臭名昭著的 20-80-80 三角形）的人就会知道，这种类型的题目往往会非常非常地复杂。

据说这是 1989 – 1990 年加拿大亚伯达省中学数学竞赛中的一道题目，当时只有一个人做对，并且解答过程用到了非常繁琐的三角函数运算。

然而，这道题实际上有一个非常漂亮的秒杀方法，完全不需要使用三角函数。

你能想到吗？
答案：把注意力集中在三角形 ABD 上。

容易看出，∠A = 180° –40° –80° = 60° 。

另外， CB 平分∠B 的外角， CD 平分∠D 的外角，因而 C 就是三角形 ABD 的一个旁心。

这说明， CA 也将平分∠A 。

因此，∠BAC = 60° / 2 = 30° 。

专题11.6三角形有关角的计算与证明大题专练30题(重难点培优)(解析版)

专题11.6三角形有关角的计算与证明大题专练30题（重难点培优）姓名：__________________班级：______________得分：_________________注意事项：本试卷试题共30题，解答30道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一．解答题（共30小题）1．（2021春•泰兴市月考）如图，在△ABC中，∠B＝40°，∠C＝110°．（1）画出下列图形：①BC边上的高AD；②∠A的角平分线AE．（2）试求∠DAE的度数．【分析】（1）利用直角三角板一条直角边与BC重合，沿BC平移使另一直角边过A画BC边上的高AD 即可；再根据角平分线的做法作∠A的角平分线AE；（2）首先计算出∠BAE的度数，再计算出∠BAD的度数，利用角的和差关系可得答案．【解析】（1）如图所示；（2）在△ABC中，∠BAC＝180°﹣∠B﹣∠ACB＝180°﹣40°﹣110°＝30°，∵AE平分∠BAC，∴∠BAE=12∠BAC＝15°，在Rt△ADB中，∠BAD＝90°﹣∠B＝50°，∴∠DAE＝∠DAB﹣∠BAE＝35°．2．（2021春•贺兰县期中）如图，FA⊥EC，垂足为E，∠F＝40°，∠C＝20°，求∠FBC的度数．【分析】根据三角形的内角和可得∠A的度数，再利用外角的性质可得∠FBC的度数．【解析】：在△AEC中，FA⊥EC，∴∠AEC＝90°，∴∠A＝90°﹣∠C＝70°．∴∠FBC＝∠A+∠F＝70°+40°＝110°．3．（2021春•福田区校级月考）已知：如图，在△ABC中，∠DAE＝10°，AD⊥BC于点D，AE平分∠BAC，∠B＝60°，求∠C的度数．【分析】由AD⊥BC，∠B＝60°及三角形内角和定理可求出∠BAD＝30°，再由∠DAE＝10°及AE平分∠BAC可求出∠BAC＝80°，在△ABC中由三角形内角和定理进而求得∠C为40°．【解析】：∵AD⊥BC，∠B＝60°，∴在△ABD中，∠BAD＝180°﹣90°﹣60°＝30°，又∵∠DAE＝10°，∴∠BAE＝∠BAD+∠DAE＝30°+10°＝40°，又∵AE平分∠BAC，∴∠BAC＝2∠BAE＝80°，∴在△ABC中，∠C＝180°﹣∠BAC﹣∠B＝180°﹣80°﹣60°＝40°．答：∠C的度数是40°．4．（2020秋•沙县期末）如图，在△ABC中，∠A＝30°，∠ACB＝80°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．（1）求∠CBE的度数；（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．【分析】（1）根据三角形的外角的性质求出∠CBD，根据角平分线的定义计算，得到答案；（2）先根据三角形外角的性质得出∠CEB＝∠ACB﹣∠CBE，再根据平行线的性质即可求出∠F＝∠CEB 即可．【解析】：（1）∵在△ABC中，∠A＝30°，∠ACB＝80°，∴∠CBD＝∠A+∠ACB＝110°，∵BE是∠CBD的平分线，∴∠CBE=12∠CBD＝55°；（2）∵∠ACB＝80°，∠CBE＝55°，∴∠CEB＝∠ACB﹣∠CBE＝80°﹣55°＝25°，∵DF∥BE，∴∠F＝∠CEB＝25°．5．（2021春•沙坪坝区期中）如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．（1）若∠B＝35°，∠E＝25°，求∠BAC的度数；（2）证明：∠BAC＝∠B+2∠E．【分析】（1）根据三角形的外角性质求出∠ECD，根据角平分线的定义求出∠ACE，再根据三角形的外角性质计算，得到答案；（2）根据角平分线的定义、三角形的外角性质计算，证明结论．【解析】（1）解：∵∠B＝35°，∠E＝25°，∴∠ECD＝∠B+∠E＝60°，∵CE平分∠ACD，∴∠ACE＝∠ECD＝60°，∴∠BAC＝∠ACE+∠E＝85°；（2）证明：∵CE平分∠ACD，∴∠ECD＝∠ACE，∵∠BAC＝∠E+∠ACE，∴∠BAC＝∠E+∠ECD，∵∠ECD＝∠B+∠E，∴∠BAC＝∠E+∠B+∠E，∴∠BAC＝2∠E+∠B．6．（2021春•亭湖区校级期中）互动学生课堂上，某小组同学对一个课题展开了探究．小亮：已知，如图三角形ABC，点D是三角形ABC内一点，连接BD，CD，试探究∠BDC与∠A、∠1、∠2之间的关系．小明：可以用三角形内角和定理去解决．小丽：用外角的相关结论也能解决．（1）请你在横线上补全小明的探究过程：∵∠BDC+∠DBC+∠BCD＝180°，（三角形内角和定理）∴∠BDC＝180°﹣∠DBC﹣∠BCD，（等式性质）∵∠A+∠1+∠2+∠DBC+∠BCD＝180°，∴∠A+∠1+∠2＝180°﹣∠DBC﹣∠BCD，∴∠BDC＝∠A+∠1+∠2．（等量代换）（2）请你按照小丽的思路完成探究过程．【分析】（1）根据三角形内角和定理、等式的性质解答；（2）延长BD交AC于E，根据三角形的外角性质证明结论．【解析】：（1）∵∠BDC+∠DBC+∠BCD＝180°，（三角形内角和定理）∴∠BDC＝180°﹣∠DBC﹣∠BCD，（等式性质）∵∠A+∠1+∠2+∠DBC+∠BCD＝180°，∴∠A+∠1+∠2＝180°﹣∠DBC﹣∠BCD，∴∠BDC＝∠A+∠1+∠2（等量代换），故答案为：三角形内角和定理；∠2；∠DBC；等量代换；（2）如图，延长BD交AC于E，由三角形的外角性质可知，∠BEC＝∠A+∠1，∠BDC＝∠BEC+∠2，∴∠BDC＝∠A+∠1+∠2．7．（2021春•东城区校级期中）如图，在△ABC中，∠ABC的角平分线交AC于点E，过点E作DF∥BC，交AB于点D，且EC平分∠BEF．（1）若∠ADE＝50°，求∠BEC的度数；（2）若∠ADE＝α，则∠AED＝90°−14α（含α的代数式表示）．【分析】（1）根据平行线的性质得到∠ABC＝∠ADE＝50°，根据角平分线的定义∠EBC＝25°，根据角平分线的定义和平行线的性质可得∠BEC＝∠C，根据三角形的内角和定理即可得到结论；（2）根据角平分线的定义和平行线的性质以及三角形的内角和定理即可得到结论．【解析】：（1）∵DF∥BC，∴∠ADE＝∠ABC＝50°，∠CEF＝∠C，∵BE平分∠ABC，∴∠DEB＝∠EBC＝25°，∵EC平分∠BEF，∴∠CEF＝∠BEC＝∠C，∵∠BEC+∠C+∠EBC＝180°，∴∠BEC＝77.5°；（2）∵DF∥BC，∴∠ADE＝∠ABC＝α，∵BE平分∠ABC，∴∠DEB＝∠EBC=12α，∵EC平分∠BEF，∴∠AED＝∠CEF=12（180°−12α）＝90°−14α．故答案为：90°−14α．8．（2021春•姑苏区期中）如图，在△ABC中，BE是△ABC角平分线，点D是AB上的一点，且满足∠DEB ＝∠DBE．（1）DE与BC平行吗？请说明理由；（2）若∠C＝50°，∠A＝45°，求∠DEB的度数．【分析】（1）根据角平分线的定义可得∠DBE＝∠EBC，从而求出∠DEB＝∠EBC，再利用内错角相等，两直线平行证明即可；（2）先根据三角形的内角和等于180°求出∠ABC，最后用角平分线求出∠DBE＝∠EBC，即可得解．【解析】：（1）DE∥BC．理由如下：∵BE是△ABC的角平分线，∴∠DBE＝∠EBC，∵∠DEB＝∠DBE，∴∠DEB＝∠EBC，∴DE∥BC；（2）在△ABC中，∠A+∠ABC+∠C＝180°，∴∠ABC＝180°﹣∠A﹣∠C＝180°﹣45°﹣50°＝85°．∵BE是△ABC的角平分线，∴∠DBE＝∠EBC＝42.5°，∴∠DEB＝∠EBC＝42.5°．9．（2021春•莲湖区期中）如图，已知∠DAE+∠CBF＝180°，CE平分∠BCD，∠BCD＝2∠E．（1）CD与EF是否平行，请说明理由．（2）若DF平分∠ADC，求∠DOC的度数（注：三角形的三个内角和等于180°）．【分析】（1）依据∠BCD＝2∠DCE，∠BCD＝2∠E，即可得出∠E＝∠DCE，进而判定CD∥EF；（2）根据同角的补角相等，即可得到∠CBF＝∠DAB，进而得到AD∥BC；依据AD∥BC，可得∠ADC+∠DCB＝180°，进而得到∠COD＝90°，即可得出CE⊥DF．【解析】：（1）CD与EF平行．∵CE平分∠BCD，∴∠BCD＝2∠DCE，又∵∠BCD＝2∠E，∴∠E＝∠DCE，∴CD∥EF；（2）∵DF平分∠ADC，∴∠CDF=12∠ADC，∵∠BCD＝2∠DCE，∴∠DCE=12∠DCB，∵∠DAE+∠CBF＝180°，∠DAE+∠DAB＝180°，∴∠CBF＝∠DAB，∴AD∥BC；∴∠ADC+∠DCB＝180°，∴∠CDF+∠DCE=12（∠ADC+∠DCB）＝90°，∴∠DOC＝90°．10．（2021春•宝应县月考）如图，△ABC中，∠ABC＝40°，∠C＝60°，AD⊥BC于D，AE是∠BAC的平分线．求∠DAE的度数．【分析】根据三角形的高和角平分线的性质，可求∠DAE的度数．【解析】：∵AD⊥BC于D，∴∠ADB＝∠ADC＝90°，∵∠ABC＝40°，∠C＝60°，∴∠BAD＝50°，∠CAD＝30°，∴∠BAC＝50°+30°＝80°，∵AE是∠BAC的平分线，∴∠BAE＝40°，∴∠DAE＝50°﹣40°＝10°．11．（2020秋•兰州期末）如图①，在△ABC中，∠BAC＝90°，AD是BC边上的高．（1）求证：∠DAC＝∠ABC；（2）如图②，△ABC的角平分线CF交AD于点E，求证：∠AFE＝∠AEF．【分析】（1）利用三角形内角和定理可得出∠ABC+∠ACB＝90°，∠DAC+∠ACB＝90°，进而可证出∠DAC＝∠ABC；（2）由CF是△ABC的角平分线，利用角平分线的定义可得出∠ACF＝∠BCF，利用三角形内角和定理可得出∠AFE+∠ACF＝90°，∠CED+∠BCF＝90°，进而可得出∠AFE＝∠CED，再结合对顶角相等即可证出∠AFE＝∠AEF．【解析】证明：（1）∵∠BAC＝90°，∴∠ABC+∠ACB＝90°，∵AD是BC边上的高，∴AD⊥BC，∴∠ADC＝90°，∴∠DAC+∠ACB＝90°，∴∠DAC＝∠ABC．（2）∵CF是△ABC的角平分线，∴∠ACF＝∠BCF，∵∠BAC＝∠ADC＝90°，∴∠AFE+∠ACF＝∠CED+∠BCF＝90°，∴∠AFE＝∠CED，又∵∠AEF＝∠CED，∴∠AFE＝∠AEF．12．（2021春•黄陂区期中）如图，在三角形ABC中，D是AB上一点，E是AC上一点，∠B＝60°，∠BDE ＝120°，∠AED＝45°．（1）求证：DE∥BC；（2）若DF平分∠ADE，交AC于点F，∠ECD＝2∠BCD，求∠CDF的度数．【分析】（1）根据平行线的判定定理即可得到结论；（2）根据平行线的性质和角平分线的定义即可得到结论．【解析】（1）证明：∵∠B＝60°，∠BDE＝120°，∴∠B+∠BDE＝60°+120°＝180°，∴DE∥BC（同旁内角互补，两直线平行）；（2）解：∵DE∥BC，∠AED＝45°，∴∠ADE＝∠B＝60°，∠ACB＝∠AED＝45°，∠EDC＝∠BCD，∵DF平分∠ADE，∴∠ADF＝∠EDF=12∠ADE＝30°，∵∠ECD＝2∠BCD，∴∠BCD=13∠ACB＝15°，∴∠EDC＝15°，∴∠CDF＝∠EDC+∠EDF＝45°．13．（2021春•海陵区校级月考）直角△ABC中，∠C＝90°，点D，E分别是边AC，BC上的点，点P是一动点，令∠PDA＝∠1，∠PEB＝∠2，∠DPE＝∠α．（1）若点P在线段AB上，如图1所示，且∠α＝50°，则∠1+∠2＝140°；（2）若点P在边AB上运动，如图2所示，则∠α、∠1、∠2之间有何关系，并说明理由；（3）如图3，若点P在斜边BA的延长线上运动（CE＜CD），请写出∠α、∠1、∠2之间的关系式．【分析】（1）根据四边形内角和定理以及邻补角的定义得出∠1+∠2＝∠C+∠α，进而得出即可；（2）利用（1）中所求得出答案即可；（3）利用三角外角的性质分三种情况讨论即可．【解析】：（1）∵∠1+∠2+∠CDP+∠CEP＝360°，∠C+∠α+∠CDP+∠CEP＝360°，∴∠1+∠2＝∠C+∠α，∵∠C＝90°，∠α＝50°，∴∠1+∠2＝140°；（2）由（1）得出：∠α+∠C＝∠1+∠2，∴∠1+∠2＝90°+α．（3）如图，分三种情况：在BA延长线上取点P，连接EP、DP，如图1，由三角形的外角性质，∠2＝∠C+∠1+∠α，∴∠2﹣∠1＝90°+∠α；如图2，∠α＝0°，∠2＝∠1+90°；如图3，∠2＝∠1﹣∠α+∠C，∴∠1﹣∠2＝∠α﹣90°．14．（2021春•海陵区校级月考）如图1，△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，CF∥AD．（1）如图1，∠B＝30°，∠ACB＝70°，求∠CFE的度数；（2）若（1）中的∠B＝α，∠ACB＝β（α＜β），则∠CFE＝12β−12α；（用α、β表示）（3）如图2，（2）中的结论还成立么？请说明理由．【分析】（1）求∠CFE的度数，求出∠DAE的度数即可，只要求出∠BAE﹣∠BAD的度数，由平分和垂直易得∠BAE和∠BAD的度数即可；（2）由（1）类推得出答案即可；（3）类比以上思路，把问题转换为∠CFE＝90°﹣∠ECF即可解决问题．【解析】：（1）∵∠B＝30°，∠ACB＝70°，∴∠BAC＝180°﹣∠B﹣∠ACB＝80°，∵AD平分∠BAC，∴∠BAD＝40°，∵AE⊥BC，∴∠AEB＝90°∴∠BAE＝60°∴∠DAE＝∠BAE﹣∠BAD＝60°﹣40°＝20°，∵CF∥AD，∠B＝α，∠ACB＝β，∴∠CFE＝∠DAE＝20°；（2）∵∠BAE＝90°﹣∠B，∠BAD=12∠BAC=12（180°﹣∠B﹣∠ACB），∵CF∥AD，∴∠CFE＝∠DAE＝∠BAE﹣∠BAD＝90°﹣∠B−12（180°﹣∠B﹣∠BCA）=12（∠ACB﹣∠B）=12β−12α，故答案为：12β−12α；（3）（2）中的结论成立．∵∠B＝α，∠ACB＝β，∴∠BAC＝180°﹣α﹣β，∵AD平分∠BAC，∴∠DAC=12∠BAC＝90°−12α−12β，∵CF∥AD，∴∠ACF＝∠DAC＝90°−12α−12β，∴∠BCF＝β+90°−12α−12β＝90°−12α+12β，∴∠ECF＝180°﹣∠BCF＝90°+12α−12β，∵AE⊥BC，∴∠FEC＝90°，∴∠CFE＝90°﹣∠ECF=12β−12α．15．（2021春•吴中区月考）如图，点O在直线AB上，OC⊥AB．在△ODE中，∠ODE＝90°，∠EOD＝60°．先将△ODE一边OE与OC重合，然后绕点O顺时针方向旋转，当OE与OB重合时停止旋转．（1）当OD在OA与OC之间，且∠COD＝25°时，则∠AOE＝125°．（2）试探索：在△ODE旋转过程中，∠AOD与∠COE大小的差是否发生变化？若不变，请求出这个差值；若变化，请说明理由；（3）在△ODE的旋转过程中，若∠AOE＝7∠COD，试求∠AOE的大小．【分析】（1）求出∠COE的度数，即可求出答案；（2）分为两种情况，根据∠AOC＝90°和∠DOE＝60°求出即可；（3）根据∠AOE＝7∠COD、∠DOE＝60°、∠AOC＝90°求出即可．【解析】：（1）∵OC⊥AB，∴∠AOC＝90°，∵OD在OA和OC之间，∠COD＝25°，∠EOD＝60°，∴∠COE＝60°﹣25°＝35°，∴∠AOE＝90°+35°＝125°，故答案为：125；（2）在△ODE旋转过程中，∠AOD与∠COE的差不发生变化，有两种情况：①如图1，∵∠AOD+∠COD＝90°，∠COD+∠COE＝60°，∴∠AOD﹣∠COE＝90°﹣60°＝30°，②如图2，∵∠AOD＝∠AOC+∠COD＝90°+∠COD，∠COE＝∠DOE+∠DOC＝60°+∠DOC，∴∠AOD﹣∠COE＝（90°+∠COD）﹣（60°+∠COD）＝30°，即△ODE在旋转过程中，∠AOD与∠COE的差不发生变化，为30°；（3）如图1、∵∠AOE＝7∠COD，∠AOC＝90°，∠DOE＝60°，∴90°+60°﹣∠COD＝7∠COD，解得：∠COD＝18.75°，∴∠AOE＝7×18.75°＝131.25°；如图2、∵∠AOE＝7∠COD，∠AOC＝90°，∠DOE＝60°，∴90°+60°+∠COD＝7∠COD，∴∠COD＝25°，∴∠AOE＝7×25°＝175°；即∠AOE＝131.25°或175°．16．（2020秋•前郭县期末）如图所示，在△ABC中，BO，CO分别平分∠ABC和∠ACB；BD、CD分别平分∠ABC和∠ACB的外角．（1）若∠BAC＝70°，求：∠BOC的度数；（2）探究∠BDC与∠A的数量关系．（直接写出结论，无需说明理由）【分析】（1）根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数，再根据三角形的内角和定理即可求出∠BOC的度数；（2）根据三角形外角平分线的性质可得∠BCD=12（∠A+∠ABC）、∠DBC=12（∠A+∠ACB）；根据三角形内角和定理可得∠BDC＝90°−12∠A．【解析】：（1）∵OB、OC分别是∠ABC和∠ACB的角平分线，∴∠OBC+∠OCB=12∠ABC+12∠ACB=12（∠ABC+∠ACB），∵∠A＝70°，∴∠OBC+∠OCB=12（180°﹣70°）＝55°，∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣55°＝125°；（2）∠BDC＝90°−12∠A．理由如下：∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线，∴∠BCD=12（∠A+∠ABC）、∠DBC=12（∠A+∠ACB），由三角形内角和定理得，∠BDC＝180°﹣∠BCD﹣∠DBC，＝180°−12[∠A+（∠A+∠ABC+∠ACB）]，＝180°−12（∠A+180°），＝90°−12∠A；17．（2021春•东台市月考）如图，EF∥GH，Rt△ABC的两个顶点A、B分别在直线EF、GH上，∠C＝90°，AC交EF于点D，若BD平分∠ABC，∠BAH＝32°，求∠BAC的度数．【分析】根据平行线的性质和已知条件求出∠DBA＝∠BAH＝32°，根据角平分线的定义得出∠CBD＝∠DBA＝32°，求出∠ABC，再根据直角三角形的性质求出答案即可．【解析】：∵∠BAH＝32°，EF∥GH，∴∠DBA＝∠BAH＝32°，∵BD平分∠ABC，∴∠CBD＝∠DBA＝32°，即∠ABC＝64°，∵∠C＝90°，∴∠BAC＝90°﹣∠ABC＝90°﹣64°＝26°．18．（2021春•青羊区校级期中）已知：△ABC中，BE是△ABC的角平分线，BD是△ABC的AC边上的高，过点A作AF∥BE，交直线BD于点F．（1）如图1，若∠ABC＝74°，∠C＝32°，则∠AFB＝21°；（2）若（1）中的∠BAC＝α，∠ACB＝β（α＞β），求∠AFB；（用α，β表示）；（3）如图2，（2）中的结论还成立吗？若成立，说明理由；若不成立，求出∠AFB．（用α，β表示）【分析】（1））先根据角平分线的定义可得∠CBE＝37°，由三角形的外角的性质可得∠AEB＝69°，最后由平行线的性质可得结论；（2）同理可得∠AFB的度数；（3）如图2，（2）中的结论不成立，先根据三角形内角和定理可得∠ABC＝180°﹣α﹣β，由角平分线的定义得∠ABE＝90°−12−12，最后由平行线的性质和三角形的内角和定理可得结论．【解析】：（1）∵∠ABC＝74°，BE平分∠ABC，∴∠CBE=12∠A=37°，△CBE中，∠AEB＝∠C+∠CBE＝32°+37°＝69°，∵BF⊥AC，∴∠BDE＝90°，∴∠EBD＝90°﹣69°＝21°，∵AF∥BE，∴∠AFB＝∠EBD＝21°，故答案为：21；（2）∵∠BAC＝α，∠ACB＝β，∴∠ABC＝180°﹣α﹣β，∵BE平分∠ABC，∴∠CBE=12∠A=90°−12−12，△CBE中，∠AEB＝∠C+∠CBE＝β+90°−12α−12β＝90°−12α+12β，∵∠BDE＝90°，∴∠EBD＝90°﹣（90°11）11，∵AF∥BE，∴∠AFB＝∠EBD=12α−12β；（3）如图2，（2）中的结论不成立，理由如下：∵∠BAC＝α，∠ACB＝β，∴∠ABC＝180°﹣α﹣β，∵BE平分∠ABC，∴∠ABE=12∠A=90°−12−12，△ABC中，∠DAB＝180°﹣∠BAC＝180°﹣α，∵AF∥BE，∴∠FAB＝∠ABE，∵∠D＝90°，∴∠ABD＝90°﹣∠DAB＝90°﹣（180°﹣α）＝α﹣90°，∴∠AFB＝180°﹣∠FAB﹣∠ABD＝180°﹣（90°−12−12）﹣（α﹣90°）＝180°+12−12α．19．（2021春•高新区校级月考）（1）如图1的图形我们把它称为“8字形”，请说明：∠A+∠B＝∠C+∠D．（2）阅读下面的内容，并解决后面的问题：（①）如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC＝36°，∠ADC＝16°，求∠P的度数．（②）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC＝36°，∠ADC＝16°，请猜想∠P的度数，并说明理由．（③）如图4中，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．【分析】（1）根据三角形的内角和等于180°列式整理即可得证；（2）①根据角平分线的定义可得∠1＝∠2，∠3＝∠4，再根据（1）的结论列出整理即可得解；②表示出∠PAD和∠PCD，再根据（1）的结论列出等式并整理即可得解；③根据四边形的内角和等于360°可得（180°﹣∠1）+∠P+∠4+∠B＝360°，∠2+∠P+（180°﹣∠3）+∠D＝360°，然后整理即可得解．【解析】：（1）∵∠A+∠B+∠AOB＝180°，∠C+∠D+∠COD＝180°，∴∠A+∠B+∠AOB＝∠C+∠D+∠COD，∵∠AOB＝∠COD，∴∠A+∠B＝∠C+∠D；（2）①如图2：∵AP、CP分别平分∠BAD、∠BCD∴∠1＝∠2，∠3＝∠4，由（1）的结论得：∠P+∠3＝∠2+∠B①，∠P+∠1＝∠4+∠D②，①+②，得2∠P+∠2+∠3＝∠1+∠4+∠B+∠D，∵∠ABC＝36°，∠ADC＝16°，∴∠P=12（∠B+∠D）＝26°．②∠P＝26°．如图3：∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，∴∠1＝∠2，∠3＝∠4，由（1）的结论得：∠PAD+∠P＝∠PCD+∠D①，∠PAB+∠P＝∠PCB+∠B②，∵∠PAB＝∠1，∠1＝∠2，∴∠PAB＝∠2，∴∠2+∠P＝∠3+∠B③，①+③得∠2+∠P+∠PAD+∠P＝∠3+∠B+∠PCD+∠D，即2∠P+180°＝∠B+∠D+180°，∴∠P=12（∠B+∠D）＝26°．③如图4，∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，∴∠1＝∠2，∠3＝∠4，∴（180°﹣2∠1）+∠B＝（180°﹣2∠4）+∠D，在四边形APCB中，（180°﹣∠1）+∠P+∠4+∠B＝360°，在四边形APCD中，∠2+∠P+（180°﹣∠3）+∠D＝360°，∴2∠P+∠B+∠D＝360°，∴∠P＝180°−12（∠B+∠D）．20．（2021春•增城区期中）如图①，直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC＝50°，∠ADC＝30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于点E．（1）求∠AEC的度数；（2）若线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E 与CE相交于E，∠PAC＝50°，∠A1D1C＝30°，求∠A1EC的度数．【分析】（1）利用平行线性质求出∠ACE和∠CAE度数，再根据三角形内角和定理即可求出∠AEC的度数；（2）利用平行线性质求出∠AA1E、∠ACE、∠A1AC的度数，再根据四边形内角和即可求出∠A1EC的度数．【解析】：（1）∵PQ∥MN，∴∠ADC＝∠QAD＝30°（两直线平行，内错角相等），∴∠PAD＝180°﹣30°＝150°，而AE平分∠PAD，∠PAC＝50°，∴∠CAE=12×150°−50°=25°，又∵PQ∥MN，∠CAQ＝130°，∴∠ACD＝180°﹣∠CAQ＝180°﹣130°＝50°（两直线平行，同旁内角互补），而CE平分∠ACD，∴∠ACE＝25°，在△ACE中，∠AEC＝180°﹣∠ACE﹣∠CAE＝180°﹣25°﹣25°＝130°，（2）∵PQ∥MN，∴∠1D1C＝∠QA1D1＝30°（两直线平行，内错角相等），∠PAC＝∠ACD1＝50°（同上），∴∠A1AC＝180°﹣50°＝130°，而CE平分∠ACD1，∴∠ACE＝25°，而∠AA1D1＝180°﹣∠QA1D1＝180°﹣30°＝150°，A1E平分∠AA1D1，∴∠AA1E＝75°，在四边形ACEA1中，∠A1EC＝360°﹣∠AA1E﹣∠ACE﹣∠A1AC＝360°﹣75°﹣25°﹣130°＝130°．21．（2021春•吴江区期中）在△ABC中，∠A＝70°，点D、E分别是边AC、AB上的点（不与A、B、C 重合），点P是平面内一动点（P与D、B不在同一直线上），设∠PEB＝∠1，∠DPE＝∠2，∠PDC＝∠3．（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠2＝∠1+∠3﹣70°；（用含有∠1、∠3的代数式表示）（2）若点P在△ABC的外部，如图（2）所示，则∠1、∠2、∠3之间有何关系？写出你的结论，并说明理由．（3）当点P在边CB的延长线上运动时，试画出相应图形，标注有关字母与数字，并写出对应的∠1、∠2、∠3之间的关系式．（不需要证明）【分析】（1）根据∠AEP＝180°﹣∠1，∠ADP＝180°﹣∠3和四边形AEPD的内角和为360°，表示出∠3，∠1，∠2之间的关系；（2）根据三角形外角的性质∠4＝∠1﹣70°，∠3＝∠5+∠2，求出∠3，∠1，∠2之间的关系；（3）画出符合条件的图形，根据图形和（2）的结论解答即可．【解析】：（1）∵∠AEP＝180°﹣∠1，∠ADP＝180°﹣∠3，∴180°﹣∠1+180°﹣∠3+∠2+70°＝360°，即∠2＝∠1+∠3﹣70°；故答案为：∠1+∠3﹣70°．（2）结论：∠3＝∠1+∠2﹣70°．如图：根据三角形外角的性质可知，∠4＝∠1﹣70°，∠3＝∠5+∠2，由对顶角可知：∠5＝∠4＝∠1﹣70°，∴∠3＝∠1﹣70°+∠2＝∠1+∠2﹣70°．（3）如图①，由外角的性质得：∠4＝∠3﹣70°，∠1＝∠5+∠2，由对顶角可知：∠5＝∠4＝∠3﹣70°，∴∠1＝∠3﹣70°+∠2＝∠3+∠2﹣70°．如图②，由外角的性质得：∠4＝∠3﹣70°，∠5＝∠2+∠1，由对顶角可知：∠5＝∠4，∴∠3﹣70°＝∠1+∠2，即∠3＝∠1+∠2+70°．综上：∠1＝∠3+∠2﹣70°或∠3＝∠1+∠2+70°．22．（2020秋•南海区校级期末）阅读理解：如果三角形满足一个角α是另一个角β的3倍时，那么我们称这个三角形为“智慧三角形”．其中α称为“智慧角”．解答问题：（1）一个角为60°的直角三角形是（填“是”或“不是”）“智慧三角形”，若是，“智慧角”是90°．（2）已知一个“智慧三角形”的“智慧角”为108°，求这个“智慧三角形”各个角的度数．【分析】（1）根据“智慧三角形”，“智慧角”的定义判断即可．（2）根据一个“智慧三角形”的“智慧角”的定义，求出三角形的另一个内角，可得结论．【解析】：（1）在直角三角形，一个内角为60°，则另一个内角为30°，∵90°＝3×30°，∴这个直角三角形是“智慧三角形”．其中90°称为“智慧角”．故答案为：是，90°．（2）∵一个“智慧三角形”的“智慧角”为108°，∴这个三角形的另一个内角为36°，∴这个三角形的三个内角分别为36°，36°，108°．23．（2021春•福田区校级期中）直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．（1）如图1，MN⊥PQ，若∠BAO＝30°，∠BAO与∠ABO的角平分线相交于点E，∠AEB的度数为135°，（2）如图2，MN⊥PQ，∠BAP与∠ABM的角平分线相交于点E，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；（3）如图3，若∠MOQ＜90°，∠BAO与∠BOQ的角平分线相交于点E，延长BA至点G，∠OAG的角平分线与射线EO相交于点F，点A、B在运动的过程中，试探索∠F与∠ABO之间的等量关系，并证明你的结论．【分析】（1）根据三角形内角和定理、角分线定义即可求得∠AEB的度数；（2）与（1）同理，只是把内角平分线转化为外角平分线，借助外角的性质即可得结论；（3）根据内角和外角平分线的定义可得∠E=12∠ABO，再利用∠EAF＝90°可得结论．【解析】：（1）∵MN⊥PQ，∴∠AOB＝90°，∵∠BAO＝30°，∴∠ABO＝60°，∵AE、BE分别是∠BAO和∠ABO的角平分线，∴∠ABE=12∠ABO＝30°，∠BAE=12∠BAO＝15°，∴∠AEB＝180°﹣∠ABE﹣∠BAE＝135°．故答案为：135°．（2）不会发生变化．∵∠BAP与∠ABM的角平分线相交于点E，∴∠EAB=12∠PAB，∠EBA=12∠MBA，∵MN⊥PQ，∴∠AOB＝90°，∵∠PAB＝∠ABO+∠AOB＝90°+∠ABO，∠MBA＝∠BAO+∠AOB＝90°+∠BAO，∴∠EAB+∠EBA=12（90°+∠ABO+90°+∠BAO）＝90°+12（∠ABO+∠BAO），∵∠ABO+∠BAO＝90°，∴∠EAB+∠EBA＝90°+45°＝135°，∴∠AEB＝180°﹣135°＝45°．（3）12∠ABO+∠F＝90°．如图：∵∠BAO与∠BOQ的角平分线相交于点E，∴∠1=12∠BAO，∠2=12∠BOQ，由外角的性质可得：∠ABO＝∠BOQ﹣∠BAO，∠E＝∠2﹣∠1，∴∠E=12∠ABO．∵AE平分∠BAO，AF平分∠GAO，∴∠EAF＝90°，∴∠E+∠F＝90°，即12∠ABO+∠F＝90°．24．（2021春•江都区月考）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．（1）如果∠A＝70°，求∠BPC的度数；（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q，∠A之间的数量关系．（3）如图③，延长线段BP，QC交于点E，在△BQE中，存在一个内角等于另一个内角的3倍，求∠A的度数．【分析】（1）根据三角形内角和定理求出∠ABC+∠ACB＝110°，根据角平分线的定义得出∠PBC=12∠ABC，∠PCB=12∠ACB，求出∠PBC+∠PCB＝55°，再根据三角形内角和定理求出即可；（2）根据三角形外角性质得出∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，求出∠MBC+∠NCB＝180°+∠A，根据角平分线的定义得出∠QBC=12∠MBC，∠QCB=12∠NCB，求出∠QBC+∠QCB＝90°+12∠A，根据三角形内角和定理求出即可；（3）根据角平分线的定义得出∠ACF＝2∠ECF，∠ABC＝2∠EBC，根据三角形外角性质得出∠ECF＝∠EBC+∠E，求出∠A＝2∠E，求出∠EBQ＝90°，分为四种情况：①∠EBQ＝3∠E＝90°，②∠EBQ ＝3∠Q，③∠Q＝3∠E，④∠E＝3∠Q，再求出答案即可．【解析】：（1）∵∠A＝70°，∴∠ABC+∠ACB＝180°﹣∠A＝110°，∵点P是∠ABC和∠ACB的角平分线的交点，∴∠PBC=12∠ABC，∠PCB=12∠ACB，∴∠PBC+∠PCB＝55°，∴∠BPC＝180°﹣（∠PBC+∠PCB）＝125°；（2）∵∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，∴∠MBC+∠NCB＝∠ACB+∠A+∠ABC+∠A＝180°+∠A，∵点Q是∠MBC和∠NCB的角平分线的交点，∴∠QBC=12∠MBC，∠QCB=12∠NCB，∴∠QBC+∠QCB=12（∠MBC+∠NCB）=12（180°+∠A）＝90°+12∠A，∴∠Q＝180°﹣（∠QBC+∠QCB）＝180°﹣（90°+12∠A）＝90°−12∠A；（3）如图③中，延长BC到F．∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF＝2∠ECF，∵BE平分∠ABC，∴∠ABC＝2∠EBC，∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠ABC+2∠E，∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E=12∠A，∵∠EBQ＝∠EBC+∠CBQ=12∠ABC+12∠MBC=12（∠ABC+∠A+∠ACB）＝90°，如果△BQE中，存在一个内角等于另一个内角的3倍，那么分为四种情况：①∠EBQ＝3∠E＝90°，则∠E＝30°，∠A＝2∠E＝60°；②∠EBQ＝3∠Q，则∠Q＝30°，∠E＝60°，∠A＝2∠E＝120°；③∠Q＝3∠E，则∠E＝22.5°，∠A＝2∠E＝45°；④∠E＝3∠Q，则∠E＝67.5°，∠A＝2∠E＝135°，综合上述，∠A的度数是45°或60°或120°或135°．25．（2021春•奉贤区期中）在△ABC中，若存在一个内角是另外一个内角度数的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝60°，∠C＝40°，可知∠A ＝2∠C，所以△ABC为2倍角三角形．（1）在△DEF中，∠E＝40°，∠F＝35°，则△DEF为3倍角三角形；（2）如图，直线MN⊥直线PQ于点O，点A、点B分别在射线OP、OM上；已知∠BAO、∠OAG的角平分线分别与∠BOQ的角平分线所在的直线交于点E、F；①说明∠ABO＝2∠E的理由；②若△AEF为4倍角三角形，直接写出∠ABO的度数．【分析】（1）由∠E＝40°，∠F＝35°可知∠D＝105°，再根据n倍角三角形的定义可得结论．（2）①根据三角形内角和定理及一个外角等于与它不相邻的两个内角和，利用角的和差计算即可求得结果．②首先证明∠EAF＝90°，分两种情形分别求出即可．【解析】：（1）∵∠E＝40°，∠F＝35°，∴∠D＝180°﹣40°﹣35°＝105°，∴∠D＝3∠F，∴△ABC为3倍角三角形，故答案为：3；（2）①∵AE平分∠BAO，OE平分∠BOQ，∴∠BAO＝2∠EAQ，∠BOG＝2∠EOQ，由外角的性质可得：∠BOQ＝∠BAO+∠ABO，∠EOQ＝∠EAQ+∠E，∴∠ABO＝2∠E．②∵AE平分∠BAO，AF平分∠OAG，∴∠EAB＝∠EAO，∠OAF＝∠FAG，∴∠EAF＝∠EAO+∠OAF=12（∠BAO+∠OAG）＝90°，∵△EAF是4倍角三角形，∴∠E=14×90°＝22.5°或15×90°＝18°，∵∠ABO＝2∠E，∴∠ABO＝45°或36°．26．（2021春•东台市月考）（1）阅读并填空：如图1，BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线．试说明∠D＝90°+12∠A的理由．解：因为BD平分∠ABC（已知），所以∠1＝12∠ABC（角平分线定义）．同理：∠2＝12∠ACB．所以∠1+∠2＝12（∠ABC+∠ACB）．因为∠A+∠ABC+∠ACB＝180°，∠1+∠2+∠D＝180°（三角形的内角和等于180°），所以∠D＝180°−12（∠ABC+∠ACB）（等式性质）．即：∠D＝90°+12∠A．（2）探究，请直接写出结果（i）如图2，BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线．试探究∠D与∠A之间的等量关系．答：∠D与∠A之间的等量关系是∠D＝90°−12∠A．（ii）如图3，BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线．试探究∠D与∠A 之间的等量关系．答：∠D与∠A之间的等量关系是∠D=12∠A．（3）拓展应用请用以上结论解决下列问题：如图4，在△ABC中，BD、CD分别平分∠ABC、∠ACB，M、N、Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF分别平分∠EBC、∠ECQ，（i）∠A＝80°，则∠F＝12.5°；（ii）∠F＝n°，则∠A＝180°﹣4n°．【分析】（1）根据角平分线的定义和三角形的内角和定理即可得到结论；（2）（i）根据角平分线的定义和三角形的内角和定理以及三角形外角的性质即可得到结论；（ii）根据角平分线的定义和三角形的内角和定理以及三角形外角的性质即可得到结论；（3）（i）根据（2）（i）中的结论即可得到结论；（ii）根据（2）（ii）中的结论即可得到结论．【解析】：（1）解：因为BD平分∠ABC（已知），所以∠1=12∠ABC（角平分线定义）．同理：∠2=12∠ACB．所以∠1+∠2=12（∠ABC+∠ACB），因为∠A+∠ABC+∠ACB＝180°，∠1+∠2+∠D＝180°，（三角形的内角和等于180°），所以∠D＝180°−12（∠ABC+∠ACB）（等式性质）．即：∠D＝90°+12∠A．故答案为：12∠ABC，12∠ACB，12（∠ABC+∠ACB），三角形的内角和等于180°，180°−12（∠ABC+∠ACB）．（2）解：（i）∠D与∠A之间的等量关系是：∠D＝90°−12∠A．理由：∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线，∴∠EBD＝∠DBC，∠BCD＝∠DCF，∴∠DBC+∠DCB+∠D＝180°，∴∠A+∠ABC+∠ACB＝180°，而∠ABC＝180°﹣2∠DBC，∠ACB＝180°﹣2∠DCB，∴∠A+180°﹣2∠DBC+180°﹣2∠DCB＝180°，∴∠A﹣2（∠DBC+∠DCB）＝﹣180°，∴∠A﹣2（180°﹣∠D）＝﹣180°，∴∠A﹣2∠D＝180°，∴∠D＝90°−12∠A，故答案为：∠D＝90°−12∠A；（ii）∠D与∠A之间的等量关系是：∠D=12∠A．理由：∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线，∴∠DCE＝∠DBC+∠D，∵∠A+2∠DBC＝2∠DCE∴∠A+2∠DBC＝2∠DBC+2∠D，∴∠A＝2∠D，即：∠D=12∠A．故答案为：∠D=12∠A；（3）（i）由（1）知：∠D＝90°+12∠A．∵∠A＝80°，∴∠D＝130°，∴∠DBC+∠DCB＝50°，∴∠MBC+∠NCB＝360°﹣50°＝310°，∵BE、CE分别平分∠MBC、∠BCN，∴∠CBE+∠BCN=12（∠MBC+∠NCB）＝155°，∴∠E＝180°﹣155°＝25°，由（2）（ii）知∠F=12∠E=12×25°＝12.5°，故答案为：12.5°；（ii）由（1）得∠D＝90°+12∠A，∵BE、CE分别平分∠MBC、∠BCN，∴2（∠EBC+∠ECB）+∠DBC+∠DCB＝360°，∵∠EBC+∠ECB＝180°﹣∠E，∠DBC+∠DCB＝180°﹣∠D，∴2（180°﹣∠E）+180°﹣∠D＝360°，∴∠E＝90°−12∠D＝90°−12（90°+12∠A）＝45°−14∠A，∴∠F＝90°−12∠E=12（45°−14∠A）＝n°，∴∠A＝180°﹣8n°．故答案为：180°﹣8n°．27．（2020秋•南山区期末）（1）如图1，则∠A、∠B、∠C、∠D之间的数量关系为∠A+∠B＝∠C+∠D．（2）如图2，AP、CP分别平分∠BAD、∠BCD．若∠B＝36°，∠D＝14°，求∠P的度数；（3）如图3，CP、AG分别平分∠BCE、∠FAD，AG反向延长线交CP于点P，请猜想∠P、∠B、∠D 之间的数量关系．并说明理由．【分析】（1）根据三角形的内角和定理，结合对顶角的性质可求解；（2）根据角平分线的定义可得∠BAP＝∠DAP，∠BCP＝∠DCP，结合（1）的结论可得2∠P＝∠B+∠D，再代入计算可求解；（3）根据角平分线的定义可得∠ECP＝∠PCB，∠FAG＝∠GAD，结合三角形的内角和定理可得∠P+∠GAD＝∠B+∠PCB，∠P+（180°﹣∠GAD）＝∠D+（180°﹣∠ECP），进而可求解．【解析】：（1）∵∠AOB+∠A+∠B＝∠COD+∠C+∠D＝180°，∠AOB＝∠COD，∴∠A+∠B＝∠C+∠D，故答案为∠A+∠B＝∠C+∠D；（2）∵AP、CP分别平分∠BAD、∠BCD，∴∠BAP＝∠DAP，∠BCP＝∠DCP，由（1）可得：∠BAP+∠B＝∠BCP+∠P，∠DAP+∠P＝∠DCP+∠D，∴∠B﹣∠P＝∠P﹣∠D，即2∠P＝∠B+∠D，∵∠B＝36°，∠D＝14°，∴∠P＝25°；（3）2∠P＝∠B+∠D．理由：∵CP、AG分别平分∠BCE、∠FAD，∴∠ECP＝∠PCB，∠FAG＝∠GAD，∵∠PAB＝∠FAG，∴∠GAD＝∠PAB，∵∠P+∠PAB＝∠B+∠PCB，∴∠P+∠GAD＝∠B+∠PCB，∵∠P+∠PAD＝∠D+∠PCD，∴∠P+（180°﹣∠GAD）＝∠D+（180°﹣∠ECP），∴2∠P＝∠B+∠D．28．（2020秋•南海区期末）已知：线段AB、CD相交于点O，连接AD、CB．（1）如图1，求证：∠A+∠D＝∠B+∠C；（2）如图2，∠ADC和∠ABC的平分线DE和BE相交于点E，并且与AB、CD分别相交于点M、N，∠A＝28°，∠C＝32°，求∠E的度数；（3）如图3，∠ADC和∠ABC的三等分线DE和BE相交于点E，并且与AB、CD分别相交于点M、N，∠CDE=13∠ADC，∠CBE=13∠ABC，试探究∠A、∠C、∠E三者之间存在的数量关系，并说明理由．【分析】（1）根据三角形的内角和定理，结合对顶角相等可求解；（2）由角平分线的定义可得∠ADE＝∠CDE，∠ABE＝∠CBE，结合（1）可得∠A+∠C＝2∠E，再代入计算即可求解；（3）由∠CDE=13∠ADC，∠CBE=13∠ABC可得∠ADE＝2∠CDE，∠ABE＝2∠CBE，结合（1）可得∠A+2∠C+∠ADE+2∠CBE＝3∠E+∠ABE+2∠CDE，进而可求解．【解析】（1）证明：∵∠A+∠D+∠AOD＝∠C+∠B+∠BOC＝180°，∠AOD＝∠BOC，∴∠A+∠D＝∠C+∠B；（2）解：∵∠ADC和∠ABC的平分线DE和BE相交于点E，∴∠ADE＝∠CDE，∠ABE＝∠CBE，由（1）可得∠A+∠ADE＝∠E+∠ABE，∠C+∠CBE＝∠E+∠CDE，∴∠A+∠C＝2∠E，∵∠A＝28°，∠C＝32°，∴∠E＝30°；（3）解：∠A+2∠C＝3∠E．理由：∵∠CDE=13∠ADC，∠CBE=13∠ABC，∴∠ADE＝2∠CDE，∠ABE＝2∠CBE，由（1）可得∠A+∠ADE＝∠E+∠ABE，∠C+∠CBE＝∠E+∠CDE，∴2∠C+2∠CBE＝2∠E+2∠CDE，∴∠A+2∠C+∠ADE+2∠CBE＝3∠E+∠ABE+2∠CDE，即∠A+2∠C＝3∠E．29．（2021春•玄武区校级月考）【概念认识】如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．【问题解决】（1）如图②，在△ABC中，∠A＝73°，∠B＝42°，若∠B的三分线BD交AC于点D，则∠BDC＝87°或101°；（2）如图③，在△ABC中，BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线，且BP⊥CP，求∠A的度数；【延伸推广】（3）在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝α°，∠B＝β°，直接写出∠BPC的度数．（用含α、β的代数式表示）【分析】（1）分为两种情况：当BD是“邻AB三分线”时，当BD′是“邻BC三分线”时，根据三角形的外角性质求出即可；（2）求出∠PBC+∠PCB＝90°，根据BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线求出∠PBC=23∠ABC，∠PCB=23∠ACB，求出∠ABC+∠ACB＝135°，再求出∠A即可；（3）画出符合的所有情况，①当BP和CP分别是“邻AB三分线”、“邻AC三分线”时，②当BP和CP分别是“邻BC三分线”、“邻AC三分线”时，③当BP和CP分别是“邻AB三分线”、“邻CD三分线”时，④当BP和CP分别是“邻BC三分线”、“邻CD三分线”时，再根据三角形的外角性质求出答案即可．【解析】：（1）如图，当BD是“邻AB三分线”时，∵∠A＝73°，∠B＝42°，∴∠BDC＝∠A+∠ABD＝73°+13×42°＝87°；当BD′是“邻BC三分线”时，∠BDC′＝∠A+∠ABD′＝73°+23×42°＝101°；故答案为：87°或101；（2）∵BP⊥CP，∴∠BPC＝90°，∴∠PBC+∠PCB＝90°，∵BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线，∴∠PBC=23∠ABC，∠PCB=23∠ACB，∴23∠ABC+23∠ACB＝90°，∴∠ABC+∠ACB＝135°，∴∠A＝180°﹣（∠ABC+∠ACB）＝180°﹣135°＝45°；（3）分为四种情况：情况一：如图1，当BP和CP分别是“邻AB三分线”、“邻AC三分线”时，由外角可得：∠PCD=23∠ACD=23（α+β），∴∠BPC＝∠PCD﹣∠PBC=23（α+β）−23β=23α；情况二：如图2，当BP和CP分别是“邻BC三分线”、“邻AC三分线”时，由外角可知：∠PCD=23∠ACD=23（α+β），∴∠BPC＝∠PCD﹣∠PBC=23（α+β）−13=2K3；情况三、当BP和CP分别是“邻AB三分线”、“邻CD三分线”时，当α＞β时，如图3，由外角可得：∠PCD=13∠ACD=13（α+β），∴∠BPC＝∠PCD﹣∠PBC=13（α+β）−23β=K3；当α＜β时，如图4，当α＜β时，如图4，由外角及对顶角可得：∠DCE＝∠PCB=13∠ACD=13（α+β），∴∠BPC＝∠FBC﹣∠PCB=23β−13（α+β）=K3；情况四、如图5，当BP和CP分别是“邻BC三分线”、“邻CD三分线”时，由外角可得：∠PCD=13∠ACD=13（α+β），∴∠BPC＝∠PCD﹣∠PBC=13（α+β）−13=13；综合上述：∠BPC的度数是23α°或（2r3）°或（K3）°或（K3）°或13U．30．（2021春•深圳期中）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．（1）如果∠A＝80°，求∠BPC的度数；（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求∠A 的度数．【分析】（1）运用三角形的内角和定理及角平分线的定义，首先求出∠1+∠2，进而求出∠BPC即可解决问题；（2）根据三角形的外角性质分别表示出∠MBC与∠BCN，再根据角平分线的性质可求得∠CBQ+∠BCQ，最后根据三角形内角和定理即可求解；（3）在△BQE中，由于∠Q＝90°−12∠A，求出∠E=12∠A，∠EBQ＝90°，所以如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况进行讨论：①∠EBQ＝2∠E＝90°；②∠EBQ＝2∠Q＝90°；③∠Q＝2∠E；④∠E＝2∠Q；分别列出方程，求解即可．【解析】（1）解：∵∠A＝80°．∴∠ABC+∠ACB＝100°，∵点P是∠ABC和∠ACB的平分线的交点，∴∠P＝180°−12（∠ABC+∠ACB）＝180°−12×100°＝130°，（2）∵外角∠MBC，∠NCB的角平分线交于点Q，∴∠QBC+∠QCB=12（∠MBC+∠NCB）=12（360°﹣∠ABC﹣∠ACB）=12（180°+∠A）＝90°+12∠A∴∠Q＝180°﹣（90°+12∠A）＝90°−12∠A；（3）延长BC至F，∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF＝2∠ECF，∵BE平分∠ABC，∴∠ABC＝2∠EBC，∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠ABC+2∠E，又∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E=12∠A；∵∠EBQ＝∠EBC+∠CBQ=12∠ABC+12∠MBC=12（∠ABC+∠A+∠ACB）＝90°．如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况：①∠EBQ＝2∠E＝90°，则∠E＝45°，∠A＝2∠E＝90°；②∠EBQ＝2∠Q＝90°，则∠Q＝45°，∠E＝45°，∠A＝2∠E＝90°；③∠Q＝2∠E，则90°−12∠A＝∠A，解得∠A＝60°；④∠E＝2∠Q，则12∠A＝2（90°−12∠A），解得∠A＝120°．综上所述，∠A的度数是90°或60°或120°．。

2022-2023学年广东省阳江市阳东区八年级(上)期中数学试卷

2022-2023学年广东省阳江市阳东区八年级（上）期中数学试卷一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A．B．C．D．2．（3分）下列三条线段能构成三角形的是（）A．1cm，2cm，3cm B．3cm，4cm，5cmC．4cm，4cm，8cm D．2cm，2cm，8cm3．（3分）如图，在△ABC中，∠C＝90°，∠A＝30°，分别以A，B两点为圆心，大于为半径画弧，两弧交于M，N两点，直线MN交AC于点D，交AB于点E，若CD＝3，则AC的长度为（）A．9B．8C．7D．64．（3分）一个多边形的每一个内角都等于140°，那么这个多边形的边数为（）A．8B．9C．10D．1 15．（3分）人字梯中间一般会设计一“拉杆”，这样做的道理是（）A．两点之间，线段最短B．垂线段最短C．三角形具有稳定性D．两直线平行，内错角相等6．（3分）如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（）A．BC＝EC，∠B＝∠E B．BC＝EC，AC＝DCC．∠B＝∠E，∠A＝∠D D．BC＝DC，∠A＝∠D7．（3分）如图，把△ABC纸片沿DE折叠，点A落在四边形DEBC内部A'，当∠A＝30°时，∠1+∠2＝（）A．30°B．40°C．50°D．60°8．（3分）如图，AD为△ABC的中线，AB＝10，AC＝4，则AD的长度可能为（）A．2.9B．5.4C．7.3D．8.89．（3分）如图，在△ABC中，AD⊥BC于点D，CE⊥AB于点E，AD、CE交于点F，已知EF＝EB＝6，AE＝8，则CF＝（）A．4B．3C．2D．110．（3分）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过O点作EF∥BC交AB于点E，交AC于点F，过点O作OD⊥AC于D，下列四个结论：①EF＝BE+CF；②∠BOC＝90°+∠A；③点O到△ABC各边的距离相等；④设OD＝m，AE+AF＝n，则S△ABF＝mn，正确的结论有（）个．A．1B．2C．3D．4二、填空题（本大题共7小题，每小题4分，共28分）11．（4分）若点A（m，﹣3），B（﹣2，n）关于y轴对称，则2m+3n的值为．12．（4分）如图，△ABC与△A′B′C′关于直线l对称，且∠A＝105°，∠C′＝30°，则∠B的度数为°．13．（4分）如图，△ABC中，∠C＝90°，∠B＝60°，BC＝2cm，则AB的长是cm．14．（4分）如图，在Rt△OCD中，∠C＝90°，OP平分∠DOC交DC于点P，若PC＝2，OD＝8，则△OPD的面积为．15．（4分）等腰三角形中有一个内角为40°，则其底角的度数是．16．（4分）如图，在△ABC中，AB＝AC，D为BC的中点，AD＝4，BD＝3，AB＝5，点P为AD边上的动点，点E为AB边上的动点，则PE+PB的最小值为．17．（4分）如图，在△ABC中，∠A＝64°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；∠A2BC和∠A2CD的平分线交于点A3，则∠A5＝．三、解答题（本大题共3小题，每小题6分，共18分）18．（6分）如图所示，CD＝CA，∠1＝∠2，EC＝BC，求证：△ABC≌△DEC．19．（6分）如图，在△ABC中，DE是AC的中垂线，分别交AC、AB于点D、E，若△BCE的周长为8，BC＝3，求AB的长．20．（6分）如图，在△ABC中，∠C＝90°．（1）尺规作图：作斜边AB的垂直平分线DE，分别交AB，BC于D、E（不写作法，保留作图痕迹）；（2）已知AC＝6cm，CB＝8cm，求△ACE的周长．四、解答题（本大题共3小题，每小题8分，共24分）21．（8分）如图，在△ABC中，AB＝AC，D是BC边上的一点，以AD为边在AD右侧作△ADE，使AE ＝AD，连接CE，∠BAC＝∠DAE＝100°．（1）试说明△BAD≌△CAE；（2）若DE＝DC，求∠CDE的度数．22．（8分）如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）．（1）在图中作出△ABC关于y轴对称的△A1B1C1；（2）△A1B1C1的面积为；（3）在y轴上画出点P，使PB+PC最小．23．（8分）如图，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，且BD＝CD．（1）图中与△BDE全等的三角形是，请加以证明；（2）若AE＝8cm，AC＝5cm，求BE的长．五、解答题（本大题共2小题，每小题10分，共20分）24．（10分）直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．（1）如图1，已知AE、BE分别是∠BAO和∠ABO的角平分线，①当∠ABO＝60°时，求∠AEB的度数；②点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况：若不发生变化，试求出∠AEB的大小；（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，请直接写出∠ABO的度数．25．（10分）如图，已知B（﹣1，0），C（1，0），A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC＝2∠BAO．（1）求证：∠ABD＝∠ACD；（2）求证：AD平分∠CDE；（3）若在D点运动的过程中，始终有DC＝DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数．参考答案一、选择题（本大题共10小题，每小题3分，共30分）1．A；2．B；3．A；4．B；5．C；6．D；7．D；8．B；9．C；10．D；二、填空题（本大题共7小题，每小题4分，共28分）11．﹣5；12．45；13．4；14．8；15．40°或70°；16．；17．2°；三、解答题（本大题共3小题，每小题6分，共18分）18．；19．5．；20．（1）见解答过程；（2）14cm．；四、解答题（本大题共3小题，每小题8分，共24分）21．；22．；23．△CFD；五、解答题（本大题共2小题，每小题10分，共20分）24．；25．（1）证明见解答；（2）证明见解答；（3）∠BAC的度数不变，为60°．。

初二数学压轴题

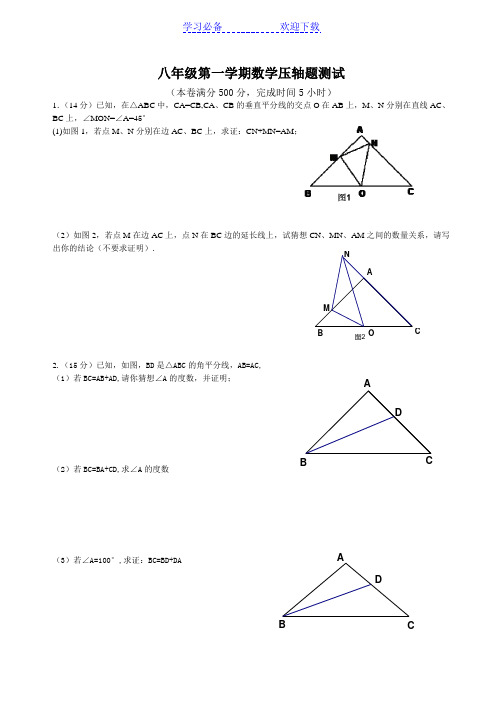
DCBAACB DN图2CB OMA八年级第一学期数学压轴题测试（本卷满分500分，完成时间5小时）1．（14分）已知，在△ABC 中，CA=CB,CA 、CB 的垂直平分线的交点O 在AB 上，M 、N 分别在直线AC 、BC 上，∠MON=∠A=45°(1)如图1，若点M 、N 分别在边AC 、BC 上，求证：CN+MN=AM ；（2）如图2，若点M 在边AC 上，点N 在BC 边的延长线上，试猜想CN 、MN 、AM 之间的数量关系，请写出你的结论（不要求证明）.2.（15分）已知，如图，BD 是△ABC 的角平分线，AB=AC, （1）若BC=AB+AD,请你猜想∠A 的度数，并证明；（2）若BC=BA+CD,求∠A 的度数（3）若∠A=100°,求证：BC=BD+DA图3E DCBA图2EDCBA 图1EDCBA3．（18分）如图，△ABC 是等边三角形，D 是三角形外一动点，满足∠ADB=600，（1）当D 点在AC 的垂直平分线上时，求证： DA+DC=DB;（2）当D 点不在AC 的垂直平分线上时，（1）中的结论是否仍然成立？请说明理由; （3）当D 点在如图的位置时，直接写出DA ，DC ，DB 的数量关系，不必证明。

DC B ADCBAD CBA4.（15分）如图，已知：点D 是△ABC 的边BC 上一动点，且AB =AC ，DA =DE ，∠BAC =∠ADE =α.⑴如图1，当α=60°时，∠BCE = ；（图1）（图2）（图3）⑵如图2，当α=90°时，试判断∠BCE 的度数是否发生改变，若变化，请指出其变化范围；若不变化，请求出其值，并给出证明；⑶如图3，当α=120°时，则∠BCE = ；5.（18分）（1）如图1，等边△ABC 中，点D 为AC 的中点，若∠EDF=120°，点E 与点B 重合，DF 与BC 的延长线交于F 点，则DE 与DF 数量关系为；BE+BF 与BC 的等量关系为 .（直接写出结论，不必证明）图1FD CB(E)A图2F EDCBA图3EDF CBA（2）将（1）中∠EDF 绕点D 顺时针旋转一定角度（如图2），DE 交AB 于E 点，DF 交BC 的延长线于F 点，其中“等边△ABC 中，点D 为AC 的中点，若∠EDF=120°”，这一条件不变，则DE 与DF 有怎样的数量关系？BE+BF 与BC 之间有怎样的等量关系？写出你的结论并加以证明.（3）将（1）中∠EDF 绕点D 顺时针旋转一定角度，DE 与AB 的延长线交于E 点，DF 交BC 的延长线于F 点（如图3），其中“等边△ABC 中，点D 为AC 的中点，若∠EDF=120°”，这一条件仍不变，则DE 与DF 数量关系为；BE 、BF 、BC 这三者的等量关系是（不必证明）6．（12分）如图，△ABC 为等边三角形，P 为AB 上一点，PE ⊥BC 于E 交AC 于F ，在BC 的延长线上截取CD=PA ，PD 交AC 于l,.Bn P PA= （1）如图，当n=1时，CD EC = ，=EDFI.(直接写出) （2）如图，当n= 时，∠EPD=600，并求出EDFI 的值，请写出证明的过程。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如图，四边形ABCD 中，连接对角线AC 、BD ，若∠ABD = 40°，∠ADB = 80°，∠CBD = 70°，∠CDB = 50°，求∠BAC 的度数。

这道题看上去似乎非常简单，但稍作尝试你就会发现，仅仅是在这几个角度之间来回倒腾，是没法求出∠BAC 的度数的。

听说过Langley 问题（就是那个臭名昭著的20-80-80 三角形）的人就会知道，这种类型的题目往往会非常非常地复杂。

据说这是1989 – 1990 年加拿大亚伯达省中学数学竞赛中的一道题目，当时只有一个人做对，并且解答过程用到了非常繁琐的三角函数运算。

然而，这道题实际上有一个非常漂亮的秒杀方法，完全不需要使用三角函数。

你能想到吗？
答案：把注意力集中在三角形ABD 上。

容易看出，∠A = 180°– 40°– 80°= 60°。

另外，CB 平分∠B 的外角，CD 平分∠D 的外角，因而C 就是三角形ABD 的一个旁心。

这说明，CA 也将平分∠A 。

因此，∠BAC = 60°
/ 2 = 30°。